Modeling Flexible Loops in the Dark-Adapted and Activated States of Rhodopsin, a Prototypical G-Protein-Coupled Receptor

Abstract

Conformational possibilities of flexible loops in rhodopsin, a prototypical G-protein-coupled receptor, were studied by modeling both in the dark-adapted (R) and activated (R*) states. Loop structures were built onto templates representing the R and R* states of the TM region of rhodopsin developed previously (G. V. Nikiforovich and G. R. Marshall. 2003. Biochemistry. 42:9110). Geometrical sampling and energy calculations were performed for each individual loop, as well as for the interacting intracellular loops IC1, IC2, and IC3 and the extracellular loops EC1, EC2, and EC3 mounted on the R and R* templates. Calculations revealed that the intra- and extracellular loops of rhodopsin possess low-energy structures corresponding to large conformational movements both in the R and R* states. Results of these calculations are in good agreement with the x-ray data available for the dark-adapted rhodopsin as well as with the available experimental biophysical data on the disulfide-linked mutants of rhodopsin. The calculated results are used to exemplify how the combined application of the results of independent calculations with emerging experimental data can be used to select plausible three-dimensional structures of the loops in rhodopsin.

INTRODUCTION

G-protein-coupled receptors (GPCRs) comprise a vast protein family involved in a variety of physiological functions. GPCRs are embedded in the cell membrane and include seven-helical transmembrane stretches (TM helices) as well as non-TM parts, namely, the N- and C-terminal fragments (the extracellular N-terminal fragment is often glycosylated) and the extra- and intracellular loops connecting the TM helices. GPCRs undergo conformational transitions bringing their inactive states (R) to the activated states (R*) during the process of transduction. Knowledge of the detailed three-dimensional (3D) structures of the R and R* states of GPCRs would be extremely relevant to wide areas of biochemistry, biophysics, and medicinal chemistry.

The largest GPCR family, containing up to 700 members, possesses distinct homology to rhodopsin, the 348-residue α-helical photoreceptor of the visual system (family A (1) or the “rhodopsin” family (2)). The 3D structure of dark-adapted rhodopsin (the R state) has been determined by x-ray crystallography (3–7); so far, it is the only 3D structure of a GPCR known with high resolution. 3D model(s) for rhodopsin have been used as templates for building 3D structures of other rhodopsin-like GPCRs in their inactive states (see, e.g., a minireview by Ballesteros et al. (8)). The 3D structure of the TM region of rhodopsin in the activated state (the R* state) was deduced from the experimental data of site-directed spin labeling (SDSL) (9); this structure is also in good agreement with the results of independent energy calculations (10).

High flexibility of the intra- and extracellular loops in rhodopsin (and in any other GPCR) presents specific challenges in determining 3D structures of the R and R* states, since even the most detailed structural information on the dark-adapted rhodopsin provided by x-ray crystallography presents only one snapshot out of many possible loop conformations. Indeed, the exact x-ray structure of fragments belonging to the intracellular loops and to the C-terminus of rhodopsin remains unknown or contradictive in five different x-ray structures obtained for bovine dark-adapted rhodopsin so far (3–7). Therefore, computational modeling of the intra- and extracellular loops in GPCRs is of special importance to provide insight into intermolecular recognition and activation of G-proteins.

This work considers modeling of the intracellular loops in rhodopsin connecting TM helices 1 and 2 (IC1), 3 and 4 (IC2), and 5 and 6 (IC3), as well as the extracellular loops connecting TM helices 2 and 3 (EC1), 4 and 5 (EC2), and 6 and 7 (EC3). We have developed an original de novo computational procedure for restoring interhelical loops in GPCRs (see Methods for details); part of this procedure has been described earlier (11). To circumvent the conflict between the thoroughness of sampling of conformational space available to a particular loop versus the required amount of computer resources (see, e.g., Fiser et al. (12) and Jacobson et al. (13)), we have decided to sacrifice a detailed description of any particular 3D structure of a loop in rhodopsin in favor of a less precise description of many structures, which then allows focusing on the major differences among them detectable by experimental procedures. The study describes the sets of low-energy conformers obtained for the intra- and extracellular loops of rhodopsin by geometrical and energy sampling performed first for each individual loop and then for the “packages” of interacting loops mounted onto the templates for the TM region of the rhodopsin developed previously (10). The obtained low-energy structures of the intra- and extracellular loops in the R state were compared to the x-ray structures available for dark-adapted rhodopsin. The low-energy structures of the intracellular loops were also compared to the available experimental biophysical data on the disulfide-linked mutants of rhodopsin. Finally, examples of employing newly emerging experimental data to select the most plausible structures of the loops from the sets of low-energy conformers obtained by calculations are discussed.

METHODS

Conformational sampling of individual loops

All loops were mounted on the “template”, i.e., on the specific 3D structure of the TM region of rhodopsin. The templates for the R and R* states were the same as those developed earlier (see Nikiforovich and Marshall (10)) and consisted of seven fragments of amino acid residues, namely, W³⁵–Q⁶⁴, L⁷²–L⁹⁹, T¹⁰⁸–V¹³⁹, E¹⁵⁰–L¹⁷², N²⁰⁰–Q²²⁵, A²⁴⁶–T²⁷⁷, and I²⁸⁶–C³²². All fragments corresponded to TM helices from TM1 to TM6, except the last one, which combined TM7 and H8, the helix located parallel to the membrane plane in the x-ray structures of rhodopsin. The N- and C-terminal fragments 1–34 and 323–348 were absent in both templates. Sampling of the loops was performed for the intracellular and extracellular regions separately from the smallest loops to the largest, i.e., from IC1 to IC2 to IC3 and from EC1 to EC3 to EC2. As soon as the resulting structures of the smaller loops were selected, the loop structure closest to the average spatial positions of the Cα atoms was included in the template, providing additional geometrical limitations for the larger loops.

The developed procedure of geometrical conformational sampling was, basically, a stepwise elongation of the loop starting from the first stem residue of the loop, which was overlapped with the corresponding residue in the template. The aim of the procedure was to cover all combinations of the possible backbone conformations for the residues in the stepwise growing loops, i.e., fragments 64–72 (IC1), 139–150 (IC2), 225–246 (IC3), 99–108 (EC1), 172–200 (EC2), and 277–286 (EC3). The conformations were selected from the set of the local minima of the Ramachandran map, namely, from the following {φ,ψ} points: −140°, 140°; −75°, 140°; −75°, 80°; −60°, −60°; and 60°, 60° (i.e., they covered all combinations of β, pII, γ′, α_R, and α_L minima). For the Gly residues, the minimum pII′ (φ,ψ = −140°, 80°) and all minima symmetrical to β, pII, γ′, and pII′ were added; in total, there were 10 local minima for Gly. For Pro, the φ,ψ points were −75°, 140°; −75°, 80°; and −75°, −60°. At each elongation step, the system of distance limitations was imposed on the growing peptide chain. First, the growing chain was required to be self-avoided, i.e., the corresponding Cα-Cα distances should not be less than D_int, which was accepted as 4.0 Å. Second, the chain had to avoid sterical clashes with the existing template; the corresponding Cα-Cα distances should not be less than D_out ≈ 5.0–8.0 Å. D_out was intentionally chosen to be larger than D_int, since in GPCRs, contrary to soluble globular proteins, the loops cannot be in too close contact with the rest of the protein to avoid the unlikely insertion of the loop into the membrane. However, for contacts of a newly built loop with already existing ones (when a loop was included in the template) and with the first three residues of the helical stems, D_out was equal to D_int. Third, the growing chain should not go too far from the starting point as well as from the target point, which are the two stem residues, 1 and M, respectively, both already existing in the template. Only those conformations were, therefore, selected where Cα-Cα distances between the current end residue of a growing chain (the ith residue) and the two stem residues of the loop were less than (i − 1) or (M − i) times a coefficient EL = 1.5 (this empirical dependence was deduced from our analysis of the protein loops in the Protein Data Bank (PDB)). This last constraint was accepted with a tolerance parameter, DEL, which varied depending on the particular situation along with D_out. Generally, several values of both parameters were considered at each step of the build-up procedure to ensure a reasonable number of selected conformers (from hundreds to hundreds of thousands; see Results). Since the EC2 loop is connected to the TM region of rhodopsin by the disulfide bridge 110–187, geometrical sampling for this loop was performed in two steps: first from residue 172 to residue 187 (assuming that the target residue is in the close position to residue 110) and then from residue 187 to residue 200, which required using negative values of DEL (see Results).

After geometrical sampling selected all potentially loop-closing conformations for a specific loop, the selected structures were subjected to energy minimization employing the ECEPP/2 force field (14,15) with rigid valence geometry and planar transpeptide groups (for prolines, the ω angles were allow to vary); the dielectric constant was chosen equal to 80 to mimic to some extent the water environment of the protruded loops. Two flanking N- and C-terminal helical fragments of three stem residues each were added to each selected loop structure, so the loops considered for energy calculations were as follows: 61–75 (IC1), 136–153 (IC2), 222–249 (IC3), 96–111 (EC1), 169–203 (EC2), and 274–289 (EC3). Spatial arrangement of the side chains according to a previously developed algorithm (16) was optimized for each backbone structure along with energy minimization. The total energy included also the sum of parabolic potentials (U₀ = 10 kcal/mol), keeping the flanking residues in the relative spatial positions they occupied in the template structures of the TM regions of R and R*. The additional parabolic potentials were added to keep residue 187 of loop EC2 in a spatial position that did not preclude the disulfide bridge 110–187, as well as to keep residue 188 in a spatial position not preventing possible interaction with retinal, covalently attached to K296. Since two sequential proline residues in the TM5 helical stem of EC2 (fragment 169–172, APPL) cannot be tolerated in a helix (the ECEPP/2 force field shows very significant sterical hindrance in this fragment), P¹⁷¹ was replaced by alanine. Note that this proline is not conserved in the rhodopsin family of GPCRs (17) contrary to P¹⁷⁰; in fact, the P¹⁷⁰–P¹⁷¹ sequence exists only in rhodopsins themselves. After energy minimization, low-energy conformers were selected as those with relative energies less than ΔE = 1 kcal/mol per residue (18). Finally, the resulting loop structures were placed back onto the templates, and those with newly emerged sterical clashes (due to changes in the dihedral angle values) were removed according to the accepted value of the D_out parameter.

Energy calculations for the interacting intra- and extracellular loops

The low-energy conformers selected by results of energy calculations for individual loops were then combined to account for the interloop interactions. In GPCRs, the loops are much more likely to interact with each other than with the TM regions of the proteins (see also observations made in Forrest and Woolf (19)), and, obviously, the intracellular loops do not interact with the extracellular loops. Accordingly, interloop interaction was studied in two separate systems: the intracellular “package” consisting of fragments 61–75 (IC1), 136–153 (IC2), 222–249 (IC3), and 303–322 (the TM7 helical stem and helix H8), and the extracellular package consisting of fragments 35–38 (the TM1 helical stem), 96–111 (EC1), 169–203 (EC2), and 274–289 (EC3); the latter contained also the disulfide bridge 110–187. In other words, the studied systems included, besides all loops, all TM helical stems and, additionally, helix H8, i.e., all elements in the rhodopsin most likely to interact with the loops. However, the TM region of rhodopsin beyond the stems was not present in the packages during energy minimization. Therefore, some low-energy conformers of the loops obtained as a result of energy minimization may occupy spatial positions with potential close contacts with the TM region of rhodopsin beyond the stems, i.e., the loops may be “inserted” into the membrane. Conformers of this class were discarded from the final results.

Typically, energy calculations for the individual loops yield a fairly large number of low-energy conformations for each loop, from tens to hundreds (see Results), which makes it virtually impossible to perform energy calculations for all their combinations. Therefore, the sets of low-energy conformers for each loop were divided into clusters by the root mean-square (rms) values of 2 Å or 3 Å (Cα-atoms only), and only the lowest-energy conformers in each cluster were selected as representatives for further consideration in the intracellular and extracellular packages. Then, for all combinations of representatives, energy calculations were performed employing the ECEPP/2 force field, as in the previous subsection. Total energy included the additional parabolic potentials (U₀ = 10 kcal/mol) between the end residues of the TM helical stems to keep them in the relative spatial positions close to those in the TM templates. Again, optimization of the spatial positions of side chains (16) was performed along with energy minimization.

RESULTS

The R state

Individual extracellular loops

Geometrical sampling was performed first for the EC1 loop (residues 99–108); all possible combinations of local minima on the Ramachandran map for each residue (see Methods) were considered for the octapeptide fragment 100–107. A total of 273 backbone conformers were selected as the loop-closing ones with parameters D_out = 7.0 Å and DEL = 2.0 Å. Energy calculations for fragment 96–111 found 119 conformers with relative energy values <16 kcal/mol, which were divided into two clusters of structures similar to each other by the rms value of 2.0 Å (here and further in this section, the presented rms values are for Cα-atoms only).

The low-energy structure of EC1 closest to the average spatial positions of the Cα-atoms (averaged over all 119 low-energy conformers of EC1) was added to the employed template of the TM region of rhodopsin in the R state, and geometrical sampling was performed for the EC3 loop (residues 277–286). Again, all possible combinations of local minima on the Ramachandran map for each residue were considered for the octapeptide fragment 278–285, and 169 backbone conformers were selected as the loop-closing ones with parameters D_out = 7.0 Å and DEL = 2.0 Å. Subsequent energy calculations (fragments 274–289) found 43 low-energy conformers (ΔE = 16 kcal/mol) that fall into four clusters with an rms value of 2.0 Å. Then, the low-energy structure of EC3 closest to the spatial positions of the Cα-atoms averaged over 43 low-energy conformers of EC3 was added to the template of the TM region.

Geometric sampling for the largest of the extracellular loops, EC2 (172–200), was performed by the build-up procedure consisting of several steps described in Table 1. At the first step, all combinations of local minima for peptide backbones were considered for fragment 173–179 and those potentially loop-closing ones were selected; after that, all combinations of local minima for peptide backbone were considered only for the newly added di- or tripeptide fragments. The negative values of DEL for elongation beyond residue 187 were used to account for limitations associated with the disulfide bridge 110–187 (see Methods). Finally, 2,155 conformers of fragment 172–200 were selected for energy calculations that, in turn, found 334 low-energy conformers of fragment 169–203 (ΔE = 35 kcal/mol). The low-energy conformers were divided into 270 clusters by the rms value of 2.0 Å.

TABLE 1.

Results of build-up procedure (starting from residue 170) of geometrical sampling for the EC2 loop

*	179	181	183	185	187	189	191	193	195	197	200
†	5.0	5.0	5.0	5.0	5.0	5.0	8.0	8.0	8.0	8.0	8.0
‡	0.0	2.0	5.0	3.0	3.0	−5.0	−5.0	−2.0	−2.0	−2.0	0.0
§	4,380	16,715	275,000	333,080	690,570	3,915	7,400	40,950	79,005	56,905	2,155

^*End residue of a fragment.

^†D_out at a given step, Å.

^‡DEL at a given step, Å.

^§Number of selected loop-closing backbone conformers.

Individual intracellular loops

In this case, again, geometrical sampling was performed first for the smallest IC1 loop. All possible combinations of local minima for each residue were considered for the heptapeptide fragment 65–71. A total of 59 backbone conformers suitable to close the loop were selected with parameters D_out = 6.0 Å and DEL = 2.0 Å. Energy calculations for fragments 61–75 yielded 24 conformers with relative energy values <15 kcal/mol, which were divided into three clusters of structures by the rms value of 2.0 Å. The low-energy structure of IC1 closest to the spatial positions of the Cα-atoms averaged over all low-energy conformers was added to the template of the TM region.

Geometrical sampling for IC2 consisted of two elongation steps. First, all possible combinations of local minima for each residue were considered for the heptapeptide fragment 140–146, and then selected conformers were elongated to the level of fragments 140–150. At both steps, the value of D_out was 6.0 Å and DEL was 2.0 Å. Geometrical sampling found 228 tentative loop-closing conformers that yielded 97 low-energy structures (ΔE = 18 kcal/mol) of fragment 136–153. Some of those structures experienced sterical clashes (D_out = 4.0 Å) with the template when mounted back onto the helical stems of TM3 and TM4 and were removed from further consideration (see Methods). Finally, 33 low-energy conformers were selected for the IC2 loop; they were divided into seven clusters by the rms value 2.0 Å. Again, the low-energy structure of IC2 closest to the spatial positions of the Cα-atoms averaged over selected 33 low-energy conformers of IC2 was added to the template of the TM region.

As in the case of EC2, geometric sampling of the largest IC3 loop required several steps of build-up procedure, described in Table 2, which is analogous to Table 1. Resulting 3,031 loop-closing conformers of fragment 225–246 yielded 687 low-energy conformers of fragment 222–249, out of which 124 were selected as those without sterical clashes with the template (D_out = 6.0 Å). They were divided into 27 clusters by the rms value of 3.0 Å.

TABLE 2.

Results of build-up procedure (starting from residue 225) of geometrical sampling for the IC3 loop

*	230	234	238	240	243	246
†	8.0	8.0	8.0	8.0	8.0	8.0
‡	2.0	0.0	0.0	0.0	0.0	0.0
§	175	1,140	2,835	2,360	9,130	3,031

^*End residue of a fragment.

^†D_out at a given step, Å.

^‡DEL at a given step, Å.

^§Number of selected loop-closing backbone conformers.

Interacting intra- and extracellular loops

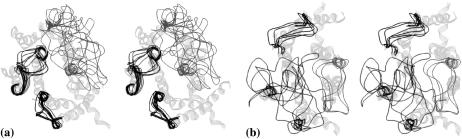
As described in Methods, all combinations of the lowest-energy representatives for all clusters of low-energy conformations of the IC1, IC2, and IC3 (or EC1, EC2, and EC3) were considered as starting points for energy calculations in the “packages” of IC1+IC2+IC3+H8 and EC1+EC2+EC3. In total, 567 conformers (3 × 7 × 27) were studied for the IC package, and 2,160 (2 × 270 × 4) were studied for the EC package. Low-energy conformers were selected as those with relative energy values less than an arbitrary cutoff of 30 kcal/mol for the intracellular part (133 conformers) and of 50 kcal/mol for the extracellular part (54 conformers). Removal of some low-energy conformers with the close contacts with the TM region of rhodopsin beyond the stems (see Methods) left 106 low-energy conformers for the intracellular part and 27 conformers for the extracellular part. Those conformers, in turn, were divided into clusters by the rms value of 3 Å (over all loops in the package), which produced 13 clusters for the intracellular part and 15 clusters for the extracellular part. The representatives of the clusters are depicted in Fig. 1; for illustrative purposes, only clusters differing by the rms value of 4 Å are shown in Fig. 1 b (the extracellular loops).

FIGURE 1.

Stereoviews showing sketches of clusters of low-energy conformers of the intracellular (a) and extracellular (b) loops of rhodopsin in the R state. Loop conformers are shown as one-line ribbons in dark gray; TM region of rhodopsin is shown as a five-line ribbon in light gray. Loops are shown in clockwise order from IC1 to IC2 to IC3 (a) or from EC2 to EC1 to EC3 (b) starting from the lower left corner of the figure. Views are from the intracellular (a) and extracellular (b) sides of the membrane, respectively.

The R* state

Individual loops

Building of 3D structures for the individual intra- and extracellular loops in the activated state of rhodopsin was based on the template for the 3D structure of the TM region of rhodopsin in the activated state (MII) developed earlier (10). The main difference between the templates for the TM region in the R and R* states is rotation of TM6 along the long axis by ∼120°, which should not significantly affect the loop closing for IC1, IC2, EC1, and EC2. Therefore, energy calculations for these loops were performed for the same structures that were selected by geometrical sampling for the R state (see above) and following the same protocol with the same selection criteria. For IC1, energy calculations found 30 low-energy structures of the backbone that were divided into two distinct clusters with an rms value of 2.0 Å. For IC2, there were 108 low-energy structures (17 structures without sterical clashes with the TM template) with three clusters with an rms value of 2.0 Å. The EC1 loop yielded 90 low-energy conformers that fit into one single cluster with an rms value of 2.0 Å. The set of the low-energy structures of the largest loop EC2 consisted of 404 conformers, which were divided into 327 clusters with an rms value of 2.0 Å.

Separate geometrical sampling was independently performed for the EC3 and IC3 loops. All possible combinations of local minima for each residue were considered for the fragment 278–285 in EC3; 1,651 backbone conformers suitable to close the loop were selected with parameters D_out =7.0 Å and DEL = 2.0 Å. Energy calculations yielded 217 low-energy conformers, which were divided into five clusters of structures by the rms value of 2.0 Å. Geometric sampling of the large IC3 loop consisted of the same several steps of build-up procedure, which are described above for the same loop in the R state (Table 2). The much larger number of potentially loop-closing conformers (39,934) was found by geometrical sampling; they result in 1,443 low-energy conformers, out of which 394 were selected as those without sterical clashes with the template (D_out = 6.0 Å). They were divided into 13 clusters with the rms value of 3.0 Å.

Interacting intra- and extracellular loops

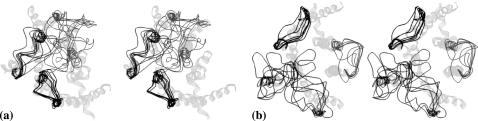
Again, this stage of calculations was performed as described above for the R state. In total, 117 conformers (3 × 3 × 13) were studied for the IC1+IC2+IC3+H8 package, and 1,635 (1 × 327 × 5) were studied for the EC1+EC2+EC3 package. Energy calculations yielded 53 low-energy conformers for the intracellular part, and 144 low-energy conformers for the extracellular part (the same energy cutoffs as for the R state were applied). Removing some low-energy conformers with close contacts with the TM region of rhodopsin in the R* state left 42 low-energy conformers for the intracellular part and 131 conformers for the extracellular part. Those conformers can be divided into clusters by the rms value of 3 Å over all loops producing 10 clusters for the intracellular part and 59 clusters for the extracellular part. The representatives of the clusters are depicted in Fig. 2 in the same projection and with the same limitations as the clusters in Fig. 1.

FIGURE 2.

Stereoviews showing sketches of clusters of low-energy conformers of the intracellular (a) and extracellular (b) loops of rhodopsin in the R* state. Loop conformers are shown as one-line ribbons in dark gray; TM region of rhodopsin is shown as a five-line ribbon in light gray. Loops are shown in clockwise order from IC1 to IC2 to IC3 (a) or from EC2 to EC1 to EC3 (b) starting from the lower left corner of the figure. Views are from the intracellular (a) and extracellular (b) sides of the membrane, respectively.

DISCUSSION

Comparison of calculation results with x-ray data

Three of the five different x-ray structures obtained for the dark-adapted bovine rhodopsin (3–5) lack some fragments of the loop IC3: fragment 235–240 in the PDB entry 1F88 and fragment 235–241 in the PDB entries 1HZX and 1L9H. Moreover, the fragments 240/241–246 are oriented in totally different directions in 1F88 and 1HZX/1L9H. The two most recent structures, the PDB entries 1GZM (6) and 1U19 (7), contain data on the entire IC3 loop though the x-ray snapshots of the loop significantly differ from each other and the B-factor values measured for the IC3 loop are unusually high (6). Therefore, we have decided to compare our calculation results with the PDB entries 1GZM and 1U19 only. Obviously, since our modeling procedure employs an unsophisticated force field and deliberately sacrifices detailed description of the system (no membrane, no water, etc.) in favor of rapid determination of sterically and energetically reasonable conformers of the loops, it would be unrealistic to expect that the closest spatial similarity to the x-ray structures will be achieved by the lowest-energy conformation. Instead, we considered our energy calculations sufficiently validated if at least one of the found low-energy conformers is in good agreement with the available x-ray snapshots of the loops.

The root mean-square deviation (rmsd) values were calculated for all low-energy conformers of the individual intra- and extracellular loops for all heavy atoms of the backbones for the loops overlapped over the corresponding helical stems of 1GZM (the so-called “global” rmsd values (13)); only atoms of the nonstem residues were included in calculations of the rmsd values. For the low-energy conformers of individual loops closest to the x-ray structure in 1GZM (or 1U19, see numbers in parentheses), the rmsd values were as follows: 1.9 (2.0) Å for the smallest loop IC1 (7 nonstem residues from 65 to 71); 1.0 (1.3) Å and 2.1 (2.0) Å for EC3 (8 residues from 278 to 285), and EC1 (8 residues from 100 to 107); 2.5 (1.8) Å for IC2 (10 residues from 140 to 149); 5.0 (5.0) Å for IC3 (20 residues from 226 to 245); and 4.7 (4.9) Å for the largest EC2 loop (27 residues from 173 to 199). These values are quite comparable with the rmsd values (Cα atoms only) reported in the recent study that modeled the shortest IC1, EC1, and EC3 loops of rhodopsin employing a previously developed complex algorithm for loop closing (20); the study found the values of 1.2, 0.8, and 1.2 Å, respectively (21). Interestingly, the mean rmsd values calculated for the lowest-energy conformers obtained for the large test sets of loops of similar sizes in globular proteins by various state-of-the-art sampling procedures that employed the force fields much more sophisticated than the ECEPP were also close to ours. Specifically, for seven-membered loops (such as IC1) the rmsd values were 1.4 Å, 1.2 Å, and 0.8 Å; for eight-membered loops (such as EC1 and EC3) 2.3 Å, 1.4 Å, and 1.0 Å; and for 10-membered loops (such as IC2) 3.5 Å, 2.2 Å, and 1.7 Å (see DePristo et al. (22), Xiang et al. (23), and Jacobson et al. (13), respectively). On the other hand, the only modeling study that considered ab initio modeling of the long IC3 loop (fragment 226–246) used multicanonical molecular dynamics (24) and yielded rmsd values as small as 3.6 Å. However, they were calculated by overlapping all residues in fragment 227–244 (the “local” rmsd values that are always smaller than the corresponding “global” ones (12)) to the x-ray structure of the 1NZX entry in the PDB where the missing fragment 236–240 was artificially restored (24).

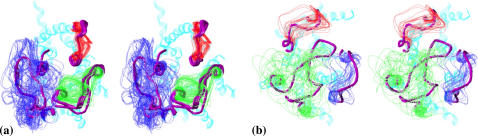
The global rmsd values for the low-energy conformers of the interacting IC1+IC2+IC3 and EC1+EC2+EC3 loops that are closest to the x-ray structure of 1GZM (1U19) were 4.2 (4.4) Å and 4.5 (4.3) Å for 37 and 43 nonstem residues, respectively. Combining these conformers with the template previously suggested for the R state of the TM region of rhodopsin (10), the total rms value (Cα atoms only) between 1GZM (fragment 35–313) and the resulting structure was of 2.9 Å for a total of 279 residues, 80 of them being the loop residues. Fig. 3 illustrates consistency between the calculated loop structures and the x-ray structures. Various x-ray snapshots for the IC3 loop from 1GZM, 1U19, 1F88, 1HZX, and 1L9H are shown in Fig. 3 a for the intracellular loops; for the extracellular loops, the five snapshots are fairly close, so only one of them is shown in Fig. 3 b.

FIGURE 3.

Stereoviews of low-energy conformers of the IC1+IC2+IC3 (a) and EC1+EC2+EC3 (b) packages compared to snapshots from the five x-ray structures of rhodopsin in the R state. Loops IC1 and EC1 are shown in red, IC2 and EC2 in green, and IC3 and EC3 in blue. Loop conformers are shown as one-line ribbons. The x-ray snapshots are shown as tubes in magenta. The TM region of rhodopsin is shown as a five-line ribbon in cyan. Views are from the intracellular (a) and extracellular (b) sides of membrane, respectively.

Conformational flexibility of the intra- and extracellular loops in the R and R* states

Our results clearly show that the intra- and extracellular loops of rhodopsin may possess sterically consistent structures that correspond to large conformational movements both in the R and R* states. The Cα-Cα distances between the central residues of the intracellular loops IC1, IC2, and IC3 (L⁶⁸, S¹⁴⁴, and A²³⁵, respectively) averaged over all low-energy conformations for the IC1+IC2+IC3 package were 18.6 Å (L⁶⁸–S¹⁴⁴), 27.1 Å (L⁶⁸–A²³⁵), and 19.0 Å (S¹⁴⁴–A²³⁵) in the R state and 15.1 Å, 22.1 Å, and 13.9 Å in the R* state. For the extracellular loops EC1, EC2, and EC3, the central residues are F¹⁰³, T¹⁹³ (for the EC2 fragment from the disulfide-bonded residue S¹⁸⁷–N²⁰⁰), and S²⁸¹; the average distances between them were 25.0 Å (F¹⁰³–T¹⁹³), 22.4 Å (F¹⁰³–S²⁸¹), and 13.1 Å (T¹⁹³–S²⁸¹) in the R state and 23.6 Å, 20.1 Å, and 20.1 Å in the R* state. In both states, there were low-energy conformers of the loops that may be considered as the “closed” and “opened” ones in terms of the above distances. Specifically, the lowest and largest distances (the latter in parentheses) between the central residues of the intracellular loops were 12.5 (24.5) Å, 19.7 (34.1) Å, and 10.0 (31.6) Å for the R state and 9.25 (20.6) Å, 13.8 (33.9) Å, and 5.3 (31.6) Å for the R* state. The corresponding distances found for the extracellular loops were 20.8 (32.2) Å, 12.2 (31.9) Å, and 7.1 (19.2) Å in the R state, and 18.2 (31.0) Å, 11.0 (24.8) Å, and 5.9 (37.5) Å in the R* state.

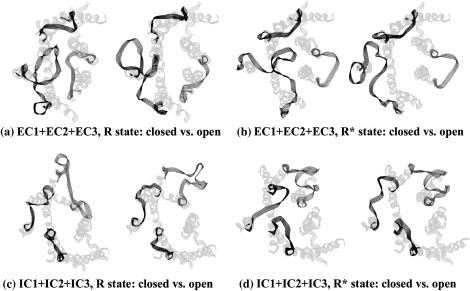
Fig. 4 schematically depicts the most “closed” and the most “opened” conformations out of those found by energy calculations for the extracellular and intracellular loops in the R and R* states. According to modeling results, the largest movements within both states may occur in spatial positions of the largest loop EC2, despite its flexibility being limited by the disulfide bridge between C¹¹⁰ and C¹⁸⁷. However, the “opening” created by the movement of EC2 in the R* state can be more profound than that in the R state (compare the right structures in Fig. 4, a and b). One of the reasons for this difference is the shift of the N-terminal part of TM5 away from the TM core in the R* state, which, in turn, is caused by rotation of the TM6 helix (see Nikiforovich and Marshall (10)). On the other hand, the most “closed” conformation of the extracellular loops is the most similar to the x-ray snapshot in the dark-adapted state (compare Fig. 4 a, left structure, and Fig. 3 b).

FIGURE 4.

Pairs of the most closed (left structures) and most opened (right structures) low-energy conformers of the extracellular (panels a and b) and the intracellular (panels c and d) for the R and R* states of rhodopsin (left and right panels, respectively). The loop structures are shown as five-line ribbons in dark gray. TM region of rhodopsin is shown as five-line ribbon in light gray. Loops are shown in clockwise order from EC2 to EC1 to EC3 (a and b) or from IC1 to IC2 to IC3 (c and d) starting from the lower left corner of the figure. Views are from the extracellular (a and b) and intracellular (c and d) sides of the membrane, respectively.

Comparison of modeling results to available biophysical data

There are few experimental biophysical data related to conformational flexibility of the loops in rhodopsin that allow interpretation in direct structural terms. The most informative data were obtained by SDSL of the TM region of rhodopsin (9). These data were employed for selection of the most plausible 3D models for the R and R* states of the TM region out of all low-energy structures suggested in our previous study (10). Accordingly, the templates for the TM regions used in this study are already in good agreement with those particular experimental data. The same is true for many of the data on the disulfide-rate formation in rhodopsin mutants with additional disulfide bonds and on disulfide-linked rhodopsin mutants that either permit or inhibit activation (see Nikiforovich and Marshall (10) for details). The experimental data related specifically to possible contacts between the loops are available, in fact, only for intracellular loops. Comparison of these data with the sets of low-energy structures found for the intracellular and extracellular loops in our study shows good consistency.

For instance, a scan by Cys residues of fragment 55–75 that encompass IC1 has found that the highest rates of spontaneous disulfide-bond formation were between residues C³¹⁶ in H8 and C⁶⁵; residues C⁶⁸ and C⁶¹ also may form disulfide bonds with C³¹⁶, though at lower rates (25); this suggested some conformational mobility of IC1 in the R state (26). The same scan for fragment 311–314 (H8) found high rates of disulfide-bond formation between positions 246–311 and 246–312 (i.e., between IC3 and H8) but not between 246–313 and 246–314 (27). Independently, it was found that the disulfide bond C⁶⁵–C³¹⁶ permits activation of rhodopsin (28), whereas the disulfide bond C²⁴⁶–C³¹² prevents activation (27).

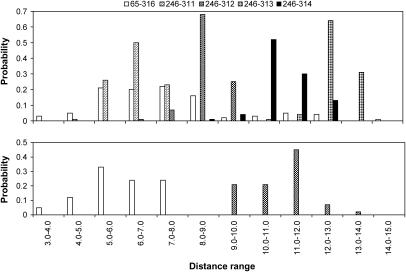
Fig. 5 (upper panel) displays distributions of distances between Cβ atoms in positions 65–316, 246–311, 246–312, 246–313, and 246–314 over all low-energy conformations found for the IC1+IC2+IC3 package in the R state. The distributions for distances 65–316, 246–311, and 246–312 were shifted toward lower values, and those for distances 246–313 and 246–314 were shifted toward higher values. The average distances were 7.3 Å for distance 65–316, 6.4 Å for 246–311, 8.6 Å for 246–312, 12.8 Å for 246–313, and 11.0 Å for 246–314. This observation rationalizes the experimental biophysical data on the rates of disulfide-bond formation in the disulfide-linked rhodopsin mutants with amino acid replacements in the loops in terms of average proximities of the corresponding positions. Interestingly, this straightforward interpretation of the decrease of disulfide-bonding rates from 246–312 to 246–313 in terms of proximity of the bonding positions has not been accepted in the original study (27) on the grounds that position 246 is equally close to positions 311–314 in the x-ray structure (1F88, (3)). In our calculations, however, the single x-ray snapshot was replaced by a variety of sterically consistent conformers that likely interconvert. The lower panel of Fig. 5 shows distributions of distances 65–316 and 246–312 over the low-energy conformations found for the IC1+IC2+IC3 package in the R* state. Whereas distribution for distance 65–316 remained basically the same as in the upper panel, distribution for distance 246–312 was shifted toward higher values. Both findings are in agreement with the experimental observations on the disulfide bonds permitting (65–316) and prohibiting (246–312) activation. The experimental data that suggest disulfide-bond formation between residues in positions 61 and 316 (25) or 65 and 312 (27) also agree with calculation results; the corresponding average Cβ-Cβ distances were 7.6 Å and 8.5 Å, respectively. However, high rates of disulfide bonding between residues in positions 68 and 316 (25) and 65 and 315 (27) do not correlate with proximities of these positions according to these calculations (the average Cβ-Cβ distances of 15.6 Å and 10.7 Å, respectively).

FIGURE 5.

Distributions of distances (in angstroms) between Cβ atoms in positions 65–316, 246–311, 246–312, 246–313, and 246–314 in the R state (upper panel) and between Cβ atoms in positions 65–316 and 246–312 in the R* state (lower panel).

Employing emerging experimental data for selection of the plausible 3D structures of the loops

As shown above, our calculation results determined sterically reasonable low-energy conformations of the intra- and extracellular loops that are in general agreement with the available experimental data. These results could also be compared with any new emerging experimental data to select the most plausible 3D models for the loop structures. For instance, some preliminary data obtained by the novel technique of double electron-electron resonance (29) suggested that the distance between spin labels inserted in positions 63 (close to IC1) and 241 (in IC3) of rhodopsin became larger by ∼6 Å (shift from ∼34 Å to ∼40 Å) upon transition from R to R* (W. L. Hubbell, UCLA, personal communication, 2005; also see Topics in EPR (30)). According to our calculated results, Cα-Cα distances between positions 63 and 241 in the low-energy conformers of the IC1+IC2+IC3 packages varied from 20.3 Å to 34.3 Å in the R state and from 14.0 Å to 32.0 Å in the R* state. The average value of distance 63–241 in the R state was 28.2 Å, which is fairly close to 27.2 Å, which is the same value averaged over the five x-ray snapshots of rhodopsin (30.7 Å in 1GZM (6), 18.6 Å in 1F88 (3), 28.8 Å in 1L9H (5), 29.2 Å in 1HZX (4), and 28.6 in 1U19 (7)). One can assume that selections of conformers with distances 63–241 below ∼26 Å for the R state (maximal distance for the R* state less 6 Å) and above ∼26 Å for the R* state (minimal distance for the R state plus 6 Å) will satisfy the above experimental observation. There are 33 low-energy conformers for the R state and 15 conformers for the R* state possessing distances within the specified limits. The average Cα-Cα distances 63–241 in these newly deduced sets of low-energy structures are 24.2 Å for the R state and 28.4 Å for the R* state. Rescaling of the interhelical distances estimated by electronic paramagnetic resonance between spin labels in position 139 and positions 248, 249, 250, 251, 252 in dark-adapted rhodopsin (31) to the Cα-Cα distances according to the x-ray data (all five available x-ray structures agree well with these distances) showed that distances between spin labels are always larger than the corresponding Cα-Cα distances by 4−9 Å (32). Assuming the same rescaling in the case of distance 63–241, the average distances between the spin labels in the deduced sets of the low-energy structures would be 28–33 Å for the R state and 32–37 Å for the R* state, whereas the experimental estimations were ∼34 Å and ∼40 Å, respectively (30). Importantly, distributions of Cβ-Cβ distances 65–316, 246–311, 246–312, 246–313, and 246–314 over the deduced sets of conformers are close to those in Fig. 5 (data not shown), which means that the narrower sets of low-energy conformers also agree with the previously available experimental data on disulfide-linked rhodopsin mutants. This exemplifies how combined application of independent calculation results and emerging experimental data can effectively narrow down the scope of possible candidates for 3D structures of the loops in rhodopsin.

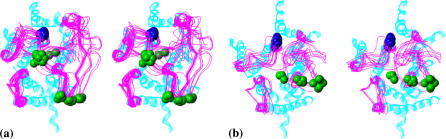
The obtained calculation results may also be used to produce structural hypotheses as to plausible 3D models of the loops to be tested by experiment. As an example, the low-energy conformers satisfying the observed differences in distances between positions 63 and 241 in the R and R* states (those deduced above) are depicted in Fig. 6, a and b, respectively. Cα atoms of residues C¹⁴⁰ (in IC2) and A²⁴¹ (in IC3) are shown in Fig. 6 in space-filled mode in blue and green, respectively. It is obvious that the conformers of the R state can be divided into two distinct groups as to distances between these two residues (see Fig. 6 a). The first group consists of 13 conformers where the distances are from 9.3 Å to 13.4 Å, and the second group involves the 20 remaining conformers where the distances are from 25.3 Å and 29.0 Å, according to the calculated results. In the R* state, the same distances vary from 16.6 Å to 26.6 Å, but here it is difficult to divide the low-energy conformers into the distinctly different groups (see Fig. 6 b). Inserting spin labels or other reporting groups at positions 140 and 241 and estimating distances between them both in the R and R* states of rhodopsin could provide new experimental data to select even more narrow sets of plausible structures for the rhodopsin loops out of the low-energy conformations suggested by the calculations.

FIGURE 6.

Stereoviews showing sketches of low-energy conformers of the intracellular loops of rhodopsin satisfying the experimentally estimated differences in distances between positions 63 and 241 in the R (a) and R* (b) states. Loop conformers are shown as one-line ribbons in magenta; TM region of rhodopsin is shown as a five-line ribbon in cyan. Cα atoms of residues 140 and 241 are shown in space-filled mode in blue and green, respectively; only those atoms are shown. Views are from the intracellular side of membrane.

CONCLUDING REMARKS

This work presents results of modeling conformational possibilities of flexible loops in rhodopsin, a prototypical GPCR, both in the dark-adapted (R) and activated (R*) states. The employed approach sacrificed a detailed description of the molecular system under consideration to sample many more, though less-precise, low-energy 3D structures of the loops. Specifically, the procedure involved geometrical and energetic sampling of the possible conformations of the large loops (up to ∼30 residues) that proved to be efficient in terms of required computer resources: all computations in this study were performed on a single PC node of 2.8 GHz and required from several minutes to several hours of computer time for a single run covering all considered conformations for a given loop at a given stage. At the same time, the approach provided significant agreement with available x-ray snapshots of the dark-adapted state of rhodopsin.

The obtained results provided insights into conformational flexibility of the loops in both the R and R* states of rhodopsin. These results agree with the experimental biophysical data on the disulfide-linked mutants of rhodopsin related to the R and R* states. Importantly, they revealed large-scale concerted molecular movements ranging from the “closed” to “opened” conformations of the intra- and extracellular loops. The modeling results obtained provide experimentalists with testable hypotheses as to the plausible 3D structures of the loops in both the R and R* states of rhodopsin; specific examples are estimating differences in distances between positions 63 and 241 as well as between positions 140 and 241.