The Geometry of the Flux Cone of a Metabolic Network

Abstract

The analysis of metabolic networks has become a major topic in biotechnology in recent years. Applications range from the enhanced production of selected outputs to the prediction of genotype-phenotype relationships. The concepts used are based on the assumption of a pseudo steady-state of the network, so that for each metabolite inputs and outputs are balanced. The stoichiometric network analysis expands the steady state into a combination of nonredundant subnetworks with positive coefficients called extremal currents. Based on the unidirectional representation of the system these subnetworks form a convex cone in the flux-space. A modification of this approach allowing for reversible reactions led to the definition of elementary modes. Extreme pathways are obtained with the same method but splitting up internal reactions into forward and backward rates. In this study, we explore the relationship between these concepts. Due to the combinatorial explosion of the number of elementary modes in large networks, we promote a further set of metabolic routes, which we call the minimal generating set. It is the smallest subset of elementary modes required to describe all steady states of the system. For large-scale networks, the size of this set is of several magnitudes smaller than that of elementary modes and of extreme pathways.

INTRODUCTION

Progress in biotechnology led to the discovery of a rapidly increasing number of genomes of different species (1,2). From the identification of enzymes, the genes encode, the biochemical reactions can be derived, and the metabolic network of the organism can be reconstructed. Two of the most frequently used tools to analyze these networks are the stoichiometric network analysis (SNA) (3) and the flux balance analysis (FBA) (4), which are closely related to each other.

The SNA is based on concepts of convex geometry. It was outlined in a seminal article by Clarke (5) to analyze the stability of chemical reaction networks. The starting point is the steady state of the system where the kinetic equations expressed in terms of fluxes represent a linear equation system, which is determined by the stoichiometry matrix. The steady-state assumption requires that a flux vector is an element of the null-space of the stoichiometry matrix. A row of this matrix can be interpreted as a hyperplane in flux space. The intersection of all these hyperplanes forms the null-space. From thermodynamic considerations, some of the reactions can be assumed to proceed only in one direction so that the backward reaction can be neglected. Provided that all reactions are unidirectional or irreversible, the intersection of the null-space with the semipositive orthant of the flux space forms a polyhedral cone, the flux cone. The intersection procedure results in a set of rays or edges starting at 0, which fully describe the cone. The edges are represented by vectors and any admissible steady state of the system is a positive combination of these vectors. Thus, the first goal of SNA is to determine the representative vectors of the edges of the flux cone.

From a biological perspective, these edges characterize important pathways of the metabolic network. In the case of a pointed cone, where 0 is a vertex, they connect inputs to outputs with a minimal set of reactions. If one of the reactions is blocked, the route containing this reaction is interrupted and gets eliminated from the pathway set. As a consequence, the cone loses an edge and shrinks. Due to the fact that most reactions are catalyzed by enzymes in metabolic networks, we can determine the minimal set of enzymes, which must be expressed for a proper functioning of a metabolic route. This relationship links the metabolic network to the genetic regulatory network. It might help to elucidate the operon and regulon structure in prokaryotes and eukaryotes, respectively (6). Furthermore, the length of these metabolic pathways might be an important determinant in the evolutionary optimization procedure since the costs for maintaining a certain route increases with the number of enzymes expressed (7).

Another system property of interest is the robustness of the network, which can be assessed by counting the number of edges per reaction or per input-output relationship. In the former case, the approach measures how many edges of the cone are eliminated if a reaction is blocked, whereas, in the latter case, the outcome tells us how many pathways are available to produce a desired output from a given input.

The minimality property of these pathways can also be exploited to determine the minimal cut sets of the network (8). A minimal cut set is defined as a minimal set of reactions required to disconnect the input from the output. Minimal cut sets are used to determine the inhibitors necessary to fully block the metabolic network. This approach can be applied against parasites where the metabolic system of the parasite is shut down by the drugs, but not the network of the host.

A complication occurs when some of the reactions are reversible. However, with the simple trick of splitting up a reversible reaction into separate forward and backward directions, the system can be written in a fully irreversible representation. The cost for this transformation is the increase in the dimension of the flux space, which augments by 1 for every split reaction. Moreover, the number of edges of the flux cone rises by this procedure. This has led to different description of the flux cone depending on the set of reversible reactions, which were partitioned in forward and backward rates. Writing all reversible reaction as two irreversible rates, the flux cone can be defined in the semipositive orthant of the flux-space. The edges of this cone are the so-called extremal currents, which were defined by Clarke (5). Schuster and co-workers (9) determined the flux cone in the original flux-space abandoning the semipositivity constraint for reversible reactions. As a consequence, representatives of edges of the flux cone may have negative entries at the positions of reversible reactions. To distinguish these flux vectors from extremal currents, they were named elementary flux modes. An intermediate approach was undertaken by Schilling et al. (10). The authors considered all internal reversible reactions as two irreversible ones, but left the reversible exchange reactions unchanged. The edges of this cone were termed extreme pathways.

The concepts of elementary modes and extreme pathways have found broad application in the analysis of metabolic networks. Stelling and co-workers (11) used a reduced model of the central carbon metabolism of Escherichia coli to study the growth behavior of the wild-type and mutated organisms. The growth of phenotypes was computationally foretold by the elementary mode analysis and the result was experimentally tested. In the overwhelming majority of cases, the flux mode analysis correctly predicted the experimental outcome. The concept of extreme pathways has been applied to the human red blood cell metabolism (12). The authors analyzed the effect of flux limitation and determined the steady-state solution space with respect to network capabilities. In bioengineering, E. coli is used to produce recombinant proteins such as green fluorescent protein. Vijayasankaran et al. (13) have applied elementary mode analysis to the metabolic network of E. coli, which led to the identification of the most efficient pathway for the production of the protein.

Recently a debate has been launched in the literature whether it is necessary to compute the elementary modes or if it is sufficient to calculate the extreme pathways (6,14–16). On the one hand, it was claimed that some of the states of the system cannot be reached by linear optimization when only the extreme pathway are considered (14). They are therefore missed in the optimization procedure, leading to incorrect results. On the other hand, it was put forward that extreme pathways are the smallest set of vectors, which describes the flux cone (10).

In this article, we show that in the original flux-space the smallest set to generate the flux cone is the minimal generating set. (Sets of generators are defined in Rockafellar (17).) However, these sets are not minimal. We term the elements of the minimal generating set generating flux modes instead of generators, due to their closed relationship to elementary flux modes. The minimal generating set we obtain is a subset of elementary modes as well as of extreme pathways, and describes the edges of the flux cone. The remaining extreme pathways and elementary modes, which can be expanded in generating modes, are all interior points. The elements of the minimal generating set are related to the result of flux balance analysis (FBA) in the following way. Based on linear programming, FBA requires that the flux cone is bounded. This can be achieved by limiting the fluxes of the input reactions and of reversible cycles. In the bacterium E. coli the target function is represented by the production of biomass due to the assumed optimization of growth (18). The solution of the linear programming problem is a vertex of the truncated flux cone. This vertex is either a representative of one of the edges of the cone (element of the minimal generating set) or an interior point, which becomes a vertex because of the flux limitations. Of course, these interior point vertices can always be written as a combination of extreme vertices, which stem from the edges of the flux cone. Therefore, phase-plane analysis of metabolic networks (19) partitions the space of selected inputs into different regions, according to the sets of extreme vertices involved in producing the optimized output.

We have recently developed a new algorithm, which calculates elementary flux modes via linear combinations of null-space basis vectors (20,21). It turned out that the null-space approach is significantly faster than previously suggested algorithms, due to its reduction in dimensionality. The mathematical basis of our method is described in Urbanczik and Wagner (21), including all proofs. Empirical evidence suggests that the null-space algorithm is polynomial in the input size and output size and shows an almost quadratic dependence of the CPU time versus the number of elementary modes. This result is obtained using the network of the central carbon metabolism of E. coli with different input sets. Application of the new method to the pyruvate metabolism in rat liver mitochondria is given in Stucki (22), including a highly simplified Mathematica program (Wolfram Research, Champaign, IL) of the null-space approach, which handles only the fully irreversible case.

In this work we use the null-space algorithm to study the geometry of the flux cone. This geometric interpretation of the method allows us to identify the edges of the cone and to elucidate the differences among elementary flux modes, extreme pathways, and the minimal generating set. Moreover, we will present the relationship between these different sets of routes and the solution of the linear optimization problem.

BASIC FRAMEWORK

We first briefly resume the null-space algorithm to calculate elementary flux modes of a reaction network. Metabolic systems are assumed to operate in the steady state so that the time derivatives of the metabolites are zero. In this case, the reaction network can be represented as

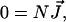(1)

where N represents the stoichiometry matrix and 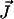the flux vector. In the following, we assume that the network consists of m independent species and of n reaction rates or fluxes. Only for illustrative purposes we arrange the fluxes in such a way that the first r reactions are reversible and the last (r + 1)…n irreversible. There are two strategies to calculate elementary modes. The primal algorithm introduced by Schuster et al. (9) starts with flux vectors fulfilling the irreversibility condition, and combines these vectors according to the stoichiometry matrix, so that the final flux vector lies in the null-space of N. It is based on an earlier suggested algorithm by Nozicka et al. (23). The starting point of this algorithm is

(2)

Here N^T is the transposed stoichiometry matrix and Id the identity matrix, which represent the set of initial flux vectors with fulfilled irreversibility condition.

Assuming only irreversible reactions, the above algorithm has a simple geometric interpretation. The initial cone is the semipositive orthant of the flux-space and the columns of N^T are hyperplanes in this space. The flux cone is then formed by the intersection of the hyperplanes with the semipositive orthant and by mutual intersections, which reduces the dimension of the cone with each hyperplane by 1. Thus, in the final stage, the flux cone is of dimension n–m.

In our dual algorithm we first calculate the kernel matrix K, which consists of null-space basis vectors and satisfies the equation

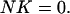(3)

Obviously, the vectors of K fulfill the null-space condition. It is well known from linear algebra that K can be put into the form (24)

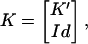(4)

where the identity matrix is now of size n–m. So the transpose of K has the very same form as the initial state of the primal algorithm (Eq. 2). At the moment we assume that all basis vectors in (Eq. 4) are irreversible, containing at least one irreversible reaction. It means that the network has neither a reversible input output path nor a reversible cycle. As a consequence, the flux cone is pointed and r ≤ m. Nonpointed cones will be considered separately in a later section. In the second step, we combine these basis vectors so that the irreversibility conditions are fulfilled. For the last n–m fluxes, these inequalities are automatically satisfied because of the identity matrix in K (Eq. 4). Therefore we are searching vectors , which lead to flux vectors 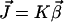fulfilling the inequalities

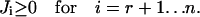(5)

Obviously, 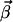is a semipositive vector since the basis vectors are all irreversible. As we have shown in our previous work (21), the 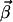vectors are obtained by a stepwise processing of the rows of K′. Each row of K is associated with a flux J_i of the network. Within a step, 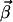vectors are constructed by pairwise annihilating the flux, which corresponds to that row. For i ≥ r + 1, only the flux vectors with semipositive entries at this position, and which are elementary, are kept for the next step. In contrast, for i ≤ r the calculated modes are only checked for its elementary property. Note that the vector 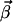is always part of the corresponding elementary mode due to the identity matrix in K (Eq. 4). Thus a projection of the elementary modes on the n–m-dimensional subspace spanned by J_m+1,J_m+2…J_n still contains all information of the flux cone.

Due to the similarities between the primal and the dual approach mentioned above, the null-space algorithm has also a more geometrical interpretation. Each row of K′ represents a hyperplane in the subspace V′ spanned by J_m+1,J_m+2…J_n. The flux cone is shaped by half-spaces defined by the hyperplanes of K′ and the inequalities given in Eq. 5. Thus, in the null-space algorithm we can directly follow the formation of the cone. This geometric interpretation also illustrates the reduction of dimensionality from n for the primal algorithm to n–m in the case of the null-space approach.

The different set of routes of a reaction network

In this section we will discuss the three different sets of network routes, which have been discussed in the literature. We will also promote a fourth set, the minimal generating set, which might become important in many applications.

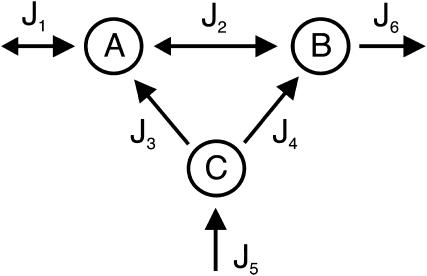
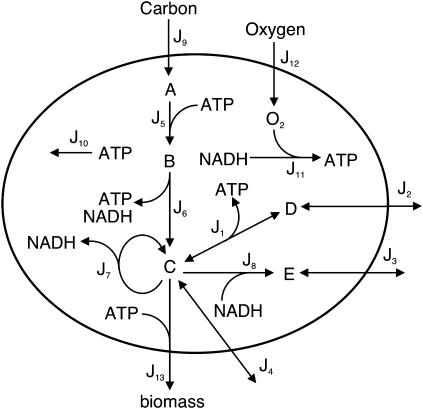
The different sets can only be compared if they are considered as elements of the same vector space. Therefore, we define our standard vector space as the n-dimensional flux-space. Elementary modes are calculated in this vector space. In contrast, to compute extremal currents the dimension of the vector space is increased by r, the number of reversible reactions. In our previous work we have shown (20), that there exists a projection operator which maps extremal currents onto elementary modes and that this mapping is reversible. By the projection operation, the spurious cycles (forward and backward reaction of a reversible reaction) get lost; however, they can be easily reconstructed when going in the opposite direction (from elementary modes to extremal currents). Thus the number of elementary modes corresponds to the number of extremal currents minus the number of reversible reactions r. Apart from this aspect, extremal currents and elementary modes describe the same set of routes but in different vector spaces. To illustrate the differences between elementary modes and extreme pathways, we will use the slightly modified example network suggested by Papin et al. (6) and displayed in Fig. 1. It consists of three species A, B, and C and of six fluxes J₁…J₆, whereof J₁ and J₂ are reversible. The stoichiometry matrix of this network reads

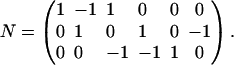(6)

The corresponding kernel matrix K is then given as

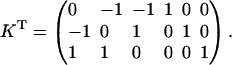(7)

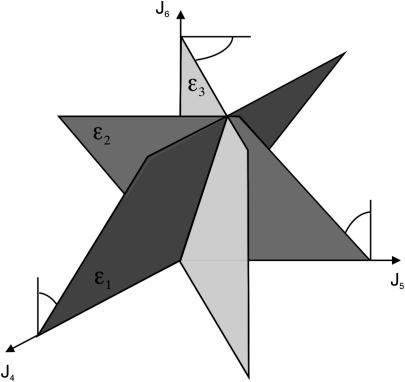
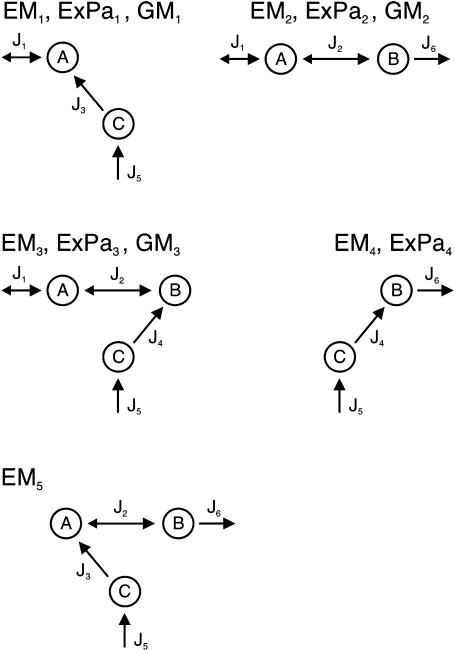
Let us call the subspace V′, which is spanned by the fluxes J₄, J₅, and J₆. Due to the fact that these reactions are irreversible, the initial cone is given by the semipositive orthant of V′. The first three columns of K^T represent hyperplanes in V′, which are linked to the fluxes J₁ to J₃ (see Fig. 2). Associated with J₃ is the plane ɛ₃. Due to the irreversibility condition imposed on J₃, only the proper half-space is admissible for the system. Therefore, the excluded half-space has to be cut off from the initial cone. For the other two hyperplanes ɛ₂ and ɛ₁ linked to the reversible fluxes J₂ and J₁, respectively, no inequality holds. Although these planes intersect the flux cone they do not contribute to its formation. The elementary flux modes of the system are now the vertices of the flux cone as well as the intersections of the hyperplanes defined by reversible fluxes (here J₁ and J₂) with the cone. They are displayed in network representation in Fig. 3 and read as flux vectors

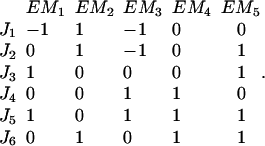(8)

FIGURE 1.

Scheme of the example network used in this study. It consists of three Species A, B, and C, and of six fluxes J₁–J₆. The first two, J₁ and J₂, are reversible; the remaining fluxes are unidirectional, given by the orientation of the arrows.

FIGURE 2.

The three hyperplanes, which may shape the flux cone. Their normal vectors are given by the columns of K^T. Thus, ɛ₃ linked to the flux J₃ is given by 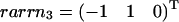, ɛ₂ linked to the flux J₂ is given by 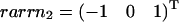, and ɛ₁ linked to the flux J₁ is given by .

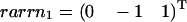FIGURE 3.

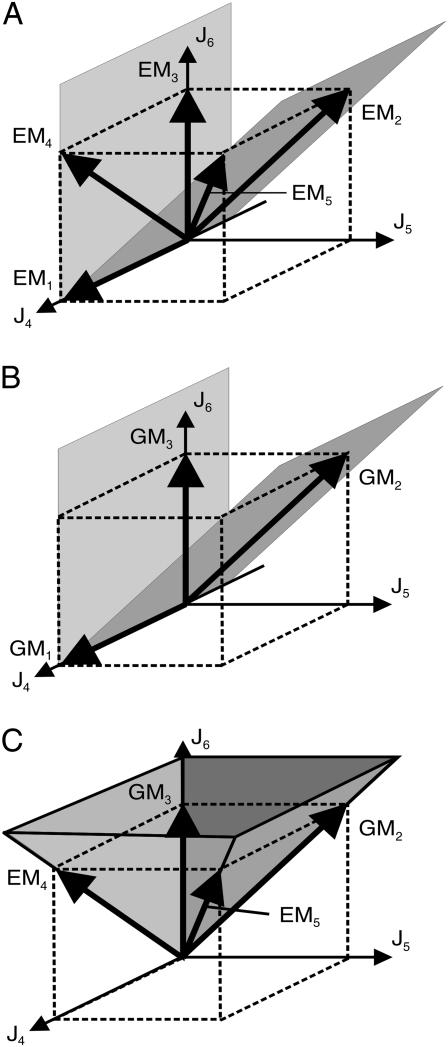
Network representation of elementary modes (5), extreme pathways (4), and generating modes (3) using the example network given in Fig. 1. The first two fluxes J₁ and J₂ are reversible, whereas the remaining ones are unidirectional. After deletion of J₂, EM₂ and EM₄ remain, whereby the former interior point EM₄ becomes a representative of an edge of the flux cone.

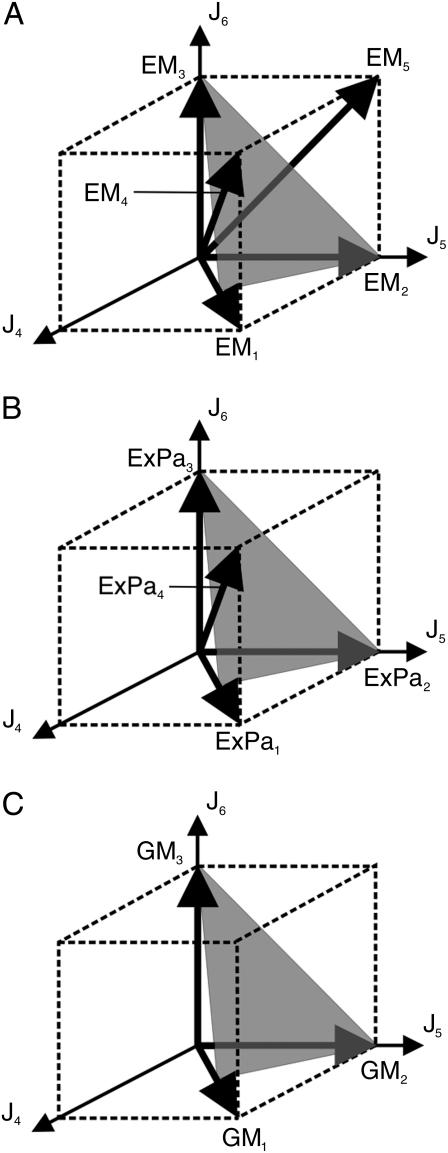
The elementary flux modes EM₁–EM₃ represent vertices of the flux cone whereas EM₄ and EM₅ are interior points (see Fig. 4 A). The modes EM₄ and EM₅ arise from the intersection of ɛ₂ and ɛ₁ with the flux cone, respectively.

FIGURE 4.

The different sets of routes of the reaction network given in Fig. 1 (spurious cycles omitted). (A) elementary flux modes (EMs), (B) extreme pathways (ExPas), and (C) generating modes (GMs). All flux vectors are projected to the components J₄–J₆. The components of the projected flux vectors represent the linear combination of null-space basis vectors.

Like extremal currents, extreme pathways are calculated in an extended vector space. For all internal reversible reactions, an additional flux in the reverse direction is introduced. In contrast, reversible exchange reactions are not split in forward and backward rates. They will simply adjust so that the steady-state condition is fulfilled. It is easy to find a projection operator that maps the extreme pathway back to the original flux-space of dimension n. These projected extreme pathways can be compared to the set of elementary modes. Again, by the projection we will lose the spurious cycles resulting from internal reversible reactions. The projection procedure also provides the insight that the detour via the extended vector space is not necessary. Extreme pathways can also be directly calculated in the n-dimensional flux-space, which can be nicely seen using the null-space approach. To obtain the extreme pathways, we take into account half-spaces of hyperplanes associated with irreversible reactions and intersections with internal reversible reactions. All hyperplanes linked to reversible exchange reactions are ignored. In our example, only J₁ corresponds to a reversible input. If we omit the intersection of ɛ₁ with the flux cone, then the elementary mode EM₅ is dropped (see Fig. 4 B). As a result, only four of the five elementary modes remain as extreme pathways.

As shown in Fig. 4, elementary modes and extremal pathways completely cover the flux cone. However, both sets of network routes still contain interior points (EM₄ and EM₅ for the set of elementary modes and ExPa₄ for the set of extreme pathways; see Fig. 4). The obvious question arises: What is the minimal set of network routes to cover the flux cone? This is the set we have called the minimal generating set (21). As a consequence of the set of inequalities given in Eq. 5, only hyperplanes linked to irreversible reactions form the flux cone. Hyperplanes related to reversible fluxes can only lead to interior points of the cone, since both half-spaces are admitted.

The intersection of half-spaces given by the identity matrix define the semipositive orthant of the subspace span[J_m+1…J_n]. All further half-spaces associated with irreversible reactions shape the flux cone whereas hyperplanes linked to reversible reactions do not. Since only half-spaces related to irreversible reactions are taken into account to calculate the minimal generating set, it is the smallest subset of elementary flux modes that covers the flux cone in the n-dimensional flux-space. In our example, only the half-space defined by ɛ₃ and J₃ ≥ 0 has to be considered. As displayed in Fig. 4 C, the three edges of the flux cone indeed correspond to the three elements of the minimal generating set GM₁ to GM₃.

Phenotype phase-plane analysis

If the metabolic network of an organism is reconstructed, the minimal generating set describes all possible states the system can assume (possibilities of the genotype). However, only a few generating modes are active at the same time. The selection of the generating modes might be the result of optimization processes during evolution as well as adaptation to the environment. It is well known from linear optimization that the state the system singles out is a vertex on the hull of the truncated flux cone (if it is not degenerated). This selection of modi is controlled by the environment (input, output) and the status of the genetic network. Thus, it becomes possible to describe the phenotype of the microorganism if the active subset of the minimal generating set can be determined. A different approach to find phenotypic behavior was put forward by Varma and Palsson (25). They applied the method of shadow prices, an approach derived in economics, to distinguish different modes of action of the system in the space of input fluxes. Here we show that the changes of the shadow prices, and therefore that of the phenotypes, go in parallel with the change of the active subset of generating modes. In silico phenotype predictions has been applied successfully to the metabolic capabilities of E. coli (26) as well as Saccharomyces cerevisiae (27) using linear optimization procedures and phenotype phase-plane analysis.

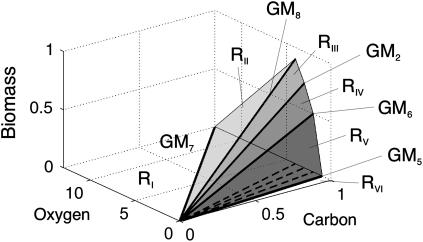
To illustrate the concept, we will use the example model introduced by Edwards et al. (19) and presented in Fig. 5. If we naively calculate elementary modes, extreme pathways, and the minimal generating set as in the example above, the number of elements would be 24, 12, and 6, respectively. However, if we want to perform an experiment the coupling to the environment must be properly defined. The exchange reactions are coupled either to sources or sinks; otherwise, the external metabolites must reach a stationary state. Obviously the direction of irreversible input and output reactions are predefined, while the direction of reversible exchange reactions is fixed by the experimental setup. Although in the latter case the exchange reactions are initially reversible, they become unidirectional by the coupling. The case where the output is coupled neither to a sink nor a source is explored in the next section. In the actual example, the inputs are J₉ and J₁₂ (the carbon and oxygen sources), while the outputs read J₂, J₃, J₄, and J₁₃ for D, E, C, and the biomass production, respectively (see Fig. 5). The minimal generating set is given in Table 1. For the phase-plane analysis, we project the five-dimensional flux cone to the three-dimensional subspace given by the two inputs, J₉ and J₁₂, and the biomass reaction, J₁₃. For fixed carbon source and free oxygen input the projected cone is displayed in Fig. 6. Due to the projection, GM₁, GM₃, and GM₄ become interior points and are not drawn. The six different regions obtained are separated by GM₂ and GM₅–GM₈. In region R_I and R_VI the system cannot process the inputs due to stoichiometric constraints. The network states in the regions R_II–R_V are positive combinations of the two flanking GMs (see Fig. 6). Thus, the minimal-generating set changes from {GM₇, GM₈} in region R_II to {GM₈, GM₂} in R_III to {GM₂, GM₆} in R_IV and finally to {GM₆, GM₅} in R_V. Under these conditions, the ratio of J₁₃/J₉ defines the efficiency of the GMs, which is optimal for GM₈. Note that a different GM becomes optimal if we fix the oxygen input J₉ and vary the carbon input J₁₂ (GM₆). Due to the defined coupling of the system to the environment, all exchange reaction is unidirectional. In addition, if J₂ is defined as output, the direction of J₁ is also given. Thus, in this case the set of elementary modes and extreme pathways collapse to the minimal generating set.

FIGURE 5.

Example model of a metabolic network taken from Edwards et al. (19). The reactions are: J₁: C ↔ 3D + ATP; J₂: D ↔ D_out; J₃: E ↔ E_out; J₄: C ↔ C_out; J₅: A + ATP → B; J₆: B → C + 2ATP + 3NADH; J₇: 5C → 4C + 10NADH; J₈: C + 2NADH → 3E; J₉: A_out → A; J₁₀: ATP →; J₁₁: NADH + O₂ → 2ATP; J₁₂: O_2,out → O₂; and J₁₃: C + 10ATP → biomass.

TABLE 1.

Generating modes GM₁–GM₈ of the model displayed in Fig. 5, represented in the space of fluxes J₁–J₁₃

	GM1	GM2	GM3	GM4	GM5	GM6	GM7	GM8
J1	1	3	0	0	0	0	0	0
J2	3	9	0	0	0	0	0	0
J3	0	0	0	0	3	3	0	0
J4	0	0	1	3	0	0	0	0
J5	1	11	1	10	1	2	1	10
J6	1	11	1	10	1	2	1	10
J7	0	0	0	0	0	0	1	1
J8	0	0	0	0	1	1	0	0
J9	1	11	1	10	1	2	1	10
J10	8	0	7	0	3	0	27	0
J11	3	33	3	30	1	4	13	40
J12	3	33	3	30	1	4	13	40
J13	0	8	0	7	0	1	0	9

FIGURE 6.

Phase-plane analysis of the example model displayed in Fig. 5 using the minimal generating set. Projection of the flux cone to input reactions J₉ and J₁₂ and biomass output J₁₃. In the regions R_I and R_VI, there is no biomass production. The regions R_II, R_III, R_IV, and R_V are associated with the generating modes {GM₇, GM₈}, {GM₈, GM₂}, {GM₂, GM₆}, and {GM₆, GM₅}, respectively.

The phenotypic behavior can be obtained via FBA or by calculating the minimal generating set. In FBA, the optimization procedure selects a single solution out of many equivalent pathways with the same objective value but different internal flux distribution (alternative solutions are obtained via mixed-integer linear programming). In contrast, using the minimal generating set, we keep control over the full solution space.

Nonpointed cone

A cone is pointed if it does not contain a one-dimensional sub-vectorspace. The set of elementary modes is unique for pointed and nonpointed cones, whereas the minimal generating set loses its uniqueness when the cone is nonpointed (24).

Based on irreversibility constraints, a network displays a nonpointed flux cone if it contains a reversible input output pathway or a reversible cycle. As a consequence, one of the basis vectors of the null-space can run in the forward and the backward direction without violating the irreversibility conditions imposed on the system. Whether the system has a pointed cone or not can be easily determined by the null-space matrix given in Eq. 4. If one of the basis vectors is reversible (containing only reversible fluxes), the flux cone is nonpointed. As an example, this condition is met when the number of reversible reactions r is larger than the number of independent metabolites m. In the following, we will consider nonpointed cones caused by reversible input output pathways and reversible cycles separately. In the latter case, further thermodynamic considerations may additionally reduce the space of admissible steady states.

As mentioned above, when the system is coupled to the environment the direction of the exchange reactions must be defined. The selection of inputs and outputs reflects the experimental condition, e.g., the ingredients of the nutrition substrate the microorganism is placed on. If all reversible exchange reactions are endowed with a direction, reversible input output pathways are removed from the system. Of course, under different conditions an input might become an output and vice versa, which just reflects the different couplings to the environment. However, during an experiment, such a change should not occur—since time-dependent phenomena are not covered by the approach and violate the steady-state assumption. There might still be the possibility that an external substance is neither defined as input nor output since it cannot be controlled experimentally. For this case we introduce external metabolites for all undefined substances and treat them as members of the network. In the stationary state all reversible branches of the network, which are connected to dead end (external) metabolites get eliminated. These branches of the network represent strictly detailed balanced subnetworks, which form a null submatrix in the kernel-matrix of the network (28). Thus, reversible input-output pathways are excluded when the system is properly coupled to the environment.

If the system is disjoined from the environment, thermodynamics requires that the network eventually reach an equilibrium state. Thus, irreversible cycles are excluded and only reversible cycles might be present (29,30). The flux cone is now represented as a sub-vectorspace and a pointed subcone. A basis of the sub-vectorspace is given by the set of reversible null-space basis vectors, whereas the subcone is defined by the irreversible elementary modes.

As an example, we consider again the network displayed in Fig. 1. However, the reversible reactions in this case are J₂, J₃, and J₄, whereas J₁, J₅, and J₆ are assumed to be irreversible. The former set forms a reversible cycle, and the latter represents unidirectional input output reactions. Thus, extremal pathways correspond to the extremal currents and, when projected back to the flux-space, J₁ to J₆, they are equivalent to the set of elementary modes. As shown in Fig. 7 A, the five elementary flux modes form a wedgelike body, which is already defined by the minimal generating set presented in Fig. 7 B. Again, the flux cone of the example network can be easily constructed using the kernel matrix K. The identity defines the space given by the semipositive J₅ and J₆ direction as well as the full J₄ axis (no semipositivity restriction on J₄). This cone is further restricted by the irreversibility condition imposed on J₁. The associated hyperplane ɛ₁ (see Fig. 7 B) then provides the wedgelike structure. Here, the thermodynamic constraints are only considered insofar as some of the reactions are unidirectional (large free energy). Any thermodynamic feasible state of the system is a combination of elements of the minimal generating set, but not vice versa. Further thermodynamic consideration for combinations of generating flux modes can additionally reduce the space of admissible steady states. An obvious supplementary constraint is that reversible cycles only operate if they are coupled to a driven input output mode. In this example, this leads to additional inequalities J₆ ≥ J₄ and J₄ ≥ 0. The associated half-spaces given by the normal vectors 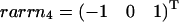and 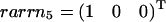are shown in Fig. 7 C. As a consequence, the flux cone becomes pointed. It is important to note that all elementary flux modes connecting input to output are thermodynamically feasible since they do not contain reversible cycles. However, by combining elementary flux modes a reversible cycle might get formed, which must comply with Kirchhoff's second law. This can be directly checked by determining the solution space of chemical potential differences. If the solution space is empty, the mode is thermodynamically unfeasible. A different approach to explore this structure was suggested by Beard et al. (31) using matroid cycles.

FIGURE 7.

Elementary modes (A) and minimal generating set (B) for the example model displayed in Fig. 1 with J₂, J₃, and J₄ as reversible, and J₁, J₅, and J₆ as irreversible reactions. The modes EM₁ and GM₁ are reversible; thus, the wedge is open in the positive and the negative J₄ directions. The reversible cycles do not operate by themselves; they must be coupled to an input output mode. This leads to two additional inequalities (see text). The resulting flux-cone is pointed, revealing a pyramidal shape (C).

DISCUSSION

Constraint-based approaches have become a major tool to analyze metabolic networks of microorganisms. A variety of applications have been suggested, including evolutionary processes, gene knockout viability studies, and optimization in biotechnology (32). However, different concepts of metabolic pathways have been proposed to be used in these approaches. Thus, the aim of this work is twofold: first, to elucidate the differences between the different set of pathways; and second, to identify the smallest set of routes that describes the flux cone and encompasses all optimal states of the network.

The different sets of metabolic pathways are best characterized when we take into account the vector space wherein they are defined. Consider a system with n reactions whereof r < n are reversible. Furthermore, k < r are reversible exchange reactions. Then, elementary modes are calculated in the n-dimensional flux-space whereas extreme pathways and extreme currents are obtained in an n+k-dimensional or, respectively, an n+r-dimensional space. In our previous work we have shown that all sets can be projected down to the n-dimensional flux space. The projection allows for comparing the different sets in the same vector-space. It turned out that neither elementary modes nor extremal pathways are, in general, the smallest set describing the flux cone. Thus, the second goal of this work is to promote the smallest set, which we named the minimal generating set. The elements thereof are called generating modes, and visualization examples are presented in Figs. 4 and 7. The minimal generating set is defined as the minimal set of modes to reach all points of the flux cone. It is obtained by completing the null-space algorithm after having processed all irreversible fluxes. For a pointed cone, all interior points are a positive combination of vertices. Thus, when interrupting the null-space algorithm after the last irreversible flux, further combinations associated with a reversible reaction always lead to an interior point of the cone. For nonpointed cones the very same algorithm holds. However, the flux cone is then described by the irreversible generating modes and the reversible ones. If the inverted reversible modes are ignored, a general description of the flux cone includes negative coefficients for reversible generating modes.

Although many of the elementary modes are interior rays, they might become an edge of the cone if one of the fluxes is inhibited. To illustrate the phenomena, we consider the example network shown in Fig. 1. If the flux J₂ is inhibited, the elementary flux modes EM₁ and EM₄ survive, spanning a two-dimensional cone. In contrast, from the minimal generating set, only GM₁ remains and we are missing the former interior elementary flux mode EM₄. In contrast to the set of elementary modes, the minimal generating set has to be recalculated after gene deletion to obtain the altered cone. However, the advantage of the minimal generating set is its reduced size. Considering the central carbon metabolism of E. coli, the computation of elementary modes requires 1–2 h (∼500,000 EMs), whereas it took <2 s to work out the minimal generating set (∼3000 GMs) (21).

An application of the minimal generating set is the phenotype phase-plane analysis, which predicts the phenotype from the genotypical possibilities and the coupling to the environment. Different modes of operation of the system are distinguished in the plane of selected inputs. Phase-plane analysis is a projection of the flux cone to a restricted space of exchange reactions. Therefore the borders, which separate different regions of the subspace, represent projection of the generating modes. However, as we already have pointed out, some of the vertices of the flux cone might become interior points by the projection. Thus, the number of vertices of the flux cone and the number of separating lines in the phase plane may differ.

In the literature, the term convex basis can be found, which was introduced in an article by Pfeiffer et al. (33) in the context of nonpointed cones, to describe a minimal subset of elementary modes covering the flux cone. Later on it has been claimed that the convex basis of a network corresponds to the set of extreme pathways (6,14,16). This statement needs some clarification. First of all, a convex basis is not a basis in the mathematical sense (34), thus this term is somehow misleading. Second, it is not clear in which vector space such a convex basis is defined. If all reversible reactions are split up in forward and backward reactions, the convex basis corresponds to the extreme currents. In contrast, if only reversible internal reactions are represented by two irreversible fluxes, then the convex basis is the same as the set of extreme pathways. Finally, if we consider the initial flux space, the convex basis is equivalent to the minimal generating set. However, neither the extreme currents nor the extreme pathways are in general equivalent to the minimal generating set if they are projected to the original flux space (see Fig. 4). Due to this confusing use of the term convex basis, we feel that the name minimal generating set is more appropriate to describe the minimal set of generators. Furthermore, Klamt et al. (14) apprehended that when considering only extreme pathways, an optimization procedure would fail to provide the optimal state. Here we show that the edges of a pointed flux cone are fully described by the minimal generating set, which is a subset of extreme pathways. Thus, all optimized states of the network are either generating flux modes or a combination thereof, as a consequence of the truncation procedure (see Fig. 6).