Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2005 Sep 16;89(6):3919–3930. doi: 10.1529/biophysj.105.065144

Reorganization and Conformational Changes in the Reduction of Tetraheme Cytochromes

A Sofia F Oliveira 1, Vitor H Teixeira 1, António M Baptista 1, Cláudio M Soares 1
PMCID: PMC1366959  PMID: 16169983

Abstract

Molecular dynamics simulation (MD) constitutes an alternative to time-consuming experiments for studying conformational changes. We apply MD on a redox system where experimental information exists for the fully oxidized and fully reduced states: tetraheme cytochrome c3. Instead of doing one simulation for each state, we apply 10 4-ns replicas for both states, which provides robust statistics to characterize the redox changes. Besides these long simulations, we perform 120 short ones (50 ps), where an equilibrated oxidized state is perturbed to a reduced state. This allows the application of a nonequilibrium method, the subtraction technique, which makes it possible to characterize the different timescales of conformational changes. Reduction induces conformational changes in the N-terminus and on the loops spanning residues 36–42 and 88–93, which correlate very well with experiments, demonstrating the applicability of this methodology. We also analyze the effect of reduction on hydrogen bonds, solvent accessible surface and bound water, the changes being found to involve the hemes and propionate groups. Redox-induced protonation is also investigated, by protonating the propionates D from hemes I and IV. Although this change in the former does not have major conformational consequences, it induces in the latter conformational changes beyond the ones obtained with reduction.

INTRODUCTION

Conformational changes play an important role in protein function, being the basis of many biological phenomena. However, in many cases, the study of these conformational changes and protein reorganization in general is difficult to be made with full atomic detail, due to technical difficulties. These limitations are more pertinent in the case of redox-driven conformational changes, which normally consist of small, but significant alterations. These phenomena are difficult to study for two reasons: 1), the eventual difficulty to experimentally isolate a particular redox state (in the case of proteins with multiple redox groups); 2), the fact that these changes are sometimes too small to be tackled efficiently by current experimental techniques, which are usually very time consuming (like x-ray crystallography and multidimensional NMR). Molecular dynamics (MD) simulation methods (1) are able to investigate the individual atomic motions as a function of time and in this way allow the study of conformation changes in biomolecules. Moreover, this type of technique can be applied under different conditions of the molecular system (in the particular case, different redox states, opening the way to perturb it and simulate the resulting conformational reorganization. As computer power increases and the force fields are becoming more adequate for simulation of proteins, more biomolecular phenomena and properties can be studied using these methodologies. There are already several studies where different redox states of a protein are analyzed with MD procedures (see for instance Yelle et al. and others (2–8)).

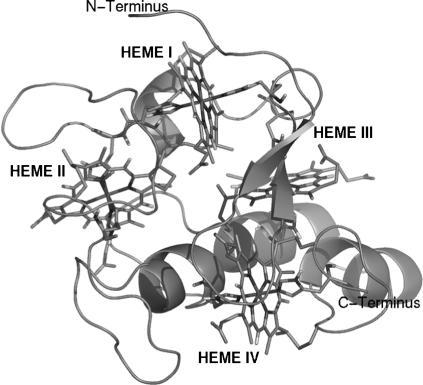
Desulfovibrio vulgaris Hildenborough cytochrome c3 is a periplasmatic 14 kDa tetraheme protein found in sulfate-reducing bacteria (9). This cytochrome plays a central role in the process of hydrogen oxidation (10,11). It is believed to be one of the redox partners of hydrogenases (12), receiving the electrons from hydrogen oxidation. Based on its protonation behavior, it has been proposed that it can also receive the protons resulting from the same reaction (10,11,13). This cytochrome has 107 residues and four heme groups covalently bound to the polypeptide chain through cysteine residues and with histidines as the fifth and sixth axial ligands of the iron (see Fig. 1).

FIGURE 1.

FIGURE 1

Open in a new tab

Cartoon representation of cytochrome c3. The four heme groups, the cysteines covalently bound, and the histidines are represented with sticks. This figure was generated with the program PyMOL (55).

Several experimental studies in this particular protein and members of its family have shown that the four heme groups are part of a network of interacting redox and protonation centers (10,14–22) that lead to the occurrence of several interesting phenomena such as positive cooperativity (higher affinity for electrons than it would be expected for independent groups) and the redox-Bohr effect (thermodynamic coupling between the reduction of redox groups and the protonation of protonatable centers). Besides its extensive experimental characterization, the redox-Bohr effect in cytochromes of this family has been carefully analyzed in our lab using theoretical methodologies (13,23–27), allowing the identification of groups that play an important role in this process, the most important being the heme propionates. Positive cooperativity is a rather interesting phenomenon, which requires in most cases that conformational changes are present during the reduction process. In the cytochrome c3 studied here, these changes have been experimentally characterized, by the fact that a structure in the fully oxidized state was obtained by x-ray diffraction (28,29) and a structure in the fully reduced state was obtained by multidimensional NMR (30). The comparison between these two structures shows the existence of small but significant differences, mostly localized near a loop close to heme I. In a related cytochrome c3 from Desulfovibrio desulfuricans ATCC 27774, structures at the fully oxidized and fully reduced states were obtained by x-ray crystallography (13,27) under the same conditions. Again in this case, the effects of reduction are small, but significant, as shown by thermodynamic calculations of the redox and protonation equilibrium, which evidence that small conformational changes in the side chains of certain groups (Glu-61, His-76, and the propionate D from heme II) have important effects on the heme redox potentials, explaining positive cooperativity effects. This study suggests that the conformational changes involved in these cooperativity effects are not conserved in the family of cytochromes c3, given that these are dissimilar between cytochromes from different species. Another similar structural study (31) in a related cytochrome of a similar type, the nine-heme cytochrome c, also showed the existence of small redox-driven conformational changes (additionally there were conformational changes due to redox-driven protonation), localized near the heme groups (propionates and groups close to them), which had important effects on the heme electron affinity. Therefore, the picture that emerges from all these studies is that this type of redox proteins display conformational changes upon reduction. Despite being small, given their proximity to the heme groups (which are considerably packed), these changes are important in modulating the redox potentials of the hemes.

The experimental studies described above were important to characterize redox-driven conformational changes, but are rather time-consuming and require complex experimental techniques (protein crystallography and multidimensional NMR). As mentioned above, molecular dynamics simulation studies represent an alternative way to investigate this type of phenomena using limited resources and in much less time. Previously, we used these techniques to study reduction effects in this same cytochrome, by simulating the first reduction event in each individual heme (7). However, at the time, the lack of computational power and problems in the force-field parameterization have prevented us to reach definite conclusions about this system, despite the fact that we could observe some interesting conformational changes. More recently, Bret et al. (32) simulate the cytochrome c3 from Desulfovibrio africanus in the fully reduced and fully oxidized states, and compared the simulated structures with the experimental ones to identify the differences between them. These authors found differences in exposed parts of the cytochrome, mostly loops and the N- and C-terminus, with the interior core (including the hemes) being invariant upon reduction, and it was claimed that these differences could be correlated with experimental data. The prime goal of this work is to use molecular dynamics simulations methods to map the conformational transitions between the fully oxidized and fully reduced forms of this protein, using a protocol that is statistically robust. It is our objective also to determine with detail the behavior of several properties of the system (e.g., hydrogen bonds, solvent accessible surface, potential energy, radial distribution functions, and others) and to have an idea of the time needed for these changes to occur.

MATERIALS AND METHODS

General setup of molecular dynamics simulation

Parameterization of the redox centers

The charges for the heme redox centers, in the oxidized and reduced states, were calculated with the program GAUSSIAN98 (33) and RESP fitting (34). The quantum chemical calculations were made with B3LYP, and with the 6-31G(d) basis set for organic atoms and the 6-31G(2df) for the iron. Only single point calculations were performed on the geometry of the heme I, axial histidines, and covalently bound cysteines side chains (up to the C-β, treated as a methyl group) of molecule A of the x-ray structure of this cytochrome (Protein Data Bank entry 2CTH) (28,29). RESP fitting was made using a united atom approach (the GROMOS96 standard), where only polar and aromatic protons are considered. The only exceptions are the aromatic protons of histidines, which are treated using the united atom approach, as any normal histidine in the GROMOS96 43A1 force field. The two histidine side chains were considered to be equal, but the same was not done for the two cysteine side chains, which were fitted separately. The values of the partial charges used for the atoms of the heme redox groups are listed in Table 1, for both oxidized and reduced states.

TABLE 1.

Partial charges for the redox group (including the heme, axial histidines, and cysteines) in the oxidized and the reduced state

Oxidized form Fe (III) Reduced form Fe (II)
HEM
 FE 1.000 1.478
 NA −0.146 −0.299
 NB −0.181 −0.324
 NC −0.176 −0.288
 ND −0.070 −0.207
 CHA 0.072 0.039
 HHA 0.060 0.087
 C1A −0.074 −0.081
 C2A −0.149 −0.113
 C3A 0.112 0.124
 C4A −0.222 −0.245
 CMA 0.085 0.035
 CAA 0.124 0.055
 CBA 0.000 0.000
 CHB −0.040 −0.027
 HHB 0.157 0.179
 C1B −0.145 −0.234
 C2B −0.049 −0.018
 C3B 0.009 0.089
 C4B 0.126 0.085
 CMB 0.097 0.047
 CAB 0.096 0.151
 CBB 0.104 0.047
 CHC −0.064 −0.104
 HHC 0.109 0.108
 C1C −0.036 −0.006
 C2C −0.066 −0.052
 C3C 0.073 0.078
 C4C −0.160 −0.247
 CMC 0.076 0.045
 CAC 0.127 0.165
 CBC 0.083 0.045
 CHD −0.105 −0.074
 HHD 0.184 0.206
 C1D −0.245 −0.310
 C2D 0.113 0.118
 C3D −0.124 −0.058
 C4D −0.024 −0.055
 CMD 0.075 0.020
 CAD 0.112 0.027
 CBD 0.000 0.000
HIS
 CB 0.164 0.106
 CG −0.036 −0.029
 ND1 −0.376 −0.498
 HD1 0.383 0.398
 CD2 0.049 0.056
 CE1 0.258 0.321
 NE2 −0.273 −0.401
Cys B
 SG −0.333 −0.431
 CB 0.211 0.228
Cys C
 SG −0.322 −0.411
 CB 0.188 0.222
Open in a new tab

This calculation considered the heme up to CBA and CBD, the axial histidines, and the covalently bond cysteines (only side chains).

Test calculations on the oxidized state on the conformation of other hemes of the x-ray structure of this cytochrome yielded similar charges.

The remaining heme bonded and nonbonded parameters were adapted from the original hemoglobin heme parameterized in GROMOS96, to reflect the differences for the C-type bis-histidinyl hemes present here.

Protonation state of protonable residues

The protonation state of each individual group in the protein at a given value of pH (in this case pH 7) has to be specified before the MD simulations. We estimated these protonation states using methodologies for studying the equilibrium thermodynamics of proton binding described elsewhere (26,35). These methodologies use a combination of continuum electrostatics, calculated with the package MEAD (version 1.1.8) (36–38), and Metropolis Monte-Carlo simulations, using the program PETIT (35). According to these calculations (results not shown), performed on the x-ray structure of this cytochrome (28,29), all lysines and arginines should be protonated, all glutamic and aspactic acids are deprotonated, the N-terminal should be in the charged state (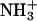Inline graphic) and the His-67 (the only free histidine) should be neutral (deprotonated at Nδ1).

General setup of MD simulations

All MD simulations were performed using the GROMACS 3.1.4 package (39,40) and the 43A1 GROMOS96 force field (41,42). The starting protein structure for all simulations was the fully oxidized conformation (28,29). Crystallographic internal water molecules, with a relative accessibility lower than 50% were included, determined using the program ASC (43,44). The different protein models were solvated in a dodecahedron box, considering a minimum distance between the protein and box walls of 9 Å that contained 5389 water molecules. Chlorine ions were added to neutralize the system, meaning that the fully oxidized system had five Cl− ions (replacing five water molecules, resulting in a final system containing 17,379 atoms), and the fully reduced system had one Cl− ion (replacing one water molecule, resulting in a final system with 17,387 atoms). Simulations were run at the constant pressure of 1 atm and at the constant temperature of 300 K by coupling the system to heat (coupling constant of 0.1 ps; separate coupling of solutes and solvent) and pressure (coupling constant of 0.5 ps) baths (45). The time step for the integration of equations of motion was 0.002 ps. A cutoff of 14 Å was used for van der Waals interactions and a smooth particle mesh Ewald method (46) was used for long-range electrostatic interactions from a 9-Å cutoff. Neighbor lists were updated every 10 steps. The LINCS algorithm (47) was employed to keep all bonds at their equilibrium values and the SETTLE algorithm (48) was used for keeping water molecules rigid.

Two distinct redox states for this cytochrome were simulated, namely the fully oxidized and the fully reduced. These two states started from the fully oxidized x-ray structure of c3. Both systems were energy minimized to remove excessive strain. First, we performed 5000 steps of steepest descent minimization of the water molecules (all protein atoms were restrained), followed by another 5000 steps of the same algorithm with restrains to the heavy atoms. Finally, we carried out 5000 steps of steepest descent restraining only the Cα atoms. The force constant used was 1000 kJ mol−1 nm−1. Next, we performed 50 ps of molecular dynamics simulations with all the heavy atoms restrained (the force constant used was 1000 kJ mol−1 nm−1) at the constant temperature of 300 K and constant pressure of 1 atm (coupling constant of 0.01 ps for temperature and 0.05 ps for pressure) followed by 50 ps with position restrains only at Cα atoms (coupling constant of 0.1 ps for temperature and 0.5 ps for pressure), ending with 50 ps with the protein totally free (same coupling constants as previously). Production simulations started from this equilibrated conformations.

Long molecular dynamics simulations

Ten molecular dynamics simulations were performed for each of the redox states in study (in a total of 20 simulations), each 4-ns long. All of the replicates of each redox model started from the same optimized system but with different sets of random velocities. The conformations along the trajectories were saved each picosecond for further analysis.

Short molecular dynamics simulations

Besides the long simulations described above, we also performed a large number of short simulations of 50 ps each. This allows us to characterize the fast events of the system and compare them with the ones observed in the long simulations, giving information on the timescale of the different phenomena. Contrary to the 4-ns simulations, we could afford to perform a large number of short simulations (120), started from the equilibrated 1 ns of the 10 oxidized state simulations, sampled each 250 ps (12 per trajectory). In each simulation, the oxidized state of all hemes was changed abruptly and the trajectory followed by 50 ps. This procedure allows the application of the subtraction technique introduced by Ciccotti et al. (49), which is very useful when dealing with nonequilibrium simulations. Given that we have a perturbed (reduced) and an unperturbed (oxidized) trajectory for each replica, we can calculate the response of the system to the perturbation (reduction) as a difference of a given property measured in both states at the same simulated time. In this way, providing that enough statistics are collected, we can see the time evolution of the response of a given property. This methodology is based on the fact that there is high correlation between the perturbed/unperturbed trajectories at short times. At long time simulations this correlation is lost, so this methodology cannot be used.

RESULTS AND DISCUSSION

The need for multiple replicas

Molecular dynamics simulations of proteins are computationally demanding, the traditional approach being to run a single long simulation from which thermodynamically meaningful averages can be computed. Of course, the implicit assumption is that the ergodic postulate holds, so that the properties of the ensemble of all protein molecules in solution can be captured by following just one of them. This should in principle be true if we restrict our analysis to properties that get enough sampling within the simulated time. But protein molecules have very complex conformational energy landscapes, with multiple minima where the system may become trapped during the simulation. These minima can be considered at different detail levels, meaning the proteins can be regarded as having a multitude of conformational substates arranged in a roughly hierarchical way (each substate having several subsubstates, and so on) (50). Although usual simulation times may be enough to sample some localized properties, they are still probably too short for most global properties, because many substates can be sufficiently long-lived to trap the protein in a transient or permanent way during the simulation. Given this situation, the use of MD replicas is becoming more frequent in protein studies, the rational being that, even if each simulation visits a few substates, each one will generally visit a different set of substates. Therefore, the combined use of temporal and ensemble (replica) averaging should help to mitigate the sampling problems. This interplay between both types of averaging becomes even more crucial in the case of perturbed systems, where temporal responses must be necessarily averaged over an ensemble of systems (51). This follows from the fact that the response to a perturbation (e.g., reduction of a previously oxidized system) depends strongly on the precise state of the system when the perturbation is applied, this being a consequence of the exponentially diverging character of MD trajectories. This state of affairs is behind approaches such as the subtraction technique (49) also used here, and explains why the simple act of assigning different initial velocities is so efficient in producing effectively different replicates: the assignment of random initial velocities creates a sudden perturbation of the system, which is thrust into a “direction” that strongly depends on the particular velocities that happened to be generated. The foregoing considerations become particularly important when different system conditions (e.g., oxidized versus reduced) want to be compared, because the changes observed between a single unperturbed/perturbed pair of simulations result partly from the alteration of conditions and partly from the diverging character of their trajectories. Therefore, the trajectory-specific features resulting from a perturbation should be eliminated by ensemble (replica) averaging, whether the perturbation is physically meaningful (e.g., reduction) or merely the result of a computational procedure (e.g., assignment of initial velocities).

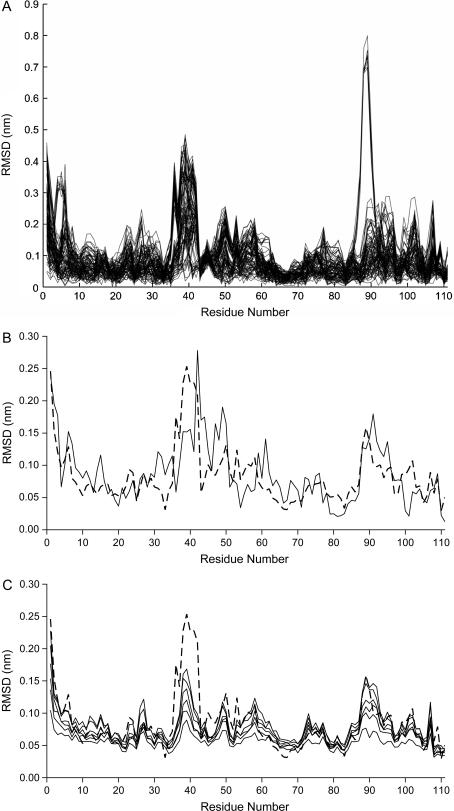
Given the above considerations, we decided to use replicas for the two system conditions being examined, running 10 MD simulations in the fully oxidized state and 10 MD simulations in the fully reduced state, all started from the same structure but with different random initial velocities. This gives 100 possible oxidized/reduced combinations, where each can be regarded as one of the nonreplica studies that could have been performed. The importance of using replicas can be strikingly illustrated by looking at the residue root mean square deviation (RMSD) profiles of all the 100 combinations, shown in Fig. 3 A (computed with the last 2-ns periods; see below). From this analysis, some of the combinations display large deviations in certain protein segments, whereas others display small deviations in these same segments. If one is unfortunate with the combination selected (i.e., with the initial velocities), totally unrealistic conclusions can be obtained. To obtain reasonable conclusions we should average all this information, and in the rest of this work all analyses are made under this perspective.

FIGURE 3.

FIGURE 3

Open in a new tab

(A) All combinations (100) of C-α RMSD between oxidized and reduced states obtained in the last 2 ns of the trajectories (average structures). (B) Average C-α RMSD between oxidized and reduced states (the average of all curves in Fig. 3 A) (dashed line). The same measure obtained for the difference between the experimental oxidized and reduced structures is also presented (solid lines). (C) The same measure as in the dashed line of Fig. 3 B, but with average RMSDs calculated from the short simulations, showing the evolution of the conformational changes. The curve obtained with the long simulations is depicted (dashed line), whereas measurements after 2, 4, 6, 10, 30, and 50 ps are presented (solid lines).

Structural differences between redox states

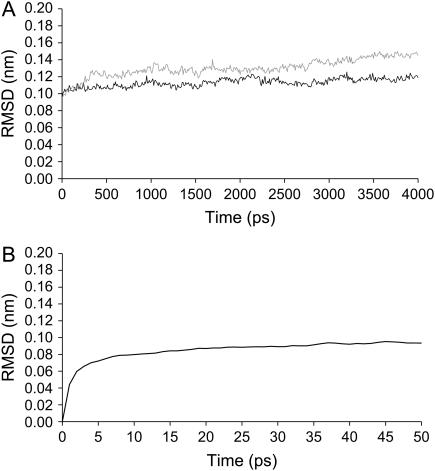
In all replicates we considered the first 2 ns as an equilibration period. Analysis of all individual simulations showed that the RMSD from the oxidized x-ray structure is mostly stabilized after these initial 2 ns. The average RMSD (over all replicas) of both oxidized and reduced states through time is presented in Fig. 2.

FIGURE 2.

FIGURE 2

Open in a new tab

(A) Time evolution of the C-α RMSD from the oxidized x-ray structure in the long 4-ns simulations. RMSD averages for all replicates are used here. The black line corresponds to the simulations in the fully oxidized form and the gray line to the ones in the fully reduced state. (B) Time evolution of the C-α RMSD between the oxidized and reduced states, using the subtraction technique applied to the short simulations.

After the stabilization period, the conformations resulting from the simulations show a global RMSD from the crystal structure of ∼0.12 nm in the fully oxidized and 0.14 nm in the fully reduced state. As expected, the conformation of the molecule in the fully reduced state is more different from the x-ray structure than the one in the fully oxidized state; this reflects the fact that the x-ray structure was obtained for the fully oxidized state.

By analyzing the RMSD between the oxidized and reduced states in the short simulations with the subtraction technique, we can perceive that fast changes occur in the first 6–10 ps after reduction and then the system seems to become pseudostabilized with small increases in its difference from the oxidized state (as judged from the property analyzed here). This may not be true with other analysis (see below).

To characterize more precisely the structural differences between the fully oxidized and fully reduced states, by identifying the residues involved in conformational changes, we decided to compare the set of oxidized and reduced conformations obtained in the simulations, by analyzing residue C-α RMSDs (Fig. 3). As stated before we decided to use the average information obtained from all 100 combinations (resulting from the 10 oxidized and 10 reduced trajectories), i.e., the curves present in Fig. 3 A were averaged to get the dashed curve in Fig. 3 B. This figure also contains the same measure obtained for the comparison of the experimental oxidized and reduced structures (solid line) for comparison.

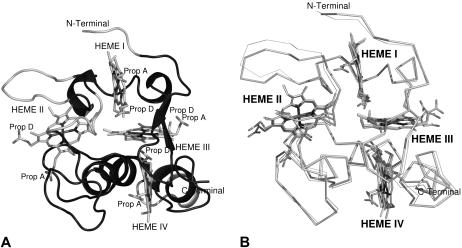
As can be seen in Fig. 3 B, the regions that show higher deviations between oxidized and reduced states in our simulations are almost the same as those presenting higher deviations in the comparison between experimental structures. This is very interesting showing that this simulation methodology is capturing the essentials of the reduction process. These variable regions are shown in Fig. 4.

FIGURE 4.

FIGURE 4

Open in a new tab

(A) Three-dimensional fold of tetraheme cytochrome c3. The variable regions are colored in gray (and correspond to residues 1–3, 36–42, and 88–93) and the invariant ones are colored in black. The variable zones correspond to residues with RMSD higher than 0.07 nm. The protein is rendered as a cartoon and the hemes are represents with sticks. (B) Comparison between the average oxidized (thick lines) and reduced (thin lines) structures, obtained in the last 2 ns of all replicas. Figures generated with the program Pymol (55).

Combining the results showed in Figs. 3 B and 4 we can see that the major difference in the backbone conformation occurs in some of the more exposed regions of this cytochrome: the N-terminus (residues 1–3) and the loops comprising residues 36–42 and 88–93. In Fig. 4 it is possible to observe that the invariant part of this cytochrome involves hemes III and IV (colored in black). Hemes I and II are both surrounded by more mobile regions (colored in gray). The same observation was made when analyzing the oxidized and reduced x-ray structures of cytochrome c3 from D. desulfuricans ATCC 27774 (13,27), with hemes I and II surrounded by more redox-sensitive zones, with the zone of hemes III and IV being more rigid upon redox changes.

The N-terminus (residues 1–3) is a rather flexible region in these proteins and is affected by the reduction process. The displacement of the polypeptide chain is associated with an electrostatics interaction between the charged N-terminus and Glu-41. After reduction, the loop between hemes I and II (residues 36–42) undergoes a significant movement. This movement reduces the solvent accessibility of hemes I and II (see Table 3 below). An additional region of interest is the one involving the segment of residues 45–50. The main chain of this zone approaches the propionate D of heme I. Similar events have been observed in the comparison between experimental oxidized and reduced structures. The loop located between hemes III and IV (residues 88–93) suffers a slight displacement after reduction. In our simulations, this movement seems to be a consequence of the disappearance of a salt bridge between Lys-93 and the propionate D of heme III. After reduction the lysine turns away into the solvent.

TABLE 3.

Average SAS (nm2) for the oxidized and reduced states

Oxidized Reduced
Protein 364.91 (0.21) 364.76 (0.35)
Heme I 9.47 (0.01) 9.44 (0.01)
Heme II 9.27 (0.01) 9.07 (0.03)
Heme III 9.44 (0.01) 9.44 (0.01)
Heme IV 9.66 (0.03) 9.68 (0.01)
Open in a new tab

These averages are computed using the last 2 ns of all replicates. See Table 2 legend for more details. To determine the SAS for the protein we consider all residues, including hemes. The hemes include the propionate groups, the axial histidines, and the covalently bond cysteine residues.

The results of Fig. 3 C shows that many conformational changes due to reduction occur rather quickly, but that the whole motion observed in the 4-ns simulations is not fully reproduced within the 50-ps time frame of the short simulations. From the analysis of the plot we are able to see that conformational changes start to appear soon after reduction (2 ps after the perturbation). The changes become higher over the following picoseconds, and after 50 ps all the major conformational differences are present, except for one involving segment 36–42, which apparently needs more time to change its conformation fully.

Variation in the number of hydrogen bonds between redox states

We determined the average number of hydrogen bonds for all replicates for the last 2 ns of the simulations, for the two redox states in study. The average of these measures is shown in Table 2.

TABLE 2.

Average number of hydrogen bonds for the oxidized and reduced states

Oxidized Reduced
Protein-protein 75.38 (0.40) 75.05 (0.09)
Heme I-protein 1.66 (0.02) 1.39 (0.08)
Heme II-protein 2.36 (0.14) 2.50 (0.06)
Heme III-protein 2.29 (0.15) 0.84 (0.12)
Heme IV-protein 6.11 (0.16) 6.62 (0.05)
Protein-solvent 297.43 (0.56) 303.89 (0.55)
Open in a new tab

These averages are computed using the last 2 ns of all replicates. Errors (in parenthesis) are shown as ±2 SD of the average, corrected for time correlations using standard techniques (analysis of statistical inefficiency and autocorrelation functions) (54). The hemes include the propionate groups, the axial histidines, and the covalently bond cysteine residues. In the determination of the number of hydrogen bonds between the protein and the solvent we consider all the residues, including the heme groups.

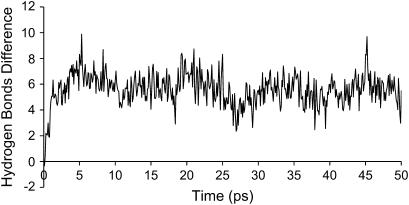
After reduction, there is an increase of hydrogen bonds between the protein and the solvent of ∼2.2% relatively to the oxidized state (after reduction the cytochrome forms, on average, six new H-bonds with the solvent). The formation of new hydrogen bonds with the solvent is a rather fast phenomenon, as shown in Fig. 5, where the results of the subtraction technique, applied to the short simulations, are presented. The timescale for this change is ∼4 ps. In contrast, the hydrogen bonds formed inside the protein are approximately constant upon reduction. It is interesting to look at what happens to the H-bonds formed between the heme groups and the residues of the protein upon reduction. For hemes I, II, and IV there are only small changes, but heme III shows a decrease of approximately one hydrogen bond from the oxidized to the reduced state. Upon a more careful analysis, we could see that the reduction induces the loss of a hydrogen bond between propionate D from heme III and Lys-83 (a salt bridge), caused by the motion of the latter into the solvent.

FIGURE 5.

FIGURE 5

Open in a new tab

Difference between the average number of protein-solvent hydrogen bonds between the oxidized and reduced states, using the subtraction technique on the short simulations.

Variation in the solvent accessible surface

Another property of the system that was studied was the total solvent accessible surface (SAS) that can be found in Table 3.

The SAS for the whole protein shows no significant change upon reduction, but the same cannot be said when we look at individual hemes. Although no significant differences (within the error) occur on hemes III and IV, there is a small but significant decrease in the SAS of heme I, and a considerably larger decrease for heme II. The alteration of the solvent accessible surface can be explained by several factors. This may be due to the movement of the surrounding segments toward hemes I and II, which could decrease the SAS. One of these segments may be the one comprised between residues 36 and 42. Analysis in the short MD simulations using the subtraction technique revealed (results not shown) that this decrease of the accessible area of hemes I and II does not occur during the 50 ps analyzed, suggesting that the conformational change in the 36–42 residue segment, is indeed responsible for this effect, given that, as seen before, this change is not accomplished in the first 50 ps.

Potential energy

Reduction has an influence on the potential energy of the system, due to two factors: the first is the simple fact that the potential energy function changes by the different charge distribution of the reduced state. The second is due to relaxation and conformational changes experimented by the system when it becomes reduced. The nonbonded potential energies (Coulomb and van der Waals) of the protein and between the protein and the solvent are shown on Table 4. Using the subtraction technique, the evolution of the same energies obtained in the short simulations is shown on Fig. 6.

TABLE 4.

Average interaction energies (in kJ mol−1) between groups for both oxidized and reduced states

Oxidized Reduced Difference
Protein intramolecular nonbonded energy 4652 (11) 3884 (14) −768
Protein-solvent interaction energy −9699 (22) −9974 (54) −275
Open in a new tab

These averages are computed using the last 2 ns of all replicates. See Table 2 legend for more details.

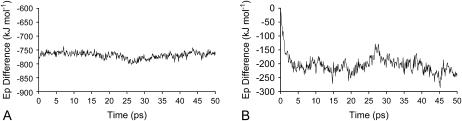
FIGURE 6.

FIGURE 6

Open in a new tab

Difference between the average energies between the oxidized and reduced states, using the subtraction technique on the short simulations. (A) Intraprotein nonbonded energy. (B) Protein-solvent nonbonded interaction energy.

As we can see, both the intramolecular nonbonded energy (Fig. 6 A) as well as the protein-solvent interaction energy (Fig. 6 B) decrease upon reduction. In the case of the intraprotein nonbonded energy this decrease is immediate, and large, given that we are dealing with strong charge-charge interactions at short range (the introduction of four negative charges inside the protein). After this there seems to be a slight pattern of change, but not as large as this initial change. In the end of the 50 ps the energy difference is similar to the one found in the long simulations, suggesting that nothing much happens to this energy after 50 ps. This decrease in energy is not paralleled by the conformational changes, which take more time to occur (as evidenced by Fig. 3 C, especially in the loop containing residues 36–42), meaning that these correspond, either to small energetic changes, or are reflected in the protein-solvent energies (in any case, let us not forget that this discussion is only strictly valid if free energies were being considered, so these remarks result from an approximation). In the case of the protein-solvent energy, there is an immediate change of around −20 kJ mol−1, which is much lower than the one observed in the intraprotein energy. This can be explained by the fact that these are dipole-charge interactions, which are lower in magnitude than charge-charge interactions, particularly at the relatively large distances between the heme cores and the solvent. After the initial instant, the system reorganizes itself and the energy difference is further reduced, being pseudostabilized after ∼6–8 ps, with a localized peak around 27 ps. The value of the energy difference reached in the short simulations is close to the value obtained in the long simulations, but still a bit higher (−230.6 kJ mol−1 as the average in the last 10 ps), suggesting that, although most of the reorganization is reached during this time, there is still a component that takes >50 ps to be reached, probably associated with the motion of loop 36–42.

Radial distribution function and water density

We determined the average radial distribution function (RDF) (52) of water molecules, calculated as a function of the distance to the whole protein and the results can be observed in Fig. 7.

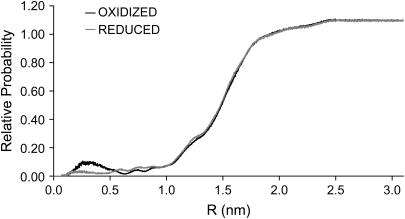
FIGURE 7.

FIGURE 7

Open in a new tab

Average RDF of the water molecules in the oxidized (black) and reduced (gray) states with respect to the whole protein (i.e., to the closest atom of the protein). This RDF is an average for all replicates in both states (oxidized and reduced) for the last 2 ns of simulation.

The first peak of the RDF (0.25–0.40 nm) is much lower in the reduced state, meaning that the density of water close to the protein is significantly reduced in this state. To identify with more detail this difference, we calculated a water probability density function (WPDF) in space using the program PEGASUS (53) and the result can be appreciated in Fig. 8.

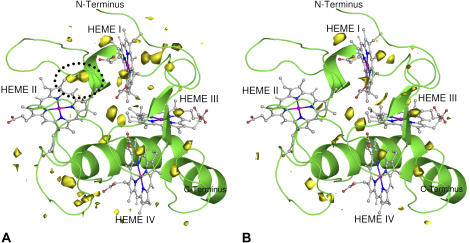
FIGURE 8.

FIGURE 8

Open in a new tab

Graphical representation of the average WPDF in the oxidized (A) and reduced (B) structures, with respect to the oxidized (A) and to the reduced replicates (B). The protein structure is rendered as a cartoon and the WPDF is represented as a yellow contour. A zone where differences are higher is encircled in the figure of the oxidized state (A) by a dotted line. The contour level for the WPDF is a probability of 0.18. The WPDF is an average calculated for all replicates over the last 2 ns of the dynamics. Figure generated with the program PyMOL (55).

A detailed analysis of the figures allows us to locate the major difference for the water density between oxidized and reduced states. In the oxidized state, a density of water is located between hemes I and II (near the loop 36–42 and encircled by a dotted line), which does not exist in the reduced state. Apart from this major difference, one can see some higher density at the left of heme I in the oxidized state and a somewhat lower density near heme III in the same state. In view of these results, the difference seen in the first peak in the RDF can be probably explained by the higher density near heme II in the oxidized state. This loss of water in the reduced state may be due to the loss of a salt bridge between Asp-42 and Arg-44, which upon reduction and due to the motion of a loop between the hemes I and II, opens the way for two internal crystallographic waters to leave this region.

Investigation of redox-linked protonations: protonating propionate D of heme I and propionate D of heme IV

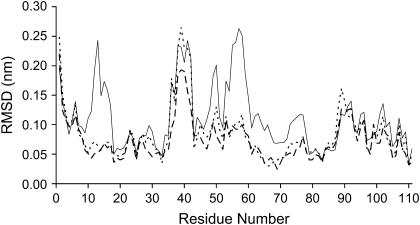
As mentioned in the Introduction, the reduction process on cytochromes c3 often leads to protonation events, mostly located at the propionate groups of the hemes. Therefore, any conformational study trying to investigate the effects of reduction of this cytochrome must also investigate concomitant protonations in key groups. The most obvious group to protonate upon reduction is the propionate D of heme I, with our calculations showing that its pKa changes from 5.03 in the fully oxidized to 6.32 in the fully reduced state (results not shown). Ten new 4-ns reduced state simulations were started from the same structure as previously, but considering this propionate protonated. The resulting RMSD per residue can be seen in Fig. 9 (short-dashed line), where the nonprotonated case is also shown (the long-dashed line). As it can be seen, the curves for the reduced protonated and reduced deprotonated structures are very similar, except for a small difference in the zone of residues 36–42, which shows a smaller displacement (lower RMSD) in the protonated situation. Therefore, it seems that the neutralization of the negative charge of this propionate has very little conformational consequences for the cytochrome.

FIGURE 9.

FIGURE 9

Open in a new tab

Comparison between the average C-α RMSD between oxidized and reduced states (see Fig. 3 B legend). The dashed line with large gaps is the same as in Fig. 3 B, corresponding to the situation where propionates D of hemes I and IV are both deprotonated, whereas the other curves correspond to the situations where propionate D of either heme I (short-dashed line) or heme IV (solid line) is protonated.

Despite the fact that the pKa calculations did not show significant redox-linked protonation for propionate D of heme IV, the oxidized and reduced structures of cytochrome c3 from D. desulfuricans ATCC 27774 at pH 7.6 (27) display considerable protonation of this group, a fact that is evident from the conformation of the propionate itself, which sits inside the structure not making hydrogen bonds with the protein. If, upon reduction, this protonation occurs in the cytochrome studied here, it is unlikely that the pKa calculations are able to predict it, given that it would require substantial conformational changes not present in the oxidized structure used in the calculations. Irrespective of this, it is interesting to study the conformational consequences of this protonation when reduction takes place. Ten new simulations in the reduced state with this protonated propionate were calculated as before and the residue RMSD results can also be appreciated in Fig. 9. In comparison with the situation with no protonation (long-dashed line), this situation (solid line) shows very significant differences, namely higher deviations in the residue zones 10–16 and 48–60. The segment that comprises residues 10–16 is located in the loop between hemes III and IV. The protonation of the propionate D of heme IV makes it neutral, which will lead to the changes in the hydrogen bond pattern (mostly with Thr-14) between this propionate and the main chain of this segment, resulting in its displacement. The 48–60 residue segment corresponds to a loop located between hemes II and IV. Apparently, this is due to several H-bonds formed in the reduced state between Arg-44 (side chain), Ala-49 (main chain), and Thr-48 (side chain), that were not present in the oxidized state. Although an indirect effect, the formation of these new hydrogen bonds in the reduced state may be the reason for the segment displacement. As can be seen, the protonation of the propionate D of heme IV has large consequences and induce substantial reorganization in the overall structure.

CONCLUSIONS

This work had two main goals: the first was to test a methodology to study conformational changes upon reduction/oxidation, based on a considerable large number (10) of MD simulations, both on the oxidized as well as on the reduced states. For that we used the experimentally well-characterized cytochrome c3, for which oxidized and reduced structures exist. One important issue in this methodology is the use of multiple replicas, which allows the simultaneous use of temporal and ensemble averages, yielding much more robust statistics to characterize the relatively small changes that occur upon reduction. The use of one simulation only for each state (as done in other works) is shown to be clearly insufficient to reach sound conclusions. Additionally, the calculation of many small reduction replicas (short simulations) and the application of the subtraction technique (49) with the corresponding unperturbed simulations, allows us to statistically characterize the fast subtle changes and, upon comparison with the long simulations, to infer the timescale of the different phenomena. Our simulation results are clearly in line with what is observed experimentally (28,30), with the most redox-sensitive zones of the protein being identified. In any case, the structural changes observed in this reduction process are mostly small. However, as we have demonstrated for other experimentally characterized cases (13,27,31), small conformational changes may have important consequences in terms of electron affinity of the redox groups, being the basis of important phenomena such as positive cooperativity. Reduction seems to induce a global movement of the backbone in some specific regions: the N-terminus, and the loops spanning 36–42 and 88–93. One interesting remark is that the major conformational change upon reduction occurs between hemes I and II, in contrast with the region surrounding hemes III and IV, which is almost invariant. These conformational changes occur within different timescales, although most are relatively fast, in the timescale of the short simulations (50 ps). Others require more time to occur and are only captured in the 4 ns of the long simulations.

The second goal of our work is the characterization of changes not easily accessible by experiments or even beyond what is possible with modern experimental techniques. For instance, we determined the average number of hydrogen bonds between the cytochrome and the solvent, and found that it increases after reduction, even if the number of intraprotein hydrogen bonds remains approximately constant. The groups responsible for this increase seem to be the propionates, which upon reduction turn to the solvent. These changes are very fast, and they are stabilized in 3–4 ps. The SAS of hemes I and II is reduced slightly upon reduction, whereas no significant changes occur for hemes III and IV. Another interesting aspect of reduction is the decrease of the first peak of water in the RDF, which may be explained by the loss of water in a cavity near heme II, due to the loss of a salt bridge that liberates two internal crystallographic water molecules in the reduced state.

Conformational effects of redox-linked protonation were also investigated, given the interplay that these two effects have in this cytochrome. Protonation of the propionate D of heme I (the most probable to protonate) does not introduce further changes upon reduction, showing that this is a low reorganization event. In contrast, the protonation of propionate D of heme IV (seen in other cytochrome c3 structures) has several conformational consequences beyond simple reduction, additionally affecting the 10–16 and 48–60 segments.

As evidenced by the work contained here, modern molecular dynamics techniques, once properly used and providing sufficient computational power to achieve robust statistics, are able to investigate redox-induced conformational changes in proteins with some confidence, and provide alternative routes to time-consuming experimental techniques for understanding these systems. Additionally, they provide access to properties and redox (and protonation) states beyond what can be achieved with modern experimental techniques.

Acknowledgments

We thank Prof. M. J. Calhorda for help with quantum chemical calculations. We gratefully acknowledge Prof. A. V. Xavier for fruitful discussions through the years concerning this line of investigation.

This work was supported by grants POCTI/BME/32789/99 and POCTI/BME/45810/2002 and by fellowship SFRH/BD/6477/2001 from Fundação para a Ciência e a Tecnologia, Portugal.

References

  • 1.Hansson, T., C. Oostenbrink, and W. F. van Gunsteren. 2002. Molecular dynamics simulations. Curr. Opin. Struct. Biol. 12:190–196. [DOI] [PubMed] [Google Scholar]
  • 2.Yelle, R. B., N. S. Park, and T. Ichiye. 1995. Molecular dynamics simulations of rubredoxin from Clostridium pasteurianum: changes in structure and electrostatic potential during redox reactions. Proteins. 22:154–167. [DOI] [PubMed] [Google Scholar]
  • 3.Shenoy, V. S., and T. Ichiye. 1993. Influence of protein flexibility on the redox potential of rubredoxin: energy minimization studies. Proteins. 17:152–160. [DOI] [PubMed] [Google Scholar]
  • 4.Leenders, R., W. Gunsteren, H. Berendsen, and A. Visser. 1994. Molecular-dynamics simulations of oxidized and reduced Clostridium-Beijerinckii flavodoxin. Biophys. J. 66:634–645. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Ludwig, M. L., K. A. Pattridge, A. L. Metzger, M. M. Dixon, M. Eren, Y. C. Feng, and R. P. Swenson. 1997. Control of oxidation-reduction potentials in flavodoxin from Clostridium beijerinckii: the role of conformation changes. Biochemistry. 36:1259–1280. [DOI] [PubMed] [Google Scholar]
  • 6.Min, T. P., M. K. Eidsness, T. Ichiye, and C. H. Kang. 2001. Regulation mechanism of redox reaction in rubredoxin. J. Microbiol. 39:149–153. [Google Scholar]
  • 7.Soares, C. M., P. J. Martel, J. Mendes, and M. A. Carrondo. 1998. Molecular dynamics simulation of cytochrome c3: studying the reduction processes using free energy calculations. Biophys. J. 74:1708–1721. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Min, T. P., C. E. Ergenekan, M. K. Eidsness, T. Ichiye, and C. H. Kang. 2001. Leucine 41 is a gate for water entry in the reduction of Clostridium pasteurianum rubredoxin. Protein Sci. 10:613–621. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Coutinho, I. B., and A. V. Xavier. 1994. Tetraheme cytochromes. Methods Enzymol. 243:119–140. [DOI] [PubMed] [Google Scholar]
  • 10.Louro, R. O., T. Catarino, C. A. Salgueiro, J. LeGall, and A. V. Xavier. 1996. Redox-Bohr effect in the tetrahaem cytochrome c3 from Desulfovibrio vulgaris: a model for energy transduction mechanisms. J. Biol. Inorg. Chem. 1:34–38. [Google Scholar]
  • 11.Louro, R. O., T. Catarino, J. LeGall, and A. V. Xavier. 1997. Redox-Bohr effect in electron/proton energy transduction: cytochrome c3 coupled to hydrogenase works as a “proton thruster” in Desulfovibrio vulgaris. J. Biol. Inorg. Chem. 2:488–491. [Google Scholar]
  • 12.Yagi, T., M. Honya, and N. Tamiya. 1968. Purification and properties of hydrogenases of different origins. Biochim. Biophys. Acta. 153:699–705. [DOI] [PubMed] [Google Scholar]
  • 13.Louro, R., I. Bento, P. M. Matias, T. Catarino, A. M. Baptista, C. M. Soares, M. A. Carrondo, D. L. Turner, and A. V. Xavier. 2001. Conformational component in the coupled transfer of multiple electrons and protons in a monomeric tetraheme cytochrome. J. Biol. Chem. 276:44044–44051. [DOI] [PubMed] [Google Scholar]
  • 14.Santos, H., J. J. G. Moura, I. Moura, J. LeGall, and A. V. Xavier. 1984. NMR studies of electron transfer mechanisms in a protein with interacting redox centres: Desulfovibrio gigas cytochrome c3. Eur. J. Biochem. 141:283–296. [DOI] [PubMed] [Google Scholar]
  • 15.Coletta, M., T. Catarino, J. LeGall, and A. V. Xavier. 1991. A thermodynamic model for the cooperative functional properties of the tetraheme cytochrome c3 from Desulfovibrio gigas. Eur. J. Biochem. 202:1101–1106. [DOI] [PubMed] [Google Scholar]
  • 16.Salgueiro, C. A., D. L. Turner, H. Santos, J. LeGall, and A. V. Xavier. 1992. Assignment of the redox potentials to the four haems in Desulfovibrio vulgaris cytochrome c3 by 2D-NMR. FEBS Lett. 314:155–158. [DOI] [PubMed] [Google Scholar]
  • 17.Turner, D. L., C. A. Salgueiro, T. Catarino, J. LeGall, and A. V. Xavier. 1994. Homotropic and heterotropic cooperativity in the tetrahaem cytochrome c3 from Desulfovibrio vulgaris. Biochim. Biophys. Acta. 1187:232–235. [DOI] [PubMed] [Google Scholar]
  • 18.Turner, D. L., C. A. Salgueiro, T. Catarino, J. LeGall, and A. V. Xavier. 1996. NMR studies from cooperativity in the tetrahaem cytochrome c3 from Desulfovibrio vulgaris. Eur. J. Biochem. 241:723–731. [DOI] [PubMed] [Google Scholar]
  • 19.Louro, R. O., I. Pacheco, D. L. Turner, J. LeGall, and A. V. Xavier. 1996. Structural and functional characterization of cytochrome c3 from D. desulfuricans ATCC 27774 by 1H-NMR. FEBS Lett. 390:59–62. [DOI] [PubMed] [Google Scholar]
  • 20.Salgueiro, C. A., D. L. Turner, J. L. LeGall, and A. V. Xavier. 1997. Reevaluation of the redox and redox-Bohr cooperativity in tetrahaem Desulfovibrio vulgaris (Miyazaki F) cytochrome c3. J. Biol. Inorg. Chem. 2:343–349. [Google Scholar]
  • 21.Louro, R. O., T. Catarino, J. LeGall, D. L. Turner, and A. V. Xavier. 2001. Cooperativity between electrons and protons in a monomeric cytochrome c3: the importance of mechano-chemical coupling for energy transduction. ChemBioChem. 2:831–837. [DOI] [PubMed] [Google Scholar]
  • 22.Pereira, P. M., I. Pacheco, D. L. Turner, and R. O. Louro. 2002. Structure-function relationship in type II cytochrome c3 from Desulfovibrio africanus: a novel function in a familiar heme core. J. Biol. Inorg. Chem. 7:815–822. [DOI] [PubMed] [Google Scholar]
  • 23.Soares, C. M., P. J. Martel, and M. A. Carrondo. 1997. Theoretical studies on the redox-Bohr effect in cytochrome c3 from Desulfovibrio vulgaris Hildenborough. J. Biol. Inorg. Chem. 2:714–727. [Google Scholar]
  • 24.Martel, P. J., C. M. Soares, A. M. Baptista, M. Fuxreiter, G. Naray-Szabo, R. O. Louro, and M. A. Carrondo. 1999. Comparative redox and pKa calculations on cytochrome c3 from several Desulfovibrio species using continuum electrostatic methods. J. Biol. Inorg. Chem. 4:73–86. [DOI] [PubMed] [Google Scholar]
  • 25.Baptista, A. M., P. J. Martel, and C. M. Soares. 1999. Simulation of electron-proton coupling with a Monte Carlo method: application to cytochrome c3 using continuum electrostatics. Biophys. J. 76:2978–2998. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Teixeira, V. H., C. M. Soares, and A. M. Baptista. 2002. Studies of the reduction and protonation behavior of tetraheme cytochromes using atomic detail. J. Biol. Inorg. Chem. 7:200–216. [DOI] [PubMed] [Google Scholar]
  • 27.Bento, I., P. M. Matias, A. M. Baptista, P. N. da Costa, W. M. A. M. van Dongen, L. M. Saraiva, T. R. Schneider, C. M. Soares, and M. A. Carrondo. 2004. Molecular basis for redox-Bohr and cooperative effects in cytochrome c3 from Desulfovibrio desulfuricans ATCC 27774: crystallographic and modelling studies of oxidised and reduced high resolution structures at pH 7.6. Proteins. 54:135–152. [DOI] [PubMed] [Google Scholar]
  • 28.Matias, P. M., C. Frazao, J. Morais, M. Coll, and M. A. Carrondo. 1993. Structure analysis of cytochrome c3 from Desulfovibrio vulgaris Hildenborough at 1.9 A resolution. J. Mol. Biol. 234:680–699. [DOI] [PubMed] [Google Scholar]
  • 29.Simoes, P., P. M. Matias, J. Morais, K. Wilson, Z. Dauter, and M. A. Carrondo. 1998. Refinement of the three-dimensional structures of cytochrome c3, from Desulfovibrio vulgaris Hildenborough at 1.67 angstrom resolution and from Desulfovibrio desulfuricans ATCC 27774 at 1.6 angstrom resolution. Inorg. Chim. Acta. 273:213–224. [Google Scholar]
  • 30.Messias, A. C., D. H. Kastrau, H. S. Costa, J. LeGall, D. L. Turner, H. Santos, and A. V. Xavier. 1998. Solution structure of Desulfovibrio vulgaris (Hildenborough) ferrocytochrome c3: structural basis for functional cooperativity. J. Mol. Biol. 281:719–739. [DOI] [PubMed] [Google Scholar]
  • 31.Bento, I., V. H. Teixeira, A. M. Baptista, C. M. Soares, P. M. Matias, and M. A. Carrondo. 2003. Redox-Bohr and other cooperativity effects in the nine heme cytochrome c from Desulfovibrio desulfuricans ATCC 27774: crystallographic and modeling studies. J. Biol. Chem. 278:36455–36469. [DOI] [PubMed] [Google Scholar]
  • 32.Bret, C., M. Roth, S. Norager, E. C. Hatchikian, and M. J. Field. 2002. Molecular dynamics study of Desulfovibrio africanus cytochrome c3 in oxidized and reduced forms. Biophys. J. 83:3049–3065. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Frisch, M. J., G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. Montgomery, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, et al. 1998. Gaussian 98. Revision A.7. Gaussian, Inc., Pittsburgh PA.
  • 34.Bayly, C. I., P. Cieplak, W. D. Cornell, and P. A. Kollman. 1993. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges - the RESP model. J. Phys. Chem. 97:10269–10280. [Google Scholar]
  • 35.Baptista, A. M., and C. M. Soares. 2001. Some theoretical and computational aspects of the inclusion of proton isomerism in the protonation equilibrium of proteins. J. Phys. Chem. 105:293–309. [Google Scholar]
  • 36.Bashford, D., and M. Karplus. 1990. pKa's of ionizable groups in proteins: atomic detail from a continuum electrostatic model. Biochemistry. 29:10219–10225. [DOI] [PubMed] [Google Scholar]
  • 37.Bashford, D., and K. Gerwert. 1992. Electrostatic calculations of the pKa values of ionizable groups in bacteriorhodopsin. J. Mol. Biol. 224:473–486. [DOI] [PubMed] [Google Scholar]
  • 38.Bashford, D. 1997. An object-oriented programming suite for electrostatic effects in biological molecules. In Scientific Computing in Object-Oriented Parallel Environments. Y. Ishikawa, R. R. Oldehoeft, J. V. M. Reynders, and M. Tholburn, editors. ISCOPE97, Springer, Berlin, Germany. 233–240.
  • 39.Berendsen, H., D. Spoel, and R. Drunen. 1995. GROMACS 3.1.4. Comput. Phys. Commun. 91:43–56. [Google Scholar]
  • 40.Lindahl, E., B. Hess, and D. van der Spoel. 2001. GROMACS 3.0: a package for molecular simulation and trajectory analysis. J. Mol. Model. [Online]. 7:306–317. [Google Scholar]
  • 41.van Gunsteren, W. F., S. R. Billeter, A. A. Eising, P. H. Hunenberger, P. Kruger, A. E. Mark, W. R. P. Scott, and I. G. Tironi. 1996. Biomolecular Simulation: The GROMOS96 Manual and User Guide. BIOMOS b.v., Groninger, Zurich, Switzerland.
  • 42.Scott, W. R. P., P. H. Hünenberger, I. G. Tironi, A. E. Mark, S. R. Billeter, J. Fennen, A. E. Torda, T. Huber, P. Krüger, and W. F. Gunsteren. 1999. The GROMOS biomolecular simulation program package. J. Phys. Chem. 103:3596–3607. [Google Scholar]
  • 43.Eisenhaber, F., and P. Argos. 1993. Improved strategy in analytic surface calculation for molecular systems: handling of singularities and computational efficiency. J. Comput. Chem. 14:1272–1280. [Google Scholar]
  • 44.Eisenhaber, F., P. Lijnzaad, P. Argos, C. Sander, and M. Scharf. 1995. The double cubic lattice method: efficient approaches to numerical-integration of surface-area and volume and to dot surface contouring of molecular assemblies. J. Comput. Chem. 16:273–284. [Google Scholar]
  • 45.Berendsen, H., J. Postma, W. van Gunsteren, A. Dinola, and J. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
  • 46.Essmann, U., L. Perera, and M. L. Berkowitz. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
  • 47.Hess, B., H. Bekker, H. J. C. Berendsen, and J. G. E. M. Fraaije. 1997. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 18:1463–1472. [Google Scholar]
  • 48.Miyamoto, S., and P. A. Kollman. 1992. SETTLE: an analytical version of the SHAKE and RATTLE algorithms for rigid water models. J. Comput. Chem. 13:952–962. [Google Scholar]
  • 49.Ciccotti, G., G. Jacucci, and I. R. McDonald. 1979. “Thought-experiments” by molecular dynamics. J. Stat. Phys. 21:1–21. [Google Scholar]
  • 50.Frauenfelder, H., S. G. Sligar, and P. G. Wolynes. 1991. The energy landscapes and motions of proteins. Science. 254:1598–1603. [DOI] [PubMed] [Google Scholar]
  • 51.Zwanzig, R. 1965. Time-correlation functions and the transport coefficients in statistical mechanics. Annu. Rev. Phys. Chem. 16:67–102. [Google Scholar]
  • 52.Leach, A. R. 1996. Molecular Modelling: Principles and Applications. Longman, Essex, UK.
  • 53.Victor, B. L., A. M. Baptista, and C. M. Soares. 2004. Theoretical identification of proton channels in the quinol oxidase aa3 from Acidianus ambivalens. Biophys. J. 87:4316–4325. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54.Allen, M. P., and D. J. Tildesley. 1987. Computer simulation of liquids. Clarendon Press, Oxford, UK.
  • 55.Delano, W. 2003. The Pymol Molecular Graphics System. Version 0.90. Delano Scientific LLC, San Carlos, CA.

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES