A Clockwork Hypothesis: Synaptic Release by Rod Photoreceptors Must Be Regular

Stan Schein; Kareem M Ahmad

doi:10.1529/biophysj.105.070623

. 2005 Sep 16;89(6):3931–3949. doi: 10.1529/biophysj.105.070623

A Clockwork Hypothesis: Synaptic Release by Rod Photoreceptors Must Be Regular

Stan Schein ^*,†, Kareem M Ahmad ^*

PMCID: PMC1366960 PMID: 16169984

Abstract

We can see at light intensities much lower than an average of one photon per rod photoreceptor, demonstrating that rods must be able to transmit a signal after absorption of a single photon. However, activation of one rhodopsin molecule (Rh*) hyperpolarizes a mammalian rod by just 1 mV. Based on the properties of the voltage-dependent Ca²⁺ channel and data on [Ca²⁺] in the rod synaptic terminal, the 1 mV hyperpolarization should reduce the rate of release of quanta of neurotransmitter by only ∼20%. If quantal release were Poisson, the distributions of quantal count in the dark and in response to one Rh* would overlap greatly. Depending on the threshold quantal count, the overlap would generate too frequent false positives in the dark, too few true positives in response to one Rh*, or both. Therefore, quantal release must be regular, giving narrower distributions of quantal count that overlap less. We model regular release as an Erlang process, essentially a mechanism that counts many Poisson events before release of a quantum of neurotransmitter. The combination of appropriately narrow distributions of quantal count and a suitable threshold can give few false positives and appropriate (e.g., 35%) efficiency for one Rh*.

INTRODUCTION

Human observers are able to detect a very small number of photons and can see at light intensities much lower than an average of one photon per rod, demonstrating that rods must be able to transmit a signal after absorption of a single photon (1,2,3–5). However, the efficiency of transmission of single-photon events from rod to rod bipolar cell may be limited by noise of several sorts. For example, in primate the continuous voltage noise in a rod, ±0.2 mV, is significant when compared with the 1-mV (peak) hyperpolarization due to activation of a rhodopsin molecule (Rh*) after absorption of one photon (6,7). There is mounting physiological evidence for a thresholding nonlinearity that could block this noise from reaching the rod bipolar cell (8–10), as first posited by Baylor, Nunn, and Schnapf (11) and van Rossum and Smith (12). Such a threshold would also block some of the photon signals, reducing the efficiency of transmission to <100% (8).

The efficiency of transmission is also limited by the small number of quanta of neurotransmitter that convey the signal from a rod to a rod bipolar cell dendrite within the integration time of the rod bipolar cell, particularly if the process for release of quanta were Poisson (13), as it is believed to be in most synapses (14–20). (In this article, “quantum” (Q) refers to one synaptic vesicle's worth of neurotransmitter, whereas “photon” refers to light.) To illustrate the problem, we assume that the integration time is ∼0.1 s. Under the assumptions that the release process is Poisson and that the quantal release rate in the dark (Q_rate,dark) is 100 quanta/sec (100 Q s⁻¹) (12,21), the quantal count (Q_count) within a 0.1-s epoch would be 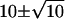Inline graphic Q (mean ± 1 SD) (Fig. 1 A). Under the further assumption that shutdown of quantal release is the signal for absorption of a photon, then one epoch out of 20,000 (or once every 2000 s) would have a Q_count of 0 Q and would represent a rare “false positive” (12,21). A “quantal threshold” higher than 0 Q would have more frequent false positives.

Quantal noise makes discrimination difficult if production of one activated rhodopsin (Rh*) causes a small decrement in quantal release rate. In this figure, continuous rod voltage noise is assumed to be zero. (A) With random (Poisson) quantal release at a rate (Q_rate,dark) of 100 Q s⁻¹, the count of quanta (Q_count) in an epoch of 0.1 s would be Q. Few (0.005%) of the epochs would contain 0 Q. Thus, if response to production of one Rh* were signaled by shutdown of quantal release, that is, the threshold were set to 0 Q, the interval between false positives would be 2000 s. (B) The amount of overlap between a Poisson distribution for a mean Q_count of 10 Q in the dark (*dark bars*) and 8 Q after production of one Rh* (*light bars*) would make it difficult for the rod bipolar cell to distinguish between the two states (dark, Rh*) of the rod. If the threshold were set between the two means (9 Q), efficiency would be high, but false positives would be very frequent. If the threshold were set very low (e.g., 0 Q), false positives would be rare but efficiency would be very low. The dark bars are placed just to the right of the tick mark, the light bars just to the left in Fig. 1, B and C. (C) With regular release, a threshold count (*dashed line*) of 8 Q distinguishes between the 10 Q and 8 Q distributions with high efficiency and few false positives. A threshold of 8 Q is represented by a dashed line between 8 Q and 9 Q to signify a “positive” event for ≤8 Q.

Inline graphic — Quantal noise makes discrimination difficult if production of one activated rhodopsin (Rh*) causes a small decrement in quantal release rate. In this figure, continuous rod voltage noise is assumed to be zero. (A) With random (Poisson) quantal release at a rate (Q_rate,dark) of 100 Q s⁻¹, the count of quanta (Q_count) in an epoch of 0.1 s would be 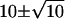Q. Few (0.005%) of the epochs would contain 0 Q. Thus, if response to production of one Rh* were signaled by shutdown of quantal release, that is, the threshold were set to 0 Q, the interval between false positives would be 2000 s. (B) The amount of overlap between a Poisson distribution for a mean Q_count of 10 Q in the dark (*dark bars*) and 8 Q after production of one Rh* (*light bars*) would make it difficult for the rod bipolar cell to distinguish between the two states (dark, Rh*) of the rod. If the threshold were set between the two means (9 Q), efficiency would be high, but false positives would be very frequent. If the threshold were set very low (e.g., 0 Q), false positives would be rare but efficiency would be very low. The dark bars are placed just to the right of the tick mark, the light bars just to the left in Fig. 1, B and C. (C) With regular release, a threshold count (*dashed line*) of 8 Q distinguishes between the 10 Q and 8 Q distributions with high efficiency and few false positives. A threshold of 8 Q is represented by a dashed line between 8 Q and 9 Q to signify a “positive” event for ≤8 Q.

However, we start with the calculation that a 1 mV hyperpolarization would not shut off quantal release (22) but would instead reduce Q_rate by a small amount, for example, from 100 to 80 Q s⁻¹. This calculation follows from the assumption that the ratio of open to closed voltage-gated Ca channels follows a Boltzmann distribution with ∼5 gating charges (23–26). If the release process were Poisson, then the rod bipolar cell dendrite would have the impossible task of efficiently discriminating Inline graphic Q from 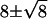Q (Fig. 1 B). We therefore propose that release of quanta of neurotransmitter by the presynaptic terminal of the rod is more regular than Poisson, allowing efficient discrimination by use of a threshold, represented by the dashed line in Fig. 1 C, between two narrow count distributions like 10 ± 0.4 Q and 8 ± 0.3 Q.

METHODS

Activation of a rhodopsin molecule by absorption of one photon produces a relatively long-lasting hyperpolarization of just ∼1 mV. This hyperpolarization causes closure of some of the Ca²⁺ channels in the presynaptic terminal of the rod, a reduction in [Ca²⁺]_int, and a reduction in the rate of release of quanta of neurotransmitter. Therefore, the first section of Methods transforms rod voltage into quantal release rate. Rod voltage is also subject to continuous voltage noise, a consequence of random activation of elements of the transduction cascade. Therefore, in the second section, we calculate the effect of this voltage noise on quantal release rate. In that section we also introduce a “counting window”, biologically related to the integration time of the quantal counter, namely, the rod bipolar cell. The resulting quantal counts are noisy, varying from epoch to epoch as a consequence of randomness in the release process. Therefore, the final section of Methods presents a method for combining the effect of continuous rod voltage noise and quantal noise to generate distributions of quantal counts.

Production of an Rh* is likely to reduce quantal release rate by ∼20%

For voltage-dependent channels, the ratio of the number of channels in the open state (N_o) to the number in the closed state (N_c) (Eq. 1) follows a Boltzmann distribution (modified from Eq. 2.21 of Hille (27)):

(1)

where V is membrane potential, V_o is the membrane potential at which half the channels are open and half are closed, n is the number of gating charges, q is the charge on the electron, k is Boltzmann's constant, T is absolute temperature, and kT/q = 26.7 mV at 37°C. For voltage-dependent channels, including the L-type Ca channels in the rod synaptic terminal (24,25,28–34), the number n of gating charges is typically 4–5 (23–26). Since kT/q ≈ 25 mV, the ratio N_o/N_c changes e-fold for corresponding changes of voltage of 5 mV to 6 mV.

It follows that the fraction of all channels that are in the open state is

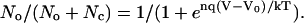(2)

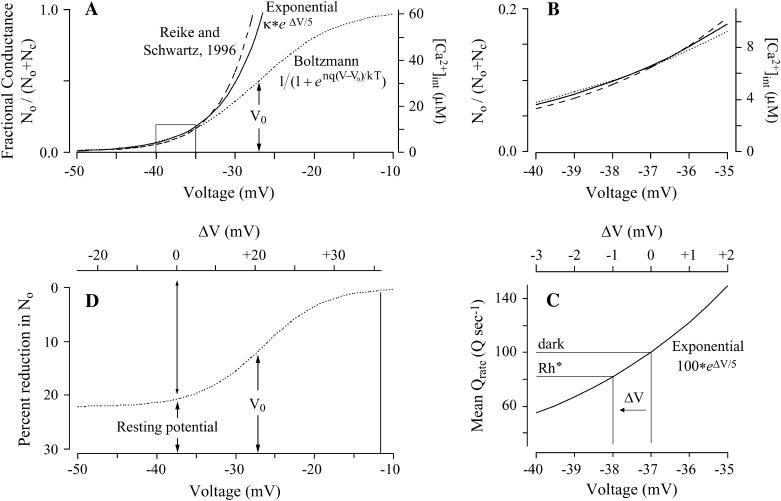
From this equation, with an e-fold change in this fraction for 5 mV (n = 5.35 gating charges) and V_o = −27 mV (within the range reported in Corey et al. (24)), the fraction of channels that are open N_o/(N_o + N_c) as a function of voltage is small at the −37-mV resting potential of the rod (23) and follows the S-shaped Boltzmann curve (dotted line) in Fig. 2 A.

A 1-mV hyperpolarization should modestly reduce quantal release rate. (A) Based on a Boltzmann distribution with five gating charges (Eq. 2), the dotted S-shaped curve shows the fraction of L-type Ca channels that are open as a function of voltage. The solid curve shows a single exponential (Eq. 3) that approximates the Boltzmann distribution over the range −40 to −35 mV. The dashed curve shows [Ca²⁺]_int in the synaptic terminal of a rod from an equation provided by Rieke and Schwartz (25) to fit the data in their Fig. 4. For their equation, 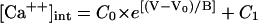: [Ca²⁺]_int is in micromoles, and the parameters C₀ = 62 μM, C₁ = 0.5 μM, and B = 4 mV are supplied by the authors. V₀ = −27 mV is omitted by the authors and estimated by us. (B) An enlarged version of the boxed region in Fig. 2 A. (C) Mean quantal release rate (Q_rate), a function of membrane potential, is computed with a single exponential (Eq. 4), a scaled version of the solid curve in A. (D) Based on the Boltzmann distribution, the greatest percent reduction in the number of open calcium channels N_o and thus Q_rate for a 1-mV hyperpolarization is achieved if the membrane potential in the dark is at the foot of the dotted curve in A.

A single exponential (Eq. 3), shown by the solid curve in Fig. 2 A, well approximates the Boltzmann curve in the region from −40 to −35 mV. The box in that region of Fig. 2 A is expanded in Fig. 2 B.

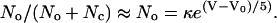(3)

In this equation, V₀ is the same as above, −27 mV, and the scaling factor κ is 0.12.

The effect of a hyperpolarization is to reduce the number of open channels, which reduces inward Ca²⁺ current and [Ca²⁺]_int. The dashed curve in Fig. 2, A and B, is a graph of the equation for [Ca²⁺]_int as a function of membrane potential from Fig. 4 of Rieke and Schwartz (25). Within the range −30 mV to −40 mV, these investigators found that [Ca²⁺]_int was reduced by ∼20% for a 1-mV hyperpolarization. [Ca²⁺]_int closely follows the number of open channels given by the Boltzmann distribution and the exponential approximation in Fig. 2, A and B.

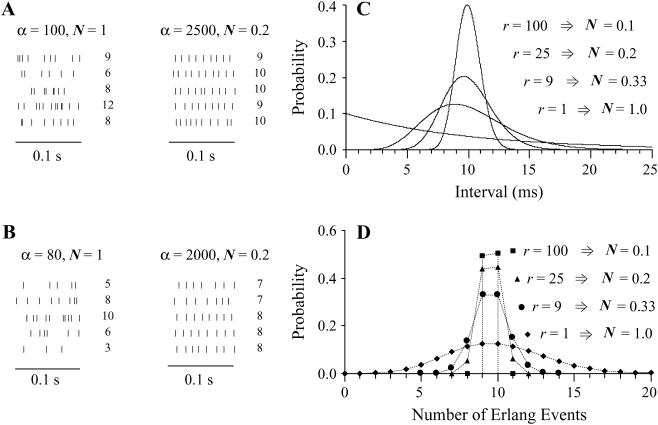
Distributions of intervals and counts within an epoch narrow as the order of an Erlang ordinary renewal process rises. (A) After an Erlang Event at time 0− (not shown), Erlang Events arrive at random times that depend on the rate (100 Erlang Events s⁻¹) and order r of the renewal process. The order r equals 1 (Poisson) for the five 0.1 s sequences on the left, corresponding to a narrowing N of 1. The order r equals 25 for the five sequences on the right, corresponding to a narrowing N of 0.2. The count in 0.1 s is listed to the right of each sequence. To maintain the same 10 ms mean interval between Erlang Events, the rate of underlying Poisson events α is the product of the rate of Erlang Events (e.g., 100 Erlang Events s⁻¹) and order r (e.g., 25 underlying Poisson events/Erlang Event), giving 2500 Poisson events s⁻¹. (B) The sequences are as described for A, except that the rate of Erlang Events is 80 Erlang Events s⁻¹. (C) Continuous distributions of intervals for an Erlang renewal process with a rate of 100 Erlang Events s⁻¹ and with several order r from 1 to 100. The intervals for a Poisson process (r = 1) are exponentially distributed. The narrowing N, the reciprocal of the square root of r, is also equal to the coefficient of variation of the distribution. (This figure follows Fig. 10.3 of Wickens (106).) (D) Discrete distribution of numbers of Erlang Events within a 0.1-s window for an ordinary Erlang renewal process with a rate of 100 Erlang Events s⁻¹ and with several orders r from 1 to 100.

The rate of quantal release (Q_rate) closely follows [Ca²⁺]_int in rod terminals (25,26,28–31), approximately linearly (35,36). Therefore, at the foot of the curve, we can use a single exponential to compute the mean Q_rate as follows:

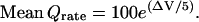(4)

We set the coefficient in this equation to 100 to give a Q_rate of 100 Q s⁻¹ in the dark when the departure from resting potential (ΔV) equals 0, that is, at the resting potential of −37 mV, and we make Q_rate change e-fold for a ΔV of 5 mV (Fig. 2 C). (A rate of 100 Q s⁻¹ was suggested by calculations in Van Rossum and Smith (12) and Rao-Mirotznik (21).) With two active zones or “ribbon synaptic units” in each rod (37), this rate for each active zone, 50 Q s⁻¹, is similar to that measured for salamander rod terminals, 400 Q s⁻¹ (25) from an average of seven ribbons (38). Nonetheless, we explore Q_rates as low as 50 Q s⁻¹ and as high as 400 Q s⁻¹ below.) At the resting potential, a hyperpolarization of 1 mV (ΔV = −1 mV) would reduce Q_rate from 100 to 81.87 Q s⁻¹, a decrement of ∼20%.

The reduction by 20% is as large as it is because the resting potential (−37 mV) is located at the foot of the Boltzmann curve, 10 mV less than V₀ (−27 mV) in Fig. 2 A. Fig. 2 D shows, as a function of resting potential, the percent by which the number of open calcium channels would be reduced by a 1-mV hyperpolarization. If resting potential were equal to V₀, the baseline fraction of open channels would be relatively high, 50% (Fig. 2 A), and the percent reduction in the number of open channels due to the 1-mV hyperpolarization would only be half as large, ∼10% (Fig. 2 D).

Rod voltage noise causes variation in mean Q_rate

The membrane potential in the dark exhibits continuous Gaussian voltage noise of ∼±0.2 mV (7), due in part to spontaneous activation of the cGMP phosphodiesterase in the rod (39). The dark curve in Fig. 3 A shows the resulting probability density function (PDF) for the departure of rod voltage from its resting potential in the dark (ΔV). The abscissa is in millivolts. The ordinate is in units of probability per millivolt, and the area under each curve is unity.

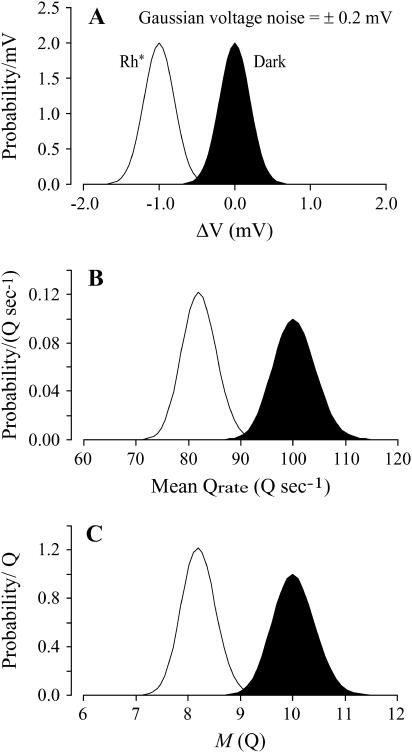
Probability distribution of rod voltage (ΔV) can be transformed into probability distributions of Q_rate and Q_count. (A) Probability density functions (PDFs) of rod voltage ΔV in the dark and after production of one Rh* reflect Gaussian noise (SD = 0.2 mV) and are centered at ΔV = 0.0 mV and −1.0 mV, respectively. (B) PDFs of mean Q_rate are calculated from mean Q_rate as a function of rod voltage ΔV (Fig. 2 B; Eq. 4) and the PDFs of rod voltage ΔV in A. (C) PDFs of M are calculated as the product of mean Q_rate from B and the duration of the counting window, assumed here to be 0.1 s.

The hyperpolarization in response to activation of one rhodopsin molecule (Rh*) in the rod outer segment lasts for ∼0.5 s and reaches a reproducible “peak” of −1 mV (6,7). The same continuous voltage noise is superimposed on this hyperpolarization (Fig. 3 A, light curve). Equation 4, providing Q_rate as a function of ΔV (illustrated in Fig. 2 B), enables us to transform the PDFs of ΔV that were shown in Fig. 3 A into the PDFs of Q_rate (Fig. 3 B). Since membrane potential in the dark is normally distributed, mean Q_rate is also distributed, ranging from 90 to 110 Q s⁻¹ in the dark and from 72 to 92 Q s⁻¹ after production of one Rh*. The abscissa is in Q s⁻¹. The ordinate is in units of probability per Q s⁻¹, and the area under each curve is unity.

Physiological and psychophysical studies suggest that the rod pathway accumulates photons over a finite period, on the order of 0.1 s. (For psychophysical evidence, see Hood and Finkelstein (1), Graham and Margaria (40), Barlow (41), Sperling and Jolliffe (42), and Baumgardt and Hillmann (43). For electroretinographic evidence, see Fig. 6 of Robson and Frishman (44). For intracellular electrophysiological evidence, see Fig. 4 A of Field and Rieke (8).) Therefore, for most of this article, we adopt the value 0.1 s for the “counting window” (or “epoch”). (We show later that its precise duration is not critical for our findings.) Because the bulk of the power in voltage noise is contained in frequencies under 3 Hz and because the peak response to a photon is not brief (6,7,11), we can treat ΔV in the rod as if it were a single value over this 0.1-s counting window. In addition, the approximately linear dependence of quantal release rate on [Ca²⁺]_int (35,36), the presence of L-type Ca²⁺-channels in the terminal, and the bandpass (1.5–4 Hz) nature of quantal release by the rod terminal (35) permit us to discount transients, and we can treat Q_rate as a single value over the 0.1-s counting window.

Quantal noise overwhelms physiological rod voltage noise in determining the probability distribution of Q_count. (A) For Poisson quantal release (Erlang order r = 1, N = 1), the distribution of Q_count with physiological (±0.2 mV) rod voltage noise (*shaded bars*), computed using the convolution described in Fig. 5 A, is compared with the distribution without noise (*open bars*). The shaded bars are placed just to the left of the tick marks, the open bars just to the right in all parts of the figure. The SD of the distribution with 0 mV voltage noise = 3.16 Q, and with ±0.2 mV voltage noise = 3.19 Q. (B) For regular quantal release (r = 25, N = 0.2), the distribution of Q_count with physiological (±0.2 mV) rod voltage noise (*shaded bars*), computed using the convolution described in Fig. 5 B, may be compared with the distribution without noise. The SD of the distribution with 0 mV voltage noise = 0.71 Q, with ±0.2 mV voltage noise = 0.82 Q. (C) For regular quantal release (r = 25, N = 0.2), the distribution of Q_count with nonphysiological (±0.4 mV) rod voltage noise (*shaded bars*) may be compared with the distribution without noise. For the distribution with 0 mV voltage noise SD = 0.71 Q, and with ±0.2 mV voltage noise, SD = 1.10 Q.

We define a parameter M in the subsection titled Grouped Poisson number distribution: Erlang process in Appendix A. But for a small correction, M can be thought of as the mean count of Erlang Events, or quanta in this case. (In fact, the value of M is slightly greater than the mean. (See Appendix Eqs. A8 and A9.))

We can calculate M for any ΔV as the product of 0.1 s and the Q_rate associated with that ΔV, the latter shown in Fig. 2 B. For example, in that figure, at ΔV = −0.3 mV, the mean Q_rate is 94.2 Q s⁻¹, so M is 9.42 Q.

We can also calculate the PDF of M. We do so by taking the product of 0.1 s and the PDF of the mean Q_rate (Fig. 3 B), giving ranges of M of 9–11 Q in the dark and 7–9 Q after production of one Rh* (Fig. 3 C). The abscissa is in quanta. The ordinate is in units of probability per quantum, and the area under each curve is unity.

The Q_count distribution depends on quantal noise as well as continuous rod voltage noise

The preceding section takes continuous rod voltage noise into account. Here, we take quantal noise, the variation in the count of quanta between epochs due to stochastic release, into account as well. For a Poisson process, events occur at some mean rate (α events s⁻¹) but at random times (Fig. 4, A and B, left panels), as described in detail in Appendix A. The mean time between events is equal to 1/α s, and the SD of the interval distribution is equal to this mean, thus also 1/α s. If α = 100 events s⁻¹, for example, the mean interval and the SD of the interval distribution both equal 0.01 s (or 10 ms). For Poisson release, each event represents release of a quantum of neurotransmitter.

We use an ordinary Erlang renewal process to model regular release. In that case, each Erlang Event represents release of a quantum of neurotransmitter. Erlang Events of order r occur at some mean rate (μ Erlang Events s⁻¹), with each Erlang Event declared at the r^th Poisson event. (A first-order Erlang process is a Poisson process.) Thus, the mean interval between Erlang Events is r times as long (r/α) as the mean interval (1/α) between Poisson events, but the SD of the interval distribution increases by a smaller factor, 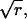Inline graphic to become 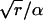(Fig. 4 C).

We use N to denote the narrowing of the interval distribution, that is, the reduction of its SD relative to the mean, so 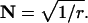Inline graphic For example, if μ = 100 25th-order Erlang Events s⁻¹, based on α = 2500 underlying Poisson events s⁻¹, the mean time between Erlang Events is 0.01 s (or 10 ms), and the SD of the interval distribution for these 25th-order Erlang Events is that of a first-order process at 100 Poisson events s⁻¹ (0.01 s) multiplied by the factor 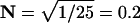Inline graphic to become 0.002 s (Fig. 4, A and B, right panels).

For a Poisson process, the mean count (λ) within some window T equals αT Poisson events, and the SD of the Poisson count distribution equals 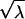Inline graphic Poisson events. Thus, for a counting window of 0.1 s and a rate of 100 Poisson events s⁻¹, the mean count is 10 Poisson events, and the SD of the count distribution is 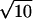Poisson events.

For an ordinary Erlang process, the parameter M is equal to 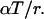Inline graphic The mean count of Erlang Events is slightly less than M (Eq. A9); for a high-order Erlang process, the shortfall approaches 0.5 Erlang Events. The SD of this “Grouped Poisson” count distribution is approximately narrowed (that is, reduced) by the factor 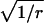(Fig. 4 D). For example, for a counting window of 0.1 s, a rate of 2500 underlying Poisson events s⁻¹, and an Erlang Event declared every 25th Poisson event, M = 10 Erlang Events, and the mean count (9.52 Erlang Events) is close to 0.5 less than 10. In this case the SD of the count distribution is reduced approximately by the factor N = 0.2 to become 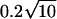Inline graphic Erlang Events.

The order r can be noninteger, in which case the process is called a gamma process. The count distribution may still be described as a Grouped Poisson distribution (Appendix A).

With these definitions in hand, the following description focuses initially on the situation in the dark. Because release is stochastic, the actual count of quanta (Q_count) for a single M varies from epoch to epoch. Examples of Poisson event streams and counts within an epoch are shown in the left panel of Fig. 4 A for M = 10 Q and r = 1. The Q_count ranges from 6 to 12 Q. Examples of Erlang Event streams are shown in the right panel of Fig. 4 A for M = 10 Q and more regular release (r = 25; N = 0.2). The Q_count ranges from 9 to 10 Q. In addition, examples of increasingly narrow count distributions for M = 10 Q and orders r = 1, 9, 25, and 100 are shown in Fig. 4 D. These distributions are discrete because numbers of quanta are integers.

Because M depends on ΔV, which varies due to continuous rod voltage noise, M itself varies from epoch to epoch (Fig. 3 C). Therefore, to compute the discrete probability distribution of quantal count (“Q_count distribution”), we convolve the PDF of ΔV with the discrete probability distribution of quantal counts for the M associated with each ΔV (Fig. 5, A and B).

Distribution of Q_count in the dark may be computed by convolving voltage noise with quantal noise. The points on the left wall (yz plane) represent the probability distribution (probability/0.05 mV) of membrane potential ΔV in the dark (y axis). The points provide a discretized version of Fig. 3 A (*dark curve*), scaled by 20 to sum to unity. Each ΔV is associated with a value of M, the product of mean Q_rate as a function of ΔV (Fig. 2 B) and 0.1 s. For each ΔV, the associated M determines a grouped Poisson distribution of Q_count, rows of boxes parallel to the x axis, and each of these Q_count distributions is weighted by the probability of its associated ΔV. Finally, all of the weighted probabilities for a given Q_count, rows of boxes parallel to the y axis are summed to produce the Q_count distribution incorporating voltage noise and quantal noise at the back panel. (A) The distribution of Q_count for rod voltage noise = ±0.2 mV and Poisson release process (Erlang order r = 1). (B) The distribution of Q_count for rod voltage noise = ±0.2 mV and regular release process (r = 25).

To ease the subsequent computational load, we sample the PDF of ΔV, the dark curve in Fig. 3 A, every 0.05 mV, so the units on the z axis for the left walls of Fig. 5, A and B, are probability/0.05 mV, and the points on that wall are a discretized and scaled version of the dark curve in Fig. 3 A. (The scaling is by 20 times to give a sum of probabilities over ΔV equal to unity.) For example, the probability/0.05 mV that ΔV = −0.3 mV is 0.0324, that is, the product of 0.648 mV⁻¹ (Fig. 3 A) and 0.05 mV, as illustrated by the short black vertical bar on the left wall of Fig. 5 A.

We can associate the probability of each ΔV on the left wall of Fig. 5 A with its corresponding M, computed as the product of Q_rate as a function of ΔV (Eq. 4 and Fig. 2 B) and the counting window 0.1 s. At ΔV = 0.3 mV, for example, the mean Q_rate is 94.2 Q s⁻¹ (Fig. 2 B). Multiplying by 0.1 s gives an M of 9.42 Q.

For each ΔV, based on the associated M, we compute the discrete distribution of quantal count—a Grouped Poisson distribution—from Appendix Eq. A9 (though in practice we use Appendix Eqs. A10 or A11). For example, for ΔV = −0.3 mV in Fig. 5 A, we compute the discrete distribution of quantal counts for M = 9.42 Q and order r = 1. We then weight that distribution by the probability of occurrence of that ΔV (e.g., 0.0324). To illustrate this step, the strip of solid boxes running parallel to the abscissa in Fig. 5 A at ΔV = −0.3 mV represents the product of 0.0324 and the Grouped Poisson distribution, with one box for each integer number of quanta (e.g., 8 Q). (The z axis on the right applies to these weighted probabilities.) We carry out these steps for ΔV from −2 mV to +2 mV at intervals of 0.05 mV.

Finally, we sum the weighted probabilities for each number of quanta (e.g., 8 Q) for every ΔV from −2 mV to +2 mV, as illustrated by the strip of boxes with black-outlined tops that runs parallel to the ΔV axis for 8 Q in Fig. 5 A. The tall distribution at the back of Fig. 5 A gives these sums and represents the Q_count distribution in the dark, taking into account both rod voltage noise and a Poisson release process (Erlang order r = 1).

Fig. 5 B illustrates the results for a more regular release process with order r = 25. The weighting factors in the left wall, the result of continuous rod voltage noise, are the same as those in Fig. 5 A, but the Q_count distribution for any particular ΔV is much narrower, and the resulting Q_count distribution at the back is much narrower.

We can compute the Q_count distribution after production of one Rh* by the same methods, except that we carry out the steps for ΔV in the range from −3 mV to +1 mV, centered at −1 mV, and we weight those discrete Grouped Poisson distributions by the probability of occurrence of each ΔV. Similar to what is described above, the latter is a discretized version of the light curve in Fig. 3 A, sampled every 0.05 mV.

RESULTS

Rod voltage noise may contribute much less than quantal noise to broadening Q_count distributions. The shaded bars in the histogram in Fig. 6 A show the Q_count distribution in the dark, taken from the back of Fig. 5 A, which was computed for physiological rod voltage noise of ±0.2 mV and Poisson release (Erlang order r = 1, hence N = 1). The open bars in the histogram show the distribution computed for rod voltage noise of zero. The difference between the two histograms is barely perceptible. Indeed, physiological voltage noise increases the SD of the Q_count distribution from 3.16 Q to 3.19 Q, a factor of just 1.01.

The shaded bars in the histogram in Fig. 6 B show the Q_count distribution in the dark, taken from the back of Fig. 5 B, which was computed for physiological rod voltage noise of ±0.2 mV and more regular release (r = 25, hence N = 0.2). The increase in SD over quantal noise alone (open bars), from 0.71 to 0.82 Q, is by a factor of only 1.16. For the same degree of regularity, a larger, nonphysiological amount of rod voltage noise, like ±0.4 mV (Fig. 6 C), is required to significantly increase the SD, from 0.71 to 1.10 Q, a factor of 1.55.

In the above descriptions, continuous rod voltage noise is expressed in units of millivolts, whereas quantal noise, the SD of a Q_count distribution, is expressed in units of quanta. In Appendix B, we show how to express continuous rod voltage noise in quanta and, conversely, how to express quantal noise in millivolts (Fig. 7 A). The conversion factor is close to 2 Q mV⁻¹. This analysis shows that the quantal noise associated with Poisson release and a mean Q_count of 10 Q is ±1.54 mV, obviously swamping the physiological ±0.2 mV of continuous rod voltage noise (Appendix B). Total noise, the square root of the sum of the squares of quantal noise and continuous rod voltage noise (Fig. 7 B, Eq. B1), is slightly increased by ±0.2 mV of continuous rod voltage noise, from ±1.54 to ±1.55 mV.

Continuous rod voltage noise, quantal noise, and total noise may be expressed in units of voltage or in units of quanta. (A) Rod voltage noise in millivolts (*RVN*_V) is equal to the SD of the PDF of membrane potential. Conversion to rod voltage noise in units of quanta (*RVN*_Q) relies on the independence of rod voltage noise and quantal noise (Eq. B1 in Appendix B). Each measurement of *RVN*_Q is obtained from the SD of a Q_count distribution with a mean of 10 Q. As expected, the conversion factor (Q/mV) is essentially independent of the degree of quantal noise (N = 1 (♦) versus N = 0.2 (□). (B) Total noise, a vector with quantal noise and voltage noise components, can be measured in units of millivolts (*left* and *top scales*) or in units of quanta (*right* and *bottom scales*). The dashed horizontal line marks physiological voltage noise of ±0.2 mV. The dotted vertical lines mark the level of quantal noise that accompanies Poisson release (N = 1) and regular release (N = 0.2).

Appendix B also shows that quantal noise is approximately proportional to the narrowing of the Q_count distribution, hence ±0.34 mV (≈ 0.2 × 1.54) for N = 0.2 and a mean Q_count of 10 Q. Even in this case total noise is increased little, to ±0.39 mV, by the physiological level of continuous rod voltage noise.

Based on the Q_count distribution in the dark, the threshold number of quanta sets the rate of false positives

The absorption of a photon by a rod produces an Rh*, which hyperpolarizes that rod, reduces its Q_rate, and reduces the number of quanta counted by the rod bipolar dendrite. A reduction to or below some “threshold” integer number of quanta (Q_T) after absorption of a photon constitutes a signal that an Rh* was produced, a “true positive”. (In our treatment, a spontaneous isomerization of rhodopsin, producing an Rh*, is also a true positive.) Conversely, a reduction to or below Q_T in the absence of an Rh* constitutes a “false positive”. False positives occur because of random fluctuations in Q_count due to continuous rod voltage noise and quantal noise.

The rate of spontaneous production of an Rh* has been measured in rods (11,45) and inferred from electrophysiological recordings of ganglion cells (46,47). Spontaneous production of an Rh* is believed to occur once every ∼160 s in each rod (11) and may account for the psychophysical “dark light”, a background “light” that sets the visual threshold in complete darkness (48,49). Therefore, in order that random fluctuations in Q_count due to continuous rod voltage noise and quantal noise not add appreciably to the rate of false positives due to spontaneous production of an Rh*, we set conditions (threshold Q_T, Erlang order r, and Q_rate,dark) to give a 1600 s interval between random fluctuations in Q_count that fall to or below Q_T, that is, 10 times longer than 160 s. We note that once in 1600 s is also equal to once in every 16,000 epochs of 0.1 s.

This choice (an interval of 1600 s between these additional false positives) is admittedly arbitrary, but we show below that the qualitative findings change little if we use an interval between these additional false positives from as low as 200 s to as high as 3200 s. We use the phrase “dark noise interval” to refer to the interval between these false positives that are due to quantal noise and continuous rod voltage noise. This phrase specifically does not refer to the interval between spontaneous Rh* events.

We set Q_T to generate false positives at the desired interval, for example, once in 16,000 epochs (1600 s). Fig. 8 A shows two Q_count distributions, the one with dark bars representing Poisson release in the dark, the other with light bars representing Poisson release after production of one Rh*. If Q_T were 9 Q, then the sum of the probabilities given by the solid bars for ≤ 9 Q, 0.458, would represent false positives due primarily to quantal noise and secondarily to continuous rod voltage noise. In this case, false positives would occur in 45.8% of the epochs, that is, once in every 2.2 epochs, or once in every 0.22 s. This dark noise interval is far too short, ∼10,000 times shorter than 1600 s.

More regular quantal release (lower N, higher r) reduces the overlap between the Q_count distributions for darkness and for one Rh* and increases efficiency. Dark bars represent the distribution of Q_count in the dark with a Q_rate,dark of 100 Q s⁻¹ and an M of 10 Q. Light bars represent the distribution of Q_count after production of one Rh* with a Q_rate,Rh* of 81.9 Q s⁻¹ and an M of 8.19 Q. The dark bars are placed just to the right of the tick marks, the light bars just to the left. The distributions of Q_count are computed by convolution (Fig. 5) for physiological (±0.2) rod voltage noise and release processes of several different N. The N have been set for the dark distributions to give one false positive in 16,000 epochs of 0.1 s for a quantal threshold Q_T (*dashed vertical lines*) of (A) 0 Q, (B) 5 Q, (C) 6 Q, and (D) 7 Q.

Clearly, the threshold Q_T must be lower. If it were 8 Q, then the sum of the probabilities given by the dark bars for ≤ 8 Q would yield dark noise intervals of 0.30 s between false positives, still not long enough. Even a Q_T of 1 Q would give a dark noise interval of 189 s. In this case, a Q_T of 0 Q would be required to obtain a dark noise interval of 2052 s, close to the target 1600 s. Thus, to determine Q_T, we begin with the interval between false positives (e.g., 1600 s), convert that rate into a probability per epoch (e.g., 1/16,000), and then consult the Q_count distribution in the dark—and only that distribution—to determine this threshold number of quanta.

Regular release improves efficiency

Upon production of an Rh*, the mean release rate would fall to 81.9 Q s⁻¹ (Fig. 2 B), and the distribution of counts (Fig. 8 A, light bars) in 0.1 s would be broad, 8.19 Q ± 2.88 Q. With a Q_T of 1 Q, the probability given by the sum of the probabilities represented by the open bars for 1 Q or fewer would be exceedingly low, just 0.26%. This value, the percent of Rh* produced that would be counted as true positives by a perfect counter of quanta of neurotransmitter, is the “efficiency”. With a Q_T of 0 Q, the efficiency would be given by the probability shown by the light bar for 0 Q alone and would be even lower, just 0.029%.

A more regular release process would narrow the continuous distribution of intervals between quantal release events and the discrete distribution of counts in an epoch. For example, if gamma order r of the release process was 8.55 and Q_rate,dark was 100 Q s⁻¹, the sum of the probabilities given by the dark bars for Q_count ≤ Q_T (representing false positives) would be 1 in 16,000 epochs for a Q_T of 5 Q (Fig. 8 B). The narrowing of the distribution of intervals, 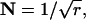Inline graphic would be 0.341. The same dark noise interval could also be achieved with Q_T = 6 Q and a correspondingly higher order release process (r = 18.11, N = 0.235) (Fig. 8 C) or with Q_T = 7 Q and an even higher order release process (r = 66.10, N = 0.123) (Fig. 8 D). The solid squares in Fig. 9 A show these data, N as a function of quantal threshold Q_T, well fit by a line labelled “100”.

Higher release rate permits quantal release with less regularity. Solid squares in all parts correspond to the standard conditions, including a Q_rate,dark of 100 Q s⁻¹. (A) For a given Q_rate,dark (50, 100, 200, and 400 Q s⁻¹) the N that is required to give one false positive in 16,000 epochs of 0.1 s falls linearly as we increase threshold Q_T by increments of 1 Q. Threshold numbers of quanta Q_T must be an integer, so the line that fits the points for a given Q_rate,dark is dashed, not solid. (B) For a given Q_rate,dark, both threshold and efficiency rise as the narrowing N of the Q_count distribution is reduced. Small numbers next to each point show the threshold Q_T for that point. Q_T must be a whole number of quanta, so dashed lines connect points with the same Q_rate,dark, not solid lines. For greater Q_rates,dark, the relationship between efficiency and N can be seen to move upward (greater efficiency) or rightward (less regular release), the latter emphasized by the dotted horizontal lines connecting points with the same efficiency. (C) For any particular efficiency, the N that is required is directly proportional to the square root of Q_rate,dark. The small number next to each point provides the value of Q_T. Threshold numbers of quanta Q_T must be integers, so the line that fits the points for a given efficiency is dashed, not solid. (D) For any particular efficiency, the reciprocal of order r is directly proportional to Q_rate,dark. Threshold Q_T must be an integer number of quanta, so the line that fits the points for a given efficiency is dashed, not solid. (E) For any particular efficiency, the integer value of Q_T rises linearly with Q_rate.

A more regular release process also narrows the distribution of Q_count after production of an Rh*. Narrowing both distributions for dark and for an Rh* reduces their overlap and permits greater efficiency (Fig. 8). Because an N of 0.341 (r = 8.58) in Fig. 8 B permits a Q_T of 5 Q, efficiency is calculated from the sum of the light bars for 5 Q and fewer. In this case, the efficiency is 1.11%. Greater regularity (N = 0.235, r = 18.0, and N = 0.123, r = 66.5) permits higher values of Q_T and yields higher efficiencies, 4.81% and 34.2% (Fig. 8, C and D). The solid squares in Fig. 9 B, efficiency as a function of N, show these data connected by the dashed curve labeled “100 Q sec⁻¹”.

Higher release rates permit less regular release

As was shown in Fig. 8 and by the solid squares in Fig. 9 B for a Q_rate,dark of 100 Q s⁻¹, narrowing the distributions of interval for quanta in the dark and after an Rh* increases separation between the two Q_count distributions and increases efficiency. This separation can be increased by other methods as well. For example, we can increase the number of samples in an epoch (Q_count) by increasing Q_rate. Therefore, we first determined the narrowing N required to produce one false positive in 16,000 epochs from dark distributions of Q_rate,dark for 50, 100, 200, and 400 Q sec⁻¹ (Fig. 9 A). N is a linear function of Q_T in all cases.

Then, we determined efficiency as a function of N for these different Q_{rates, dark} (Fig. 9 B). As Q_rate,dark increases, a particular efficiency may be achieved with less regular release, that is, greater N. For example, as shown by the uppermost dotted horizontal line labeled 34.2% in Fig. 9 B, an efficiency of 34.2% may be achieved with N = 0.087, 0.123, 0.173, and 0.245 for release rates of 50, 100, 200, and 400 Q s⁻¹. In fact, for a particular efficiency, a graph of N as a function of the square root of Q_rate,dark is a line through the origin (Fig. 9 C). Since Inline graphic the same data, graphed with 1/r as a function of Q_rate,dark (Fig. 9 D), is also fit by a line through the origin (Fig. 9 D). The important conclusion is that interchanging order r and Q_rate,dark gives the same efficiency, and we can generalize the efficiency results (Fig. 9 B) to all combinations of Q_rate,dark and r whose product is the same.

Quantal thresholds Q_T are marked on the points in Fig. 9, B–D. For the same 34.2% efficiency, as Q_rate,dark rises from 50 to 100 to 200 to 400 Q s⁻¹, Q_T rises from 3 to 7 to 15 to 31 Q. (Again, see the uppermost dotted horizontal line in Fig. 9 B) The situation is similar for efficiencies of 4.81% and 1.11% (see Fig. 9 B, middle and lower horizontal lines). Indeed, for any given efficiency, threshold Q_T increases linearly with Q_r_ate,dark (Fig. 9 E).

For a Q_rate,dark of 100 Q s⁻¹, the highest efficiency is 34% (Fig. 9 B). Not surprisingly, higher efficiencies may be achieved with higher Q_rates,dark, like 200 Q s⁻¹ or 400 Q s⁻¹ (Fig. 9 B). However, efficiencies >34% may also be achieved for Q_rates,dark somewhat lower than 100 Q s⁻¹. Consider a Q_rate,dark like 95 Q s⁻¹, yielding a mean Q_count in 0.1 s that is 95% as great. (In that case, the appropriately low rate of false positives must be achieved for the same Q_T (7 Q) as was used with 100 Q s⁻¹ to achieve 34.2% efficiency by more severely narrowing the Q_count distribution in the dark, that is, with a higher Erlang order r.) The lower Q_rate would also lower the mean Q_count for one Rh*, place a greater percent of the Q_count distribution associated with one Rh* at or below the Q_T, and thus achieve a higher efficiency.

A longer counting window would also increase the number of samples. Consequently, a longer counting window permits use of higher N, that is, a less regular release process. Similar to the situation in Fig. 9 C, for any given efficiency, N depends on the square root of the duration of the counting window (data not shown). Also, similar to the situation in Fig. 9 A, for any given Q_rate,dark and counting window, N is a linear function of Q_T (data not shown).

Efficiency and N are not very sensitive to dark noise interval

To this point N has been set to give a dark noise interval (due to continuous rod voltage noise and quantal noise of 1600 s (cf. Fig. 9), 10 times longer than the interval between spontaneous production of Rh*s. A dark noise interval shorter than 1600 s means that more total noise, generating more frequent false positives, would be permitted. Since continuous rod voltage noise is constant (±0.2 mV), the increase in total noise is achieved by an increase in quantal noise. In other words, for any given Q_T, larger values of N would be permitted for shorter dark noise intervals (Fig. 10 A). In addition, efficiency for any given Q_T would be greater (Fig. 10 B) for shorter dark noise intervals. For example, for Q_T = 7 Q and an interval of 3200 s, the requisite N is 0.113, and efficiency is 33.7%. For the same Q_T and an interval of 200 s, the requisite N would be greater, but only slightly, 0.160, and the efficiency would be 36.2%. Thus, particularly for a high efficiency like ∼35%, requiring a high threshold Q_T like 7 Q, the differences in N over wide variation in dark noise interval are small (Fig. 10 B).

Shorter dark noise interval permits slightly less regular release. (A) For any given threshold Q_T—the small numbers associated with each line—the narrowing N that is required to achieve any particular dark noise interval rises linearly but not steeply as dark noise interval falls. Here an epoch is 0.1 s, so a dark noise interval in seconds may be expressed as 10 times that number of epochs. The solid squares correspond to the standard conditions, including a dark noise interval of 1600 s and a Q_rate,dark of 100 Q s⁻¹. (B) Shorter dark noise intervals yield higher efficiencies for any given threshold Q_T (small numbers). The points marked by solid squares for a dark noise interval of 1600 s are the same as those in Fig. 9 *B. Q*_T must be an integer number of quanta, so points with the same dark noise interval but different Q_T are connected by a dashed line, not a solid line.

Larger decrements reduce the degree of regularity needed

In all of the calculations thus far, we assumed an e-fold change in the number of open Ca²⁺ channels for 5 mV. For the 1 mV hyperpolarization associated with production of an Rh*, this value resulted in an 18.1% decrement in Q_rate from 100 to 81.9 Q s⁻¹ (Eq. 4) and a decrement in M from 10.0 to 8.19 Q. To explore the effect of this parameter, we considered e-fold changes for 10, 5, 3, and 2 mV, corresponding to decrements in Q_rate of 9.5%, 18.1%, 28.3%, and 39.3%. The corresponding M for a 1-mV hyperpolarization would fall to 9.1, 8.2, 7.2, and 6.1 Q from 10.0 Q in the dark. Increasing the decrement beyond 18.1%, a fall from 10.0 to 8.19 Q, causes the distribution of rod voltage noise in the dark (Fig. 3 A) to be transformed to a slightly wider distribution of Q_rate (Fig. 3 B). Therefore, to maintain the dark noise interval at 1600 s as the decrement rises, it is necessary to reduce quantal noise (and thus N) by a small amount (Fig. 11 A).

Larger decrement between Q_rate,dark and Q_rate,Rh* permits less regular release. The decrement is determined by the voltage sensitivity of the Ca²⁺ channels in the presynaptic terminal. Decrements of 9.5%, 18.1%, 28.3%, and 39.3% are obtained for e-fold changes in conductance for 10, 5, 3, and 2 mV. For this figure, Q_rate is 100 Q s⁻¹. (A) For a given Q_T, increasing the decrement widens the distribution of mean Q_rate,dark due to voltage noise (cf. Fig. 3 B) and thus increases voltage noise. To maintain the dark noise interval at 1600 s, quantal noise must be reduced by reducing N. (B) Increasing the decrement reduces the overlap between Q_count distributions, thus increasing the efficiency for any Q_T (small numbers). The solid squares are the same as those in Fig. 9 B. Threshold Q_T must be an integer number of quanta, so dashed lines, not solid lines, connect points with the same decrement.

Increasing the decrement causes a much larger separation between the Q_count distributions in the dark and after production of an Rh*. However, regular release is still necessary (Fig. 11 B). For example, to obtain efficiencies in the range 35–45% (Fig. 11 B, uppermost points), for any given Q_T, N rises from 0.123 to 0.227 as the decrement rises from 18.1% to 39.4%. Conversely, reducing the decrement to 9.5% yields less separation between the Q_count distributions. In that case, for a Q_rate,dark of 100 Q s⁻¹, no efficiency in this range can be achieved.

DISCUSSION

Overlap between Q_count distributions in the dark and in the light reduces efficiency

Discrimination between the “large” number of quanta released by a rod within some counting window in the dark (Q_count,dark) and the “small” number after production of an Rh* (Q_count,Rh*) requires setting a “threshold” count (Q_T). If the Q_count,dark distribution were wide, due to quantal noise and continuous rod voltage noise, Q_T would have to be set to a very low value, much lower than the mean Q_count,dark, to avoid a high rate of false positives. For example, with “standard assumptions” (a Poisson quantal release process, a Q_rate,dark of 100 Q s⁻¹, a hyperpolarization of 1 mV for one Rh*, an e-fold change in Q_rate for 5 mV, a counting window (epoch) of 0.1 s, and continuous rod voltage noise of ±0.2 mV), the bipolar dendrite would count ∼10 Q in the dark, and Q_T would have to be 0 Q to give an interval of ∼1600 s between false positives (Fig. 8 A).

Even this low threshold, 0 Q, would not be a problem if quantal release were completely halted by the 1 mV hyperpolarization that follows production of an Rh*. However, we argue that a 1 mV hyperpolarization should reduce Q_rate from 100 Q s⁻¹ to 82 Q s⁻¹, not to 0 Q s⁻¹, and thus reduce mean Q_count from 10 Q to 8.2 Q, not to 0 Q (Fig. 2). With a mean Q_count,Rh* of 8.2 Q and Poisson quantal release, only 0.029% of epochs after production of an Rh* would have 0 Q, giving an efficiency of just 0.029% (Fig. 8 A).

Far more “favorable” assumptions would still give low efficiencies in the face of Poisson release. For example, although available data suggests that the conductance of the presynaptic Ca²⁺ channel changes e-fold for 5 mV, one study of toad rod reported 2.3 mV (50), a value that would produce a 35% decrement in Q_rate for a 1-mV hyperpolarization (cf. Eq. 4). Fig. 11 shows that Poisson release and a decrement of 39.3% in response to one photon, corresponding to an e-fold change for 2 mV, gives an efficiency of just 0.26%. If in addition we assumed that Q_rate,dark were higher, like 200 Q s⁻¹, giving a mean Q_count,dark of 20 Q and a mean Q_count,Rh* of 13 Q, Q_T would rise to 4 Q, but that value would still be much less than 13 Q. Efficiency would rise only to 0.91% (data not shown).

In our analysis we accepted the hypothesis that the psychophysical dark light was mainly due to spontaneous production of Rh* (2,48,49), so we generally set the interval between false positives due to quantal noise and continuous rod voltage noise at 1600 s. However, measurements of the rate of spontaneous production of Rh* and of the dark light are highly variable and rely on questionable assumptions (7,41,51,52). To these challenges to the hypothesis, we add that 35% efficiency at the rod-to-rod-bipolar synapse (8, and see our Fig. 12) means that at most 35% of spontaneous Rh* can contribute to the dark light.

Efficiency estimated from rod bipolar cell responses to dim flashes of light, the original data from a study by Field and Rieke (8). (A) These two datasets are redrawn from Fig. 4 C in Field and Rieke (8). They show, for each of two rod bipolar cells, the distribution of normalized response amplitudes to light flashes that produced an average of 0.25 Rh* per rod. (B) Open triangles show the distribution of number of Rh* signaled by bipolar cell 1 after conversion of normalized amplitudes in A into number of Rh*. Points and error bars are these numbers of responses ± the square root of these numbers of responses. As described in the text, solid squares connected by a dashed line represent the probability (right ordinate) of signals for 0–4 Rh* calculated by a binomial method for a pool of eight intact rods and an efficiency of transmission from each rod to its rod bipolar cell of 35%. These parameters minimize the error calculated by least squares. (C) The same analysis as in B for rod bipolar cell 2. Here, the parameters of the calculated distribution (▪) are 11 intact rods and an efficiency of 39%.

Moreover, the magnitude of the contribution of other sources of noise—particularly quantal noise—that arise along the path from rod bipolar cell to ganglion cell to human performance is uncertain (53). Therefore, we investigated the effect of allowing more quantal noise in rod release by reducing the interval between false positives (due to quantal noise and continuous rod voltage noise) to a value as short as that between spontaneous Rh* events, ∼200 s. We found that the requirement for regular release (N) was relaxed by only a trivial amount (Fig. 10).

Release must be regular

To achieve an efficiency of 35–40% with the standard assumptions, we claim that the intervals between quanta must be very regular; that is, the interval distribution must be narrowed greatly, for example, by the factor N = 0.123 compared to a Poisson release process (N = 1) (Fig. 8 D). This clockwork release narrows the distribution of Q_count,dark and places the threshold Q_T (to produce false positives once every 1600 s) at 7 Q instead of 0 Q, slightly less than the mean Q_count,Rh* (8 Q). Correspondingly, Field and Rieke (8), who describe threshold in terms of rod voltage, place the threshold at −1.3 mV, beyond the average rod response to a photon of −1.0 mV.

Clearly, regular release helps to overcome quantal noise only if there is a mechanism that can discriminate a low count (≤ Q_T) from a high count (> Q_T) at the synapse between each rod and rod bipolar dendrite. The need for such a threshold was recognized years ago, albeit for a different purpose, to block transmission of the ±0.2-mV continuous voltage noise from each of the 25–100 rods converging onto a single rod bipolar cell (11,13). Subsequently, van Rossum and Smith (12) proposed a biological mechanism for such a threshold: Their mechanism involves an enzyme in the rod bipolar dendrite that reduces the concentration of an internal messenger (like cyclic GMP) that opens messenger-gated channels in the bipolar cell dendrite. Ultimately sensitive to the high rate of glutamate release by the rod in the dark, the resulting high activity of the enzyme in the dark would hold the concentration of the internal messenger at zero. The rate of glutamate release would have to fall below a threshold level before the activity of the enzyme would fall enough to permit messenger concentration to rise above zero and open messenger-gated channels.

One common strategy for setting a threshold to discriminate between low-mean count and high-mean count distributions is to use a maximum likelihood criterion (chapter A.15 of Rieke et al.) (54). For example, Fig. 8 A shows two Q_count distributions, one with dark bars representing Poisson release in the dark, the other with light bars representing Poisson release after production of one Rh*. The figure shows that the cause of a Q_count ≤ 9 Q is more likely to be an Rh* than darkness, whereas the cause of a Q_count > 9 Q is more likely to be darkness. Thus, the maximum likelihood setting of Q_T would be 9 Q. As we described in Results, that criterion would produce far too many false positives.

Here we point out a more fundamental reason for rejecting that criterion (or any criterion set by an ideal observer). The ideal observer sets the threshold based on the Q_count,dark distribution and the Q_count,Rh* distribution (55). However, to set the interval between false positives, the rod bipolar should consult only the distribution in the dark. Moreover, an ideal observer would need to know which positive events (Q_count ≤ Q_T) were true positives and which were false positives, that is, which positives arose from an Rh* and which arose from noise. This is exactly what the dendrite of a bipolar cell cannot do.

Efficiency of transmission

After slicing a mouse retina, Field and Rieke (8) suggested that ∼½ of a pool of 20 rods still contacted the rod bipolar cell from which they recorded. Nonetheless, a high proportion of the flashes that provided several photons to this pool of rods failed to generate a response in the bipolar cell. They suggested that a threshold 1.3 times as large as the average response to an Rh* blocked transmission at each synapse of rod voltage noise and most (75%) single Rh* events. The value of 75% blockage—hence a value of 25% efficiency—was obtained from the proportion of flashes that failed to generate a response in the bipolar cell.

Field and Rieke's Fig. 4 C provides the distribution of normalized amplitudes of current responses to flashes of light that generated an average of 0.25 Rh*/rod in two voltage-clamped rod bipolar cells. We reproduce these distributions in our Fig. 12 A. From these data we estimate the number of intact rods and the synaptic efficiency. To obtain the values of these two parameters, we calculate the probability of transmission of a signal from each rod as the product of 0.25 Rh*/rod and the efficiency of transmission of that signal across its synapse onto the rod bipolar cell. For example, if efficiency was 36%, then the probability p of a signal from each rod would be 0.25 × 36% = 9.0%. Then we calculate the probability of k = 0, 1, 2, 3, etc. signals being transmitted by the pool of N intact rods, each with p = 9.0%:

(5)

The parameters that best fit the observed distributions are eight intact rods with 35% efficiency for one rod bipolar cell (Fig. 12 B) and 11 intact rods with 39% efficiency for a second (Fig. 12 C). These efficiencies are between the 25% reported in Field and Rieke (8) and the 60% reported more recently (53,56).

Regular release could also be modeled by a refractory period

We modeled regularity by assuming a high-order counting process, but we could have assumed some other mechanism, such as a refractory period after each quantal release event. Indeed, regular spiking in retinal cells has been described in those terms (57–59). The mapping between descriptions may be illustrated as follows: Assume that quanta were released according to a Poisson process and that the mean interval between quantal events was 1 ms. The SD of the interval distribution would equal 1 ms as well (see Eq. A1 and associated text in Appendix A). If each release event were followed by an absolute refractory period of 9 ms, the mean interval would increase to 10 ms, but the SD would remain 1 ms (instead of 10 ms), and N would be 0.1.

In some central synapses only one of 10–20 docked vesicles fuse in response to a spike (19,20,60–64), and the next fusion event is delayed by what has been described as a “refractory period” of ∼10 ms (60,65). (We discuss multivesicular release below.) The mechanism of the refractory period in this case is unknown, however. Only one of the docked vesicles might be competent, or the fusion of one vesicle might block fusion of the remainder for a period of time. The special challenge for such a mechanism in the rod terminal would be to span two ribbon-associated active zones, ∼2 μm in total length (37) and with many times 20 docked vesicles.

However, a refractory period that would satisfactorily regularize release would create the following problems. First, in the above example, to generate release in ∼1 ms (after the 9-ms refractory period) the Q_rate during that 1 ms would have to be 1000 Q s⁻¹. Second, to reduce Q_rate from 100 to 80 Q s⁻¹, the total interval between quanta would have to increase from 10 to 12.5 ms. Assuming that the refractory period is constant, activation of one Rh* would have to increase the nonrefractory interval from 1 to 3.5 ms, requiring an almost fourfold reduction in Q_rate, from 1000 to 286 Q s⁻¹, after the 9-ms refractory period. Therefore, this assumption is likely to be incorrect, and to account for the dependence of Q_rate on [Ca²⁺]_int, the duration of the refractory period would have to depend on [Ca²⁺]_int as well.

Two kinds of biological mechanism could regularize release of quanta

We distinguish two types of biological mechanism that could account for the regularity of the quantal release process, one based on an internal mechanism that would operate in an isolated rod, the other requiring an intact synapse. Examples of an internal mechanism include an internal oscillator and an internal counter. As precedent for the latter, variation in the single-photon response in the rod is reduced by the requirement for multiple phosphorylations to deactivate Rh* (66–68). Indeed, several proteins in presynaptic terminals that are involved in synaptic release have large numbers of phosphorylation sites, including 30 on bassoon and 16 on piccolo (69).

In contrast, an intact synapse would be needed if regularity were imposed by feedback. Several candidate mechanisms have been reported. For example, glutamate activates autoreceptors in vertebrate cones (70,71). Also, the release of the contents of the synaptic vesicle might briefly reduce the pH in the synaptic cleft underlying the active zone and shift the voltage-sensitive range of the Ca²⁺ channels, possibly with participation of Ca²⁺-dependent Cl⁻ channels (34,72–75).

After expressing synaptopHluorin (76) in hippocampal neurons, Gandhi and Stevens (77) were able to monitor release of individual quanta. Using the styryl dye FM1-43, Arvanis, Pyle, and Tsien (78) were also able to monitor release of single quanta. With better sensitivity and time resolution, such methods might be able to test the clockwork hypothesis in isolated rods and also in “intact” rod circuits in retinal slices. Moreover, either method might be used to measure the effect of absorption of single photons on release rate by rods.

Each quantum represents a large number of Poisson events

We suggest that several mechanisms, both presynaptic and postsynaptic, contribute to reducing quantal noise at the synapse between a rod and a rod bipolar cell dendrite. Presynaptically, Q_rate is high, and the Erlang order of the regular release process is high. Postsynaptically, each rod bipolar cell dendrite counts many Erlang Events (quanta) in its counting window. For example, to achieve 34% efficiency with a Q_rate,dark of 100 Q s⁻¹ and mean counts of 10 Q in the dark and 8.2 Q for one Rh*, Erlang order would need to be ∼66 (Fig. 8 D). Since each Erlang Event—release of one quantum—would “represent” 66 Poisson events, the (no photon/photon) “decision” would depend on the difference between 660 Poisson events (10 Q × 66 Poisson events/Q) and 530 Poisson events (8.2 Q × 66 Poisson events/Q).

From the point of view of the presynaptic terminal of the rod, the alternative to releasing ten 66^th-order “Erlang quanta” in a counting window of 0.1 s is to release 660 “Poisson quanta” in that time, an unsustainable rate (79,80). Therefore, by incorporating a mechanism that counts Poisson events and permits low Q_rates, the rod terminal expends far less of the energy associated with manufacture, release, and recycling of quanta, perhaps at the relatively minor cost of phosphorylating a number of sites on some protein in the presynaptic terminal.

Cone bipolar cells add another mechanism to increase their count: They sample many synaptic ribbons. Nonetheless, we suggest that quantal release at each cone ribbon must be regular as well. Specifically, a foveal ON midget bipolar cell provides dendrites (“central elements”) to the active zones associated with ∼16 synaptic ribbons of one cone (81). This cone bipolar cell has the same mGluR6 receptor as the rod bipolar cell (82,83), so it can sum several quanta in its counting window, estimated as ∼50 ms (1).

The base of a synaptic ribbon in a cone is shorter (∼0.6 μm) (84) than that in a rod (∼2 μm), so we assume that Q_rate,dark is 40 Q s⁻¹ at each cone synaptic ribbon. (This assumption is generous, as Berntson and Taylor (85) estimate ∼20 Q s⁻¹.) In that case each central element would count 2 Q over 50 ms, and the ON midget bipolar cell would sum just 32 Q from its 16 central elements in a counting window, more than the number of quanta (e.g., 10 Q) counted by a rod bipolar cell dendrite. If the Erlang order regularizing quantal release at a cone ribbon equaled 66, this quantal count in the dark would correspond to 2112 Poisson events, more than the rod (660 above), enabling the cone to encode more levels of stimulation (as it must) than the two (no photon/photon) encoded by a rod under starlight conditions. Laughlin and de Ruyter van Steveninck (86) made a similar argument for a large number of quanta at the output of an invertebrate photoreceptor.

Synaptic ribbons are associated with high rates of release but not necessarily regular release

Synaptic ribbon-like structures are also found in hair cells in the lateral line system of fish and its evolutionary descendants, namely auditory, vestibular, and electrosensory systems (87). These receptor cells are also able to transmit extremely small signals (< 1 mV) to their target neurons, so these cells too must overcome quantal noise.

In response to appropriate stimuli, the cells postsynaptic to these receptor cells show regular spiking, but the firing of an afferent fiber in auditory nerve, for example, is regular because it is phase-locked to a periodic stimulus (sound). Indeed, in the absence of a tone, an auditory afferent fiber fires at random intervals (88). If each afferent spike follows release of one quantum or one coordinated release of several quanta by an inner hair cell (88–90), and if the afferent fiber receives all of its input at a single synaptic ribbon of an inner hair cell (91,92), then quantal release events—both single and multivesicular—at the ribbon in the unstimulated inner hair cell must occur at random intervals. The lateral line system may function similarly (93): Spiking in this afferent is phase-locked to sinusoidal vibration (94) but is irregular in the absence of stimulation. Thus, although ribbons may serve different specialized purposes in different receptor cells (95,96), the mere presence of a synaptic ribbon does not insure regular release. Indeed, a single photon is an aperiodic stimulus, so regular quantal release by a rod must be accomplished by a mechanism that may or may not be connected to the presence of a synaptic ribbon.

At some central synapses (97), at ribbon synapses made by hair cell terminals (89,98,99), and at ribbon synapses made by bipolar cell terminals (100,101), multivesicular release and/or compound exocytosis occur, perhaps to overcome the postspike refractory period and sustain a high firing rate in the target neuron (89). (By contrast, the synaptic target of the rod does not fire action potentials.) If the number of vesicles that fused before each multivesicular release event were fixed, and if all release events were of this sort, then it is conceivable that multivesicular release could be a presynaptic counting mechanism that increases Erlang order and regularizes quantal release.

However, if the number of vesicles in a multivesicular release event is not fixed (89,97), a multivesicular event is like a burst that contains several quantal release events at very small intervals. Bursting reduces regularity, even producing interval distributions with coefficients of variation that can be larger than unity. Therefore, multivesicular release and compound exocytosis generally increase randomness, and variation in number of quanta participating in multivesicular events increases quantal noise.

Up to this point we have assumed that the narrowing N of the distribution of intervals between quantal release events in the dark and the distribution of intervals for one Rh* are the same. However, there is the possibility that the intrinsic regularity of quantal release might differ for the unstimulated and the stimulated conditions in the rod, analogous to our description of what happens in the auditory system. Correspondingly, the difference between the quantal stream for darkness and the quantal stream for one Rh* would be greater if the Erlang order were high for the first and low for the second.

If efficiency is < 50%, as we believe it to be, threshold Q_T would be less than mean Q_count,Rh*. In that case, a broader Q_count,Rh* distribution, as in Fig. 13, would place more counts to the left of Q_T and consequently increase efficiency. In that figure, the Q_count,dark distribution (dark bars) was taken from Fig. 8 C with N = 0.235, where a Q_T of 6 Q gave 4.81% efficiency. By contrast, the Q_count,Rh* distribution (light bars) was taken from Fig. 8 A with N = 1, that is, assuming Poisson release. Efficiency for a Q_T of 6 Q would rise to 29.2%. The improvement of efficiency that accompanies a narrowing of the Q_count,dark distribution but not of the Q_count,Rh* distribution would be an example of stochastic resonance (102,103).

Less regularity in quantal release after production of Rh* can improve efficiency. The Q_count distribution represented by the solid bars is taken from Fig. 8 C. The fine dotted line without bars shows the distribution for one Rh* and is also taken from Fig. 8 C. Both distributions derive from a regular release process (N = 0.235). The distribution represented by the open bars is taken from Fig. 8 A for a random (Poisson) release process (N = 1) in response to one Rh*. In this case, the part of the Rh* distribution that is at or to the left of the threshold (Q_T = 6) is greater for Poisson release than for regular release.

Similarly, spiking in retinal ganglion cells is phase-locked to periodic stimuli (104) but random when unstimulated (after correction for bursts of ∼3 spikes per spontaneous Rh*) (46,105). This situation resembles that described above for auditory nerve fibers. Thus, a difference in the regularity of quantal release or spiking between the stimulated and the unstimulated conditions could increase efficiency in all of these highly sensitive sensory systems.

Acknowledgments

We thank Karen Migdale for discussions that triggered this work and Robert Smith for generously and consistently providing insightful discussion. We also thank Laura Frishman, Julie Schnapf, and Robert Smith for critical comments on the manuscript. We thank Thomas Wickens for help with the statistical distributions.

APPENDIX A: QUANTAL NOISE

Some of the equations and figures that follow can be found in textbooks and online, but we present them here for three reasons. First, it is important to have a consistent terminology with consistent symbols. Second, some familiarity with these probability concepts and distributions is helpful. At the same time, and third, great sophistication is not necessary, and readers should not have to pore over textbooks to understand this material.

Interarrival time (interval) distributions

Poisson process

In a Poisson renewal process, events arrive at some rate α (Poisson events s⁻¹) with constant probability at any time after the last event (Fig. 4, A and B, left panels) (chapter 2.3 of Cox (106)). The time between events, the interarrival time (or “interval”), follows an exponential distribution (Eq. A1), as illustrated by the r = 1 curve in Fig. 4 C.

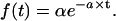(A1)

The mean interval μ (in seconds) equals 1/α, the variance σ² of the distribution of intervals equals 1/α² (modified from Eq. A.46 of Wickens (107)), and the standard variation σ of the distribution equals 1/α, the same as the mean. In the example in the left panel of Fig. 4 A, the rate α is 100 Poisson events s⁻¹, so the mean interval and the SD are both 0.01 s.

Erlang process

An r^th-order ordinary Erlang renewal process declares an Erlang Event (here with an uppercase “E”) when r underlying Poisson events (with a lowercase “e”) of rate α have accumulated, where r is a positive integer. (An Erlang process with order r = 1 is a Poisson process.) With r > 1, the process becomes more regular, as shown by the examples in the right panels of Fig. 4, A and B, for r = 25. The mean interval for an Erlang Event (μ) is the Erlang order r (underlying Poisson events per Erlang Event) divided by the Poisson rate α (underlying Poisson events s⁻¹), that is, μ = r/α. The distribution of interval (t) until the r^th Poisson event, that is, until the next Erlang Event, is a probability density function (Eq. A2) (modified from Eq. A.49 of Wickens (107)).

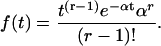(A2)

The variance σ² = r /α², and the standard deviation Inline graphic The coefficient of variation (CV) of this interval time distribution equals the SD (σ) divided by the mean interval (μ); thus,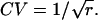

To appreciate the effect of increasing r on the width of the distribution of interarrival times, it is convenient to keep the mean interval μ constant by increasing the rate of underlying Poisson events α along with the order r. Then it becomes clear that the distribution of intervals progressively narrows as r increases from 1 to 9 to 25 to 100 (and α increases from 100 to 900 to 2500 to 10,000) (Fig. 4 C). The SD is reduced by the factor 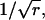Inline graphic a quantity that we refer to as “narrowing” (or N for short). Since 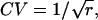the CV of an interval distribution is reduced by the same factor N.

Gamma process

A gamma renewal process is the same as an Erlang process but generalized to include positive noninteger values of r. In that case, Eq. A2 is replaced by Eq. A3 (modified from Eq. A.52 of Wickens (107)),

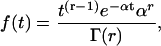(A3)

where Γ(r) is the gamma function (modified from Eq. A.50 of Wickens (107)).

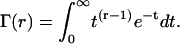(A4)

Number distribution

Poisson process

If a counter accumulates Poisson events within a window of duration T, the product of rate α and time T gives the expected number λ of Poisson events. For example, in the left panel of Fig. 4 A, the combination of a rate α of 100 events s⁻¹ and a time T of 0.1 s yields an expected number λ of 10 Poisson events. If release of quanta of neurotransmitter were a Poisson process, the probability distribution of number of quanta (x) depends on λ as given by Eq. A5 from Eq. A.12 of Wickens (107):

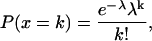(A5)

where P(x = k) is the probability that k Poisson events arrived in that window T. This number distribution is shown by the r = 1 curve in Fig. 4 D. (Numbers of events are whole numbers; the curve connects related points but is dashed instead of solid to emphasize that fractional events are not meaningful.) This number distribution is characterized by a variance σ² that equals the mean λ, 10 in this case; thus, standard deviation 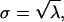Inline graphic 3.162 in this case. CV = σ/λ, 31.62% in this case. The probabilities summed over all x equals one.

Grouped Poisson number distribution: Erlang process

Recall that an r^th-order Erlang renewal process declares an Erlang Event when r underlying Poisson events of rate α have accumulated. (In this case an Event could represent release of one quantum of neurotransmitter, and α could represent the average rate of underlying Poisson events.) In an “ordinary” renewal process, the counting begins immediately after the last (0th) Erlang Event, with 0 Poisson events accumulated (chapter 2.1 of Cox (106)). The probability of K Erlang Events in time T is equal to the sum of the probabilities of rK Poisson events, rK + 1 Poisson events, rK + 2 Poisson events, etc., up to r(K + 1) − 1 Poisson events. For example, the probability of ten 4th-order Erlang Events is equal to the sum of the probabilities of k = 40–43 underlying Poisson events, as shown by the summation limits in the equation for the discrete probability distribution of the number of Erlang Events (Eq. A6) (108, modified from Eq. 4 of chapter 3.1 of Cox (106) and Eq. 4.131 of Johnson et al. (109)),

(A6)

If release of quanta is an Erlang process, the distribution of number of quanta (X) would depend on the order r and the expected number λ = αT of underlying Poisson events, where α is the rate of underlying Poisson events and T is the duration of the counting window. If α = 400 underlying Poisson events s⁻¹, and T = 0.1 s, λ = αT would be 40 underlying Poisson events. We define a quantity M that is equal to λ/r. With λ = 40 underlying Poisson events and r = 4 in this example, M would be 10 Erlang Events, and λ = αT = rM = 40 underlying Poisson events. Fig. 4 D shows progressively narrower count distributions for several r, increasing from 1 to 100. For this reason, the count distribution that results from an ordinary Erlang renewal process has been called a Grouped Poisson distribution (chapter 12.5 of Johnson et al. (109)).

In an ordinary renewal process, M does not equal the expected number of Erlang Events because “excess” Poisson events are rounded down. For example, the probability of ten 4th-order Erlang Events is the sum of the probabilities for 40, 41, 42, and 43 underlying Poisson events. None of the “excess” (1, 2, and 3) Poisson events over 40 add to the number 10 of 4th-order Erlang Events, yielding 0, 0.25, 0.5, and 0.75 uncounted 4th-order Erlang Events, an average loss of 0.375 Erlang Events. The actual expected number of Erlang Events in this case, 9.625, is 10 – 0.375. The expected number of Erlang Events is always less than M by the amount calculated in Eqs. A7 and A8, where r is the order.

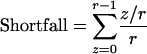(A7)

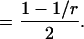(A8)

Hence,

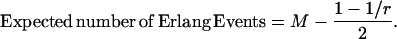(A9)

As r increases, irrespective of M, the shortfall approaches 0.5 Erlang Events. Thus, for an M of 10 and a high order r (e.g., 25), slightly more than half of the counts of Erlang Events would be 10, and slightly less than half would be 9. The expected number of Erlang Events would be 9.52, illustrated by the highly regular Erlang Event train in Fig. 4 A, right panel, giving the narrow, discrete r = 25 number distribution in Fig. 4 D.

The expected (mean) number of Erlang Events is thus <M. The shortfall depends only on r and would be 0.375 for a 4th-order renewal process. Thus, to achieve an expected number of 4th-order Erlang Events equal to 10, it would be necessary to use a larger Poisson rate α or a longer T to set M to 10.375.

In an “equilibrium” renewal process the counting begins at a random time (Cox (106)), implying that some random number of Poisson events have already been accumulated. It may appear more natural to model the counting of quanta of neurotransmitter—Erlang Events—by a rod bipolar cell dendrite on this kind of renewal process, since the bipolar cell is continuously counting quanta. Then, the already accumulated Poisson events balance the excess Poisson events, and the expected number of Erlang Events is equal to M. However, in this kind of renewal process the time to the first Erlang Event has a different distribution from that of intervals for subsequent Erlang Events, and Eq. A6 does not apply. For that reason, we use an ordinary renewal process in this article. Moreover, an ordinary renewal process with M and some expected number of Erlang Events yields the same distribution as an equilibrium renewal process with its mean set to that expected number. In addition, comparison of two number distributions generated by ordinary renewal processes with the same order r is unaffected because the two distributions have the same shortfall (Eq. A8).

For the distribution of the number of Erlang Events (Fig. 4 D), one might assume that variance σ² of the count would equal M/r, the standard deviation σ of the count would equal 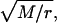Inline graphic and the CV would fall as the narrowing N = 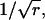analogous to what occurs with the distribution of intervals. This assumption is approximately correct for values of r < 25. However, for higher-order r the SD of the number distribution begins to depend on M as well as r. There are two extreme cases for large r (>25). For values of M that result in means that are integers, the SD falls to zero. For values of M that are integers, the SD asymptotes to 0.5.

Grouped Poisson number distribution: gamma process

If release of quanta follows an ordinary gamma renewal process instead of an Erlang renewal process, that is, if order r is noninteger, then the distribution of the number of quanta (X) in Eq. A10 would depend on the same parameters as the distribution for an Erlang process as described above (108, modified from Eq. 4.130 of Johnson et al. (109)):

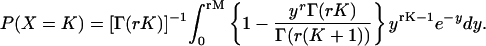(A10)

The expected number of Events can be calculated as we did for an Erlang process (Eq. A9), the SD of the number distribution is approximated as we described above for an Erlang process, and the SD is reduced approximately by N = 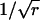Inline graphic for order r < 25. The count distribution that results from an ordinary gamma renewal process may also be called a Grouped Poisson distribution.

Microsoft Excel 2000 (Microsoft, Redmond, WA) functions can be used to compute Eq. A10 as follows:

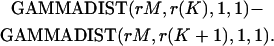(A11)

Excel is unable to compute the GAMMADIST function for large K and large rM. Therefore, we used Mathematica 4.2 (Wolfram Research, Champaign, IL) and Mathlink (Mathematica Link for Excel) 2.1 (Wolfram Research, Champaign, IL) to compute the gamma probabilities. The corresponding equation and functions in Mathematica are as follows:

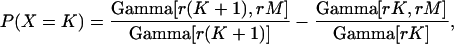(A12)

where the gamma function, Gamma[x], already shown as Eq. A4, has integration limits from 0 to ∞. Gamma[x,y], the (upper) incomplete gamma function, resembles Eq. A4 but has integration limits from y to ∞.

APPENDIX B: QUANTAL NOISE CAN BE EXPRESSED IN UNITS OF MILLIVOLTS

Continuous rod voltage noise (RVN), the SD of the distribution of rod voltage, is typically expressed in units of millivolts (e.g., 0.2 mV, as in Fig. 3 A). Quantal noise (QN), the SD of a Q_count distribution in the absence of rod voltage noise, is expressed in units of quanta. Because continuous rod voltage noise and quantal noise are independent, total noise (TN) may be computed as the square root of the sum of the squares of rod voltage noise and quantal noise. To compute total noise, however, rod voltage noise and quantal noise must be in the same units, either both in quanta or both in millivolts.

To transform the SD of continuous rod voltage noise in millivolts (RVN_V) to quanta (RVN_Q), we take advantage of Eq. B1,

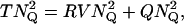(B1)

where quantal noise QN_Q is the SD of the Q_count distribution with zero voltage noise, expressed in quanta, and total noise TN_Q is the SD of the Q_count distribution with both continuous voltage noise and quantal noise, expressed in quanta. The convolution method (Fig. 5) is used to generate both of these Q_count distributions. From both standard deviations TN_Q and QN_Q in quanta and Eq. B1, continuous rod voltage noise may be computed in quanta (RVN_Q) as well.

Therefore, we first set continuous rod voltage noise RVN_V to 0 mV. (As examples, the open bars in Fig. 6 A and the open bars in Fig. 6 B show Q_count distributions for RVN_V of 0 mV for N = 1 and N = 0.2.) The resulting SDs of the Q_count distributions reflect quantal noise alone, hence QN_Q for N = 1 and N = 0.2.

Second, we measured the SD of Q_count distributions (TN_Q) in the presence of both continuous rod voltage noise (0.1, 0.2, 0.3, or 0.4 mV) and quantal noise for N = 1.0. With QN_Q and TN_Q in hand, we applied Eq. B1 to solve for RVN_Q, as shown by the solid points in Fig. 7 A. For N = 1, the slope of the relationship in Fig. 7 A is 2.06 Q/mV. We repeated the exercise with N = 0.2, with the results shown by the open points in Fig. 7 A, and then again for N = 0.25, 0.33, and 0.5 (data not shown). All of these data were obtained with a mean count of 10 Q, with the requisite Q_rate obtained by use of Eq. 4. For N = 0.2, the slope is trivially different at 2.11 Q/mV; for the intermediate N, the slopes are intermediate (data not shown). These slopes are close to 2 Q/mV, because M changes by slightly less than 2 Q (from 10 to 8.2 Q) for departure of voltage from ΔV = 0 to −1 mV (Fig. 3) and by slightly more than 2 Q for departure of voltage from ΔV = 0 to +1 mV.

Therefore, we can graph continuous rod voltage noise in units of millivolts (RVN_V) or in quanta (RVN_Q) against quantal noise in units of millivolts (QN_V) or quanta (QN_Q) and obtain total noise in units of millivolts (TN_V) or quanta (TN_Q) (Fig. 7 B).

This analysis has three virtues. First we can transform quantal noise into millivolts for comparison with continuous rod voltage noise. (Expressing quantal noise in millivolts corresponds to referring noise to the input, a standard practice (110).) Consider quantal noise for a mean count of 10 Q and N = 1, for which 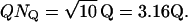Inline graphic In that case, quantal noise could be expressed as 1.54 mV (= 3.16 Q × 1 mV/2.06 Q), clearly dominating the physiological 0.2 mV of continuous rod voltage noise. Total noise would be 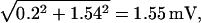so continuous rod voltage noise would cause total noise to increase just 1.01 times over quantal noise alone, as reported in the first section of Results. This total noise has also been called “effective noise” (chapter 3.1 of Rieke et al. (54)).

Now consider quantal noise for a mean count of 10 Q and N = 0.2, for which QN_Q = 0.71 Q. (This value is close to Inline graphic but not equal to it because the SD of the number distribution for N < 1 is only approximated by N ×) In that case, quantal noise could be expressed as 0.34 mV (0.71 Q × 1 mV/2.11 Q), still dominating the physiological 0.2 mV of rod voltage noise. Total noise would be 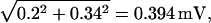so continuous rod voltage noise would cause total noise to increase just 1.16 times over quantal noise alone, also as reported in the first section in Results.

Second, if one wished to take into account other independent sources of noise that affect the Q_count distribution, one could easily do so with a simple extension of Eq. B1.

Third, although we obtained TN_Q in the presence of continuous rod voltage noise and quantal noise by use of the convolution method, it is possible to estimate TN_Q more simply by use of Eq. B1 and the factor that transforms continuous rod voltage noise into quanta. To illustrate the last point, we compute the SD corresponding to 0.2 mV of continuous rod voltage noise as 0.412 Q (0.2 mV × 1 mV/2.06 Q). We compute QN_Q, the SD in the absence of continuous rod voltage noise, for a mean count of 10 Q and 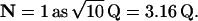Inline graphic Then, from Eq. B1 we estimate TN_Q when both are present as 3.19 Q, exactly what we measured by the convolution method. Similarly, we can compute the QN_Q for a mean count of 10 Q and 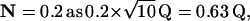so from Eq. B1 we estimate TN_Q when both are present as 0.76 Q, just 8% less than what we measured by the convolution method, 0.82 Q. The small difference occurs because the SD of the discrete count distribution is well approximated—but only approximated—by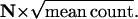 Inline graphic

References

1.Hood, D. C., and M. A. Finkelstein. 1986. Sensitivity to light. In Handbook of Perception and Human Performance, Vol. 1: Sensory Processes and Perception. K. R. Boff, L. Kaufman, and J. P. Thomas, editors. John Wiley & Sons, New York. Chapter 5.
2.Rodieck, R. W. 1998. The First Steps in Seeing. Sinauer, Sunderland, MA. Chapter 7.
3.Hecht, S., S. Shlaer, and M. H. Pirenne. 1942. Energy quanta and vision. J. Gen. Physiol. 25:819–840. [DOI] [PMC free article] [PubMed] [Google Scholar]
4.van der Velden, H. A. 1946. The number of quanta necessary for the perception of light in the human eye. Ophthalmologica. 111:321–331. [DOI] [PubMed] [Google Scholar]
5.Sakitt, B. 1972. Counting every quantum. J. Physiol. 223:131–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
6.Schneeweis, D. M., and J. L. Schnapf. 1995. Photovoltage of rods and cones in the macaque retina. Science. 268:1053–1056. [DOI] [PubMed] [Google Scholar]
7.Schneeweis, D. M., and J. L. Schnapf. 2000. Noise and light adaptation in rods of the macaque monkey. Vis. Neurosci. 17:659–666. [DOI] [PubMed] [Google Scholar]
8.Field, G. D., and F. Rieke. 2002a. Nonlinear signal transfer from mouse rods to bipolar cells and implications for visual sensitivity. Neuron. 34:773–785. [DOI] [PubMed] [Google Scholar]
9.Robson, J. G., H. Maeda, S. M. Saszik, and L. J. Frishman. 2004. In vivo studies of signaling in rod pathways of the mouse using the electroretinogram. Vision Res. 44:3253–3268. [DOI] [PubMed] [Google Scholar]
10.Sampath, A. P., and F. Rieke. 2004. Selective transmission of single photon responses by saturation at the rod-to-rod bipolar synapse. Neuron. 41:431–443. [DOI] [PubMed] [Google Scholar]
11.Baylor, D. A., B. J. Nunn, and J. L. Schnapf. 1984. The photocurrent, noise and spectral sensitivity of rods of the monkey Macaca fascicularis. J. Physiol. 357:575–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
12.van Rossum, M. C., and R. G. Smith. 1998. Noise removal at the rod synapse of mammalian retina. Vis. Neurosci. 15:809–821. [DOI] [PubMed] [Google Scholar]
13.Falk, G., and P. Fatt. 1972. Physical changes induced by light in the rod outer segment of vertebrates. In Handbook of Sensory Physiology, Vol. VII/1. H. J. A. Dartnall, editor. Springer-Verlag. Berlin. 200–244.
14.Fatt, P., and B. Katz. 1952. Spontaneous subthreshold activity at motor nerve endings. J. Physiol. 117:109–128. [PMC free article] [PubMed] [Google Scholar]
15.del Castillo, J., and J. B. Katz. 1953. Statistical nature of facilitation at a single nerve-muscle junction. Nature. 171:1016–1017. [DOI] [PubMed] [Google Scholar]
16.Katz, B., and R. Miledi. 1965. The measurement of synaptic delay, and the time course of acetylcholine release at the neuromuscular junction. Proc. R. Soc. Lond. B Biol. Sci. 161:483–495. [DOI] [PubMed] [Google Scholar]
17.Katz, B. 1969. The release of neural transmitter substances. Liverpool University Press, Liverpool.
18.Barrett, E. F., and C. F. Stevens. 1972. The kinetics of transmitter release at the frog neuromuscular junction. J. Physiol. 227:691–708. [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Allen, C., and C. F. Stevens. 1994. An evaluation of causes for unreliability of synaptic transmission. Proc. Natl. Acad. Sci. USA. 91:10380–10383. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Bekkers, J. M., and C. F. Stevens. 1994. The nature of quantal transmission at central excitatory synapses. Adv. Second Messenger Phosphoprotein Res. 29:261–273. [DOI] [PubMed] [Google Scholar]
21.Rao-Mirotznik, R., G. Buchsbaum, and P. Sterling. 1998. Transmitter concentration at a three-dimensional synapse. J. Neurophysiol. 80:3163–3172. [DOI] [PubMed] [Google Scholar]
22.Baylor, D. 1996. How photons start vision. Proc. Natl. Acad. Sci. USA. 93:560–565. [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Bader, C. R., D. Bertrand, and E. A. Schwartz. 1982. Voltage-activated and calcium-activated currents studied in solitary rod inner segments from the salamander retina. J. Physiol. 331:253–284. [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Corey, D. P., J. M. Dubinsky, and E. A. Schwartz. 1984. The calcium current in inner segments of rods from the salamander (Ambystoma tigrinum) retina. J. Physiol. 354:557–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Rieke, F., and E. A. Schwartz. 1996. Asynchronous transmitter release: control of exocytosis and endocytosis at the salamander rod synapse. J. Physiol. 493:1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Taylor, W. R., and C. Morgans. 1998. Localization and properties of voltage-gated calcium channels in cone photoreceptors of Tupaia belangeri. Vis. Neurosci. 15:541–552. [DOI] [PubMed] [Google Scholar]
27.Hille, B. 1984. Ionic channels of excitable membranes. Sinauer Associates: Sunderland, MA.
28.Rieke, F., and E. A. Schwartz. 1994. A cGMP-gated current can control exocytosis at cone synapses. Neuron. 13:863–873. [DOI] [PubMed] [Google Scholar]
29.Wilkinson, M. F., and S. Barnes. 1996. The dihydropyridine-sensitive calcium channel subtype in cone photoreceptors. J. Gen. Physiol. 107:621–630. [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Schmitz, Y., and P. Witkovsky. 1997. Dependence of photoreceptor glutamate release on a dihydropyridine-sensitive calcium channel. Neuroscience. 78:1209–1216. [DOI] [PubMed] [Google Scholar]
31.Witkovsky, P., Y. Schmitz, A. Akopian, D. Krizaj, and D. Tranchina. 1997. Gain of rod to horizontal cell synaptic transfer: relation to glutamate release and a dihydropyridine-sensitive calcium current. J. Neurosci. 17:7297–7306. [DOI] [PMC free article] [PubMed] [Google Scholar]
32.Nachman-Clewner, M., R. St. Jules, and E. Townes-Anderson. 1999. L-type calcium channels in the photoreceptor ribbon synapse: localization and role in plasticity. J. Comp. Neurol. 415:1–16. [PubMed] [Google Scholar]
33.Wässle, H., S. Haverkamp, U. Grünert, and C. W. Morgans. 2003. The cone pedicle, the first synapse in the retina. In The Neural Basis of Early Vision. A. Kaneko, editor. Springer Verlag, Tokyo. 19–38.
34.Thoreson, W. B., R. Nitzan, and R. F. Miller. 1997. Reducing extracellular Cl⁻ suppresses dihydropyridine-sensitive Ca²⁺ currents and synaptic transmission in amphibian photoreceptors. J. Neurophysiol. 77:2175–2190. [DOI] [PubMed] [Google Scholar]
35.Armstrong-Gold, C. E., and F. Rieke. 2003. Bandpass filtering at the rod to second-order cell synapse in salamander (Ambystoma tigrinum) retina. J. Neurosci. 23:3796–3806. [DOI] [PMC free article] [PubMed] [Google Scholar]
36.Thoreson, W. B., R. Katalin, E. Townes-Anderson, and R. Heidelberger. 2004. A highly Ca²⁺-sensitive pool of vesicles contributes to linearity at the rod photoreceptor ribbon synapse. Neuron. 42:595–605. [DOI] [PMC free article] [PubMed] [Google Scholar]
37.Migdale, K., S. Herr, K. Klug, K. Ahmad, K. Linberg, P. Sterling, and S. Schein. 2003. Two ribbon synaptic units in rod photoreceptors of macaque, human, and cat. J. Comp. Neurol. 455:100–112. [DOI] [PubMed] [Google Scholar]
38.Townes-Anderson, E., P. R. MacLeish, and E. Raviola. 1985. Rod cells dissociated from mature salamander retina: ultrastructure and uptake of horseradish peroxidase. J. Cell Biol. 100:175–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
39.Rieke, F., and D. A. Baylor. 1996. Molecular origin of continuous dark noise in rod photoreceptors. Biophys. J. 71:2553–2572. [DOI] [PMC free article] [PubMed] [Google Scholar]
40.Graham, C. H., and R. Margaria. 1935. Area and the intensity-time relation in the peripheral retina. Am. J. Physiol. 113:299–305. [Google Scholar]
41.Barlow, H. B. 1957. Increment thresholds at low intensities considered as signal/noise discrimination. J. Physiol. 136:469–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
42.Sperling, H. G., and C. L. Jolliffe. 1965. Intensity-time relationships at threshold for spectral stimuli in human vision. J. Opt. Soc. Am. 55:191–199. [Google Scholar]
43.Baumgardt, E., and B. Hillmann. 1961. Duration and size as determinants of peripheral retinal response. J. Opt. Soc. Am. 51:340–344. [DOI] [PubMed] [Google Scholar]
44.Robson, J. G., and L. J. Frishman. 1999. Dissecting the dark-adapted electroretinogram. Doc. Ophthalmol. 95:187–215. [DOI] [PubMed] [Google Scholar]
45.Baylor, D. A., G. Matthews, and K.-W. Yau. 1980. Two components electrical dark noise in toad rod outer segments. J. Physiol. 309:591–621. [DOI] [PMC free article] [PubMed] [Google Scholar]
46.Mastronarde, D. N. 1983. Correlated firing of cat retinal ganglion cells. II. Responses of X- and Y-cells to single quantal events. J. Neurophysiol. 49:325–349. [DOI] [PubMed] [Google Scholar]
47.Copenhagen, D. R., K. Donner, and T. Reuter. 1987. Ganglion cell performance at absolute threshold in toad retina: Effects of dark events in rods. J. Physiol. 393:667–680. [DOI] [PMC free article] [PubMed] [Google Scholar]
48.Barlow, H. B. 1956. Retinal noise and absolute threshold. J. Opt. Soc. Am. 8:634–639. [DOI] [PubMed] [Google Scholar]
49.Donner, K. 1992. Noise and the absolute thresholds of cone and rod vision. Vision Res. 32:853–866. [DOI] [PubMed] [Google Scholar]
50.Belgum, J. H., and D. R. Copenhagen. 1988. Synaptic transfer of rod signals to horizontal and bipolar cells in the retina of the toad (Bufo marinus). J. Physiol. 396:225–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
51.Walraven, J., C. Enroth-Cugell, D. C. Hood, D. I. A. MacLeod, and J. L. Schnapf. 1990. Control of visual sensitivity. In Visual Perception: The Neurophysiological Foundations. L. Spillman, and J. S. Werner, editors. Academic Press, San Diego. 53–101.
52.Field, G. D., A. P. Sampath, and F. Rieke. 2005. Retinal processing near absolute threshold: from behavior to mechanism. In Annual Review of Physiology, Vol. 67. J. F. Hoffman, editor. Annual Reviews, Palo Alto, CA. 491–514. [DOI] [PubMed]
53.Taylor, W. R., and R. G. Smith. 2004. Transmission of scotopic signals from the rod to rod-bipolar cell in the mammalian retina. Vision Res. 44:3269–3276. [DOI] [PubMed] [Google Scholar]
54.Rieke, F., and D. Warland. R. R. de Ruyter van Steveninck, and W. Bialek. 1997. Spikes: Exploring the Neural Code. MIT Press, Cambridge, MA.
55.Green, D. M., and J. A. Swets. 1966. Signal Detection Theory and Psychophysics. John Wiley, New York. 151–179.
56.Berntson, A., R. G. Smith, and W. R. Taylor. 2004. Transmission of single photon signals through a binary synapse in the mammalian retina. Vis. Neurosci. 21:693–702. [DOI] [PubMed] [Google Scholar]
57.de Ruyter van Steveninck, R. R., G. D. Lewen, S. P. Strong, R. Koberle, and W. Bialek. 1997. Reproducibility and variability in neural spike trains. Science. 275:1805–1808. [DOI] [PubMed] [Google Scholar]
58.Berry, M. J., and M. Meister. 1998. Refractoriness and neural precision. J. Neurosci. 18:2200–2211. [DOI] [PMC free article] [PubMed] [Google Scholar]
59.Uzzell, V. J., and E. J. Chichilnisky. 2004. Precision of spike trains in primate retinal ganglion cells. J. Neurophysiol. 92:780–789. [DOI] [PubMed] [Google Scholar]
60.Stevens, C. F., and Y. Wang. 1995. Facilitation and depression at single central synapses. Neuron. 14:795–802. [DOI] [PubMed] [Google Scholar]
61.Korn, H., A. Mallet, A. Triller, and D. S. Faber. 1982. Transmission at a central inhibitory synapse. II. Quantal description of release, with a physical correlate for binomial n. J. Neurophysiol. 48:679–707. [DOI] [PubMed] [Google Scholar]
62.Redman, S. 1990. Quantal analysis of synaptic potentials in neurons of the central nervous system. Physiol. Rev. 70:165–198. [DOI] [PubMed] [Google Scholar]
63.Korn, H., and D. S. Faber. 1991. Quantal analysis and synaptic efficacy in the CNS. Trends Neurosci. 14:439–445. [DOI] [PubMed] [Google Scholar]
64.Schikorski, T., and C. F. Stevens. 1997. Quantitative ultrastructural analysis of hippocampal excitatory synapses. J. Neurosci. 17:5858–5867. [DOI] [PMC free article] [PubMed] [Google Scholar]
65.Hjelmstad, G. O., R. A. Nicoll, and R. C. Malenka. 1997. Synaptic refractory period provides a measure of probability of release in the hippocampus. Neuron. 19:1309–1318. [DOI] [PubMed] [Google Scholar]
66.Rieke, F., and D. A. Baylor. 1998. Origin of reproducibility in the responses of retinal rods to single photons. Biophys. J. 75:1836–1857. [DOI] [PMC free article] [PubMed] [Google Scholar]
67.Field, G. D., and F. Rieke. 2002b. Mechanisms regulating variability of the single photon responses of mammalian rod photoreceptors. Neuron. 35:733–747. [DOI] [PubMed] [Google Scholar]
68.Hamer, R. D., S. C. Nicholas, D. Tranchina, P. A. Liebman, and T. D. Lamb. 2004. Multiple steps of phosphorylation of activated rhodopsin can account for the reproducibility of vertebrate rod single-photon responses. J. Gen. Physiol. 122:419–444. [DOI] [PMC free article] [PubMed] [Google Scholar]
69.Collins, M. O., Y. Lu, M. P. Coba, H. Husi, I. Campuzano, W. P. Blackstock, J. S. Choudhary, and S. G. N. Grant. 2005. Proteomic analysis of in vivo phosphorylated synaptic proteins. J. Biol. Chem. 280:5972–5982. [DOI] [PubMed] [Google Scholar]
70.Picaud, S., H. P. Larsson, D. P. Wellis, H. Lecar, and F. Werblin. 1995. Cone photoreceptors respond to their own glutamate release in the tiger salamander. Proc. Natl. Acad. Sci. USA. 92:9417–9421. [DOI] [PMC free article] [PubMed] [Google Scholar]
71.Koulen, P. 1999. Clustering of neurotransmitter receptors in the mammalian retina. J. Membr. Biol. 171:97–105. [DOI] [PubMed] [Google Scholar]
72.Barnes, S., and Q. Bui. 1991. Modulation of calcium-activated chloride current via pH-induced changes of calcium channel properties in cone photoreceptors. J. Neurosci. 11:4015–4023. [DOI] [PMC free article] [PubMed] [Google Scholar]
73.Barnes, S., V. Merchant, and F. Mahmud. 1993. Modulation of transmission gain by protons at the photoreceptor output synapse. Proc. Natl. Acad. Sci. USA. 90:10081–10085.7694280 [Google Scholar]
74.DeVries, S. H. 2001. Exocytosed protons feedback to suppress the Ca2+ current in mammalian cone photoreceptors. Neuron. 32:1107–1117. [DOI] [PubMed] [Google Scholar]
75.Hirasawa, H., and A. Kaneko. 2003. pH changes in the invaginating synaptic cleft mediate feedback from horizontal cells to cone photoreceptors by modulating Ca2+ channels. J. Gen. Physiol. 122:657–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
76.Miesenbock, G., D. A. De Angelis, and J. E. Rothman. 1998. Visualizing secretion and synaptic transmission with pH-sensitive green fluorescent proteins. Nature. 394:192–195. [DOI] [PubMed] [Google Scholar]
77.Gandhi, S. P., and C. F. Stevens. 2003. Three modes of synaptic vesicular recycling revealed by single-vesicle imaging. Nature. 423:607–613. [DOI] [PubMed] [Google Scholar]
78.Aravanis, A. M., J. L. Pyle, and R. W. Tsien. 2003. Single synaptic vesicles fusing transiently and successively without loss of identity. Nature. 423:643–647. [DOI] [PubMed] [Google Scholar]
79.von Gersdorff, H., and G. Matthews. 1994. Dynamics of synaptic vesicle exocytosis and membrane retrieval in synaptic terminals. Nature. 367:735–739. [DOI] [PubMed] [Google Scholar]
80.von Gersdorff, H., N. Vardi, G. Matthews, and P. Sterling. 1996. Evidence that vesicles on the synaptic ribbon of retinal bipolar neurons can be rapidly released. Neuron. 16:1221–1227. [DOI] [PubMed] [Google Scholar]
81.Herr, S., K. Klug, P. Sterling, and S. Schein. 2003. Inner S-cone bipolar cells provide all of the central elements for S cones in Macaque retina. J. Comp. Neurol. 457:185–201. [DOI] [PubMed] [Google Scholar]
82.Nakajima, Y., H. Iwakabe, C. Akazawa, H. Nawa, R. Shigemoto, N. Mizuno, and S. Nakanishi. 1993. Molecular characterization of a novel retinal metabotropic glutamate receptor mGluR6 with a high agonist selectivity for L-2-amino-4-phosphonobutyrate. J. Biol. Chem. 268:11868–11873. [PubMed] [Google Scholar]
83.Vardi, N., and K. Morigiwa. 1997. ON cone bipolar cells in rat express the metabotropic receptor mGluR6. Vis. Neurosci. 14:789–794. [DOI] [PubMed] [Google Scholar]
84.Haverkamp, S., U. Grünert, and H. Wässle. 2001. The synaptic architecture of AMPA receptors at the cone pedicle of the primate retina. J. Neurosci. 21:2488–2500. [DOI] [PMC free article] [PubMed] [Google Scholar]
85.Berntson, A., and W. R. Taylor. 2003. The unitary event amplitude of mouse retinal on-cone bipolar cells. Vis. Neurosci. 20:621–626. [DOI] [PubMed] [Google Scholar]
86.Laughlin, B., and R. R. de Ruyter van Steveninck. 1996. Measurements of signal transfer and noise suggest new model for graded transmission at an adapting retinal synapse. J. Physiol. 494:19. [Google Scholar]
87.Fain, G. 2003. Sensory Transduction. Sinauer Associates, Sunderland, MA.
88.Geisler, C. D. 1998. From Sound to Synapse. Physiology of the Mammalian Ear. Oxford University Press, New York..
89.Glowatzki, E., and P. A. Fuchs. 2002. Transmitter release at the hair cell ribbon synapse. Nat. Neurosci. 5:147–154. [DOI] [PubMed] [Google Scholar]
90.Siegel, J. H. 1992. Spontaneous synaptic potentials from afferent terminals in the guinea pig cochlea. Hear. Res. 59:85–92. [DOI] [PubMed] [Google Scholar]
91.Liberman, M. C. 1980. Morphological differences among radial afferent fibers in the cat cochlea: an electron-microscopic study of serial sections. Hear. Res. 3:45–63. [DOI] [PubMed] [Google Scholar]
92.Liberman, M. C. 1982. Single-neuron labeling in the cat auditory nerve. Science. 216:1239–1241. [DOI] [PubMed] [Google Scholar]
93.Sewell, W. F. 1990. Synaptic potentials in afferent fibers innervating hair cells of the lateral line organ in Xenopus laevis. Hear. Res. 44:71–81. [DOI] [PubMed] [Google Scholar]
94.Tricas, T. C., and S. M. Highstein. 1991. Action of the octavolateralis efferent system upon the lateral line of free-swimming toadfish, Opsanus tau. J. Comp. Physiol. [A]. 169:25–37. [DOI] [PubMed] [Google Scholar]
95.von Gersdorff, H. 2001. Synaptic ribbons: versatile signal transducers. Neuron. 29:7–10. [DOI] [PubMed] [Google Scholar]
96.Sterling, P., and G. Matthews. 2005. Structure and function of ribbon synapses. Trends Neurosci. 28:20–29. [DOI] [PubMed] [Google Scholar]
97.Auger, C., and A. Marty. 2000. Quantal currents at single-site central synapses. J. Physiol. 526:3–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
98.Edmonds, B. W., F. D. Gregory, and F. E. Schweizer. 2004. Evidence that fast exocytosis can be predominantly mediated by vesicles not docked at active zones in frog saccular hair cells. J. Physiol. 560:439–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
99.Parsons, T. D., and P. Sterling. 2003. Synaptic ribbon: conveyor belt or safety belt? Neuron. 37:379–382. [DOI] [PubMed] [Google Scholar]
100.Heidelberger, R., C. Heinemann, E. Neher, and G. Matthews. 1994. Calcium dependence of the rate of exocytosis in a synaptic terminal. Nature. 371:513–515. [DOI] [PubMed] [Google Scholar]
101.Singer, J. H., L. Lassova, N. Vardi, and J. S. Diamond. 2004. Coordinated multivesicular release at a mammalian ribbon synapse. Nat. Neurosci. 7:826–833. [DOI] [PubMed] [Google Scholar]
102.Douglass, J. K., L. Wilkens, L. Pantazelou, and F. Moss. 1993. Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance. Nature. 365:337–340. [DOI] [PubMed] [Google Scholar]
103.Gammaitoni, L., P. M. Hanggi, P. Jung, and F. Marchesoni. 1998. Stochastic resonance. Rev. Mod. Phys. 70:223–287. [Google Scholar]
104.Kara, P., P. Reinagel, and R. C. Reid. 2000. Low response variability in simultaneously recorded retinal, thalamic, and cortical neurons. Neuron. 27:635–646. [DOI] [PubMed] [Google Scholar]
105.Barlow, H. B., W. R. Levick, and M. Yoon. 1971. Responses to single quanta of light in retinal ganglion cells of the cat. Vision Res. S3:87–101. [DOI] [PubMed] [Google Scholar]
106.Cox, D. R. 1962. Renewal Theory. Methuen, London.
107.Wickens, T. D. 1982. Models for Behavior: Stochastic Processes in Psychology. W. H. Freeman, San Francisco.
108.Morlat, G., and É. Borel. 1952. Sur une généralisation de loi de Poisson. Comptes Rendus. 234:933–935. [Google Scholar]
109.Johnson, N. L., S. Kotz, and A. W. Kemp. 1992. Univariate Discrete Distributions, 2nd ed. Wiley Interscience. John Wiley & Sons, New York.
110.Horowitz, P., and W. Hill. 1980. The Art of Electronics. Cambridge University Press, Cambridge.

[bib1] 1.Hood, D. C., and M. A. Finkelstein. 1986. Sensitivity to light. In Handbook of Perception and Human Performance, Vol. 1: Sensory Processes and Perception. K. R. Boff, L. Kaufman, and J. P. Thomas, editors. John Wiley & Sons, New York. Chapter 5.

[bib2] 2.Rodieck, R. W. 1998. The First Steps in Seeing. Sinauer, Sunderland, MA. Chapter 7.

[bib3] 3.Hecht, S., S. Shlaer, and M. H. Pirenne. 1942. Energy quanta and vision. J. Gen. Physiol. 25:819–840. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib4] 4.van der Velden, H. A. 1946. The number of quanta necessary for the perception of light in the human eye. Ophthalmologica. 111:321–331. [DOI] [PubMed] [Google Scholar]

[bib5] 5.Sakitt, B. 1972. Counting every quantum. J. Physiol. 223:131–150. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib6] 6.Schneeweis, D. M., and J. L. Schnapf. 1995. Photovoltage of rods and cones in the macaque retina. Science. 268:1053–1056. [DOI] [PubMed] [Google Scholar]

[bib7] 7.Schneeweis, D. M., and J. L. Schnapf. 2000. Noise and light adaptation in rods of the macaque monkey. Vis. Neurosci. 17:659–666. [DOI] [PubMed] [Google Scholar]

[bib8] 8.Field, G. D., and F. Rieke. 2002a. Nonlinear signal transfer from mouse rods to bipolar cells and implications for visual sensitivity. Neuron. 34:773–785. [DOI] [PubMed] [Google Scholar]

[bib9] 9.Robson, J. G., H. Maeda, S. M. Saszik, and L. J. Frishman. 2004. In vivo studies of signaling in rod pathways of the mouse using the electroretinogram. Vision Res. 44:3253–3268. [DOI] [PubMed] [Google Scholar]

[bib10] 10.Sampath, A. P., and F. Rieke. 2004. Selective transmission of single photon responses by saturation at the rod-to-rod bipolar synapse. Neuron. 41:431–443. [DOI] [PubMed] [Google Scholar]

[bib11] 11.Baylor, D. A., B. J. Nunn, and J. L. Schnapf. 1984. The photocurrent, noise and spectral sensitivity of rods of the monkey Macaca fascicularis. J. Physiol. 357:575–607. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib12] 12.van Rossum, M. C., and R. G. Smith. 1998. Noise removal at the rod synapse of mammalian retina. Vis. Neurosci. 15:809–821. [DOI] [PubMed] [Google Scholar]

[bib13] 13.Falk, G., and P. Fatt. 1972. Physical changes induced by light in the rod outer segment of vertebrates. In Handbook of Sensory Physiology, Vol. VII/1. H. J. A. Dartnall, editor. Springer-Verlag. Berlin. 200–244.

[bib14] 14.Fatt, P., and B. Katz. 1952. Spontaneous subthreshold activity at motor nerve endings. J. Physiol. 117:109–128. [PMC free article] [PubMed] [Google Scholar]

[bib15] 15.del Castillo, J., and J. B. Katz. 1953. Statistical nature of facilitation at a single nerve-muscle junction. Nature. 171:1016–1017. [DOI] [PubMed] [Google Scholar]

[bib16] 16.Katz, B., and R. Miledi. 1965. The measurement of synaptic delay, and the time course of acetylcholine release at the neuromuscular junction. Proc. R. Soc. Lond. B Biol. Sci. 161:483–495. [DOI] [PubMed] [Google Scholar]

[bib17] 17.Katz, B. 1969. The release of neural transmitter substances. Liverpool University Press, Liverpool.

[bib18] 18.Barrett, E. F., and C. F. Stevens. 1972. The kinetics of transmitter release at the frog neuromuscular junction. J. Physiol. 227:691–708. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib19] 19.Allen, C., and C. F. Stevens. 1994. An evaluation of causes for unreliability of synaptic transmission. Proc. Natl. Acad. Sci. USA. 91:10380–10383. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib20] 20.Bekkers, J. M., and C. F. Stevens. 1994. The nature of quantal transmission at central excitatory synapses. Adv. Second Messenger Phosphoprotein Res. 29:261–273. [DOI] [PubMed] [Google Scholar]

[bib21] 21.Rao-Mirotznik, R., G. Buchsbaum, and P. Sterling. 1998. Transmitter concentration at a three-dimensional synapse. J. Neurophysiol. 80:3163–3172. [DOI] [PubMed] [Google Scholar]

[bib22] 22.Baylor, D. 1996. How photons start vision. Proc. Natl. Acad. Sci. USA. 93:560–565. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib23] 23.Bader, C. R., D. Bertrand, and E. A. Schwartz. 1982. Voltage-activated and calcium-activated currents studied in solitary rod inner segments from the salamander retina. J. Physiol. 331:253–284. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib24] 24.Corey, D. P., J. M. Dubinsky, and E. A. Schwartz. 1984. The calcium current in inner segments of rods from the salamander (Ambystoma tigrinum) retina. J. Physiol. 354:557–575. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib25] 25.Rieke, F., and E. A. Schwartz. 1996. Asynchronous transmitter release: control of exocytosis and endocytosis at the salamander rod synapse. J. Physiol. 493:1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib26] 26.Taylor, W. R., and C. Morgans. 1998. Localization and properties of voltage-gated calcium channels in cone photoreceptors of Tupaia belangeri. Vis. Neurosci. 15:541–552. [DOI] [PubMed] [Google Scholar]

[bib27] 27.Hille, B. 1984. Ionic channels of excitable membranes. Sinauer Associates: Sunderland, MA.

[bib28] 28.Rieke, F., and E. A. Schwartz. 1994. A cGMP-gated current can control exocytosis at cone synapses. Neuron. 13:863–873. [DOI] [PubMed] [Google Scholar]

[bib29] 29.Wilkinson, M. F., and S. Barnes. 1996. The dihydropyridine-sensitive calcium channel subtype in cone photoreceptors. J. Gen. Physiol. 107:621–630. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib30] 30.Schmitz, Y., and P. Witkovsky. 1997. Dependence of photoreceptor glutamate release on a dihydropyridine-sensitive calcium channel. Neuroscience. 78:1209–1216. [DOI] [PubMed] [Google Scholar]

[bib31] 31.Witkovsky, P., Y. Schmitz, A. Akopian, D. Krizaj, and D. Tranchina. 1997. Gain of rod to horizontal cell synaptic transfer: relation to glutamate release and a dihydropyridine-sensitive calcium current. J. Neurosci. 17:7297–7306. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib32] 32.Nachman-Clewner, M., R. St. Jules, and E. Townes-Anderson. 1999. L-type calcium channels in the photoreceptor ribbon synapse: localization and role in plasticity. J. Comp. Neurol. 415:1–16. [PubMed] [Google Scholar]

[bib33] 33.Wässle, H., S. Haverkamp, U. Grünert, and C. W. Morgans. 2003. The cone pedicle, the first synapse in the retina. In The Neural Basis of Early Vision. A. Kaneko, editor. Springer Verlag, Tokyo. 19–38.

[bib34] 34.Thoreson, W. B., R. Nitzan, and R. F. Miller. 1997. Reducing extracellular Cl⁻ suppresses dihydropyridine-sensitive Ca²⁺ currents and synaptic transmission in amphibian photoreceptors. J. Neurophysiol. 77:2175–2190. [DOI] [PubMed] [Google Scholar]

[bib35] 35.Armstrong-Gold, C. E., and F. Rieke. 2003. Bandpass filtering at the rod to second-order cell synapse in salamander (Ambystoma tigrinum) retina. J. Neurosci. 23:3796–3806. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib36] 36.Thoreson, W. B., R. Katalin, E. Townes-Anderson, and R. Heidelberger. 2004. A highly Ca²⁺-sensitive pool of vesicles contributes to linearity at the rod photoreceptor ribbon synapse. Neuron. 42:595–605. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib37] 37.Migdale, K., S. Herr, K. Klug, K. Ahmad, K. Linberg, P. Sterling, and S. Schein. 2003. Two ribbon synaptic units in rod photoreceptors of macaque, human, and cat. J. Comp. Neurol. 455:100–112. [DOI] [PubMed] [Google Scholar]

[bib38] 38.Townes-Anderson, E., P. R. MacLeish, and E. Raviola. 1985. Rod cells dissociated from mature salamander retina: ultrastructure and uptake of horseradish peroxidase. J. Cell Biol. 100:175–188. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib39] 39.Rieke, F., and D. A. Baylor. 1996. Molecular origin of continuous dark noise in rod photoreceptors. Biophys. J. 71:2553–2572. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib40] 40.Graham, C. H., and R. Margaria. 1935. Area and the intensity-time relation in the peripheral retina. Am. J. Physiol. 113:299–305. [Google Scholar]

[bib41] 41.Barlow, H. B. 1957. Increment thresholds at low intensities considered as signal/noise discrimination. J. Physiol. 136:469–488. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib42] 42.Sperling, H. G., and C. L. Jolliffe. 1965. Intensity-time relationships at threshold for spectral stimuli in human vision. J. Opt. Soc. Am. 55:191–199. [Google Scholar]

[bib43] 43.Baumgardt, E., and B. Hillmann. 1961. Duration and size as determinants of peripheral retinal response. J. Opt. Soc. Am. 51:340–344. [DOI] [PubMed] [Google Scholar]

[bib44] 44.Robson, J. G., and L. J. Frishman. 1999. Dissecting the dark-adapted electroretinogram. Doc. Ophthalmol. 95:187–215. [DOI] [PubMed] [Google Scholar]

[bib45] 45.Baylor, D. A., G. Matthews, and K.-W. Yau. 1980. Two components electrical dark noise in toad rod outer segments. J. Physiol. 309:591–621. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib46] 46.Mastronarde, D. N. 1983. Correlated firing of cat retinal ganglion cells. II. Responses of X- and Y-cells to single quantal events. J. Neurophysiol. 49:325–349. [DOI] [PubMed] [Google Scholar]

[bib47] 47.Copenhagen, D. R., K. Donner, and T. Reuter. 1987. Ganglion cell performance at absolute threshold in toad retina: Effects of dark events in rods. J. Physiol. 393:667–680. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib48] 48.Barlow, H. B. 1956. Retinal noise and absolute threshold. J. Opt. Soc. Am. 8:634–639. [DOI] [PubMed] [Google Scholar]

[bib49] 49.Donner, K. 1992. Noise and the absolute thresholds of cone and rod vision. Vision Res. 32:853–866. [DOI] [PubMed] [Google Scholar]

[bib50] 50.Belgum, J. H., and D. R. Copenhagen. 1988. Synaptic transfer of rod signals to horizontal and bipolar cells in the retina of the toad (Bufo marinus). J. Physiol. 396:225–245. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib51] 51.Walraven, J., C. Enroth-Cugell, D. C. Hood, D. I. A. MacLeod, and J. L. Schnapf. 1990. Control of visual sensitivity. In Visual Perception: The Neurophysiological Foundations. L. Spillman, and J. S. Werner, editors. Academic Press, San Diego. 53–101.

[bib52] 52.Field, G. D., A. P. Sampath, and F. Rieke. 2005. Retinal processing near absolute threshold: from behavior to mechanism. In Annual Review of Physiology, Vol. 67. J. F. Hoffman, editor. Annual Reviews, Palo Alto, CA. 491–514. [DOI] [PubMed]

[bib53] 53.Taylor, W. R., and R. G. Smith. 2004. Transmission of scotopic signals from the rod to rod-bipolar cell in the mammalian retina. Vision Res. 44:3269–3276. [DOI] [PubMed] [Google Scholar]

[bib54] 54.Rieke, F., and D. Warland. R. R. de Ruyter van Steveninck, and W. Bialek. 1997. Spikes: Exploring the Neural Code. MIT Press, Cambridge, MA.

[bib55] 55.Green, D. M., and J. A. Swets. 1966. Signal Detection Theory and Psychophysics. John Wiley, New York. 151–179.

[bib56] 56.Berntson, A., R. G. Smith, and W. R. Taylor. 2004. Transmission of single photon signals through a binary synapse in the mammalian retina. Vis. Neurosci. 21:693–702. [DOI] [PubMed] [Google Scholar]

[bib57] 57.de Ruyter van Steveninck, R. R., G. D. Lewen, S. P. Strong, R. Koberle, and W. Bialek. 1997. Reproducibility and variability in neural spike trains. Science. 275:1805–1808. [DOI] [PubMed] [Google Scholar]

[bib58] 58.Berry, M. J., and M. Meister. 1998. Refractoriness and neural precision. J. Neurosci. 18:2200–2211. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib59] 59.Uzzell, V. J., and E. J. Chichilnisky. 2004. Precision of spike trains in primate retinal ganglion cells. J. Neurophysiol. 92:780–789. [DOI] [PubMed] [Google Scholar]

[bib60] 60.Stevens, C. F., and Y. Wang. 1995. Facilitation and depression at single central synapses. Neuron. 14:795–802. [DOI] [PubMed] [Google Scholar]

[bib61] 61.Korn, H., A. Mallet, A. Triller, and D. S. Faber. 1982. Transmission at a central inhibitory synapse. II. Quantal description of release, with a physical correlate for binomial n. J. Neurophysiol. 48:679–707. [DOI] [PubMed] [Google Scholar]

[bib62] 62.Redman, S. 1990. Quantal analysis of synaptic potentials in neurons of the central nervous system. Physiol. Rev. 70:165–198. [DOI] [PubMed] [Google Scholar]

[bib63] 63.Korn, H., and D. S. Faber. 1991. Quantal analysis and synaptic efficacy in the CNS. Trends Neurosci. 14:439–445. [DOI] [PubMed] [Google Scholar]

[bib64] 64.Schikorski, T., and C. F. Stevens. 1997. Quantitative ultrastructural analysis of hippocampal excitatory synapses. J. Neurosci. 17:5858–5867. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib65] 65.Hjelmstad, G. O., R. A. Nicoll, and R. C. Malenka. 1997. Synaptic refractory period provides a measure of probability of release in the hippocampus. Neuron. 19:1309–1318. [DOI] [PubMed] [Google Scholar]

[bib66] 66.Rieke, F., and D. A. Baylor. 1998. Origin of reproducibility in the responses of retinal rods to single photons. Biophys. J. 75:1836–1857. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib67] 67.Field, G. D., and F. Rieke. 2002b. Mechanisms regulating variability of the single photon responses of mammalian rod photoreceptors. Neuron. 35:733–747. [DOI] [PubMed] [Google Scholar]

[bib68] 68.Hamer, R. D., S. C. Nicholas, D. Tranchina, P. A. Liebman, and T. D. Lamb. 2004. Multiple steps of phosphorylation of activated rhodopsin can account for the reproducibility of vertebrate rod single-photon responses. J. Gen. Physiol. 122:419–444. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib69] 69.Collins, M. O., Y. Lu, M. P. Coba, H. Husi, I. Campuzano, W. P. Blackstock, J. S. Choudhary, and S. G. N. Grant. 2005. Proteomic analysis of in vivo phosphorylated synaptic proteins. J. Biol. Chem. 280:5972–5982. [DOI] [PubMed] [Google Scholar]

[bib70] 70.Picaud, S., H. P. Larsson, D. P. Wellis, H. Lecar, and F. Werblin. 1995. Cone photoreceptors respond to their own glutamate release in the tiger salamander. Proc. Natl. Acad. Sci. USA. 92:9417–9421. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib71] 71.Koulen, P. 1999. Clustering of neurotransmitter receptors in the mammalian retina. J. Membr. Biol. 171:97–105. [DOI] [PubMed] [Google Scholar]

[bib72] 72.Barnes, S., and Q. Bui. 1991. Modulation of calcium-activated chloride current via pH-induced changes of calcium channel properties in cone photoreceptors. J. Neurosci. 11:4015–4023. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib73] 73.Barnes, S., V. Merchant, and F. Mahmud. 1993. Modulation of transmission gain by protons at the photoreceptor output synapse. Proc. Natl. Acad. Sci. USA. 90:10081–10085.7694280 [Google Scholar]

[bib74] 74.DeVries, S. H. 2001. Exocytosed protons feedback to suppress the Ca2+ current in mammalian cone photoreceptors. Neuron. 32:1107–1117. [DOI] [PubMed] [Google Scholar]

[bib75] 75.Hirasawa, H., and A. Kaneko. 2003. pH changes in the invaginating synaptic cleft mediate feedback from horizontal cells to cone photoreceptors by modulating Ca2+ channels. J. Gen. Physiol. 122:657–671. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib76] 76.Miesenbock, G., D. A. De Angelis, and J. E. Rothman. 1998. Visualizing secretion and synaptic transmission with pH-sensitive green fluorescent proteins. Nature. 394:192–195. [DOI] [PubMed] [Google Scholar]

[bib77] 77.Gandhi, S. P., and C. F. Stevens. 2003. Three modes of synaptic vesicular recycling revealed by single-vesicle imaging. Nature. 423:607–613. [DOI] [PubMed] [Google Scholar]

[bib78] 78.Aravanis, A. M., J. L. Pyle, and R. W. Tsien. 2003. Single synaptic vesicles fusing transiently and successively without loss of identity. Nature. 423:643–647. [DOI] [PubMed] [Google Scholar]

[bib79] 79.von Gersdorff, H., and G. Matthews. 1994. Dynamics of synaptic vesicle exocytosis and membrane retrieval in synaptic terminals. Nature. 367:735–739. [DOI] [PubMed] [Google Scholar]

[bib80] 80.von Gersdorff, H., N. Vardi, G. Matthews, and P. Sterling. 1996. Evidence that vesicles on the synaptic ribbon of retinal bipolar neurons can be rapidly released. Neuron. 16:1221–1227. [DOI] [PubMed] [Google Scholar]

[bib81] 81.Herr, S., K. Klug, P. Sterling, and S. Schein. 2003. Inner S-cone bipolar cells provide all of the central elements for S cones in Macaque retina. J. Comp. Neurol. 457:185–201. [DOI] [PubMed] [Google Scholar]

[bib82] 82.Nakajima, Y., H. Iwakabe, C. Akazawa, H. Nawa, R. Shigemoto, N. Mizuno, and S. Nakanishi. 1993. Molecular characterization of a novel retinal metabotropic glutamate receptor mGluR6 with a high agonist selectivity for L-2-amino-4-phosphonobutyrate. J. Biol. Chem. 268:11868–11873. [PubMed] [Google Scholar]

[bib83] 83.Vardi, N., and K. Morigiwa. 1997. ON cone bipolar cells in rat express the metabotropic receptor mGluR6. Vis. Neurosci. 14:789–794. [DOI] [PubMed] [Google Scholar]

[bib84] 84.Haverkamp, S., U. Grünert, and H. Wässle. 2001. The synaptic architecture of AMPA receptors at the cone pedicle of the primate retina. J. Neurosci. 21:2488–2500. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib85] 85.Berntson, A., and W. R. Taylor. 2003. The unitary event amplitude of mouse retinal on-cone bipolar cells. Vis. Neurosci. 20:621–626. [DOI] [PubMed] [Google Scholar]

[bib86] 86.Laughlin, B., and R. R. de Ruyter van Steveninck. 1996. Measurements of signal transfer and noise suggest new model for graded transmission at an adapting retinal synapse. J. Physiol. 494:19. [Google Scholar]

[bib87] 87.Fain, G. 2003. Sensory Transduction. Sinauer Associates, Sunderland, MA.

[bib88] 88.Geisler, C. D. 1998. From Sound to Synapse. Physiology of the Mammalian Ear. Oxford University Press, New York..

[bib89] 89.Glowatzki, E., and P. A. Fuchs. 2002. Transmitter release at the hair cell ribbon synapse. Nat. Neurosci. 5:147–154. [DOI] [PubMed] [Google Scholar]

[bib90] 90.Siegel, J. H. 1992. Spontaneous synaptic potentials from afferent terminals in the guinea pig cochlea. Hear. Res. 59:85–92. [DOI] [PubMed] [Google Scholar]

[bib91] 91.Liberman, M. C. 1980. Morphological differences among radial afferent fibers in the cat cochlea: an electron-microscopic study of serial sections. Hear. Res. 3:45–63. [DOI] [PubMed] [Google Scholar]

[bib92] 92.Liberman, M. C. 1982. Single-neuron labeling in the cat auditory nerve. Science. 216:1239–1241. [DOI] [PubMed] [Google Scholar]

[bib93] 93.Sewell, W. F. 1990. Synaptic potentials in afferent fibers innervating hair cells of the lateral line organ in Xenopus laevis. Hear. Res. 44:71–81. [DOI] [PubMed] [Google Scholar]

[bib94] 94.Tricas, T. C., and S. M. Highstein. 1991. Action of the octavolateralis efferent system upon the lateral line of free-swimming toadfish, Opsanus tau. J. Comp. Physiol. [A]. 169:25–37. [DOI] [PubMed] [Google Scholar]

[bib95] 95.von Gersdorff, H. 2001. Synaptic ribbons: versatile signal transducers. Neuron. 29:7–10. [DOI] [PubMed] [Google Scholar]

[bib96] 96.Sterling, P., and G. Matthews. 2005. Structure and function of ribbon synapses. Trends Neurosci. 28:20–29. [DOI] [PubMed] [Google Scholar]

[bib97] 97.Auger, C., and A. Marty. 2000. Quantal currents at single-site central synapses. J. Physiol. 526:3–11. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib98] 98.Edmonds, B. W., F. D. Gregory, and F. E. Schweizer. 2004. Evidence that fast exocytosis can be predominantly mediated by vesicles not docked at active zones in frog saccular hair cells. J. Physiol. 560:439–450. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib99] 99.Parsons, T. D., and P. Sterling. 2003. Synaptic ribbon: conveyor belt or safety belt? Neuron. 37:379–382. [DOI] [PubMed] [Google Scholar]

[bib100] 100.Heidelberger, R., C. Heinemann, E. Neher, and G. Matthews. 1994. Calcium dependence of the rate of exocytosis in a synaptic terminal. Nature. 371:513–515. [DOI] [PubMed] [Google Scholar]

[bib101] 101.Singer, J. H., L. Lassova, N. Vardi, and J. S. Diamond. 2004. Coordinated multivesicular release at a mammalian ribbon synapse. Nat. Neurosci. 7:826–833. [DOI] [PubMed] [Google Scholar]

[bib102] 102.Douglass, J. K., L. Wilkens, L. Pantazelou, and F. Moss. 1993. Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance. Nature. 365:337–340. [DOI] [PubMed] [Google Scholar]

[bib103] 103.Gammaitoni, L., P. M. Hanggi, P. Jung, and F. Marchesoni. 1998. Stochastic resonance. Rev. Mod. Phys. 70:223–287. [Google Scholar]

[bib104] 104.Kara, P., P. Reinagel, and R. C. Reid. 2000. Low response variability in simultaneously recorded retinal, thalamic, and cortical neurons. Neuron. 27:635–646. [DOI] [PubMed] [Google Scholar]

[bib105] 105.Barlow, H. B., W. R. Levick, and M. Yoon. 1971. Responses to single quanta of light in retinal ganglion cells of the cat. Vision Res. S3:87–101. [DOI] [PubMed] [Google Scholar]

[bib106] 106.Cox, D. R. 1962. Renewal Theory. Methuen, London.

[bib107] 107.Wickens, T. D. 1982. Models for Behavior: Stochastic Processes in Psychology. W. H. Freeman, San Francisco.

[bib108] 108.Morlat, G., and É. Borel. 1952. Sur une généralisation de loi de Poisson. Comptes Rendus. 234:933–935. [Google Scholar]

[bib109] 109.Johnson, N. L., S. Kotz, and A. W. Kemp. 1992. Univariate Discrete Distributions, 2nd ed. Wiley Interscience. John Wiley & Sons, New York.

[bib110] 110.Horowitz, P., and W. Hill. 1980. The Art of Electronics. Cambridge University Press, Cambridge.

PERMALINK

A Clockwork Hypothesis: Synaptic Release by Rod Photoreceptors Must Be Regular

Stan Schein

Kareem M Ahmad

Abstract

INTRODUCTION

FIGURE 1.

METHODS

Production of an Rh* is likely to reduce quantal release rate by ∼20%

FIGURE 2.

FIGURE 4.

Rod voltage noise causes variation in mean Qrate

FIGURE 3.

FIGURE 6.

The Qcount distribution depends on quantal noise as well as continuous rod voltage noise

FIGURE 5.

RESULTS

FIGURE 7.

Based on the Qcount distribution in the dark, the threshold number of quanta sets the rate of false positives

FIGURE 8.

Regular release improves efficiency

FIGURE 9.

Higher release rates permit less regular release

Efficiency and N are not very sensitive to dark noise interval

FIGURE 10.

Larger decrements reduce the degree of regularity needed

FIGURE 11.

DISCUSSION

Overlap between Qcount distributions in the dark and in the light reduces efficiency

FIGURE 12.

Release must be regular

Efficiency of transmission

Regular release could also be modeled by a refractory period

Two kinds of biological mechanism could regularize release of quanta

Each quantum represents a large number of Poisson events

Synaptic ribbons are associated with high rates of release but not necessarily regular release

FIGURE 13.

Acknowledgments

APPENDIX A: QUANTAL NOISE

Interarrival time (interval) distributions

Poisson process

Erlang process

Gamma process

Number distribution

Poisson process

Grouped Poisson number distribution: Erlang process

Grouped Poisson number distribution: gamma process

APPENDIX B: QUANTAL NOISE CAN BE EXPRESSED IN UNITS OF MILLIVOLTS

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Rod voltage noise causes variation in mean Q_rate

The Q_count distribution depends on quantal noise as well as continuous rod voltage noise

Based on the Q_count distribution in the dark, the threshold number of quanta sets the rate of false positives

Overlap between Q_count distributions in the dark and in the light reduces efficiency