Abstract
Recently we have shown that the free energy for pore formation induced by antimicrobial peptides contains a term representing peptide-peptide interactions mediated by membrane thinning. This many-body effect gives rise to the cooperative concentration dependence of peptide activities. Here we performed oriented circular dichroism and x-ray diffraction experiments to study the lipid dependence of this many-body effect. In particular we studied the correlation between lipid's spontaneous curvature and peptide's threshold concentration for pore formation by adding phosphatidylethanolamine and lysophosphocholine to phosphocholine bilayers. Previously it was argued that this correlation exhibited by magainin and melittin supported the toroidal model for the pores. Here we found similar correlations exhibited by melittin and alamethicin. We found that the main effect of varying the spontaneous curvature of lipid is to change the degree of membrane thinning, which in turn influences the threshold concentration for pore formation. We discuss how to interpret the lipid dependence of membrane thinning.
INTRODUCTION
One universal feature of antimicrobial peptides is the cooperative (often described as all-or-none) concentration dependence of their activities. This includes both the bactericidal and hemolytic activities of antimicrobial peptides, only that the lethal concentrations for hemolysis are two to three orders of magnitude higher than that for bactericide (reviewed by Merrifield et al. (1)). This difference is due to the fact that almost all antimicrobial peptides are strongly cationic so they are attracted to the negatively charged lipids on the outer leaflets of bacterial membranes, whereas such electrostatic effect is absent for mammalian membranes, whose outer leaflets are electrically neutral. Indeed a careful analysis by Wieprecht et al. (2) showed that if the bulk peptide concentrations are replaced by surface concentrations (i.e., excluding the electrostatic effect), similar binding constants and similar threshold concentrations for pore formation are obtained for neutral and negatively charged membranes. Excluding the electrostatic effect for the initial binding, the strongly cooperative concentration dependence of the peptide activities implies that the peptide-membrane interactions include a collective (or many-body) effect. The purpose of this article is to show the lipid dependence of this collective effect, and to demonstrate the importance of this effect in the analysis of the mechanism of antimicrobial peptides.
Clearly, the binding states of peptide below and above the threshold concentration are different. When the bound peptide/lipid molar ratio P/L is below the threshold value P/L*, no pores are formed in the membrane (3) and, correspondingly, no leakage is observed from vesicles (2,4–7). This is called the S state (8). All experiments, in particular solid-state NMR (9–12) and fluorescence energy transfer (FET) (13–15), have shown that peptides in the S state are monomers adsorbed on the polar-nonpolar interface of the lipid leaflet. The pore states (the I states) appear only when the concentration P/L exceeds a threshold (2–7). How does the concentration drive the S state toward the I state? One of the most interesting properties of membranes is the possibility that proteins embedded in a membrane can interact with one another via lipid modulation. Although this possibility has long been speculated (16–19), there have not been many explicit examples (20,21) to demonstrate it. We believe that it is the peptide-peptide interaction in the S state mediated by membrane thinning that elevates the energy level of the S state as a function of the peptide concentration P/L. When P/L exceeds the threshold, the energy level of the S state exceeds that of the I state, hence causing the transition from the surface state to the pore state. In a recent series of articles (22–25), we provided a thermodynamic description of this collective effect, and supported it quantitatively with extensive data.
When a factor influences the threshold concentration of an antimicrobial peptide, it can do so by its effect on three aspects of the peptide-lipid interactions: the energy level of the S state, the energy level of the I state, and/or the collective effect. It has been a common practice to study how the threshold concentration is influenced by the variation of peptides or lipids, to gain insight into the mechanism of the peptides (1,5,26,27). For example, correlations have been found between the spontaneous curvature of the lipid and the threshold concentration for vesicle leakage (5,27). This has been argued as a support for the toroidal model. Here we will reanalyze this correlation by experiments that exhibit the many-body effect.
The possibility that amphipathic peptides can form two types of pore has been a fascinating issue. In the barrel-stave model (28), amphipathic peptides form a cylindrical barrel and insert transmembrane; the surrounding lipid molecules are supposed to remain in the bilayer form. In the toroidal model (3,29,30), the lipid leaflet bends continuously through the pore so the two originally separated leaflets are now connected and become one (a topological change that increases the genus by one). On the rim of a toroidal pore the peptides are bound to the interface just as in the S state. From the P/L ratio and the pore size (deduced from neutron in-plane scattering), we found that there are not enough peptides to entirely line the rims of the pores (30). We suggested that peptides are fillers in the headgroup region of the positively curved lipid monolayer so as to relieve the bending stress (30). However neither model has been directly observed. The evidence for either type is, up to now, still indirect (3). It is of great interest to provide experimental support for either model. Using the correlation between the spontaneous curvature of lipid and the threshold concentration to support the toroidal model is intuitively based on the structural difference between the two models. However, this assumes that the spontaneous curvature of lipid mainly affects the energy level of the pore state. Our experiment here will show that the spontaneous curvature of lipid has such a strong effect on membrane thinning that it affects the threshold concentrations of alamethicin and melittin almost equally. Since there is a strong support for the alamethicin pores to be of the barrel-stave type (3), this correlation cannot be used to support the toroidal model.
Earlier, we extensively investigated the behaviors of four different peptides, alamethicin (22–24,31,32), magainin (30,33–36), protegrin (35–38), and melittin (3,22–25,36), in a wide variety of lipid bilayers. We found that the peptide-lipid interactions of magainin, protegrin, and melittin are qualitatively similar, all consistent with forming toroidal pores (3). As mentioned above, alamethicin is consistent with forming barrel-stave pores (3). Thus, in this study, we select alamethicin and melittin as two representative peptides. We study their behaviors in bilayers of varying lipid compositions corresponding to different spontaneous curvatures.
MATERIALS AND METHODS
Materials
1,2-Diphytanoyl-sn-glycero-3-phosphocholine (DPhPC), 1,2-diphytanoyl-sn-glycero-3-phosphoethanolamine (DPhPE), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE), and 1-oleoyl-2-hydroxy-sn-glycero-3-phosphocholine (18:1 LysoPC) were purchased from Avanti Polar Lipids (Alabaster, AL). Alamethicin and melittin were purchased from Sigma Aldrich Chemical (St. Louis, MO). Melittin was of purity 93% HPLC (product No. M-2272). Earlier we compared this product with the sequencing grade (product No. M-1407) (23) and with pure synthetic melittin (3). We did not detect differences in the types of experiments performed here. Polyethylene glycol (PEG400) was purchased from Merck (Hohenfrunn, Germany). All materials were used as delivered.
Sample preparation
In this study, two experimental methods were used. One was oriented circular dichroism (OCD (39,40)) for the measurement of peptide orientation in lipid bilayers. Another was lamellar x-ray diffraction (LXD) for the measurement of membrane thickness. The samples used in both methods were in the form of oriented multilayers, a stack of parallel hydrated lipid bilayers on a solid substrate. The preparation of such oriented samples followed the method described in Ludtke et al. (34). Briefly, lipid and peptide of the chosen peptide/lipid molar ratio (P/L) were codissolved in a solvent of 1:1 (v/v) methanol and chloroform. The lipid concentration was ∼1 mg per 20 μl solvent. The appropriate amount of solution was spread onto a cleaned quartz surface: 5 μl or less solution (depending on the P/L) onto a 12-mm-diameter area for OCD, or 60 μl solution onto an area 18 × 18 mm2 for LXD. When the solvent dried, the sample was vacuumed to remove the remaining solvent residue, and then slowly hydrated with water vapor until it appeared transparent. A good sample was visually smooth, and showed at least five orders of Bragg diffraction by LXD. Four peptide/lipid systems were studied systematically, i.e., melittin in DOPC/DOPE mixtures, melittin in DOPC/18:1 LysoPC mixtures, alamethicin in DPhPC/DPhPE mixtures, and alamethicin in DPhPC/18:1 LysoPC mixtures. These peptide-lipid combinations were chosen for reasons explained in the Results and Analysis section.
OCD measurement
The sample chamber was a cylindrical construction as described in Chen et al. (22). The light beam of the CD spectropolarimeter was along the cylindrical axis, perpendicular to the two parallel quartz windows. One of the windows was the quartz plate on whose inside surface the sample was deposited. The space between the windows was sealed. The rim of this space was used to hold distilled water for a full hydration measurement or a PEG solution for a less than full hydration measurement. The humidity corresponding to a polyethylene glycol (PEG400) solution was measured by a hygrometer in a calibration chamber provided by the hygrometer manufacturer (Rotronic Instrument Co., Huntington, NY). A typical concentration used in this study was 1.00 g of PEG400 in 4.00 g water, which gave a 98.0% relative humidity at 30°C. The outer part of the sample chamber was a thermostat. The temperature was monitored by a Pt100 thermoresistor and controlled by a computer via a feedback thermoelectric module. The temperature could be controlled from 10° to 40°C with the stability of ±0.1°C for several days. The cylindrical sample chamber was allowed to rotate around its axis for the purpose of rotational averaging.
The hydration equilibrium of the sample was ensured by an agreement of at least three OCD spectra measured over a period of 6 h. OCD was measured with a Jasco J-810 spectropolarimeter, with light incident normal to the sample surface (40). The sample was allowed to rotate around the incident light at eight angles equally spaced in one complete rotation. The averaged spectrum of the measurements at eight rotational angles was used for analysis. The rotational average ensured the elimination of possible artifacts due to linear dichroism (40). The background OCD spectra of pure lipid bilayers (i.e., without peptides) were measured separately and were removed from the spectra of the corresponding samples containing peptide.
The reason we chose 98% relative humidity (RH) rather than 100% RH for this experiment was that for both OCD and LXD measurements the sample substrate was oriented vertically. At levels of humidity >98% RH, the membranes on an open sample (i.e., on one substrate) would flow. This is not to say it is impossible to make measurements at 100% RH. An oriented membrane sample could be covered with another substrate to prevent the sample flow, as we have done previously for OCD (22,40) and for LXD (41–43). However, it would take a long equilibrating time to change the hydration of a covered (i.e., two-substrate) sample, and hydration changes are necessary in x-ray experiments for the purpose of phase determination. In our previous experiments (22,23) we have shown that the dependence of the threshold concentration on hydration is gradual. There is no qualitative difference between the states of peptides measured at 98% RH and 100% RH (22,23).
The OCD spectra for the S state and the I state of alamethicin were measured in Chen et al. (22). The OCD spectra for the S state and the I state of melittin were measured previously by Yang et al. (3) in DMPC bilayers in another laboratory. These spectra were remeasured and reproduced here using the instrument described here.
LXD measurement
The sample chamber for LXD was the same as used in our previous studies (44,45), except that the relative humidity was controlled by a series of PEG solutions enclosed inside the chamber. This was to ensure that the hydration levels of the sample were the same in the OCD and LXD measurements. The temperature was set at 30°C, the same temperature for the OCD measurement. In addition to the measurement at 98%RH, a series of measurements were made at lower levels of humidity for the purpose of phase determination. Precise reading for these lower-level humidities was not necessary, because the swelling method for phase determination depended on the precise reading of lamellar repeat spacing only.
LXD was measured with Cu Kα radiation generated from a sealed tube at 30 kV/30 mA by θ-2θ scan from θ = 0.5–7.5° with a step size Δθ = 0.01° at 1 s/step. The equilibrium of the sample at each humidity setting was ensured by an agreement of at least three consecutive diffraction patterns whose average was subsequently analyzed. Only samples that produced at least five discernible diffraction peaks were accepted. Each peptide-lipid combination was measured with at least two separately prepared samples. Each sample was measured twice separately at least 10 h apart to check the reproducibility.
The procedure for data reduction was described in many previous works (34,41,42,44,45). Briefly, the procedure started with the background removal, and the absorption and diffraction volume corrections. Then the integrated peak intensities were corrected for the polarization and the Lorentz factors. The magnitude of the diffraction amplitude was the square root of the integrated intensity. The phases of the amplitudes were determined by the swelling method (46,47). With their phases determined, the diffraction amplitudes were Fourier transformed to obtain the transbilayer electron density profiles. The profiles were not normalized to the absolute scale, but they gave the correct peak-to-peak distances, since the latter are independent of normalization (42).
RESULTS AND ANALYSIS
The experiments were designed to vary the spontaneous curvature of the lipid leaflet by adding phosphoethanolamine (PE) or lysoPC to a PC bilayer (48) and examine its consequences on the threshold concentration P/L*. Since the effect of peptide is most readily measurable in the concentration range from P/L ∼1:10 to ∼1:150, DOPC and DPhPC were chosen for melittin and alamethicin, respectively. (The upper limit of the P/L range is due to the increasing possibility of sample inhomogeneity for P/L >1:10.) The threshold concentration of melittin in pure DOPC is 1:99, and the threshold concentration of alamethicin in pure DPhPC is 1:58 (24). These values of P/L* are in the middle of the measurable range of P/L, allowing room for varying the P/L* in both the positive and negative directions. (For reference, the P/L* for melittin in pure DPhPC is 1:30—too high, and the P/L* for alamethicin in pure DOPC is <1:200—too low (24).)
Peptide orientation by OCD
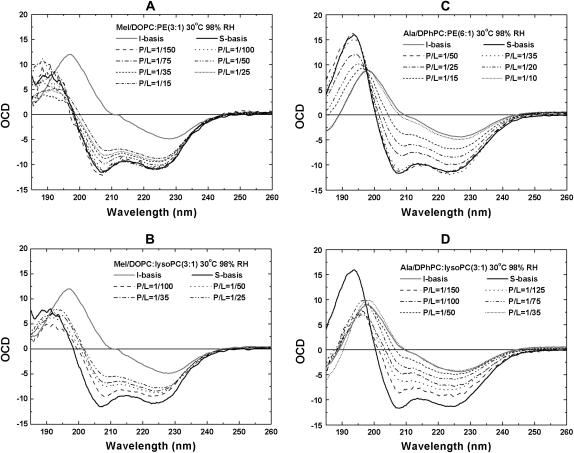
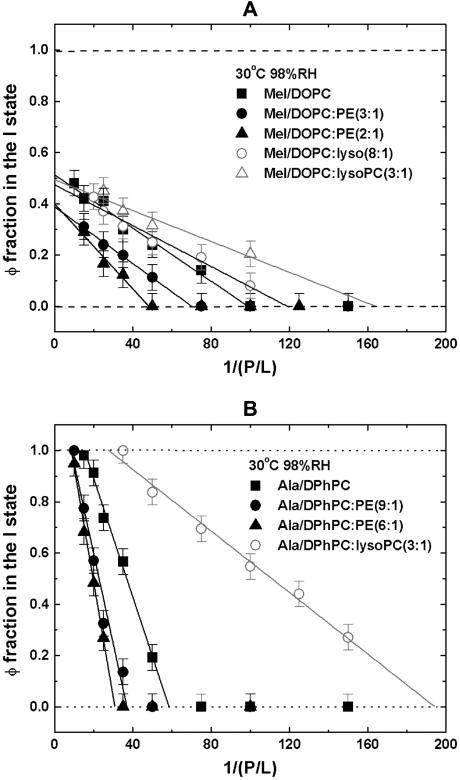
The helical orientation of melittin was measured in five lipid compositions: pure DOPC, DOPC/18:1 lysoPC (3:1), DOPC/18:1 lysoPC (8:1), DOPC/DOPE (2:1), and DOPC/DOPE (3:1). In each lipid composition, the OCD was measured for a series of P/L, including one without peptide (P/L = 0) for the background removal. Two representative series are shown in Fig. 1. The analysis of OCD spectra follows Chen et al. (23). Briefly we found that each spectrum can be fit very well to a linear combination of an I state spectrum and an S state spectrum α[φI + (1 − φ)S], where α is a normalization factor. The I and S spectra were obtained from melittin in DMPC bilayers as described in Yang et al. (3). According to the theory of OCD (40), the I spectrum represents a helix oriented perpendicular to the plane of bilayers and the S spectrum represents a helix oriented parallel to the plane. Furthermore, these two basis spectra have been correlated with neutron in-plane scattering experiments performed on samples showing the same OCD spectra. The I spectrum corresponds to the pore state and the S spectrum corresponds to a state with no pores (3). The linear decompositions of the spectra in Fig. 1, A and B, give the fraction of melittin in the I state, φ, plotted as a function of 1/(P/L) in Fig. 2. We have shown previously that, in all the cases we have measured, if φ is plotted as a function of 1/(P/L) the data break into two straight sections (22), one for the data on  and another for the data
and another for the data 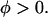 The intersection of these two straight sections defines the threshold concentration P/L* (the theoretical basis is expounded in (22)). Fig. 2 A shows the fraction of melittin in the I state versus 1/(P/L) for all five lipid compositions.
The intersection of these two straight sections defines the threshold concentration P/L* (the theoretical basis is expounded in (22)). Fig. 2 A shows the fraction of melittin in the I state versus 1/(P/L) for all five lipid compositions.
FIGURE 1.
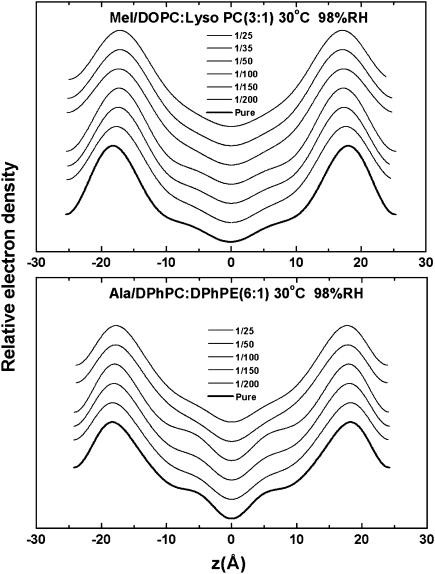
Oriented circular dichroism spectra of melittin in DOPC/DOPE (3:1) (A) and DOPC/18:1 lysoPC (3:1) (B), and of alamethicin in DPhPC/DPhPE (6:1) (C) and DPhPC/18:1 lysoPC (3:1) (D). All measurements were made in a series of P/L at 30°C and 98% RH. The lipid background has been removed from each spectrum. In each melittin panel, the basis spectra for the S state and the I state, obtained independently from melittin in DMPC (3), are shown. In each alamethicin panel, the basis spectra for the S state and the I state were obtained from alamethicin in pure DPhPC (22). Each OCD spectrum is fit with a linear combination of S and I to obtain the fraction of the peptide in the I state.
FIGURE 2.
(A) Fraction of melittin in the I state (or the pore state), φ, is plotted against 1/(P/L) for different lipid systems. (B) The fraction of alamethicin in the I state, φ, is plotted against 1/(P/L) for different lipid systems. The error bars represent the ranges of reproducibility from two independently prepared samples. The data points in the φ > 0 region are least-squares fit to a straight line. The intersection of the line with the φ = 0 base gives the threshold concentration P/L* for each peptide/lipid combination.
The helical orientation of alamethicin was measured in four lipid compositions: pure DPhPC, DPhPC/DPhPE (9:1), DPhPC/DPhPE (6:1), and DPhPC/18:1 lysoPC (3:1). The measurement and analysis of alamethicin OCD are similar to melittin as described previously in Chen et al. (22,23). The I and S spectra of alamethicin have also been independently correlated to the pore states and states without pores, respectively, by neutron in-plane scattering experiments (49,50). Two representative P/L series of OCD spectra are shown in Fig. 1, C and D. The fraction of alamethicin in the I state versus 1/(P/L) for all four lipid compositions are shown in Fig. 2 B.
Membrane thinning by LXD
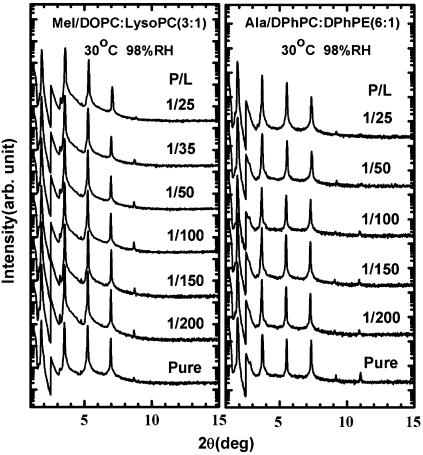
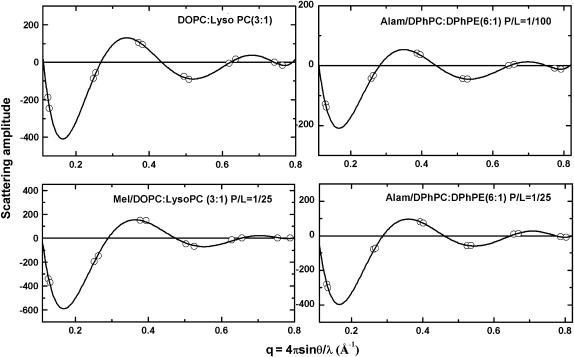
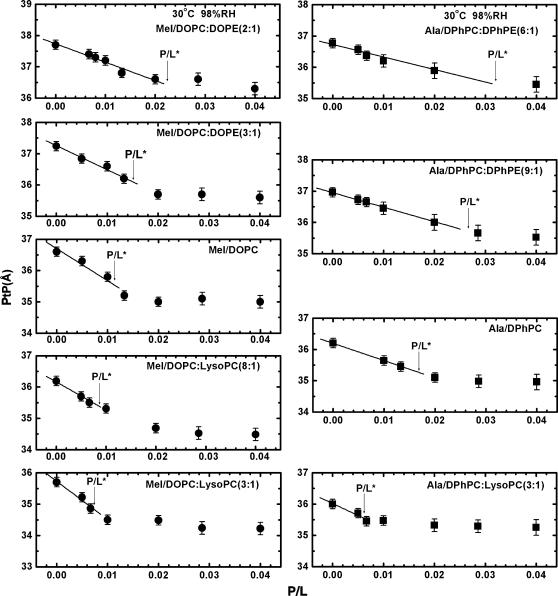
Every OCD sample was measured by LXD under the same condition in which OCD was measured, and at a few lower humidity levels for the purpose of determining the phases of diffraction amplitudes. Representative diffraction patterns, phasing diagrams, and the transmembrane electron density profiles are shown in Figs. 3–5, respectively. Very importantly, we note that every diffraction pattern has only one Bragg series, indicating the homogeneity of the peptide-lipid mixtures. For every lipid mixture, we were concerned about the possibility of phase separations, but we did not find them. From each electron density profile, we measured the peak-to-peak distance (PtP) corresponding to the phosphate-to-phosphate distance, and plot the result as a function of P/L for each lipid composition (Fig. 6). In Fig. 6, we marked the threshold concentration P/L* as determined from the OCD measurements Fig. 2. The data points for P/L < P/L* are least-squares fit to a line. The slope of this line is used for the following analysis.
FIGURE 3.
Representative diffraction patterns. An attenuator was used for the first-order Bragg peak to prevent the photon count from exceeding 104/s. The patterns are displaced for clarity. Note that each pattern consists of one Bragg series only, indicating the homogeneity of the sample.
FIGURE 4.
Representative phasing diagrams by the swelling method. The phases are chosen so that a form factor Fourier-constructed from the diffraction amplitudes measured at one humidity level will go through all the data points (47).
FIGURE 5.
Representative electron density profiles constructed from the measured diffraction amplitudes, displaced for a series of P/L.
FIGURE 6.
Peak-to-peak distance (PtP) versus P/L. The error bars represent the ranges of reproducibility from four measurements, two measurements for each of two independently prepared samples. The arrows indicate the threshold concentration P/L* measured from OCD (Fig. 2). The data points for P/L < P/L* are least-squares fit to a straight line. The slope is used to calculate the membrane area expansion AP per peptide.
Membrane thinning linearly proportional to P/L has been noted since 1995 by Wu et al. (42) (see more references in Lee et al. (24)). This is because the inclusion of peptides at the interface stretches the membrane area. The stretching occurs under the condition that the peptides do not insert transmembrane (the S state). The volume of the hydrocarbon region is conserved. Thus the fractional area increase dA/A is equal to the fractional thickness decrease of the hydrocarbon region 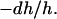 The thickness of the hydrocarbon region h is
The thickness of the hydrocarbon region h is 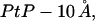 or PtP minus twice the length of the glycerol region (from the phosphate to the first methylene of the hydrocarbon chains). The latter is very close to 10 Å (51–53). We introduce the quantity AP as the area increase due to the addition of one peptide in the S state. Let AL be the cross-sectional area per lipid which is calculated by AL = (chain volume)/(h/2). Then we have
or PtP minus twice the length of the glycerol region (from the phosphate to the first methylene of the hydrocarbon chains). The latter is very close to 10 Å (51–53). We introduce the quantity AP as the area increase due to the addition of one peptide in the S state. Let AL be the cross-sectional area per lipid which is calculated by AL = (chain volume)/(h/2). Then we have 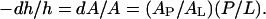 The slope of each line in Fig. 6 is
The slope of each line in Fig. 6 is 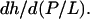 Thus AP is practically a directly measured quantity, i.e., from the measurement of PtP and the well-known values for the lipid chain volumes (52). The measured values of AP for melittin and alamethicin in various lipid compositions are listed in Table 1.
Thus AP is practically a directly measured quantity, i.e., from the measurement of PtP and the well-known values for the lipid chain volumes (52). The measured values of AP for melittin and alamethicin in various lipid compositions are listed in Table 1.
TABLE 1.
Experimental parameters of peptide-lipid interaction pertinent to the mechanism of pore formation
| Peptide | Melittin
|
Alamethicin
|
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Lipid | DOPC/ lysoPC (3:1) | DOPC/ lysoPC (8:1) | DOPC | DOPC/ DOPE (3:1) | DOPC/ DOPE (2:1) | DPhPC/ lysoPC (3:1) | DPhPC | DPhPC/ DPhPE (9:1) | DPhPC/ DPhPE (6:1) |
| h (Å) | 25.7 | 26 | 26.6 | 27.2 | 27.7 | 26 | 26.2 | 27 | 26.8 |
| AL (Å2) | 67 | 71.5 | 74 | 72 | 71 | 78 | 91 | 88 | 89 |
| AP (Å2) | 324 | 271 | 246 | 196 | 162 | 233 | 193 | 165 | 153 |
| (P/L)* | 1/164 | 1/119 | 1/99 | 1/70 | 1/48 | 1/194 | 1/58 | 1/37 | 1/31 |
| β | −1.02 | −1.11 | −0.95 | −1.57 | −1.5 | 0.14 | 0.24 | 0.23 | 0.26 |
| δɛ (kcal/mol) | 6.7 | 6.3 | 5.6 | 6.8 | 6.7 | 1.1 | 1.9 | 2.2 | 2.2 |
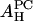 (Å2) (Å2) |
60.3 | 60.1 | 75.6 | 77.6 | |||||
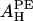 (Å2) (Å2) |
— | 29.5 | — | 40.6 | |||||
Thermodynamic analysis
In four previous articles (22–25) we expounded a thermodynamic theory to explain the observed peptide orientation change and membrane thinning as a function of P/L. We proposed a free energy including three terms: 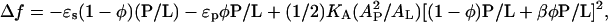 where ɛs and ɛp are the energy per peptide in the S state and the I state, respectively; KA is the area stretch modulus of bilayer (54); and β is a parameter expressing the effect of the I state on the bilayer thickness relative to that of the S state. The meaning of the first two terms is obvious: they represent the two possible states for the peptide. The third term is the elastic energy for thinning the bilayer. The thinning is caused by the peptide adsorption in the bilayer. It is this term that describes the peptide-peptide interaction mediated by membrane deformation (thinning). This interaction is extended, involving all the peptides in the bilayer—a many-body effect.
where ɛs and ɛp are the energy per peptide in the S state and the I state, respectively; KA is the area stretch modulus of bilayer (54); and β is a parameter expressing the effect of the I state on the bilayer thickness relative to that of the S state. The meaning of the first two terms is obvious: they represent the two possible states for the peptide. The third term is the elastic energy for thinning the bilayer. The thinning is caused by the peptide adsorption in the bilayer. It is this term that describes the peptide-peptide interaction mediated by membrane deformation (thinning). This interaction is extended, involving all the peptides in the bilayer—a many-body effect.
The minimization of Δf with respect to φ gives the relation
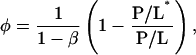 |
(1) |
with the threshold concentration P/L* given by
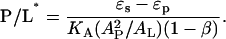 |
(2) |
Equation 1 explains why the fraction of the peptide in the I state φ is a linear function of 1/(P/L). Since the threshold concentration P/L* has been determined by OCD (Fig. 2), the parameter β can be determined from the slope of φ versus 1/(P/L). Thus all the parameters appearing in the free energy Δf are independently determined, except for the energies of the S state and the I state relative to the peptide in solution. Only the relative energy 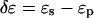 is determined by Eq. 2. The physical meaning for each of the parameters has been discussed extensively in Lee et al. (24). We list the parameter values in Table 1 that will be discussed below.
is determined by Eq. 2. The physical meaning for each of the parameters has been discussed extensively in Lee et al. (24). We list the parameter values in Table 1 that will be discussed below.
DISCUSSION
Research on membrane-active antimicrobial peptides started in the 1960s, when a number of such peptides were discovered (see review by Latorre and Alvarez (55)). Alamethicin from the fungus Trichoderma viride (56) and melittin from bee venom (57,58) were among those more commonly studied. These peptides were noted for their amphiphilicity and their ability to cause ion conduction across membranes. In the 1970s they were mainly studied as molecular models for voltage-gated channels (see reviews for alamethicin(55) and melittin (59)). These experiments were conducted at extremely low peptide concentrations so as to observe single-channel ion conductions. Alamethicin-like peptides could induce fluctuating ion-conducting single channels in such low peptide concentrations under an electric field. (More refined experiments were done later (60).) Melittin also induced fluctuating ion conductance, but unlike alamethicin, its discrete conductance steps were poorly defined, and not reproducible from one laboratory to another (see references in Yang et al. (3)).
The discoveries of cecropins (61), defensins (62), and magainin (63) from animals in the 1980s refocused the peptide-membrane research to peptides' antimicrobial mechanisms. It was noted from the beginning that the lethal concentrations of these peptides are in the micrometer range, corresponding to the bound peptide/lipid molar ratios P/L ∼1:10 to ∼1:100 (1). However, in the early stage of this research much confusion about the states of bound peptides arose from comparisons of experiments performed at different peptide concentrations (31). By now there is at least a universal agreement on the state of bound peptides below the threshold concentrations, i.e., the S state. In this state, the amphiphilic peptides are bound to the polar-nonpolar interface of the lipid bilayer (64). Solid-state NMR (9–12) has consistently shown that helical peptides are bound as monomers, each with its helical axis parallel to the plane of the membrane and rotating rapidly with respect to the membrane normal. In this article, we focus on the question: what causes this state to become unstable at higher peptide concentrations so that peptides make a transition to a state forming pores in the membrane?
Many investigators considered the possibility of peptide association or aggregation. However, repeated experiments with the method of FET (13–15) failed to detect peptide association or aggregation. A careful analysis by Schumann et al. (15) found that not only the peptides were bound to the membrane surface as monomers, but the measured energy transfer was lower than predicted for a random distribution of monomeric peptides (see below). This result is consistent with the fast rotation of peptide around the membrane normal observed by solid-state NMR (11,12). Indeed the Coulomb repulsion should make direct association or aggregation unlikely for highly charged peptides (unless at the presence of di- or trivalent counterions).
A cooperative concentration dependence due to aggregation would make sense if it were in solution, as occurs in critical phenomena of micellar aggregation (65), because in solution there would be no other way for the molecules to interact with each other. However, it has long been realized (16–19) that proteins in membrane can interact with one another via lipid modulation without a direct protein-protein contact. A clear example is the peptide-induced membrane thinning that has been observed in extensive measurements with four different peptides, including alamethicin (22–25,42,43), magainin (34), protegrin (38) and melittin (23–25). A peptide adsorbed at the interface locally expands the area and reduces the chain thickness of the lipid monolayer. Due to the monolayer's resistance to bending, the area of the local thinning extends to a range of 20–50 Å (depending on the values of the monolayer's elastic constants (25,66)). As the concentration of bound peptides increases, the areas of local deformation by individual peptides overlap, resulting in an overall membrane thinning. In such a state, individual peptides experience short-range repulsion from one another due to the monolayer elasticity (66). This is consistent with the FET observation by Schumann et al. (15) that the measured energy transfer was lower than predicted for a random distribution of monomeric peptides.
It should be pointed out that the phenomena described above have been observed both in oriented multilayer experiments and in vesicle experiments. In a vesicle aspiration experiment with melittin, Longo et al. (6) observed a membrane area expansion without a volume change (no leakage) at low peptide concentration, whereas at high peptide concentrations, they observed a membrane area expansion followed by a volume increase, indicating the formation of transmembrane pores.
Correlations between spontaneous curvature and threshold concentration
In this experiment we have examined the effect of PE and lysoPC on the threshold concentration P/L*. Parallel experiments on vesicle leakage have been performed with magainin (5) and melittin (27). Our result for melittin is consistent with the vesicle experiments, i.e., addition of PE increases the peptide threshold concentration for pore formation or vesicle leakage, whereas addition of lysoPC decreases the threshold concentration. However, quantitative comparisons between the structural experiments performed with oriented multilayers and the leakage experiments performed with vesicles are difficult for the following reasons. In a multilayer sample, the P/L ratio is uniform, so it is more likely to exhibit a well-defined threshold concentration for pore formation. In a vesicle experiment, the bound peptide/lipid ratio is likely to vary somewhat from one vesicle to another, so it is less likely to exhibit a sharp threshold concentration. Furthermore, a leakage experiment is a time-dependent measurement depending on many variables, such as the number of pores in a vesicle, the size of the pores, the size of the dye molecules, etc. The degree of leakage should be characterized by a time curve, not by a number.
Nevertheless, both types of experiments showed that PE inhibits and lysoPC facilitates pore formation or vesicle leakage. Since it is well known that PE has a more negative spontaneous curvature than PC (both DOPC and DOPE have a negative curvature (67)), and lysoPC has a positive curvature (68), there is a close correlation between the spontaneous curvature and the threshold concentration. There is also a common perception that the lipid leaflet of a toroidal pore has an overall positive mean curvature whereas the lipid leaflet around a barrel-stave pore has approximately zero curvature. Therefore the evidence of the correlation seems to support the idea that magainin and melittin form toroidal pores, rather than barrel-stave pores (5,27).
As we see in Table 1, the same correlations for melittin, between PE and P/L* and between lysoPC and P/L*, also exist for alamethicin. Furthermore, the degree of change in P/L* from the addition of PE and lysoPC is similar for both peptides. Since it is fairly well established that alamethicin forms barrel-stave pores (see discussion and references in Yang et al. (3)), the effect of PE and lysoPC cannot be used to support toroidal pores.
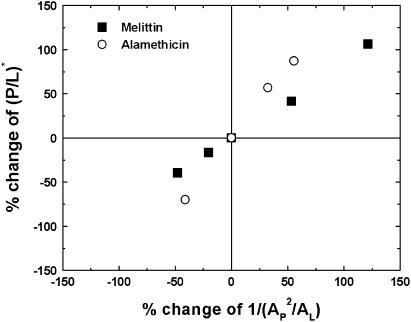
This is because adding PE or lysoPC has a strong effect on membrane thinning regardless of the type of peptide. The membrane thinning effect is directly measured by the value of AP for each peptide in each lipid composition. We see in Table 1 that the value of AP correlates with the value of P/L* for both peptides. The larger the AP, the smaller the threshold concentration P/L* that is equivalent to a stronger peptide activity. If we use the theoretical expression in Eq. 2 for P/L*, the factor depending on the lipid composition is 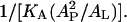 The area stretch modulus KA has been measured for a large number of unsaturated-chain lipids and found to be practically the same for all, ∼240 pN/nm (54). (Here, we assume that DPhPC and DPhPE have a KA similar to that of unsaturated-chain lipids.) Fig. 7 shows that the change in P/L* strongly correlates with the change in the factor
The area stretch modulus KA has been measured for a large number of unsaturated-chain lipids and found to be practically the same for all, ∼240 pN/nm (54). (Here, we assume that DPhPC and DPhPE have a KA similar to that of unsaturated-chain lipids.) Fig. 7 shows that the change in P/L* strongly correlates with the change in the factor 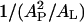 for both melittin and alamethicin.
for both melittin and alamethicin.
FIGURE 7.
Correlation between the threshold concentration P/L* and the thinning effect. Melittin in pure DOPC and alamethicin in pure DPhPC are taken as the reference (central) point. The percent change of P/L* is plotted against the percent change of the factor 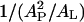 as a result of adding PE or lysoPC to the pure PC bilayers.
as a result of adding PE or lysoPC to the pure PC bilayers.
The energy of the I state relative to the energy of the S state, 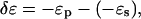 is three times higher for the melittin pore than for the alamethicin pore (Table 1).
is three times higher for the melittin pore than for the alamethicin pore (Table 1). 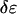 did not change much by the addition of PE or lysoPC (Table 1). It is possible that, in the case of a toroidal pore, the curvature stress of the lipid has been largely relieved by the participation of peptides in the pore structure. If that were the case, the addition of PE or lysoPC might not have a significant effect on the energy of pore formation. However this issue cannot be clarified until the pore structures are resolved. As pointed out previously in Chen et al. (23) and Lee et al. (24), the clearest distinction between the putative toroidal pores of melittin and the putative barrel-stave pores of alamethicin is that the parameter β is negative for the former but is positive for the latter (Table 1). A positive β represents a thinning effect by the pore on the lipid bilayer; a negative β represents a thickening effect by the pore. From the values shown in Table 1, we see that PE increases the thickening effect by the melittin pores, whereas lysoPC has little effect. In contrast, lysoPC decreases the thinning effect by the alamethicin pores, whereas PE has little effect.
did not change much by the addition of PE or lysoPC (Table 1). It is possible that, in the case of a toroidal pore, the curvature stress of the lipid has been largely relieved by the participation of peptides in the pore structure. If that were the case, the addition of PE or lysoPC might not have a significant effect on the energy of pore formation. However this issue cannot be clarified until the pore structures are resolved. As pointed out previously in Chen et al. (23) and Lee et al. (24), the clearest distinction between the putative toroidal pores of melittin and the putative barrel-stave pores of alamethicin is that the parameter β is negative for the former but is positive for the latter (Table 1). A positive β represents a thinning effect by the pore on the lipid bilayer; a negative β represents a thickening effect by the pore. From the values shown in Table 1, we see that PE increases the thickening effect by the melittin pores, whereas lysoPC has little effect. In contrast, lysoPC decreases the thinning effect by the alamethicin pores, whereas PE has little effect.
How AP changes with lipid
From the discussion above, we see that the parameter AP characterizes the major effect of the binding of an amphipathic peptide to a lipid bilayer. At first sight, AP seems to represent the cross-sectional area of the peptide bound at the interface. If that were the case, AP should be a constant. How then does it vary with lipid? We will now try to understand the lipid dependence of AP.
The lengthwise cross section of the melittin helix has been measured by crystallography (Terwilliger et al. (69), who took into account the solvent content) to be ∼400 Å2, whereas the monolayer study (70) gave a cross section of 368 Å2. For a 26-amino-acid helix, 400 Å2 seems reasonable, and we will use the 10 × 40 Å2 cross section in the following analysis. In alamethicin crystals (71), six helices are packed in a unit cell of a = 33.33 Å, b = 29.62 Å, c = 23.20 Å, and β = 120.4°. The length 33.33 Å is apparently the length of the 20-amino-acid helix. The width can be taken as the average of 29.62/3 and 23.20/2, or ∼10.7 Å. However, the solvent content of the crystals is 30%. It is not clear how to take this into account. For simplicity we will assume the cross section of alamethicin to be 10 × 30 Å2.
The smaller values for AP as compared with the peptide cross section can be explained if some water molecules are released from the headgroup region when the peptide is embedded. Normally in the headgroup region, the lipid cross section AL is occupied by the headgroup of cross section AH and water molecules. We assume that these water molecules are not tightly bound and are released from the headgroup region when a peptide is embedded next to this lipid molecule. (AH may include a number of tightly bound water molecules.) From the dimension of the peptide and the cross section of lipid AL, we can estimate the number of lipids nL surrounding a bound peptide: 11 for melittin and 8 for alamethicin. Let ΣP be the cross section of the peptide. We assume that 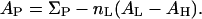 Take the example of melittin in DOPC/DOPE mixtures. Let x be the fraction of DOPE in the DOPC/DOPE mixture. The AH of the mixture is a linear combination of
Take the example of melittin in DOPC/DOPE mixtures. Let x be the fraction of DOPE in the DOPC/DOPE mixture. The AH of the mixture is a linear combination of 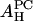 and
and 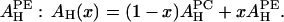 Thus, we obtain a formula
Thus, we obtain a formula
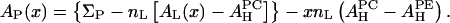 |
(3) |
By fitting the formula to the experimental data AP(x) in Table 1, we obtain the values for 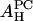 and
and 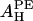 shown in the second column of the
shown in the second column of the 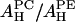 rows of Table 1.
rows of Table 1.
When 18:1 lysoPC is mixed with DOPC, we let x be the fraction of lysoPC in the mixture. In this case we have
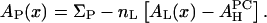 |
(4) |
The value of 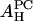 obtained from the lysoPC experiment is shown in the first column of the
obtained from the lysoPC experiment is shown in the first column of the 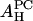 row in Table 1. The same analyses were applied to the alamethicin data and shown in the third and fourth columns.
row in Table 1. The same analyses were applied to the alamethicin data and shown in the third and fourth columns.
It is satisfying to see that the values of 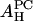 obtained from the melittin/PE experiment and from the melittin/lysoPC experiment are consistent with each other. So are the values of
obtained from the melittin/PE experiment and from the melittin/lysoPC experiment are consistent with each other. So are the values of 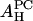 from the alamethicin/PE and the alamethicin/lysoPC experiments. Because the value of AH depends on the peptide's ability to release the water molecules from the headgroup region, it is not unreasonable that the values of
from the alamethicin/PE and the alamethicin/lysoPC experiments. Because the value of AH depends on the peptide's ability to release the water molecules from the headgroup region, it is not unreasonable that the values of 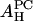 and
and 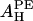 obtained from the melittin experiment are different from those from the alamethicin experiment. Melittin has five basic side chains, thus carrying, including the N-terminal, net +6 charges at pH 7. In comparison, alamethicin carries only one acidic side chain, Glu-18. It appears that melittin is better able than alamethicin to remove water molecules from the headgroups of lipid molecules.
obtained from the melittin experiment are different from those from the alamethicin experiment. Melittin has five basic side chains, thus carrying, including the N-terminal, net +6 charges at pH 7. In comparison, alamethicin carries only one acidic side chain, Glu-18. It appears that melittin is better able than alamethicin to remove water molecules from the headgroups of lipid molecules.
Although each peptide has its own specific affinity with water molecules, in all cases AP decreases with the chain-headgroup area differential 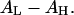 In general, introducing smaller headgroups such as PE (increasing
In general, introducing smaller headgroups such as PE (increasing 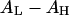 ) gives more room in the headgroup region to accommodate peptide adsorption, which lessens the membrane-thinning effect, reduces the value of AP, and therefore increases the threshold concentration P/L*, which is equivalent to reducing the peptide's activity. Conversely, introducing lysoPC or decreasing
) gives more room in the headgroup region to accommodate peptide adsorption, which lessens the membrane-thinning effect, reduces the value of AP, and therefore increases the threshold concentration P/L*, which is equivalent to reducing the peptide's activity. Conversely, introducing lysoPC or decreasing 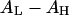 has the opposite effect.
has the opposite effect.
We summarize our results as follows:
The concentration dependence of peptide activities can be understood as mediated by the membrane-thinning effect caused by peptide binding. If one assumes that the mechanism of antimicrobial peptides is via peptide aggregation, it would be difficult to explain the effect of PE and lysoPC.
Introducing PE or lysoPC into PC bilayers affects the threshold concentrations of melittin and alamethicin to a similar degree. One cannot use the correlations between the spontaneous curvature of lipid and the threshold concentration to determine whether the pores are of the toroidal type or the barrel-stave type. The major effect of changing the spontaneous curvature of lipid is changing the degree of membrane thinning when the peptide is adsorbed.
We propose use of the membrane area expansion per peptide AP as a key parameter to characterize the effect of an amphipathic peptide binding onto a membrane.
Acknowledgments
This work was supported by National Science Council (Taiwan) contract NSC93-2112-M-145-002 (to W.-C.H.), by National Science Council (Taiwan) contract NSC 93-2112-M-008-033 and by University System of Taiwan BRC938202 (to F.-Y.C.), and by National Institutes of Health grants GM55203 and RR14812 and the Robert A. Welch Foundation grant C-0991 (to H.W.H).
Ming Tao-Lee and Wei-Chin Hung contributed equally to this work.
Ming Tao-Lee's present address is National Synchrotron Radiation Research Center, Hsinchu 30076, Taiwan.
References
- 1.Merrifield, R. B., E. L. Merrifield, P. Juvvadi, D. Andreu, and H. G. Boman. 1994. Design and synthesis of antimicrobial peptides. In Antimicrobial Peptides. Ciba Foundation Symposium 186. H. G. Boman, J. Marsh, and J. A. Goode, editors. John Wiley, New York. 5–26. [PubMed]
- 2.Wieprecht, T., O. Apostolov, M. Beyermann, and J. Seelig. 2000. Membrane binding and pore formation of the antimicrobial peptide PGLa: thermodynamic and mechanistic aspects. Biochemistry. 39:442–452. [DOI] [PubMed] [Google Scholar]
- 3.Yang, L., T. A. Harroun, T. M. Weiss, L. Ding, and H. W. Huang. 2001. Barrel-stave model or toroidal model? A case study on melittin pores. Biophys. J. 81:1475–1485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Williams, R. W., R. Starman, K. M. P. Taylor, K. Gable, T. Beeler, and M. Zasloff. 1990. Raman spectroscopy of synthetic antimicrobial frog peptides magainin 2a and PGLa. Biochemistry. 29:4490–4496. [DOI] [PubMed] [Google Scholar]
- 5.Matsuzaki, K., K. Sugishita, N. Ishibe, M. Ueha, S. Nakata, K. Miyajima, and R. M. Epand. 1998. Relationship of membrane curvature to the formation of pores by magainin 2. Biochemistry. 37:11856–11863. [DOI] [PubMed] [Google Scholar]
- 6.Longo, M. L., A. J. Waring, L. M. Gordon, and D. A. Hammer. 1998. Area expansion and permeation of phospholipid membrane bilayers by influenza fusion peptides and melittin. Langmuir. 14:2385–2395. [Google Scholar]
- 7.Blazyk, J., R. Wiegand, J. Klein, J. Hammer, R. M. Epand, R. F. Epand, W. L. Maloy, and U. P. Kari. 2001. A novel linear amphipathic beta-sheet cationic antimicrobial peptide with enhanced selectivity for bacterial lipids. J. Biol. Chem. 276:27899–27906. [DOI] [PubMed] [Google Scholar]
- 8.Huang, H. W. 2000. Action of antimicrobial peptides: Two-state model. Biochemistry. 39:8347–8352. [DOI] [PubMed] [Google Scholar]
- 9.Bechinger, B., Y. Kim, L. E. Chirlian, J. Gesell, J.-M. Neumann, M. Motal, J. Tomich, M. Zasloff, and S. J. Opella. 1991. Orientation of amphipathic helical peptides in membrane bilayers determined by solid-state NMR spectroscopy. J. Biomol. NMR. 1:167–173. [DOI] [PubMed] [Google Scholar]
- 10.Marassi, F. M., S. J. Opella, P. Juvvadi, and R. B. Merrifield. 1999. Orientation of cecropin A helices in phospholipid bilayers determined by solid-state NMR spectroscopy. Biophys. J. 77:3152–3155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yamaguchi, S., D. Huster, A. Waring, R. I. Lehrer, W. Kearney, B. F. Tack, and M. Hong. 2001. Orientation and dynamics of an antimicrobial peptide in the lipid bilayer by solid-state NMR. Biophys. J. 81:2203–2214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Glaser, R. W., C. Sachse, U. H. N. Durr, P. Wadhwani, S. Afonin, E. Strandberg, and A. Ulrich. 2005. Concentration-dependent realignment of the antimicrobial peptide PGLa in lipid membranes observed by solid-state 19F-NMR. Biophys. J. 88:3392–3397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gazit, E., A. Boman, H. G. Boman, and Y. Shai. 1994. Mode of action of the antimicrobial cecropin B2: a spectrofluorometric study. Biochemistry. 33:10681–10692. [DOI] [PubMed] [Google Scholar]
- 14.Gazit, E., A. Boman, H. G. Boman, and Y. Shai. 1995. Interaction of the mammalian antibacterial peptide cecropin P1 with phospholipid vesicles. Biochemistry. 34:11479–11488. [DOI] [PubMed] [Google Scholar]
- 15.Schumann, M., M. Dathe, T. Wieprecht, M. Beyermann, and M. Bienert. 1997. The tendency of magainin to associate upon binding to phospholipid bilayers. Biochemistry. 36:4345–4351. [DOI] [PubMed] [Google Scholar]
- 16.Marcelja, S. 1976. Lipid-mediated protein interaction in membranes. Biochim. Biophys. Acta. 455:1–7. [DOI] [PubMed] [Google Scholar]
- 17.Lewis, B. A., and D. M. Engelman. 1983. Bacteriorhodopsin remains dispersed in fluid phospholipid bilayers over a wide range of bilayer thickness. J. Mol. Biol. 166:203–210. [DOI] [PubMed] [Google Scholar]
- 18.Pearson, L. T., J. Edelman, and S. I. Chan. 1984. Statistical mechanics of lipid membranes. Protein correlation functions and lipid ordering. Biophys. J. 45:863–871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Huang, H. W. 1986. Deformation free energy of bilayer membrane and its effect on gramicidin channel lifetime. Biophys. J. 50:1061–1070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Harroun, T. A., W. T. Heller, T. M. Weiss, L. Yang, and H. W. Huang. 1999. a. Experimental evidence for hydrophobic matching and membrane-mediated interactions in lipid bilayers containing gramicidin. Biophys. J. 76:937–945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Harroun, T. A., W. T. Heller, T. M. Weiss, L. Yang, and H. W. Huang. 1999. b. Theoretical analysis of hydrophobic matching and membrane-mediated interactions in lipid bilayers containing gramicidin. Biophys. J. 76:3176–3185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chen, F. Y., M. T. Lee, and H. W. Huang. 2002. Sigmoidal concentration dependence of antimicrobial peptide activities: a case study on alamethicin. Biophys. J. 82:908–914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chen, F. Y., M. T. Lee, and H. W. Huang. 2003. Evidence for membrane thinning effect as the mechanism for peptide-induced pore formation. Biophys. J. 84:3751–3758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lee, M. T., F. Y. Chen, and H. W. Huang. 2004. Energetics of pore formation induced by antimicrobial peptides. Biochemistry. 43:3590–3599. [DOI] [PubMed] [Google Scholar]
- 25.Huang, H. W., F. Y. Chen, and M. T. Lee, 2004. Molecular mechanism of peptide induced pores in membranes. Phys. Rev. Lett. 92:198304. [DOI] [PubMed] [Google Scholar]
- 26.Sitaram, N., and R. Nagaraj. 1999. Interaction of antimicrobial peptides with biological and model membranes: structural and charge requirements for activity. Biochim. Biophys. Acta. 1462:29–54. [DOI] [PubMed] [Google Scholar]
- 27.Allende, D., S. A. Simon, and T. J. McIntosh. 2005. Melittin-induced bilayer leakage depends on lipid material properties; evidence for toroidal pores. Biophys. J. 88:1828–1837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Baumann, G., and P. Mueller. 1974. A molecular model of membrane excitability. J. Supramol. Struct. 2:538–557. [DOI] [PubMed] [Google Scholar]
- 29.Matsuzaki, K., O. Murase, H. Tokuda, N. Fujii, and K. Miyajima. 1996. An antimicrobial peptide, magainin 2, induced rapid flip-flop of phospholipids coupled with pore formation and peptide translocation. Biochemistry. 35:11361–11368. [DOI] [PubMed] [Google Scholar]
- 30.Ludtke, S. J., K. He, W. T. Heller, T. A. Harroun, L. Yang, and H. W. Huang. 1996. Membrane pores induced by magainin. Biochemistry. 35:13723–13728. [DOI] [PubMed] [Google Scholar]
- 31.Huang, H. W., and Y. Wu. 1991. Lipid-alamethicin interactions influence alamethicin orientation. Biophys. J. 60:1079–1087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Heller, W. T., K. He, S. J. Ludtke, T. A. Harroun, and H. W. Huang. 1997. Effect of changing the size of lipid headgroup on peptide insertion into membranes. Biophys. J. 73:239–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ludtke, S. J., K. He, Y. Wu, and H. W. Huang. 1994. Cooperative membrane insertion of magainin correlated with its cytolytic activity. Biochim. Biophys. Acta. 1190:181–184. [DOI] [PubMed] [Google Scholar]
- 34.Ludtke, S., K. He, and H. W. Huang. 1995. Membrane thinning caused by magainin 2. Biochemistry. 34:16764–16769. [DOI] [PubMed] [Google Scholar]
- 35.Yang, L., T. M. Weiss, R. I. Lehrer, and H. W. Huang. 2000. Crystallization of antimicrobial pores in membranes: magainin and protegrin. Biophys. J. 79:2002–2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Ding, L., L. Yang, T. M. Weiss, A. J. Waring, R. I. Lehrer, and H. W. Huang. 2003. Interaction of antimicrobial peptides with lipopolysaccharides. Biochemistry. 42:12251–12259. [DOI] [PubMed] [Google Scholar]
- 37.Heller, W. T., A. J. Waring, R. I. Lehrer, and H. W. Huang. 1998. Multiple states of β-sheet peptide protegrin in lipid bilayers. Biochemistry. 37:17331–17338. [DOI] [PubMed] [Google Scholar]
- 38.Heller, W. T., A. J. Waring, R. I. Lehrer, T. A. Harroun, T. M. Weiss, L. Yang, and H. W. Huang. 2000. Membrane thinning effect of the β-sheet antimicrobial protegrin. Biochemistry. 39:139–145. [DOI] [PubMed] [Google Scholar]
- 39.Olah, G. A., and H. W. Huang. 1988. Circular dichroism of oriented α-helices. I. Proof of the exciton theory. J. Chem. Phys. 89:2531–2538. [Google Scholar]
- 40.Wu, Y., H. W. Huang, and G. A. Olah. 1990. Method of oriented circular dichroism. Biophys. J. 57:797–806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Olah, G. A., H. W. Huang, W. Liu, and Y. Wu. 1991. Location of ion binding sites in the gramicidin channel by x-ray diffraction. J. Mol. Biol. 218:847–858. [DOI] [PubMed] [Google Scholar]
- 42.Wu, Y., K. He, S. J. Ludtke, and H. W. Huang. 1995. X-ray diffraction study of lipid bilayer membrane interacting with amphiphilic helical peptides: diphytanoyl phosphatidylcholine with alamethicin at low concentrations. Biophys. J. 68:2361–2369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.He, K., S. J. Ludtke, W. T. Heller, and H. W. Huang. 1996. b. Mechanism of alamethicin insertion into lipid bilayers. Biophys. J. 71:2669–2679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chen, F. Y., W. C. Hung, and H. W. Huang. 1997. Critical swelling of phospholipid bilayers. Phys. Rev. Lett. 79:4026–4029. [Google Scholar]
- 45.Hung, W. C., F. Y. Chen, and H. W. Huang. 2000. Order-disorder transition in bilayers of diphytanoyl phosphatidylcholine. Biochim. Biophys. Acta. 1467:198–206. [DOI] [PubMed] [Google Scholar]
- 46.Blaurock, A. E. 1971. Structure of the nerve myelin membrane: proof of the low resolution profile. J. Mol. Biol. 56:35–52. [DOI] [PubMed] [Google Scholar]
- 47.Torbet, J., and M. H. F. Wilkins. 1976. X-ray diffraction studies of lecithin bilayers. J. Theor. Biol. 62:447–458. [DOI] [PubMed] [Google Scholar]
- 48.Chen, Z., and R. P. Rand. 1997. The influence of cholesterol on phospholipid membrane curvature and bending elasticity. Biophys. J. 73:267–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.He, K., S. J. Ludtke, D. L. Worcester, and H. W. Huang. 1995. Antimicrobial peptide pores in membranes detected by neutron in-plane scattering. Biochemistry. 34:15614–15618. [DOI] [PubMed] [Google Scholar]
- 50.He, K., S. J. Ludtke, D. L. Worcester, and H. W. Huang. 1996. Neutron scattering in the plane of membranes: structure of alamethicin pores. Biophys. J. 70:2659–2666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.McIntosh, T. J., and S. A. Simon. 1986. Area per molecule and distribution of water in fully hydrated dilauroylphosphatidylethanolamine bilayers. Biochemistry. 25:4948–4952. [DOI] [PubMed] [Google Scholar]
- 52.Nagle, J. F., and S. Tristram-Nagle. 2000. Structure of lipid bilayers. Biochim. Biophys. Acta. 1469:159–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Hung, W. C., and F. Y. Chen. 2003. The hydrophobic-hydrophilic interface of phospholipid membranes studied by lamellar X-ray diffraction. Chinese J. Phys. 41:85–91. [Google Scholar]
- 54.Rawicz, W., K. C. Olbrich, T. McIntosh, D. Needham, and E. Evans. 2000. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 79:328–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Latorre, R., and O. Alvarez. 1981. Voltage-dependent channels in plannar lipid bilayer membranes. Physiol. Rev. 61:77–150. [DOI] [PubMed] [Google Scholar]
- 56.Meyer, P., and F. Reusser. 1967. A polypeptide antibacterial agent isolated from Trichoderma viride. Experientia. 23:85–86. [DOI] [PubMed] [Google Scholar]
- 57.Habermann, E., and J. Jentsch. 1967. Sequenzanalyse des Melittins aus seinen tryptischen und peptischen Spaltstucken. Hoppe Seylers Z. Physiol. Chem. 348:37–50. [PubMed] [Google Scholar]
- 58.Habermann, E. 1972. Bee and wasp venoms. Science. 177:314–322. [DOI] [PubMed] [Google Scholar]
- 59.Tosteson, M. T., and D. C. Tosteson. 1981. The sting: melittin forms channels in lipid bilayers. Biophys. J. 36:109–116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Mak, D. D., and W. W. Webb. 1995. Two classes of alamethicin transmembrane channels: molecular models form single-channel properties. Biophys. J. 69:2323–2336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Hultmark, D., H. Steiner, T. Rasmuson, and H. G. Boman. 1980. Insect immunity: purification and properties of three inducible bactericidal proteins from hemolymph of immunized pupae of Hyalophora cecropia. Eur. J. Biochem. 106:7–16. [DOI] [PubMed] [Google Scholar]
- 62.Selsted, M. E., D. M. Brown, R. J. DeLange, and R. I. Lehrer. 1983. Primary structures of MCP-1 and MCP-2, natural peptide antibiotics of rabbit lung macrophages. J. Biol. Chem. 258:14485–14489. [PubMed] [Google Scholar]
- 63.Zasloff, M. 1987. Magainins, a class of antimicrobial peptides from Xenopus skin: isolation, characterization of two active forms, and partial cDNA sequence of a precursor. Proc. Natl. Acad. Sci. USA. 84:5449–5453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Hirsh, D. J., J. Hammer, W. L. Maloy, J. Blazyk, and J. Schaefer. 1996. Secondary structure and location of a magainin analogue in synthetic phospholipid bilayers. Biochemistry. 35:12733–12741. [DOI] [PubMed] [Google Scholar]
- 65.Blankschtein, D., G. M. Thurston, and G. B. Benedek. 1986. Phenomenological theory of equilibrium thermodynamic properties and phase separation of micellar solutions. J. Chem. Phys. 85:7268–7288. [Google Scholar]
- 66.Huang, H. W. 1995. Elasticity of lipid bilayer interacting with amphiphilic helical peptides. Journal de Physique II. 5:1427–1431. [Google Scholar]
- 67.Rand, R. P., N. L. Fuller, S. M. Gruner, and V. A. Parsegian. 1990. Membrane curvature, lipid segregation, and structural transitions for phospholipids under dual-solvent stress. Biochemistry. 29:76–87. [DOI] [PubMed] [Google Scholar]
- 68.Fuller, N., and R. P. Rand. 2001. The influence of lysolipids on the spontaneous curvature and bending elasticity of phospholipid membranes. Biophys. J. 81:243–254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Terwilliger, T. C., L. Weissman, and D. Eisenberg. 1982. The structure of melittin in the form I crystals and its implication for melittin's lytic and surface activities. Biophys. J. 37:353–361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.DeGrado, W. F., F. J. Kezdy, and E. T. Kaiser. 1981. Design, synthesis and characterization of a cytotoxic peptide with melittin-like activity. J. Am. Chem. Soc. 103:679–681. [Google Scholar]
- 71.Fox, R. O., and F. M. Richards. 1982. A voltage-gated ion channel model inferred from the crystal structure of alamethicin at 1.5-Å resolution. Nature. 300:325–330. [DOI] [PubMed] [Google Scholar]