Abstract
To probe the complexity of the cell membrane organization and dynamics, it is important to obtain simple physical observables from experiments on live cells. Here we show that fluorescence correlation spectroscopy (FCS) measurements at different spatial scales enable distinguishing between different submicron confinement models. By plotting the diffusion time versus the transverse area of the confocal volume, we introduce the so-called FCS diffusion law, which is the key concept throughout this article. First, we report experimental FCS diffusion laws for two membrane constituents, which are respectively a putative raft marker and a cytoskeleton-hindered transmembrane protein. We find that these two constituents exhibit very distinct behaviors. To understand these results, we propose different models, which account for the diffusion of molecules either in a membrane comprising isolated microdomains or in a meshwork. By simulating FCS experiments for these two types of organization, we obtain FCS diffusion laws in agreement with our experimental observations. We also demonstrate that simple observables derived from these FCS diffusion laws are strongly related to confinement parameters such as the partition of molecules in microdomains and the average confinement time of molecules in a microdomain or a single mesh of a meshwork.
INTRODUCTION
The processes responsible for the molecular confinement in live cell plasma membranes have been widely investigated in the last past years. These studies have demonstrated the existence of different mechanisms that could be responsible for the confinement of lipids and proteins in the plasma membrane, such as the cytoskeleton, the molecular clustering, or the extracellular matrix (1). Among them, the actin cytoskeleton has been shown to be responsible for confining transmembrane proteins (2) as well as lipids (3). In this case, the actin filaments act as barriers that hinder the diffusion of membrane components. Beside this cytoskeleton confinement, models of the membrane structure have included lateral lipid heterogeneities, thereby enriching the fluid mosaic view initially proposed by Singer and Nicolson (4). Evidences for membrane domains come mainly from biochemical studies, which show that some membrane constituents are resistant to solubilization by nonionic detergents at low temperature (5). The remaining detergent resistant membranes are found to be enriched in cholesterol and sphingolipids. These results have led to a postulate for the organization of the plasma membrane in which cholesterol and sphingolipid-rich domains coexist with more fluid domains enriched in phospholipids with unsaturated hydrocarbon chains (6,7). Though increasing evidences that those domains exist, the data regarding their structure and dynamics are still very few and mainly indirect.
This lack of data principally results from the absence of appropriate tools. Indeed, optical tools such as confocal microscopy have not enabled the observation of separate domains and suggest that the size of the domains is below the optical resolution (<200 nm) (8). Alternative approaches, such as single-particle tracking (2,9,10) and optical tweezers (11), have a better spatial resolution and have shed a new light on this question. Single particle tracking and single dye tracking have proved to be valuable tools to measure the diffusion properties in membranes and to unravel hop diffusion. Nevertheless they suffer from two drawbacks: i), in most cases, these experiments require the labeling of a single molecule with a bead or a gold colloidal particle, which proves to be difficult; and ii), a large number of trajectories need to be recorded and analyzed to fit statistical criteria. One must be cautious in interpreting experimental results on a few diffusing particles, since distributions of hopping rates may be broad (12) and the detection of transiently confining structures thus requires the study of many molecules. In this respect, FCS may appear as a more appropriate technique since it analyzes an ensemble of molecules diffusing in the detection volume. Although FCS studies have reported anomalous diffusion in live cells (13), it has not been applied to study confinement in membranes. Here, we detail the rationales of the FCS analysis performed at various spatial scales to probe the submicron organization of the cell membrane. The method that we proposed recently (14) has been independently implemented in another context by Okamato's group (15,16).
FCS is a mature and powerful technique for measuring diffusion coefficients and chemical reaction rates both in vivo and in vitro (17). It measures the spontaneous fluctuations of fluorescence in an open volume defined by a focused laser and confocal optics. These fluctuations can arise in particular from the diffusion of fluorescent molecules into or out of this open sampling volume. To analyze statistically the fluctuations, one computes the time ACF, which provides information on diffusion properties.
Though the size of the detection volume is diffraction limited, the ACF can be altered by processes occurring on smaller spatial scales. It has been recently shown (18,19) that confinement in small cell compartments modifies ACFs computed by FCS. In these studies, analytical formula taking into account the volume and geometry of confined regions are proposed to fit experimental ACFs. Although this approach might be useful to determine diffusion coefficients in small volume compartments, its validity is restricted to simple geometries and its implementation is difficult without any a priori knowledge of the geometry.
In this article, we suggest observables that can be obtained from FCS and that are useful to detect confinement in microdomains. First, we emphasize the problems encountered when fitting ACFs, and point out the need for measuring the so-called FCS diffusion laws, instead of only interpreting the shape of ACFs measured at a single size of waist.
The manuscript is organized as follows: we first introduce and show FCS experimental diffusion laws for a lipid and a transmembrane protein. The studied lipid is FL-GM1, which is considered to be a raft marker, and the transmembrane protein is TfR-GFP, diffusion of which is supposed to be hindered by the cytoskeleton meshwork. Interestingly, these two constituents exhibit two different FCS diffusion laws. To explain these results, we simulate in the second part different diffusion processes, which could explain the FCS diffusion laws that have been measured experimentally. We first address the basic issue of confinement of a molecule freely diffusing in an impermeable or permeable 2D domain, and then focus on restricted diffusion in multiple microdomains in mosaic geometries. Two geometries are explored more accurately: the first one accounts for isolated microdomains, in which molecules can partition dynamically (“partitioning microdomains”); and the second accounts for the actin meshwork. Finally, the experimental FCS diffusion laws are reinterpreted thanks to the new light shed by the simulations.
MATERIALS AND METHODS:
A list of the parameters used in the following is given in Table 1.
TABLE 1.
Main parameters used in the simulations
| Parameter description | Symbol | Value/Range of values/Calculation |
|---|---|---|
| Simulation parameters | ||
| Time step | Δt0 | 2.10−6s |
| Simulation box | A | Square, 10 × 10 μm2 |
| Total simulated time | > 4.103 s | |
| Half-size of the domains | r | Radius of a circular domain/Half-size of the side of a square domain. Varied between 50 nm and 100 nm. |
| Mean elementary jump length | σ | Between r/100 and r/20 |
| Microscopic diffusion coefficient | Dmicro | Between 1.0 and 10.0 μm2/s |
| Waist of the excitation focal spot | w | Between 0 and 1 μm |
| Calculated parameters | ||
| Apparent diffusion time | 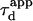 |
FWHM of the autocorrelation function |
| Free diffusion time in the focal spot | 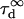 |
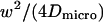 |
| Free diffusion time in a single domain | 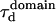 |
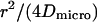 in a circular domain of radius r, in a circular domain of radius r, 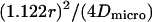 in a square domain in a square domain |
| Confinement time in a single domain | τconf | |
| Confinement strength | Sconf | 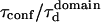 |
| Confinement size parameter | Xc |  |
| Specific parameters for isolated microdomains | ||
| Density of the domains | d | 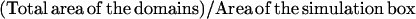 |
| Microscopic diffusion coefficient inside the domains | 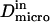 |
Between 1.0 and 5.0 μm2/s |
| Microscopic diffusion coefficient outside of the domains | 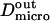 |
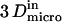 (Dietrich et al. (29)) (Dietrich et al. (29)) |
| Probability of going into a domain | 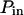 |
Between 0 and 1 (for r/σ = 30) |
| Probability of going out of a domain | Pout | Between 10−3 and 1 (for r/σ = 30) |
| Specific parameters for the meshwork | ||
| Probability of crossing a barrier | P | Between 6.10−3 and 1 (for r/σ = 5) |
| Experimental outcomes | ||
| Intercept time of the diffusion law in regime iii | t0 | |
| Effective diffusion coefficient | Deff | |
| Partition of the molecules in microdomains | α | 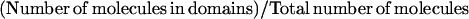 |
Cell culture and staining
All experiments are carried out on COS-7 cells (American Type Culture Collection No. CRL-1657).
Fluorescent conjugated lipid probe BODIPY-ganglioside GM1 (FL-GM1) (Molecular Probes, Eugene, OR) is incorporated in the plasma membrane by a lipid exchange procedure (20).
To obtain the TfR-GFP recombinant protein expression, cells are transiently transfected with a mixture of the plasmid and ExGen 500 reagent (Euromedex, Souffelweyersheim, France).
FCS measurements are performed at 37°C at least 16 h after each of these incorporations.
FCS setup
Confocal fluorescence microscopy and fluorescence correlation spectroscopy are performed on a custom apparatus, which has been developed from an Axiovert 200 inverted microscope (Zeiss, Jena, Germany). The excitation light of the 488 nm line of an Ar+-ion laser is focused onto the sample through a Zeiss C-Apochromat 40×, numerical aperture =1.2, water immersion objective. The fluorescence is collected by the same objective, separated from the excitation light by a dichroic mirror, then split by a 50/50 cube splitter and sent onto two avalanche photodiodes through 525–565 nm bandpass filters. Cross correlation between the two channels is preferred to autocorrelation of one channel, since it reduces artifacts due to the dead time of each detector and after pulses. A confocal pinhole (20 or 50 μm in diameter) reduces the out-of-plane fluorescence. Precise positioning of the cell membrane in the confocal volume is obtained by moving the sample step-by-step with a three-axis piezo-scanner, which is controlled by a digital controller (Physik Instrumente, Karlsruhe, Germany). Scanning softwares are written with LabView (National Instruments, Austin, TX).
FCS measurements are performed by illuminating the sample with an excitation power of 3.5 μW at the back-aperture of the objective. Auto-correlation is processed by a hardware correlator (ALV-GmBH, Langen, Germany). Data are analyzed with built-in functions of IgorPro (Wavemetrics, Lake Oswego, OR).
Fitting of autocorrelation functions
In a standard FCS experiment, a diffusion measurement is carried out for a single size of the confocal volume, i.e., a single value of the laser beam transversal waist w at the focal plane of the focusing objective. The diffusion coefficient is determined from the measurement of the apparent diffusion time 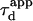 of a fluorescent molecule through the confocal volume, which is defined as the FWHM of the ACF. For free translational two-dimension diffusion,
of a fluorescent molecule through the confocal volume, which is defined as the FWHM of the ACF. For free translational two-dimension diffusion, 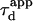 matches the actual diffusion time through the confocal volume
matches the actual diffusion time through the confocal volume 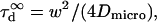 where
where 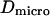 is the microscopic diffusion coefficient of the fluorescent molecule in the plane of diffusion. If the diffusion is free, and in the case of a Gaussian approximation of the detectable emission intensity distribution, the ACF is given by (21)
is the microscopic diffusion coefficient of the fluorescent molecule in the plane of diffusion. If the diffusion is free, and in the case of a Gaussian approximation of the detectable emission intensity distribution, the ACF is given by (21)
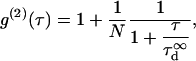 |
(1) |
where N is the average number of molecules in the detection volume.
For anomalous diffusion, the mean-square displacement of particles is no longer proportional to time t as for free diffusion, but rather to tα, with 0 < α ≤ 1. This diffusion mode corresponds to molecules diffusing in the presence of multiple energy potential traps with binding energies that vary over wide ranges of time and space (22). Anomalous diffusion can also result from diffusion on a percolating cluster at the threshold. In FCS, if diffusion is anomalous, α can be determined from the ACF, which is given by
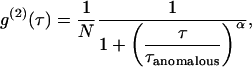 |
(2) |
where 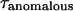 is equal to
is equal to 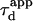 if α = 1.
if α = 1.
When diffusion is free, then α = 1. We will show in the Experimental Evidence section that the converse is false.
Size of the confocal volume
The size of the confocal volume can be controlled by selecting either with a diaphragm or a variable telescope (14,16) the lateral extension of the laser excitation beam falling onto the back-aperture of the microscope objective. Similar approaches have been implemented in fluorescence recovery after photobleaching experiments (23,24).
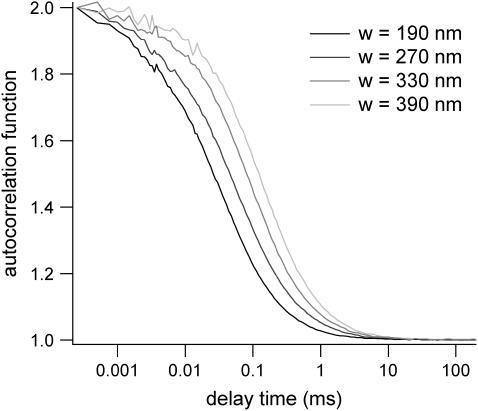
The size of the confocal volume can be inferred from the free diffusion time 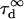 of a fluorophore in the open confocal volume, and its known diffusion coefficient (Fig. 1). Here, Rh6G, of which the diffusion coefficient is known (
of a fluorophore in the open confocal volume, and its known diffusion coefficient (Fig. 1). Here, Rh6G, of which the diffusion coefficient is known (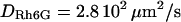 ) (21) is used to calibrate the size of the confocal volume. The radius of the illuminated observation area can be modulated between 190 and 400 nm. The Rh6G diffusion time through the confocal volume obtained by fulfilling the rear-aperture of the microscope objective allows the determination of the smallest waist accessible with our setup: wmin=190 nm. In all experiments, the excitation power at the back-aperture of the objective is kept constant for all waist sizes. To validate the calibration protocol of the waists in the context of 2D diffusion measurements, we have studied the diffusion of Bodipy-PC probes freely diffusing in giant unilamellar vesicles (14). We have checked that the determination of the diffusion coefficient is correct and independent on the size of the waist as expected for free 2D diffusion.
) (21) is used to calibrate the size of the confocal volume. The radius of the illuminated observation area can be modulated between 190 and 400 nm. The Rh6G diffusion time through the confocal volume obtained by fulfilling the rear-aperture of the microscope objective allows the determination of the smallest waist accessible with our setup: wmin=190 nm. In all experiments, the excitation power at the back-aperture of the objective is kept constant for all waist sizes. To validate the calibration protocol of the waists in the context of 2D diffusion measurements, we have studied the diffusion of Bodipy-PC probes freely diffusing in giant unilamellar vesicles (14). We have checked that the determination of the diffusion coefficient is correct and independent on the size of the waist as expected for free 2D diffusion.
FIGURE 1.
Rh6G autocorrelation functions measured by FCS at various beam waists w. The diffusion time is used to calibrate w.
Simulations of confined diffusion and FCS
Scheme of simulations
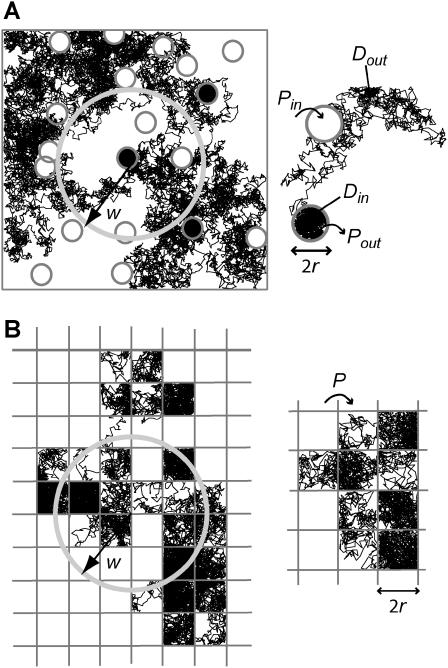
We have implemented simulations as close as possible to real FCS experiments. We have included a fluorescent molecule in an area A, which is composed of a single domain or of multiple domains (Fig. 2). If not otherwise stated, the excitation laser beam is supposed to be Gaussian: 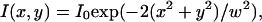 where x and y are the Cartesian coordinates originating at the center of the area A. Depending on the objective back-aperture filling used, w can vary from 200 nm to 400 nm in a standard FCS setup.
where x and y are the Cartesian coordinates originating at the center of the area A. Depending on the objective back-aperture filling used, w can vary from 200 nm to 400 nm in a standard FCS setup.
FIGURE 2.
Simulated trajectories of a molecule in the cell membrane drawn for two models of confined diffusion. Fluorescence fluctuations arise from the detection volume of size w that is defined by a laser beam. In real optics, the diffraction limit sets in the minimum size w to wmin ∼ 190 nm. (A) Model for isolated microdomains: static circular microdomains of radius r are embedded in a fluid phase. The molecules have a Brownian motion as long as they stay in the same phase. The probabilities of going into and out of the microdomains, Pin and Pout respectively, can be asymmetric. Here, r = 100 nm, w = 600 nm, Pin = 0.05, and Pout = 0.02. (B) Meshwork model: molecules have to jump over regularly spaced barriers. The molecules have a Brownian motion described by a microscopic diffusion coefficient Dmicro as long as they stay within the same mesh. The probability that the molecule can cross the barrier is P. Here r = 100 nm, w = 500 nm, and P = 0.05.
The fluorescent molecule performs a random walk from a starting position that is randomly selected in the surface A. For the sake of simplicity and without any loss of generality, we simulate the walk of a single molecule. Simulating independent multiple molecules would not change the ACF profile but only its amplitude.
The random walk is performed as follows:
At each time step Δt0, the particle performs a jump (ΔX, ΔY), which is determined by two independent random variables with a Gaussian distribution centered on 0 and a standard deviation 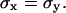 The jump length
The jump length 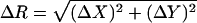 is therefore a random variable with a standard deviation
is therefore a random variable with a standard deviation 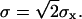 The microscopic diffusion coefficient Dmicro is related to σ by
The microscopic diffusion coefficient Dmicro is related to σ by 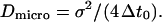 Typically, 109–1010 steps are calculated for a trajectory. The mean elementary jump length is kept small (from 1/100 to 1/20) with respect to the size of domains (see below).
Typically, 109–1010 steps are calculated for a trajectory. The mean elementary jump length is kept small (from 1/100 to 1/20) with respect to the size of domains (see below).
Detection and ACF
At each time step, the detected intensity is computed assuming a Poisson distribution; the number of detected fluorescence photons nph for a particle at position (x, y) is given by a random variable following a Poisson distribution function with parameter 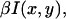 where β describes the collection efficiency of the setup (25). To analyze fluorescence fluctuations, the normalized time autocorrelation function ACF is defined as
where β describes the collection efficiency of the setup (25). To analyze fluorescence fluctuations, the normalized time autocorrelation function ACF is defined as
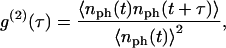 |
(3) |
where 〈 〉 represents a time average.
In our simulations, the ACF is calculated either after the whole trajectory of the particle has been obtained or in parallel. The software correlator used to compute the ACFs follows the architecture proposed by (26) and described in (25). It has a logarithmic timescale, each channel having an individual sampling time and delay time.
Domains and barriers
Domains are considered to be regions in which the diffusion is free but restricted by barriers. These barriers can represent physical obstacles (cytoskeleton fences) or energy barriers (phase separations). Barriers are considered to be infinitely thin: they are lines that the molecule can cross with a given probability P. The probability P of crossing a barrier is independent of time. External boundaries of the surface A are impermeable. When the molecule hits the external boundaries, it is reflected at the wall.
When the molecule hits a barrier, a number rand is drawn at random between 0 and 1 and compared to the probability P of crossing the barrier. rand is generated by a number generator of Park and Miller with Bays-Durham shuffle and added safeguards, and has a period of ∼2 × 109 (27). If rand < P, the barrier is crossed; if not, the molecule remains at its previous position. This condition seems appropriate for biological membranes that are viscous.
Confinement in a permeable domain: definition of the confinement strength
This section aims at defining the input parameters and the associated physical parameters that are relevant to study the transient confinement in domains. In particular, we define the confinement time and the confinement strength, and give their expression as functions of the input parameters.
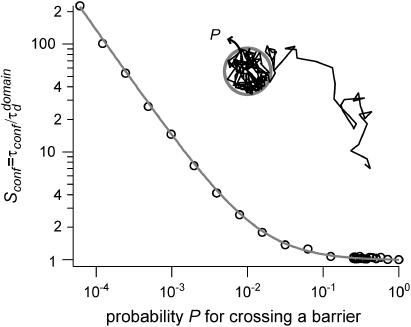
A circular permeable domain is now embedded in a square area. We define the confinement time 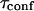 as the average time needed by a molecule placed at the center of the domain to escape from it. We have studied the ratio of the confinement time over the free diffusion time in the domain
as the average time needed by a molecule placed at the center of the domain to escape from it. We have studied the ratio of the confinement time over the free diffusion time in the domain 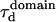 as a function of P (Fig. 3).
as a function of P (Fig. 3).
FIGURE 3.
Confinement strength of a circular domain as a function of the probability P of crossing the barrier.
Results can be approximated by a curve of the form:
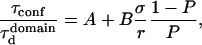 |
(4) |
where A and B are two positive constants: A = 1 (by definition) and B = 0.95 (fitted value).
This curve has the same shape as that derived by Saxton for the mean escape time from a corral (12). Nevertheless, different definitions for the escape time and the diffusion time were chosen in Saxton (12), which were more adapted to a single-particle tracking study, leading to different values for the two parameters A and B.
With our definition, parameter A is equal to 1, which means that the confinement time in a domain surrounded by fully permeable barriers is equal to the free diffusion time in the domain. When the probability P of crossing the barrier is <1, the confinement time gets longer than the diffusion time. The ratio 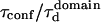 is the key parameter expressing the height of the barrier that molecules have to pass. In the following, we will define the confinement strength as
is the key parameter expressing the height of the barrier that molecules have to pass. In the following, we will define the confinement strength as 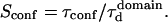 It has to be noted that this confinement strength is not only a function of P, but also a function of the mean diffusion step length σ and the radius r of the domain (see Eq. 4).
It has to be noted that this confinement strength is not only a function of P, but also a function of the mean diffusion step length σ and the radius r of the domain (see Eq. 4).
One may wonder if 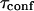 is an accessible parameter, not only with single-particle analysis, but also from a FCS study. To assess this point, we simulate a FCS experiment with a laser spot centered on the permeable domain. The laser beam waist w is chosen equal to the radius r of the domain, so that the apparent diffusion time
is an accessible parameter, not only with single-particle analysis, but also from a FCS study. To assess this point, we simulate a FCS experiment with a laser spot centered on the permeable domain. The laser beam waist w is chosen equal to the radius r of the domain, so that the apparent diffusion time 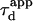 represents the average time spent by a molecule in the domain. In this case, we found that
represents the average time spent by a molecule in the domain. In this case, we found that 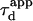 matches
matches 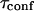 as a function of P. As a result,
as a function of P. As a result, 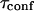 is still easy to determine with a FCS analysis.
is still easy to determine with a FCS analysis.
In the case where the confinement area is a square, the value of the radius of the circle is simply replaced in Eq. 4 by the average length between the center of the square and the side of the square. This length is equal to 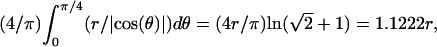 where θ is the angle that a line from the center of the square makes with one side. Doing the same analysis leads to coefficients A = 1 and B = 1.34.
where θ is the angle that a line from the center of the square makes with one side. Doing the same analysis leads to coefficients A = 1 and B = 1.34.
Simulations and data analysis
We have implemented the simulations in C++ (Microsoft Visual C++, Version 6.0). They are run on a PC (Pentium III processor). Results have been analyzed and fitted with Igor Pro software (Wavemetrics).
EXPERIMENTAL EVIDENCE: NEED FOR FCS DIFFUSION LAW MEASUREMENTS
To connect our simulations to real experiments, FCS measurements at various spatial scales have been carried out for a lipid and a transmembrane protein inserted in the cell plasma membrane. The experimental results that are explained here have to be considered as a support to our theoretical considerations; they are representative of a large number of experimental results that have been carried out and that will be presented in details in P.-F. Lenne, L. Wawrezinieck, F. Conchonaud, O. Wurtz, A. Boned, H. Rigneault, and D. Marguet (unpublished).
This section points out the need for performing FCS diffusion law measurements, instead of the sole study of the shape of the autocorrelation function at a single waist.
Experimental autocorrelation functions
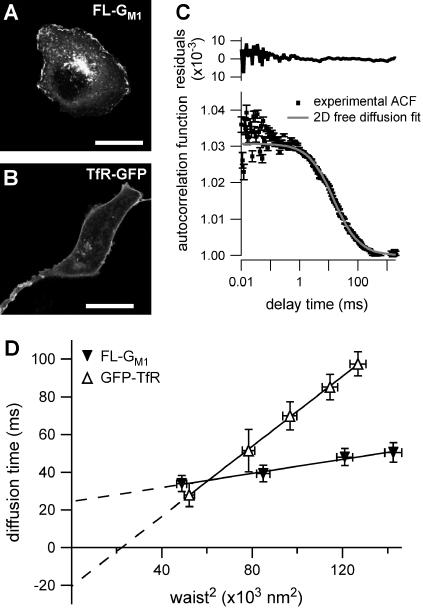
Confocal images of COS-7 cells after staining with fluorescent lipids FL-GM1 showed a uniform distribution of the probes in the plasma membrane and a vesicular staining figured by intracellular small dots (Fig. 4 A). Confocal images for TfR-GFP expressing cells (Fig. 4 B) show comparable intracellular and membrane fluorescence signal distribution.
FIGURE 4.
Experimental results on COS-7 cells for FL-GM1 and TfR-GFP. (A) Confocal image of a cell stained with FL-GM1 (scale bar, 20 μm). (B) Confocal image of a TfR-GFP stained cell (scale bar, 20 μm). (C) ACF measured by FCS on FL-GM1 stained cells. (D) Experimental FCS diffusion laws obtained for FL-GM1 and TfR-GFP. Curves are extrapolated to zero beam waist to make the time intercepts more visible, even if the diffusion law at small waists can be different.
Fig. 4 C shows the experimental ACF obtained for FL-GM1 diffusing in the plasma membrane of COS-7 cells. In this case, fitting the experimental ACF with an anomalous fit leads to an anomalous diffusion coefficient 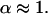 The studied diffusion is therefore not anomalous, which means that the potential trap energies do not vary over a wide range of time and space. Nevertheless, the diffusion of lipids at the cell membrane is certainly constrained, since the measured diffusion time is ∼10 times longer than the diffusion time of lipids in an artificial membrane (28).
The studied diffusion is therefore not anomalous, which means that the potential trap energies do not vary over a wide range of time and space. Nevertheless, the diffusion of lipids at the cell membrane is certainly constrained, since the measured diffusion time is ∼10 times longer than the diffusion time of lipids in an artificial membrane (28).
This example shows that fitting the ACF obtained with fluorescent lipids diffusing in the plasma membrane does not permit determination of their diffusion mode. On the contrary, measuring the diffusion time at different sizes of the confocal volume is an interesting way of studying the confinement.
Experimental FCS diffusion law
For an experimentalist, it is possible to vary the waist w by changing the extension of the laser beam falling on the microscope objective back-aperture. We name “FCS diffusion law” the plot of the apparent diffusion time 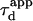 of a membrane component measured by FCS as a function of the square of the waist w2
of a membrane component measured by FCS as a function of the square of the waist w2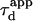 is defined as the FWHM of the ACF. We will show that this representation is very fruitful to study the constrained submicron diffusion in the cell membrane.
is defined as the FWHM of the ACF. We will show that this representation is very fruitful to study the constrained submicron diffusion in the cell membrane.
Although the 1-species free 2D diffusion curve seems to fit nicely the experimental ACFs obtained for FL-GM1 and TfR-GFP, the FCS diffusion laws do not reflect free diffusion. Indeed, in both cases the diffusion time is not proportional to the square of the waist w2 as it is expected for free diffusion, where 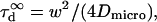 but is an affine function of w2 (
but is an affine function of w2 (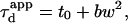 with t0 ≠ 0). The intersection of the line with the time axis is strictly positive in the case of FL-GM1 (t0 = 25 ± 3 ms), and strictly negative in the case of TfR-GFP (t0 = − 20 ± 2 ms) (Fig. 4 D). Knowing that GM1 is a putative raft marker and that TfR could be sensitive to the cytoskeleton through its cytoplasmic tail, these two different FCS diffusion laws may be signatures for two different diffusion processes.
with t0 ≠ 0). The intersection of the line with the time axis is strictly positive in the case of FL-GM1 (t0 = 25 ± 3 ms), and strictly negative in the case of TfR-GFP (t0 = − 20 ± 2 ms) (Fig. 4 D). Knowing that GM1 is a putative raft marker and that TfR could be sensitive to the cytoskeleton through its cytoplasmic tail, these two different FCS diffusion laws may be signatures for two different diffusion processes.
For diffusive processes, it is expected to have a zero diffusion time at zero beam waist. However, the extrapolation of the experimental diffusion curve to zero beam waist can be nonzero independently of the real value of the diffusion time. In the next core section of this study, we will try to explain the two different intercepts and slopes of the measured diffusion laws with two models for the diffusion of membrane constituents. We will also show that these experimental results (free-like ACFs, but FCS diffusion laws that are not normal) are not paradoxical but can indeed reflect diffusion processes in a submicron structured membrane.
SIMULATION RESULTS
To explain the two experimental behaviors that we have shown in the first section, we propose and test different models. First, we give a simple example of total confinement in which a molecule is enclosed in an impermeable box. Then we propose two more refined models to account for i), the diffusion of molecules transiently sequestered in lipid microdomains and ii), the diffusion of molecules hindered by the cytoskeleton meshwork.
Simulated confinement in one impermeable domain
The purpose of this study is to determine how the diffusion behavior of a molecule (as measured by FCS) is sensitive to the presence of impermeable barriers. Moreover, this is useful in determining the minimum size of the simulation area which prevents FCS measurements from boundary effects.
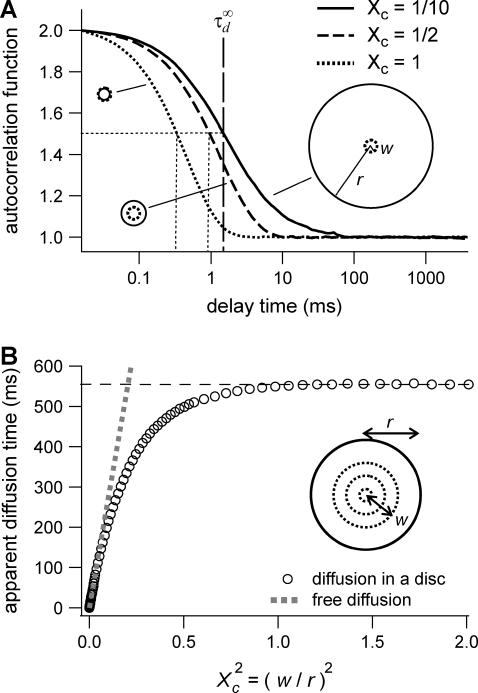
Let us first analyze how ACFs are changed by the confinement of molecules in a single domain with impermeable barriers. We assume a circular domain on the center of which a laser beam is focused. The domain has a radius r and the waist of the laser beam is w. The key parameter is 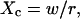 which reflects the confinement probed by the laser beam. Fig. 5 A shows autocorrelation functions obtained for different values of r and a fixed value of w. The microscopic diffusion coefficient Dmicro is kept the same in all these simulations:
which reflects the confinement probed by the laser beam. Fig. 5 A shows autocorrelation functions obtained for different values of r and a fixed value of w. The microscopic diffusion coefficient Dmicro is kept the same in all these simulations: 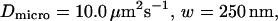 and thus
and thus 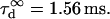 Fig. 5 A clearly shows that the so-called apparent diffusion time
Fig. 5 A clearly shows that the so-called apparent diffusion time 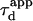 (FWHM of the ACF) does not generally match the free diffusion time
(FWHM of the ACF) does not generally match the free diffusion time 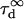 and depends strongly on the confinement: it decreases when the size of the domain decreases. The decrease of
and depends strongly on the confinement: it decreases when the size of the domain decreases. The decrease of 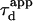 is a direct consequence of the reduction of the area available for diffusion, which is not defined anymore by the laser beam extension. In the presence of confinement, a diffusion measurement using FCS should not be made at a single value of the waist, since the diffusion law is not that of free diffusion: it leads practically to an overestimation of Dmicro when estimated by
is a direct consequence of the reduction of the area available for diffusion, which is not defined anymore by the laser beam extension. In the presence of confinement, a diffusion measurement using FCS should not be made at a single value of the waist, since the diffusion law is not that of free diffusion: it leads practically to an overestimation of Dmicro when estimated by 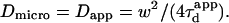
FIGURE 5.
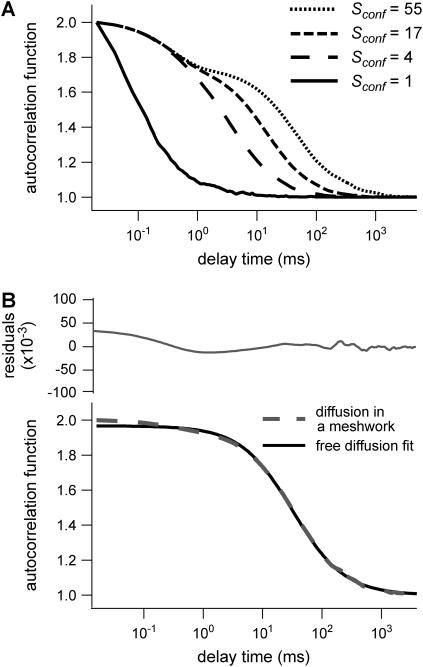
Simulation results for a molecule diffusing in a single impermeable domain. (A) ACFs obtained by FCS. Effect of the domain size on the shape of ACFs drawn for three values of the confinement parameter 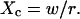 (B) Apparent diffusion time measured from ACFs as a function of the confinement parameter squared, plotted for a fixed size of the impermeable domain.
(B) Apparent diffusion time measured from ACFs as a function of the confinement parameter squared, plotted for a fixed size of the impermeable domain.
Let us thus assume now that the diffusion law is probed by varying w while the domain size is kept constant. Fig. 5 B shows the variation of 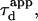 with
with 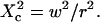 Three different regimes are observed. For
Three different regimes are observed. For 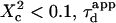 increases linearly with
increases linearly with 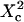 as predicted for free diffusion. For intermediate values,
as predicted for free diffusion. For intermediate values, 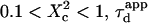 increases more slowly with
increases more slowly with 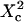 and deviates from the standard formula. For
and deviates from the standard formula. For 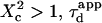 reaches a saturation value. This regime is dominated by a domain size effect: as a further proof, we have verified that the saturation value of
reaches a saturation value. This regime is dominated by a domain size effect: as a further proof, we have verified that the saturation value of 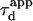 is proportional to
is proportional to 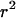 (data not shown).
(data not shown).
It has to be noted that these conclusions can be extended to the case of a square domain of side 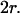 The confinement probed by the laser beam is then defined by
The confinement probed by the laser beam is then defined by 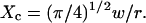 The proportional coefficient
The proportional coefficient 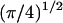 is chosen so that
is chosen so that 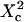 is still the ratio of the excitation beam surface area (
is still the ratio of the excitation beam surface area (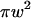 ) over the confinement area (
) over the confinement area (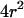 ). Here again, the free diffusion regime is only obtained when
). Here again, the free diffusion regime is only obtained when 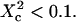
The shape of the ACF has already been studied in the case of a square domain in Gennerich and Schild (19).
Simulated confinement in multiple microdomains
In the following, we will distinguish between two hindering processes, and propose a model for both of them. First, we will focus our study on isolated circular microdomains, which try to account for lipid microdomains. Then we will study the diffusion of molecules in a meshwork, which is supposed to model the cytoskeleton.
Isolated microdomains
We have modeled rafts as permeable isolated microdomains surrounded by energy barriers. This model should be able to account for lipid rafts as well as other kinds of domains. We have simulated the diffusion of a molecule in a model membrane where microdomains (phase II) are embedded in a larger square surface of phase I (Fig. 2 A). Microdomains are considered as static entities that are separated from phase I by barriers. They can be either periodically or randomly distributed. We assume that domains are identical disks of radius r distributed over the surface. We make the assumption that the microscopic diffusion coefficients in and out of microdomains, respectively 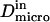 and
and 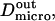 are linked by
are linked by 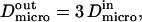 as it has been previously measured on artificial membranes (29).
as it has been previously measured on artificial membranes (29). 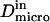 and
and 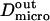 stand for the microscopic diffusion coefficients in liquid-ordered and liquid-disordered phases, respectively. In each simulation, the following parameters are chosen: the microscopic diffusion coefficient outside of the domains is
stand for the microscopic diffusion coefficients in liquid-ordered and liquid-disordered phases, respectively. In each simulation, the following parameters are chosen: the microscopic diffusion coefficient outside of the domains is 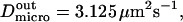 and the mean jump length is
and the mean jump length is 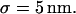 The size of the radius of the circular domain is r = 100 nm, and the square simulation box A has an area of 100 μm2.
The size of the radius of the circular domain is r = 100 nm, and the square simulation box A has an area of 100 μm2.
Probabilities of going out of or into a microdomain are Pin and Pout, respectively. If not otherwise stated, these two probabilities have the same value, P. The confinement probed by the laser beam is defined here by 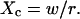 In the following,
In the following, 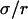 is kept constant, so that the confinement strength
is kept constant, so that the confinement strength 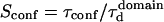 is only a function of the probability P.
is only a function of the probability P.
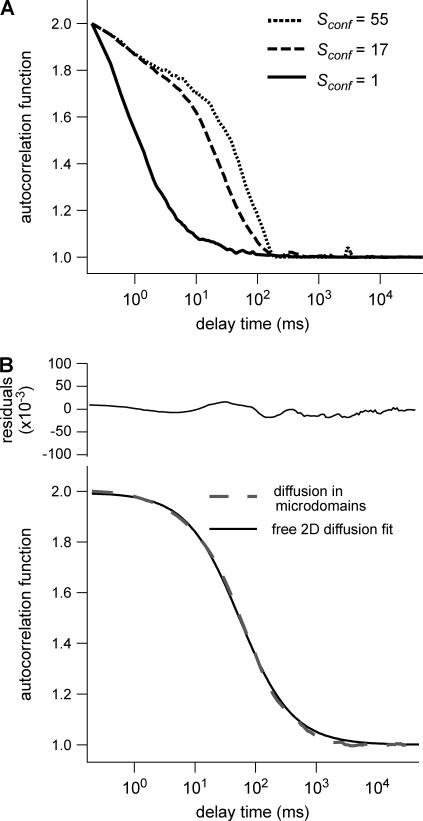
Shapes of ACFs obtained for different probabilities P of crossing a barrier
Fig. 6 A shows ACFs which have been obtained for different probabilities of crossing the barriers and for w = r, for a laser spot centered on a domain. When P decreases, i.e., when barriers are more impermeable and the confinement strength 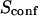 increases, the diffusion time increases. Two distinct decay times can be observed for high values of
increases, the diffusion time increases. Two distinct decay times can be observed for high values of 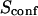 and small values of
and small values of 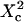 : the short time is related to the diffusion time within a single domain and the longer one is related to the diffusion time through the whole illuminated area. The detection of the first bump is a signature of the presence of a domain that can be on the order of or even smaller (data not shown) than the beam extension (30).
: the short time is related to the diffusion time within a single domain and the longer one is related to the diffusion time through the whole illuminated area. The detection of the first bump is a signature of the presence of a domain that can be on the order of or even smaller (data not shown) than the beam extension (30).
FIGURE 6.
Simulated intensity ACFs for a single molecule diffusing in microdomains delimited by permeable barriers. (A) ACFs are calculated for a confinement parameter 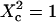 and for different probabilities P of crossing the barriers. (B) ACF calculated for a confinement parameter
and for different probabilities P of crossing the barriers. (B) ACF calculated for a confinement parameter 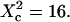 It is well fitted by a free 2D diffusion fit.
It is well fitted by a free 2D diffusion fit.
On the contrary, ACFs obtained for large waists (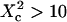 ) can be quite nicely fitted by a 1-species 2D free diffusion fit (Fig. 6 B).
) can be quite nicely fitted by a 1-species 2D free diffusion fit (Fig. 6 B).
We put forward 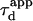 as an observable of physical meaning that is easy to determine since it does not require the implementation of a complex fit. By varying w, we can explore FCS diffusion laws by observing
as an observable of physical meaning that is easy to determine since it does not require the implementation of a complex fit. By varying w, we can explore FCS diffusion laws by observing 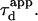 It is simply related in the case of free 2D diffusion to the microscopic diffusion coefficient by
It is simply related in the case of free 2D diffusion to the microscopic diffusion coefficient by 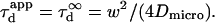 In the presence of microdomains, we expect a deviation from this law depending in particular on
In the presence of microdomains, we expect a deviation from this law depending in particular on 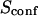 and on the size and density of microdomains.
and on the size and density of microdomains.
Diffusion laws for fixed size and density of domains and variable probability P of crossing a barrier
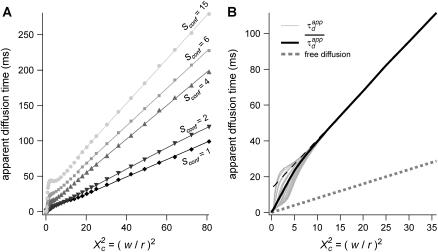
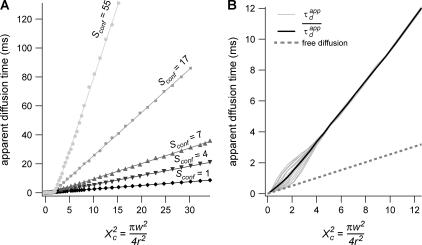
To evaluate the different regimes that a FCS experiment can probe, we have determined the variation of the apparent diffusion time with respect to w (having r fixed). We first plot 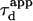 as a function of
as a function of 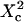 with the laser spot centered on a microdomain, a density of microdomains d = 0.5 and different confinement strengths
with the laser spot centered on a microdomain, a density of microdomains d = 0.5 and different confinement strengths 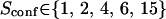 (Fig. 7 A). When
(Fig. 7 A). When 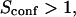 i.e., when the diffusion is not free, three regimes can be distinguished. If
i.e., when the diffusion is not free, three regimes can be distinguished. If 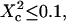 particles appear to diffuse freely, and
particles appear to diffuse freely, and 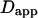 matches
matches 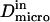 (regime i): FCS measurements probe the microscopic diffusion coefficient within the microdomain. A transient regime is observed when
(regime i): FCS measurements probe the microscopic diffusion coefficient within the microdomain. A transient regime is observed when 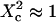 : complex diffusion occurs because of barrier effects (regime ii). Last, when
: complex diffusion occurs because of barrier effects (regime ii). Last, when 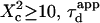 scales linearly with w2 (regime iii). However, it differs significantly from regime i: the intersection with the time axis becomes strictly positive and the line slope increases. The positive intercept as well as the slope are increasing functions of the probability
scales linearly with w2 (regime iii). However, it differs significantly from regime i: the intersection with the time axis becomes strictly positive and the line slope increases. The positive intercept as well as the slope are increasing functions of the probability 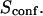
FIGURE 7.
Simulated diffusion laws obtained by FCS: the apparent diffusion time measured from ACFs is plotted as a function of the confinement parameter squared 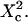 In each case, the chosen probabilities
In each case, the chosen probabilities 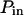 and
and 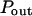 are equal. (A) Diffusion laws obtained for five confinement strengths
are equal. (A) Diffusion laws obtained for five confinement strengths 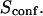 Here the laser spot is centered on a microdomain. (B) The diffusion law is averaged on all possible positions of the excitation beam for
Here the laser spot is centered on a microdomain. (B) The diffusion law is averaged on all possible positions of the excitation beam for 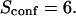 It is compared to diffusion laws plotted for different positions of the laser spot.
It is compared to diffusion laws plotted for different positions of the laser spot.
To be closer to experimental conditions, one averages the values of 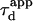 obtained for different positions of the laser spot on the surface of the membrane. Fig. 7 B shows the average value
obtained for different positions of the laser spot on the surface of the membrane. Fig. 7 B shows the average value  as an affine function of
as an affine function of 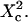 The first two regimes, i and ii, cannot be distinguished anymore. When
The first two regimes, i and ii, cannot be distinguished anymore. When 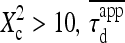 is a linear function of w2. We find that regime iii is described by the same line as the one obtained when no average is done on the position of the laser waist. In the following, all the diffusion laws will be given with the laser spot centered on one domain. This leads to no change in the description of regime iii, which is the regime we are mostly interested in, since we expect to have w/r > few units in experiments. If the sole regime iii is indeed probed experimentally, an upper limit can be given to the microdomain radius since this regime starts at
is a linear function of w2. We find that regime iii is described by the same line as the one obtained when no average is done on the position of the laser waist. In the following, all the diffusion laws will be given with the laser spot centered on one domain. This leads to no change in the description of regime iii, which is the regime we are mostly interested in, since we expect to have w/r > few units in experiments. If the sole regime iii is indeed probed experimentally, an upper limit can be given to the microdomain radius since this regime starts at 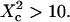
We also verified that the same regime iii is obtained for periodically and nonperiodically distributed microdomains as long as there is no percolation (data not shown).
Diffusion laws for a fixed size of domains, a fixed probability P of crossing a barrier and various densities of domains
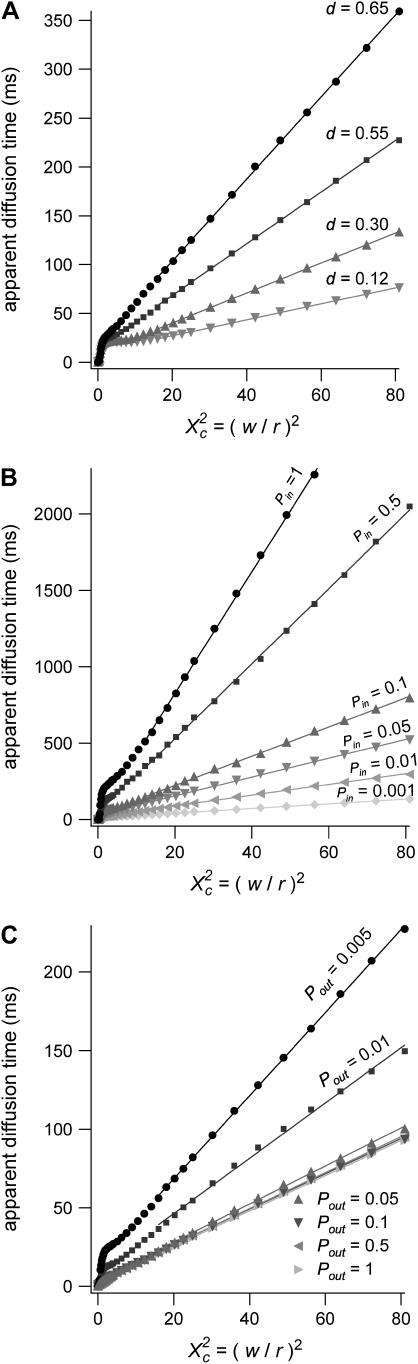
The same study is carried out for densities ranging from 0.1 to the percolation threshold, with a periodical distribution of microdomains.
Fig. 8 A shows that the intercept and the slope of the line describing regime iii are increasing functions of the density d.
FIGURE 8.
Simulated diffusion laws obtained by FCS for the microdomain geometry, when d, Pin, or Pout are changed. (A) Diffusion laws as a function of the density of microdomains (i.e., as a function of the ratio of the surface of all microdomains over the whole surface A) for 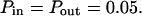 (B) Diffusion laws obtained for different probabilities of going Pin into microdomains (for
(B) Diffusion laws obtained for different probabilities of going Pin into microdomains (for 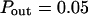 ). (C) Diffusion laws obtained for different probabilities Pout of going out of microdomains (for
). (C) Diffusion laws obtained for different probabilities Pout of going out of microdomains (for 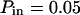 ).
).
Diffusion laws for fixed size and densities of domains and different probabilities Pin and Pout of entering and exiting a domain
In the following, the study is carried out with 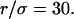
The probability of entering a microdomain may not be the same as the probability of exiting the microdomain. To study this case, the diffusion laws have first been drawn for a fixed probability 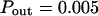 and a variable value of Pin (Fig. 8 B).
and a variable value of Pin (Fig. 8 B).
Regime iii are lines, whatever the value of Pin is. The intercepts and the slopes are two increasing functions of Pin. They behave as power laws of Pin.
The diffusion laws have also been drawn for a fixed probability 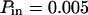 and a variable value of Pout (Fig. 8 C). In this case, regime iii is still a line, the intercepts and the slopes being decreasing functions of Pout. It can be pointed out that the different simulated diffusion laws obtained for high values of Pout (
and a variable value of Pout (Fig. 8 C). In this case, regime iii is still a line, the intercepts and the slopes being decreasing functions of Pout. It can be pointed out that the different simulated diffusion laws obtained for high values of Pout (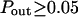 ) are approximately the same. These high values of Pout lead to a confinement time on the order of the diffusion time in a domain (
) are approximately the same. These high values of Pout lead to a confinement time on the order of the diffusion time in a domain (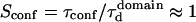 ). These cases correspond to a low confinement of the molecules in the domain, whereas the probability of entering a domain is low: the diffusion law is very close to the one obtained for impermeable obstacles.
). These cases correspond to a low confinement of the molecules in the domain, whereas the probability of entering a domain is low: the diffusion law is very close to the one obtained for impermeable obstacles.
Regime iii of the diffusion laws is a line for densities of microdomains ranging from 0.1 to 0.65, and when 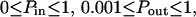 for
for 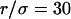 (which corresponds to confinement strengths ranging from 1 to 15).
(which corresponds to confinement strengths ranging from 1 to 15).
Meshwork
We will now show that the diffusion law is different when the molecule diffusion is hindered by a meshwork instead of isolated microdomains. We consider the case of multiple adjacent domains separated by barriers (Fig. 2 B). This situation may be representative of the diffusion of transmembrane proteins in a cytoskeletal network (e.g., the actin meshwork in COS-7 cells).
For reasons of simplicity, domains are squares separated by straight barriers spaced by a distance of 2r. In each simulation, the following parameters are chosen: the microscopic diffusion coefficient is 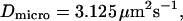 the jump length
the jump length 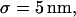 and the size of the half-side of the squares
and the size of the half-side of the squares 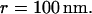
The confinement probed by the laser beam is defined here by 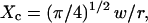 with the laser beam centered on a knot of the meshwork.
with the laser beam centered on a knot of the meshwork.
Fixed size of confinement and variable probability P of crossing the barrier
Fig. 9 A shows ACFs obtained for a fixed illumination laser waist and for different values of 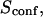 corresponding to different values of P, since σ/r is kept constant.
corresponding to different values of P, since σ/r is kept constant.
FIGURE 9.
Simulated results obtained by FCS for permeable meshwork geometry. (A) ACFs are calculated for a confinement parameter 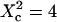 and for different probabilities P of crossing the barriers. Effect of the confinement strength on the shape of ACFs. (B) ACF calculated for a confinement parameter
and for different probabilities P of crossing the barriers. Effect of the confinement strength on the shape of ACFs. (B) ACF calculated for a confinement parameter 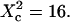 It is well fitted by a 2D free diffusion fit.
It is well fitted by a 2D free diffusion fit.
As for isolated microdomains, the apparent diffusion time increases when P decreases, and two decay times are obtained for large confinement strengths and small values of 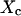 (
(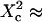 few units, depending on the confinement strength). Moreover, ACFs obtained for large waists (
few units, depending on the confinement strength). Moreover, ACFs obtained for large waists (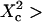 few units) are well fitted by a 1-species 2D free-diffusion fit (Fig. 9 B). As in the case of isolated microdomains, study of the shape of the ACF does not give any information on the diffusion mode if the area of the focal spot is more than a few times larger than the area of a single mesh.
few units) are well fitted by a 1-species 2D free-diffusion fit (Fig. 9 B). As in the case of isolated microdomains, study of the shape of the ACF does not give any information on the diffusion mode if the area of the focal spot is more than a few times larger than the area of a single mesh.
Apparent diffusion time when w varies
Fig. 10 A shows 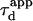 as a function of
as a function of 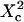 for different values of
for different values of 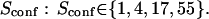 As expected,
As expected, 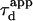 matches
matches 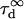 when
when 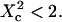 For intermediate values of
For intermediate values of 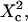 i.e.,
i.e., 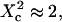 a short transition regime is observed. When
a short transition regime is observed. When 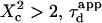 is a linear function of
is a linear function of 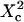 : its slope is dependent on
: its slope is dependent on 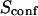 and the intersection with the time axis is negative. The slope and the absolute value of the intersection with the time axis are two increasing functions of the confinement strength
and the intersection with the time axis is negative. The slope and the absolute value of the intersection with the time axis are two increasing functions of the confinement strength 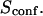 Fig. 10 B shows the average value
Fig. 10 B shows the average value  as a function of
as a function of 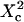 for
for 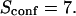 The first two regimes i and ii cannot be distinguished anymore in the case of isolated microdomains. When
The first two regimes i and ii cannot be distinguished anymore in the case of isolated microdomains. When 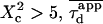 is the same linear function of w2 as the one obtained when no average is done on the position of the laser waist.
is the same linear function of w2 as the one obtained when no average is done on the position of the laser waist.
FIGURE 10.
(A) Diffusion laws obtained for five confinement strengths 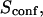 and a single position of the excitation beam (the laser spot is centered on a knot of the meshwork). (B) The diffusion law is averaged on all possible positions of the excitation beam (for
and a single position of the excitation beam (the laser spot is centered on a knot of the meshwork). (B) The diffusion law is averaged on all possible positions of the excitation beam (for 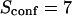 ). It is compared to diffusion laws plotted for different positions of the laser spot.
). It is compared to diffusion laws plotted for different positions of the laser spot.
DISCUSSION
The major applications of FCS are measurements of diffusion coefficients D (31,32). For free diffusion, the standard treatment of FCS data, which consists in fitting ACFs measured at a single size of the waist, is well adapted to determine D. However, a large number of membrane proteins and lipids are partially confined in substructures of sizes ranging from tens of nanometers to micrometers; some are impeded by the cytoskeleton, some others are thought to be raft-associated (33,34). Although sophisticated fits can give some clues on the mode of diffusion in some specific cases, we have shown here that the FCS approach can be revisited to understand diffusion in membranes and to allow inferences on membrane structures. We have introduced the “FCS diffusion law” concept that requires performing several FCS measurements for different sizes of the observation volume, a parameter defined by the transverse laser waist w and can be easily changed in a FCS setup by underfilling the microscope objective back-aperture. With such a technique, we have easily performed measurements for waists w ranging from 200 nm to 400 nm, which corresponds to a fourfold increase of 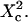
The determination of the apparent diffusion time 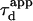 for different values of w permits one to infer the process of diffusion; in particular, we emphasize that
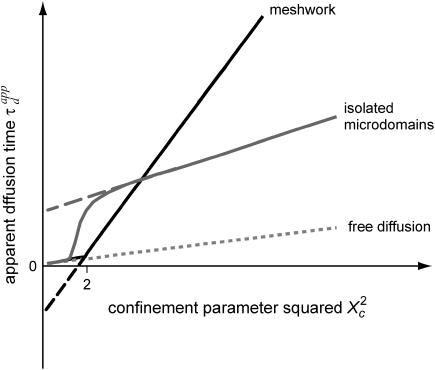
for different values of w permits one to infer the process of diffusion; in particular, we emphasize that 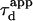 can bring information on the confinement. Fig. 11 summarizes our different results and is presented as a guide for discussion.
can bring information on the confinement. Fig. 11 summarizes our different results and is presented as a guide for discussion.
FIGURE 11.
Apparent diffusion time with respect to 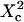 for different geometries of diffusion.
for different geometries of diffusion.
When the size of w is small with respect to the domain size (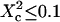 (regime i)), the diffusion appears to be free: the size of the beam does not permit probing the complexity of the system (either skeletal corrals or isolated microdomains). On the other hand, FCS can then give access to microscopic diffusion coefficients and will be sensitive to heterogeneities: it can be used to determine a two-dimension map of microscopic diffusion coefficients. For laser waists comparable to the size of the domains (
(regime i)), the diffusion appears to be free: the size of the beam does not permit probing the complexity of the system (either skeletal corrals or isolated microdomains). On the other hand, FCS can then give access to microscopic diffusion coefficients and will be sensitive to heterogeneities: it can be used to determine a two-dimension map of microscopic diffusion coefficients. For laser waists comparable to the size of the domains (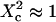 (regime ii)), a transitional diffusion regime is observed. In this regime and for a small probability of crossing the barriers, we expect to detect confinement by a noticeable change of ACFs, which exhibit two different decay times associated respectively to diffusion through the domain and the observation volume (see Figs. 6 A and 9 A). For laser waists larger than the size of the domains (
(regime ii)), a transitional diffusion regime is observed. In this regime and for a small probability of crossing the barriers, we expect to detect confinement by a noticeable change of ACFs, which exhibit two different decay times associated respectively to diffusion through the domain and the observation volume (see Figs. 6 A and 9 A). For laser waists larger than the size of the domains (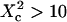 for isolated domains and
for isolated domains and 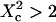 for a meshwork (regime iii)), diffusion is normal again, with an apparent diffusion coefficient
for a meshwork (regime iii)), diffusion is normal again, with an apparent diffusion coefficient 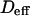 depending on the probability of crossing the barriers, the microscopic diffusion coefficients, and the density of domains (in the case of isolated microdomains). This regime can be approximated by a function of the form
depending on the probability of crossing the barriers, the microscopic diffusion coefficients, and the density of domains (in the case of isolated microdomains). This regime can be approximated by a function of the form
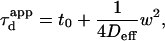 |
(5) |
where 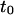 and
and 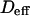 are two constants. Interestingly, in simulations, t0 is positive for diffusion in isolated microdomains and negative for corrals.
are two constants. Interestingly, in simulations, t0 is positive for diffusion in isolated microdomains and negative for corrals.
Phenomenological models for the regime iii of the FCS diffusion law obtained in rafts and corrals
Regime iii is of particular interest since it corresponds to the experimental case when the size of the microdomains is a few times smaller than the diffraction limit. In this section, we focus on the interpretation of parameters 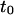 and
and 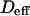 (Eq. 5) that are easily deduced from the FCS diffusion laws in this regime.
(Eq. 5) that are easily deduced from the FCS diffusion laws in this regime.
Diffusion laws in microdomains as a function of the molecular partition inside microdomains
We have shown that the intercept t0 and the slope 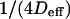 of these lines depend on parameters such as the density and the probabilities of entering or exiting microdomains. They also depend on the diffusion coefficients inside and outside microdomains.
of these lines depend on parameters such as the density and the probabilities of entering or exiting microdomains. They also depend on the diffusion coefficients inside and outside microdomains.
Nevertheless, more physical parameters are needed to explain the experimental FCS diffusion laws.
The partition coefficient α of molecules into raft microdomains can be evaluated independently through biochemical studies. The partition coefficient α corresponds to the ratio measured at a given instant of molecules of a certain kind that are inside microdomains over all molecules of this kind. It can also be calculated with our simulations, since the duration of the whole simulated trajectory is much longer than the time needed for the molecule to visit all the allowed points of the state-space (ergodic principle). Hence, α is obtained from the simulated trajectory by calculating the time the molecule spends in microdomains over the whole simulation time.
In the Appendix, we show that the time intercept t0 can be quite well described by a function of α and the confinement time
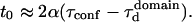 |
(6) |
Since α can be measured from biochemical studies, one can now evaluate the confinement time in a single microdomain 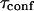 under the usually admitted assumption that
under the usually admitted assumption that 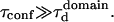
To go further, we give now a possible expression for the slope 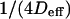 of the line describing the regime iii: the total time needed by a molecule to diffuse through the focal spot is the sum of the time it is confined in microdomains and
of the line describing the regime iii: the total time needed by a molecule to diffuse through the focal spot is the sum of the time it is confined in microdomains and 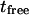 the time it is not being confined. In this case, one can write
the time it is not being confined. In this case, one can write 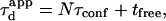 with N the average number of domains that are being crossed.
with N the average number of domains that are being crossed.
But as mentioned before, the partition is defined (in the time description) by the time a molecule spends in microdomains over the total diffusion time, which can be written as 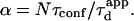
This leads to 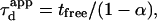 which is equivalent to
which is equivalent to 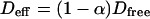 in terms of diffusion coefficients.
in terms of diffusion coefficients.
If molecules enter easily in microdomains, which is the case if the partition is ∼>0.5, Dfree is equal to Dout. If molecules do not enter easily in microdomains, which is the case if the partition is ∼<0.5, they diffuse among microdomains as if they were impermeable obstacles and Dfree is equal to Dobst, which is the effective diffusion coefficient among impermeable obstacles. An expression of Dobst in terms of the surface density covered by the obstacles is given in the Appendix.
As a consequence, this leads to the following expression for the effective diffusion coefficient in the presence of permeable microdomains:
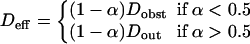 |
(7) |
Diffusion laws in a meshwork as a function of the confinement strength
In all diffusion simulations in a meshwork, the particle visits a certain number of meshes during its diffusion in the confocal volume. The average number N of meshes that are crossed is only a function of the waist of the focal spot, not of the probability of passing a barrier. The mean diffusion time through the focal spot is equal to the number of crossed meshes multiplied by the confinement time in a single mesh so that 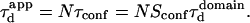 In the case of free diffusion, the diffusion time in the focal spot is given by the number of crossed meshes multiplied by the diffusion time in a single mesh:
In the case of free diffusion, the diffusion time in the focal spot is given by the number of crossed meshes multiplied by the diffusion time in a single mesh: 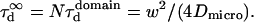 As a consequence, the asymptotic diffusion law needs to be a line with a slope equal to
As a consequence, the asymptotic diffusion law needs to be a line with a slope equal to 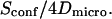 For spatial scales much smaller than the mesh size, one expects to obtain a free diffusion law, i.e., a line with a slope equal to
For spatial scales much smaller than the mesh size, one expects to obtain a free diffusion law, i.e., a line with a slope equal to 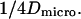 Finally, the spatial scale at which regime ii and regime iii cross should be close to the mesh size. It can be seen from the simulated FCS diffusion laws that the crossover is found for
Finally, the spatial scale at which regime ii and regime iii cross should be close to the mesh size. It can be seen from the simulated FCS diffusion laws that the crossover is found for 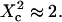 The actual FCS diffusion law can be calculated from the slopes derived from this intuitive model, and the crossover obtained from the simulations; we find
The actual FCS diffusion law can be calculated from the slopes derived from this intuitive model, and the crossover obtained from the simulations; we find
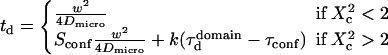 |
(8),(9) |
with 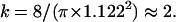
These equations fit quite nicely the FCS diffusion laws obtained from the simulations (data not shown). Note that the determination of the crossover point provides a measure of the mesh size.
Interpretation of the experimental results
Diffusion modes encountered in COS-7 cells
To end up our discussion, we now come back on the experimental results that have been presented in Fig. 4. In the framework of our model, the diffusion modes of both the FL-GM1 and the TfR-GFP can now be inferred from the shapes of the measured FCS diffusion laws. For FL-GM1, the large waists diffusion law (regime iii) can be fitted by a line with a positive intercept. This diffusion law is well described by the microdomain model. This can be related to the fact that FL-GM1 is a putative raft marker, which means that biochemical studies show that it partitions into rafts.
For TfR-GFP, the large waists diffusion law (regime iii) is a line with a negative intercept, which is compatible with a diffusion hindered by the cytoskeleton meshwork.
Confinement time values
Through biochemical studies, it has be shown that 40% of GM1 partition into detergent resistant membranes (35,36), whereas its fluorescent analog FL-GM1 is expected to have a much smaller partition coefficient (37). Thus, a lower limit of the confinement time into microdomains can be inferred from the partition α and the intercept 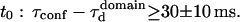
An upper limit can be given to the microdomain radius, because the sole affine regime (iii) is observed experimentally. Since this regime corresponds to 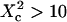 and the experimental waist is >200 nm (diffraction-limited), the maximum value for the microdomain radius should be ∼60 nm. Moreover, at a waist of 200 nm, we measured a diffusion time of 30 ms. Thus, the diffusion time through a domain would be at most 3 ms. The time intercept being much larger than this time, we can conclude that τconf ≫ τdiff and
and the experimental waist is >200 nm (diffraction-limited), the maximum value for the microdomain radius should be ∼60 nm. Moreover, at a waist of 200 nm, we measured a diffusion time of 30 ms. Thus, the diffusion time through a domain would be at most 3 ms. The time intercept being much larger than this time, we can conclude that τconf ≫ τdiff and 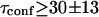 ms.
ms.
The confinement time in a mesh of the cytoskeleton can also be calculated from the negative time intercept of TfR-GFP diffusion law, since 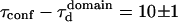 ms.
ms.
As mentioned before, these two diffusion examples are representative of some more experimental results that will be presented in detail in Lenne et al. (unpublished).
CONCLUSION
Because FCS has a high temporal resolution, it can easily capture millisecond range phenomena, in particular transient confinements, which are difficult to study with other techniques. In this article, we have shown that the “FCS diffusion laws”, which are obtained by FCS measurements at various spatial scales, give valuable information on the diffusion processes taking place in the membranes. The shape of such FCS diffusion laws distinguishes between two different diffusion modes: diffusion among isolated microdomains (as for FL-GM1) and diffusion hindered by a meshwork (as for TfR-GFP). In the regime where the laser waist w is much larger than the domain or mesh extension, we have demonstrated that the FCS diffusion laws can provide physical parameters such as the residence time into a single microdomain or mesh and an effective diffusion coefficient. Furthermore, we have shown that the FCS diffusion laws split in various regimes depending on the ratio of the waist w over the size of the microdomains (or meshes). The validity of the models has been extensively tested in membranes of live cells (more examples are given and exploited in Lenne et al. (unpublished)). These results show that FCS diffusion laws are relevant to study confinement and permit inferences about the dynamic organization of the cell membrane. We hope that these “FCS diffusion laws” will constitute a framework to study complex diffusion in model systems and membranes of live cells.
From a biological point of view, this will unravel the relationship between molecular confinement and biological functions such as signaling processes. From a physical point of view, this offers a new tool to study the transition from anomalous to normal diffusion (38).
Acknowledgments
We thank H. Qasmi and N. Bertaux for technical help in simulations and P. Pelcé for helpful discussions.
This work was supported by institutional grants from the Centre National de la Recherche Scientifique and Institut National de la Santé et de la Recherche Médicale, and by specific grants from the Fondation pour la Recherche Médicale, Ministère de l'Education Nationale, de l'Enseignement Supérieur et de la Recherche, and Centre National de la Recherche Scientifique. L.W. is recipient of a doctoral fellowship from the Ministère de l'Education Nationale, de l'Enseignement Supérieur et de la Recherche.
APPENDIX: EFFECTIVE DIFFUSION COEFFICIENT AND TIME INTERCEPT FOR THE MICRODOMAIN MODEL
When domains are fully impermeable and molecules are restricted to diffuse outside of them, the diffusion law in regime iii is a line with a null intercept, which gives an effective diffusion coefficient Dobst:
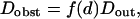 |
where f(d) is a function of the surface density d covered by the obstacles. In the case of periodically distributed impermeable circular obstacles and for 0.1<d<0.6, we obtain from fit 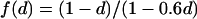 (data not shown).
(data not shown).
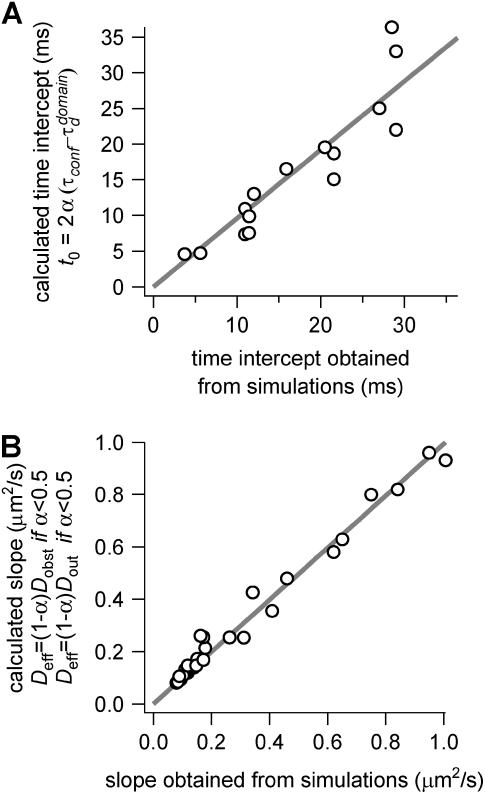
To confront our heuristic model with the simulation results, we compare the calculated time intercept and slope given by Eqs. 6 and 7 with those obtained from our simulations. Fig. 12 shows that both the time intercept and the effective diffusion coefficient are very well described by Eqs. 6 and 7.
FIGURE 12.
Parameters of the line describing regime iii of molecules in isolated domains geometry. (A) Time intercept 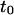 as calculated by Eq. 6 versus the time intercept obtained from the simulations. (B) Slope
as calculated by Eq. 6 versus the time intercept obtained from the simulations. (B) Slope 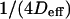 calculated by Eq. 7 as a function of the slope obtained from the simulations.
calculated by Eq. 7 as a function of the slope obtained from the simulations.
Abbreviations used: FCS, fluorescence correlation spectroscopy; ACF, autocorrelation function; GFP, green fluorescent protein; BODIPY, 4,4-difluoro-5,7-dimethyl-4-bora-3a, 4a-diaza-s-indacene; FL-GM1, BODIPY-ganglioside GM1; TfR, human transferrin receptor; RhG6, rhodamine 6G; FWHM, full width at half-maximum; 2D, two-dimensional.
References
- 1.Jacobson, K., E. D. Sheets, and R. Simson. 1995. Revisiting the fluid mosaic model of membranes. Science. 268:1441–1442. [DOI] [PubMed] [Google Scholar]
- 2.Kusumi, A., Y. Sako, and M. Yamamoto. 1993. Confined lateral diffusion of membrane receptors as studied by single particle tracking (nanovid microscopy). Effects of calcium-induced differentiation in cultured epithelial cells. Biophys. J. 65:2021–2040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fujiwara, T., K. Ritchie, H. Murakoshi, K. Jacobson, and A. Kusumi. 2002. Phospholipids undergo hop diffusion in compartmentalized cell membrane. J. Cell Biol. 157:1071–1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Singer, S. J., and G. L. Nicolson. 1972. The fluid mosaic model of the structure of cell membranes. Science. 175:720–731. [DOI] [PubMed] [Google Scholar]
- 5.Brown, D. A., and J. K. Rose. 1992. Sorting of GPI-anchored proteins to glycolipid-enriched membrane subdomains during transport to the apical cell surface. Cell. 68:533–544. [DOI] [PubMed] [Google Scholar]
- 6.Simons, K., and E. Ikonen. 1997. Functional rafts in cell membranes. Nature. 387:569–572. [DOI] [PubMed] [Google Scholar]
- 7.Brown, D. A., and E. London. 2000. Structure and function of sphingolipid- and cholesterol-rich membrane rafts. J. Biol. Chem. 275:17221–17224. [DOI] [PubMed] [Google Scholar]
- 8.Varma, R., and S. Mayor. 1998. GPI-anchored proteins are organized in submicron domains at the cell surface. Nature. 394:798–801. [DOI] [PubMed] [Google Scholar]
- 9.Saxton, M. J., and K. Jacobson. 1997. Single-particle tracking: applications to membrane dynamics. Annu. Rev. Biophys. Biomol. Struct. 26:373–399. [DOI] [PubMed] [Google Scholar]
- 10.Schutz, G. J., G. Kada, V. P. Pastushenko, and H. Schindler. 2000. Properties of lipid microdomains in a muscle cell membrane visualized by single molecule microscopy. EMBO J. 19:892–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Pralle, A., P. Keller, E. L. Florin, K. Simons, and J. K. Horber. 2000. Sphingolipid-cholesterol rafts diffuse as small entities in the plasma membrane of mammalian cells. J. Cell Biol. 148:997–1008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Saxton, M. J. 1995. Single-particle tracking: effects of corrals. Biophys. J. 69:389–398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Weiss, M., H. Hashimoto, and T. Nilsson. 2003. Anomalous protein diffusion in living cells as seen by fluorescence correlation spectroscopy. Biophys. J. 84:4043–4052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wawrezinieck, L., P.-F. Lenne, D. Marguet, and H. Rigneault. 2004. Fluorescence correlation spectroscopy to determine diffusion laws: application to live cell membranes. Proc. SPIE Int. Soc. Opt. Eng. 5462:92–103. [Google Scholar]
- 15.Masuda, A., K. Ushida, and T. Okamoto. 2003. Japanese Patent Application. (Published as Japanese Patent Publication No. 2005–043278, Feb. 17, 2005). Tokyo, Japan.
- 16.Masuda, A., K. Ushida, and T. Okamoto. 2005. New fluorescence correlation spectroscopy enabling direct observation of spatiotemporal dependence of diffusion constants as an evidence of anomalous transport in extracellular matrices. Biophys. J. 88:3584–3591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schwille, P. 2001. Fluorescence correlation spectroscopy and its potential for intracellular applications. Cell Biochem. Biophys. 34:383–408. [DOI] [PubMed] [Google Scholar]
- 18.Gennerich, A., and D. Schild. 2002. Anisotropic diffusion in mitral cell dendrites revealed by fluorescence correlation spectroscopy. Biophys. J. 83:510–522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gennerich, A., and D. Schild. 2000. Fluorescence correlation spectroscopy in small cytosolic compartments depends critically on the diffusion model used. Biophys. J. 79:3294–3306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pagano, R. E., and O. C. Martin. 1998. Cell Biology: A Laboratory Handbook. Academic Press, San Diego, CA.
- 21.Elson, E. L., and D. Magde. 1974. Fluorescence correlation spectroscopy. Biopolymers. 13:1–27. [DOI] [PubMed] [Google Scholar]
- 22.Bouchaud, J. P., and A. Georges. 1990. Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Phys. Rep. 195:127–293. [Google Scholar]
- 23.Yechiel, E., and M. Edidin. 1987. Micrometer-scale domains in fibroblast plasma membranes. J. Cell Biol. 105:755–760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lopez, A., L. Dupou, A. Altibelli, J. Trotard, and J. F. Tocanne. 1988. Fluorescence recovery after photobleaching (FRAP) experiments under conditions of uniform disk illumination. Critical comparison of analytical solutions, and a new mathematical method for calculation of diffusion coefficient D. Biophys. J. 53:963–970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wohland, T., R. Rigler, and H. Vogel. 2001. The standard deviation in fluorescence correlation spectroscopy. Biophys. J. 80:2987–2999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Schätzel, K. 1985. New concepts in correlator design. In Institute of Physics Conference Series. Hilger, London. 77:175–184.
- 27.Press, W. H., S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. 1992. Numerical Recipes in C: The Art of Scientific Computing. Cambridge University Press, Cambridge, U.K.
- 28.Fahey, P. F., D. E. Koppel, L. S. Barak, D. E. Wolf, E. L. Elson, and W. W. Webb. 1977. Lateral diffusion in planar lipid bilayers. Science. 195:305–306. [DOI] [PubMed] [Google Scholar]
- 29.Dietrich, C., L. A. Bagatolli, Z. N. Volovyk, N. L. Thompson, M. Levi, K. Jacobson, and E. Gratton. 2001. Lipid rafts reconstituted in model membranes. Biophys. J. 80:1417–1428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lenne, P.-F., E. Etienne, and H. Rigneault. 2002. Subwavelength patterns and high detection efficiency in fluorescence correlation spectroscopy using photonic structures. Appl. Phys. Lett. 80:4106–4108. [Google Scholar]
- 31.Hess, S. T., S. Huang, A. A. Heikal, and W. W. Webb. 2002. Biological and chemical applications of fluorescence correlation spectroscopy: a review. Biochemistry. 41:697–705. [DOI] [PubMed] [Google Scholar]
- 32.Schwille, P., U. Haupts, S. Maiti, and W. W. Webb. 1999. Molecular dynamics in living cells observed by fluorescence correlation spectroscopy with one- and two-photon excitation. Biophys. J. 77:2251–2265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kusumi, A., C. Nakada, K. Ritchie, K. Murase, K. Suzuki, H. Murakoshi, R. S. Kasai, J. Kondo, and T. Fujiwara. 2005. Paradigm shift of the plasma membrane concept from the two-dimensional continuum fluid to the partitioned fluid: high-speed single-molecule tracking of membrane molecules. Annu. Rev. Biophys. Biomol. Struct. 34:351–378. [DOI] [PubMed] [Google Scholar]
- 34.Simson, R., B. Yang, S. E. Moore, P. Doherty, F. S. Walsh, and K. A. Jacobson. 1998. Structural mosaicism on the submicron scale in the plasma membrane. Biophys. J. 74:297–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Fra, A. M., E. Williamson, K. Simons, and R. G. Parton. 1994. Detergent-insoluble glycolipid microdomains in lymphocytes in the absence of caveolae. J. Biol. Chem. 269:30745–30748. [PubMed] [Google Scholar]
- 36.Blank, N., C. Gabler, M. Schiller, M. Kriegel, J. R. Kalden, and H. M. Lorenz. 2002. A fast, simple and sensitive method for the detection and quantification of detergent-resistant membranes. J. Immunol. Methods. 271:25–35. [DOI] [PubMed] [Google Scholar]
- 37.Kuerschner, L., C. S. Ejsing, K. Ekroos, A. Shevchenko, K. I. Anderson, and C. Thiele. 2005. Polyene-lipids: a new tool to image lipids. Nat. Methods. 2:39–45. [DOI] [PubMed] [Google Scholar]
- 38.Saxton, M. J. 1996. Anomalous diffusion due to binding: a Monte Carlo study. Biophys. J. 70:1250–1262. [DOI] [PMC free article] [PubMed] [Google Scholar]