Interactions between Charged Polypeptides and Nonionic Surfactants

Abstract

The influence of molecular characteristics on the mutual interaction between peptides and nonionic surfactants has been investigated by studying the effects of surfactants on amphiphilic, random copolymers of α-L-amino acids containing lysine residues as the hydrophilic parts. The hydrophobic residues were either phenylalanine or tyrosine. The peptide-surfactant interactions were studied by means of circular dichroism spectroscopy and binding isotherms, as well as by 1D and 2D NMR. The binding of surfactant to the peptides was found to be a cooperative process, appearing at surfactant concentrations just below the critical micellar concentration. However, a certain degree of peptide hydrophobicity is necessary to obtain an interaction with nonionic surfactant. When this prerequisite is fulfilled, the peptide mainly interacts with self-assembled, micelle-like surfactant aggregates formed onto the peptide chain. Therefore, the peptide-surfactant complex is best described in terms of a necklace model, with the peptide interacting primarily with the palisade region of the micelles via its hydrophobic side chains. The interaction yields an increased amount of α-helix conformation in the peptide. Surfactants that combine small headgroups with a propensity to form small, nearly spherical micelles were shown to give the largest increase in α-helix content.

INTRODUCTION

Many peptides and proteins interact strongly with amphiphilic molecules and these interactions are of vast importance, not only in vivo but also in technical applications. The conformational changes in prion proteins provide a pertinent example. Here, interactions with amphiphiles may stabilize the α-helical conformation of the protein and hence decrease the risk for the devastating β-sheet formation (1). Similarly, interactions between peptides and amphiphiles (lipids) are inherent features of the mechanism of membrane binding peptides, including antibiotic ones (2–10). A large group of peptide antibiotics fold into an amphipathic α-helical conformation when interacting with the target membranes (7). Examples of other native peptides and proteins that undergo α-helix formation upon membrane binding include plasma apolipoproteins, mitochondrial presequences, virus fusion peptides, and antibacterial peptides (11). For example, the binding of magainin to a nonionic vesicle has been shown to be an enthalpy-driven process, primarily driven by the increased formation of α-helix (2–6). Similarly, the peptides melittin and cecropin A show a transition from random coil to α-helix upon interaction with micelles (12,13) and gelatin has been shown to display a coil-helix transition in the presence of nonionic surfactants (14,15).

That interactions with surfactants and other amphiphiles lead to an increased amount of α-helix conformation in peptides is thus well known from the literature. Nevertheless, the understanding of surfactant binding, concentration-dependent effects, and the nature of peptide-surfactant complexes still seems somewhat sketchy. Furthermore, the influence of surfactant and peptide molecular characteristics on the α-helix formation has not been studied in a systematic fashion.

In this study, we have examined a range of nonionic surfactants in terms of their ability to stabilize the α-helical conformation of peptides. These studies have been supplemented by a thorough investigation of the specific intermolecular interactions between peptides and surfactants, as well as their dependence on molecular characteristics. The prime objectives of the study are to identify the molecular properties of the peptides and surfactants that primarily govern their mutual interaction. For this reason, the study comprises simple model peptides, with well-defined secondary conformation. More precisely, the peptides in this work are random copolymers containing lysine as the hydrophilic part and either phenylalanine or tyrosine as the hydrophobic part. For these peptides, random coil and α-helix are the only two conformations that need to be taken into account under the pH conditions used in the study (16). Similarly, peptide aggregation is strongly disfavored under these conditions, for electrostatic reasons (16). The model peptides make it possible to derive detailed information, at the molecular level, about the roles of hydrophilic and hydrophobic side chains in the interactions between peptide and surfactant. They also make it possible to directly correlate these interactions with conformational changes (random coil to α-helix) of the peptide. To avoid end effects, model peptides with a large degree of polymerization (generally >200 amino acid residues, corresponding to >40 kDa) were selected.

A more specific objective of this study is to pave the way for a rational selection of surfactants for pharmaceutical formulations containing peptides. In such formulations, surfactants provide a means to enhance the physical stability by preventing undesirable conformational changes, aggregation, and surface adsorption caused by changes in pH, temperature, and other parameters (17,18). An important contributing factor to physical instability of peptide formulations is the propensity of many peptides to form intramolecular β-sheets. In general, this formation leads to precipitation of the peptide, which is clearly detrimental for product performance. The β-sheet formation in pharmaceutical peptides may be inhibited by stabilization of the α-helical conformation and this, in turn, can be achieved by addition of a suitable surfactant. It is preferable to use nonionic surfactants, since they tend to be less potent irritants on mucosa and other biointerfaces than ionic surfactants (17). Nevertheless, detrimental effects on mucosa and epithelia are observed also for nonionic surfactants, and these effects are concentration-dependent (19). For this reason, it is desirable to select a surfactant that provides a high enough physical stability of the peptide (i.e., preventing peptide aggregation) at a sufficiently low concentration. However, a clear rationale for this selection has not been established, partly due to the incomplete understanding of the details of peptide-surfactant interactions in aqueous solution.

This study focuses on alkylglycoside surfactants, but also comprises a comparison with surfactants based on polyethyleneoxide (PEO). PEO-based surfactants are approved for use in pharmaceutics and are extensively used in formulation. The alkylglycosides, on the other hand, are a class of surfactants frequently used for membrane protein solubilization, since they generally do not unfold the protein (20). Their chemical stability and high biocompatibility mean that they can be regarded as strong candidates for future use in drug formulations.

MATERIALS AND METHODS

Chemicals

Co-poly-L-(lysine, phenylalanine) HBr, poly-L-lysine HCl and two different types of co-poly-L-(lysine, tyrosine) were purchased from Sigma Chemicals (Steinheim, Germany). They were stored at −18°C and used as received. The mean molecular weight determined by viscosimetry, 〈M_w〉_vis, the corresponding average degree of polymerization, D_p, and the molar ratio between the amino acids, all as stated by the manufacturer, are listed in Table 1. The table also presents the shorthand notations henceforth used to refer to the various peptides.

TABLE 1.

Mean molecular weight, degree of polymerization, and molar ratio of the poly-L-amino acids used

Polypeptide	Shorthand notation	(〈Mw〉vis (kDa)	Dp	Molar ratio
Poly-L-lysine HCl	Kn	52.5	319	—
Co-poly-L-(lysine, phenylalanine) 1:1 HBr	(KF)n	49.0*	275*	52:48
		42.2†	237†	52:48
Co-poly-L-(lysine, tyrosine) 1:1 HBr	(KY)n	128	684	53:47
Co-poly-L-(lysine, tyrosine) 4:1 HBr	(K4Y)n	24.6	123	80:20

The degree of polymerization, D_p, refers to the number of amino acid residues in each peptide chain.

^*Used for NMR and binding isotherm.

^†Used for all other studies.

n-Heptyl-β-D-glucoside (β-C₇G₁), n-octyl-β-D-glucoside (β-C₈G₁), n-nonyl-β-D-glucoside (β-C₉G₁), n-octyl-β-D-maltoside (β-C₈G₂), n-decyl-β-D-maltoside (β-C₁₀G₂), n-dodecyl-β-D-maltoside (β-C₁₂G₂), n-tetradecyl-β-D-maltoside (β-C₁₄G₂), n-dodecyl-α-D-maltoside (α-C₁₂G₂), and n-dodecyl-β-D-maltotrioside (β-C₁₂G₃) were obtained from Anatrace (Maumee, OH) and were of Anagrade quality. Representative examples of the molecular structure of these alkylglycosides are given in Fig. 1. Monodisperse samples of pentaethyleneglycol mono n-dodecyl ether (C₁₂E₅), hexaethyleneglycol mono n-dodecyl ether (C₁₂E₆), and octaethyleneglycol mono n-dodecyl ether (C₁₂E₈) were provided by Nikkol Chemical (Tokyo, Japan).

FIGURE 1.

Chemical structure of three different alkylglycosides: n-octyl-β-D-glucoside (β-C₈G₁), n-dodecyl-α-D-maltoside (α-C₁₂G₂), and n-dodecyl-β-D-maltotrioside (β-C₁₂G₃). Note the difference between alkylglycosides (surfactants with an undefined number of sugar units in the headgroup) and alkylglucosides (surfactants with one sugar unit in the headgroup).

Acetic acid, NaCl, and sodium acetate (p.A. grade), HCl and NaOH (Titrisol grade), and D-(+)− glucose (“for microbiology” grade) were purchased from Merck (Darmstadt, Germany). Sodium hydrogen carbonate (p.A. grade) was purchased from Fluka (Buchs, Switzerland). Deuterium oxide, acetic acid-D4, and sodium deuteroxide, with an isotopic purity of 99.9%, 99.5%, and 99.5%, respectively, were purchased from Cambridge Isotope Laboratories (Andover, MA). Distilled water, purified on a PureLab Plus water purification apparatus and filtered through a 0.10-μm filter, was used in all experiments.

Spectra/Por regenerated cellulose membrane discs, with a molecular weight cutoff of 6–8 kDa, were purchased from Spectrum Laboratories (Breda, The Netherlands).

Circular dichroism spectroscopy

Circular dichroism (CD) spectra of the peptides were recorded on a Jasco J715 spectropolarimeter with the samples enclosed in standard cuvettes made of quartz and with an optical pathlength of 1.000 cm. For each sample, 30–50 individual spectra were collected and added. All measurements, except the temperature study of C₁₂E₆, were carried out at 20°C. The temperature was controlled by a Peltier-type temperature control system.

A peptide concentration of 25 μg/ml (which equals 0.14 mM of amino acid residues) was used, and the samples were buffered at pH 4.90 (±0.02) with 20 mM acetate buffer. All measurements were performed within 1 h of sample preparation. For (KF)_n + β-C₈G₁, measurements were also performed in deuterated solutions, to allow for a direct comparison with the binding isotherm experiments. However, no significant difference in the α-helix content of (KF)_n was observed when deuterated solutions were used.

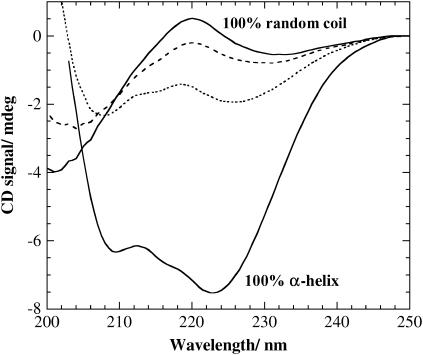
The CD signal recorded at 225 nm was used in calculations of the α-helix content. However, CD spectra were recorded between 220 and 250 nm to verify absence of secondary conformations other than α-helix and random coil (e.g., β-sheets and β-turns). Additionally, for (KF)_n, the absence of peptide conformations other than random coil and α-helix was verified by measuring the CD spectra in a wider wavelength region (200–250 nm), before and after addition of 2 mM β-C₁₂G₂ (results not shown) or 0.2 M β-C₈G₁ (Fig. 2). For these studies, a cuvette with an optical pathlength of 0.100 cm was used to allow for data acquisition in the far-UV region.

FIGURE 2.

CD spectra for (KF)_n with (dotted trace) and without (dashed trace) addition of 0.2 M β-C₈G₁. The reference spectra for 100% α-helix and 100% random coil (solid traces) are given for comparison. A (KF)_n concentration of 25 μg/ml (which equals 0.14 mM of amino acid residues) was used in the CD measurements. All measurements were performed in a 20-mM acetate buffer at pH 4.9.

A baseline offset of <1.4 mdeg was observed in most measurements. This offset is a normal effect of minor instrument misalignments and changes slightly every time the instrument is restarted. When the data were evaluated the offset was subtracted by assuming that the CD signal is zero at 250 nm. However, in the (KY)_n and (K₄Y)_n case, no baseline correction was applied, since the tyrosine residues give a significant CD contribution at wavelengths around 250 nm.

The total CD signal depends linearly on the CD signals of the different types of secondary conformation in the peptide. The peptides used in this study only form α-helical and/or random coil conformation under the relevant conditions. Hence, the recorded CD signal at any given wavelength, A, can be expressed as

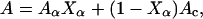(1)

where A_α and A_c are the CD signals for a peptide in a 100% α-helix and a 100% random coil conformation, respectively, and X_α is the fraction of the peptide in α-helical conformation. Eq. 1 can be rewritten as

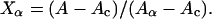(2)

For K_n, conditions for obtaining 100% α-helix or 100% random coil conformation can be found in the literature. At a 0.01–0.06% concentration, K_n has been reported to form a 100% random coil conformation at pH 5 and 22°C, whereas it forms a 100% α-helix conformation at pH 11 and 22°C (21,22). In this study, a 0.15-mM (amino acid residue concentration) solution of K_n in 0.1 M HCl and 0.1 M NaOH was used to determine the 100% random coil and 100% α-helix spectra, respectively. In contrast to K_n, it was found necessary to use a medium with very low ionic strength (0.02 M acetic acid) to achieve 100% random coil conformation in (KF)_n. Similarly, formation of 100% α-helix in (KF)_n requires addition of nonionic surfactant. Consequently, the α-helix spectrum of this peptide was recorded in 0.1 M NaOH solution containing 5 mM β-C₁₂G₂, as has previously been reported (16).

For (K₄Y)_n and (KY)_n, 100% α-helix conformation is impossible to obtain by titration, due to the fact that tyrosine residues (pK_a = 10.07) (23) are charged under pH conditions where the lysine residues (pK_a = 10.53) (24) are uncharged, and vice versa. Furthermore, the CD results for the tyrosine-containing peptides cannot be evaluated using the 100% α-helix spectra for K_n or (KF)_n, since the tyrosine residues absorb in the region of the characteristic α-helix minima and random coil maximum. Therefore, the results from the tyrosine-containing peptides are only reported in terms of absolute changes in CD signal upon addition of surfactant, ΔCD.

Using the spectra for the all-coil and all-helix reference solutions, A_α and A_c for K_n and (KF)_n were determined. From these values, X_α were calculated for any given sample by means of Eq. 2.

The increased amount of peptide in α-helix conformation obtained upon addition of surfactant, ΔX_α, is calculated as the difference between X_α at surfactant concentrations ≥10 × CMC (critical micellar concentration, where the fraction of peptide in α-helix conformation is independent of the surfactant concentration) and X_α observed in the absence of surfactant.

Tensiometry

A KSV Sigma 70 tensiometer equipped with a du Nouy ring made of platinum was used to determine the liquid/air surface tension as a function of surfactant concentration. The system was temperature-controlled at 20°C by a circulating water bath. The surfactant solutions were prepared in 20 mM acetate buffer at pH 4.90. At each measurement, the surface tension was recorded after a maximum of 1 h of equilibration. With time, a small drift toward lower surface tension was observed. However, the drift was not affecting the determination of the CMC, except for β-C₁₄G₂. For this surfactant, the very low CMC renders the measurements difficult, and a larger drift was observed. As a consequence, the CMC determination for β-C₁₄G₂ is less accurate than for the other surfactants.

NMR spectroscopy

All samples were prepared in 20 mM deuterated acetate buffer at pD 5.0, as measured with a pH meter. All ¹H chemical shifts are referenced to the residual HDO signal set to 4.75 ppm. Indirect chemical shift referencing is employed for ¹³C using the frequency ratio Ξ = ν_C/ν_H = 0.25145002, where ν_C and ν_H correspond to the ¹³C and ¹H frequencies, respectively, of the methyl resonances (0 ppm) in tetramethylsilane in H₂O (25). All studies were performed at 25°C.

In the investigation of the binding isotherm of β-C₈G₁ to (KF)_n, 1D ¹H spectra were acquired on a 400 MHz Varian INOVA spectrometer equipped with a 5-mm ¹H-¹³C switchable gradient probe (Nalorac, Martinez, CA). All spectra were recorded with a spectral width of 6250 Hz, 24,992 complex points, and a spectra total relaxation delay of 4 s between each scan. For each experiment, 512 scans were recorded. Automatic gain adjustment was employed. The NMR data were processed with a pure cosine window function, zero-filled to 128,000 before the Fourier transform, and followed by automatic baseline correction.

Initial studies of possible interactions between various peptides and the surfactant β-C₁₂G₂ were performed by acquiring standard 1D ¹H spectra on 400 and 500 MHz Varian INOVA spectrometers on seven separate samples, namely (KF)_n, K_n, (K₄Y)_n, β-C₁₂G₂, (KF)_n + β-C₁₂G₂, K_n + β-C₁₂G₂, and (K₄Y)_n + β-C₁₂G₂. The NMR samples contained 0.25–0.65 mM of polypeptide (which corresponds to 80 mM of amino acid residues) and/or 40 mM surfactant. More detailed studies were performed on samples of (KF)_n, β-C₁₂G₂, (KF)_n + β-C₁₂G₂, and (K₄Y)_n + β-C₁₂G₂ using 2D NMR techniques. Nearly complete ¹H and ¹³C chemical shift assignments were obtained for these four samples by recording ¹³C–¹H heteronuclear single quantum correlation (HSQC) (26,27), ¹H nuclear Overhauser enhancement spectroscopy (NOESY) (28,29), and ¹H total correlation spectroscopy spectra (30,31) with a DIPSI-2 relaxation-compensated isotropic sequence (32). Intermolecular contacts were studied from a series of 2D NOESY spectra with mixing times from 15 to 200 ms. All 2D spectra were acquired on a 500 MHz Varian INOVA spectrometer equipped with a 5-mm ¹H/¹³C/¹⁵N triple-resonance probe.

Dialysis and binding isotherm measurements

The binding of β-C₈G₁ to (KF)_n was determined by equilibrium dialysis, using a Spectrum equilibrium dialyzer with semi-micro cells. We used 800-μl aliquots of solutions containing a peptide concentration of 18 μM (5 mM of amino acid residues) and 0.5 mM β-C₈G₁ dialyzed against 800 μl aliquots of β-C₈G₁ in the concentration range 0.5–60 mM. All solutions were prepared in 20 mM deuterated acetate buffer at pD 5.0. The dialyzer was run at maximum speed (30 rpm) until equilibrium was reached (∼70 h). At equilibrium, the free β-C₈G₁ concentration in the peptide-free dialysis cell halves was determined by ¹H NMR from the area of the signals in three different regions of the ¹H NMR spectra, namely 0.66–1.03, 1.03–1.53, and 1.53–1.83 ppm. The regions were carefully selected so that all chemical shift changes observed in the studied concentration interval were taken into account. The integral values were corrected for the various gain parameters employed (as given in the preceding section) and evaluated with reference to standard curves for β-C₈G₁ measured in the range 0.5–40 mM. The reference curves displayed a linear regression coefficient R ≥ 0.9996.

Attempts were made to determine the binding isotherm also for the binding of β-C₉G₁ to (KF)_n (results not shown). In this case, the establishment of dialysis equilibrium was found to be exceedingly time-consuming (dialysis times of ≫300 h). The membrane pore size used (molecular weight cutoff = 6–8 kDa) is smaller than the size of both β-C₈G₁ and β-C₉G₁ micelles, implying that only surfactant monomers pass through the membrane pores. However, the propensity of β-C₉G₁ (33) to form elongated aggregates may open the possibility for surfactant monolayer coverage of the membrane. This stronger interaction with the dialysis membrane could possibly lead to a concomitant bilayer coverage of the membrane pores, which would dramatically decrease the membrane permeability. Such a scenario could possibly serve as an explanation for the huge decrease in dialysis equilibrium rate between β-C₈G₁ and β-C₉G₁.

Dynamic light scattering

Dynamic light scattering (DLS) experiments were performed at 20°C on a Brookhaven ZetaPALS instrument (Brookhaven Instruments, Holtsville, NY). The instrument was equipped with a thermostated sample cell and a laser operating at 532 nm. The scattered light was measured at an angle of 90° with the samples enclosed in 1.00-cm polystyrene cuvettes. The samples contained 10 g/L of surfactant, dissolved in 20 mM acetate buffer at pH 4.90. All solutions used in the DLS experiments were filtered through an Acrodisc filter with a pore size of 0.1 or 0.2 μm. Data were collected for 10 min for each sample and analyzed by means of the software supplied with the instrument (Brookhaven DLS software, ver. 2.13). The analysis is based on the method of cumulants (34).

The analysis yields the diffusion coefficient D of the particles in the system. The effective hydrodynamic diameter, d_H, reported in this work is derived directly from Stoke-Einstein's equation (Eq. 3) using the diffusion coefficient, D:

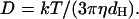(3)

Here, k is the Boltzmann constant, T the absolute temperature of the solution, and η the solvent viscosity.

Since the micelles may be elongated objects and the Stoke-Einstein equation strictly applies only to hard spheres, the effective hydrodynamic diameter is to be considered merely as an alternative way to represent the primary DLS data, namely the diffusion coefficient D.

RESULTS

Effects of surfactants on peptide conformation

The pK_a for lysine in solution is 10.53 (24) and the lysine residues in K_n, (KF)_n, (KY)_n and (K₄Y)_n are therefore protonated and charged under the pH conditions used in this study (pH 4.9). The high charge of the peptides at pH 4.9 means that their conformation is predominantly random coil and that peptide aggregation is strongly disfavored for electrostatic reasons. Previous work on K_n and (KF)_n shows that β-sheet formation with concomitant aggregation and precipitation only occur at pH >9 for (KF)_n (16). For K_n, β-sheet formation occurs at pH >11 and elevated temperatures (>35°C) and/or very high peptide concentrations (35–37). However, the CD spectra of aqueous peptide solutions at pH 4.9 reveal that addition of 5 mM β-C₁₂G₂ significantly increases the amount of α-helix conformation in (KF)_n and (KY)_n (Table 2). In contrast, the conformation of the more hydrophilic peptides K_n and (K₄Y)_n is unaffected by addition of surfactant (Table 2). These results clearly indicate that nonionic surfactants interact with peptides, provided that the peptide comprises a high enough relative number of hydrophobic amino acid residues. This is in agreement with previous studies, where (KF)_n was shown to interact with net neutral phosphatidylcholine liposomes (38).

TABLE 2.

Stabilizing effect of different surfactants on peptide α-helix

Peptide	Surfactant	ΔXα (%)
Kn	β-C12G2	0
(K4Y)n	β-C12G2	0
(KY)n	β-C12G2	ΔCD = 2.7 ± 0.1 mdeg*
(KY)n	α-C12G2	ΔCD = 1.0 ± 0.1 mdeg*
(KF)n	β-C12G2	14.7 ± 0.3
(KF)n	α-C12G2	11.3 ± 0.1
(KF)n	β-C8G2	14.3 ± 0.6
(KF)n	β-C10G2	15.1 ± 0.3
(KF)n	β-C14G2	15.8 ± 0.1
(KF)n	β-C7G1	22.4†
(KF)n	β-C8G1	22.9 ± 0.3
(KF)n	β-C9G1	17.7 ± 0.8
(KF)n	β-C12G3	12.5 ± 0.1
(KF)n	C12E5	17.2 ± 0.8
(KF)n	C12E6	16.7 ± 0.6
(KF)n	C12E8	15.1 ± 0.4

The stabilizing effect is expressed as the increase in peptide α-helix fraction, ΔX_α, at surfactant concentration ≥10 × CMC. The values represent the mean value from at least three independent measurements ± 1 SD. Standard deviations ≤0.1 are given as ±0.1.

^*For (KY)_n, it is not possible to determine an absolute value for the increased amount of α-helix, due to inherent limitations of the CD technique (see Materials and Methods).

^†The (KF)_n CMC required extremely large amounts of surfactant, and because of cost considerations, only one sample solution was prepared.

The amount of surfactant required to induce an increased amount of α-helix was determined by measuring the CD signal of (KF)_n solutions as a function of surfactant concentration. The stabilization of the α-helix conformation was found to be a cooperative effect, the onset of which occurs at a surfactant concentration somewhat lower than the CMC of each pure surfactant (Figs. 3 and 4, Tables 2 and 3). Upon increasing surfactant concentration, the amount of α-helix increases drastically within a relatively narrow concentration range and then levels off. At high surfactant concentrations (≥10 × CMC), the peptide conformation is thus independent of surfactant concentration. As described above, this limiting amount of α-helix stabilization is referred to as ΔX_α.

FIGURE 3.

Surface tension (▴) and the fraction of (KF)_n in α-helix conformation (X_α, ♦) as a function of β-C₁₂G₂ concentration. A (KF)_n concentration of 25 μg/ml (which equals 0.14 mM of amino acid residues) was used in the CD measurements. All measurements were performed in a 20-mM acetate buffer at pH 4.9. The kink in the tensiometric data indicates the CMC of β-C₁₂G₂. The solid traces are added as guides for the eye.

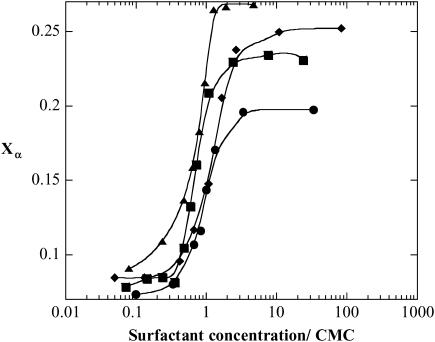
FIGURE 4.

The fraction of (KF)_n in α-helix conformation, X_α, as a function of surfactant concentration for α-C₁₂G₂ (•), β-C₁₂G₂ (▪), β-C₉G₁ (▴), and C₁₂E₅ (♦). All curves are normalized to the CMC of the specific surfactant. A (KF)_n concentration of 25 μg/ml (which equals 0.14 mM of amino acid residues) was used, and the measurements were performed in a 20-mM acetate buffer at pH 4.9. The solid traces are added as guides for the eye.

TABLE 3.

Critical micellar concentration for the different surfactants

Surfactant	Shorthand notation	CMC* (mM) (this work)	CMC (mM) (literature values)
n-Dodecyl-β-D-maltoside	β-C12G2	0.21	0.16†
n-Dodecyl-α-D-maltoside	α-C12G2		0.15‡
n-Octyl-β-D-maltoside	β-C8G2		26.5§
n-Decyl-β-D-maltoside	β-C10G2		2.0¶
n-Tetradecyl-β-D-maltoside	β-C14G2	0.014 (H2O)	0.01‡
n-Heptyl-β-D-glucoside	β-C7G1		70‡
n-Octyl-β-D-glucoside	β-C8G1		22†
n-Nonyl-β-D-glucoside	β-C9G1	6.3 6.9 (H2O)	6.5†
n-Dodecyl-β-D-maltotrioside	β-C12G3		0.2§
Pentaethyleneglycol mono n-dodecyl ether	C12E5	0.060	0.057**
Hexaethyleneglycol mono n-dodecyl ether	C12E6		0.087**
Octaethyleneglycol mono n-dodecyl ether	C12E8		0.092**

^*Determined in 20 mM acetate buffer, pH 4.9, unless otherwise stated.

^†Determined in H₂O (67,68).

^‡Determined in H₂O by Anatrace.

^§Determined in 0.15 mM KCl (69).

^¶Determined in 0.01 M NaCl (70).

^**Determined in H₂O (71).

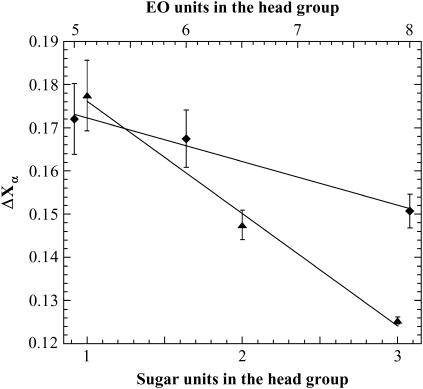
Variation of the surfactant headgroup was found to strongly influence the stabilization of α-helix conformation, as measured in terms of ΔX_α (Table 2, Fig. 4). For sugar surfactants, a larger headgroup makes the surfactant less efficient as stabilizer for the α-helix conformation (Fig. 5). In addition, the ability of alkylmaltosides to stabilize α-helix also depends on headgroup conformation, as is evident when α-C₁₂G₂ is compared with β-C₁₂G₂ (Fig. 4, Table 2). In terms of the effect of headgroup size on α-helix stabilization, surfactants based on PEO display the same trend as the sugar surfactants (Table 2, Fig. 5).

FIGURE 5.

Increase in peptide α-helix conformation, ΔX_α, (determined with CD spectroscopy) as a function of surfactant headgroup size, for β-C₁₂G_X surfactants (▴) and C₁₂E_X surfactants (♦). A (KF)_n concentration of 25 μg/ml (which equals 0.14 mM of amino acid residues) was used, and the measurements were performed in a 20-mM acetate buffer at pH 4.9. Since the Krafft point of β-C₁₂G₁ is above room temperature, it cannot be used for comparison. The glucosides are therefore represented by β-C₉G₁. The data points represent the mean value from at least three independent measurements, and the error bars correspond to 1 SD.

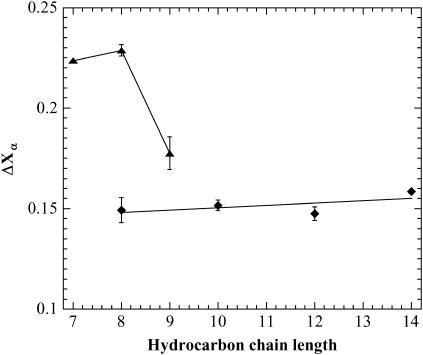
For alkylglycosides, the effect of the surfactant hydrocarbon chain length on the peptide α-helix content actually depends on the surfactant headgroup (Fig. 6). For the alkylmaltosides investigated here, the α-helix stabilization is independent of the hydrocarbon chain length, thus suggesting that the headgroup size is the limiting factor for ΔX_α. Similarly, there is no difference in α-helix stabilization between the short-chain alkylglucosides β-C₇G₁ and β-C₈G₁. On the other hand, for β-C₉G₁, the stabilization effect is markedly lower. Since β-C₇G₁ and β-C₈G₁ both form small, nearly spherical micelles, whereas β-C₉G₁ forms elongated ones (33,39), the observed differences in α-helix stabilization may be due to differences in preferred aggregate morphology and hence to differences in critical packing parameter (CPP). To further investigate this possibility, the conformation of (KF)_n in the presence of C₁₂E₆ was determined as a function of temperature. As for all PEO-based surfactants, the CPP for C₁₂E₆ increases with temperature, which leads to a dramatic increase of the hydrodynamic diameter of C₁₂E₆ micelles at higher temperatures (Fig. 7). It is known from literature that the micelles preferentially grow in one dimension (40,41). As can be seen in Fig. 7, the α-helix content of (KF)_n at constant C₁₂E₆ concentration indeed decreases with increasing temperature, which lends strong support to the idea that CPP and preferred micelle morphology play a role in the efficiency of the α-helix stabilization. In contrast, the effect of temperature on (KF)_n conformation in the absence of surfactant was found to be minute.

FIGURE 6.

Increase in peptide α-helix conformation, ΔX_α, as determined with CD spectroscopy, as a function of surfactant hydrocarbon chain length, for β-C_XG₁ surfactants (▴) and β-C_XG₂ surfactants (♦). Data represent systems with a surfactant concentration of ≥10 × CMC and a (KF)_n concentration of 25 μg/ml (which equals 0.14 mM of amino acid residues) in a 20-mM acetate buffer at pH 4.9. The solid traces are added as guides for the eye. The data points represent the mean value from at least three independent measurements, and the error bars correspond to 1 SD.

FIGURE 7.

Increase in peptide α-helix conformation, ΔX_α, (♦) (measured with CD spectroscopy) and the effective hydrodynamic diameter, d_H, (▴) (measured with DLS) as a function of (A) temperature for C₁₂E₆ and (B) hydrocarbon chain length for β-C_XG₁. A surfactant concentration of ≥10 × CMC and a (KF)_n concentration of 25 μg/ml (which equals 0.14 mM of amino acid residues) were used. The measurements were performed in a 20-mM acetate buffer at pH 4.9. The DLS measurements were performed on solutions of pure surfactant (no peptide added). The solid traces are added as guides for the eye.

The surfactant binding isotherm

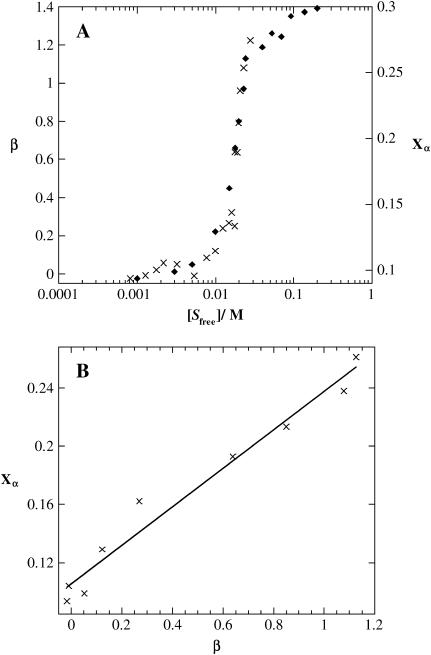
In agreement with the CD studies of surfactant effects on peptide conformation, the binding isotherm of β-C₈G₁ to (KF)_n, as determined by equilibrium dialysis combined with 1D ¹H NMR spectroscopy, displays a strong binding of the surfactant slightly below the surfactant CMC of the pure surfactant (22 mM; Fig. 8) This strongly suggests the binding is a cooperative process that produces micellar-like self-assembled surfactant structures on the peptide chain. We may therefore assume that the presence of surfactant aggregates is a key feature in the stabilization of α-helix (Fig. 8). On the average, more than one surfactant monomer bind each peptide amino acid residue at high surfactant concentration. The binding isotherm does not afford any information about the aggregation number of the self-assembled structures (micelles) on the peptide chain. However, a rough estimate of the number of micelle aggregates bound to each peptide chain can be calculated if the aggregation number is assumed to be identical to that in the corresponding pure surfactant solution. At 29 mM, the approximate micellar aggregation number for β-C₈G₁ micelles is 54 (42). According to the binding isotherm data, the number of bound surfactant molecules per amino acid residue (β) is 1.2 at this surfactant concentration. Considering that the average degree of polymerization of (KF)_n is 275 (Table 1), this would correspond to six micelles per peptide molecule, assuming that the micelle aggregation number is unaffected by the presence of peptide.

FIGURE 8.

Number of bound β-C₈G₁ molecules per amino acid residue in (KF)_n (β) as a function of free β-C₈G₁ concentration [S_free]. [S_free] as determined by equilibrium dialysis and subsequent NMR assay of surfactant concentration. The data points represent the average of values calculated from signals in three different regions in the NMR spectra, and the error bars correspond to 1 SD. The solid trace is a fit to the Hill equation (Eq. 5), whereas the dashed trace is a fit to the Scatchard equation (noncooperative binding, Eq. 5 with n = 1) and the dotted line to the Satake-Yang equation (Eq. 4).

The binding isotherm is analyzed in more detail in the Discussion section.

Characterization of the peptide-surfactant complex

1D and 2D NMR spectra were acquired at 400 and 500 MHz spectrometers to characterize the peptide-surfactant complex. Three peptides, (KF)_n, K_n, and (K₄Y)_n, were studied separately in the absence and presence of β-C₁₂G₂. Since all samples were prepared in D₂O, no exchangeable protons were observed and the results presented here mainly rely on the amino acid side chains. In other words, no conclusions can be drawn about possible surfactant interaction, either with the amide protons in the backbone or with the amine end group of the lysine residues.

It is noteworthy that the NMR spectra of (KF)_n and (K₄Y)_n show significantly sharper resonance lines for lysine protons than for the phenylalanine and tyrosine protons, both in the absence and presence of β-C₁₂G₂. The line broadening is more pronounced for (KF)_n than for (K₄Y)_n, which may reflect the larger size of the former peptide (275 residues) compared to that of the latter (123 residues). The broader signals from tyrosine and phenylalanine compared to lysine side chains seemingly imply that the correlation time of the lysine side chain is shorter, i.e., that lysine residues are more flexible. This could be explained by a higher degree of solvent exposure for the lysine residues than for the aromatic ones; for example, aromatic residues may take part in the formation of transient, intramolecular hydrophobic domains. A complementary or alternative explanation would be that the aromatic side chains experience more chemical exchange on the microsecond to millisecond timescales than do lysine side chains and thereby get an extra contribution to the transverse relaxation rate, resulting in broader resonance lines. Such chemical exchange would be compatible with the idea that the motion of the hydrophobic side chains is more restricted, due to intramolecular hydrophobic interactions. In addition, some apparent line broadening is likely to be a consequence of the natural sequence variation in these random polypeptides. More in-depth studies would be required to establish the exact structural and dynamic origin(s) of the observed line broadening in the peptides themselves. However, the primary aim of these studies is to investigate effects due to intermolecular interactions between the surfactant and peptide molecules. Therefore, the NMR results presented and discussed henceforth are focused on the differences between the spectra of individual peptides and surfactants on the one hand, and the spectra of the corresponding binary mixtures on the other.

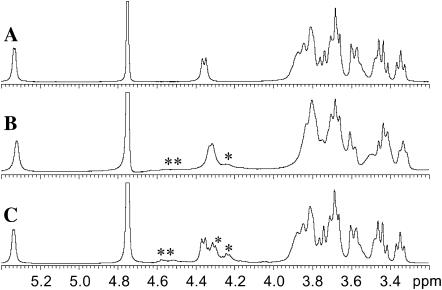
Addition of β-C₁₂G₂ to the peptide solutions showed no effect on line shapes or chemical shifts of the proton resonance lines for K_n or (K₄Y)_n in the 1D ¹H NMR spectra. In contrast, the proton signals of the phenyl rings in (KF)_n were clearly broadened and altered, consistent with appreciable peptide-surfactant interaction (Fig. 9). The side-chain proton peaks of the lysine residues in (KF)_n were, however, unaffected upon addition of surfactant. This suggests that peptide and surfactant mainly interact through the aromatic rings of the peptide. The NMR data therefore substantiate the assumption that a certain minimum fraction of hydrophobic and/or aromatic amino acid residues is necessary for surfactant-peptide interaction. The NMR signals of the surfactant tell the same story. The ¹H peaks of β-C₁₂G₂ are both shifted and broadened by addition of (KF)_n, but seemingly unchanged by addition of (K₄Y)_n or K_n. This observation is illustrated by Fig. 10, which displays the 1D ¹H spectral region containing the sugar protons of the β-C₁₂G₂ alone and mixed with (KF)_n and (K₄Y)_n, respectively (data for K_n not shown).

FIGURE 9.

Expansion of the aromatic region of 1D ¹H NMR spectra acquired at 500 MHz for (A) 80 mM (KF)_n, (B) 80 mM (KF)_n + 40 mM β-C₁₂G₂, (C) 80 mM (K₄Y)_n, and (D) 80 mM (K₄Y)_n + 40 mM β-C₁₂G₂. All concentrations are given as amino acid residue concentrations. All solutions were prepared in 20 mM deuterated acetate buffer, pD 5.

FIGURE 10.

Expansion of 1D ¹H NMR spectra recorded at 500 MHz showing the sugar proton resonances for (A) 40 mM β-C₁₂G₂, (B) 40 mM β-C₁₂G₂ + 80 mM (KF)_n, and (C) 40 mM β-C₁₂G₂ + 80 mM (K₄Y)_n. H^α peaks of lysine and phenylalanine are indicated by * and **, respectively, in B. Similarly, in C, * and ** indicate the H^α peaks of lysine and tyrosine. For the peptides, all concentrations are given as the amino acid residue concentrations. All solutions were prepared in 20 mM deuterated acetate buffer, pD 5.

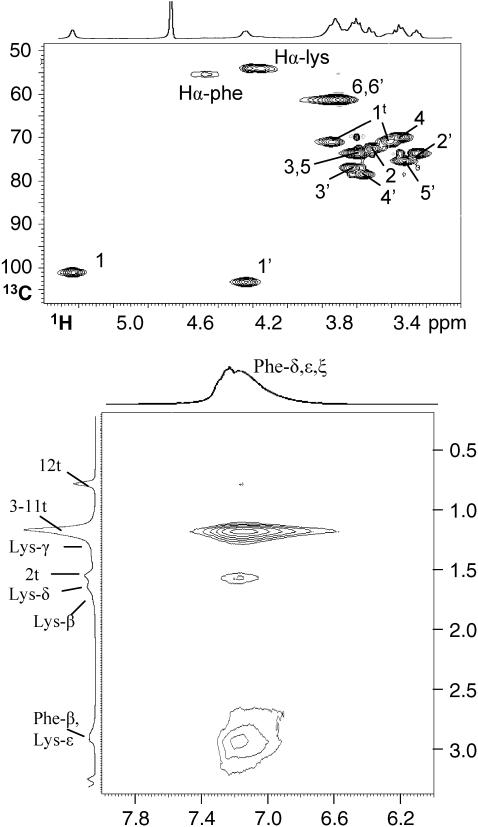
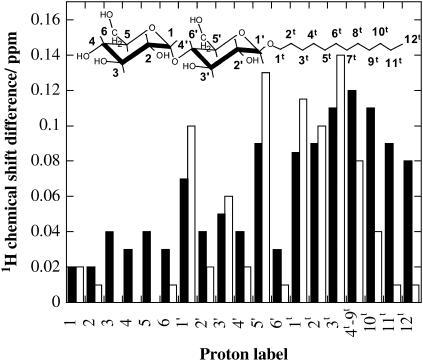
To investigate the peptide-surfactant interaction in more detail, 2D NMR spectra were acquired for (KF)_n and β-C₁₂G₂, separately as well as when mixed (Tables 4 and 5). The ¹H and ¹³C chemical shift assignments of both the peptide and the surfactant were readily obtained by standard 2D NMR techniques, as described in the Materials and Methods section. Even the chemical shifts of the crowded spectral region of the sugar protons proved possible to resolve by means of ¹H-¹³C correlated spectroscopy (Fig. 11, top). The chemical shift assignments demonstrate that the protons of β-C₁₂G₂ are significantly affected by the peptide, and that the effect is most pronounced for the inner sugar ring and the hydrocarbon tail (Fig. 12). The chemical shift distributions of the protons in the surfactant hydrocarbon chain do not allow for any definite conclusion to be drawn about the exact location of the hydrophobic peptide side chain within the micelle core. This is mainly a consequence of the statistical distribution of the CH₂ and CH₃ groups in the alkyl chain within a spherical or ellipsoidal shaped micellar core, where a large fraction of the hydrocarbon chain segments are located in the vicinity of the core surface (43–45).

TABLE 4.

¹H and ¹³C chemical shift for 40 mM β-C₁₂G₂ in acetate buffer with and without addition of 80 mM (KF)_n

	β-C12G2		β-C12G2 + (KF)n		Chemical shift difference
Position	1H (ppm)	13C (ppm)	1H (ppm)	13C (ppm)	1H (ppm)	13C (ppm)
1	5.34	101.10	5.32	101.10	0.02	0.00
2	3.60	72.60	3.58	72.80	0.02	−0.20
3	3.70	73.70	3.66	73.70	0.04	0.00
4	3.45	70.00	3.42	70.10	0.03	−0.10
5	3.70	73.70	3.66	73.70	0.04	0.00
6*	3.82	61.30	3.79	61.30	0.03	0.00
1′	4.37	103.40	4.30	103.40	0.07	0.00
2′	3.36	73.70	3.32	73.70	0.04	0.00
3′	3.75	77.10	3.70	77.10	0.05	0.00
4′	3.68	78.50	3.64	78.40	0.04	0.10
5′	3.48	75.50	3.39	75.4	0.09	0.10
6′*	3.82	61.30	3.79	61.30	0.03	0.00
1t	3.89/3.57	71.20	3.81/3.48	71.10	0.08/0.09	0.10
2t	1.66	30.30	1.57	30.40	0.09	−0.10
3t	1.34	26.90	1.23	26.90	0.11	0.00
4t–9t†	∼1.29	∼30.60	∼1.17	∼30.80	∼0.12	∼−0.20
10t	1.27	32.90	1.16	32.90	0.11	0.00
11t	1.28	23.50	1.19	23.60	0.09	−0.10
12t	0.87	14.70	0.79	14.70	0.08	0.00

¹H chemical shifts are referenced to the residual HDO signal set to 4.75 ppm. Indirect chemical shift referencing is employed for ¹³C using the frequency ratio Ξ = ν_C/ν_H = 0.25145002, where ν_C and ν_H correspond to the ¹³C and ¹H frequency, respectively, of the methyl resonances (0 ppm) in tetramethylsilane in H₂O. The error limits are ±0.01 ppm for the ¹H signals and ±0.3 ppm for the ¹³C signals. The proton positions are numbered as in Fig. 12.

^*Total overlap in ¹³C HSQC.

^†Total overlap in ¹³C HSQC.

TABLE 5.

¹H and ¹³C chemical shift for 80 mM (KF)_n in acetate buffer with and without addition of 40 mM β-C₁₂G₂

	(KF)n		(KF)n + β-C12G2		Chemical shift difference
Position	1H (ppm)	13C (ppm)	1H (ppm)	13C (ppm)	1H (ppm)	13C (ppm)
	Lys		Lys		Lys
α	4.24	54.30	4.26	54.1	−0.02	0.20
β	1.70	31.40	1.71	31.30	−0.01	0.10
γ	1.40/1.32	22.90	1.40/1.32	23.00	0.00	−0.10
δ	1.66	27.20	1.66	27.10	0.00	0.10
ɛ	2.96*	40.00	2.97*	40.00	−0.01	0.00
	Phe		Phe		Phe
α	4.55	55.40	4.55	55.50	0.00	−0.10
β	2.96*	38.00	2.97*	38.00	−0.01	0.00

¹H chemical shifts are referenced to the residual HDO signal set to 4.75 ppm. Indirect chemical shift referencing is employed for ¹³C using the frequency ratio Ξ = ν_C/ν_H = 0.25145002, where ν_C and ν_H correspond to the ¹³C and ¹H frequency of the methyl resonances (0 ppm), respectively, in tetramethylsilane in H₂O. The error limits are ±0.01 ppm for the ¹H signals and ±0.3 ppm for the ¹³C signals.

^*Total overlap in ¹³C HSQC.

FIGURE 11.

Expansions of the 2D ¹H-¹³C HSQC spectrum (top) and the 2D ¹H NOESY spectrum, using a mixing time of 15 ms (bottom), of a mixture of 80 mM (KF)_n and 40 mM β-C₁₂G₂ solution in 20 mM deuterated acetate buffer, pD 5. For peptides, all concentrations are given as the amino acid residue concentrations. The atom-specific assignment is indicated with the numbering presented in Fig. 12. The NOESY spectrum shows NOE crosspeaks between the aromatic ring protons of the phenylalanine residues and the protons in the aliphatic hydrocarbon chain of β-C₁₂G₂. Atom-specific assignments of the ¹H peaks are presented in the corresponding regions of the 1D ¹H spectrum displayed along the edges of the 2D spectrum.

FIGURE 12.

¹H chemical shift difference for 40 mM β-C₁₂G₂ in acetate buffer observed upon addition of 80 mM (KF)_n. (solid bars) and 9.3 mM naphthylacetate (open bars). For peptides, all concentrations are given as the amino acid residue concentrations. Small chemical shift differences (≤∼0.04 ppm) could simply be explained by subtle sample variations (e.g., pH and ionic strength) rather than significant peptide-surfactant interactions.

There are no significant changes in the ¹³C chemical shifts of the surfactant in the absence or presence of peptide. In strong contrast to the surfactant, the ¹H and ¹³C chemical shifts of (KF)_n are virtually unchanged (see Tables 4 and 5), although, as already stated, the proton signals of the phenyl ring are clearly broadened. The absence of changes in the H^α and C^α chemical shifts upon addition of surfactant is noteworthy, considering the clear increase in α-helical content observed from the CD data (46). In some sense, based on the chemical shift data, it appears as if the peptide affects the surfactant micelles more than the micelles affect the peptide.

Although the chemical shift analyses strongly suggest that (KF)_n and β-C₁₂G₂ interact, more robust and unambiguous proofs of intermolecular interactions are obtained from 2D ¹H-¹H NOESY experiments. This type of 2D spectrum displays NOE crosspeaks located at the chemical shifts of protons that are correlated through magnetization transfer mediated by dipole-dipole interactions. The effect occurs through space and is independent of covalent bonds. It is strongly distance-dependent and the protons normally need to be separated by <∼5 Å to be observed in NOESY spectra. NOE crosspeaks are observed between the aromatic rings of (KF)_n and the aliphatic hydrocarbon chain of β-C₁₂G₂, as shown in Fig. 11 (bottom). Weak NOE crosspeaks are observed also between the phenyl ring and the surfactant headgroup. This finding shows that the aromatic rings and the hydrophobic tail of the surfactant, at least on an average level, are spatially close (like CD spectroscopy, NMR only captures the ensemble- and time-averaged properties of the sample). In contrast, no intermolecular NOEs are observed between (K₄Y)_n and β-C₁₂G₂ (data not shown). It is noteworthy that no obvious NOEs are observed between the lysine and phenylalanine side chains in (KF)_n, even if these should, at least transiently, interact since they reside within the same molecule. However, these crosspeaks may be obscured by the strong and adjacent intermolecular (KF)_n–β-C₁₂G₂ crosspeaks in the 2D spectra. Similarly, no unambiguous intermolecular contacts are found between lysine side chains and surfactant. In this case, the crosspeaks may be difficult to observe, due to potential crosspeak overlap and/or proximity to the strong diagonal of autocrosspeaks in the aliphatic proton region of the 2D NOESY spectra.

Taking all NMR data together, the results support the notion that important interactions take place between aromatic rings of the peptides and the surfactant alkyl chain, with possible interaction also with the inner sugar ring of the micellar headgroup.

DISCUSSION

Peptide-surfactant binding

CD spectroscopic and isotherm data show that both the α-helix stabilization and the surfactant binding are cooperative processes. Furthermore, by comparing the surfactant binding isotherm (Fig. 8) with the α-helix content of (KF)_n as a function of surfactant concentration (Fig. 13), it is obvious that the surfactant binding as such leads to the coil-helix transition in the peptide. These observations strongly suggest that the main surfactant-peptide interaction is due to formation of surfactant micellar-like self-assembled structures on the peptide, whereas the number of randomly bound surfactant monomers may be assumed to be negligible. The observation that the onset of cooperative surfactant binding occurs at a concentration slightly lower than the CMC of the pure surfactant is in agreement with results on manifold other surfactant-polymer systems in which either the surfactant or polymer is uncharged. The surfactant concentration required to achieve surfactant aggregation in the presence of a polymer is often referred to as the critical aggregation concentration. Just as is observed in our systems, critical aggregation concentration of nonionic surfactants interacting with charged polymers is often marginally lower than CMC, meaning that the binding of the surfactant to the polymer has relatively little effect on the surfactant monomer concentration (47,48).

FIGURE 13.

(A) Number of bound β-C₈G₁ molecules per (KF)_n monomers (β, ×) as determined by equilibrium dialysis and the fraction of (KF)_n in α-helix conformation (X_α, ♦; determined by CD spectroscopy) as a function of free β-C₈G₁ concentration [S_free]. (B) The number of bound β-C₈G₁ molecules per (KF)_n amino acid monomers (β) as a function of the fraction of (KF)_n in α-helix conformation (X_α) plotted for the same free β-C₈G₁ concentration.

A number of different models may be applied in the analysis of surfactant binding to a protein, peptide, or polymer. The two most common ones are the closed association model, described by the Hill equation (49), and the Satake-Yang model (50), which is based on the Zimm-Bragg theory (51).

The Satake-Yang model, first introduced to explain the coil-helix transition in polypeptide chains induced by binding of oppositely charged surfactants, can be expressed as

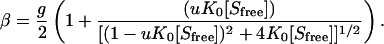(4)

Here, β is the number of bound surfactant molecules per amino acid residue, [S_free] is the unbound (free) surfactant concentration, and g is the number of binding sites per amino acid residue. K₀ is the binding constant for the binding of a surfactant molecule to a binding site where both neighboring binding sites are unoccupied; for binding to sites where these conditions are not met the binding constant is uK₀. The variable u is referred to as a cooperativity parameter.

The Hill equation (49), on the other hand, is expressed as

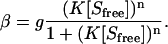(5)

As in Eq. 4, g is the number of binding sites per amino acid residue, whereas K is the association constant (comparable with uK₀ in the Satake-Yang model) and n is the Hill coefficient. The Hill coefficient reflects the aggregation number of the bound surfactant micelles. For a noncooperative binding (where n = 1), Eq. 5 reduces to a Langmuir-type equation often called the Scatchard equation (52–55).

As can be seen in Fig. 8, both the Satake-Yang and the Hill equations fit the experimental data well. However, the quality of the fit as such can obviously not be used as a tool to assess the physical relevance of the models. There is one fundamental and, in this context, quite discriminative difference between the two models. The Satake-Yang model describes the binding of surfactant molecules to the peptide without accounting for packing effects favoring a particular shape or aggregation number of the self-associated micellar-like surfactant aggregates. The Hill model, on the other hand, describes a micelle formation process modified by peptide binding, neglecting possible random, noncooperative (monomeric) surfactant-peptide binding. Considering what our data tell us about the surfactant-peptide interaction, the Hill model is preferred. In addition, previous investigations show that since the Satake-Yang model does not include micellar size, the fitting results are in qualitative disagreement with experimental results for polyelectrolyte-surfactant interactions (56). Hereafter, the analysis of the binding isotherm will therefore be based on the Hill equation. Fitting the data in Fig. 8 to the Hill equation (Eq. 5) by least-squares fit yields g = 1.4 ± 0.2, K = 51.8 ± 3.1 M⁻¹, and n = 5.9 ± 1.4, where error limits are given as the standard error of the mean. As previously mentioned, a Hill coefficient greater than unity is an indication of a cooperative binding.

It is interesting to compare our results on the binding of β-C₈G₁ to (KF)_n with previous results on the binding of the same surfactant to globular proteins. Such a comparison reveals a number of important differences between peptides and proteins in terms of surfactant interaction. First, we find that the total number of binding sites per protein/peptide residue (g) is almost 200 times larger in the β-C₈G₁-(KF)_n system (g = 1.4 ± 0.2) than in systems containing β-C₈G₁ and globular proteins (g = 0.0081 ± 0.0010) (57). The huge difference may, at least in part, be explained by the fact that (KF)_n behaves as a rather flexible chain in which the amino acid residues are exposed to the surrounding media, whereas globular proteins are folded into a compact tertiary conformation, in which a large fraction of the hydrophobic amino acid residues are hidden in the interior of the globule and therefore less accessible for surfactant micellar binding. The isotherm binding data therefore highlight a pertinent difference in behavior between peptides and proteins in solution.

The association constant K obtained from the Hill equation (Eq. 5) amounts to a change in Gibbs free energy on binding of −9.7 kJ mol⁻¹ per mole of free surfactant, which corresponds to −4 kT for the binding of β-C₈G₁ to (KF)_n. This change in Gibbs free energy is in good agreement with previously obtained results on binding of β-C₈G₁ to different globular proteins (ΔG⁰ = −10.8 ± 0.6 kJ mol⁻¹) (57).

Influence of surfactant characteristics on peptide conformation

The peptides (KF)_n and (KY)_n show an increased amount of α-helix upon surfactant addition, whereas K_n and (K₄Y)_n do not. This study therefore shows that nonionic surfactants stabilize the α-helical conformation of peptides, provided that the peptide contains a sufficient amount of hydrophobic amino acid residues. The results on K_n agree with previous studies, in which no surfactant-induced α-helix stabilization was observed (58). Additionally, it has previously been shown that nonionic surfactants interact with polymers, only if the polymer is sufficiently hydrophobic (59,60).

For all surfactants studied in this work, the onset of the α-helix stabilization effect, i.e., increased X_α, occurs just below the surfactant CMC. By combining our CD and binding isotherm data, we see that the onset of stabilization coincides with the onset of appreciable surfactant binding to the peptide. A further increase of the surfactant concentration above CMC does not increase the amount of peptide in α-helix conformation. Rather, the amount of α-helix as a function of surfactant content levels off at a constant value. However, the limiting value of α-helix stabilization, ΔX_α, observed at high surfactant concentration varies with surfactant characteristics.

The CMC (Table 3) of any given surfactant does not correlate with ΔX_α. Rather, the size of the surfactant headgroup, as well as surfactant characteristics related to the preferred micellar morphology, are the factors that govern ΔX_α. We will discuss these factors one by one, starting with the most clear-cut, namely the headgroup size.

The increased amount of α-helix in (KF)_n is directly dependent on headgroup size in the sense that increasing headgroup size within a homologous series of surfactants leads to decreasing ΔX_α. This is evident when comparing the homologs C₁₂E₅, C₁₂E₆, and C₁₂E₈, as well as alkylmaltotriosides, -maltosides, and -glucosides. In the case of large headgroups, ΔX_α shows little or no dependence on the surfactant hydrocarbon chain length. It is also independent of the CPP, and therefore of the preferred micelle size and morphology of the surfactant.

For surfactants with large headgroup, the conformation provides an additional factor that needs to be taken into account. This is exemplified by β-C₁₂G₂ and α-C₁₂G₂ (Table 2). The headgroup in α-C₁₂G₂ is known to be more compact due to the smaller angle between the hydrocarbon chain and the headgroup in comparison to β-C₁₂G₂ (61).

For surfactants with small headgroup, exemplified by the alkylglucosides and PEO-based surfactants, the situation is different. Here, CPP influences the capacity to stabilize α-helix. As can be seen for the alkylglucosides (Fig. 7), the α-helix stabilization is independent of the hydrocarbon chain length for a given headgroup, as long as the hydrocarbon chain length is short enough for the surfactant to preferentially form small, nearly spherical micelles (β-C₇G₁ and β-C₈G₁) (39). For surfactants with longer hydrocarbon chains, i.e., surfactants with a large CPP and an inherent tendency to form elongated micelles (β-C₉G₁) (33,39,62), a lower degree of peptide α-helix stabilization is obtained.

In conclusion, the largest peptide stabilization effect (highest ΔX_α) is obtained when surfactants with low CPP and small headgroups are used (β-C₇G₁ or β-C₈G₁). This effect can be rationalized once we have discussed the properties of the peptide-surfactant complex.

Characteristics of the peptide-surfactant complex

In 1D ¹H NMR spectra, the peptide-surfactant interaction is evident as changes in the chemical shift of the surfactant proton signals upon addition of peptide (Fig. 10). This effect resembles previously reported surfactant proton shifts observed for alkylglucoside-cyclodextrin inclusion complexes (63). The peptide-surfactant interaction is also evident as an alteration and broadening of the proton signals of the (KF)_n phenyl rings (Fig. 9), which bears a close resemblance to the results previously obtained for cresol red when bound to β-C₁₂G₂ (64). However, the combination of 1D and 2D NMR results in this work provides much more detailed information as to the properties of the peptide-surfactant complex.

From the data in Fig. 12, it is clear that the ¹H chemical-shift changes, and thereby the peptide-surfactant interaction, are largest for the surfactant hydrocarbon chain region and the inner sugar ring, whereas the outer sugar ring only displays smaller signal shifts. Similarly, NOE crosspeaks are observed between the surfactant hydrocarbon chain and the peptide phenyl ring (Fig. 11, bottom). It is highly relevant to compare these results to NMR data on solubilization of small aromatic molecules in alkylglycoside micelles. Data on solubilization of naphthylacetate (Fig. 12) shows that this relatively small and weakly amphiphilic molecule is localized as a cosurfactant in the surfactant micelle. The most hydrophilic part of naphthylacetate is located in the micelle palisade layer, whereas the hydrophobic part is totally enclosed in the hydrocarbon chain micellar core (61).

The most notable difference between the surfactant interaction with naphthylacetate and peptides is the ability for naphthylacetate to be fully enclosed in one micelle. Due to the large size of the peptides in the study (Table 1) the whole peptide chain can never be enclosed in one micelle-like surfactant aggregate. The consequence is that part of the peptide chain needs to be located in the outer headgroup sugar ring (Fig. 12), whereas for naphthylacetate the interaction with the outer headgroup sugar ring is negligible (Fig. 12).

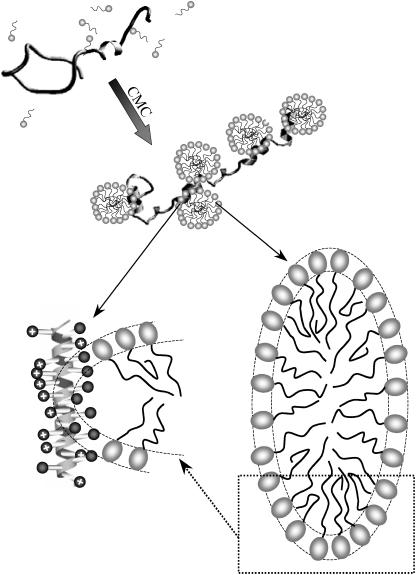
According to the NMR data, the complex between (FK)_n and β-C₁₂G₂ is thus best described by a necklace model, in which surfactant micelles bind to the peptide chains, primarily through interaction with the aromatic groups. The suggested peptide-surfactant complex is schematically represented in Fig. 14 and is similar to the structure previously proposed for the complex between charged poly(acrylic acid) and PEO-based surfactants (48). It is important to clearly distinguish the structure of this type of complex from that of complexes in which the micelle core encloses the peptide chains. In this case, the peptide is located in the interface between the headgroup and the micellar hydrocarbon chain core, with an appreciable number of the hydrophobic, aromatic side chains sticking into the micelle core region. Location of charged lysine residues in the core region would be highly energetically unfavorable and the lysine residues would therefore be expected to point away from the micelle, in agreement with experimental data.

FIGURE 14.

Schematic view of the surfactant-peptide binding. The upper left panel illustrates the surfactant micelle-peptide binding above CMC, yielding an increased fraction of peptide in α-helix conformation. The enlargements of the β-C₁₂G₂ micelle and the (KF)_n-β-C₁₂G₂ complex (lower left and right) are drawn to scale. Previously reported (72,73) dimensions of the oblate ellipsoid β-C₁₂G₂ micelle have been used. Thus, the radii of the hydrocarbon region (r_small = 14.1 Å and r_large = 28.2 Å) and the thickness of the headgroup region (6.2 Å) as well as the micelle aggregation number (132, assuming an unchanged aggregation number upon peptide binding) are taken from literature data on the “free” micelle. In the lower left panel, the peptide-micelle complex is sketched based on the NMR results and by using the number of amino acid (3.6) and the pitch (5.4 Å) per α-helix turn (74), and an approximate amino acid side-chain length (for a fully stretched chain) of 6 Å, assuming that the side-chain length of phenylalanine is the same as for lysine side chain as presented in the literature (75). For clarity, only part of the micelle and the peptide chain is drawn for the peptide-micelle complex in the lower left panel.

In principle, it would be possible to envisage an alternative explanation, in which hydrophobic blocks in the random (KF)_n and (KY)_n peptides are assumed to be long enough to be fully enclosed by surfactant micelles. The increased α-helix content would then be attributable to α-helix formation within these blocks. However, the probability that the hydrophobic blocks in a random polymer are large enough for this model to make sense is minute. According to the first-order Marcov model of copolymerization (65), the number-average segment length of a 1:1 copolypeptide is 2, assuming equal amino acid monomer reactivity for lysine, phenylalanine, and tyrosine. Assuming spherical micelles with a C₁₂ chain, at least 24 subsequent amino acid residues would need to be hydrophobic to form an all-hydrophobic α-helix long enough to span the entire micelle core region. Statistically, only <0.2 ppm of a random 1:1 copolymer contains unbroken blocks of 24 amino acids or longer (65,66), which clearly makes this model highly implausible.

Origin of the α-helix stabilization

The proposed structure of the peptide-surfactant complex makes it possible to rationalize the influence of surfactant characteristics on α-helix stabilization. The lower efficiency of surfactants with large headgroups can be understood as a steric effect, where a bulky headgroup sterically hinders the hydrophobic residues on the peptide from interacting with the micelle core. As for the influence of the surfactant CPP, we note that the unfavorable contact between water and the surfactant hydrophobic hydrocarbon chain region is largest for small spherical micelles (small CPP), due to a larger curvature of the hydrophobic hydrocarbon chain core. Consequently, small micelles have more to gain in terms of screening of their hydrocarbon-water contact through interaction with hydrophobic peptide residues. This serves as an explanation for the correlation between the preferred micelle morphology of a given surfactant and its ability to stabilize α-helix.

The cause of the increased amount of peptide in α-helix conformation upon interaction with surfactant micelles can, at least partly, be understood from the fact that formation of an α-helical turn in a random coil domain is entropically costly. However, when a random coil peptide chain is bound to a surfactant micelle, the peptide chain entropy is markedly lower as compared to a free peptide chain. Consequently, the further entropy loss suffered upon α-helix formation can be assumed to be considerably lower than is the case for a free peptide chain in solution.

CONCLUSIONS

Nonionic surfactants have been shown to interact with sufficiently hydrophobic peptides, thereby inducing an increased amount of α-helix conformation. The onset of α-helix stabilization occurs at surfactant concentrations slightly lower than the CMC of the surfactant, and the α-helix content levels off toward a constant value at surfactant concentrations above CMC. The surfactant-peptide binding process is cooperative. Surfactant micelles on the peptide chain, rather than randomly adsorbed surfactant monomers, are therefore the likely cause of the α-helix stabilization.

The propensity of a given surfactant to stabilize the α-helix conformation depends on a number of its characteristics, namely

• The headgroup size, where a larger headgroup is less favorable than a smaller one.

• The headgroup conformation (observed for surfactants with a large headgroup).

• The surfactant CPP, where a larger CPP is less favorable than a smaller one (observed for surfactants with a small headgroup).

In other words, the largest increase in peptide α-helix conformation is obtained for surfactants with a small headgroup and low CPP value.

The peptide-micelle complex can best be described by a necklace model, as illustrated in Fig. 14. The surfactant-peptide interaction occurs mainly between the surfactant hydrophobic micellar core and the inner surfactant sugar ring and the phenyl rings of the (KF)_n peptide. This type of complex is fully compatible with the observed correlation between surfactant characteristics and α-helix stabilization.