Chromatin Dynamics in Interphase Cells Revealed by Tracking in a Two-Photon Excitation Microscope

Abstract

Increasing evidence points to a dynamical compartmentalization of the cell nucleus, yet the mechanisms by which interphase chromatin moves and is positioned within nuclei remain unclear. Here, we study the dynamics of chromatin in vivo applying a novel particle-tracking method in a two-photon microscope that provides ∼10-fold higher spatial and temporal resolutions than previous measurements. We followed the motion of a chromatin sequence containing a lac-operator repeat in cells stably expressing lac repressor fused with enhanced green fluorescent protein, observing long periods of apparent constrained diffusion interrupted by relatively abrupt jumps of ∼150 nm lasting 0.3–2 s. During these jumps, the particle moved an average of four times faster than in the periods between jumps and in paths more rectilinear than predicted for random diffusion motion. Additionally, the jumps were sensitive to the temperature and absent after ATP depletion. These experimental results point to an energy-dependent mechanism driving fast motion of chromatin in interphase cells.

INTRODUCTION

Significant advances in the fields of microscopy and molecular biology have in recent years allowed direct visualization of chromatin structure and dynamics in live cells, changing the initial vision of an interphase nucleus containing randomly arranged and static DNA (1).

A significant breakthrough in the field was the development of a novel approach to label specific DNA sequences in live cells, which consist of the insertion of a lac-operator repeat in the DNA and the expression of the lac repressor protein fused to the enhanced green fluorescence protein (EGFP) (2,3). This new approach made it possible for the first time to study the dynamics of chromatin in vivo.

Using this methodology, several studies in Saccharomyces cerevisiae (4), mammalian cells (5), and Drosophila (6) have described the motion of specific chromatin regions as undergoing apparent Brownian motion limited to a nuclear subregion.

However, the general dynamic organization of DNA seems to be more complex. Heun et al. (7) reported that early and late origins of replication in S. cerevisiae are more mobile in the G1 phase than in the S phase. Also, the movement in the G1 phase was highly sensitive to ATP depletion and to changes in metabolic status.

The interior versus peripheral intranuclear location of early- versus late-replicating DNA regions is established early in G1 (8); similarly, changes in the transcriptional activity of certain genes have been shown to be correlated with changes in their intranuclear location (9). In a simplified experimental system, the targeting of the VP16 transcriptional activator to a specific DNA region in Chinese hamster ovary (CHO) cells leads to a repositioning of this region from the nuclear periphery to the interior (10).

These results suggest that important nuclear functions such as DNA transcription are accompanied by defined changes in the position of the sequence. However, as concluded by Gasser (11), there is little experimental support to date for an active mechanism driving these chromatin movements.

This divergence could be explained by the fact that the methods used for the observations do not have the temporal and/or spatial resolutions required for detecting such a motion. Also, it is important that the phototoxicity generated under imaging conditions that produce no other obvious phenotypes can significantly change chromatin dynamics (A. S. Belmont and C. H. Chuang, unpublished data).

In this work, we reexamine interphase chromatin dynamics using a new, two-photon microscopy fluorescent particle-tracking method (12). This method has spatial and temporal resolutions of 20 nm and 30 ms, respectively, i.e., ∼10-fold higher than the resolution of methods previously used to study chromatin dynamics in vivo. The method is especially well suited for biological applications since it provides significantly lower out-of-focus photodamage and photobleaching (13).

Our results reveal that chromatin undergoes an apparently confined random motion alternating with moments of fast curvilinear motion. These jumps are ATP-dependent and appear to be the manifestation of active, versus passive diffusive, mechanisms for interphase chromosome movements.

MATERIALS AND METHODS

Establishment of DHFR-BAC cell line

A 256-copy lac-operator direct repeat (14) was inserted into the dihydrofolate reductase (DHFR) bacterial artificial chromosome (BAC) (clone 057L22 from the CITB mouse library). This BAC clone contains the 31-kb DHFR locus together with 132 kb of upstream and 5.5 kb of downstream sequence inserted into the pBeloBAC11 vector. Insertion of the lac-operator repeat used Tn5 transposition. A Tn5 transposon was constructed using the pSP2 plasmid (15). The pSP2 polylinker was modified by insertion of an adaptor (AATTGACAGCTGTCGATC) containing a PshAI/PyuII site between the EcoR1 and BamH1 sites, creating pPvuII. The transposon 〈Kan-2〉 (Epicentre Technologies, Madison, WI) was inserted into pPvuII using the PshAI/PyuII site, creating p[Kan]. The 8.32 lac-operator repeat was cut out of pSV2-DHFR-8.32 (14) using a Sal I and XhoI digest and inserted into p[Kan] linearized with Sal I to create p[Kan-8.32].

Transposons were generated by digestion of p[Kan-8.32] with PyuII and purification from an agarose gel using Gelase (Epicentre Technologies). Transposition into the DHFR-BAC used the EZ:TN Tn5 transposition system (Epicentre Technologies) according to the manufacturer's instructions. Screening of transposition insertions by restriction enzyme digest were done to identify clones containing the full lac-operator insertion, followed by DNA sequencing into the BAC from both ends of the transposon to verify that no BAC sequence was lost during transposon insertion and to identify the insertion location.

The 057-K-8.32-C29 BAC clone we identified contained a transposon insertion 75 kb 5′ to the DHFR locus and was used for subsequent CHO cell transformation. CHO DG44 cells with a double deletion of the endogenous DHFR locus were used (16). CHO DG44 cells stably expressing EGFP-lac repressor (dimeric form) were transfected using FuGENE 6 reagent (Roche Applied Science, Indianapolis, IN) according to the manufacturer's instructions. Stable transformants were cloned by serial dilution and selected for cell clones containing multiple, closely located fluorescent dots within interphase nuclei. The B9 subclone we identified contained a maximum of 7–10 fluorescent dots cointegrated at a single mitotic chromosome location.

Cell culture and preparation for microscopy measurements

CHO cells were cultured as described (14). For the tracking experiments, cells were plated for 2–3 days in fibronectin-coated dishes with an optic glass in the bottom. During the tracking experiments the temperature was kept at 37°C using a ΔT3 system (Bioptechs, Butler, CA), with a coverslip seal to maintain constant pH.

ATP depletion was carried out by incubating cells at 37°C for 1 h in the presence of 50 mM deoxyglucose (ICN Biomedicals, Irvine, CA) and 20 mM sodium azide (Acros Organics, Belgium) before the tracking experiment (17).

To fix the cells, they were incubated at room temperature with 1.6% formaldehyde in Dulbecco's phosphate-buffered saline for 10 min and washed several times with the phosphate-buffered saline.

Microscope setup

The tracking experiments were carried out with the Olympus IX70 microscope previously described (12). The two-photon excitation source was a mode-locked titanium-sapphire laser (Mira 900, Coherent, Palo Alto, CA) pumped by an argon ion laser (Innova 300, Coherent) tuned to 920 nm. The laser power at the sample was in the 1- to 10-mW range. The light is directed into the microscope by two galvomotor-driven scanning mirrors (Cambridge Technologies, Watertown, MA) through a scanning lens. During the tracking procedure, the two scanning mirrors are moved independently by two synchronized voltage sine waves shifted 90° relative to each other and generated in a computer card (three-axis card, ISS, Champaign, IL). As a consequence, the laser moves in a circular path. The frequency of the circular orbit (f_orbit) was 250 Hz. The position of the scanning center is determined by the offset values of the sine waves.

The laser light is reflected with a low-pass dichroic mirror (transmission between 370 and 630 nm, Chroma Technology, Brattleboro, VT) and focused on the sample with a 63× (dry) 0.8-NA objective. Fluorescence emission collected by the objective passes through the dichroic and a short-pass filter, exiting the microscope through the side port. A Hamamatsu H7422P-40 photomultiplier tube was used as a detector with its output amplified, passed through a photon counting discriminator (PX01 Photon Counting Electronics, ISS), and counted with a data acquisition card (ISS). The experiments are controlled by a data acquisition program (SimFCS, Laboratory for Fluorescence Dynamics, Champaign, IL).

A cMOS camera (Pixelink, Ottawa, ON) was placed on the top port of the microscope to take differential interference contrast (DIC) images of the cells. In the microscope, the emission filter is placed immediately before the detector so that the near-infrared laser used for the two-photon excitation is not blocked in the camera path and can be imaged.

Tracking procedure

The particle-tracking method used in this work was similar to that described previously (12) and adapted to tracking in two dimensions. Briefly, with a fast raster scan, the fluorescence image of a large area of the sample is obtained and the particle of interest is chosen by clicking it on the image. This directs the laser beam to the particle by changing the DC offset values of the x and y outputs of the three-axis driver card. This point is considered as the initial coordinates for the tracking.

During each cycle of the tracking routine, the excitation beam does eight circular orbits with a radius of 250 nm, equal to half the x,y width of the point spread function, and centered at the initial coordinates set before. The fluorescence intensity is collected at high frequency (f_data = 32,000 Hz) as the laser moves around the particle (Fig. 1). Thus, in a typical experiment with f_orbit = 250 Hz, we measure the fluorescence intensity at 128 different points of the orbit. By performing several orbits in each cycle, we improved the signal/noise ratio.

FIGURE 1.

Schematic representation of the tracking procedure. The diagrams depict the laser beam (blue) orbiting around the particle (red). The simulated intensity collected during two circular orbits is represented as a function of the orbit angle for four different positions of the particle with respect to the center of scanning. Note the changes on the intensity profile (top part of the plots) with the particle position.

As was demonstrated by Kis-Petikova and Gratton (18) and Berland et al. (19), the fluorescence intensity (F) during the scanning is a periodic function of time (t),

(1)

where w₀ is the beam waist, B is the background intensity, and F₀ is a constant. The subscripts p and s refer to the particle and the scanner coordinates, respectively.

For known radius of scanning, beam waist, and background, the measured intensity function can be fitted to determine the position of the particle. As can be observed in Fig. 1, the width of the peak in the intensity trace is related to the distance from the center of scanning to the particle whereas the phase of the intensity signal is determined by the relative angle between two vectors defined from the center of scanning to the starting point of the orbit and to the particle.

According to Eq. 1, the absolute position of the particle can be determined by measuring the fluorescence intensity while moving the laser beam as a function of time. The phase and modulation of the fluorescence signal are calculated by fast Fourier transform after each cycle of the tracking routine and from these values, the current coordinates of the particle are determined. Then, the center of scanning is moved to this new position and a new cycle of the tracking routine starts. In other words, during the tracking routine, the scanner follows the particle by changing its position to that determined for the particle in the previous cycle. In an ideal tracking experiment, the scanner is always on top of the particle and the position of the center of scanning is identical to the position calculated for the particle.

The method described above can also be used to track two particles simultaneously. The initial positions for the particles are set by selecting them interactively from the fluorescence image computer display. The tracking routine starts on top of one of the particles; after a given number of cycles, the laser jumps to the position of the second particle where it performs the same routine for tracking. Then, the center of scanning is moved to the new position determined previously for the first particle. Thus the positions of the particles are recovered alternately.

In a recent article (12), we performed control experiments—tracking fluorescent microspheres moving in known paths—in which we demonstrated that the method can recover trajectories up to 10 μm with 20-nm precision and a time resolution of 32 ms. The performance of the tracking was shown to be equally good in the x and y directions. Also, we showed that the accuracy of the position determination is approximately constant for a signal/noise ratio >2.

The rotation of an asymmetric particle will not be detected by the current method since the algorithm only minimizes the modulation of the first harmonic and this rotation would only affect higher-order harmonics.

Using two-photon microscopy makes this method well suited for biological applications since it provides significantly lower out-of-focus photodamage and photobleaching than other fluorescence microscopy (13). Also, during the tracking we focus the laser in a small volume surrounding the particle, resulting in reduced photodamage of the rest of the sample. In contrast, methods that employ video cameras (see, e.g., Hicks and Angelides (20) and Wilson et al. (21)) require repetitive exposures of large sample volumes that could result in significant damage.

Calculation of diffusion coefficients

For each two-dimensional trajectory, the mean square displacement (MSD) was calculated as a function of lag time (τ):

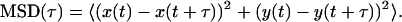(2)

MSD was plotted as a function of τ and the diffusion coefficients were calculated by fitting the following equation to the experimental data (22),

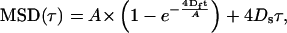(3)

where A is the characteristic confinement area and D_f and D_s represent the fast and slow diffusion coefficients.

This model considers a short-term confined diffusion overlapped with a long-term random diffusion.

RESULTS

Two-photon imaging and tracking of EGFP-tagged chromatin

Two cell lines, each stably expressing EGFP-lac repressor and containing chromosome sites labeled with lac-operator sites, were used in the experiments (Fig. 2 A). The C6-14 CHO cell line, previously described (10), has 10–20 copies of a plasmid containing lac-operator repeats and a DHFR cDNA transgene driven by a viral promoter. These copies are integrated at a single, internal chromosome site. The DHFR-BAC CHO cell line contains multiple copies (∼8–10) of a BAC with a 170-kbp mouse genomic DNA insertion including the DHFR locus. A 256-copy, lac-operator direct repeat was inserted ∼75 kbp upstream of the DHFR gene. In mitotic chromosomes these BAC copies appear integrated at a single spot (data not shown).

FIGURE 2.

EGFP labeling of chromatin in vivo. (A) Construction of the C6-14 and DHFR-BAC cell lines. Scale bar, 2 μm. (B) Intensity distribution of the fluorescent-tagged sequence in a C6-14 cell.

To assess whether the tracking method is suitable to follow the fluorescent-tagged sequences, we first analyzed the fluorescence intensity distribution of the cells under two-photon excitation. Fig. 2 A shows representative images obtained for C6-14 and DHFR-BAC cells. The lac-operator repeat in both cell lines is detected as a single spot or multiple bright spots, respectively. The background fluorescence observed in both cell lines is due to molecules of EGFP-lac repressor freely diffusing in the nucleus.

As an example, Fig. 2 B shows the intensity distribution in a region of the image of a C6-14 cell that includes the bright spot. The ratio between the intensity of the spot and the background ranged from 3 to 10 (N = 39).

To verify the capability of the two-photon tracking system to follow the motion of the lac-operator tandem, we first performed the tracking of the bright sequence in fixed C6-14 cells (Fig. 3 A). The spot presented a highly constrained motion in an area of ∼50-nm radius, in the order of the fluctuations in the position observed when tracking immobilized fluorescent beads. It is important that we did not observe photobleaching of the fluorescent-tagged sequence for our runs that lasted for <20 min.

FIGURE 3.

Dynamics of the EGFP-tagged DNA sequences. (A) Representative trajectory of the fluorescent-tagged sequence in a fixed C6-14 cell. (B) Trajectory registered in a live C6-14 cell, where the regions of confined motion are painted with different colors. Both trajectories were obtained with a time resolution of 32 ms. The trajectory of the labeled sequence (yellow) is overlaid on the DIC image of the cell (left). Scale bar, 2 μm.

Dynamics of chromatin in C6-14 cells

To study the motion of the lac-operator tandem sequence in C6-14 cells, we plated the cells for 2–3 days in fibronectin-coated dishes. The dishes were sealed to avoid contact with the air and placed in the microscope stage, keeping the temperature at 37°C.

After detecting the fluorescent-tagged sequence by imaging the cell, we followed its motion for 5–20 min as described in Materials and Methods.

We took DIC images of each studied cell before and after the tracking experiment. By comparing these images, we determined whether there was obvious motion of the nucleus or the whole cell, in which case we discarded the trajectory. Also, we determined the position of the fluorescent-tagged sequence in the nucleus by recording another DIC image of the cell after placing the laser exactly in the position last determined for the sequence (see Materials and Methods). In 86% of the C6-14 cells analyzed (N = 60) we observed a close association of the sequence with either the nucleolus (54%) or the nuclear envelope (32%).

Fig. 3 B shows a representative trajectory recovered for a C6-14 cell. In contrast to the fixed cells, 77% of the trajectories (N = 60) presented larger regions of apparent constrained diffusion connected through curvilinear paths or jumps.

From the analysis of these trajectories, we determined that the characteristic value for the jump size was 150 nm (Fig. 4 A). Also, we calculated the characteristic time of residence in a region of confined motion before jumping to another region and obtained a value of 56 s (Fig. 4 B). From the analysis of the number of points in the trajectory during the jumps we could estimate that they occur in 0.3–2 s.

FIGURE 4.

Jump characterization. (A) The size of the jump in different trajectories was determined as the distance between the centers of mass of two connected regions of confined motion. The histogram of jump size was constructed with 70 jumps and was fitted with a lognormal distribution function 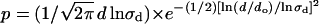centered at d_o = 151 ± 6 nm, with a standard deviation σ_d = 1.42 ± 0.06 (continuous line). (B) The residence time was calculated as the time interval in which the sequence remains in a region of confined motion before jumping to another region. The histogram of residence time (t) includes 59 regions of confined motion and was fitted with a lognormal function where t_o = 0.94 ± 0.07 min and σ_t = 1.9 ± 0.1 (continuous line).

Interestingly, in some of the trajectories measured for the fluorescent tagged sequence, we observed loops that extend beyond the apparent regions of confined motion (see, for example, Fig. 6 A).

FIGURE 6.

Velocity distribution in the trajectories of the DNA labeled sequence in untreated (A) and ATP-depleted (B) C6-14 cells. The data points in the trajectories, obtained with a time resolution of 32 ms, were classified as fast (blue) or slow (pink), as described in the text. The boxes show the details of two jumps between regions of confined motion. Most of the points in these regions are blue high-velocity data.

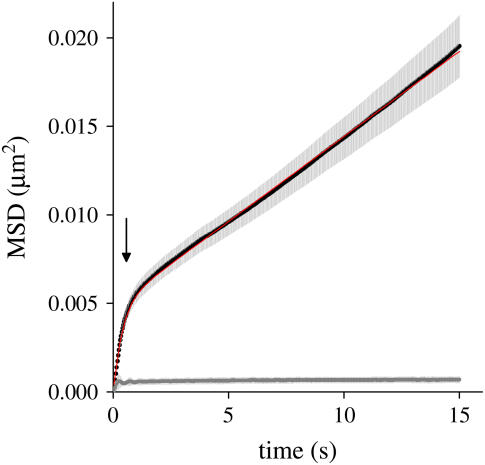
To characterize the motion of the sequence in the confined regions, we plotted the MSD as a function of time for each trajectory (Fig. 5). This plot shows a bilinear behavior that could be fitted with a model that considers a superposition between a short-term confined diffusion with a long-term random walk. The best fit of Eq. 3 to the experimental data was obtained with a confinement area A = 4.83 × 10⁻³ ± 0.01 × 10⁻³ μm², and slow and fast diffusion coefficients D_s = 2.400 × 10⁻⁴ ± 0.004 × 10⁻⁴ μm²/s and D_f = 3.13 × 10⁻³ ± 0.05 × 10⁻³ μm²/s.

FIGURE 5.

Diffusion of the EGFP-tagged sequence. The plot shows the average MSD obtained from 39 live (black) and six fixed (gray) C6-14 cells as a function of the lag time. The standard error of the experimental data is shown in light gray. The arrow shows approximately the limit between the fast and slow diffusion regime regions. The red line shows the fitting of Eq. 3 with the parameters indicated in the text.

The jumps are not a consequence of random diffusion

Using a combination of experimental measurements, theoretical analysis, and Monte Carlo simulations, Saxton studied several motion models that could explain trajectories observed in biological systems (e.g., 23–27). The trajectories observed in our work have characteristics similar to those predicted for theoretical models such as diffusion within corrals with transitions between the corrals (26) and the conveyor belt model of directed transport in which a particle moving randomly has a probability of binding to a conveyor belt that moves at a constant velocity (25). The first of these models has been used to explain the hop motion of lipids and proteins in membranes (see references in Kusumi et al. (28)). The second model was proposed to explain the trajectories of cargoes transported through the cytoskeleton.

However, the apparent similarity of trajectories does not imply that the physical mechanism driving the motion is the same. In particular, in our case the fluorescence sequence is constrained by the polymer chain that has a complex nonrandom structure. Therefore, the models proposed for motion of isolated particles are not applicable a priori to our system. Also, the jumps we observed in the trajectories cannot be detected by the MSD analysis since they seem to be a rare event in the trajectories. Thus, we followed a different experimental and theoretical approach to characterize the physical processes that are responsible for the chromatin position jumps.

First, we calculated the absolute instantaneous velocity in each trajectory, at all the trajectory points. The points were then painted in two different colors, according to a median velocity threshold for which 50% of the points are above (blue) or below (pink) the threshold (Fig. 6). If the velocity were homogeneous through the trajectory, we would expect ∼50% of blue points in any trajectory region. We examined the color distribution during the curvilinear transitions between regions of confined motion and verified that of 27 jumps, 23 presented an average of 87% of blue points. (The remaining four jumps contain only 48% of blue points). In comparison, the analysis of the trajectories of fluorescent beads randomly diffusing in an agarose mesh showed that the mean velocity in the pore regions between areas of confined diffusion is not significantly different than the mean velocity within the overall bead trajectory (not shown). These results suggest that the observed high-velocity jumps in live cells are not a consequence of passive chromatin diffusion through nucleoplasm pores or channels.

A second statistical analysis of the trajectories also supports the model of an active process driving the motion of the sequence during the jumps. Specifically, if the transitions between regions of confined motion are the result of random motion, we would expect the average time spent in the curvilinear path (τ_jump) to be equal to 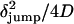, where δ_jump is the net displacement from the starting point to the end point of the jump. We determined the values of τ_jump and δ_jump for 18 different transitions and verified that 72% of the jumps occurred, on average, four times faster than predicted according to a random diffusion model. The rest of the transitions presented τ_jump values compatible with this model.

In a third analysis of the trajectories of the fluorescent-labeled sequence in live C6-14 cells, we correlated the direction and distance traveled by the sequence over a long timescale. We defined vectors between every two trajectory points separated by n data points and determined the absolute size of these sliding vectors (d_i,i+n) and the angle between adjacent vectors. Then, we calculated an index J according to:

(4)

where 〈d_i,i+n〉 is the average size of the vector measured for the trajectory and α_i is an index equal to 1 if the absolute angle between the contiguous vectors (i, i + n) and (i + 1, i + 1 + n) is ≤20° for at least five consecutives points and equal to zero otherwise.

According to this definition, J values different from zero indicate regions where the sequence undergoes an approximately curvilinear motion. For our calculations, n = 1000, which means that the vector was calculated between points far from each other in 32 s, i.e., approximately the maximum of the distribution of residence time in confined regions (Fig. 4). This condition allows us to discriminate those long segments resulting from transitions between regions of confined motion from other segments that can stochastically occur in a confined random motion. If n were smaller (i.e., if d_i,i+n were calculated between data points very near each other) there would be a higher probability of finding segments within the constrained random motion regions similar in size to that observed during the jumps. We also set the requirement that the angle should be <20^o for at least five data points (i.e., 0.16 s, which is in the order of the jump duration) to distinguish short-duration episodes of linear motion from those in which the sequence moves persistently in a given direction for a longer period.

By plotting J as a function of time, we observed that the sequence trajectories present clustered regions with J values higher than zero when the sequence is undergoing a jump. This analysis was also done in trajectories obtained by simulating a particle diffusing randomly in a two-dimensional grid. In this case, we observed a homogeneous distribution of J throughout the trajectory, without clustered, nonzero regions (Fig. 7).

FIGURE 7.

J analysis. The trajectories determined for the fluorescent tagged sequence in a C6-14 cell (A) and a simulated particle moving in a two-dimensional grid under a random diffusion regime with D = 2.4 × 10⁻⁴ μm²/s (B) were analyzed according to the description in the article. The J values obtained for the sequence (C) and the simulated particle (D) are plotted as a function of time. The double arrow represents the time interval in which the jump is observed.

The jumps are sensitive to temperature and ATP

The analyses presented in the previous section show that the fluorescent-tagged sequence trajectories in live cells cannot be explained by random diffusion models. Two other experimental lines of evidence support the same conclusion.

First, we followed the motion of the fluorescent-tagged sequences in C6-14 or DHFR-BAC cells in which ATP levels had been depleted by previous incubation with sodium azide and 2-deoxyglucose (Fig. 6 B). After ATP depletion, we did not observe jumps in the trajectories measured in either cell line (N = 30), indicating that these curvilinear jump movements are not the consequence of passive diffusion but occur through an energy-dependent process.

Second, we measured the chromatin dynamics in C6-14 cells at 21°C after preincubating the cells for 4 h at this temperature. In contrast to the very small changes in motion expected for diffusive processes (29) the number of trajectories presenting jumps decreased from 77% to 47% (N = 36).

Dynamics of chromatin in DHFR-BAC cells

To further distinguish chromatin dynamics from small submicrometer motion of the nucleus or the cell, we simultaneously tracked two EGFP-tagged sequences within DHFR-BAC nuclei. In 36% of the observed cells (N = 80), similar jumps were observed in the trajectories to those seen for C6-14 cells (Fig. 8). The rest of the trajectories showed either confined motion (25%) or mixed behaviors not easily classifiable.

FIGURE 8.

Trajectories registered by simultaneous tracking of two labeled sequences in the DHFR-BAC cell line. DIC image of a DHFR-BAC cell overlaid with the trajectories of the tracked sequences. The time resolution was 32 ms. Scale bar, 2 μm (left). One of the sequences undergoes a constrained diffusion motion (blue), whereas the trajectory of the other shows jumps between regions of confined motion (red).

In 71% of the DHFR-BAC cells, there was no association between the fluorescent tagged sequences and the nuclear envelope or nucleoli observed by DIC imaging and only 9% of the spots associated with the nuclear envelope or nucleolus had jumps in their trajectories. Therefore, the jumps are not a consequence of the association of the sequences with these nuclear substructures.

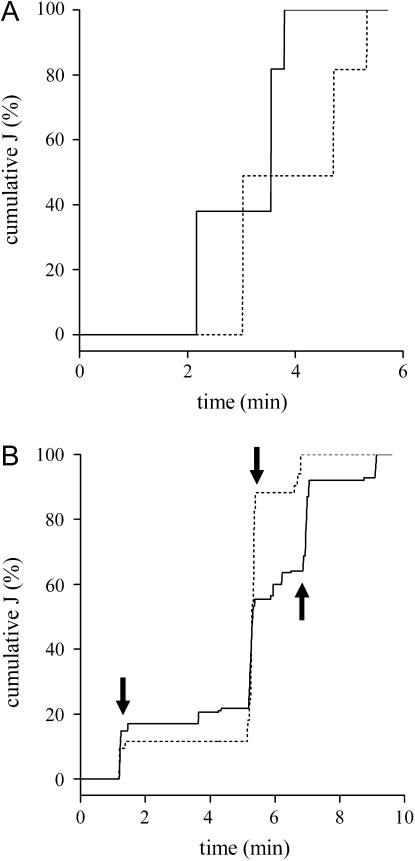
For those DHFR-BAC cells that showed jumps in both trajectories, we analyzed whether they occurred simultaneously by doing a J analysis similar to that shown in the previous section. First, we calculated the value of J for the two trajectories obtained for each DHFR-BAC nucleus. Then, we computed a cumulative function J. In this way, the jumps are detected as fast increments in the cumulative J and we can easily see whether they occur at the same time in both trajectories. By doing this analysis, we observed that the jumps are not correlated in 90% of the cells. Fig. 9 shows the results obtained from this analysis for two different cells, one of them presenting simultaneous jumps whereas the other only shows uncorrelated jumps. This result indicates that most jumps are due to local processes which are not transmitted long distances through the chromatin chain or nuclear subregion.

FIGURE 9.

Analysis of simultaneous jumps in DHFR-BAC cells. The J parameter was calculated as described in the text for the trajectories obtained in DHFR-BAC nuclei. The cumulative value of J obtained for each trajectory was plotted as a function of time. The panels show DHFR-BAC cells in which trajectories represent uncorrelated (A) and correlated (B) jumps. The continuous and dotted lines correspond to the cumulative J calculated for different spots in the same cell. The cumulative J is expressed as a percentage of the maximum obtained for the trajectory. The arrows in B show jumps that occur simultaneously in both trajectories.

DISCUSSION

Summary

In this work, we studied the dynamics of fluorescent-labeled chromatin loci in interphase cells. Previous studies have been done on the mobility of interphase chromatin loci in several different cell lines (4–7). The general conclusion reached from all of those studies is that interphase chromatin mobility follows a constrained random diffusion model. The biological interpretation of such findings is that interphase chromatin is tethered to different nuclear structures, with mobility produced by diffusion of chromatin loci on variable-length chromatin tethers. However, all of those studies used experimental methodologies with time and spatial resolutions significantly lower than in the particle-tracking method we applied in this study. Instead, we now describe a significantly more complex nature to the observed interphase chromatin mobility, with at least three different chromatin motion regimes described.

Jumps in chromatin position

Perhaps the most intriguing observed mobility regime, which we describe here for the first time that we know of, is the rapid transition between different localized motion regimes via jumps in which the locus appears to move in a curvilinear path. These jumps, averaging 150 nm, occur over a time duration ranging from 0.3 to 2 s. Previous methods used to observe chromatin mobility had insufficient time and spatial resolution to resolve this mobility behavior.

For several reasons we believe these jumps represent bona fide, local chromatin movements. First, similar jumps were observed for the single-spot cell line, C6-14, and the DHFR-BAC cell line containing multiple spots. Simultaneous particle tracking revealed that in these DHFR-BAC cell nuclei, two EGFP-labeled sequences that are typically separated by <1–2 μm, i.e., a small fraction of the nuclear diameter, do not show correlated jumps. Therefore these jumps do not represent movements of the entire nucleus. Second, because the multiple BAC transgene insertions were localized in metaphase chromosomes to an area less than one full chromosome band, we estimate that they cointegrated within several Mbp. Therefore the lack of correlation between jumps on individual chromatin spots in these cells implies that the observed motion does not correspond to movement of an entire chromosome or chromosome arm, but is restricted to a several-Mbp DNA segment or smaller.

Moreover, our results indicate that these jumps likely reflect energy-dependent chromatin movements rather than diffusive motions driven by thermal fluctuations. This conclusion is suggested by the elimination of jumps after sodium azide depletion of ATP pools. ATP depletion has been used to suggest metabolic-dependent transport of promyelocytic leukaemia nuclear bodies (30) and Cajal bodies (17). The latter authors reported no changes in chromatin structure after treatment with azide and deoxyglucose in conditions similar to those used in this work. However, there is a recent report indicating that this treatment could lead to changes in chromatin structure (31). We note, though, that in the DHFR-BAC cell line, multiple insertions of the lac-operator repeats are visualized as a linear string of spots. No alteration of this linear arrangement is observed with ATP depletion (not shown), arguing against a major change in large-scale chromatin structure as an explanation for the disappearance of jumps.

An independent experimental manipulation also suggesting that these jumps arise through an active process is provided by decreasing temperature from 37°C to 21°C. Under these conditions, jump frequency was significantly reduced, counter to what would be expected from thermal-driven diffusive movements.

The energy-driven motion of chromatin is also supported by a careful inspection of the details of the motion during the jumps. Particularly, we verified a sustained faster motion and a linear path for the sequence movement during these jumps.

The average jump length is 150 nm. However as the jump was determined by two-dimensional tracking we are probably underestimating its size. If we consider that the jump is equally probable in all directions, the average jump length would be ∼185 nm. This movement could arise through translocation of a local interphase chromosome region and/or condensation or decondensation of a local interphase chromosome region.

If a local change in chromatin compaction is involved, this conformational change could occur at several different levels of structure. For example, it could occur at the level of the folding of beads-on-a-string, 10-nm chromatin fibers into 30-nm chromatin fibers. With a linker distance of ∼30 nm between nucleosomes in the beads-on-a-string structure (32), an elongation of 180 nm would be produced by the unfolding of one turn of a 30-nm chromatin fiber (six nucleosomes). Cui and Bustamante (33) estimated the internucleosomal attractive energy as ∼3.4 kT by measuring the force involved in the extension of a single chromatin fiber. According to this value, the probability of spontaneous unfolding of a complete turn of a 30-nm fiber is very low, confirming that if such an event occurs, it requires an energy-dependent interaction with the cell machinery. RNA or DNA polymerases, chromatin-remodeling complexes, or chromatin-modifying complexes are all possible candidates for such unfolding. Alternatively, this conformational change could occur in the large-scale chromatin folding motifs involving folding of 10- and 30-nm chromatin fibers in higher-order structures (34). The processes controlling these higher levels of chromatin folding are poorly understood.

The observed jumps in the trajectories could reflect active translocation of chromatin regions. Nuclear myosin I is the first molecular motor said to be present in the nucleus (35). Recently it was demonstrated that this nuclear motor, in conjunction with nuclear actin, is required for RNA polymerase I transcription (36), and it has been proposed that nuclear myosin I is necessary for RNA polymerase II function (35) as well. Also, it has been suggested that nuclear myosin mediates the dynamics of some nuclear processes, such as the motion of promyelocytic leukaemia nuclear bodies (30), based on the sensitivity of this motion to specific actin-dependent myosin inhibitors. These data make complexes of nuclear myosin I and actin possible candidates to account for the motion of chromatin observed in this work. Future experiments are planned that will use molecular methods to inhibit specific candidate proteins to determine their possible role in these jumps in chromatin position.

Two time regimes for “diffusive” chromatin motion

We analyzed the trajectories obtained for C6-14 cells during the periods of motion between jumps where the spot was confined to localized regions by plotting the MSD as a function of the lag time. A biphasic MSD plot was observed (Fig. 5) which consisted of two different linear regions. At small lag-time values <0.6 s a steeper slope was observed; this was followed by an approximately linear behavior with lower slope for values of τ > 0.6 s. Our results are consistent with previous reports in Drosophila of an anomalously fast-motion component at very short lag times (6); however, these authors could not describe quantitatively the fast component of the motion since it occurred on a timescale comparable to their sampling time.

We first tried to fit the MSD experimental data with an anomalous diffusion model, since this is the simplest model that could explain negative deviations in MSD plots with respect to the linear behavior expected for a pure random diffusion (37). However, the fit presented a clear bias (not shown), indicating that such a model cannot explain our experimental results.

Then, we considered a model that takes into account that the particle moves randomly in a confined region that is itself moving (22). As can be observed in Fig. 5, this model satisfactorily fitted the experimental data. These results indicate that there are at least two regimes of motion operating on different timescales.

The predicted confinement radius for the observed rapid, short-timescale motion is ∼40 nm, roughly comparable to the diameter of 30-nm chromatin fibers. Thus, this fast, confined motion very likely could reflect local oscillations in chromatin folding. The slow-diffusion coefficient is in the order of the diffusion coefficients determined for DNA in mammalian cells (5). Vazquez et al. (6) showed that the slow-diffusion constant changes with the cell cycle, suggesting that this diffusion rate reflects dynamic interactions between chromatin and internal nuclear structures that contribute to large-scale reorganization of chromatin within the nucleus.

CONCLUSIONS

Our data, though consistent with previous lower-resolution analysis of chromatin movement within mammalian interphase nuclei, now at higher spatial and temporal resolution reveals short, high-velocity, curvilinear jumps, over a timescale of ∼1 s, connecting localized regions of apparent constrained diffusion. The motion of the sequence in these constrained regions appears to consist of a fast motion over a short timescale of <0.6 s, possibly reflecting oscillations on local chromatin structures, with a slower, longer-range movement, which may reflect interactions of large-scale ordered chromatin with internal nuclear structures. The jumps connecting these regions of constrained mobility are ATP-dependent and thus appear to be the manifestation of active, versus passive diffusive, mechanisms for interphase chromosome movements.

Future experiments will apply the new two-photon particle-tracking method described in this article to test candidate proteins, including nuclear myosin, RNA polymerases, and chromatin remodeling and modification complexes, for their role in producing different features of interphase chromatin mobility.