Multiple Membrane Tethers Probed by Atomic Force Microscopy

Abstract

Using the atomic force microscope to locally probe the cell membrane, we observed the formation of multiple tethers (thin nanotubes, each requiring a similar pulling force) as reproducible features within force profiles recorded on individual cells. Forces obtained with Chinese hamster ovary cells, a malignant human brain tumor cell line, and human endothelial cells (EA hy926) were found to be 28 ± 10 pN, 29 ± 9 pN, and 29 ± 10 pN, respectively, independent of the nature of attachment to the cantilever. The rather large variation of the tether pulling forces measured at several locations on individual cells points to the existence of heterogeneity in the membrane properties of a morphologically homogeneous cell. Measurement of the summary lengths of the simultaneously extracted tethers provides a measure of the size of the available membrane reservoir through which co-existing tethers are associated. As expected, partial disruption of the actin cytoskeleton and removal of the hyaluronan backbone of the glycocalyx were observed to result in a marked decrease (30–50%) in the magnitude and a significant sharpening of the force distribution indicating reduced heterogeneity of membrane properties. Taken together, our results demonstrate the ability of the plasma membrane to locally produce multiple interdependent tethers—a process that could play an important role in the mechanical association of cells with their environment.

INTRODUCTION

The plasma membrane of mammalian cells is a highly dynamic structure and its biomechanical properties are vital to the regulation of many cellular functions, such as adhesion, migration, signaling, and morphology (1). One of the most dynamic processes within these membranes is the formation of tethers or thin nanotubes. These structures have been implicated in cell-cell adhesion (2) and recent studies suggest they might also provide a pathway for intracellular and intercellular communication (3–7).

In vivo, tethers form during the primary adhesion and rolling motion of activated leukocytes on vascular endothelial cells or platelets along the walls of blood vessels (2,8,9). Hence, tether formation corresponds to the initial event leading to the extravasation of activated white blood cells at the sites of inflammatory reactions (10). In these systems, membrane tethers originate from pre-existing microvilli through specific selectin/glycoprotein bond formation between cells under hemodynamic conditions (11).

Membrane nanotubes have also been observed between liposomes and have been shown to readily form in red blood cells (12,13), neutrophils (14), neurons (15), fibroblasts (16,17), as well as epithelial (18) and endothelial cells (19). Several experimental methods have been used to characterize the mechanical properties of membrane tethers, such as micropipette aspiration assays (12,13,20–23) and optical tweezers (15,24,25). In these experiments, tethers are observed in force-versus-distance curves as well-defined plateaus occurring at constant force. The presence of plateaus can be understood in terms of a membrane reservoir being gradually depleted upon pulling on the bilayer (16). These studies also revealed that tether length (i.e., available membrane reservoir) and tether formation force are influenced by the various components of the cytoskeleton. On the intracellular side, the membrane is connected to the cytoskeleton through a variety of proteins and other complexes (26,27) and this association has been proposed to play a major role in cell membrane cohesion. The influence of cytoskeletal integrity on the force needed to form tethers has been investigated earlier (28). These experiments demonstrated that the disruption of the cytoskeleton leads to a decrease of the force required to extract and elongate tethers. On the extracellular side, the cell membrane is covered by a glycosaminoglycan and proteoglycan network, the glycocalyx. Whether or not the glycocalyx influences the properties of membrane tether formation has not been explored. Another important question concerns the possible heterogeneity in the interaction of the cytoskeleton/glycocalyx with the membrane over a morphologically homogeneous cellular surface.

Tether formation in cell motility and cellular adhesion is likely to involve the simultaneous formation of multiple tethers. To our knowledge, the tether pulling experiments performed until now have primarily addressed the formation of single tethers. One recent study explored dual tether extraction using the micropipette aspiration technique. Here the tethers were observed not in force-elongation profiles, but rather through the analysis of the dependence of the pulling force on the growth velocities of the tethers (29). Other recent work has demonstrated that multiple membrane tethers can be formed in a minimal system composed of a giant unilamellar vesicle, kinesin-coated beads, microtubules, and ATP as energy source (3,5,30). Beyond these examples, little is known about the behavior of multiple, simultaneously existing tethers in real cells, and their coupling with the overall membrane reservoir or their association with each other. Whether or not multiple membrane tethers can be simultaneously extracted from the membranes of living cells is still a matter of controversy. Indeed, multiple tethers extracted from close locations along the membrane surface are expected to rapidly coalesce. In a recent theoretical article, Derényi et al. (31) predicted that, in the absence of pinning forces, multiple membrane tethers coalesce smoothly. However, this study also points out that in real cells, membrane heterogeneities or coupling to the cytoskeleton may prevent tether fusion.

To extract multiple tethers, a large initial adhesion force has to be overcome. For this, a force transducer with the ability to measure a broad range of forces (such as those encountered in specific and nonspecific cellular adhesion events) is needed. The atomic force microscope (AFM) (32) has proven to be a powerful tool for single molecular investigations, to observe biological structures and to study intramolecular and intermolecular interactions (for reviews on the subject, see (33,34)). Recently, a variety of biologically relevant binding forces have been characterized by force spectroscopy including the rupture force of a covalent bond (35), unfolding forces in individual biomolecules (36–40), rupture forces between various ligands and receptors (41,42), unbinding forces of cadherins (43), and cell-cell interaction forces (44,45). The ability of AFM cantilevers to detect a large range of forces (picoNewtons to nanoNewtons) provides the opportunity to simultaneously monitor the formation of individual or multiple tethers and to bring new insight into the behavior of multipally extracted tethers. In this study, we used the AFM to extract multiple tethers, using a variety of cells with different morphology and origin, including Chinese hamster ovary (CHO) cells, a malignant human brain tumor cell line (HB), and endothelial cells. These studies were aimed at demonstrating that formation of multiple membrane nanotubes is a ubiquitous phenomenon, largely independent of particular cell type. In particular, we show that multiple tether formation can be induced locally through contact of the AFM cantilever with the cell membrane, and that the tethers extracted are interdependent. By measuring the contributions of both the cytoskeleton and the glycocalyx to the tether forces, we bring new insights into the mechanism of membrane tether formation and the behavior of multiple, simultaneously extracted tethers.

MATERIALS AND METHODS

Cell culture and treatments

Chinese hamster ovary cells (CHO-K1 cells, American Type Culture Collection, Manassas, VA) and the human brain tumor cell line (HB) (46) were cultured in DMEM (Invitrogen, Carlsbad, CA) supplemented with 10% fetal bovine serum (Sigma-Aldrich, St. Louis, MO) and 1% penicillin/streptomycin mixture (Sigma-Aldrich) following standard procedures. The human endothelial cells EA hy926 were a generous gift of Dr. C-J S. Edgell (47), and were maintained in HAM'S F-12 supplemented with 20% fetal bovine serum (Sigma-Aldrich). Cells were plated on glass coverslips (Pierce Biotechnology, Rockford, IL), placed in 35-mm plastic petri dishes (Techno Plastic Products, Trasadingen, Switzerland), or plated directly in petri dishes, and cultured at 37°C in a 5% CO₂ incubator typically for 24 h. In cytoskeletal disruption experiments, the cells were in regular medium supplemented with latrunculin A (Sigma), a specific actin polymerization inhibitor (48–50) at various concentrations (0.1, 0.2, 0.5, and 1.0 μM) for 30 min before the measurement. The importance of the glycocalyx in the fomation of membrane nanotubes was studied through one of its major components, the glycosaminoglycan hyaluronan (51). The removal of hyaluronan from the surface of substrate-attached cells was achieved by a 30-min incubation in the presence of hyaluronidase (500 IU/ml) (Sigma-Aldrich) in serum- and polysaccharide-free medium. For surface modification assays, cantilevers (Veeco, Santa Barbara, CA) and glass coverslips (Pierce Biotechnology) were put in the 0.1 mg/ml Poly-L-Lysine solution (Sigma) for 15 min, then rinsed with Milli-Q water (Millipore, Billerica, MA) and air-dried. The effect of a collagen-coated surface was measured by incubation of cantilevers in a type I collagen solution (1 mg/ml; Sigma) at 4°C for 60 min, then rinsing with Milli-Q water and air-drying in a laminar flow hood.

Force spectroscopy measurements

Our in-house-built force measurement device, based on the design and operation of an AFM, was attached to the stage of an inverted optical microscope (Olympus IX70, Olympus America, Melville, NY). This arrangement allowed for precise positioning of the cantilever on the area of interest along the cell membrane. Soft silicon nitride cantilevers (Veeco, Santa Barbara, CA) were cleaned in 70% ethanol, rinsed in Milli-Q water, and then sterilized with UV light for 15 min. Each cantilever was calibrated after a given experiment using thermal noise amplitude analysis (52,53). The measured spring constants were between 8 and 11 mN/m, in agreement with the nominal spring constant of 10 mN/m.

Cells were placed under the force device in CO₂-independent medium (Invitrogen, Carlsbad, CA) containing 2% fetal bovine serum at room temperature. A typical experiment was performed as follows: the cantilever was moved toward the surface until contact with the cell membrane (observed from the deflection of the cantilever) was established (Fig. 1). Contact was maintained for 2–30 s, and then the cantilever was retracted from the cell surface (Fig. 1 B). A typical retraction resulted in a series of rupturelike discontinuities in force, as shown schematically in Fig. 1 B. Loading rates were maintained between 3 and 5 μm/s. Force elongation profiles were recorded using a number of cells from each cell type, with each cell subjected to multiple retraction experiments. Several hundred discrete events were used for data analysis for each of the three cell lines.

FIGURE 1.

(A) Optical image showing positioning of the cantilever on the cell surface (an HB cell is shown). (B) Schematic representation of events during retraction. The individual force steps derive from recycling of single tethers.

Visualization of membrane nanotubes with quantum dot-labeled cells

Endothelial cells (EA hy926) were washed three times in phosphate-buffered saline (Fisher Scientific, Pittsburgh, PA) to remove culture medium followed by incubation with sulfo-NHS-biotin (Sigma, St. Louis, MO) at a concentration of 100 μg/ml for 15 min at room temperature. Subsequently, cells were washed four times in HAM'S F-12 cell culture medium (Wisent, St. Bruno, Canada) and incubated with streptavidin-conjugated Q-dots (Quantum Dot, Hayward, CA) with a fluorescence maximum at 605 nm. Finally, cells were rinsed an additional three times to remove unbound Q-dots and micrographs were obtained with an inverted epifluorescence microscope (Axiovert 200, Zeiss, Thornwood, NY) on which the force spectrometer was mounted. Images were taken (40× objective) with an ME2 CCD camera (Finger Lakes Instrumentation, Lima, NY) at a resolution of 768 × 512 pixels. Membrane tethers were formed by contacting an individual cell with the AFM cantilever, followed by a simultaneous vertical and lateral retraction allowing individual tether visualization.

RESULTS

Multiple tether formation and rupture

Formation of membrane tethers between cells and untreated AFM cantilevers was demonstrated by labeling the cell surface with fluorescent quantum dots and probing the cell in a manner similar to that used in the force measurements. Fig. 2 shows a membrane tether formed after contact of the AFM cantilever with an endothelial cell. The two fluorescent images correspond to two different positions of the cantilever and demonstrate the fluid nature of membrane tethers. This visual control provides confirmation that the features present in the retraction profiles are the result of tether extraction from the cell membrane. However, fluorescence imaging did not permit resolving multiple tethers, possibly due to their close proximity and small diameter. An alternative explanation could be the large extension (several microns) required for their observation using AFM, which favors observation of multiple tethers in close proximity as one. Indeed, in a typical imaging experiment, to bring the full length of the tether into focus, the cell is contacted through the vertical movement of the AFM cantilever, followed by its extensive horizontal displacement.

FIGURE 2.

A tether pulled by horizontal movement of the cantilever is observed by labeling the cell membrane with fluorescent quantum dots. The arrows indicate the tethers, which move freely as they follow the movement of the cantilever.

The retraction profiles recorded with three different cell types exhibited an initial high force region followed by distinct, multiple plateaus separated by force steps (Fig. 3). The existence of the high force region indicates that, to initiate the tether extraction process, a substantial effort is needed. The height of this region, as well as the number of plateaus in a given retraction experiment, were found to be sensitive to the duration of contact, but the magnitude of the force steps between plateaus, ΔF, was not. In previous experiments, performed with optical traps, plateaus in force-elongation profiles were associated with the pulling of individual membrane tethers (“tether force” in what follows), composed of freely diffusing membrane components—mainly phospholipids and membrane proteins (16). The length of the plateau was correlated with the extent of the membrane reservoir. In most of our experiments, multiple plateaus were observed along the entire extension, and within an individual force-extension profile. Since the discrete force steps between consecutive plateaus were markedly comparable (Fig. 3), we interpret them as the simultaneous elongation and sequential loss of multiple membrane tethers formed between the cell and the cantilever. Consequently, ΔF can be associated with the force needed to pull a single tether, whereas the total force at which a given plateau occurs corresponds to the force necessary to pull all existing tethers.

FIGURE 3.

Typical retraction-force curves as a function of cantilever extension for three cell lines. Numbers on the graphs denote the values of the individual force steps between consecutive plateaus. Note the very similar force drops in the quasi-constant force elongation regime, and that zero force is not reached at the end of the retractions, indicating tethers are still attached. Inset shows timescale for a typical force drop.

Our retraction traces did not exhibit the exponential rise of the force-versus-length observed in optical tweezers experiments at the end of the plateau region that is attributed to a depleted membrane reservoir (see inset in Fig. 3 (16)). The length scale (several microns) over which plateaus were observed, however, is consistent with the earlier finding that tethers form and grow by the gradual depletion of the cell's membrane reservoir (16,18). These observations provide further evidence that the measured force-steps correspond to the force required to pull a tether, rather than the force required in the process by which the tether bridge is lost.

We suggest that the size of the overall membrane reservoir, shared by all the tethers, can be characterized by the length of the last observed tether. Alternatively, the reservoir size can be evaluated at each discrete force-step by multiplying the number of tethers being pulled on a given plateau before a force drop by the length at which the rupture occurs. This is true despite the fact that at the force-steps the local membrane reservoirs are not yet fully depleted. This procedure is illustrated in Fig. 4, which shows a force-elongation profile with multiple plateaus corresponding to simultaneously pulled tethers and their sequential loss. Using Fig. 4 to evaluate the membrane reservoir in terms of tether length, we obtain the consistent values of 7.8 μm, 7.2 μm, and 7.2 μm from the last three plateaus, representing three, two, and a single tether, respectively. This observation is in accord with the assumption that multiple, simultaneously existing tethers are interdependent in terms of the cell's overall membrane reservoir: the material of a ruptured tether is rapidly recycled and its local membrane reservoir becomes available for the continued elongation of the still intact ones (15). The existence of an overall cellular membrane reservoir, composed of interconnected local reservoirs, is also supported by the earlier finding that—as a consequence of the plasma membrane's fluid character, with repeated pull-retract cycles of single tethers—the onset of the exponential regime is shifted to later times and thus longer plateaus (16). Even though the result obtained using Fig. 4 is highly suggestive, it is not fully representative for the following reasons. Any loss of membrane material to the AFM cantilever surface after a given tether bridge is lost, will cause a depletion of the available membrane reservoir, unless the force-steps correspond to the detachment of the tether from the AFM tip (which will be argued to be the case; see Discussion). Furthermore, Fig. 4 is special in the sense that it represents an experiment in which all tethers have been lost. More typically, not all tethers are lost when our device reaches its extension limit, in which case the above analysis must be performed with the assumption that the last observed plateau corresponds to more than one tether. When performed on the profiles shown in Fig. 3, the analysis leads to consistent results for the CHO and HB cell, assuming that, respectively, two or three tethers are present before the last force-step seen in the plots (which is not inconsistent with the zero of the vertical axis). The analysis is less satisfactory for the particular curve used in Fig. 3 representing endothelial cells.

FIGURE 4.

A force profile for an untreated endothelial cell is presented to illustrate the method of measuring the size of the membrane reservoir. The schematics on the top illustrate the state of the experiment at points A, B, and C along the retraction curve. A, B, and C correspond, respectively, to points with three tethers attached (L = 3 × 2.6 = 7.8 μm), two tethers attached (L = 2 × 3.6 = 7.2 μm), and one tether attached (L = 7.2 μm). Here, L stands for the total length of all simultaneously pulled tethers.

Experiments in which the chemical nature of the cantilever surface was changed were conducted to clarify that the tether force is independent of the nature of the attachment. AFM tips coated with poly-L-lysine or collagen were used to extract tethers from CHO cells and no significant differences were found in tether force (26 ± 7 pN and 29 ± 7 pN, respectively; compare with 28 ± 10 pN, for untreated cantilever; see Table 1). These results are consistent with earlier observations that tether growth, once underway, does not depend on the chemical nature of the attachment of tethers to the force transducer (54).

TABLE 1.

Summary of all tether force measurements performed in this study

		Latrunculin A treatment				Hyaluronidase 500 IU/ml
	Control	0.1 μM	0.2 μM	0.5 μM	1 μM
Endothelial cells	29 ± 10	28 ± 8	17 ± 6	15 ± 6	15 ± 8	21 ± 10
HB cells	29 ± 9	22 ± 13	15 ± 10	17 ± 6	15 ± 8	19 ± 7
CHO cells	28 ± 10	21 ± 4	16 ± 5	16 ± 7	14 ± 5	19 ± 6

Values for the forces are given in pN.

Histograms of tether forces measured between distinct plateaus for untreated CHO, HB, and endothelial cells are presented in Fig. 5 (upper row). In all histograms, a Gaussian fit was used to identify the average force needed to pull a single tether. At the pulling rate used (3 μm/s), the tether forces did not show significant variation among CHO cells (28 ± 10 pN), HB cells (29 ± 9 pN), and endothelial cells (29 ± 10 pN). These results suggest that small differences in membrane composition, surely present across the three strongly differing cell lines, do not significantly affect the magnitude of the tether force. Differences in membrane composition could affect the initiation force. In addition, they provide further support for the ubiquitous character of tether formation resulting from local external forces acting on cells, and suggest that multiple tether formation may represent an important mechanism for cell attachment. The rather broad distribution of the forces (ΔF) observed in our histograms results from the heterogeneity in the properties of the membrane across the cell surface. This heterogeneity could be, in part, the consequence of the varying association of the cytoskeleton and the glycocalyx with the membrane.

FIGURE 5.

Single-tether force distributions for untreated and treated cells. Note the narrowing of these distributions upon LATA or hyaluronidase treatment. Results shown are for 1 μM LATA and 500 IU/ml hyaluronidase concentrations.

Role of membrane-associated macromolecules

Treatment of cells with latrunculin A (LATA) is well known to disrupt the actin cytoskeleton in a concentration-dependent manner and leads to significant changes in overall morphology (48,49,55). In particular, transmembrane proteins (e.g., cadherins, integrins) lose their attachment to F-actin (56,57). Thus, LATA treatment results in the concentration-dependent decoupling of the actin cytoskeleton from the plasma membrane. In our experiments, this effect is evident from the rounding of the cells and is manifest in the 50% reduced magnitude (for 1 μM LATA concentration) of the observed tether forces for all cell types (Fig. 5, middle row). More interestingly, a noticeable narrowing of the force distribution is observed in the histograms. The changes in width obtained from the standard deviation of Gaussian fits were found to be 4, 2, and 10 pN for endothelial, HB, and CHO cells, respectively. This narrowing could be a direct consequence of the LATA-induced homogenization of membrane properties over the surface of the cell. LATA treatment reached its maximal effect at ∼0.2 μM (see Table 1)—a value in good agreement with the previously reported in vitro F-actin/LATA equilibrium dissociation constant, K_d = 0.2 μM (50).

The glycocalyx backbone hyaluronan of CHO, HB, and endothelial cells was disrupted by treatment with hyaluronidase. Hyaluronidase cleaves hyaluronan into disaccharides, which, in the present context, is equivalent to digesting part of the glycocalyx (51). The tether force measured after hyaluronidase treatment was ∼30% lower than for untreated cells (Fig. 5, bottom row and Table 1). As with the experiments using LATA, one again observes a narrowing in the force distribution (at least for the HB and CHO cells, with the respective changes in width of 4 and 8 pN; for the endothelial cells, the width remained unchanged), suggesting that the glycocalyx also contributes to the heterogeneity of plasma membrane properties. Overall, these findings show the importance of the macromolecular networks on both the intra- and extracellular sides of the cell membrane in the biomechanical integrity of the cell.

DISCUSSION

Formation of a tether requires large changes in membrane curvature. The associated energy cost depends on the biomechanical properties (i.e., bending rigidity, effective surface tension (58,59)) of the bilayer, as well as its association with the cytoskeleton and glycocalyx. AFM provides an alternative means to directly probe these properties through multiple tether extraction and pulling studies. Among the three cell lines used in our experiments, at the applied pulling rate, no major variation in single tether forces was found, implying that specific local cell membrane characteristics in these three cell types do not influence the growth of tethers. This finding also suggests that multiple tether formation is a ubiquitous phenomenon that can be initiated by nonspecific binding between a cell and its environment (e.g., other cells), and it is primarily a property of the plasma membrane itself that may be utilized in vastly differing circumstances.

Our measured values of tether forces are in good agreement with previously published data ranging from 10 to 60 pN for a variety of immobilized cells. Tether forces similar to those reported here have been measured at comparable pulling rates for fibroblasts (16), melanoma cell lines (18), neuronal growth cone membranes (24), and red blood cells (21). In contrast to previous studies using optical traps and micropipette aspiration that have the ability to extract individual tethers, with the AFM cantilever we simultaneously extracted multiple tethers, but retained the sensitivity to detect the loss of individual tethers as the membrane reservoir was gradually depleted. Initiation of multiple tether extraction requires overcoming a large initial potential barrier visible in the force profiles in Fig. 3. The force required to overcome the initial adhesion is typically larger than the maximum force that can be attained using optical traps or micropipette aspiration. One must therefore be careful how much surface area contacts the cell when using these techniques to ensure that the number of tethers extracted does not exceed the limiting forces. Attainment of the forces necessary to initiate extraction of multiple tethers is possible with the AFM.

The observation of discrete force steps in our experiments raises the question of the origin of these rupturelike events. First, tethers could snap along their length. However, this would require overcoming close-to-lytic membrane tensions and, correspondingly, as experiments (15) and theory (60) indicate, forces of ∼100 pN, considerably higher than our measured values. Second, it has been suggested that heterogeneities within the membrane could locally decrease its tension and lead to tether fission (61). This effect is expected to be cell-type-dependent and thus not likely to act in our experiments, in which no significant differences in tether force were observed. Third, theory suggests that multiple tethers extracted locally from the membrane reservoir in synthetic vesicles could fuse, but that pinning forces may prevent fusion (31). The glycocalyx and the cytoskeleton, absent in synthetic vesicles, provide ample possibilities for local pinning, thus fusion of tethers in living cells is highly regulated by these structures. Since in our experiments at least one of these macromolecular networks is always intact, the probability for fusion should be quite low. Experimental confirmation of tether fusion in synthetic vesicles has recently been provided (62). They showed that as fusion proceeds, a sudden change, similar to the discontinuities in Fig. 3, occurs in the components of the pulling force. The components parallel and perpendicular to the axis of the fused tethers respectively decrease and increase abruptly, while the overall force remains constant (for a given membrane tension). Interestingly, these results also strongly suggest that, in our experiments, tethers do not fuse. Fusion of tethers takes time. In the experiments of Cuvelier et al. (62), under static conditions (no pulling force exerted) the velocity of fusion was found to be ∼80 μm/s, and thus the time for two tethers to fuse along a 12-μm section to be 150 ms. Fusion in living cells, if it takes place, should be considerably slower due to heterogeneities in the membrane. However, as results in Fig. 3 show, force-steps occur much faster at comparable tether length. In fact, with the time-resolution of our device (<10 ms), we can estimate the time of a force-step to be an order-of-magnitude less than the time needed for fusion. Finally, tethers can detach from the cantilever. Considering that we do not reach the force necessary for tether rupture, and our force-steps occur on a timescale inconsistent with the fusion of tethers, we can assume that the force-steps result from detachment of the tethers from the cantilever.

As we pull groups of tethers with the AFM cantilever, they typically break off one by one. The extended membrane is then reincorporated into the membrane reservoir and the process continues until all of the tethers are released. The rigidity of the plasma membrane, conferred through the properties of its intrinsic components and peripherally associated macromolecules, defines the limits of the reservoir available to form tethers. This aspect is best illustrated by the measurement of the extent of the membrane reservoir as shown in Fig. 4. When measured within an individual force elongation profile, the size of the membrane reservoir probed was found to be approximately constant for each rupture event between consecutive plateaus. This result suggests that, when probed locally with an AFM tip, multiple simultaneously extracted membrane tethers are equally coupled to the membrane reservoir of the cell.

Previous studies demonstrated that tether properties depend on both actin microfilaments and microtubules—major components of the cytoskeleton (16). Our results support these earlier findings. Indeed, we observed an ∼50% decrease in tether force after the inhibition of actin polymerization, indicating that cytoskeletal integrity is crucial in the regulation of the membrane's biomechanical characteristics. In contrast to the rather well-established function of the intracellular cortical cytoskeleton in the biomechanical role of the cell membrane, relatively little is known about the role of the proteoglycan complexes covering the extracellular surface of the phospholipid bilayer. Our finding of a 30% decrease in single tether force due to the disruption of the glycocalyx highlights the importance of glycosaminoglycans on the mechanical properties of the lipid bilayer. Hence the hyaluronan backbone of the glycocalyx has a distinct effect on the mechanical properties of the plasma membrane in intact cells (51).

Multiple tethers are manifest in AFM pulling experiments as plateaus separated by well-defined steps in the force profile. In this study, we evaluated the force required to pull individual tethers directly from the measurement of these force steps. Therefore, each force histogram presented in Fig. 5 represents an ensemble of measurements performed at many different positions on many cells. It is expected that, over the entire cell surface, heterogeneity exists in the coupling between the glycocalyx, cytoskeleton, and the membrane. Although the change in the peak values in the histograms after the two treatments is a specific measure of the coupling between the membrane and its peripheral macromolecular networks, the heterogeneity of the coupling is manifest through the broad distribution in the histograms for the nontreated cells. The marked narrowing of the histograms in LATA- and hyaluronidase-treated cells illustrates the reduction of this heterogeneity achieved through disruption of the cytoskeleton and glycocalyx.

It has been shown that as a first approximation, the total force, F_t, necessary to extract a tether, can be considered to be the sum of all macromolecular contributions (18). Following this approach, F_t can be expressed in terms of the individual contributions due to the association between the cytoskeleton and the membrane (F_c/m), the coupling between the glycocalyx and the membrane (F_g/m), and the force to pull a tether composed of a pure cellular membrane (F_m):

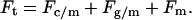(1)

In our study, the contributions of the cytoskeleton and the glycocalyx were measured by selectively disrupting these macromolecular networks. The difference between the tether forces measured on intact cells (F_t) and on cells depleted of their cytoskeleton or glycocalyx could provide an estimate for F_c/m and F_g/m, respectively. Our experiments with the endothelial, HB, and CHO cells (untreated, 1 μM LATA-, and 500 IU/ml hyaluronidase-treated) allow us to calculate F_m values of 7 pN, 5 pN, and 5 pN, respectively. These values are obtained from Eq. 1, by assuming that LATA and hyaluronidase treatments results, respectively, in F_c/m = 0 and F_g/m = 0. An experiment in which cells are treated with both LATA and hyaluronidase (i.e., F_t ≈ F_m) could have allowed us to simultaneously eliminate the glycocalyx and the cytoskeletal contributions. However, it was not possible to perform such an experiment due to extensive desorption of the cells from the surface. Nevertheless, our calculated estimate for the F_m component in the total tether force is in good agreement with the experimental value of 8 pN measured for a phospholipid membrane decoupled from the cytoskeleton (18), and the theoretical value of 13 pN for a pure phospholipid vesicle (31).

Based on these findings, we propose that any cellular process that significantly affects the molecular networks interacting with the phospholipid bilayer influences its effective mechanical properties, and that this effect can be measured using atomic force microscopy. Furthermore, our results indicate that living cells can maintain multiple tethers. Local compositional modifications in the plasma membrane, as well as its association with the cytoskeleton and glycocalyx, through heterogeneities, can prevent the fusion of these coexisting nanotubes and thus control their number. This may provide living cells with an additional mechanism to regulate their adhesive properties.