Abstract
Slow waves are rhythmic depolarizations that underlie mechanical activity of many smooth muscles. Slow waves result through rhythmic Ca2+ release from intracellular Ca2+ stores through inositol 1,4,5-trisphosphate (IP3) sensitive receptors and Ca2+-induced Ca2+ release. Ca2+ oscillations are transformed into membrane depolarizations by generation of a Ca2+-activated inward current. Importantly, the store Ca2+ oscillations that underlie slow waves are entrained across many cells over large distances. It has been shown that IP3 receptor-mediated Ca2+ release is enhanced by membrane depolarization. Previous studies have implicated diffusion of Ca2+ or the second messenger IP3 across gap junctions in synchronization of Ca2+ oscillations. In this study, a novel mechanism of Ca2+ store entrainment through depolarization-induced IP3 receptor-mediated Ca2+ release is investigated. This mechanism is significantly different from chemical coupling-based mechanisms, as membrane potential has a coupling effect over distances several orders of magnitude greater than either diffusion of Ca2+ or IP3 through gap junctions. It is shown that electrical coupling acting through voltage-dependent modulation of store Ca2+ release is able to synchronize oscillations of cells even when cells are widely separated and have different intrinsic frequencies of oscillation.
INTRODUCTION
The mechanical activity of many smooth muscles is controlled by a cyclical depolarization known as slow waves (1–3). Slow waves result through rhythmic Ca2+ release from intracellular Ca2+ stores through inositol 1,4,5-trisphosphate (IP3) sensitive receptors and Ca2+-induced Ca2+ release (4–8). Ca2+ oscillations are transformed into membrane depolarizations by generation of a Ca2+-activated inward current (9–11). Importantly, the store Ca2+ oscillations that underlie slow waves are entrained across many cells over large distances (12,13). It has been shown that IP3 receptor-mediated Ca2+ release is enhanced by membrane depolarization (6,7), and it is this positive feedback that underlies the long-range entrainment of Ca2+ stores (12). This study examines the mechanisms underlying such store entrainment.
Entrainment of Ca2+ oscillations and wave propagation have been shown to occur through two pathways; one by means of diffusion of cytoplasmic messengers through gap junctions, and the other through paracrine messengers diffusing in the extracellular space. This study relates to the former mechanism and is relevant to systems where blockade of gap junctions leads to disruption of the Ca2+ signal (12,14). In the gap junction-connected class of models, diffusion of Ca2+ (15–20) or the second messenger IP3 (21) across gap junctions has been implicated in synchronization of Ca2+ oscillations. In a recent work, Tsaneva-Atanasova et al. (20) have shown that coupling through diffusion of Ca2+ is facilitated by diffusion of IP3. In our study, a novel mechanism of Ca2+ store entrainment through depolarization-induced IP3 receptor-mediated Ca2+ release (12) is investigated. This mechanism is significantly different from the chemical coupling-based class of models, as membrane potential has a coupling effect over distances many orders of magnitude greater than either diffusion of Ca2+ or IP3 through gap junctions.
The coupling scheme presented in (12) and investigated here is based on the following experimental observations:
The cyclical release of Ca2+ from intracellular stores occurs in response to IP3 and Ca2+ in the cytosol (4–9,12,22). This excitability of the cytosolic-store Ca2+ system is enhanced by IP3 and Ca2+.
Ca2+ oscillations in the cytosol are transformed into membrane-potential oscillations due to a Ca2+-activated inward current (9–11).
Membrane potential modulates Ca2+ release from intracellular Ca2+ stores (6,7). This can occur by the following means: a), A positive feedback of membrane potential on the synthesis of IP3 (23,24). b), Voltage-dependent Ca2+ influx into the cytosol (e.g., through L-Ca2+ channels). i), Since Ca2+ release from intracellular stores is enhanced by Ca2+ (i.e., Ca2+-induced Ca2+ release), membrane depolarization enhances release of Ca2+ from stores. ii), In some cell types Ca2+ has been shown to have a positive feedback on IP3 synthesis (25,26). Thus, membrane potential can enhance release of Ca2+ from stores utilizing this pathway.
Cells connected by gap junctions can interact through current flow and modulate the membrane potential of other cells within the network (2,27,28).
The range of diffusion of Ca2+ or IP3 across gap junctions is in the order of microns (29), whereas the electrical length constant is in the range of millimeters (see (12)).
The experimental observations predicate that electrically coupled cells can interact and modulate Ca2+ excitability and oscillations of other cells through voltage-dependent enhancement of store Ca2+ release through one or more of the pathways given above. We encapsulate this in a generic model, Fig. 1, as a system of coupled oscillators where: 1), each local oscillator is composed of a cytosolic-store Ca2+ excitable system; 2), local Ca2+ oscillations are coupled to membrane potential; and, 3), membrane potential influences the local Ca2+ oscillator through a positive feedback loop. In a previous study (30), a theoretical model was presented to elucidate the role of voltage-dependent IP3 synthesis in the generation of slow waves in an isopotential system. In our work here, we construct a coupled system of cells according to the general schema outlined above (Fig. 1) using our previously presented single-cell model (30). Here we use the specific case of voltage-dependent IP3 synthesis to model the positive feedback of membrane potential on cytosolic-store excitability (slow waves).
FIGURE 1.
A general schematic representation of the two cell system. Each cell is a local oscillator composed of a cytosolic-store Ca2+ excitable system. The cytosolic Ca2+ of each oscillator is transformed into membrane potential (V) oscillations by a Ca2+-acitvated inward current. The membrane potentials of the cells are strongly linked. Each local oscillator is weakly linked to the membrane potential by a voltage-dependent feedback loop such as voltage-dependent IP3 synthesis or voltage-dependent Ca2+ influx. A specific implementation of this general system is given in the Appendix and Fig. 16.
The understanding of global calcium signaling is facilitated by studying the dynamical properties of simple networks of coupled calcium oscillators (15). A small number of such studies has been conducted (15,16,19,20,31,32). Here we use a two-cell network to understand how voltage-dependent modulation of store Ca2+ release can synchronize Ca2+ oscillations and thus act as a signaling mechanism.
The theoretical study presented confirms that voltage-dependent modulation of store Ca2+ release is an effective signaling mechanism. This mechanism could be significant in excitable (6,7,23,33,34) and nonexcitable (35–37) systems where voltage-dependent IP3 synthesis is likely to exist. The results of this article provide a basis for further study of synchronization and waves in cellular systems where voltage-dependent modulation of store Ca2+ release exists and acts as a coupling mechanism.
We begin with the study of cell pairs that are connected by strong electrical connection only (no chemical coupling). We show that an electrically connected homogenous cell pair (i.e., both cells have the same properties) displays a variety of dynamical interactions, some of which are counterintuitive. A homogenous cell pair can display in-phase oscillations (0° phase difference), phase-locked oscillations (phase difference >0°), anti-phase oscillations (180° phase difference), and bistable (in-phase and anti-phase) oscillations. These dynamical features depend on the strength of stimulation. Then, a more realistic heterogeneous cell pair system is investigated, where the sensitivity of the intracellular store receptor to IP3 is used as a heterogeneity parameter. Cells in biological tissues will differ in dynamical properties, i.e., have different intrinsic frequencies. Therefore, the study of a heterogeneous cell pair system is highly relevant to the understanding of cellular systems. An electrically connected heterogeneous pair of cells can display phase-locked, phase-trapped (oscillating phase difference), n/m phase-locked, period-doubling, and quasiperiodic oscillations. Once again, these dynamical features depend on the strength of stimulation.
Next, the effect of electrical coupling strength on synchronization of heterogeneous cell pair is studied. It is shown that weak electrical coupling is sufficient to synchronize even heterogeneous cell pairs. Finally, a comparison is made between electrical and chemical coupling (through diffusion of Ca2+ or IP3). It is shown that chemical coupling is not effective when cells are weakly coupled and have different intrinsic frequencies. The results of this study show that electrical coupling acting through voltage-dependent modulation of store Ca2+ release is able to synchronize oscillations of cells even when cells are weakly coupled (or widely separated) and have different intrinsic frequencies of oscillation.
NUMERICAL METHODS
Bifurcation analysis was carried out using AUTO (38) included in the numerical package XPPAUT (39). Schematic bifurcation diagrams, which were based on the bifurcation analysis, are presented in the text. Numerical simulation and analysis were performed using MATLAB (The MathWorks, Natick, MA) and XPPAUT.
MODEL
The model system is composed of two cells that are gap junction connected. Dynamics of each cell involves interaction between four state variables; cytosolic Ca2+ concentration ([Ca2+]c) Z, intracellular store Ca2+ concentration ([Ca2+]s) Y, cytosolic IP3 concentration ([IP3]c) P, and membrane potential V. The essential features of this model are summarized in Fig. 1. Each cell has a local cytosolic-store Ca2+ excitable system, which is transformed into membrane-potential oscillations through a Ca2+-activated inward current. The excitability and oscillatory behavior of the cytosolic-store Ca2+ excitable system depends upon [IP3]c and sensitivity of the store-receptor to IP3 (denoted by σ). A positive feedback of membrane potential on local cytosolic-store Ca2+ excitability is implemented here through a voltage-dependent IP3 synthesis, although other mechanisms are possible as discussed earlier. Thus, [IP3]c depends on membrane potential and external stimulus. These relationships can be summarized as follows:
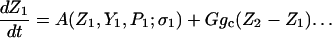 |
(1) |
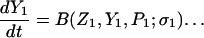 |
(2) |
 |
(3) |
 |
(4) |
where subscripts 1 and 2 denote the two cells. The last terms in Eqs. 1, 3, and 4 are the coupling terms. Here we assume simple linear symmetrical coupling through gap junctions. Electrical coupling between the cells is given by the last term in Eq. 3, where gV is the gap junction conductance. Chemical coupling between cells occurs through diffusion of Ca2+ and IP3 with diffusion coefficients gc and gP, respectively. The term G is used as a unitless quantity to denote the strength of coupling between cells. It is used as a parameter to study the effect of spatial separation and strength of coupling between cells. When G = 0, cells are uncoupled or separated by very large spatial distances, and when G = 1, cells are strongly coupled so that their membrane potentials are the same.
We use our previous experimentally derived model of an isopotential cell (30) to represent the dynamics of a single cell in the model presented here. A brief summary and parameter values for the single-cell model is given in the Appendix.
RESULTS
Response of single oscillator to current pulses: phase-response curve
The response of a single uncoupled cell to current injection provides insight into the interaction of the coupled cell pair. When a current pulse is injected into a single cell, it alters the dynamics of the cell through voltage-dependent IP3 synthesis (Fig. 2). A small perturbation in the membrane potential of a cell results in delayed or advanced appearance of the next Ca2+ peak, but causes no change in the future dynamics of the cell. In such a case, the perturbation is said to have advanced or delayed the phase of the cell. For example, a depolarizing pulse (marked in Fig. 2 A with a “++” symbol), causes an increase in [IP3]c (marked with double asterisks in Fig. 2 B), and results in an early appearance of the next Ca2+ peak (Fig. 2 C, thin dashed line). However, a depolarizing pulse (marked in Fig. 2 A with a “+” symbol) can also cause delayed appearance of the next Ca2+ peak depending on the timing of the pulse (Fig. 2 C, (thick dashed line). Similarly, a hyperpolarizing pulse can cause an early (not shown) or delayed appearance of the next Ca2+ peak (thin solid line). Thus, a current pulse of either polarity can delay or advance the appearance of the next Ca2+ peak depending on the timing of the pulse. A plot of change in phase (Δφ) versus timing (tp) of injected pulse with respect to period of oscillation (T) is known as a phase-response curve (PRC). Fig. 2, D and E, show PRCs generated by injecting +15 mA and −15 mA current pulses, respectively, into an uncoupled cell. A single cycle of Ca2+ oscillation is shown above the PRCs for timing reference (upper curve labeled Z). Fig. 2 D shows that depolarizing pulses injected at times tp < 0.5 T (approximately) delay the next pulse; thus the PRC is negative, and the opposite is true for tp > 0.5 T (approximately). Similarly, Fig. 2 E shows that almost no change in phase occurs for hyperpolarizing pulses applied at time tp < 0.5 T (approximately), whereas phase is delayed for 0.5 T < tp < 0.95 T (approximately). Thus the PRCs show that a depolarizing pulse is more effective in advancing, whereas a hyperpolarizing pulse is more effective in delaying the phase of the oscillator.
FIGURE 2.
Response of a single cell to current injection. (A) Unperturbed membrane potential of a single cell (thick line), and when a 15 mA depolarizing (dashed line) or hyperpolarizing (thin line) current pulse is injected into the cell. Another 15 mA depolarizing pulse applied before t = T/2 is given by thick dashed lines. (B) Corresponding oscillations in [IP3]c. Single plus symbol in A marks the depolarizing pulse applied before t = T/2, which caused an increase in [IP3]c marked by the single asterisks. The double plus and asterisks symbols mark the time where the depolarizing or hyperpolarizing current pulses are injected and cause corresponding increase and decrease in [IP3]c, respectively. (C) Corresponding oscillations in [Ca2+]c. Note the early and delayed appearance of the Ca2+ peaks in response to depolarizing and hyperpolarizing current injections, respectively. (D) Phase-response curve (PRC) where the input is a +15 mA current pulse. (E) PRC same as D but for −15 mA current pulse injections. Shown above the PRCs are one cycle of normalized Ca2+ oscillation for relative location of pulse timing (tp).
Coupling through voltage-dependent IP3 synthesis
A homogenous cell pair consisting of two identical cells (with IP3 sensitivities σ1 = σ2 = 3.5 μM) is studied to elucidate the mechanism of interaction between the coupled cells. The cells are strongly connected with a gap junction that only allows flow of current but not Ca2+ or IP3 (G = 1, gV = 400 mS, gc = 0 min−1, gP = 0 min−1). Both cells are stimulated with the same level of stimulus (β = 0.2 μM). Cells in the coupled system interact through voltage-dependent IP3 synthesis (Fig. 3). Initially, the cells are not connected through the gap junction and oscillate separately out of phase (Fig. 3 A). At t = 50 min, gap junctional connectivity is enabled. Now as the leading cell (cell 1) releases Ca2+ and depolarizes, it causes a depolarization in cell 2 (marked with an asterisk in Fig. 3 B) due to current flow into cell 2 through the gap junction (Fig. 3 C). The cell 1-induced depolarization in cell 2 induces synthesis of IP3, and now [IP3]c in cell 2 begins to rise, but with a delay arising from the time it takes for IP3 to be produced (upward arrowhead in Fig. 3 D). Eventually, this causes cell 2 to release Ca2+ (marked with downward arrowhead in Fig. 3 A). The net result of the interaction is that cell 2 has released Ca2+ earlier than it would have if uncoupled (i.e., its phase has been advanced). Thus cell 1 has advanced the phase of cell 2 acting through voltage-dependent IP3 synthesis. Therefore, by this means, a cell can influence cytosolic-store Ca2+ excitability and the oscillatory phase of an electrically connected cell through voltage-dependent IP3 synthesis. The outcome of the interaction is governed by the PRC as discussed below.
FIGURE 3.
Interaction between two cells through voltage-dependent IP3 synthesis. Initially, the two uncoupled cells oscillated out of phase. When they were coupled at time 50 min, Ca2+ release (A) in cell 1 (solid line) caused membrane depolarization in cell 1 (B). This depolarization in cell 1 caused an electrotonic depolarization in cell 2 (asterisk) due to current flow into cell 2 through gap junction (C). The depolarization induced in cell 2 caused an increase in [IP3]c of cell 2 (upward arrowhead in panel D), which caused cell 2 to release Ca2+ marked by downward arrowhead in panel A. Vertical bars indicate time when cells were coupled. β = 0.2 μM.
When coupling was enabled at t = 50 min, cell 2 was past its T/2 cycle (Fig. 3 A). Therefore, as predicted from the PRC (Fig. 2 D), the depolarization induced in cell 2 (by cell 1) will cause its phase to advance significantly. Similarly, cell 1 experiences current drain past 0.6 T of its cycle due to coupling, and hence its phase will be slightly delayed as predicted by the PRC (Fig. 2 E). An examination of Fig. 4 shows that this is indeed the case. The subsequent oscillations (Fig. 4 A) are such that cell 1 (solid line) continues to experience decreasing phase delays whereas the phase of cell 2 is advanced by decreasing amounts (Fig. 4 B). The net result is reduction of phase difference between the two oscillators at each cycle (Fig. 4 C), and eventually both oscillators synchronize and oscillate with a zero phase difference (Δφ = 0) (Fig. 4 A). Note that although the membrane potential of the cells is strongly coupled, the interaction between the cells is limited. This is because of the relatively weak link between the cytosolic-store excitability and membrane potential of each cell through voltage-dependent IP3 synthesis. Therefore, phase compression occurs over multiple cycles before the coupled system settles into a steady synchronized state. The weak interaction between the cells due to voltage-dependent enhancement of store Ca2+ release suggests that the two cells may be interacting as a system of weakly coupled oscillators. Some results on coupled oscillators (40,41) are available based on averaging theory, and now we use that to predict the behavior of the two coupled cells.
FIGURE 4.
In-phase oscillations of the homogenous cell pair. (A) [Ca2+]c of the homogenous cell pair initially oscillated out of phase, but when gap junction coupled they synchronized and oscillated in-phase (Δφ = 0). (B) Period of the two cells. Upon coupling, the period of one cell increased whereas that of the other decreased, and finally both cells reach same period which was equal to the uncoupled period. Lower panel shows expanded view of the upper panel. Circles are period of cell 2. (C) Phase difference between the two cells. Arrows indicate time when coupling was enabled. β = 0.2 μM.
Weakly coupled oscillators
Averaging theory of weakly coupled oscillators
When the influence of coupling between oscillators is weak compared to the limit cycle attraction, the dynamics of the coupled system can be reduced to a system of coupled phase oscillators (40,41). A brief summary of the reduction to coupled-phase oscillators is given below.
Let Zi(t) denote the T periodic Ca2+ oscillation of an uncoupled oscillator i within the stimulus domain βH1 < β < βH2 (see below). This periodic Ca2+ oscillation can be represented as a function of phase θi as Z(θi). Given the weak coupling, the coupled system can be represented by a system of coupled phase oscillators,
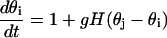 |
 |
where g is a weak coupling and H is a T-periodic interaction function that depends on the nature of coupling and the uncoupled limit cycle. Here this function is computed numerically using xppaut.
Let the phase difference be φ(t) = θj(t) − θi(t). Then phase-locked solutions exist when phase difference between the oscillators is constant, i.e., dφ(t)/dt = 0. For symmetrical coupling, the equation reduces to
 |
where Hodd is the odd part of the interaction function H. The even parts of H cancel due to symmetry. Thus stable phase-locked solutions are those where Hodd is zero with a slope >0.
Weak-coupling analysis
We use the results of the theory of weakly coupled oscillators to predict synchrony of the two electrically coupled identical oscillators. Three modes of stable synchrony are predicted depending on the stimulus β. A schematic bifurcation diagram of the coupled phase oscillators with respect to stimulus β, given in Fig. 5 A, summarizes the response of the system within the oscillatory stimulus domain βH1 < β < βH2.
FIGURE 5.
Weak-coupling analysis of the homogenous cell pair. (A) A schematic bifurcation diagram of the coupled phase oscillators with respect to stimulus β summarizes the response of the system within the oscillatory stimulus domain βH1 < β < βH2. (B) For low levels of stimulation β, the odd part of the interaction function (Hodd) has stable steady states for synchronous 0 phase difference (in-phase) oscillations. (C) At a critical value of β, new fixed points of Hodd appear that lie between 0 and T/2, indicating phase-locked oscillations. (D) At a critical level of stimulus, phase-locked steady states merge and become stable at T/2 so that cells now oscillate exactly half a cycle out of phase (anti-phase). Stimulus: for panels B, C, and D, β = 0.2, 1.1, and 1.4 μM, respectively.
For low levels of stimulation β, but within the oscillatory domain (βH1 < β < βH2), the odd part of the interaction function (Hodd) has stable steady states for synchronous 0 phase difference (in-phase) oscillations (Fig. 5 B). The in-phase steady state continues to be stable with increasing stimulus β. But at a critical value of β, new fixed points of Hodd appear, which lie between 0 and T/2 (Fig. 5 C). Simultaneously, the in-phase fixed point loses stability, which is gained by the new fixed points. This indicates that in-phase oscillations are no longer stable, but instead oscillations with phase difference 0 < Δφ < T/2 (phase-locked) become stable. Phase-locked steady states of the Hodd continue to exist with further increase in stimulus but approach the point T/2. This indicates that the phase-locked oscillations approach toward a half cycle out of phase state. At a critical level of stimulus, phase-locked steady states merge and become stable at T/2 (Fig. 5 D). This means that cells now oscillate exactly half a cycle out of phase (anti-phase).
The above weak-coupling analysis shows that synchrony in the full model would depend on the frequency of oscillations as determined by the stimulus β. As frequency of oscillations increase, the interaction function changes shape so that in-phase, phase-locked, and finally anti-phase oscillations occur in the coupled system. Thus, with increasing frequency, synchrony becomes less stable. This also predicts that synchrony will be more sensitive to differences in the intrinsic frequencies of the coupled cells at higher levels of stimulus β (i.e., at higher frequencies). We now proceed to the study of the full system and see if the predictions of the weakly coupled phase oscillator model hold.
Effect of stimulation on synchronization
The dynamics and synchronization properties of the coupled system change at different levels of stimulation. The dynamical features of the system in response to the whole range of stimulus strength were studied using bifurcation analysis of the full system. A schematic one-parameter bifurcation diagram of [Ca2+]c with β as the bifurcation parameter summarizes the dynamics of the coupled system with changing stimulus (Fig. 6). The solid traces in Fig. 6 give the maximum and minimum values of [Ca2+]c for both cells for each value of the stimulus β. The original one-cell system was oscillatory only within a specific range of stimulus strength (β). These oscillations appeared and disappeared through two Hopf points (see Figs. 2 D and 3 B in Imtiaz et al. (30)). Now, the coupled system has four Hopf points. Two of these Hopf points, HS1 and HS2, are the synchronous Hopf points. The other two Hopf points, HA1 and HA2, are the asynchronous Hopf points. The system is in stable steady state before HS1 and after HA2. This means that the coupled cells are oscillatory only if stimulus strength is between HS1 and HA2.
FIGURE 6.
Schematic one-parameter bifurcation diagram of [Ca2+]c (Z) with stimulus (β) as the bifurcation parameter for the homogenous cell pair. The coupled system has four Hopf points. Two of these Hopf points, HS1 and HS2, are the synchronous Hopf points. The other two Hopf points, HA1 and HA2, are the asynchronous Hopf points. The system is in stable steady state before HS1 and after HA2. Stable and unstable branches are shown in solid and dotted lines, respectively. See text for further details.
The coupled cells display three basic types of synchronization modes (Fig. 6, solid lines) depending on the strength of applied stimulus (β); 1), in-phase, 2), phase-locked, and 3), anti-phase oscillations. Some other dynamical features such as period doubling branches bifurcations (PD1 and PD2 in Fig. 6) are also present, but their range is very small and therefore they will not be considered any further. The above given dynamical features will now be discussed in detail.
In-phase oscillations
Oscillations are in-phase when oscillations occur with a zero phase difference (Δφ = 0). In-phase oscillations occur on the branch s1 (Fig. 6). Increasing stimulus within the range of s1 increases the frequency of oscillations, but the coupled cells continue to oscillate in-phase. The case analyzed in the previous section (Fig. 4) is an example of in-phase oscillation. The frequency of the coupled system on this branch is the same as that of the uncoupled system (Fig. 4 B).
Phase-locked oscillations
Oscillations are said to be phase-locked if they occur with a constant phase difference Δφ > 0. Phase-locked oscillations occur when the coupled system is on branch b (Fig. 6). An example of phase-locked oscillations is given in Fig. 7 A. Initial conditions were chosen such that uncoupled cells oscillated with a large phase difference (upper panel). At t = 50 min, cells were gap junction coupled. After a transient change in dynamics, cells oscillated with a constant phase difference (Δφ > 0), i.e., oscillations became phase-locked (Fig. 7 A, lower panel). Uncoupled cells oscillated with equal amplitude of Ca2+ release, but when coupled, the amplitude of Ca2+ oscillations in the two cells differed by a small fixed value. Cells in the coupled system oscillated at a frequency slightly higher compared to the uncoupled system. The system reached steady phase-locked oscillations in ∼350 min. The final phase difference between cells was ∼0.2 T and remained constant (Fig. 7 B). When stimulus was increased further, so that the system remained on branch b, the frequency of the coupled system increased but cells remain phase-locked.
FIGURE 7.
Phase-locked and anti-phase oscillations of the homogenous cell pair. (A) When uncoupled, the cell pair oscillated out of phase (upper panel), but when coupled, oscillated with a fixed-phase difference >0 (lower panel). (B) Plot of the phase difference between cells in panel A. (C) An example of anti-phase oscillations. Ca2+ oscillations of the cells before (upper panel) and after coupling (lower panel). (D) A plot of the phase difference between cells in panel C. β = 1.1 μM for panels A and B. β = 1.4 μM for panels A and B.
Anti-phase oscillations
Oscillations are said to be anti-phase if they occur with a constant phase difference of 0.5 T, i.e., half a cycle out of phase. Anti-phase oscillations occur when the coupled system is on branch a2 (Fig. 6). An example of anti-phase oscillations is given in Fig. 7 C. Initial conditions were chosen such that uncoupled cells oscillated with a small phase difference (upper panel). At t = 50 min, cells were coupled through the gap junctions. However, despite being coupled when the phase difference between the cells was small, after a transient change in dynamics, cells oscillated with a 0.5 T phase difference, i.e., oscillations became anti-phase (lower panel). Uncoupled cells oscillated with equal amplitude of Ca2+ release. When coupled together, cells continued to oscillate with equal amplitude. However, the amplitude of the Ca2+ oscillations in the coupled system was lower than that of the uncoupled system. Cells in the coupled system oscillated at a higher frequency compared to the uncoupled system. The system reached steady anti-phase oscillations in ∼250 min. The final phase difference between cells was ∼0.5 T and remained constant (Fig. 7 D). When stimulus was increased further so that the system remained on branch a2, the frequency of the coupled system increased but cells remain anti-phase locked.
Bistable oscillations
Branch s3 represents in-phase oscillations. However, branches s3 and a2 (Fig. 6) coexist; therefore, when stimulus is in the range of branch s3, the system is in a periodic bistable state. Coupled cells will either oscillate with large amplitude anti-phase or small amplitude in-phase Ca2+ release. The system can be in one or the other state depending on initial conditions, and can be switched from one state to the other by perturbations (not shown).
The above analysis shows that cells coupled through current exchange can interact by modulating [IP3]c of a connected cell through voltage-dependent IP3 synthesis. This interaction leads to in-phase, phase-locked, anti-phase, and bistable synchronization of the identical coupled cell depending on the level of stimulation. Thus, the prediction of the reduced weakly coupled phase oscillators model is in agreement to the response of the full model. This further confirms that the interaction between the coupled oscillators through voltage-dependent enhancement of store Ca2+ release results in weak interaction.
Dynamics of a heterogeneous cell pair
Cells in biological systems display heterogeneity for different reasons, such as variation in receptor density or size, etc. The aim of this section is study a more realistic system composed of two heterogeneous cells. We begin the study with a cell pair with IP3 sensitivities σ1 = 0.35 μM (cell 1) and σ2 = 0.45 μM (cell 2). Once again, the cells are strongly connected with a gap junction that only allows flow of current but not Ca2+ or IP3 (G = 1, gV = 400 mS, gc = 0 min−1, gP = 0 min−1). Then we extend the results of this specific case by studying the effect of 1), heterogeneity (i.e., varying σ2 with respect to σ1), and 2), strength of gap junction coupling and spatial separation by varying coupling parameter G.
One-parameter bifurcation diagram
A schematic one-parameter bifurcation diagram of [Ca2+]c with respect to stimulus (β) summarizes the various dynamical features of this system (Fig. 8). Only the maximum oscillation points are given for the sake of clarity. Once again the coupled system has four Hopf points. Two of these (H11 and H12) belong to cell 1 and the other two (H21 and H22) to cell 2. Note that cell 1 is more sensitive to IP3, therefore the Hopf points for cell 1 lie to the left of the respective Hopf points of cell 2 (i.e., at lower values of stimulus β). The system is at stable steady state before cell 1 Hopf point 1 (H11) and after cell 2 Hopf point 2 (H22). Stable phase-locked oscillations arise in both cells simultaneously as branch P1 (P1 collectively refers to P11 and P12, where the subscripts denote cell number with which the branch is associated). Note that the amplitude of branch P1 is different for the two cells; cell 2 oscillates with a larger amplitude. Branch P1 changes into PT, where phase-trapped oscillations emerge. Once again, the amplitude of oscillations is different for the two cells on this branch. Branch PT changes to branch P2, where cells are no long oscillating with the same frequency. Branch P2 changes into PD, where period-doubling oscillations occur with different amplitudes. Branch Q is the branch of quasiperiodic oscillations. Branch Q changes to branch P3, where once again phase-trapped oscillations occur. Note that the membrane potentials of the two cells oscillate with equal amplitude, which is due to the large electrical coupling between the cells. However, the same dynamical features exist in membrane-potential bifurcation diagram (not shown). The above given synchronization states will be defined and discussed below.
FIGURE 8.
Schematic one-parameter bifurcation diagram of [Ca2+]c (Z) with stimulus (β) as the bifurcation parameter for a heterogeneous cell pair. The amplitude of [Ca2+]c of cell 1 and cell 2 is different. P1 = phase locked, P3 = PT = phase trapped, P2 = n/m phase locked, PD = period doubling, and Q = quasiperiodic oscillations. Hopf points H11 and H12 belong to cell 1, and the other two (H21 and H22) to cell 2. Subscripts on the branch labels indicate the cell number with which the branch is associated. See text for further details.
Phase-locked oscillations
Branch P1 emerges from the Hopf points through an unstable oscillatory branch (not shown). Ca2+ oscillations of the two cells are phase-locked on this branch, but cell 2 (Fig. 8, upper trace) shows larger amplitude Ca2+ peaks than cell 1. An example of phase-locked oscillations is given in Fig. 9. When uncoupled, cell 2 is nonoscillatory, whereas cell 1 is oscillatory (Fig. 9 A). However, when coupling is enabled, cell 2 also starts to oscillate and the amplitude of cell 1 Ca2+ oscillations decrease (Fig. 9 B). Both cells oscillate with the same frequency, which is higher than the uncoupled frequency of cell 1. The coupled cells remain phase-locked with a constant phase difference. The dynamics of the coupled system is governed by voltage-dependent IP3 synthesis as explained below.
FIGURE 9.
Mechanism of phase locking in the heterogeneous cell pair. [Ca2+]c plot of cell 1 and cell 2 before (A) and after (B) coupling. [Ca2+]c (C) and [IP3]c (E) for the two cells when coupled and oscillating in a phase-locked state. Note that [IP3]c for both cells have the same kinetics as the membrane potential of the two cells (D) due to large electrical coupling. The dynamics are shown in Z-Y (F) and Z-P (G) phase space. Increase in [IP3]c due to cell 1 Ca2+ release-induced depolarization occurs (marked with downward arrowheads in panels E, F, and G) when cell 2 is in a resting but excitable state. Therefore cell 2 responds with large Ca2+ release. On the other hand, when an increase in [IP3]c occurs due to cell 2 depolarization (marked with upward arrowheads in panels E, F, and G), cell 1 is in a refractory phase. Response of cell 1 is denoted by solid lines and cell 2 by dashed lines in this and all subsequent figures.
Ca2+ oscillations in the coupled cells are phase-locked with a phase difference >0, whereas the membrane potentials of the cells oscillate in-phase (Fig. 9 D). This is due to the large gap junctional conductance that makes the cells isopotential. Since membrane potential modulates IP3 in each cell, [IP3]c in the cells oscillate in-phase (Fig. 9 E). When cell 1 releases Ca2+, there is a depolarization and an increase in [IP3]c (downward arrowhead in Fig. 9 E) in each cell due to voltage-dependent IP3 synthesis. This [IP3]c increase in cell 2 causes it to release Ca2+, after which it returns to steady state again. Thus cell 1 has evoked an excitable response from cell 2. Since there is a delay in the increase of [IP3]c, cell 2 oscillations lag behind cell 1 oscillations. Cell 2 oscillations also cause an increase in IP3 (marked with upward arrowhead in Fig. 9 E); however, this increase in IP3 does not evoke a response from cell 1. The reason for this can be ascertained by an examination of the system dynamics in the Z-Y and Z-P phase space (Fig. 9, F and G, respectively. Increase in [IP3]c due to cell 1 Ca2+ release-induced depolarization occurs (marked with downward arrowhead in Fig. 9, E–G) when cell 2 is in a resting but excitable state. Therefore cell 2 responds with large Ca2+ release. On the other hand, when an increase in [IP3]c occurs due to cell 2 depolarization (marked with upward arrowhead in Fig. 9, C, E, and F), cell 1 is in a refractory phase. Therefore, cell 1 does not respond. The net effect is that cell 1, although being not significantly affected by cell 2, is able to evoke response from cell 2 at each cycle. Note that cell 2 cannot be considered oscillatory—it is only responding to periodic current injections from cell 1. Also, the phase difference between the two oscillators never decreases to zero as there is a finite delay between the change in membrane potential and change in [IP3]c.
Phase-trapped oscillations
Oscillations are said to be phase-trapped when they occur with an oscillating phase difference. Phase-trapped oscillations occur on the branch PT (Fig. 8). An example of phase-trapped oscillations is given in Fig. 10 A. In the uncoupled system, cell 2 did not oscillate (upper panel); however, when coupled to cell 1, it also became oscillatory (lower panel). After undergoing a transient change in dynamics, cells interact so that the phase difference between cells oscillates but remains within a bounded region. In the coupled system, cell 1 Ca2+ oscillates with lower amplitude than the uncoupled state. The amplitude of Ca2+ oscillations in cell 2 was also oscillatory with four different peak values. The frequency of the coupled system was lower than the frequency of uncoupled cell 1. Phase difference between the cells is oscillatory (Fig. 10 B). Similar phase-trapped oscillations occur on branch P3; however, now the amplitude of the Ca2+ oscillations in cell 1 is much smaller than cell 2 (not shown).
FIGURE 10.
Phase-trapped and n/m phase-locked oscillations. (A) [Ca2+]c plot of the cell pair before (upper panel) and after (lower panel) coupling. Upon coupling the oscillations become phase-trapped as seen by the phase-difference plot (B). Plot of [Ca2+]c (C) and membrane potential (D) showing uncoupled oscillations (upper panels) and n/m phase-locked oscillations after coupling (lower panels). Stimulus β = 0.19 μM for A and B. Stimulus β = 0.2 μM for C and D.
n/m phase-locked oscillations
In the preceding coupled system dynamics, every oscillation of cell 1 was followed by an oscillation of cell 2. Dynamics of this type are said to be 1:1, that is, there is one/one correspondence between the peaks of the oscillating cells. On branch P2 (Fig. 8), this 1:1 oscillatory behavior of the cells does not exist any longer. Now for every three oscillations of cell 1, there are two oscillations of cell 2 (Fig. 10 C). In this case, cell 1 and cell 2 are said to be 3:2 phase-locked. This ratio can change and generally cells are said to be n/m phase-locked. When cells are n/m phase-locked, such that n/m ≠ 1, the relationship between membrane potential and Ca2+ oscillations is fca < fv, where fca and fv are the frequency of Ca2+ and membrane-potential oscillations of either cell, respectively (Fig. 10, C and D).
Period-doubling oscillations
Branch PD (Fig. 8) represents a region where one or both of the cells, when coupled, oscillate at nearly twice the frequency of the uncoupled state. An example of period-doubling oscillations is given in Fig. 11. In the uncoupled system, both cell 1 and cell 2 are oscillatory (Fig. 11, upper panel). At t = 50 min, gap junction coupling is enabled. The frequency of cell 1 is increased, whereas the frequency of cell 2 shows an even greater increase to approximately twice that of the uncoupled state (Fig. 11, lower panel). In the coupled system, the amplitude of cell 1 Ca2+ oscillations decreased, whereas those of cell 2 increased.
FIGURE 11.
Period-doubling oscillations. [Ca2+]c plot of the cell pair before (upper panel) and after (lower panel) coupling. Both cells are oscillatory in the uncoupled state. β = 0.3 μM.
Quasiperiodic oscillations
An n/m phase-locked oscillation is quasiperiodic if n/m is an irrational number. All dynamics of coupled cells 1 and 2 on branch Q (Fig. 8) are quasiperiodic. Quasiperiodic oscillations are characterized by oscillating amplitudes. An example of quasiperiodic oscillation on branch Q is shown in Fig. 12 A. The peak Ca2+ amplitudes of cell 2 oscillates with time (Fig. 12 B). The period of oscillations is also oscillatory (Fig. 12 C). Poncaire sections show that cell 2 (lower intrinsic frequency) shows quasiperiodic, whereas cell 1 has more complex oscillations (Fig. 12 D). However, further down this branch (increased stimulus), both cells clearly show quasiperiodic oscillations (Fig. 12 E). The overall dynamics of the cells is similar to the beat phenomenon, which is usually observed in uncoupled systems of slightly different frequencies. However, quasiperiodic oscillations are more complex. Quasiperiodic oscillations are frequently observed in smooth muscle Ca2+ and membrane-potential oscillations (see (42)).
FIGURE 12.
Quasiperiodic oscillations. (A) [Ca2+]c plot of the cell pair before (upper panel) and after (lower panel) coupling. (B) Peak values of [Ca2+]c oscillations for the two cells. (C) Periods of the two cells showing oscillations. β = 0.5 μM. (D) Poncaire sections show that cell 2 (lower intrinsic frequency) shows quasiperiodic, whereas cell 1 has more complex (β = 0.5 μM). (E) However, further down this branch (increased stimulus β = 0.8 μM) both cells clearly show quasiperiodic oscillations.
Effect of heterogeneity
The previous section has shown that introducing heterogeneity between the oscillators results in complex synchronization dynamics of the coupled system. The relative IP3 sensitivities of the two cells (σ2/σ1) determine the degree of heterogeneity of the coupled system. As the dynamics of the two cells become more disparate and deviate from a 1:1 phase relationship, a simple measure of phase difference (Δφ) is not sufficient to quantify the overall system dynamics. Therefore, now we introduce another measure of synchronization as follows.
In the coupled system, the frequency of the oscillators does not generally remain constant; therefore, we define an instantaneous frequency of the oscillator (also see (43)). First we detect the peaks of each oscillator and define a vector of peak times 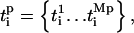 where Mp is the total number of peaks for oscillator i. For example,
where Mp is the total number of peaks for oscillator i. For example, 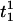 and
and 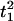 are the times when oscillator reached its first and second peaks, respectively. Then the instantaneous frequency (fi) and phase (θi) of oscillator i is given as
are the times when oscillator reached its first and second peaks, respectively. Then the instantaneous frequency (fi) and phase (θi) of oscillator i is given as
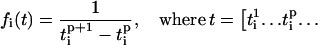 |
(5) |
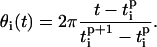 |
(6) |
Now we define a synchrony index S (44) to measure the degree of synchronization between the phases of the oscillators,
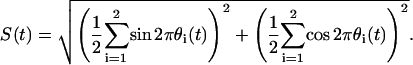 |
(7) |
If the phases of the oscillators are completely synchronized, S = 1, and 0 when there is no synchrony. We also define average values of S and f as follows:
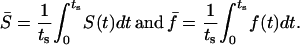 |
(8) |
The effect of heterogeneity on synchronization of the coupled cell pair is now studied by fixing cell 1 at IP3 sensitivity σ1 = 0.35 μM while varying the sensitivity of cell 2 (σ2) (Fig. 13). The system was typically integrated for 50–100 min and the average synchronization index  and average frequency
and average frequency  were calculated for each σ2/σ1 case. Thus each point on the graphs represents the averaged response of a unique heterogeneity combination (σ2/σ1). At the point σ2/σ1 = 1, cell 1 is coupled to an identical cell; for σ2/σ1 < 1, cell 1 is coupled to a cell more sensitive to IP3 than itself, i.e., with higher intrinsic frequency, and the opposite when σ2/σ1 > 1.
were calculated for each σ2/σ1 case. Thus each point on the graphs represents the averaged response of a unique heterogeneity combination (σ2/σ1). At the point σ2/σ1 = 1, cell 1 is coupled to an identical cell; for σ2/σ1 < 1, cell 1 is coupled to a cell more sensitive to IP3 than itself, i.e., with higher intrinsic frequency, and the opposite when σ2/σ1 > 1.
FIGURE 13.
Effect of heterogeneity and stimulus β (i.e., IP3) on synchrony. The effect of heterogeneity on synchronization of the coupled cell pair was studied by fixing cell 1 at IP3 sensitivity σ1 = 0.35 μM while varying the sensitivity of cell 2 (σ2). Each point on the plots denotes the mean response of a cell pair with sensitivity ratio σ2/σ1. (A) Relative frequency responses of the cells are given by color codes as indicated in the legend. Subscripts 1 and 2 denote the cell number, whereas c and u denote coupled and uncoupled state. For example, 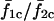 is the ratio of average frequencies of cell 1 and 2 in the coupled state. (B) Average synchrony index (
is the ratio of average frequencies of cell 1 and 2 in the coupled state. (B) Average synchrony index (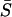 ) corresponding to panel A. (C–E) Same as A but for different stimulus β-values as indicated in the panels. (F) A comparison of the average synchrony index
) corresponding to panel A. (C–E) Same as A but for different stimulus β-values as indicated in the panels. (F) A comparison of the average synchrony index  for stimulus values of β = 0.2, 0.3, 0.4, 0.5, and 0.6 μM. The outermost curve is for β = 0.2 μM, and each succeeding inner curve corresponds to increasing values of stimulus. Note that cells are electrically coupled only (G = 1, gV = 400 mS, gc = 0 min−1, and gP = 0 min−1).
for stimulus values of β = 0.2, 0.3, 0.4, 0.5, and 0.6 μM. The outermost curve is for β = 0.2 μM, and each succeeding inner curve corresponds to increasing values of stimulus. Note that cells are electrically coupled only (G = 1, gV = 400 mS, gc = 0 min−1, and gP = 0 min−1).
Fig. 13 A shows the devil's staircase plot (45) to study the response of such cell pairs when stimulated with a fixed value of β = 0.2 μM. The ratio of intrinsic uncoupled frequencies of cell 1 and 2 is given by the curve  where the subscript u denotes that cells are uncoupled. A similar plot of frequencies
where the subscript u denotes that cells are uncoupled. A similar plot of frequencies  but in the coupled state is given by the thick trace. When cell 2 is more sensitive to IP3 than cell 1 (σ2 < σ1), it oscillates at a higher intrinsic frequency, therefore the curve
but in the coupled state is given by the thick trace. When cell 2 is more sensitive to IP3 than cell 1 (σ2 < σ1), it oscillates at a higher intrinsic frequency, therefore the curve 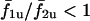 for σ2/σ1 < 1; similarly
for σ2/σ1 < 1; similarly  for σ2/σ1 > 1. It is clear that coupling the cells alters the frequency response of the cells because the
for σ2/σ1 > 1. It is clear that coupling the cells alters the frequency response of the cells because the 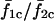 curve deviates from the
curve deviates from the 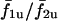 curve and shows abrupt increases or plateaus, instead of a smooth monotonic increase. For example,
curve and shows abrupt increases or plateaus, instead of a smooth monotonic increase. For example,  is same for different σ2/σ1 cases in the region marked by the arrowhead (Fig. 13 A), and forms a plateau. This shows that when coupled, all σ2/σ1 cases in this region result in the same average dynamics despite different intrinsic frequencies of cell 2 in each case. An examination of the average synchronization index
is same for different σ2/σ1 cases in the region marked by the arrowhead (Fig. 13 A), and forms a plateau. This shows that when coupled, all σ2/σ1 cases in this region result in the same average dynamics despite different intrinsic frequencies of cell 2 in each case. An examination of the average synchronization index 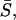 Fig. 13 B, shows that these cell pairs show a very low degree of phase synchronization. This indicates that the frequencies of the two cells are locked in an average sense but not synchronized on a peak-to-peak basis. The deviation of a cell from its intrinsic frequency due to coupling is indicated by the ratio of coupled versus uncoupled frequencies. For example, the curve f1c/f1u (Fig. 13 A) shows that in this region of σ2/σ1 (arrowhead), cell 1 has increased its frequency whereas cell 2
Fig. 13 B, shows that these cell pairs show a very low degree of phase synchronization. This indicates that the frequencies of the two cells are locked in an average sense but not synchronized on a peak-to-peak basis. The deviation of a cell from its intrinsic frequency due to coupling is indicated by the ratio of coupled versus uncoupled frequencies. For example, the curve f1c/f1u (Fig. 13 A) shows that in this region of σ2/σ1 (arrowhead), cell 1 has increased its frequency whereas cell 2 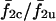 (Fig. 13 A) has not significantly changed its frequency. Moreover, cell 1 had to increase its frequency less in each of these ensuing cases due to decreasing heterogeneity, and thus all the σ2/σ1 combinations in this region resulted in the same 2:1 (cell 2/cell 1) phase-locked state and formed a plateau.
(Fig. 13 A) has not significantly changed its frequency. Moreover, cell 1 had to increase its frequency less in each of these ensuing cases due to decreasing heterogeneity, and thus all the σ2/σ1 combinations in this region resulted in the same 2:1 (cell 2/cell 1) phase-locked state and formed a plateau.
The sizes of the plateaus increase as σ2/σ1 approaches 1. Around σ2/σ1 = 1, the frequency ratio 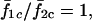 i.e., oscillations, are 1:1 synchronized. However, Fig. 13 B shows that in this region,
i.e., oscillations, are 1:1 synchronized. However, Fig. 13 B shows that in this region,  although the cells are 1:1 coupled, indicating that the cell pairs are phase locked with a phase difference >0, except at σ2/σ1 = 1, where the system degenerates to the homogenous case discussed earlier.
although the cells are 1:1 coupled, indicating that the cell pairs are phase locked with a phase difference >0, except at σ2/σ1 = 1, where the system degenerates to the homogenous case discussed earlier.
The 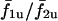 trace does not extend beyond a certain value of IP3 sensitivity (σ2 ≈ 1.1) because cell 2 is not oscillatory at the given stimulus (β = 0.2 μM) at these sensitivities. However, in the coupled state (
trace does not extend beyond a certain value of IP3 sensitivity (σ2 ≈ 1.1) because cell 2 is not oscillatory at the given stimulus (β = 0.2 μM) at these sensitivities. However, in the coupled state (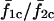 ), cell 2 becomes oscillatory due to being paced by cell 1, and the cell pair oscillates in a phase-locked synchrony as has been shown in a previous section. With decreasing IP3 sensitivity (increasing σ2), cell 2 becomes less excitable; however, cell 1 is still able to pace it in a 1:1 phase-locked mode. This appears as the plateau around σ2/σ1 > 1. As σ2 increases in value, refilling of the cell 2 store requires longer duration, and hence cell 2 remains in refractory period longer. Under such conditions, a current flow from cell 1 triggers an increase in IP3 but is unable to evoke an excitable response from cell 2 until it refills. Thus with increasing σ2, cell 2 becomes less excitable and now the 1:1 is replaced by 1:2 (cell 2/cell 1) phase-locked mode. This trend of n/m phase-locked synchrony continues with increasing heterogeneity until cell 2 reaches such a low level of excitability that cell 1 can no longer trigger it to release Ca2+ and it remains nonoscillatory.
), cell 2 becomes oscillatory due to being paced by cell 1, and the cell pair oscillates in a phase-locked synchrony as has been shown in a previous section. With decreasing IP3 sensitivity (increasing σ2), cell 2 becomes less excitable; however, cell 1 is still able to pace it in a 1:1 phase-locked mode. This appears as the plateau around σ2/σ1 > 1. As σ2 increases in value, refilling of the cell 2 store requires longer duration, and hence cell 2 remains in refractory period longer. Under such conditions, a current flow from cell 1 triggers an increase in IP3 but is unable to evoke an excitable response from cell 2 until it refills. Thus with increasing σ2, cell 2 becomes less excitable and now the 1:1 is replaced by 1:2 (cell 2/cell 1) phase-locked mode. This trend of n/m phase-locked synchrony continues with increasing heterogeneity until cell 2 reaches such a low level of excitability that cell 1 can no longer trigger it to release Ca2+ and it remains nonoscillatory.
In summary, a feature of the phase locking is that the cell with the lower intrinsic frequency adjusts its frequency significantly to achieve the global compromise frequency. Thus, when σ2/σ1 < 1, cell 2, which has the higher intrinsic frequency, remains close to its intrinsic frequency, whereas cell 1 increases its frequency to reach the compromise frequency. Similarly, for σ2/σ1 > 1, cell 2, with the lower intrinsic frequency adjusts its frequency to reach the compromise frequency. Finally, a cell can also pace a nonoscillatory but sufficiently excitable cell through voltage-dependent IP3 synthesis.
Stimulus (agonist) dependent synchrony
An important feature of this coupled cell pair is that the degree of synchrony is dependent on the intrinsic frequencies of the cells, i.e., different stimulus conditions can result in different degrees of synchrony. The above analysis was carried out at a fixed stimulus of β = 0.2 μM. Now Fig. 13 C shows the response of the system at β = 0.4 μM. It is apparent that the plateaus that existed for σ2/σ1 ≪ 1 are lost and that around σ2/σ1 = 1 is significantly reduced. This shows that increasing stimulus β from 0.2 μM to 0.4 μM has reduced the ability of heterogeneous cells to synchronize. Similarly, increasing stimulus to 0.5 μM and 0.6 μM (Fig. 13, D and E, respectively) results in even more loss of the phase-locked plateaus. Also it should be noted that as the strength of stimulus β is increased (Fig. 13 A, C–E), the f1c/f2c curve deviates less and less from the 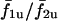 curve. This observation confirms that there is a general loss of synchrony with increasing stimulus. However, with increasing stimulus, cell 1 is able to pace cell 2 with low IP3 sensitivities (σ2) which it was unable to pace at lower stimulus. This is because with increasing stimulus, cell 2 becomes more excitable; thus cell 1 is able to evoke a response from it.
curve. This observation confirms that there is a general loss of synchrony with increasing stimulus. However, with increasing stimulus, cell 1 is able to pace cell 2 with low IP3 sensitivities (σ2) which it was unable to pace at lower stimulus. This is because with increasing stimulus, cell 2 becomes more excitable; thus cell 1 is able to evoke a response from it.
This frequency dependence of synchronization is summarized by plotting average synchrony index ( ) curves for different values of stimulus for the same range of σ2/σ1 (Fig. 13 F). The outermost curve is for β = 0.2 μM and each succeeding inner curve corresponds to increasing values of stimulus. This figure shows that generally, synchrony is reduced with increasing stimulus, i.e., with increasing intrinsic frequency of the oscillators. This confirms the prediction of the weak-coupling analysis, where it was shown that at higher levels of stimulus β (i.e., at higher frequencies), the interaction function changed so that synchrony becomes less stable and more sensitive to differences in the intrinsic frequencies of the coupled cells.
) curves for different values of stimulus for the same range of σ2/σ1 (Fig. 13 F). The outermost curve is for β = 0.2 μM and each succeeding inner curve corresponds to increasing values of stimulus. This figure shows that generally, synchrony is reduced with increasing stimulus, i.e., with increasing intrinsic frequency of the oscillators. This confirms the prediction of the weak-coupling analysis, where it was shown that at higher levels of stimulus β (i.e., at higher frequencies), the interaction function changed so that synchrony becomes less stable and more sensitive to differences in the intrinsic frequencies of the coupled cells.
Electrically mediated IP3 versus chemical coupling
The analysis given so far was carried out under conditions where the cells were coupled by large electrical coupling only and not by diffusion of Ca2+ or IP3 (G = 1, gV = 4 00 mS, gc = gP = 0 min−1). This enabled us to elucidate the role of electrical coupling in synchronization of cells through voltage-dependent excitability of Ca2+ oscillations. The aim of this section is to investigate whether cells separated by large distances, i.e., coupled with small gap junction conductance, can display the synchronization features similar to the case of large electrical coupling. Finally, a comparison will be made between synchronization achieved through electrical- versus chemical-mediated coupling.
Long-range synchronization: weak-coupling analysis
We now use the results of weak-coupling analysis to compare the long-range synchronization features of coupling achieved through diffusion of Ca2+, IP3, and voltage-dependent enhancement of store Ca2+ release. Gap junction coupling (G) was used as a parameter to simulate the distance between oscillators; decreasing G is equivalent to increasing the distance between the oscillators.
Weak-coupling analysis shows that coupling through diffusion of Ca2+ is able to synchronize cells that are in close proximity (G ≈ 1). At low frequencies, bistable synchrony appears where in-phase and anti-phase synchrony are simultaneously stable (Fig. 14 A). With increasing frequency (stimulus β), only in-phase oscillations are stable (Fig. 14 B). In the case of coupling through diffusion of IP3, synchrony at lower frequencies is phased-locked (not in-phase) (Fig. 14 C), and then become anti-phase at higher frequencies (Fig. 14 D).
FIGURE 14.
Weak-coupling analysis for long-range synchronization. Weak-coupling analysis shows that coupling through diffusion of Ca2+ is able to synchronize cells that are in close proximity (G ≈ 1). (A) At low frequencies, bistable synchrony appears where in-phase and anti-phase synchrony are simultaneously stable. (B) With increasing frequency (stimulus β), only in-phase oscillations are stable. (C) In the case of coupling through diffusion of IP3, synchrony at lower frequencies are phased-locked (not in-phase), and then (D) become anti-phase at higher frequencies. (E) Phase-response curves were produced for injected pulses of Ca2+, IP3, and membrane potential for different strengths of coupling inputs. Note the 20 times expansion of the Ca2+ PRC at G = 0.1. (F) The derivate of uncoupled normalized limit cycle.
Now we proceed to compare long-range (G ≪ 1) synchronization features achieved through chemical versus electrical coupling. In weakly connected systems, synchrony can be predicted by the shape of PRC and derivative of the uncoupled limit cycle (see Ermentrout (46) for details). Phase-response curves were produced for injected pulses of Ca2+, IP3, and membrane potential for different strengths of coupling inputs (Fig. 14 E). As coupling is reduced, i.e., as cells are moved apart, PRCs begin to change due to lower amplitude of coupling current or chemical influx. For G = 0.1, the amplitude of PRCs generated by current injections is slightly reduced (thick solid line); however, the general shape remains unaltered. Therefore, the integral of this PRC and derivate of uncoupled voltage limit cycle (Fig. 14 F) will be positive after the spike. Thus, synchronization by means of electrical coupling through voltage-dependent IP3 synthesis will remain effective even for G = 0.1 or 10 times larger separation. In the case of Ca2+ coupling, the PRC is reduced to almost zero (Fig. 14 E, thin solid line; notice multiplication by 20). Moreover, this PRC lies entirely above the zero axis, i.e., has no negative region. Therefore, the integral of this PRC and derivate of uncoupled Ca2+ limit cycle (Fig. 14 F) will be negative or nearly zero after the spike. Therefore, coupling by Ca2+ at G = 0.1 will not result in in-phase synchronization. Similar results are obtained for coupling by diffusion of IP3.
Thus, it is predicted that electrical coupling through voltage-dependent IP3 synthesis is an effective long-range signaling mechanism, whereas chemical coupling through diffusion of Ca2+ or IP3 is only effective over small spatial separations. These results also show that chemical coupling at long-range would be far more unstable in the presence of oscillator heterogeneities as compared to electrically mediated coupling through voltage-dependent enhancement of Ca2+ release. Now we proceed with analysis of the full system to confirm these results.
Electrical coupling
In the preceding analysis of the full model, cells were electrically isopotential, i.e., their membrane potentials were identical (see Fig. 9 D) due to the large electrical coupling (G = 1, gV = 400 mS, gc = gP = 0 min−1) between the cells. Here we relax this condition and study the effect of the electrical coupling strength on the synchronization properties of the coupled cell pair. As the gap junction coupling strength is reduced, the cells will no longer have identical membrane potential. Fig. 15 shows the effect of gap junction coupling strength on the synchronization of the coupled cell pair studied earlier (IP3 sensitivities; σ1 = 0.35 and σ2 = 0.4 μM). Fig. 15 A (lowest trace) shows the frequency ratios of cell 1 versus cell 2 ( ) for gap junction coupling G from 0 to 1 (i.e., electrical coupling strengths from 0 to 400 mS), when stimulated at β = 0.2 μM. It can be seen that the cell pair remains 1:1 phase locked even when coupled by negligibly small gap junctional conductances (not visible in Fig. 15 A; G ≈ 0.00005, equivalent to electrical coupling of gV ≈ 0.02 mS). Fig. 15 B (uppermost trace) shows that the corresponding average synchrony index
) for gap junction coupling G from 0 to 1 (i.e., electrical coupling strengths from 0 to 400 mS), when stimulated at β = 0.2 μM. It can be seen that the cell pair remains 1:1 phase locked even when coupled by negligibly small gap junctional conductances (not visible in Fig. 15 A; G ≈ 0.00005, equivalent to electrical coupling of gV ≈ 0.02 mS). Fig. 15 B (uppermost trace) shows that the corresponding average synchrony index 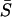 remains high for this value of gap junction coupling. The system reaches a response equal to the isopotential case (G = 1, gV = 400 mS, i.e., identical membrane potentials) even for very small values of gap junction coupling (not visible in Fig. 15 A; G ≈ 0.0025; equivalent to electrical coupling of gV ≈ 1 mS) i.e., even when the membrane potentials of the two cells are not identical. When the same cell pair is stimulated with β = 0.3 μM, they still maintain a 1:1 locking (Fig. 15 A, lowest trace). However, now the corresponding average synchrony index (Fig. 15 B, second top trace) is reduced, indicating increased phase difference. Now for β = 0.3 μM, a larger coupling (not visible in Fig. 15, A and B; G ≈ 0.01–0.025; equivalent to electrical coupling of gV ≈ 4–10 mS) is required to reach a response equal to the isopotential case. This shows that the electrically coupled cell pair can maintain 1:1 phase locking for very small electrical coupling and at varying stimulations. Thus, cells do not need to be strongly electrically coupled (i.e., have identical membrane potentials) to display synchronization features displayed by cells coupled by large electrical coupling.
remains high for this value of gap junction coupling. The system reaches a response equal to the isopotential case (G = 1, gV = 400 mS, i.e., identical membrane potentials) even for very small values of gap junction coupling (not visible in Fig. 15 A; G ≈ 0.0025; equivalent to electrical coupling of gV ≈ 1 mS) i.e., even when the membrane potentials of the two cells are not identical. When the same cell pair is stimulated with β = 0.3 μM, they still maintain a 1:1 locking (Fig. 15 A, lowest trace). However, now the corresponding average synchrony index (Fig. 15 B, second top trace) is reduced, indicating increased phase difference. Now for β = 0.3 μM, a larger coupling (not visible in Fig. 15, A and B; G ≈ 0.01–0.025; equivalent to electrical coupling of gV ≈ 4–10 mS) is required to reach a response equal to the isopotential case. This shows that the electrically coupled cell pair can maintain 1:1 phase locking for very small electrical coupling and at varying stimulations. Thus, cells do not need to be strongly electrically coupled (i.e., have identical membrane potentials) to display synchronization features displayed by cells coupled by large electrical coupling.
FIGURE 15.
Electrical versus chemical coupling. Panels A and B show the dependence of synchrony on gap junction coupling strength. (A) Relative mean frequency response of cell 2/cell 1 (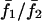 ) for a cell pair with IP3 sensitivities σ1 = 0.35 μM and σ2 = 0.40 μM when coupled by gap junction permeability between G = 0–1. Each point on the plots denotes the mean response of a cell pair. Four cases are shown: 1), coupled by diffusion of Ca2+ only, and 2), electrically coupled only, and cases (1) and (2) for stimulus strengths β = 0.2 and 0.3 μM. (B) Average synchrony index (
) for a cell pair with IP3 sensitivities σ1 = 0.35 μM and σ2 = 0.40 μM when coupled by gap junction permeability between G = 0–1. Each point on the plots denotes the mean response of a cell pair. Four cases are shown: 1), coupled by diffusion of Ca2+ only, and 2), electrically coupled only, and cases (1) and (2) for stimulus strengths β = 0.2 and 0.3 μM. (B) Average synchrony index ( ) corresponding to panel A. (C) The effect of heterogeneity on synchronization of cell pairs when only electrically coupled. (D) The effect of heterogeneity on synchronization of cell pairs when coupled only by diffusion of Ca2+. Note that cells connected only by Ca2+ diffusion cannot synchronize even though they are coupled by a gap junction coupling that is 10 times stronger than in the case of electrically coupled cells (C). (E) A comparison of the average synchrony index
) corresponding to panel A. (C) The effect of heterogeneity on synchronization of cell pairs when only electrically coupled. (D) The effect of heterogeneity on synchronization of cell pairs when coupled only by diffusion of Ca2+. Note that cells connected only by Ca2+ diffusion cannot synchronize even though they are coupled by a gap junction coupling that is 10 times stronger than in the case of electrically coupled cells (C). (E) A comparison of the average synchrony index 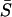 for gap junction coupling strengths of G = 0.0025, 0.0125, 0.025, and 1: in the presence of electrical coupling only. The outermost curve is G = 1, and each succeeding inner curve corresponds to decreasing values of gap junction coupling strengths. (F) Similar to panel E but now only coupled by diffusion of Ca2+.
for gap junction coupling strengths of G = 0.0025, 0.0125, 0.025, and 1: in the presence of electrical coupling only. The outermost curve is G = 1, and each succeeding inner curve corresponds to decreasing values of gap junction coupling strengths. (F) Similar to panel E but now only coupled by diffusion of Ca2+.
Electrical versus chemical coupling
The synchronization features of the cell pair when coupled electrically through voltage-dependent IP3 synthesis are significantly different to that when coupled by diffusion of Ca2+ or IP3 through gap junctions. The cell pair (IP3 sensitivities; σ1 = 0.35 and σ2 = 0.4 μM) of the above example, when coupled only by diffusion of Ca2+ (G = 1, gV = 0 mS, gP = 0 min−1, gc = 1 min−1) through gap junctions cannot synchronize in a 1:1 phase-locked state; instead it reaches a 1:2 (cell 1/cell 2) phase-locked state, and then only for gap junction permeability of G > 0.062 (Fig. 15 A, (uppermost trace β = 0.2). Moreover, in this case the average synchronization index 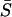 is significantly lower (Fig. 15 B, lowermost trace). The electrically coupled cells maintain a 1:1 phase locking even when stimulus is increased to β = 0.3 μM (Fig. 15 A, lowest trace), whereas the Ca2+-coupled cells even lose the 1:2 phase locking (Fig. 15 A, middle trace) and the average synchrony index remains significantly lower than that for electrical coupling. Thus, it is clear that electrically mediated IP3 coupling is significantly more effective in synchronizing cells compared to chemical coupling through diffusion of Ca2+.
is significantly lower (Fig. 15 B, lowermost trace). The electrically coupled cells maintain a 1:1 phase locking even when stimulus is increased to β = 0.3 μM (Fig. 15 A, lowest trace), whereas the Ca2+-coupled cells even lose the 1:2 phase locking (Fig. 15 A, middle trace) and the average synchrony index remains significantly lower than that for electrical coupling. Thus, it is clear that electrically mediated IP3 coupling is significantly more effective in synchronizing cells compared to chemical coupling through diffusion of Ca2+.
Fig. 15 C shows the synchronization properties of cell pairs with respect to heterogeneity (σ2/σ1) when electrically coupled (no chemical coupling) by a gap junction coupling of G = 0.0025 (i.e., weak electrical coupling). The cell pairs show synchronization plateaus, indicating that even weak electrical coupling is sufficient to synchronize heterogeneous cell pairs through voltage-dependent IP3 synthesis. In contrast, when cells are coupled by diffusion of Ca2+, and no other coupling, even with 10 times larger gap junction coupling of G = 0.025, no synchronization plateaus are achieved (Fig. 15 D), and the coupled frequency ratio f1c/f2c remains close to that of the uncoupled ratio 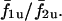 A plot of average frequency index
A plot of average frequency index  with respect to heterogeneity (σ2/σ1) (Fig. 15 E) shows that reducing gap junction conductance between electrically coupled cells (without Ca2+ coupling) does not have a significant effect on the synchronization properties of the cell pair. In contrast, when cells are coupled only by diffusion of Ca2+, the average frequency index
with respect to heterogeneity (σ2/σ1) (Fig. 15 E) shows that reducing gap junction conductance between electrically coupled cells (without Ca2+ coupling) does not have a significant effect on the synchronization properties of the cell pair. In contrast, when cells are coupled only by diffusion of Ca2+, the average frequency index 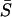 (Fig. 15 F) is reduced so that it is close to the uncoupled state for all σ2/σ1 cases except the homogenous case. Synchronization properties of cells coupled by only diffusion of IP3 were found to be similar to that of cells coupled only through diffusion of Ca2+. These results show that electrical coupling through voltage-dependent IP3 synthesis is orders of magnitude more effective than chemical coupling through diffusion of Ca2+ or IP3.
(Fig. 15 F) is reduced so that it is close to the uncoupled state for all σ2/σ1 cases except the homogenous case. Synchronization properties of cells coupled by only diffusion of IP3 were found to be similar to that of cells coupled only through diffusion of Ca2+. These results show that electrical coupling through voltage-dependent IP3 synthesis is orders of magnitude more effective than chemical coupling through diffusion of Ca2+ or IP3.
The influence of chemical fluxes through gap junctions is reduced with increasing separation of cells. Thus, an implication of the above results is that heterogeneous cells that are not adjacent, but separated by large distances due to intervening cells, are able to synchronize their Ca2+ oscillations through electrical coupling by means of voltage-dependent IP3 synthesis. In contrast, chemical coupling would be virtually ineffective once the distance between the cells is increased and the intrinsic frequencies (σ2, σ1) of the cells are different. Thus, it can be concluded that electrical coupling through voltage-dependent IP3 synthesis is an effective long-range signaling mechanism, whereas chemical coupling through diffusion of Ca2+ or IP3 is only effective over small spatial separations and only when intrinsic frequencies of the cells are not significantly different.
DISCUSSION
We have presented a theoretical analysis of a novel mechanism of intercellular communication where coupling occurs through voltage-dependent IP3 receptor mediated Ca2+ release between electrically connected cells (12). The model presented here is composed of two interacting systems, a cytosolic-store excitable system and a membrane potential-IP3 feedback loop. The cytosolic-store system is linked to membrane potential by a Ca2+-activated inward current that transforms cytosolic Ca2+ oscillations into membrane-potential oscillations. When cells are electrically coupled through gap junctions, they are able to interact with the cytosolic-store excitable system of other cells through voltage-dependent IP3 synthesis and modulate Ca2+ excitability and oscillatory properties of other connected cells. This interaction can result in synchronization of the connected cells.
It is important to note that the exact nature of the cytosolic-store Ca2+ excitable system is not significant here. It is the weak connection (voltage-dependent IP3 synthesis) between excitable systems (cytosolic-store Ca2+) through a long-range coupling mechanism (membrane potential) that is fundamental to the construction of the overall system and results in the synchronized states. Therefore it is not surprising that we have been able to obtain qualitatively similar results when the Dupont-Goldbeter model of Ca2+ oscillation is replaced with generic FitzHugh-Nagumo oscillators (47,48) or specific models of intracellular Ca2+ oscillations (16,49,50) (M. S. Imtiaz, unpublished observations). Similarly the voltage-dependent IP3 synthesis feedback loop can be replaced with other mechanisms that link membrane potential with the cytosolic-store Ca2+ excitability, such as voltage-dependent Ca2+ entry. For example, the results of this study are also relevant to lymphatic smooth muscle where oscillatory release of Ca2+ through IP3 receptors and voltage-dependent Ca2+ influx through L-Ca2+ channels underlie rhythmic vasomotion (51). In this system, subthreshold activation of voltage-dependent L-Ca2+ channels serve the same role as voltage-dependent IP3 synthesis in gastric smooth muscle (52,53).
Several modeling studies have been undertaken to understand the basic mechanism of synchronization of Ca2+ oscillations. Two of these studies (15,16) concluded that diffusion of Ca2+ across gap junction is a sufficient coupling mechanism and cells thus coupled can reach in-phase, anti-phase, phase-drift, and harmonic synchronized states. On the other hand, some studies (54) have implicated diffusion of IP3 as being sufficient for synchronization of Ca2+ oscillations. The results of our study agree that Ca2+ and IP3 coupling are capable of synchronizing cells that are closely located (strongly coupled), but also predict that with increasing cell heterogeneity and distance (weak coupling), chemical coupling is not an effective coupling mechanism. A recent work (18) has investigated the role of electrical, Ca2+, and IP3 (including phospholipase C-δ-dependent IP3 synthesis) coupling in synchronization of Ca2+ oscillators. The authors concluded that coupling through Ca2+, but not IP3 or electrical current, is capable of synchronizing Ca2+ oscillations. Although these authors have studied ensemble of cells, the intrinsic frequencies of the cells were chosen to be same or very similar. We also note that the authors have simulated a population of ∼90 cells where cells away from the boundary are connected to six nearest neighbors. Thus, the proximity between cells is not large, and therefore their results do not apply to long-range signaling. In such a case where proximity between cells is not large, chemical coupling was effective in synchronizing the cell ensemble, as also predicted by our study. Thus our study supports their findings in the limit of close proximity between cells, but further shows that large population of heterogeneous cells that are separated over large distances will not synchronize in the presence of chemical coupling only. In the tissue of our study, the gastric smooth muscle, cells have different intrinsic frequencies (see van Helden and Imtiaz (12)). Therefore, electrical, but not chemical (Ca2+ and IP3) coupling is necessary for long-range synchronization in the system studied here.
Long-range signaling
Long-range signaling and synchronization of Ca2+ oscillations require strong coupling between oscillators, but on the other hand nonphysiologically strong chemical coupling abolishes many experimentally observed phenomena. For example, long chains of our oscillators when strongly chemically coupled (i.e., by adopting extraordinarily high, nonphysiological chemical diffusion) display synchronization at high levels of stimulus, but remain nonoscillatory and do not display asynchronous oscillations under subthreshold stimulations (M. S. Imtiaz, unpublished observations). These phenomena are usually observed in weakly connected systems, and strong coupling reduces the dynamics of the coupled system to a narrow deterministic range. Thus, contradictory constraints are placed on the coupling mechanism. This dilemma is solved by the current proposed mechanism by combining a strong coupling agent (electrical coupling) with a weak-coupling mechanism of voltage-dependent modulation of store Ca2+ release. The voltage-dependent store Ca2+ release feedback loop works locally within cells to weakly couple each cell to the strong coupling link provided by membrane potential (see Figs. 1 and 16).
FIGURE 16.
Schematic representation of the two-cell system. This schematic shows a specific implementation of the general system given in Fig. 1. It shows the interaction of the major fluxes and feedback loops in the cytosolic-store Ca2+ excitable system, Ca2+ activated depolarization, and voltage-dependent IP3 synthesis in each cell. The two cells are connected by gap junctions.
The proposed coupling mechanism has the advantage that cells retain a large degree of autonomy of Ca2+ oscillations and are also able to interact with cells separated by large distances and modulate their local Ca2+ dynamics to the ensemble average. The outcome of such interaction in identical cells is in-phase, phase-locked, and anti-phase synchrony. The introduction of heterogeneity immediately destroys the anti-phase synchrony; therefore, a more biologically relevant outcome is the in-phase and phase-locked synchrony of identical or near identical cells. In nonidentical cells, the outcome can be anywhere from strongly phase-locked to n/m phase-locked states, dependent on the degree of heterogeneity and stimulation; but generally cells remain phase locked.
Weak-coupling analysis was carried out to predict the effect of gap junction conductance and spatial separation on the synchrony of the coupled cells. With decreasing coupling (increasing distance), the PRCs for electrical pulses did not change significantly and retained general shape. This indicated that long-range signaling could be achieved by electrical coupling via voltage-dependent modulation of store Ca2+ release. These predictions were confirmed in the full model, where it was found that synchronization occurred for negligibly small values of gap junction conductance (∼0.02 mS) and reached the dynamics similar to those of infinitely coupled cells even for small values of gap junction conductance (∼1 mS). This shows that not only cells that are adjacent to each other or within isopotential range, but also those distant to each other, can interact through this mechanism and successfully reach a synchronized or phase-locked state. Contrary to this, it was shown that with decreasing gap junction coupling (increasing distance), the PRCs for chemical coupling changed in such a way as to destabilize synchrony. This was confirmed in the full model, where it was shown that diffusion of Ca2+ or IP3 could act as a strong coupling agent only for large gap junction permeability, i.e., for cells that are located adjacent or in near proximity to each other, but it was virtually ineffective for cells that were distant to each other. In a previous study (12), we have shown that large two-dimensional arrays of our oscillators reach synchrony even in the presence of heterogeneities and large spatial spread of the population.
Frequency-dependent synchrony
Another important aspect of our coupling mechanism is the frequency-dependent synchrony of the coupled cells. It has been shown that timing of the interaction of the oscillators compared to the duration of the action potentials determines synchronization (55). Weak-coupling analysis showed that the interaction function changes with stimulus, favoring greater synchrony at lower frequencies. Thus, cells oscillating at low frequencies, i.e., when stimulated with low levels of agonist, reached a greater degree of synchrony (Fig. 13). Therefore, at any given level of stimulus, cells that are most sensitive will be oscillating with the highest frequency and therefore will also show the least degree of synchrony. On the other hand, at the same stimulus level, cells that are oscillating at lower frequency will show a greater degree of synchrony. The outcome of this result is that different groups of synchronized cells will emerge at different levels of stimulation. This has significant consequences in the pacemaking process of cell ensembles, i.e., pacemaker group of cells within a cell ensemble will change with changing stimulation.
Another implication of this result is that as stimulus is increased, cells in an ensemble will lose synchrony and their average response will be noise. This could underlie such phenomena as spasm observed in overstimulated lymphatic (51), blood (56), and gastric smooth muscles (7). Similar frequency-dependent synchrony has been observed in the locus ceruleus region of the brain (57). Using experimental and modeling studies, the authors concluded that a combination of electrotonic coupling and firing frequency are the key elements that regulate synchrony in the adult animals. These results are in complete agreement to the results of our study where synchrony was found to be dependent on intrinsic frequency (stimulus) and electrical coupling. This agreement further corroborates the idea that the overall structure of the proposed mechanism is generic and not dependent on the exact nature of the excitable system. Thus, using any model of Ca2+ oscillation, and replacing voltage-dependent IP3 synthesis with another voltage-dependent agonist of cytosolic-store Ca2+, excitability would produce the same result as long as the overall system is maintained.
Future directions
The oscillators in our study were modeled as point sources; that is, did not take into account diffusion within the cell. Although a point oscillator cannot predict all possible outcomes, it presents a reasonably accurate picture (20). We note that the current analysis does not imply that the qualitative outcomes of the model are necessarily observed in two coupled smooth muscle cells, or indeed the synchrony modes presented are exhaustive. However, the main aim of this study was to compare various coupling mechanisms effective for long-range signaling, and the point oscillator model provides a reasonable analysis for this purpose. Future studies will involve a more detailed analysis using models that take into account diffusion within single cells.
Further studies are also under way to study large gastrointestinal system using our coupling mechanism using voltage-dependent enhancement of store Ca2+ release.
CONCLUSION
The results of this study indicate that chemical coupling through diffusion of Ca2+ and IP3 is effective only in synchronizing Ca2+ oscillations of cells that are closely located. However, with increasing heterogeneity (intrinsic frequencies) and distance between cells, chemical coupling fails to be an effective synchronizing mechanism. Based on previous experimental observations, this study has shown that electrical coupling, acting through voltage-dependent modulation of cytosolic-store excitability, is sufficient in synchronizing oscillations of cells even in the absence of chemical coupling.
It is known that membrane potential can enhance release of Ca2+ from intracellular stores by various mechanisms such as voltage-dependent Ca2+ influx, voltage-dependent synthesis of IP3, or a combination of the two. In this study, a specific case was presented where electrical coupling occurred through voltage-dependent synthesis of IP3. It was shown that it is the combination of local weak coupling through voltage-dependent enhancement of store Ca2+ release and strong coupling through membrane potential that underlies long-range coupling. Importantly, unlike chemical coupling, this mechanism is effective in coupling cells over a large range of spatial separations and heterogeneity of intrinsic frequencies.
Voltage-dependent modulation of store-Ca2+ release has been shown to exist in various other gap junction-connected multicellular systems, such as lymphatic and vascular smooth muscles. Therefore, the outcome of this study is also relevant to synchrony and long-range signaling in these and possibly other systems.
Acknowledgments
The authors thank Associate Professor Derek Laver, The Neuroscience Group, School of Biomedical Sciences, Faculty of Health, The University of Newcastle, Callaghan NSW 2308, Australia, for a critical review of the manuscript.
D. F. van Helden and M. S. Imtiaz were supported by The National Health and Medical Research Council of Australia and The Hunter Heart-Lung Research Guild.
APPENDIX
We use our previous experimentally derived model of a single cell (30) to represent the dynamics of each cell in the current model. Here we present a brief summary of this single-cell model. The single-pool model of Dupont and Goldbeter (58) is used here to describe the Ca2+ dynamics of the single cell. However, as noted earlier in the text, the qualitative outcome of the two-cell model is not dependent on this particular choice of model. The single-cell model has four state variables: cytosolic Ca2+ concentration ([Ca2+]c) Z, Ca2+ concentration in the intracellular store ([Ca2+]s) Y, IP3 concentration in the cytosol ([IP3]c) P, and membrane potential V. A schematic given in Fig. 16 shows the main feedback loops and fluxes comprising the system. Dropping the subscripts that denoted the cell number, the Ca2+ dynamics of the single cell is
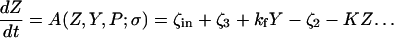 |
(5) |
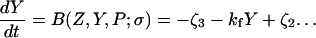 |
(6) |
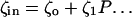 |
(7) |
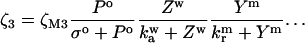 |
(8) |
 |
(9) |
Influx of Ca2+ into cytosol from extracellular space (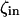 ) occurs through IP3-dependent and independent components,
) occurs through IP3-dependent and independent components, 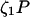 and
and  respectively. The flux of Ca2+ from the store through an IP3-sensitive receptor is given by
respectively. The flux of Ca2+ from the store through an IP3-sensitive receptor is given by 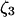 (Eq. 8). This release of Ca2+ from the store depends on the IP3 concentration and sensitivity of the receptor to IP3, as given by the first term in Eq. 8. Release of Ca2+ from the receptor is further enhanced by [Ca2+]c, and dependent on Ca2+ concentration in the store, as given by the second and third terms in Eq. 8, respectively. A [Ca2+]c-dependent efflux of Ca2+ from the cytosol is given by the last term in Eq. 5. The store is refilled by a [Ca2+]c-dependent pump
(Eq. 8). This release of Ca2+ from the store depends on the IP3 concentration and sensitivity of the receptor to IP3, as given by the first term in Eq. 8. Release of Ca2+ from the receptor is further enhanced by [Ca2+]c, and dependent on Ca2+ concentration in the store, as given by the second and third terms in Eq. 8, respectively. A [Ca2+]c-dependent efflux of Ca2+ from the cytosol is given by the last term in Eq. 5. The store is refilled by a [Ca2+]c-dependent pump 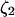 (Eq. 9). There is also a [Ca2+]s-dependent leakage from the store into the cytosol given by the term
(Eq. 9). There is also a [Ca2+]s-dependent leakage from the store into the cytosol given by the term 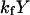 in Eqs. 5 and 6. Parameters for the system defined by Eqs. 5–9 are summarized in Table 1.
in Eqs. 5 and 6. Parameters for the system defined by Eqs. 5–9 are summarized in Table 1.
TABLE 1.
| Parameter | Description | Value |
|---|---|---|
| ζ0 | Constant Ca2+ influx from extracellular space into cytosol | 3.4 μM/min |
| ζ1 | Rate constant for IP3-dependent Ca2+ influx from extracellular space into cytosol | 3.4 min−1 |
| kf | Rate constant for Ca2+ leak from store to cytosol | 1 min−1 |
| K | Rate constant for Ca2+ extrusion from the cytosol | 10 min−1 |
| ζM2 | Maximal value for Ca2+ pump into the store | 50 μM/min |
| n | Hill coefficient | 2 |
| k2 | Cytosolic Ca2+-dependent threshold constant for ζ2 | 1 μM |
| ζM3 | Maximal value for Ca2+ release from the store | 650 μM/min |
| w | Hill coefficient | 4 |
| ka | Cytosolic Ca2+-dependent threshold constant for ζ3 | 0.9 μM |
| kr | Store Ca2+-dependent threshold constant for ζ3 | 2 μM |
| m | Hill coefficient | 2 |
| σ | IP3-dependent threshold constant for ζ3 | See text (μM) |
| o | Hill coefficient | 4 |
Membrane potential of the cell is given as follows:
 |
(10) |
The first term is the net current due to the passive ionic fluxes. The second term is a Ca2+-activated inward current and is responsible for transforming the [Ca2+]c oscillations into membrane-potential oscillations. Parameters for the system defined by Eq. 10 are summarized in Table 2.
TABLE 2.
Parameters related to membrane voltage and currents given by Eq. 10
| Parameter | Description | Value |
|---|---|---|
| Cm | Membrane capacitance | 0.0017 F |
| Gionic | Lumped conductance of passive ionic channels | 1.12 mS |
| Eionic | Lumped reversal/null potential of passive ionic channels | −67.2 mV |
| Eca | Reversal/null potential for the Ca2+modulated current(s) | −20 mV |
| GMca | Maximal value of Gca | 4 mS |
| kca | Half saturation constant for GCa | 1.4 μM |
| q | Hill coefficient | 4 |
The IP3 dynamics of the cell is given by
 |
(11) |
An externally applied stimulus β results in synthesis of IP3 and sets the base level of [IP3]c. However, a component of IP3 that depends on membrane potential further modulates the cytosolic IP3 concentration as given by the second term in Eq. 11. IP3 is degraded by a linear and nonlinear process as given by the third and fourth terms in Eq. 11. Parameters for the system defined by Eq. 11 are summarized in Table 3.
TABLE 3.
Parameters related to IP3 dynamics given by Eq. 11
| Parameter | Description | Value |
|---|---|---|
| PMV | Maximal rate of voltage-dependent IP3 synthesis | 0.8 μM/min |
| kV | Half saturation constant for voltage-dependent IP3 synthesis | −58 mV |
| r | Hill coefficient | 8 |
| β | External stimulus generated IP3 | See text (μM/min) |
| ɛ | Rate constant for linear IP3 degradation | 0.9 min−1 |
| PM4 | Maximal value for the nonlinear IP3 degradation | 2 μM/min |
| k4 | Half saturation constant for the nonlinear IP3 degradation | 0.5 μM |
| u | Hill coefficient | 4 |
References
- 1.Bolton, T. B. 1971. On the nature of the oscillations of the membrane potential (slow waves) produced by acetylcholine or carbachol in intestinal smooth muscle. J. Physiol. (Lond.). 216:403–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Tomita, T. 1981. Electrical activity (spikes and slow waves) in gastrointestinal smooth muscles. In Smooth Muscle: An Assessment of Current Knowledge. E. Bulbring, A. F. Brading, A. W. Jones, and T. Tomita, editors. University of Texas Press, Austin, TX. 127–156.
- 3.Prosser, C. L., and A. W. Mangel. 1982. Cellular Pacemakers. John Wiley & Sons, New York.
- 4.Liu, L. W., L. Thuneberg, and J. D. Huizinga. 1995. Cyclopiazonic acid, inhibiting the endoplasmic reticulum calcium pump, reduces the canine colonic pacemaker frequency. J. Pharmacol. Exp. Ther. 275:1058–1068. [PubMed] [Google Scholar]
- 5.Hashitani, H., D. F. Van Helden, and H. Suzuki. 1996. Properties of spontaneous depolarizations in circular smooth muscle cells of rabbit urethra. Br. J. Pharmacol. 118:1627–1632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Suzuki, H., and G. D. Hirst. 1999. Regenerative potentials evoked in circular smooth muscle of the antral region of guinea-pig stomach. J. Physiol. 517:563–573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.van Helden, D. F., M. S. Imtiaz, K. Nurgaliyeva, P. von der Weid, and P. J. Dosen. 2000. Role of calcium stores and membrane voltage in the generation of slow wave action potentials in guinea-pig gastric pylorus. J. Physiol. 524:245–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ward, S. M., T. Ordog, S. D. Koh, S. Abu Baker, J. Y. Jun, G. Amberg, K. Monaghan, and K. M. Sanders. 2000. Pacemaking in interstitial cells of Cajal depends upon calcium handling by endoplasmic reticulum and mitochondria. J. Physiol. 525:355–361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.van Helden, D. F. 1991. Spontaneous and noradrenaline-induced transient depolarizations in the smooth muscle of guinea-pig mesenteric vein. J. Physiol. 437:511–541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wang, Q., R. C. Hogg, and W. A. Large. 1992. Properties of spontaneous inward currents recorded in smooth muscle cells isolated from the rabbit portal vein. J. Physiol. 451:525–537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hirst, G. D. S., N. J. Bramich, H. Teramoto, H. Suzuki, and F. R. Edwards. 2002. Regenerative component of slow waves in the guinea pig gastric antrum involves a delayed increase in Ca2+i and Cl− channels. J. Physiol. 540:907–919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.van Helden, D. F., and M. S. Imtiaz. 2003. Ca2+ phase waves: a basis for cellular pacemaking and long-range synchronicity in the guinea-pig gastric pylorus. J. Physiol. 548.1:271–296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.van Helden, D. F., and M. S. Imtiaz. 2003. Ca2+ phase waves emerge. Physiology News. 52:7–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tordjmann, T., B. Berthon, M. Claret, and L. Combettes. 1997. Coordinated intercellular calcium waves induced by noradrenaline in rat hepatocytes: dual control by gap junction permeability and agonist. EMBO J. 16:5398–5407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bindschadler, M., and J. Sneyd. 2001. A bifurcation analysis of two coupled calcium oscillators. Chaos. 11:237–246. [DOI] [PubMed] [Google Scholar]
- 16.Hofer, T. 1999. Model of intercellular calcium oscillations in hepatocytes: synchronization of heterogeneous cells. Biophys. J. 77:1244–1256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hofer, T., L. Venance, and C. Giaume. 2002. Control and plasticity of intercellular calcium waves in astrocytes: a modeling approach. J. Neurosci. 22:4850–4859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Koenigsberger, M., R. Sauser, M. Lamboley, J. L. Beny, and J. J. Meister. 2004. Ca2+ dynamics in a population of smooth muscle cells: modeling the recruitment and synchronization. Biophys. J. 87:92–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Roth, B. J., S. V. Yagodin, L. Holtzclaw, and J. T. Russell. 1995. A mathematical model of agonist-induced propagation of calcium waves in astrocytes. Cell Calcium. 17:53–64. [DOI] [PubMed] [Google Scholar]
- 20.Tsaneva-Atanasova, K. T., D. Yule, and J. Sneyd. 2004. Calcium oscillations in a triplet of pancreatic acinar cells. Biophys. J. 88:1535–1551 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jafri, M. S., and J. Keizer. 1994. Diffusion of inositol 1,4,5-trisphosphate but not Ca2+ is necessary for a class of inositol 1,4,5-trisphosphate-induced Ca2+ waves. Proc. Natl. Acad. Sci. USA. 91:9485–9489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.van Helden, D. F. 1993. Pacemaker potentials in lymphatic smooth muscle of the guinea-pig mesentery. J. Physiol. 471:465–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Best, L., and T. B. Bolton. 1986. Depolarisation of guinea-pig visceral smooth muscle causes hydrolysis of inositol phospholipids. Naunyn Schmiedebergs Arch. Pharmacol. 333:78–82. [DOI] [PubMed] [Google Scholar]
- 24.Itoh, T., N. Seki, S. Suzuki, S. Ito, J. Kajikuri, and H. Kuriyama. 1992. Membrane hyperpolarization inhibits agonist-induced synthesis of inositol 1,4,5-trisphosphate in rabbit mesenteric artery. J. Physiol. 451:307–328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Harootunian, A. T., J. P. Kao, S. Paranjape, S. R. Adams, B. V. Potter, and R. Y. Tsien. 1991. Cytosolic Ca2+ oscillations in REF52 fibroblasts: Ca(2+)-stimulated IP3 production or voltage-dependent Ca2+ channels as key positive feedback elements. Cell Calcium. 12:153–164. [DOI] [PubMed] [Google Scholar]
- 26.Harootunian, A. T., J. P. Kao, S. Paranjape, and R. Y. Tsien. 1991. Generation of calcium oscillations in fibroblasts by positive feedback between calcium and IP3. Science. 251:75–78. [DOI] [PubMed] [Google Scholar]
- 27.Daniel, E. E. 1987. Gap junctions in smooth muscle. In Cell-to-Cell Communication. W. C. De Mello, editor. Plenum Press, New York. 149–185.
- 28.Kuriyama, H. 1981. Excitation-contraction coupling in various visceral smooth muscles. In Smooth Muscle: An Assessment of Current Knowledge. E. Bulbring, A. F. Brading, A. W. Jones, and T. Tomita, T., editor. University of Texas Press, Austin, TX. 171–197.
- 29.Allbritton, N. L., T. Meyer, and L. Stryer. 1992. Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science. 258:1812–1815. [DOI] [PubMed] [Google Scholar]
- 30.Imtiaz, M. S., D. W. Smith, and D. F. Van Helden. 2002. A theoretical model of slow wave regulation using voltage-dependent synthesis of inositol 1,4,5-trisphosphate. Biophys. J. 83:1877–1890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Dupont, G., S. Swillens, C. Clair, T. Tordjmann, and L. Combettes. 2000. Hierarchical organization of calcium signals in hepatocytes: from experiments to models. Biochim. Biophys. Acta. 1498:134–152. [DOI] [PubMed] [Google Scholar]
- 32.Jafri, M. S., and B. Gillo. 1994. A membrane potential model with counterions for cytosolic calcium oscillations. Cell Calcium. 16:9–19. [DOI] [PubMed] [Google Scholar]
- 33.Donaldson, S. K., N. D. Goldberg, T. F. Walseth, and D. A. Huetteman. 1988. Voltage dependence of inositol 1,4,5-trisphosphate-induced Ca2+ release in peeled skeletal muscle fibers. Proc. Natl. Acad. Sci. USA. 85:5749–5753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Vergara, J., R. Y. Tsien, and M. Delay. 1985. Inositol 1,4,5-trisphosphate: a possible chemical link in excitation-contraction coupling in muscle. Proc. Natl. Acad. Sci. USA. 82:6352–6356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Mahaut-Smith, M. P., J. F. Hussain, and M. J. Mason. 1999. Depolarization-evoked Ca2+ release in a non-excitable cell, the rat megakaryocyte. J. Physiol. 515:385–390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Mason, M. J., J. F. Hussain, and M. P. Mahaut-Smith. 2000. A novel role for membrane potential in the modulation of intracellular Ca2+ oscillations in rat megakaryocytes. J. Physiol. 524:437–446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mason, M. J., and M. P. Mahaut-Smith. 2001. Voltage-dependent Ca2+ release in rat megakaryocytes requires functional IP3 receptors. J. Physiol. 533:175–183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Doedel, E., and J. P. Kernevez. 1986. AUTO:Software for Continuation and Bifurcation Problems in Ordinary Differential Equations. California Institute of Technology, Pasadena, CA.
- 39.Ermentrout, B. 2002. Simulating, Analyzing, and Animating Dynamical Systems: A Guide to Xppaut for Researchers and Students. SIAM, Philadelphia.
- 40.Kuramoto, Y. 1984. Chemical Oscillations, Waves, and Turbulence. Springer-Verlag, New York.
- 41.Ermentrout, G. B., and N. Kopell. 1984. Frequency plateaus in a chain of weakly coupled oscillators. SIAM J. Math. Anal. 15:215–237. [Google Scholar]
- 42.Imtiaz, M. S. 2003. Distributed Pacemaking through Coupled Oscillator-Based Mechanisms: A Basis for Long-Range Signalling in Smooth Muscle. The University of Newcastle, Newcastle, Australia.
- 43.De Blasio, B. F., J. G. Iversen, and J. A. Rottingen. 2004. Intercellular calcium signalling in cultured renal epithelia: a theoretical study of synchronization mode and pacemaker activity. Eur. Biophys. J. 33:657–670 (Epub.). [DOI] [PubMed] [Google Scholar]
- 44.Goel, P., and B. Ermentrout. 2002. Synchrony, stability, and firing patterns in pulse-coupled oscillators. Physica D. 163:191–216. [Google Scholar]
- 45.Glass, L., and M. C. Mackey. 1988. From Clocks to Chaos: The Rhythms Of Life. Princeton University Press, Princeton, N.J.
- 46.Ermentrout, B. 1996. Type I membranes, phase resetting curves, and synchrony. Neural Comput. 8:979–1001. [DOI] [PubMed] [Google Scholar]
- 47.FitzHugh, R. 1961. Impulses and physiological states in theoretical models of nerve membrane. Biophys. J. 1:445–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Nagumo, J., S. Arimoto, and S. Yoshizawa. 1962. An active pulse transmission line simulating nerve axon. Proc. Institute of Radio Engineers. 50:2061–2070. [Google Scholar]
- 49.Atri, A., J. Amundson, D. Clapham, and J. Sneyd. 1993. A single-pool model for intracellular calcium oscillations and waves in the Xenopus laevis oocyte. Biophys. J. 65:1727–1739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.De Young, G. W., and J. Keizer. 1992. A single-pool inositol 1,4,5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proc. Natl. Acad. Sci. USA. 89:9895–9899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Zhao, J., and D. F. van Helden. 2003. ET-1-associated vasomotion and vasospasm in lymphatic vessels of the guinea-pig mesentery. Br. J. Pharmacol. 140:1399–1413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Imtiaz, M. S., J. Zhao, and D. F. van Helden. 2002. A theoretical study of Ca2+ oscillations and pacemaker potentials underlying vasomotion in guinea-pig lymphatic smooth muscle. Proc. Aust. Health Med. Res. Cong. Abstr. 1148.
- 53.Zhao, J., M. Imtiaz, and D. van Helden. 2002. Ca2+ oscillations and pacemaker potentials underlying vasomotion of guinea-pig lymphatic smooth muscle. Proc. Aust. Health Med. Res. Cong. Abstr. 1149.
- 54.Dupont, G., T. Tordjmann, C. Clair, S. Swillens, M. Claret, and L. Combettes. 2000. Mechanism of receptor-oriented intercellular calcium wave propagation in hepatocytes. FASEB J. 14:279–289. [DOI] [PubMed] [Google Scholar]
- 55.Van Vreeswijk, C., L. F. Abbott, and G. B. Ermentrout. 1994. When inhibition not excitation synchronizes neural firing. J. Comput. Neurosci. 1:313–321. [DOI] [PubMed] [Google Scholar]
- 56.Haddock, R. E., and C. E. Hill. 2002. Differential activation of ion channels by inositol 1,4,5-trisphosphate (IP(3))- and ryanodine-sensitive calcium stores in rat basilar artery vasomotion. J. Physiol. 545:615–627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Alvarez, V. A., C. C. Chow, E. J. Van Bockstaele, and J. T. Williams. 2002. Frequency-dependent synchrony in locus ceruleus: role of electrotonic coupling. Proc. Natl. Acad. Sci. USA. 99:4032–4036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Dupont, G., and A. Goldbeter. 1993. One-pool model for Ca2+ oscillations involving Ca2+ and inositol 1,4,5-trisphosphate as co-agonists for Ca2+ release. Cell Calcium. 14:311–322. [DOI] [PubMed] [Google Scholar]


















