Ca²⁺ Changes the Force Sensitivity of the Hair-Cell Transduction Channel

Abstract

The mechanically gated transduction channels of vertebrate hair cells tend to close in ∼1 ms after their activation by hair bundle deflection. This fast adaptation is correlated with a quick negative movement of the bundle (a “twitch”), which can exert force and may mediate an active mechanical amplification of sound stimuli in hearing organs. We used an optical trap to deflect bullfrog hair bundles and to measure bundle movement while controlling Ca²⁺ entry with a voltage clamp. The twitch elicited by repolarization of the cell varied with force applied to the bundle, going to zero where channels were all open or closed. The force dependence is quantitatively consistent with a model in which a Ca²⁺-bound channel requires ∼3 pN more force to open, and rules out other models for the site of Ca²⁺ action. In addition, we characterized a faster, voltage-dependent “flick”, which requires intact tip links but not current through transduction channels.

INTRODUCTION

The extraordinarily high sensitivity and sharp frequency tuning of mammalian hearing require the presence of an active mechanical amplification, a process that apparently resides within the mechanosensitive hair cells themselves (1,2). By selectively increasing the vibration of the basilar membrane on which hair cells ride, this “cochlear amplifier” contributes up to 50 dB of gain to the acoustic signal (3).

Two different mechanisms have been proposed to underlie the cochlear amplifier: a shortening of cochlear outer hair cells driven by depolarization (“electromotility”) (4,5), and a quick negative movement of the hair cells' mechanosensitive stereocilia caused by Ca²⁺ entry through transduction channels, which is associated with “fast adaptation” (6–8). In fast adaptation, Ca²⁺ entering through transduction channels at the tips of stereocilia is thought to bind directly to the channels or to associated components of the transduction apparatus, thereby promoting channel closure and rapidly reducing the receptor current. When they close, the channels would exert a small force on the filamentous linkages between stereocilia and move the bundle of stereocilia by a few nanometers (the “twitch”) (6). Bundles pushing back against the overlying tectorial membrane, if in phase with the stimulus, might then amplify the mechanical stimulus (9,10). Since fast adaptation has been observed in a variety of species and hair cell organs (6,8,11–14), the hair-bundle-based mechanism is attractive for nonmammalian hearing organs, which lack electromotility but have cochlear amplification qualitatively similar to that found in mammals (15). This mechanism is also attractive for the mammalian cochlea: because fast adaptation is associated with ion entry through transduction channels rather than with the subsequent receptor potential, it might operate at higher speeds.

To determine whether fast adaptation and its associated movement could mediate amplification, we must understand how it works. Several Ca²⁺-dependent mechanisms for fast adaptation have been proposed that could produce both the decline in current and a corresponding twitch movement: First, Ca²⁺ could bind directly to the transduction channel to stabilize the closed state and thereby shift the P_o(F) relation (6,8). Second, Ca²⁺ could bind to an intracellular elastic “reclosure element” in series with the channel, reducing its spring constant, and the reduced tension would allow channels to close (16). Third, Ca²⁺ could bind to a “release element” in series with the channel so as to lengthen it by a fixed distance, releasing tension in an elastic element and again allowing closure (17). An understanding of the biophysics of the underlying mechanism would permit a quantitative assessment of whether fast adaptation could mediate the cochlear amplifier, and would provide data on its force and speed that could be incorporated into amplification models.

To distinguish among these three potential mechanisms, we have made simultaneous electrical and mechanical measurements of fast adaptation in single bullfrog hair cells. Receptor currents were recorded and Ca²⁺ entry was controlled using whole-cell patch-clamp techniques, while a gradient-force optical trap was used to apply forces to hair bundles and to measure force- and Ca²⁺-dependent bundle movements. We found that fast adaptation is only consistent with a model in which Ca²⁺ directly promotes channel closure, and in which channels altered by Ca²⁺ binding require 2.9 ± 0.5 pN more force to open. In addition, we characterized another voltage-dependent movement (the “flick”) that is apparently associated with transduction channels but not with their mechanical gating.

MATERIALS AND METHODS

Electrophysiological recording

Single hair cells were dissociated from the saccule of adult bullfrogs (Rana catesbeiana) in low-Ca²⁺ saline composed of (in mM) 120 Na⁺, 2 K⁺, 0.1 Ca²⁺, 122 Cl⁻, 3 dextrose, and 5 HEPES, pH 7.27, as previously described (18). The basal surface of the sensory epithelium was additionally bathed in 1 mM EGTA and 1 mM Mg²⁺ for 15 min before its removal from the whole saccule, to loosen the hair cells. The sensory epithelium was then treated with 50 μg/ml protease XXIV (Sigma, St. Louis, MO) for 22 min and 60 μg/ml deoxyribonuclease (type I, Sigma) for 5 min, and the otolithic membrane was removed. Using an eyelash (90-μm base diameter tapering to 20 μm), the hair cells were dissociated from the whole epithelium onto a clean coverslip and the bath was replaced with an external solution containing (in mM) 120 Na⁺, 2 K⁺, 5 Cs⁺, 4 Ca²⁺, 135 Cl⁻, 3 dextrose, and 5 HEPES, pH 7.27. The chamber was continuously perfused throughout experiments unless otherwise indicated. In some experiments, the external solution was exchanged with one containing 0.1 Ca²⁺, or one with 0.1 Ca²⁺ and 0.2 mM gentamicin (Sigma). Pipettes were filled with an internal solution containing (in mM) 105 Cs⁺, 3 Mg²⁺, 111 Cl⁻, 3 NaATP, 1 BAPTA, and 5 HEPES, pH 7.25. All solutions were at room temperature (22–23°C) and, except for the internal solution, were all oxygenated.

Whole-cell patch-clamp recordings were made using conventional patch-clamp techniques (200B, Axon Instruments, Union City, CA) with acquisition and analysis programs written in LabView 5.1 (National Instruments, Austin, TX). The acquisition program generated the voltage and two-dimensional mechanical commands synchronously via two hardware-connected A/D boards (National Instruments). For recordings using voltage steps, the borosilicate recording pipettes were coated with Sylgard (Dow Corning, Midland, MI) to reduce capacitance. The residual series resistance was 2–5 MΩ after ∼85% compensation. The time constant of the clamp was 40–80 μs; the voltage error was 2–5 mV for ΔV = 180 mV, the largest voltage step applied. Records were filtered with a Bessel filter (Krohn-Hite, Brockton, MA) at 20 kHz.

The magnitudes of fast and slow adaptation were measured using the inferred shift of the instantaneous I(X) curve (19). Since both forms of adaptation act by shifting the nonlinear instantaneous activation curve while preserving its slope and amplitude (see Results), the extent of adaptation at each point in time can be calculated from the value of the current and compared with I(X) to see how far the curve must have shifted to produce that value. Fits to the extent of adaptation with a sum of two exponentials give the time constant and amplitude (in units of extent shift) of fast and slow adaptation; complete adaptation produces extent shift that equals the bundle deflection.

Optical trap

An optical trap was constructed using a Nd:YAG laser (Spectra Physics, Mountain View, CA) on an inverted microscope (Zeiss IM-35) with a high numerical aperture microscope objective (Nikon Fluor 40X, NA = 1.3). The beam was deflected with a two-dimensional acousto-optic deflection (AOD) system (IntraAction, Bellwood, IL), following the design of Visscher and Block (20). To exert sufficient force (>100 pN) on the hair bundle, a high power laser (∼2 W at 1064 nm) was used to form the optical trap.

A digital frequency synthesizer controlled the two axes of the AODs separately, and the AODs were positioned such that an angle change of the beam by the AODs would result in pure translation of the beam at the specimen. The trap position in the specimen plane could be controlled both electronically using the AODs and manually by moving a lens; using the AODs, the trap could be displaced by ∼5 μm in the x and y planes with constant trap stiffness.

To deliver beads near the hair cells without damaging the bundles, a dilute solution of 2.03 ± 0.03 μm polystyrene beads (mean ± SD, catalogue No. PS05N, lot No. 1072, Bangs Laboratories, Fischer, IN) in external solution (0.1 μg/ml) was slowly introduced to the bottom of the recording dish via a glass pipette. A single bead was trapped and its position signal was calibrated, and then the bead was attached to the kinociliary bulb of a hair cell using the trap to press it against the bulb. Only hair cells whose beads were well attached to the bulbs and whose cell bodies were well adhered to the coverslip were analyzed. After the bead was attached, the patch pipette was brought close to the cell, a gigaseal was established, and the cell membrane was ruptured to allow whole-cell recording. Care was taken to keep the pipette away from the detection beam path. Displacement traces made before and after the patch pipette was introduced for some cells showed that the pipette itself did not alter the displacement calibration. Because our beam displacement was two-dimensional, there was no constraint as to the orientation of the cell relative to the patch pipette. We saw the same behavior regardless of cell orientations, so possible systematic errors caused by electrostriction of the headstage and pipette apparatus are unlikely.

The detection of bead movements also followed the strategy of Visscher and Block (20). The deflection of the hair-cell bundles was measured using a lower-powered HeNe laser (JDS-Uniphase, San Jose, CA, 633 nm, 5 mW) using the same beam path as the optical trap. After passing through the bead, the light was imaged onto a quadrant photodiode positioned along the beam axis in the aperture plane such that only a relative displacement of the bead and HeNe laser, but not the movement of bead and laser together, would change the signal. The displacement of every bead was calibrated and recorded with step displacements of the trap before attaching it to the bundle. Calibration procedures are described in Supplementary Material.

The force of the optical trap was linear with displacements up to 550 nm, and so the trap could be characterized as a spring with a fixed stiffness. We generally operated with a laser power corresponding to a trap stiffness of 125 μN/m. The stiffness of hair bundles in these cells was typically ∼300 μN/m, significantly more than trap stiffness, so displacement of the trap center approximated a force stimulus to the bundle. With the detection beam, we measured the displacement of the bead relative to the trap center and calculated the force on the bead by Hooke's law. Using the acousto-optic deflectors, the trapping beam could be moved in ∼15 μs. The rise time for bundle deflection was then limited by the parallel stiffness of the trap and bundle and by the viscous drag on the bead and bundle, and was typically 200–400 μs.

THEORY

Model for repolarization-evoked twitch

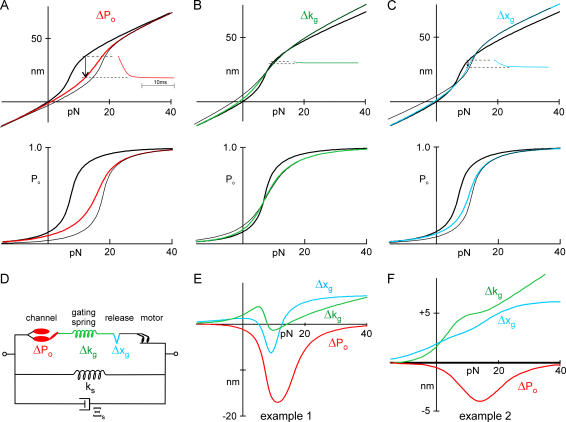
To differentiate among three possible sites of Ca²⁺ action, we used a common model of bundle mechanics (6,8,19) that incorporates five main elements (Fig. 1 D, values in Table 1): the viscous drag on the bundle Ξ_s, the stereocilia pivot spring K_s, the gating springs K_g, the gates of the transduction channels with swing d and force dependence P_o(F), and myosin-based adaptation motors. The myosin motor, simplified in Fig. 1 D, consists of a force generator F_m, a dashpot with drag Ξ_m, and an additional “extent spring” with stiffness K_e to account for incomplete adaptation. To the model we added three possible Ca²⁺ binding sites: at a channel whose open probability as a function of force, P_o(F), was shifted by Ca²⁺ binding; at a release element that relaxed by a fixed distance when Ca²⁺ bound; or at a gating spring with a stiffness that was changed by Ca²⁺ binding.

FIGURE 1.

Calculation of bundle movement for three sites of Ca²⁺ binding. See text for details. (A–C) Models in which Ca²⁺ affects the force dependence of channel open probability (ΔP_o), the stiffness of the gating spring (Δk_g), or the relaxation of a release element (Δx_g). Top: Predicted X(F) relation as measured at the tip of a hair bundle. (Inset) Predicted movement of a bundle upon Ca²⁺ entry. (Bottom) Predicted P_o(F) curve. (Thick lines) Ca²⁺ sites unbound; (thin lines) Ca²⁺ sites bound; (colored lines) steady-state and incorporate probability of site occupancy. (D) Schematic of model elements. (E) Predicted bundle movement upon Ca²⁺ entry for three models, with extreme parameters (Table 1) for channel number and gate swing. (F) Predicted bundle movement upon Ca²⁺ entry for three models, with parameters as measured for the cell in Fig 7.

TABLE 1.

Parameters for model predictions and fits to data

	Example 1 Fig. 1 E	Example 2 Fig. 1 F	Fit of Fig. 2	Fit of Fig. 7	Average fit (±SE, n = 6)	Model Fig. 8	Units
Ks	400	270	40	270	112 ± 27	40	μN m−1
Ξb	12	12	150	12	12	150	nN s m−1
Nc	80	25	28	25	24.1 ± 3.3	30	channels
Nt	40	12.5	14	12.5	12.0 ± 1.6	15	tip links
Kg	550	390	200	390	152 ± 44	200	μN m−1
κg ( = Kg/(Ntγ2))	702	1592	729	1592	763 ± 218	680	μN m−1
d	4	1.7	2.44	1.7	2.5 ± 0.5	3.15	nm
z ( = dκgγ)	393	379	249	379	212 ± 39	300	fN
x0 (Ca unbound)	20	20	36.7	13.8		29.3	nm
Δfo ( tip-link axis, upon Ca2+ binding)	1.3	2.8	7.9	1.5	2.9 ± 0.5	28.6	pN
Δxg ( tip-link axis, upon Ca2+ binding)	2.1	2.1		−0.29			nm
Δκg ( tip-link axis, upon Ca2+ binding)	−191.3	−432.7		35.1			μN m−1
[Ca2+]P = 1	40	40	40	40	40	40	μM
[Ca2+]P = 0	0.015	0.015	0.015	0.015	0.015	0.015	μM
kon	10.2	10.2	10.2	10.2	10.2	10.2	× 106 M−1s−1
koff	150	150	150	150	150	150	s−1
Fm(Ca2+ bound)						130	pN
Fm(Ca2+ unbound)			225	225		250	pN
Kd(motor)						120	μM
Ke			54	134		550	μN m−1
Ξm			1.3	4.3		4.3	μN s m−1
Ktrap			125	125		125	μN m−1

K_s is the stiffness of the bundle and Ξ_b is the damping coefficient (in tip coordinates), the geometry factor γ (=0.14) is the ratio of tip shear to tip deflection, N_t is the number of tip links, N_c ( = 2N_t) is the number of transduction channels, κ_g is the stiffness of an individual gating spring, K_g ( = N_tγ²κ_g) is the combined stiffness of all gating springs, d is the gating swing of the transduction channel, z ( = dκ_gγ) is the gating sensitivity, and x₀ is the activation curve offset (to P_o = 0.5) when Ca²⁺ is unbound. Three parameters describe three possible actions of Ca²⁺: Δf_o is the additional force to open an individual Ca²⁺-bound channel, Δx_g is the relaxation of an individual release element, and Δκ_g is the change in stiffness of an individual gating spring. Ca²⁺ binding to the fast adaptation site and to the slow adaptation motor has seven parameters: [Ca²⁺]_{P = 1} and [Ca²⁺]_{P = 0} are the concentration near an open or closed transduction channel, k_on is the binding rate to the fast adaptation site and k_off the unbinding rate, F_m(Ca²⁺-bound) is the force exerted by all the slow adaptation motors when Ca²⁺ is bound, and F_m(Ca²⁺ unbound) the force when unbound in tip coordinates, and K_d(motor) is the Ca²⁺ dissociation constant for the motor. K_e is the stiffness of all the extent springs, Ξ_m is the damping coefficient that characterizes the speed of the adaptation motor, and K_trap is the stiffness of the optical trap.

In earlier models of hair-cell transduction, it was assumed that the extracellular tip links were the morphological correlate of the gating springs. More recently, it has been argued that the tip links are stiff and that the gating spring is more likely to be intracellular (21–23). In this analysis, all the elastic elements that are in series with the transduction channel are combined in a single element, so that if part or all of the gating spring is intracellular, then Ca²⁺ influx might affect its stiffness.

Behavior of individual transduction elements was modeled and converted to forces and distances measurable at the tip of a hair bundle, based on the number and dimensions of bullfrog stereocilia. In brief, distances were adjusted by the geometric factor γ = 0.14, which is the shear between adjacent stereocilia (and the approximate stretch of each gating spring) divided by the deflection at the tip of the kinocilium. Forces were adjusted for the number of tip links and number of stereocilia per bundle. In the model, the release elements, gating springs, and transduction channels of a hair bundle were each lumped into a single element. Although the effect of Ca²⁺ binding is properly calculated by summing two populations of transduction elements, those with and without Ca²⁺ bound, we used for simplicity single elements with a Ca²⁺-dependent parameter that was intermediate between the two extremes, based on the proportion of sites bound (8).

Instantaneous bundle mechanics

The open probability of transduction channels (measured at the tip) depends on the extension of the gating spring and its stiffness κ_g and on the swing of the channel's gate d, and it is characterized as the gating sensitivity of the channel z = κ_gdγ, where γ is the bundle's geometric factor (6). The extension of the gating spring, in tip coordinates, is X_s−X_e, where X_s is the position of the tip and X_e (the extension of the extent spring) is a measure of myosin-based adaptation. X_o is an offset that accounts for an open probability <0.5 at the rest position. Then

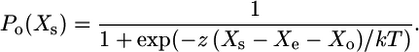(1)

The instantaneous force on the bundle is then

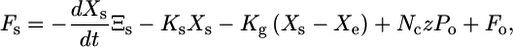(2)

where the first term is the viscous drag, the second is exerted by stereocilia pivots, the third is exerted by gating springs, the fourth incorporates gating stiffness, and F_o is an offset force reflecting static myosin motors.

Current was calculated using Eq. 1, and movement of the bundle was calculated using an iterative solution to Eq. 2.

Ca²⁺ dynamics

Since Ca²⁺ concentration is estimated to equilibrate near the channel within microseconds of channel opening (24), the concentration of Ca²⁺ near the binding site was assumed to be instantaneously proportional to P_o. Lumpkin and Hudspeth (24) calculated that Ca²⁺ concentration near the channel is 33 μM when the channels are open and 0.05 μM when closed, with the cell at −60 mV and with 4 mM external [Ca²⁺]. We assumed Ca²⁺ binding and unbinding rate constants k_on = 10⁷ M⁻¹ s⁻¹ and k_off = 150 s⁻¹ to match the initial time course of fast adaptation and to give a K_d of 15 μM, and we assumed its effect is proportional to the fraction of sites bound.

Predictions of the model

We first explored the action of Ca²⁺ using parameters that are extreme relative to those measured from frog hair cells, to emphasize the differences among the models. The myosin-based slow adaptation was omitted for this exploration because its contribution is relatively small at these short timescales.

In each case, the predicted relation between bundle deflection and force, X(F), would be linear up to the point where channels begin to open (Fig. 1, A–C, top, thick lines). The slope would then increase over the channel activation range due to the gate swing of the channel (6) before returning to linearity where all channels are open. We considered the mechanical consequences of Ca²⁺ binding to each of three different binding sites: when Ca²⁺ bound to the channel to shift the P_o(F) relation, the force to open a channel was increased (Δf₀) by 1.3 pN; when Ca²⁺ bound to the gating spring, its stiffness was decreased (Δκ_g) by ∼190 μN m⁻¹; when Ca²⁺ bound to the release element, it lengthened (Δx_g) by 2.1 nm (see Table 1, Example 1).

P_o(F) shift

If Ca²⁺-bound channels require a larger force to open, the Ca²⁺-bound X(F) curve (Fig. 1 A, thin black line) would be identical to the unbound curve at large negative and positive forces, but would be shifted along the line representing the parallel stiffness of K_s + K_g.

Experimental application of a fixed force to a resting bundle (∼12 pN in this example) would move the bundle to the coordinate position on the Ca²⁺-unbound X(F) curve (∼35 nm in this example) and would open channels. Sudden entry and binding of Ca²⁺, either from channel opening or from repolarization to allow Ca²⁺ entry through open channels, would move the bundle from its unbound X(F) curve toward its bound curve; as channels then close, the bundle would move in the negative direction (by ∼20 nm in this example; arrow in Fig. 1 A). Because Ca²⁺ influx is low when a channel's open probability is low, the channels' Ca²⁺ binding sites might not be saturated for moderate forces that partially activate channels. Thus we can calculate a steady-state X(F) curve, which takes into account the open probability and represents a transition from unbound to bound curves (Fig. 1 A, red line). The difference between the X(F) curve at steady state and with Ca²⁺ unbound represents the predicted movement upon Ca²⁺ entry; it shows a large negative peak near the center of the activation curve but increases to zero for large positive and negative forces (Fig. 1 E, red line). The inset of Fig. 1 A (red line) shows the expected bundle movement as a function of time due to Ca²⁺ entry after repolarization, with 12 pN applied to the bundle. A separate plot of the open probability P_o(F) (Fig. 1 A, bottom) shows adaptation by the shift to the right (thin black line); at steady state, the activation curve would broaden (red line).

Gating spring stiffness

A qualitatively similar movement might result from binding to other intracellular elements associated with the transduction apparatus. Bozovic and Hudspeth (16) have suggested that Ca²⁺ could bind to an elastic “reclosure element” in series with the gating spring, decreasing its stiffness. This element might be the gating spring itself or in series with it; either way, the effective stiffness K_g would be reduced by Ca²⁺ binding. The activation curve is determined by the product of the channel gate swing and K_g, and so a decrease in K_g would broaden it (Fig. 1 B, bottom: thick black line, Ca²⁺ unbound; thin black line, Ca²⁺ bound; green line, steady state). The overall X(F) curve would become shallower when Ca²⁺ binds, because of a decrease in overall bundle stiffness and the broader activation curve (Fig. 1 B, top, green line).

For a sufficiently large gate swing, the change in activation slope is large enough that for some range of forces the bound X(F) curve (Fig. 1 B, top, thin black line) is below the unbound curve (Fig. 1 B, top, thick line), indicating that the bundle would move in the negative direction upon Ca²⁺ binding. The difference curve between the unbound state and steady-state (Fig. 1 E, green line) would be negative only near the center of the activation curve, and so the bundle movement after Ca²⁺ entry would be negative only in this range. In qualitative terms, resting tension in the gating spring normally pulls a bundle in the negative direction, and Ca²⁺-dependent reduction in K_g should generally reduce tension and allow a positive bundle movement. Over a certain range of parameters, decreased tension on a channel allows it to close, but the large gate swing paradoxically increases the tension on the gating spring sufficiently that the bundle moves negatively. Using the same bundle parameters used in the inset of Fig. 1 A, we simulated the bundle movement after Ca²⁺ entry at a force step corresponding to the largest negative movement (Fig. 1 B, inset). Similar simulations were done for a range of forces (Fig. 1 E, green line).

Release element

A Ca²⁺-dependent element could release the gating spring by a fixed distance Δx_g (17). In this model, the X(F) curve would shift along a line representing the pivot stiffness K_s when Ca²⁺ binds. For most values of force, the Ca²⁺-bound X(F) curve would be above the unbound curve (Fig. 1 C, thick black and thin black lines, respectively), and relaxation of a release element would cause the bundle to relax forward. Around the center of the activation curve, a large gate swing can allow paradoxical movement in the negative direction upon Ca²⁺ binding. Similar bundle movement (arrow) is shown in the inset using the same bundle parameters as in Fig. 1, A and B, and a force step corresponding to ∼10 pN. Predicted movement as a function of force is shown in Fig. 1 E (blue line). As in the ΔP_o example, the P_o(F) curve would be shifted without broadening when Ca²⁺ binds (Fig. 1 C, bottom, thin black line).

Summary of predictions

Although the three versions all produce negative movement for some range of force with these extreme parameters, we can distinguish among them from their quantitatively different predictions of bundle movement due to Ca²⁺ binding, especially at large values of force (e.g., Fig. 1 E). Also, the two release element versions produce the “paradoxical” backward movement only for large values of d and K_g. If we use real bundle parameters, averaged from measurements on seven cells, the differences between these Ca²⁺ sites is even more pronounced: the bundle would only move backward if Ca²⁺ directly shifted the P_o(F) relation (Fig. 1 F). We used these three versions of the model to fit our data. Each fit used bundle and transduction parameters measured independently and had only one free parameter—Δf₀, Δκ_g, or Δx_g—corresponding to the Ca²⁺ binding site for that version.

RESULTS

Movement of a hair bundle in response to force steps

We dissociated hair cells from bullfrog saccules, and used the whole-cell patch clamp method to control transmembrane voltage and record receptor current. To deflect a hair bundle and measure its movement, we attached a polystyrene bead to the bulb of the bundle's kinocilium, which is itself attached to the adjacent stereocilia. Forces were applied to the bead by means of an optical trap using infrared laser of 1064-nm wavelength focused on the specimen plane. With a second beam of wavelength 633 nm, we measured the bead position and calculated the force on it. Bundle deflection rise time was limited by the viscous drag on the bead and bundle, and was typically 200–400 μs.

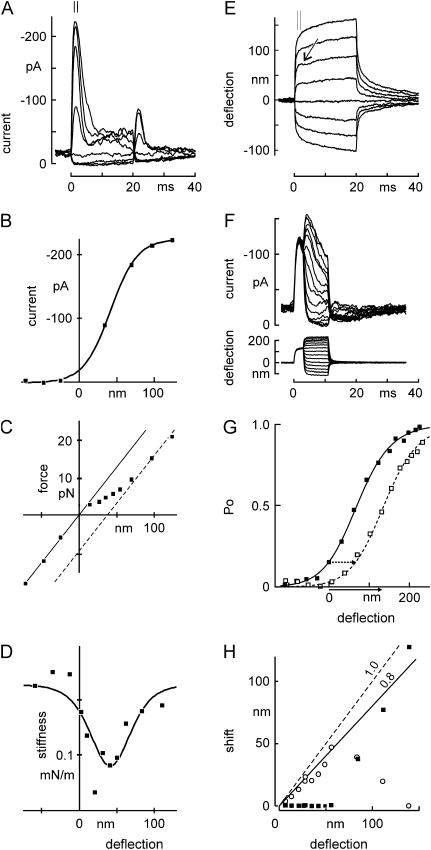
We first asked whether hair cells stimulated in this manner showed the same electrical and mechanical responses as previously observed. Positive force steps, which deflect a bundle toward its kinocilium, elicited rapidly activating transduction currents which saturated with 100- to 150-nm bundle deflection (Fig. 2 A). The activation curve thus measured (Fig. 2 B) was narrower than previously measured for bullfrog hair cells by our group using stimulators with slower rise times (19), but comparable to those measured with fast stimulators in bullfrog and turtle (6,8,25). These force steps elicited rapid deflections of the hair bundle (Fig. 2 E), whose initial amplitude was not linear with force applied to the bead (Fig. 2 C). Instead, the relationship between force and deflection was linear (displaying a bundle stiffness of 240 μN/m) up to the point where transduction channels began to open, then showed a lower slope over the range where channels opened, and returned to linearity with the initial slope once all channels were open. This form of F(X) curve results from the conformational change associated with channel opening (6). The derivative of the curve (Fig. 2 D) represents the bundle stiffness as a function of deflection; the stiffness dip has been termed “gating compliance”, and the number of transduction channels and their gate swing can be calculated from a fit to this curve (6; see Methods). Based on these calculations, this cell had 30 channels and the “gate swing” was 2.5 nm, assuming one channel at each end of a tip link. The number of channels and their gate swing can be independently calculated from the instantaneous I(X) curve, if the single-channel conductance and gating-spring stiffness are known. Using those methods, the cell had 28 channels with a gate swing of 2.2 nm, assuming a single-channel conductance of 100 pS and gating-spring stiffness K_g of 200 μN/m, relative to the tip of the bundle (or κ_g = 729 μN/m relative to the tip-link axis). In eight cells, we found an average of 23 ± 3 channels and a gate swing of 2.5 ± 0.5 nm (channels at each end of the tip link, mean ± SE).

FIGURE 2.

Mechanical and electrical responses to a family of force steps. (A) Receptor current elicited by deflection of a hair bundle with the optical trap. The receptor current showed a rapid activation for positive deflections, followed by a fast (∼5-ms) phase of adaptation. A second phase of slower adaptation was apparent with longer stimuli. Negative deflections also produced adaptation, as shown by a rebound transient current upon termination. Inward current is shown as upwards. (B) Peak receptor current as a function of deflection. The current was averaged from 1.0 to 2.0 ms after deflection (indicated by bars in A). Deflections were measured from E during the same time interval. The smooth curve is a first-order Boltzmann relation with midpoint at 41 nm and steepness of 18 nm. (C) Force versus deflection, with force measured at the peak of the receptor current. Deflections are from E, and forces were calculated from the deviation between bead position and trap center. Note that the figure has axes reversed from Fig. 1, A–C, top, but illustrates the same phenomena. Consistent with the gating-spring model of transduction, the “instantaneous” F(X) relation lies between two lines of the same slope, corresponding to transduction channels all closed (solid line) or all open (dotted line). (D) Instantaneous stiffness of the bundle as a function of bundle deflection. The stiffness (calculated by stepwise differentiating the force with respect to displacement in C) showed the characteristic dip near the center of the I(X) curve due to gating compliance. The curve is the derivative of a fit by eye to the data in C. (E) Bundle movement with two phases. The bundle movement corresponding to A showed a fast (0.2-ms) deflection followed by a slow relaxation for large deflections. For small positive deflections, an additional small and rapid negative movement occurred at the same timescale (2–4 ms) as the fast phase of adaptation (arrow). (F) Stimulus protocol to test the mechanism of fast adaptation. An adapting step of 130 nm was presented for 3 ms and followed by test steps of amplitudes between −112 and + 226 nm. A different cell is depicted from that of A–E. (G) I(X) curves measured with (open symbols, data from F) or without (solid symbols, data not shown) a 3-ms adapting step of 130 nm. The solid line is a fit by eye to the resting I(X) curve; the dashed line is the same but shifted to the right by 67 nm. (H) Amplitudes of fast and slow adaptation with increasing deflection, in a third cell. Adaptation was measured as an inferred shift with time (calculated from the receptor current and the measured I(X) relation), and the shift with time was fitted with a double exponential relation. The fast phase of I(X) shift (○) showed near-complete adaptation for small steps but declined for larger steps, whereas the slower phase (▪) was negligible for small steps, and rose to ∼80% for larger steps.

After its initial activation by bundle deflection, the transduction current rapidly adapted toward the resting level (Fig. 2 A). Adaptation to positive stimuli occurred in two phases: a fast phase with a time constant of ∼2 ms, and a slower phase of tens of milliseconds (more apparent in longer deflections; see Fig. 6). Fast adaptation was coincident with a small, negative movement of the bundle, sometimes called a “twitch” (Fig. 2 E, arrow). The slower phase of adaptation had the same time course as a slower, positive relaxation of the bundle, as has been seen in bullfrog hair cells (6,11).

FIGURE 6.

Kinetics of fast adaptation and the twitch. Ca²⁺ influx was reduced by a change in membrane potential delivered 30 ms before a force step. The time course of fast adaptation (indicated by parallel lines) matched that of the negative-going twitch. Both slowed at more positive potentials by a similar amount. 4 mM Ca²⁺ external solution.

Both fast and slow adaptation have been characterized as a shift of the I(X) curve without a change in amplitude, although experimental protocols to observe the I(X) shift directly have primarily measured the slow component (12,26). In other cells, we asked whether the fast component could also be described as a simple shift, by giving adapting steps of one amplitude, followed in 3 ms by test steps of variable amplitude (Fig. 2 F). The I(X) curve measured after 3 ms could be fitted well by shifting the unadapted I(X) curve without changing its amplitude (Fig. 2 G). In this cell, the curve shifted by 67 nm for a test step amplitude of 130 nm; slow adaptation could account for only ∼10 nm of shift, so the shift is mostly a result of fast adaptation. Measurements in other cells and with other adapting amplitudes gave the same result.

Fast adaptation was much more pronounced for small deflections, in the range of 0–50 nm, whereas slow adaptation had a larger relative amplitude for large deflections (Fig. 2 H). A similar distinction between fast and slow adaptation has been seen in turtle, mouse, and frog hair cells (8,14). In this Ca²⁺ concentration, the sum of fast and slow adaptation was typically ∼80%, similar to that observed earlier in bullfrog hair cells (19).

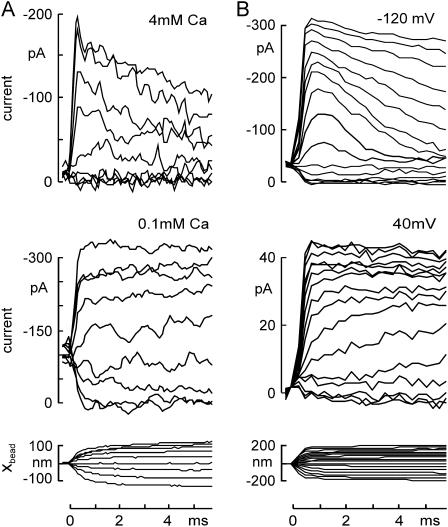
The rate and extent of adaptation in hair cells depends upon the entry of Ca²⁺ through the transduction channels (26–30). We found that fast adaptation after force steps was slowed either by reducing the external Ca²⁺ concentration (from 4 to 0.1 mM Ca²⁺; Fig. 3 A) or by depolarizing the cell to lower the driving force for Ca²⁺ entry (from −120 to +40 mV; Fig. 3 B).

FIGURE 3.

Changing adaptation rate by influencing Ca²⁺ influx through transduction channels. (A) Adaptation slowed by reducing external Ca²⁺ concentration. Transduction currents, evoked by a family of 6-ms force steps and recorded at −80 mV, showed robust adaptation in 4 mM Ca²⁺ external solution (top), which was slowed by reducing the external Ca²⁺ concentration to 0.1 mM (middle). The corresponding bundle deflection in 4 mM Ca²⁺ is shown (bottom). Force steps were from −30 to +65 pN. (B) Adaptation slowed by depolarizing the cell. Holding potential was changed to −120 mV (top) or to +40 mV (middle) 4 ms before the force steps. Adaptation of the transduction current was largely abolished at +40 mV. In addition, channels appeared to open more slowly. The bundle deflection at −120 mV is shown (bottom).

In all these respects, bullfrog hair cells stimulated by force steps from the optical trap behaved like bullfrog, turtle, mouse and rat vestibular and cochlear hair cells when stimulated with fast mechanical probes (6,13,14,30), validating the new stimulus method.

Three phases of movement evoked by depolarization

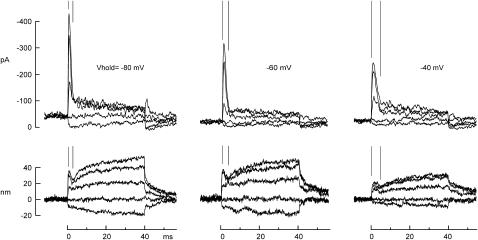
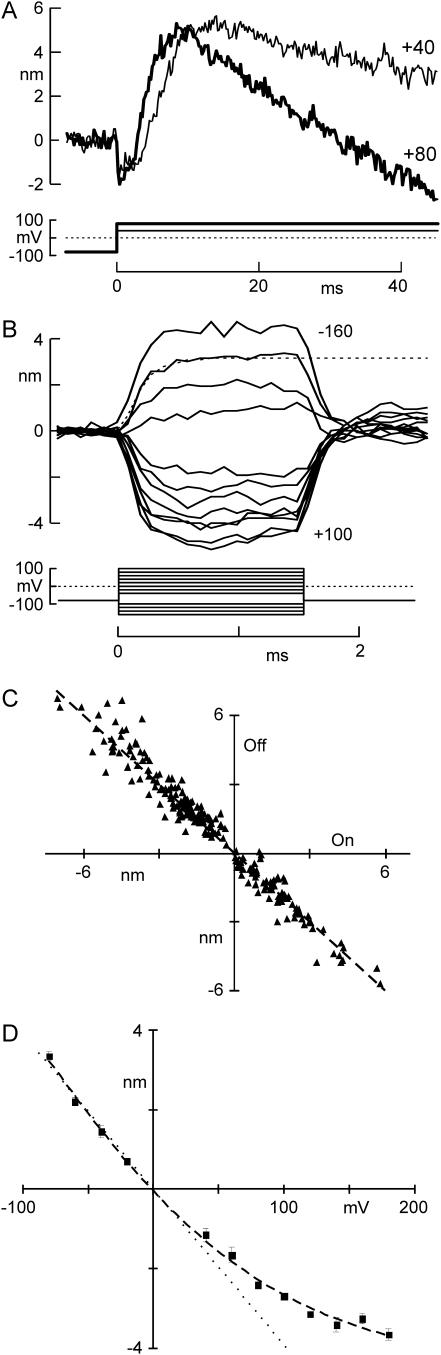
By changing Ca²⁺ influx through open transduction channels and thus changing the forces produced by the fast and slow adaptation processes, voltage alone can produce movement of a hair bundle (10,26,28). In response to a depolarizing voltage step, we found that a freestanding hair bundle moved in three distinct phases (Fig. 4 A). The slowest phase occurred in tens of milliseconds and was negative-going; it is thought to be the mechanical correlate of slow adaptation and is attributed to the myosin-1c motor complex climbing up the actin cores of stereocilia (8,12,26,31). This phase occurred more rapidly for depolarizations to +80 mV than for those to +40 mV, so the regulation of myosin-1c was apparently sensitive to the slight difference in Ca²⁺ influx between these two voltages. The middle phase was positive-going and took place in a few milliseconds, the same timescale as fast adaptation; it is thought to be a voltage-induced twitch corresponding to the relaxation in tip link tension when channels open after Ca²⁺ unbinds from some intracellular element (10,25,30). The fastest phase was a negative movement with depolarization, which we term the “flick”. This movement was previously observed in turtle hair cells, where it was described as being linearly voltage-dependent and occurring as fast as the voltage clamp could depolarize the cell (30).

FIGURE 4.

Hair bundle movement induced by voltage steps. (A) Depolarization-evoked movement of unrestrained hair bundles occurred in three phases: a fast negative phase (“flick”), a subsequent positive phase (“twitch”) and a slow negative phase (slow adaptation). Stepping to +80 mV produced faster movements for the two later phases than stepping to +40mV, but did not affect the time course of the flick. (B) Short voltage steps applied to measure the flick in isolation from slower phases. Hyperpolarizations produced positive movements, whereas depolarizations caused negative movements. The dashed line is an exponential fit with a time constant τ = 165 μs. (C) Equal magnitude of the flick at the onset and offset of the voltage steps (least-squares fit: slope = −1.03, R = 0.978, N = 18 cells). (D) Voltage dependence of flick, shown as change from the holding potential of −80 mV. The flick depended linearly on voltage changes from −80 to +140 mV, but became sublinear for more positive voltages. Dashed line is a Boltzmann fit with dx = 96 mV and x₀ = −102 mV.

The “flick”: a fast, voltage-dependent movement

We first characterized the flick to determine whether it was related to fast adaptation or represented an independent phenomenon. We applied 1.5 ms voltage steps to unrestrained hair cells and measured the movement of a bead attached to the kinociliary bulb (Fig. 4 B). The magnitude of the flick varied from cell to cell, ranging from 1 to 6 nm with an average of 3.2 ± 1.4 nm (N = 6) for a 160-mV depolarization from −80mV. Cells with larger transduction currents tended to have larger flick amplitudes (least-squares fit R = 0.3, P < 0.0001, N = 64). The magnitudes of the on and off phases were the same (Fig. 4 C). The movement was roughly linear with the change in voltage for steps ranging from −80 to +40 mV, but began to saturate at larger depolarizations (Fig. 4 D). The time course of the flick could be fitted with a single exponential function, which had similar time constants for the on and off phases, 213 ± 84 μs and 201 ± 68 μs respectively (N = 18). This was slower than the 40- to 80-μs rise time of the voltage step, and most likely reflects the mechanical time constant of the bundle due to its drag and stiffness.

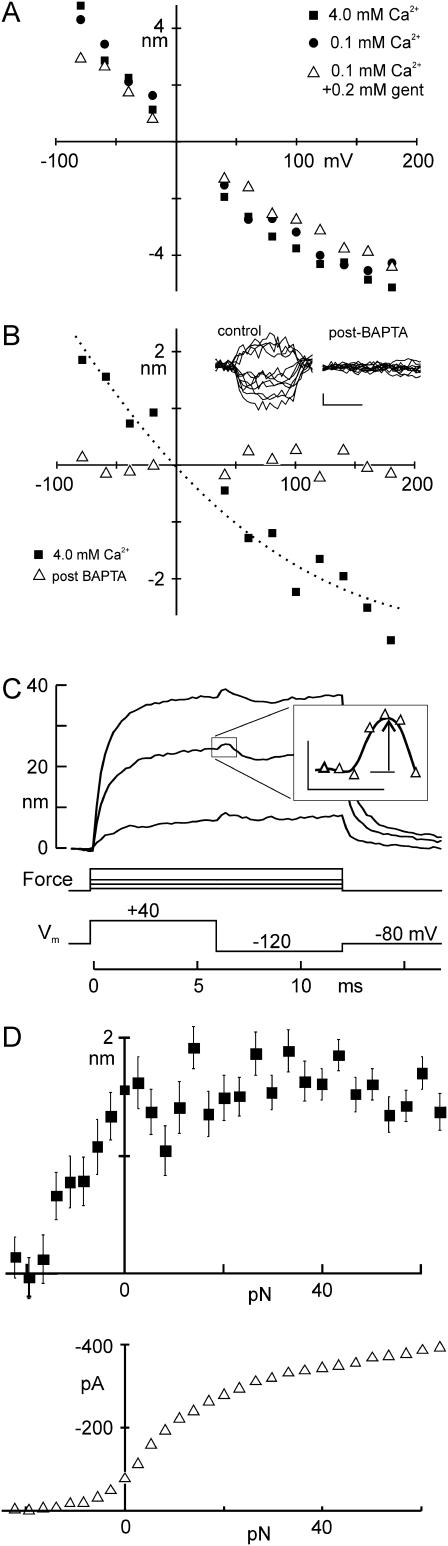
Both fast and slow adaptation are affected by Ca²⁺ influx into the stereocilia, and a phenomenon derived from either of these two processes should also be Ca²⁺-sensitive. Because the flick was nearly linear with voltage from −80 mV to +40 mV, it is unlikely to depend on Ca²⁺ entry, which would instead have an exponential voltage dependence. In fact, reducing the Ca²⁺ concentration in the external solution from 4 to 0.1 mM greatly slowed adaptation (Fig. 3 A) but did not change the size of the flick (Fig. 5 A). We blocked residual Ca²⁺ influx through transduction channels by adding 200 μM gentamicin—a channel blocker—to the 0.1-mM-Ca²⁺ external solution, which once again did not significantly change the size of the flick (Fig. 5 A). The flick is apparently not a Ca²⁺-dependent process, nor does it require any ion influx through transduction channels.

FIGURE 5.

Effects of altering transduction on the flick. (A) Effects of external Ca²⁺ and of gentamicin, a transduction channel blocker. The flick as a function of voltage was not significantly different with 4 mM Ca²⁺ (▪), with 0.1 mM Ca²⁺ (•), or with 0.1 mM Ca²⁺ + 0.2 mM gentamicin (▵) in the external solution. Five other cells showed the same effect. (B) Flick as a function of voltage before (▪) and after (▵) bath application of BAPTA to break tip links (5 mM for 10–20 s, until the receptor current was abolished). Both data sets were recorded with 4 mM Ca²⁺ in the bath solution. The flick was abolished by BAPTA treatment. Four other cells showed the same effect. (Inset) Example of flick movements before and after BAPTA. Scale represents 1 nm and 1 ms. (C) Flick evoked with varying gating spring tension. A cell was depolarized to +40 mV and one of a family of 29 force steps was simultaneously applied to deflect the bundle. Six milliseconds after the start of each force step, the voltage was stepped back to −120 mV, producing a positive-going flick. To measure the size of the flick, bundle positions were averaged 0–0.2 ms before and 0.2–0.4 ms after the voltage step (inset: scale, 1 ms, 1 nm). (D) Flick as a function of force. The flick due to the −160-mV hyperpolarization in C was constant for positive bundle deflections, but rapidly declined to zero below force steps of −16 pN, or −48 nm of bundle deflection. The corresponding receptor current (bottom), measured 1.2 ms after the deflection, declined to near zero at ∼−10 pN.

On the other hand, the flick seems to require intact tip links. Application of the Ca²⁺ chelator BAPTA cuts the tip links and eliminates transduction (18). A brief application of BAPTA abolished transduction (data not shown) and abolished the flick: the response to a 160-mV depolarization was reduced from 2.44 nm to 0.05 nm in the cell shown (Fig. 5 B, and inset). The hair bundles and kinocilium of all tested cells (N = 5) remained attached to each other after brief BAPTA treatment and showed no visible damage. Their stiffnesses were reduced by BAPTA, as expected for cutting tip links.

In addition, the flick required taut tip links. Myosin-based adaptation serves to maintain a resting tension on tip links; slackening them with a large negative deflection reduced the size of the flick, whereas tensioning the tip links did not change its size. With the optical trap, we applied a family of force steps to bias bundle position while the cell was depolarized to +40 mV. Six milliseconds after the start of the force step, we stepped the voltage back to −120 mV to measure the flick (Fig. 5 C). For the cell shown in Fig. 5 D, the flick elicited by the 160-mV hyperpolarization was constant for positive bundle positions but disappeared for force stimuli more negative than −16 pN, corresponding to a bundle deflection of −48 nm.

We measured the transduction current after the hyperpolarizing step to correlate the force dependence of the flick with the force dependence of channel activation (Fig. 5 D). In the positive direction, the flick had constant amplitude in a regime where the channels continued to open; in the negative direction the flick was still present where most channels were closed. In five other cells, the deflection below which the flick disappeared was −110 ± 58 nm, whereas the open probability of the channels was <0.01 for bundle deflection more negative than −34 ± 44 nm. Thus, the flick seems unrelated to force-dependent channel gating, although it might still involve a voltage-dependent conformational change of the channel.

Since the flick is not Ca²⁺-sensitive and therefore not related to fast adaptation, we subtracted its contribution to voltage-dependent bundle movements to measure the movement corresponding to fast adaptation.

The “twitch”: a mechanical correlate of fast adaptation

We found that fast adaptation of the mechanosensitive current was slowed either by reducing external Ca²⁺ or by depolarizing the cell to reduce Ca²⁺ influx (Fig. 3). We next asked whether the mechanical twitch after positive bundle deflections was similarly affected. As in Fig. 2, we applied force steps with the optical trap while simultaneously recording the evoked transduction currents and bundle deflections. Smaller forces were used to produce deflections up to 50 nm, where fast adaptation was more pronounced (Fig. 6). In the cell in Fig. 6, fast adaptation was complete in ∼3 ms at a holding potential of −80 mV. The negative-going twitch was also complete in this time, and was followed by a slower positive movement attributed to myosin-1c slipping. Depolarizing the cell to −60 or −40 mV, which reduces Ca²⁺ influx through transduction channels, slowed the fast adaptation and the twitch commensurately. In turtle and bullfrog hair cells the twitch time course depends on extracellular Ca²⁺, on holding potential, and on intracellular Ca²⁺ buffers (25,30,32). Our observations support the idea that the twitch is a mechanical correlate of fast adaptation and that it follows from Ca²⁺ entry through transduction channels. Next, we wanted to determine where Ca²⁺ acts to mediate this twitch.

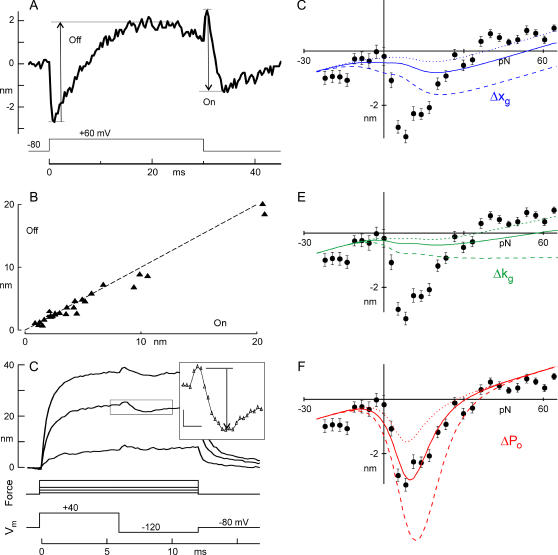
To measure in detail the mechanical correlates of Ca²⁺ action, we again controlled Ca²⁺ entry by changing the membrane potential but focused on the second phase of bundle movement (the twitch). For a depolarization to +60 mV, a freestanding bundle exhibited a negative, submillisecond flick, and a slower positive twitch (Fig. 7 A). Thirty milliseconds later, a repolarizing step back to −80 mV produced flick and twitch in the reverse directions. We measured the amplitude of the twitch after the flick (Fig. 7 A, arrows). The “off” twitch for depolarization (in which Ca²⁺ is expected to unbind) had the same magnitude as the “on” twitch for repolarization (Fig. 7 B), suggesting that the twitch involves a reversible binding reaction with a fixed mechanical correlate. When we reduced Ca²⁺ in the external solution, reducing fast adaptation in the receptor current, we reduced the voltage-induced twitch in both directions—further evidence that the voltage-induced twitch is generated by the same mechanism as the deflection-induced twitch (data not shown).

FIGURE 7.

Characteristics of the twitch, and predictions from three models for fast adaptation. (A) Twitch evoked by depolarization and repolarization. The twitch was measured as shown in the figure, or, when the repolarization twitch was so fast that it overlapped with the flick, was calculated from bundle positions a few milliseconds before and after the repolarization, adding the flick amplitude measured after depolarization. “Off” and “On” refer to Ca²⁺ unbinding and binding. (B) Magnitudes of the “on” and “off” twitch induced by voltage changes with no mechanical deflection. (N = 15 cells; dotted line with slope of 1.0). The twitch process appears reversible over tens of milliseconds. (C) Voltage-evoked twitch during bias by force steps. Fig. 5 C is replotted, now showing the magnitude of the twitch after repolarizing from +40 to −120 mV (inset, arrow; scale bar, 1 ms, 1 nm). Movement traces from 3 of the 29 force steps are shown. (D) Magnitude of the twitch for a range of forces, fitted with the Δx_g model. The model used parameters derived from fitting the I(X) and F(X) data of this cell, as in Fig. 2 (parameters below), and allowed only changes in Δx_g to fit. The solid line is the best fit (Δx_g = −0.29 nm); dashed lines are fits with values of Δx_g twice or half the best-fit value. Best fit was determined by least-squares error. (E) Magnitude of the twitch, fitted with the Δk_g model. The model allowed only changes in Δκ_g to fit. The solid line is the best fit (Δκ_g = +35 μN m⁻¹); dashed lines are fits with values of Δκ_g twice or half the best-fit value. (F) Magnitude of the twitch, fitted with the ΔP_o model. The solid line is the best fit (Δf_o = 1.5 pN); dashed lines are fits with values of Δf_o twice or half the best-fit value. Parameters measured from the I(X) and F(X) curves: N = 25 channels, gating sensitivity z = 379 fN, K_g = 390 μN/m, K_s = 270 μN/m, and the stiffness along the tip-link axis of an individual gating spring κ_g = 1592 μN/m, gate swing d = 1.7 nm. In six other cells, only the ΔP_o model gave a reasonable fit.

The twitch movement was slower for depolarization to +60 mV than for repolarization to −80 mV: the time constants were 6.3 ± 4.1 ms and 1.8 ± 0.5 ms, respectively (N = 12). Qualitatively similar results were seen in turtle by Ricci and Fettiplace (30), with slower off rates than on rates. The twitch time constant on repolarization to −80 mV was the same as fast adaptation of the receptor current after bundle deflection (1.8 ± 0.6 ms, N = 22, V_hold = −80 mV), consistent with the same Ca²⁺-binding process mediating the deflection-induced and repolarization-induced twitch.

Predicting the force dependence of repolarization twitch

Howard and Hudspeth (6) originally suggested that fast adaptation occurs when Ca²⁺ entering through mechanically opened transduction channels binds to an internal site that affects channel open probability. To understand the twitch quantitatively, we first asked how Ca²⁺ binding would affect the position-force relation of a hair bundle. We began with a simplified mechanical model (Fig. 1 D) which treats the bundle as a stereocilia pivot spring (stiffness K_s) in parallel with the transduction complex. The transduction channel is in series with an elastic gating spring (stiffness K_g) and in series with the myosin motor mediating slow adaptation. This simple model can account for the gating compliance illustrated in Fig. 2 D and for slow adaptation (19).

Ca²⁺ might act on any of these elements to cause a movement of the bundle. We considered three possibilities (see Fig. 1 and legend for details of the model): First, Ca²⁺ might bind to the transduction channel to change the relationship between force and open probability. If Ca²⁺ changes the P_o(F) relation so that more force is required to open a Ca²⁺-bound channel (8), then Ca²⁺ entry will tend to close channels and the closure will tend to pull the bundle in the negative direction. Such movement would occur only in the range where channels could open or close, but not when an applied force strongly biases the hair bundle in either the negative or positive direction (e.g., Benser et al. (32)). Second, Ca²⁺ might bind to an internal elastic element that is the gating spring or in series with it, to change its stiffness (16). If Ca²⁺ binding reduces stiffness, thereby relaxing tension on the channel, the bundle will tend to move in the positive direction, pushed by the resting tension in stereocilia pivot spring. If the channel gating swing is large, the reduced tension on the channel can close it, tightening the gating spring more and paradoxically moving the bundle backward. Finally, Ca²⁺ could bind to an internal element that changes conformation to lengthen slightly. Again, the bundle would move positively, but again, if the gating swing is large the channel could close to cause a paradoxical negative movement.

With certain parameters, in particular if the gating swing is large and the gating spring is stiff, all three models can produce qualitatively similar negative bundle movements over some range of force steps (see Fig. 1 for a graphical illustration of twitch production). If the gating swing is small or the gating spring soft, however, only the first model can produce a twitch. For any parameters, the three models can clearly be distinguished if the twitch upon Ca²⁺ entry is measured over a range of applied force (Fig. 1, E and F).

Measuring the force dependence of the twitch

We deflected bundles with a series of force steps while Ca²⁺ influx into the stereocilia was halted by a depolarization to +40 mV. We waited for 6 ms, sufficiently long for the channel open probability to equilibrate, and then hyperpolarized the cell to −120 mV to allow Ca²⁺ entry (Fig. 7 C). To subtract the voltage-dependent flick, we measured bundle movement from the peak of the flick to the plateau of the twitch, but before much movement from slow adaptation had occurred (Fig. 7 C, inset). For this cell, repolarization caused a maximum negative movement of ∼3 nm when the bundle was biased with 12 pN of force (Fig. 7 E).

These data were compared with predictions of the three different models, using a quantitative model of bundle mechanics to simulate the movement of the bundle with the same stimulus protocol as above (see Theory section). For each cell, the relevant parameters could be measured from data as described for Fig. 2, leaving just one free parameter for fitting. For the cell in Fig. 7 C, for instance, the amplitude and steepness of the I(X) curve gave N = 25 channels and gating sensitivity z = 379 fN (data not shown). The F(X) curve of the bundle (as in Fig. 2, D and E) gave the effective gating spring stiffness K_g = 390 μN/m, the stereocilia pivot stiffness K_s = 270 μN/m, and the stiffness along the tip-link axis of an individual gating spring κ_g = 1592 μN/m. The gating swing, assuming a channel at each end of the tip link, was d = 1.7 nm. We also added to the models the movement corresponding to the small amount of slow adaptation that occurred during 1.5 ms, measured from the slow phase of the voltage-induced movement.

Using these values, we had only one free parameter for each of the models. In the third model (Δx_g), we could vary the change in gating spring set point upon Ca²⁺ binding. Fig. 7 E shows the best fit, with Δx_g = −0.29 nm (a shortening with Ca²⁺), and fits with Δx_g at twice and half that value. In the second model (Δk_g), we varied the change in spring stiffness upon Ca²⁺ binding. Fig. 7 F shows the best fit, with Δκ_g = +35.1 μN/m (a stiffening with Ca²⁺) and twice and half that value. In the first (ΔP_o), we could vary the shift of the P_o(F) curve upon Ca²⁺ binding. Fig. 7 G shows a fit with Δf_o = 1.5 pN (lowered probability with Ca²⁺).

Only one model—a Ca²⁺-dependent shift of P_o(F)—could account for our experimental results. The best fits to the movement for the Δk_g or Δx_g models were with parameters opposite in sign to the predictions of the models, and so tension would increase and channels would open rather than close upon Ca²⁺ entry. Moreover, these variable parameters did not produce negative movement for any bias force in a model using the measured parameters for this cell, yet the cell displayed a twitch upon repolarization. In contrast, the ΔP_o model fit this twitch reasonably well for all bias forces, and predicted the observed channel closure. Finally, the quality of the fit was much better for the ΔP_o model. We even varied all the other parameters with the Δk_g or Δx_g models to attempt a better fit, making each twice or half the measured value and then optimizing Δκ_g or Δx_g to minimize error. The smallest fitting error for the Δk_g and Δx_g models with all parameters varied (variance = 30 nm² and 26 nm², respectively) was still much larger than the error for the ΔP_o model (variance = 4 nm²).

A similar fit to the voltage-dependent twitch was done for five other cells. The average values measured from force steps were N_c = 24.1 ± 3.3 channels (average ± SE), bundle pivot stiffness K_s = 112 ± 27 μN/m, gating-spring stiffness K_g = 152 ± 44 μN/m (or κ_g = 763 ± 218 μN/m) and gate swing d = 2.5 ± 0.5 nm. In all six cases the ΔP_o model fit the data well and the other two models did not. Overall, the variance between the data and the best fits was 75% larger for the Δk_g model than for the ΔP_o model (p < 0.035) and 116% larger for the Δx_g model (p < 0.0003).

Finally, we can determine the effect of Ca²⁺ on channel sensitivity. The P_o(F) curve measured relative to the bundle shifted by 8.3 ± 1.3 pN due to Ca²⁺ binding, or a single channel with Ca²⁺ bound requires 2.9 ± 0.5 pN more force along the tip-link axis to open.

DISCUSSION

Dissociated bullfrog saccular hair cells stimulated with an optical trap displayed all of the features previously seen in bullfrog and turtle hair cells driven by fast, flexible-fiber stimulus probes. These include a narrow activation curve of ∼100-nm width, a gating compliance over the same range, fast adaptation in the receptor current after moderate positive deflections, a rebound or twitch of the hair bundle with the same stimulus range and time course as fast adaptation, and a very fast voltage-dependent movement that we term the “flick”(6,11,14,25,30,32,33). We also observed spontaneous oscillations of hair bundles in freshly dissociated hair cells (data not shown), similar to those seen in bullfrog hair cells of intact epithelia (11,32,34–36). Despite the intense infrared beam passing near the bundle, the optical trap apparatus did not damage hair cells over recording times of 10–20 min. The optical trap has high stimulus speed due to a negligible fluid drag on the 2-μm bead attached to the bundle. For force stimuli, the rise time is limited by the drag coefficient of the bundle and stimulator. Flexible fiber probes alone have typical coefficients of 25–120 nN s m⁻¹ (36,37), which are larger than that of the bead and bundle together (10–20 nN s m⁻¹). Because the time required to move the beam and thus to change the force was 10–15 μs, the overall deflection time of 200–400 μs was limited by the bundle.

Simultaneous whole-cell voltage clamp allowed us to correlate electrical and mechanical assays of channel gating and adaptation. For instance, we found that both fast adaptation and the twitch time course changed commensurately with depolarized holding potentials, providing further evidence that the twitch is the mechanical correlate of the fast-adaptation process. Mechanical measurements resolved ambiguities in the cause of electrical phenomena: fast and slow adaptation both reduce the receptor current, both are Ca²⁺-dependent and both shift the I(X) curve in the same direction, but they could be distinguished by mechanical correlates of opposite polarity. Finally, mechanical measurements revealed behavior of the hair bundle that has no electrical manifestation, such as the voltage-dependent flick.

The flick may be driven by a transmembrane component of the transduction apparatus

Several lines of evidence suggest that the submillisecond flick movement evoked by a voltage step is associated with the transduction apparatus. First, the size of the movement tended to saturate at large positive voltages, reminiscent of a voltage-dependent conformational change. Assuming that the flick saturated symmetrically for large hyperpolarizations, we fitted the voltage dependence of all cells with a two-state Boltzmann relation and found an equivalent charge of 0.23 electron charges (Fig. 4 D, N = 6 cells). Second, the flick was not dependent on influx of Ca²⁺ or any ion through the transduction channels: neither lowering external Ca²⁺ concentration nor blocking the channels with gentamicin affected this movement. Thus, the flick is unlikely to be an initial phase of either fast or slow adaptation but seems to be driven by a transmembrane element that directly senses the membrane potential. Third, this movement seems to be transmitted through the tip links, since it was abolished by BAPTA, which severs tip links, and was reduced by large negative deflections that are expected to slacken tip links (26,38). One transmembrane element that is mechanically coupled to tip links is the transduction channel itself. The flick might represent a weakly voltage-dependent conformational change of the transduction channel that is not coupled to the mechanical gating, since the flick amplitude did not change over the channel's force-dependent activation range. The flick amplitude was constant over a range of positive bundle deflections, which suggests a fixed displacement of an inelastic element, such as a conformational change of a protein, rather than an increase in a stiffness of a spring, which would produce increasing amplitude for increasing holding force. We found that the bundle movement for a 160-mV depolarization was 3.2 nm on average, from which we can calculate using the stiffnesses and the factor γ an average 0.84 nm conformational movement along the tip-link axis. If the data of Fig. 4 D represent a Boltzmann distribution, as fitted, we can infer a maximum conformational movement of ∼1.6 nm of the voltage-sensing protein.

Movement might instead be caused by a bulk property of the lipid membrane. Zhang et al. (39) reported movements of an entire patch-clamped HEK cell to be ∼1 nm/100 mV. Shrinkage and expansion of the bundle lipid itself could conceivably produce a deflection perpendicular to the stereocilia axis. The flick seems to require taut tip links, however, and it is not clear how that could be consistent with a lipid-based voltage-dependent movement.

Fast adaptation is consistent with a Ca²⁺-dependent change in the force sensitivity of the transduction channel

Ca²⁺ affects the rates of both fast and slow adaptation, acting at intracellular sites near the transduction channels in the tips of stereocilia (28,40). For fast adaptation, it was initially proposed that Ca²⁺ binds to the transduction channel itself and promotes its closure (6). Experiments with Ca²⁺ buffers have supported a binding site near the channel, and quantitative models incorporating a Ca²⁺-dependent shift of the P_o(F) relation are consistent with adaptation of the transduction current (8). Yet Ca²⁺ might instead act on other intracellular components of the transduction apparatus, to change the force on a channel rather than its force dependence (16).

By exploring the mechanical consequences of Ca²⁺ entry over a range of forces applied to a hair bundle, we found that the Ca²⁺ effects on the force-displacement relation are consistent with only one of three possible Ca²⁺ actions: Ca²⁺ apparently shifts the transduction channel activation curve so that an additional 3–4 pN is required to open a Ca²⁺-bound channel. We cannot say exactly where Ca²⁺ acts, but its effect on channel activation suggests a binding site on the transduction channel or an associated subunit.

A mechanical model duplicates the observed mechanical and electrical responses of hair cells

We have assumed, in this analysis, that the sole effect of voltage on the twitch-like movement is as a fast modulator of Ca²⁺ entry. If the transduction channel has an intrinsic voltage dependence it could confuse the interpretation; however, to affect our conclusions a voltage-dependent conformational change would have to be slower than the mechanical activation of ∼100 μs (38) but have the same time course as the twitch and fast adaptation induced by bundle deflection.

To test whether our understanding of the site of Ca²⁺ action can account for the observed receptor currents and bundle movements, we incorporated a Ca²⁺-dependent shift of the P_o(F) curve into a quantitative model of bundle mechanics (see Theory). The model also included the voltage-dependent flick process, as measured here, and the slow myosin-based adaptation as modeled by Shepherd and Corey (19).

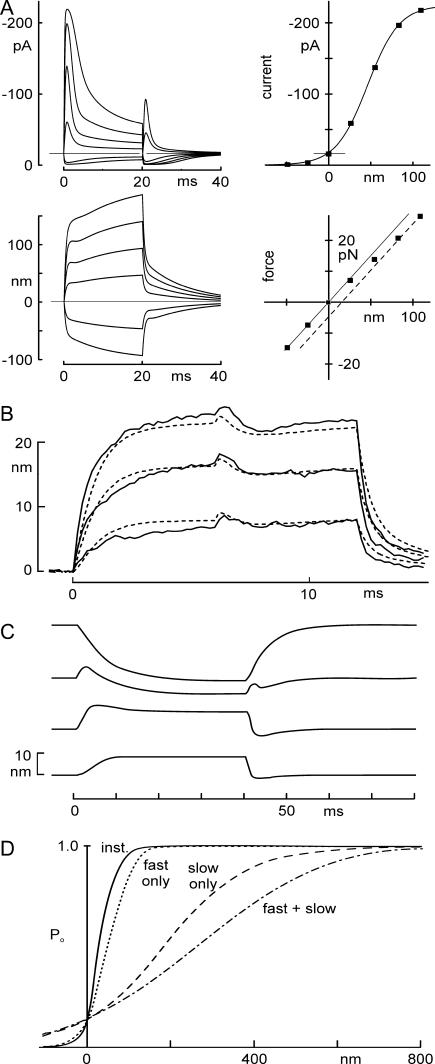
We first used the model to simulate electrical and mechanical responses to the mechanical stimuli of Fig. 2. Receptor currents and bundle motions were calculated for step displacements of one end of a spring representing the optical trap stiffness. The model reproduces the transduction current and bundle movement in the time domain reasonably well (Fig. 8 A). The twitch was predicted for intermediate bundle deflections, as observed experimentally. Peak currents and initial bundle positions were measured from the model traces, and plots of I(X) and F(X) mimicked those seen experimentally.

FIGURE 8.

Predictions of receptor current and bundle motion for a model in which Ca²⁺ changes P_o(F). (A) Currents and bundle displacements in response to a family of optical trap displacements predicted using the mechanical model, with parameters from Fig. 2. It included a Ca²⁺-dependent channel closure due to change in force dependence, a myosin-type slow adaptation modeled as in Shepherd and Corey (19), and a voltage-dependent flick measured from short voltage steps. Four predictions (top left, transduction current I(t); bottom left, bundle movement X(t); top right, peak current-displacement I(X); bottom right, force-displacement F(X)) adequately mimicked the experimentally measured data shown in Fig. 2. (B) Measured motion (solid line) and predicted motion (dashed line) of a bundle during 12-ms-long force steps, with the cell depolarized at 0 ms and repolarized at 6 ms. Data replotted from Fig. 7 C. The model used bundle parameters from the cell of Fig. 7 (listed in Fig. 7 legend). One free parameter—the additional force needed to open a transduction channel when Ca²⁺ is bound—was determined by fitting the data of Fig 6 C. (C) Modeling of bundle movement evoked by depolarization. The model used to predict responses to force steps at a normal holding potential (Fig. 8 A) could also predict the depolarization-evoked movement and the reversal of its polarity seen with varying force bias. Parameters in Table 1. (D) Time-dependent sensitivity of activation. The instantaneous P(X) curve (solid line) has an activation range of ∼100 nm. If fast adaptation (occurring in 1–2 ms) is included, the P(X) curve (dotted line, calculated as the response to maintained steps of different amplitudes) is ∼1.5-fold less sensitive. With only the slow myosin-dependent process (occurring in 10–30 ms), it is broader (dashed line), and with both processes, it is even broader than with myosin adaptation alone (long dashed line). The sensitivity thus depends on the speed of the stimulus. Parameters used were the averages from six cells.

We then modeled the bundle movements occurring on repolarization from +40 mV, with force steps and bundle parameters as in Fig. 7 C. Model traces overlaid on experimental traces (Fig. 8 B) showed a reasonable match to the data, including both flick and twitch movements.

Ricci et al. (25) measured the movement of turtle hair bundles upon depolarization, and observed that a fast, positive bundle movement (similar to that in Fig. 4 A) was replaced with a slower, negative movement as the bundle was biased positively by force. They speculated that the fast component was caused by channels opening when Ca²⁺ unbound, but that the movement disappeared with positive bias because the bias applied sufficient force to keep channels open even with Ca²⁺ bound. The reversal can be explained qualitatively as follows (25): With no static bias, the force applied by myosin motors is sufficient to keep transduction channels open 10–15% of the time. More would be open at the resting force but Ca²⁺ influx and binding closes some fraction of them. Upon depolarization, Ca²⁺ influx ceases and the concentration drops, Ca²⁺ unbinds, many of the previously bound channels open, and the relaxation of tip-link tension allows the bundle to move forward. With increased static bias, more channels are already open at the time of the depolarization and the additional opening upon Ca²⁺ unbinding is less. When the bias is sufficient to open all channels before the depolarization, there is no further positive relaxation when the Ca²⁺ concentration drops and Ca²⁺ unbinds.

At the same time, the depolarization also reduces the Ca²⁺ regulating the myosin-1c motors. At low Ca²⁺, the motor tends to climb, tightening tip-link tension and pulling the bundle in the negative direction. Climbing is slower, so the negative bundle movement follows after the initial positive relaxation. When there is no force bias and channels are mostly closed, resting Ca²⁺ near the motors is low, the further lowering with depolarization is less significant, and the change in myosin tension is less. With a large bias that opens most channels, the resting Ca²⁺ is higher, the motors exert less tension, the increase in tension is greater when Ca²⁺ entry is stopped by depolarization, and there is consequently a larger myosin-based movement.

We observed similar reversals in bundle movement with positive force bias, and found that our model can account for the reversal and can reproduce the results of Ricci et al. (25) (Fig. 8 C).

Comparison to mammalian hair cells

In outer hair cells of the rat cochlea, Kennedy et al. (13) observed a fast adaptation of the receptor current with similar characteristics and Ca²⁺ dependence. The time constants for adaptation are faster in rat cochlea than in bullfrog saccule, which can be explained partly by the larger average transduction currents (and presumed larger Ca²⁺ influx) in rat. For similarly sized transduction currents, the rat hair cells' adaptation is about twice as fast as in bullfrog. In subsequent experiments using force stimuli, Kennedy et al. (41) found that adaptation corresponds in time course to a large positive movement of the hair bundle. This movement is opposite in polarity and much larger than that in turtle and bullfrog; it cannot be explained by the model proposed here, nor could it result from a prestin-based movement because their cells were voltage-clamped. It may be that cochlear hair cells have an additional fast force production mechanism, although its molecular basis is unclear.

In an in vitro preparation of the gerbil cochlea, Chan and Hudspeth (10) found that electrical stimuli applied across the organ of Corti caused fast movement of hair bundles with a similar time course. Both this movement and a compressive nonlinearity characteristic of the cochlear amplifier require Ca²⁺ influx but not a receptor current carried by K⁺. These results are as expected from work in bullfrog and turtle, but might involve additional mechanisms.

Two phases of adaptation successively broaden the hair cell's activation curve

“Adaptation”—mediated both by closure of the transduction channel with Ca²⁺ binding and by the slower movement of myosin-1c—serves several functions in hair cells. It provides a transient response to slow or static stimuli, emphasizing changes in force; it positions the transduction element in the most sensitive part of its activation curve to maximize responsiveness, both during development and during physiological stimuli; it prevents saturation of the transducer with larger stimuli; and it may mediate frequency tuning in auditory organs through its effect on bundle mechanics (9). Because both fast and slow phases of adaptation are limited in extent, it also is manifest as a time-dependent sensitivity. The model shows how an activation range of ∼100 nm is broadened to ∼150 nm as the fast, Ca²⁺-binding mechanism occurs in a few milliseconds (Fig. 8 D), and is further broadened to ∼700 nm after the myosin-1c movement has occurred in tens of milliseconds (Fig. 8 D) (19). Only the fastest stimuli are received with the highest sensitivity.

Implications

It has long been recognized that Ca²⁺ entering through hair-cell transduction channels binds within nanometers to promote closure of the channel (8). Our measurements, tested by three models, strongly suggest how: that Ca²⁺ shifts the force dependence of activation such that ∼3 pN more force, equivalent to 1–2 kT, is needed to open a Ca²⁺-bound channel. It has been proposed that such a mechanism may mediate frequency tuning in auditory organs (6), and a model incorporating such a mechanism produces amplification of bundle movement for small stimuli of appropriate frequency (7). Thus, understanding the site of Ca²⁺ action narrows the search for the cochlear amplifier in molecular terms. Because the amplifier exhibits tonotopic variation in frequency in most auditory organs, this also narrows the search for a variable element underlying tonotopy.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.