In Silico Studies of the African Swine Fever Virus DNA Polymerase X Support an Induced-Fit Mechanism

Abstract

The African swine fever virus DNA polymerase X (pol X), a member of the X family of DNA polymerases, is thought to be involved in base excision repair. Kinetics data indicate that pol X catalyzes DNA polymerization with low fidelity, suggesting a role in viral mutagenesis. Though pol X lacks the fingers domain that binds the DNA in other members of the X family, it binds DNA tightly. To help interpret details of this interaction, molecular dynamics simulations of free pol X at different salt concentrations and of pol X bound to gapped DNA, in the presence and in the absence of the incoming nucleotide, are performed. Anchors for the simulations are two NMR structures of pol X without DNA and a model of one NMR structure plus DNA and incoming nucleotide. Our results show that, in its free form, pol X can exist in two stable conformations that interconvert to one another depending on the salt concentration. When gapped double stranded DNA is introduced near the active site, pol X prefers an open conformation, regardless of the salt concentration. Finally, under physiological conditions, in the presence of both gapped DNA and correct incoming nucleotide, and two divalent ions, the thumb subdomain of pol X undergoes a large conformational change, closing upon the DNA. These results predict for pol X a substrate-induced conformational change triggered by the presence of DNA and the correct incoming nucleotide in the active site, as in DNA polymerase β. The simulations also suggest specific experiments (e.g., for mutants Phe-102Ala, Val-120Gly, and Lys-85Val that may reveal crucial DNA binding and active-site organization roles) to further elucidate the fidelity mechanism of pol X.

INTRODUCTION

DNA is continuously damaged by both environmental factors, like smoke, light, and low-dose radiations, and endogenous oxidants, like reactive oxygen species (ROS) from metabolic activity (1–3). To preserve the integrity of the genetic material, many organisms have developed intricate repair systems to excise damaged bases and replace them with undamaged units, as specified by the template DNA strand (4,5). Understanding fidelity mechanisms of the enzymes involved in the base excision repair (BER) pathway, namely, DNA polymerases, remains a major biological challenge. The fidelity of DNA polymerases, defined as the inverse of misinsertion error frequency, refers to their ability to incorporate correct rather that incorrect nucleotides complementary to the template DNA (6). Such fidelities span a wide range, from one error per 10⁶ nucleotides incorporated for high fidelity polymerases (7,8), to one error per nucleotide for low fidelity polymerases (9,10).

From studies of mechanisms of several DNA polymerases that participate in the BER pathway, it has been suggested that these enzymes enhance fidelity by efficiently inserting the correct nucleotide rather than strongly disfavoring incorrect units; low fidelity polymerases, on the other hand, are inefficient and insert the correct nucleotide slowly (6,11). Recently, a novel class of ultralow fidelity polymerases has been discovered. These Y family members appear to be important in translesion DNA synthesis, since they can synthesize DNA past a damaged base and thus overcome stalling that characterizes replicative polymerases (12–14).

The reaction catalyzed by DNA polymerases is a nucleotidyl transfer with a general mechanism that involves two metal ions coordinated with conserved carboxylate residues (15–19). Even though the detailed pathway for nucleotide incorporation is not known, on the basis of extensive kinetics measurements and structural studies for several higher fidelity DNA polymerases (20–28), a common pathway for nucleotide insertion has been delineated, as follows. The enzyme alternates between an open and closed conformation in which the free enzyme is open and binds the DNA; upon dNTP binding, this newly formed ternary complex undergoes a large conformational change from open to closed state. After the chemical incorporation of dNTP, the complex undergoes a second conformational change and opens, releasing the products. These conformational changes are thought to represent key mechanisms used by some polymerases to enhance fidelity (29). However, not all polymerases may have well-defined open and closed states, and a few exceptions (to closed complexes when bound to substrate versus open complexes without substrate) have been reported. Among them are the binary-DNA complex of DNA polymerase λ (30) and an open ternary complex of Klentaq (A-family) (31).

Despite being phylogenetically unrelated, most polymerases share a common architecture that can be described as a hand with three characteristic subdomains: a “palm” subdomain that catalyzes the phosphoryl transfer, a “fingers” subdomain that stabilizes the incoming nucleotide and the template base, and a “thumb” subdomain that helps position the DNA strand (32,33). Members of the X family of DNA polymerases are left-handed, unlike other families. Consequently, the nomenclature for thumb and fingers is inverted (34). A well-characterized protein in this X family is DNA polymerase β (pol β), an enzyme involved in the BER pathway (7,35,36).

The African swine fever virus (ASFV) polymerase X (pol X) is a DNA-directed polymerase also in the X family (37). Pol X is a Spartan enzyme: it lacks the fingers subdomain (37). Nonetheless, it has significant sequence and structural similarity with human pol β, suggesting that pol X participates in a viral BER pathway (37,38). Experiments on the insertion fidelity of pol X on gapped DNA and its lyase activity on abasic sites lends support to this hypothesis (39). Indeed, the host cell for ASFV is the swine macrophage, known to produce ROS under certain conditions (40). ROS can cause various insults to the cells such as oxidized purines and pyrimidines (2), and these lesions are in general repaired via BER pathway. It was therefore suggested that ASFV might have developed a BER enzyme as an adaptive response to its environmental stresses (39).

Kinetic studies have shown that pol X's fidelity is low, with a preference for purine bases (10,39). In presteady-state kinetics experiments, fidelity values—measured as [(k_pol/K_d,app)_cor + (k_pol/K_d,app)_inc]/(k_pol/K_d,app)_inc, where k_pol is the rate of first nucleotide incorporation for first-enzyme turnover, K_d,app is the apparent equilibrium dissociation constant, and the subscripts “cor” and “inc” refer to the correct and incorrect nucleotide incorporation, respectively—range from 7700 for the C:C basepair to 1.9 for the G:G basepair, yielding an insertion rate of the G:G mispair comparable to the four correct Watson-Crick basepairs (10). Steady-state kinetics data, however, show significantly different catalytic efficiencies for correct and incorrect nucleotide insertions (39). Consequently, according to this later study, fidelity values for pol X are higher, with misinsertion rates between 10⁻³ and 10⁻⁵. The reasons for this discrepancy in the kinetic data are not clear. The different experimental conditions used for the kinetics measurements (especially pH) may in part explain these results.

Two groups have independently determined NMR solution structures of pol X in its free form (without any DNA bound) (41,42). The protein has two domains, an N-terminal domain that contains the catalytic site for the nucleotidyl transfer reaction and a C-terminal domain responsible for DNA binding and nucleotide selection. Because pol X is homologous to the C-terminal region of pol β, the N-terminal domain is referred to as the palm subdomain, whereas the C-terminal domain is called the thumb subdomain.

The two NMR structures are very similar to each other but differ slightly in the positioning of the thumb subdomain. As Beard and Wilson noted in presenting the NMR works, the structure determined by Maciejewski and co-workers is reminiscent of the “closed” conformation of DNA pol β whereas the other, determined by Showalter and co-workers, is more “open”, even if the difference between the two is not as marked as in the two conformations of pol β (43). For pol β, closed and open conformations are easily defined by the relative orientation of the thumb when the palm subdomain is superimposed (see Fig. 1).

FIGURE 1.

Comparison of the structures of human pol β with the NMR-determined structures of pol X. For pol β, only residues 145–335 (corresponding to the palm and thumb domain) are shown. In both figures, the open conformation of pol β (1BPX) is represented in green and the closed conformation (1BPY) is in red. In panel a, pol β structures are compared with free pol X structure A (initially closed) (41), and in panel b, pol β structures are superimposed with pol X structure B (initially open) (42). The inset identifies the region of proteins where most of the differences lie (helix N for pol β, and helix E for pol X. Residues of the catalytic triad and adjacent ones are used in the superimposition (residues 49–51 and 99–101 for pol X; residues 190–192 and 255–257 for pol β).

The experimental conditions used for the two solution structures are different. The buffer solution is 500 mM NaCl, 10 mM dithiothreitol (DTT)—a reducing agent—and pH 6.5 for Maciejewski et al. (41), whereas the salt concentration is 50 mM, 1 mM DTT, and pH 7.5 for Showalter et al. (42). Notably, a disulfide bond was not observed in the first structure, probably because of the stronger reducing conditions. Overall, it is possible that the slight differences between the two structures are due to variations in experimental conditions. It is also possible that both conformations are stable and may interconvert from one into the other by varying the conditions. Such systematic and relatively small configurational variations are good targets for molecular dynamics investigations (44).

Because the fingers subdomain, responsible in pol β for DNA binding, is absent in pol X, its overall shape is not hand-like. Interestingly, DNA binding assays (42) have shown that pol X can bind as tightly to gapped DNA as pol β, suggesting a novel mode of protein-DNA interaction. From the electrostatic surface potential map (42), it is clear that the thumb subdomain forms a highly positively charged patch that can readily interact with the DNA. Chemical shift perturbation experiments of gapped DNA or dNTP-Mg²⁺ binding by pol X suggest that the thumb subdomain likely interacts with the DNA, since many of the thumb residues undergo shifts in the thumb (41,42). Specifically, residues on the helix E were most heavily perturbed, suggesting a possible DNA binding region. This interpretation gains further support from a comparison of the solution structures of free pol X with its relative pol β, suggesting that the specific contacts within and between protein subdomains may be altered on template-primer-dNTP-Mg²⁺ binding. To investigate this hypothesis of induced fit (45,46), we perform and analyze molecular dynamics simulations of pol X-DNA complexes in the presence and absence of the incoming nucleotide. Despite the well-known modeling approximations and limitations, dynamics simulations are well suited to probe molecular details of protein-protein and protein-DNA interactions, can help biological interpretations of structure-flexibility relationships, and can make predictions which can ultimately be tested (44,47,48).

Specifically, we simulated both the binary complex (pol X and gapped DNA) and the ternary complex (pol X, gapped DNA, and incoming nucleotide). In the initial starting structure for the ternary complex, the DNA was incorporated into one DNA-free NMR structure (structure “B” below). As a control, simulations were performed from the two currently available NMR solution structures of free pol X obtained under different experimental conditions, as described under Computational Methodology. In agreement with the structural information, our results show that the two NMR structures interconvert to one another depending on the salt concentration. In addition, our simulations support the induced-fit mechanism for pol X-DNA in the presence of the correct incoming nucleotide and propose a possible sequence of events for the conformational change. Finally, we also suggest specific residues that could control fidelity.

COMPUTATIONAL METHODOLOGY

System setup for free pol X

Two independently determined NMR structures are available for ASFV pol X (41,42). For simplicity we refer to them as structure A (41) and structure B (42). Since structure A resembles more the closed conformation of human pol β (43), we also term it initially closed. Structure B, on the other hand, is more similar to the open conformation of pol β and we term it initially open. Molecular dynamics simulations were started from both forms. Since the NMR structures did not contain DNA, we also refer to structures A and B as the free pol X forms.

The coordinates for the free pol X structures were obtained from the Protein Data Bank (1JAJ for structure A and 1JQR for structure B). In each NMR ensemble the structure that best fit the experimental data, as indicated by the authors (model 20 for structure A and model 1 for structure B), was selected as the initial structure for the simulations. The models were solvated using the program PBCAID (49). A box of water molecules with a smallest image distance of 10 Å was created around the protein. Counterions (Cl⁻ and Na⁺) were added to neutralize the charges at ionic strengths of 150 mM and 500 mM with the DELPHI package (50). The ions were placed in the positions of water molecules with either minimal (for Na⁺) or maximal (for Cl⁻) electrostatic potentials at the oxygen atoms. The counterions were positioned at least 8 Å away from the protein and from each other. Both final systems contained 37 Cl⁻ ions and 15 Na⁺ ions. The initially closed structure A has two more hydrogen atoms relative to structure B, since a disulfide bond between Cys-81 and Cys-86 is lacking. At the ionic strength 150 mM, the solvated structure A contains 9,557 water molecules for a total of 31,721 atoms, whereas structure B contains 9,565 molecules of bulk water molecules for a total of 31,751 atoms. At the ionic strength 500 mM, solvated structure A contains 9,437 bulk water molecules for a total of 31,489 atoms, whereas solvated structure B has 9,445 water molecules and a total of 31,511 atoms.

System setup and initial models for pol X-DNA complexes

The starting model for the pol X-DNA complex was kindly provided to us by M. D. Tsai, The Ohio State University, Columbus, OH. This model was constructed by superimposing the conserved catalytic triad of pol X (structure B) with that of pol β in the crystallographically determined ternary complex (1BPY). Subsequently, the pol β protein sequence was deleted, leaving pol X with an unchanged DNA template-primer sequence and incoming nucleotide as in ternary pol β (1BPY) crystal structure. After modeling, initial steric clashes between protein and downstream DNA strand were removed by minimization. The resulting model includes a template strand, a primer, the corresponding downstream strand, the incoming dCTP nucleotide, and the two Mg²⁺ ions (catalytic and nucleotide binding) in the active site. This ternary complex (pol X-DNA-incoming nucleotide) was solvated using the program PBCAID. A box of water was created around the system with a total of 11,783 water molecules. Counterions were placed to neutralize the charge, as explained for the free pol X models. The final system contains 35 Cl⁻ and 28 Na⁺ in addition to the bulk water for a total of 39,441 atoms.

A binary complex was similarly constructed from the ternary model by deleting the incoming nucleotide and the metal ions, leaving the positions of protein and DNA unchanged. The system contains the same number of counterions and water molecules as the ternary complex. An additional binary system was constructed at ionic strength 500 mM, which contains 96 Cl⁻ and 103 Na⁺ ions, and 11,647 bulk water molecules for a total of 39,127 atoms.

Simulation protocol for free pol X and pol X-DNA systems

We performed nine simulations in total as summarized in Table 1: four for the free protein (two at physiological conditions and two at 500 mM salt concentration) and five for DNA-protein complexes (three for the ternary complex at physiological conditions and different computational algorithms, and two for the binary complex at 150 and 500 mM salt concentrations). Computational details of all nine simulations are described next.

TABLE 1.

Summary of simulations performed

Simulation number	System simulated	Salt concentration (mM)	Force field/MD integrator	Results (helix-E conformation)
1	Free pol X, structure A (initially closed)	150	CHARMM/LN	Opening trend
2	Free pol X, structure B (initially open)	150	CHARMM/LN	Remains open
3	Free pol X, structure A (initially closed)	500	CHARMM/LN	Remains closed
4	Free pol X, structure B (initially open)	500	CHARMM/LN	Closing trend
5	Pol X/DNA	500	CHARMM/PME	Remains open
6	Pol X/DNA	150	CHARMM/LN	Remains open
7	Pol X/DNA/dCTP	150	CHARMM/LN	Closing trend
8	Pol X/DNA/dCTP	150	CHARMM/PME	Closing trend
9	Pol X/DNA/dCTP	150	CHARMM/LN/different initial velocity	Closing trend

For the free pol X structures, all minimizations, equilibrations, and dynamics simulations were performed using the program CHARMM (Chemistry Department, Harvard University, Cambridge, MA) (51) and the all-atom force field version 26a2 (52). The initial structures for the free pol X were minimized using 10,000 steps of steepest descent method followed by 20,000 steps of adopted basis Newton Raphson (ABNR) minimization (51,53) with fixed positions for the protein heavy atoms. The procedure was then repeated, allowing all the atoms to move. The system was subsequently equilibrated at room temperature for 60 ps using the Langevin multiple timestep LN integrator (see Yang et al. (54) and references therein for a detailed discussion of the characteristics of the multiple timestep method).

The pol X DNA ternary and binary complexes were minimized with 10,000 steps of steepest descent, followed by 20,000 steps of ABNR with all heavy atoms for the protein, and DNA fixed. The minimization procedure was repeated without fixing the heavy atoms until the gradient of root mean-square deviations (RMSD) was ≤10⁻⁶ kcal/mol Å. The systems were then equilibrated for 30 ps and then minimized again. Finally, both systems were reequilibrated for 45 ps at 300 K by LN before starting the production dynamics.

Dynamics simulations for all the free pol X structures and the binary and ternary DNA complexes at physiological conditions were performed using CHARMM. For the ternary complex, a dynamic simulation with different set of velocities was also performed to ensure that simulations are not too sensitive to the choice of initial conditions. The parameters used during all the equilibration and dynamics runs were 1 fs for the short timestep Δτ (used to update the bond, angle, and dihedral energy terms), 2 fs for the medium timestep (used to update the nonbonded interaction within a 7 Å distance), and 150 fs for the long timestep (used to update all the other nonbonded interactions within a certain cutoff, set here to 14 Å). The SHAKE algorithm (55) was used in all runs to fix all bond lengths involving hydrogen atoms. A Langevin damping constant of γ = 10 ps⁻¹ is used. Electrostatic and van der Waals interactions are smoothed to zero at 12 Å with a shift function and a switch function, respectively. All molecular dynamics simulations with the CHARMM program were run for 10.5 ns.

Two additional simulations of pol X-DNA-incoming nucleotide ternary complex at 150 mM and pol X-DNA binary complex at 500 mM salt concentration were performed using the particle mesh Ewald (PME) algorithm (56). For these, systems energy minimizations equilibrations and molecular dynamics simulations were performed using the program NAMD (57) with CHARMM version C26a2 (58). First, each system was energy minimized with fixed position of all protein and DNA heavy atoms using the Powell algorithm. Systems were then equilibrated for 100 ps at constant pressure and temperature. Pressure was maintained at 1 atm using the Langevin piston method (59), with a piston period of 200 fs, a damping time constant of 100 fs, and piston temperature of 300 K. Temperature coupling was enforced by velocity reassignment every 2 ps. Then, production dynamics was performed at constant temperature and volume. The temperature was maintained at 300 K using weakly coupled Langevin dynamics of nonhydrogen atoms with a damping coefficient γ = 5 ps⁻¹. Bonds to all hydrogen atoms were kept rigid using SHAKE (55), permitting a time step of 2 fs. The system was simulated in periodic boundary conditions, with full electrostatics computed using the PME method (56) with a grid spacing on the order of 1 Å or less. Short-range nonbonded terms were evaluated every step using a 12 Å cutoff for van der Waals interactions and a smooth switching function. The total simulation length for both systems is 10.5 ns.

Molecular dynamics simulations using the LN algorithm in the CHARMM package were performed on local Silicon Graphics Origin 3000, 120 MHz processor machines at New York University and supercomputer time provided on SGI Origin machines at the National Cancer Institute. Typically, for free pol X systems, it takes 14.1 days per nanosecond of CPU time on four parallel processors. Simulations in NAMD were run on NCSA's IA32 Linux Cluster at UIUC and required ∼1.15 days per nanosecond on 16 CPUs in parallel for pol X-DNA systems.

The results and the dynamics trajectories are analyzed using Insight II (Accelrys, San Diego, CA) and the Visual Molecular Dynamics software package (60). RMSD plots and distance plots are generated using XMgrace.

RESULTS

Despite the absence in pol X of the fingers subdomain, responsible in other polymerases for DNA binding, pol X was shown to bind gapped DNA fragments tightly (42). The binding details are not known, since no structural data are available for the complex of pol X-DNA. To elucidate the interaction between pol X and the DNA, we performed molecular dynamics simulations on a ternary complex that included the protein, gapped DNA, and incoming nucleotide (simulation 7), and a binary complex where only the protein and the gapped DNA were present (simulation 6). In the ternary complex, two Mg²⁺ ions, required for catalysis, were included.

To ensure that our observations are independent on the choice of the initial conditions, simulations for the ternary complex were repeated using a different set of initial velocities (simulation 9). Also, stability of charged systems can be sensitive to the electrostatic treatment. The LN algorithm used here employs a long-distance cutoff with shift and switch variants and has been successfully applied to the study of several protein-DNA complexes (54,61,62). Indeed, it has been shown that such treatments are equally effective for nucleic acid systems (63–65). To further confirm the stability of our simulations, we performed simulations of the pol X-DNA-incoming nucleotide (dCTP) ternary complex using efficient PME method without cutoff (simulation 8). Satisfactorily, we obtained similar results from all our trajectories.

Convergence of the two free pol X configurations to one another

The subtle differences noted in the two reported NMR solution structures of ASFV pol X (41,42) involve the position of the C-terminal subdomain relative to the N-terminal domain. In the Maciejewski et al. structure (structure A), the C-terminal domain is rotated toward the N-terminal, conferring a more closed conformation to the protein.

Our molecular dynamics simulations at physiological conditions (150 mM salt concentration, pH 7.0) on both free pol X forms are more similar to the buffer concentration for structure B (open) (42); the high salt concentration (500 mM salt concentration, pH 7.0) is more similar to the buffer concentration for structure A (closed) (41).

Subdomain motions

At physiological conditions (simulations 1 and 2), after 10.5 ns of molecular dynamics simulations, the pol X structure B (initially open) remains like the starting conformation, whereas structure A (initially closed) tends to open (see Fig. 2 a). At the high salt concentration (simulations 3 and 4), on the other hand, structure A does not change its conformation, but structure B closes to a conformation very similar to the initial structure A (see Fig. 2 b). This behavior indicates that the different conformations captured in the two NMR pol X forms largely reflect the different salt environments.

FIGURE 2.

Comparison of the initial and final structures obtained for the dynamics simulation of free pol X at (a) 150 mM salt concentration (simulations 1 and 2) and (b) 500 mM salt concentration (simulations 3 and 4). The structures are superimposed on the backbone of residues 1–105 (palm subdomain). For clarity, only helix E and the adjoining residues (117–132) are shown.

The opening/closing movement occurs predominantly in helix E (see Fig. 2, a and b). For simulation performed under physiological conditions, analysis of the time evolution of the RMSD of helix E by superimposing palm subdomain reveals that structure A diverges from its original structure much more significantly than structure B (Fig 3 a). Interestingly, the RMSD values decrease in time if structure A is superimposed on the initial structure B rather than on itself (Fig 3 b). This result clearly shows that structure A converges to structure B at the end of the dynamics trajectory.

FIGURE 3.

RMSD plots for helix E of the free pol X structures obtained by superimposing the palm (residues 1–105) for simulations performed at physiological, 150 mM (a and b) (simulations 1 and 2), and high salt concentration, 500 mM (c and d) (simulations 3 and 4). (a) Time evolution plots of the RMSD values for both structure A (initially closed) and structure B (initially open) with respect to initial conformation at physiological conditions. (b) RMSD values obtained by superimposing the palm of structure A in the trajectory with initial structure A and initial structure B. This plot clearly shows that final structure A (at the 10 ns) superimposes better with structure B (average RMSD for the final 2 ns ∼3.5 Å) than with the initial structure A (average RMSD for the final 2 ns ∼5.5 Å). (c) Time evolution plots of the RMSD values for both structure A (initially closed) and structure B (initially open) with respect to initial conformation at high salt. (d) RMSD of structure B plotted with respect to its starting conformation and with respect to structure A. RMSD with respect to structure A is corrected for translational motion following earlier works (see Arora and Schlick (61)) and shows that the final structure B superimposes better with structure A than with initial structure B.

At high salt concentration, after 10 ns, the situation is reversed as expected based on the experimental data. Structure A (initially closed) does not evolve from its original conformation considerably, whereas structure B (initially open) undergoes a conformational change (see Figs. 2 and 3 c). Again, the RMSD of structure B with respect to structure A and starting conformation of structure B, as depicted in Fig. 3 d, shows that structure B evolves toward structure A.

Indeed, the positioning of helix E in the thumb subdomain of simulated structure B is very similar to the final conformation obtained in the simulated ternary complex (see below). However, these two structures (the simulated ternary complex at physiological conditions and structure B at high salt concentration) are similar in the positioning of the helix E and adjacent residues but different substantially in the arrangement of the active site residues, as discussed below (see ternary complex results).

Local residue motions

At physiological conditions, a detailed analysis of the dynamics trajectories (simulations 1 and 2) shows that two aspartates of the catalytic triad in the active site display interesting movements. In particular, although Asp-51 does not change its position considerably, the side chain of Asp-100 rotates in both trajectories, allowing the residue to form a hydrogen bond with Lys-85. Interestingly, this bond formation was also observed in the simulation of the ternary complex (see below). Asp-49 also rotates during the simulation started from structure A, but its final position differs from the one found in structure B. Asp-49 does not rotate during the simulation of structure B.

In the simulation at high salt concentration (simulation 4), structure B undergoes some of the same-residue flips observed in the ternary complex closing (such as for His-115 and Phe-116), with some exceptions. In particular, Phe-102, does not flip during the simulation and the three aspartate residues in the catalytic triad do not exhibit any significant motions, yielding an overall active-site architecture different than the one achieved in the ternary complex.

Small fluctuations in the binary complex

Subdomain motions

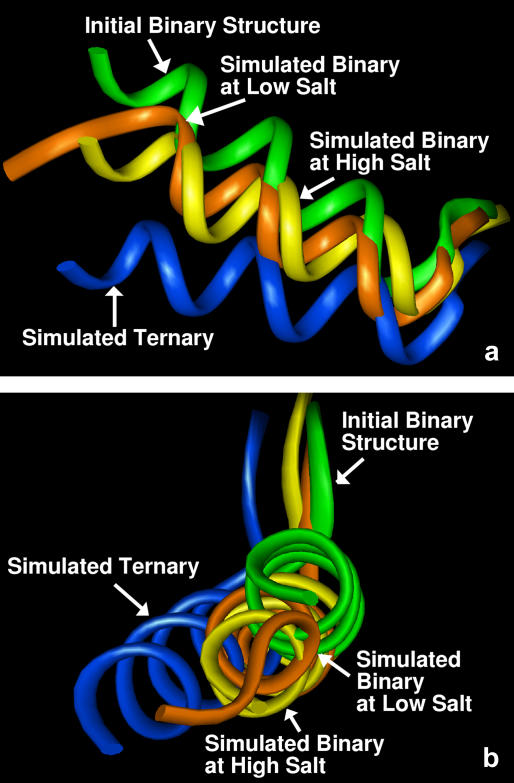
Simulations for the binary complex were performed using the LN algorithm at physiological conditions and the PME algorithm at 500 mM salt concentration (simulation 5). Dynamics simulations of the binary Pol X-DNA complex showed that the protein retained its original configuration, which is a more open form since structure B was used for building the model. Even when the simulation was carried out at high salt concentration, the thumb subdomain did not exhibit a large movement with respect to its original position (Fig. 4). These results show that, once the DNA is present, the protein assumes a conformation that is independent from the salt concentration and can be described as more similar to the open conformation (structure B).

FIGURE 4.

Comparison of the final structures of the binary pol X-DNA complexes with the starting structure (shown in green) and the simulated ternary structure (shown in blue, simulation 7). The simulated binary structure at physiological condition (simulation 6) is shown in orange, and at one obtained at high salt concentration (simulation 5) is yellow. All structures are superimposed on the C_α atoms of the palm subdomain (residues 1–105). Lateral (a) and front (b) view of helix E and the adjacent residues (117–132) are shown in the pictures.

At physiological conditions, the tip of helix E unwinds somewhat, allowing Lys-136 to approach the DNA. However the relative positioning of the helix as a whole is clearly more open than closed, as shown by the comparison with the ternary complex (see Fig. 9). A similar configuration is also obtained at high salt concentration, in contrast to the results obtained for the free protein.

FIGURE 9.

Dihedral plots for some key residues that rotate during the dynamics simulation of the ternary complex (simulation 7). In the lower panel the residues are shown before (green) and after (blue) the dynamics simulation. Dihedral plot for His-115 is not shown, but its flip occurs in the same time range as Phe-116.

Local residue motions

At the atomic level, we found a notable difference in the relative position of His-115 and Phe-116 compared to the ternary complex. The side chain of His-115 flips during the trajectory of the binary complex, whereas Phe-116 does not. In contrast, both residues flip to initiate the thumb closing in the ternary complex (see below). In addition, His-115 is hydrogen bonded to the incoming nucleotide in the ternary complex, making it more rigid. When this nucleotide is not present, this residue is freer to move.

Around the active site, we note that Phe-102 and Asp-49 (one aspartate of the catalytic triad) undergo minor transitions, but not so as to change the overall architecture of the active cavity. In addition, the DNA does not approach the active site. In fact, very few residues are within 4 Å of the DNA by the end of the simulations.

Pol X-DNA motions in the presence of the correct incoming nucleotide

Subdomain motions

After 10 ns of simulation (simulation 7), the pol X-DNA-dCTP ternary complex exhibited a large movement in the thumb subdomain (Fig. 5, a and b). Overall, the movement can be described as a closing of the protein on the DNA (Fig. 5 b). Indeed, a comparison of the final structure for the ternary complex with the known crystal structures of pol β reveals that by the end of the simulation, pol X superimposes well with the closed pol β form (Fig 5 c). Analyses also show that an initial movement occurs at ∼2 ns and then another conformational change takes place after ∼6 ns. By plotting the distance between atoms of pol X residues and the DNA strand (Fig. 6), we observe that this large motion brings the protein and the DNA closer. The residues that exhibit this marked movement are located on helix E and the adjoining β-strand (Asn-134, Lys-136, Gln-139, Asn-145, and Gln-146). Some of these distances change as much as 10 Å. For most of these residues, the predominant conformational change occurs after 6 ns. Analyses show that the changes occur both in the protein and in the DNA and involve bringing them to spatial proximity. The movement of three residues close to the “hinge” of helix E, namely, His-115, Phe-116, and Val-120, appears to initiate the large thumb movement. His-115 and Phe-116 move first, right at the beginning of the dynamics, and subsequently Val-120 flips, causing an opening of the loop that precedes the helix E and allowing the movement of the helix. Interestingly, these motions are observed also in the closing of the free pol X structure B at high salt concentration, confirming that these residue flips are essential for the thumb movement. In addition, as mentioned above, His-115 flips in the binary complex, but Phe-116 does not. That this latter flip does not occur in the absence of the incoming nucleotide likely explains why the protein remains open in the binary complex.

FIGURE 5.

(a) Comparison of the initial structure of pol X in the ternary complex (green) with the final structure obtained after 10.5 ns of simulation (blue) (simulation 7). The DNA is not shown for clarity. (b) Cartoon representation of the thumb subdomain of pol X (residues 105–173) before (green) and after (blue) the dynamics. Helix E in the foreground moves as much as 10 Å. Part of the DNA in the simulated structure is shown in red. (c) Comparison with the open (green) and closed (red) forms of pol β. The structures are superimposed on the catalytic triad (Asp-49, -51, and -100 for pol X and Asp-190, -192, and -256 for pol β).

FIGURE 6.

Plots of representative distances between protein residues and DNA that change significantly during the dynamics trajectory of the pol X-DNA-dCTP ternary complex (simulation 7). In the top left panel, the residues are shown in the simulated structure.

A comparison of the simulated ternary structure with the free NMR pol X structures reveals that the simulated ternary complex is approaching, but not quite superimposable with, the initial structure A as shown in Fig. 7.

FIGURE 7.

Comparison of the simulated ternary structure at isotonic conditions (blue, simulation 7) with the free pol X structures: free pol X structure A (initially closed) is shown in red, free pol X structure B is shown in yellow, and the equilibrated initial ternary model is shown in green. The structures are superimposed on the C_α atoms of the palm subdomain (residues 1–105). Only helix E and adjacent residues (117–132) are shown in the pictures. (a) Lateral view; (b) front view.

Rearrangement of active site residues

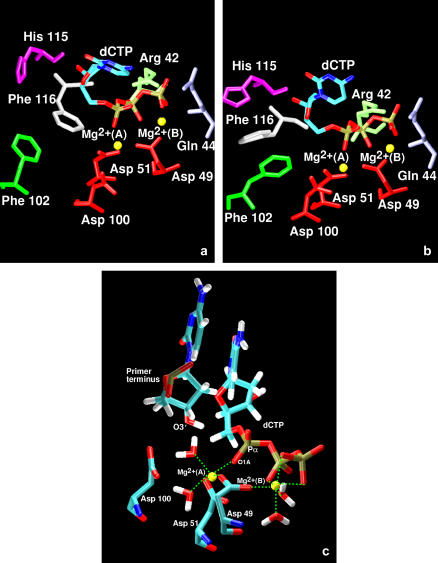
During the early stages of the simulations, the active site geometry changes (Fig. 8, a and b). In particular, we observe that the three residues Asp-100, Phe-102, and Gln-139 move closer to the incoming nucleotide. Asp-100, one of the aspartates in the catalytic triad, flips after 4 ns of dynamics, and one of the oxygen atoms in the carboxylate group comes to within 3.5 Å of the catalytic Mg²⁺ ion.

FIGURE 8.

Active site of the ternary complex (pol X-DNA-dCTP) (a) before and (b) after 10.5 ns of molecular dynamics (simulation 7). (c) Coordination spheres for the catalytic (A) and nucleotide binding (B) magnesium ions at the end of the dynamics trajectory.

This flip also allows Asp-100 to hydrogen bond to Lys-85 and Gln-98 and, at the same time, move closer to the incoming nucleotide. Four other residues, Lys-85, Phe-102, His-115, and Phe-116, also flip during the dynamics, as shown from the dihedral angle plots (Fig. 9). Interestingly, the dihedral angle of Lys-85 transits through an intermediate value before reaching a stable conformation.

During the dynamics, Phe-102 also approaches the incoming nucleotide, dCTP. Phe-102 is the analog of Arg-258 in pol β, a residue found to be important in the closing and opening of the protein during its catalytic cycle (26,54,61,66–69). Interestingly, in the simulated free pol X structure B, Phe-102 does not flip. This might explain why the active site geometry in this structure is different from the one obtained here.

During the early stages of the dynamics, the cytosine base forms the correct Watson-Crick hydrogen bond with the template base, whereas His-115 forms a hydrogen bond with the O3′ of dCTP.

The position of the two Mg²⁺ ions does not change considerably. By the end of the simulation, both ions are hexa-coordinated (Fig. 8 c). The nucleotide-binding Mg²⁺ ion is coordinated with two water molecules, the phosphoryl oxygen atoms of β- and γ-phosphate groups of the incoming nucleotide dCTP, and the oxygen atom Oδ₂ of Asp-49. The catalytic Mg²⁺ ion also has two coordination sites occupied by water molecules, whereas the other positions are taken by one oxygen atom of the α-phosphate of the dCTP and the oxygen atoms of the side chains of Asp-49 and Asp-51. The third aspartate of the catalytic triad, Asp-100, moves closer to the catalytic magnesium, but not close enough to displace the water molecule that is occupying the coordination site.

Nucleotidyl transfer geometry and magnesium ion coordination

Evidence from kinetic and structural studies for several polymerases suggests that the large thumb subdomain conformational change is followed by the nucleotidyl transfer chemical reaction, resulting in elongation of the primer strand by one base (29,70,71). Presumably, this chemical reaction occurs either by means of a metal-assisted (catalytic Mg²⁺) dissociative mechanism or associative in-line nucleophilic attack by the 3′-OH group of the primer terminus on the Pα of the incoming nucleotide, producing an extended DNA primer. The ideal Pα and 3′-OH distance for the phosphoryl transfer reaction to proceed via a dissociative mechanism should be ∼3.3 Å (72). In our simulation of pol X-DNA ternary complex in the presence of correct nucleotide performed using both LN and PME (simulations 7 and 8) at physiological concentration (150 mM), we observe that the crucial Pα and 3′-OH distance is ∼5 Å, larger than ideal distance required for chemistry to proceed. A larger than expected distance between the 3′-OH of the primer with the Pα was also observed in the prechemistry simulation of pol β closing in the presence of the correct incoming nucleotide (61,68) and yet larger for incorrect incoming nucleotides (62). These works indicated that mere force-field artifacts are not the reason for this departure and that such subtle small distortions in distances have likely biological implications for polymerase fidelity (62). Related studies suggest the existence of other subtle rearrangements involved in the enzyme active site after this large subdomain motion and before the chemical reaction (R. Radhakrishnan, E. Waters, and D. Nguyen, unpublished). Indeed, for pol β, (73) mixed quantum mechanical and molecular mechanics studies are suggesting that the enzyme can be stabilized in different closed states and that the chemical reaction proceeds through a high-energy barrier.

Finally, the coordination spheres for the two Mg²⁺ ions for pol X is quite similar to that observed in the simulations of pol β closing (61). Here too we found that the O1A oxygen atom of the α-phosphate group (also designated as pro-S) is coordinated only with the catalytic Mg²⁺ and not bridging the two metal ions as in the closed structure of pol β. In addition, we found that the catalytic magnesium ion is not coordinated to all three aspartates of the catalytic triad, as required for the chemical step. Only Asp-49 and Asp-51 are in close contact with the ion, whereas Asp-100 is further away (3.5 Å) by the end of the simulation. The coordination of Asp-100 is replaced by a water molecule that moves in the active site at the beginning of the dynamics and remains there throughout the trajectory. Interestingly, transition path sampling studies on pol β closing revealed that the coordination of the third catalytic aspartate to the Mg²⁺ ion (Asp-256) occurs late in the closing reaction pathway (68). Perhaps the Asp residue in pol X will ligand magnesium ion in later stages, too. The structural determination of the ternary complex of pol X-DNA will be required to examine this prediction.

DISCUSSION

Free pol X exists in two stable conformations depending on the salt concentration

Details regarding the interactions of DNA polymerases with their target DNA and the nucleotide incorporation mechanism are crucial for understanding the fidelity mechanisms involved in DNA synthesis and repair. Currently, there are no experimentally determined structures of the complex of pol X with DNA, although these are expected in the near future. Our dynamics simulations started from the two available DNA-free structures of pol X determined by NMR (41,42) revealed convergence of the two forms. The preference of one versus the other is determined by the salt concentration, with the more open preferred at physiological salt concentration, whereas the more closed state is predominant at high salt concentration. The reasons of this salt-induced transition between the two forms are not clear. However, the simulations performed here may explain the subtle differences observed in the two experimentally determined NMR structures.

The relevance of two stable conformations in vivo is also not clear. The high degree of flexibility revealed by our RMSD plots at physiological conditions suggests that these two subtly related conformations interconvert into one another in vivo, with a preference for the open conformation in the absence of target DNA. This is in agreement with observations for other DNA polymerases, like pol β, found in open conformation before they bind to the DNA and the incoming nucleotide (11).

Evidence for an induced-fit mechanism in pol X triggered by the correct incoming nucleotide and comparison with pol β

The molecular details of the interaction of pol X with its target DNA are not known from experiment, but our analyses of two pol X-DNA complexes with and without the correct incoming nucleotide reveal a large conformational change only in the presence of the incoming nucleotide, to close the complex. In addition, our results suggest that although the free protein exists in, and possibly interconvert between, two slightly different conformations (one more open and the other more closed), pol X assumes a unique, more open conformation that is not salt dependent once the gapped DNA is present. It is possible that this more open conformation favors nucleotide binding and that, once the nucleotide is in position, the system undergoes a conformational transition from open to closed form in preparation for the chemical reaction.

The study of several binary and ternary DNA-polymerase complexes has indicated that a series of structural changes must occur to achieve the right geometry and produce an active complex (22,29,74–79). This substrate-induced movement is usually described as a closing of the protein around the DNA according to an induced-fit mechanism (31,45,80,81). Our simulations for the binary and ternary complexes pol X-DNA agree with this generalized induced-fit mechanism.

For pol β, such closing was simulated when an intermediate structure was chosen as the starting point, suggesting a higher energy barrier than for pol X (61). The fact that we were able to observe the closing for pol X during the 10.5 ns of dynamics (simulations 7) suggests that this conformational change is relatively fast and that the barrier may be smaller for pol X. The large positively charged patch on the thumb subdomain of pol X may help drive this change. Indeed, experimental data show that pol X binds as tightly to DNA as human pol β despite the lack of the fingers subdomain, suggesting a strong interaction between the thumb and the DNA (42). Interestingly, fast conformational transitions between the crystal binary and ternary states may be characteristic of low-fidelity polymerases.

Our simulations indicate that the DNA binding region is located predominantly in the thumb subdomain. Specifically, helix E and the adjacent β-strand undergo the largest rearrangement during the simulation. Chemical shift perturbation experiments performed in the presence of gapped DNA show that several residues on helix E are affected, thus corroborating our finding that helix E is involved in DNA binding (41,42).

During the thumb closing, we observe the rearrangement of key residues in the active site. In particular, Asp-100, Phe-102, His-115, Phe-116, and Lys-85 undergo the most significant changes. For pol β, it is indeed known that a concerted movement of many active site residues is required to achieve the right closed geometry (29,61,68,69,82). For pol X, the rearrangement of a few key residues is necessary to induce a conformational change and this movement occurs rapidly. This less restrained active site for pol X relative to pol β is also consistent with the lower fidelity exhibited by pol X, a consequence of pol X's inability to tailor fit the correct Watson-Crick basepair tightly.

As expected, the sequence of events that triggers the closing in the two polymerases varies (see Table 2). A recent study that employed transition path sampling to simulate the entire reaction pathway elucidated the sequence of events in pol β closing (68). According to that study, an initial movement of the thumb subdomain toward closing is accompanied by the repositioning of the incoming nucleotide. Subsequently, Asp-192 flips, followed by the partial rotation of Arg-258 and subsequent flip of Phe-272 that positions itself between Arg-258 and Asp-192. In pol X, on the other hand, His-115 and Phe-116 (analogous to Tyr-271 and Phe-272) flip right at the onset of the simulation, and this is immediately followed by the rotation of Phe-102 (analogous to Arg-258) and subsequently Val-120 (analogous to Asp-276). These concerted movements initiate the large thumb rearrangement. After the major conformational change, Asp-100 (analogous to Asp-256) rotates and coordinates with Lys-85. These differences in the residues involved in the active site movement could explain in part the different substrate specificity of pol X versus pol β and the why pol X can accommodate a G:G mispair easily (10).

TABLE 2.

Key residues in pol X and analogues in pol β

Residue in pol X	Residue in pol β	Comments
Asp-49	Asp-190	Catalytic triad: Asp-100 flips and coordinates to Lys-85 and Gln-98
Asp-51	Asp-192
Asp-100	Asp-256
Lys-85	Lys-234	Conserved Lys residue: flips and forms H-bond with Asp-100 during the dynamics
Phe-102	Arg-258	Flips after Phe-116
His-115	Tyr-271	Both flip at the beginning of the dynamics
Phe-116	Phe-272
Val-120	Asp-276	Its flip initiates the thumb movement

Suggested site-specific mutagenesis experiments based on simulations results

The results presented here suggest a series of events for the closing of pol X (Table 2). A natural way to test this possible pathway is to study specific mutants of key residues involved.

From analogy with pol β, it would be interesting to test whether the mutation of Phe-102 has a similar effect on pol X as the mutation of Arg-258 on pol β. Targeted molecular dynamics simulations (54,67), stochastic path approach (61), and transition path sampling studies (68) have shown that a conformational rearrangement of this residue is a key slow step in the subdomain motion. Kinetics studies on the mutant R258A show that the nucleotide incorporation rate increases (W. A. Beard and S. H. Wilson, unpublished), and molecular dynamics simulations on this mutant (L. Yang, K. Arora, R. Radhakrishnan, and T. Schlick, unpublished) reveal that closing is facilitated, confirming the role of Arg-258 in the wild type (82). A mutant of Phe-102 such as Phe-102Ala, would provide insights on the importance of this residue in pol X.

Another suggested residue to investigate is Val-120, corresponding to Asp-276 in pol β. In pol β, Asp-276 influences the enzyme's catalytic efficiency and nucleotide binding affinity by forming van der Waals interactions with the nascent basepair (25). Val-120 in pol X, on the other hand, gets farther away from the incoming nucleotide during the dynamics. Whether this residue is important for nucleotide binding affinity could be tested by mutating it with a smaller (e.g., glycine) or charged residues, like aspartate or glutamate.

Finally, Lys-85, a conserved lysine residue, appears to be important in the reorganization of the active site. Whether the newly formed hydrogen bond between this residue and Asp-100 is important for catalysis could be tested by substituting Lys-85 with a hydrophobic residue like valine, leucine, or isoleucine.

CONCLUSIONS

Our dynamics simulations show that free pol X can exist in two stable configurations that interconvert to one another depending on the salt concentration, in agreement with the experimental data. At physiological conditions, the preferred free form is a more open conformation. The pol X-gapped DNA complex also remains open, though the relative positioning of the thumb domain shows some minor changes; in contrast, the complex closes its thumb subdomain upon the DNA when the incoming correct nucleotide and the divalent ions are also present. A closing is also achieved in the free protein at high salt concentration, but the active-site geometry is distorted and not suitably correct nucleotide binding. Together, these results point to an induced-fit mechanism for pol X, like pol β, upon DNA and substrate (dCTP) binding (29,61,68).

This study represents a first attempt to describe in atomic details the interaction of pol X with the DNA. A natural next step is to examine pol X complexes in the presence of mispairs, particularly G:G, to probe why pol X easily misincorporates dGTP opposite to G template (10,39). Preliminary results show that a conformational change in the thumb subdomain is achieved in the presence of a G:G mispair but not in the case of other mispairs like A:G or C:C, in agreement with the kinetic data (B. A. Sampoli Benitez, K. Arora, and T. Schlick, in preparation) In addition, the experimental determination of pol X-DNA complexes, on the horizon, will also shed further insights into the structures and mechanisms of pol X and fidelity mechanisms in general.