Simulation Study of the Contribution of Oligomer/Oligomer Binding to Capsid Assembly Kinetics

Abstract

The process by which hundreds of identical capsid proteins self-assemble into icosahedral structures is complex and poorly understood. Establishing constraints on the assembly pathways is crucial to building reliable theoretical models. For example, it is currently an open question to what degree overall assembly kinetics are dominated by one or a few most efficient pathways versus the enormous number theoretically possible. The importance of this question, however, is often overlooked due to the difficulties of addressing it in either theoretical or experimental practice. We apply a computer model based on a discrete-event simulation method to evaluate the contributions of nondominant pathways to overall assembly kinetics. This is accomplished by comparing two possible assembly models: one allowing growth to proceed only by the accretion of individual assembly subunits and the other allowing the binding of sterically compatible assembly intermediates any sizes. Simulations show that the two models perform almost identically under low binding rate conditions, where growth is strongly nucleation-limited, but sharply diverge under conditions of higher association rates or coat protein concentrations. The results suggest the importance of identifying the actual binding pattern if one is to build reliable models of capsid assembly or other complex self-assembly processes.

INTRODUCTION

Virus capsid self-assembly is a process by which many, typically chemically identical, coat protein subunits spontaneously form into larger, complex structures. Understanding of virus capsid assembly has traditionally been based on the Caspar and Klug theory of “quasi-equivalence”. This theory explained the icosahedral symmetries of typical spherical viruses, which are often categorized based on the number (T) of protein subunits in an asymmetric unit (1). Investigations of these complex and efficient self-assembly systems are important for understanding the basic biology of viruses and other complex self-assembly systems and may prove useful in developing drug treatments to interfere with viral infection processes (2–4) and providing a paradigm for designing novel self-assembly systems (5). However, many aspects of the assembly process are not well understood due to our limited ability to experimentally observe and manipulate assembly reactions on the nanometer scale. Various computer simulation models have been developed to study different aspects of capsid self-assembly behavior, such as the equilibrium behavior of assembly systems (6,7), favored assembly pathways (8,9), mechanisms behind unusual “nonquasiequivalent” structures (10,11), and the overall reaction kinetics of the assembly process (7,12,13). Several simulation models (14–16) have also been developed based on a theory of virus assembly called local rules (17), which proposed that virus capsid formation could be directed by simple local interaction of virus coat protein subunits. These local rule models created a unified conceptual model for representing structures with diverse geometries and assembly patterns and allowed exploration of many issues inaccessible to other models, such as the possible roles of interactions between assembly intermediates (13,14).

Despite rapid advances in the understanding of capsid self-assembly from the synergy of computational and experimental approaches, quantitative description of capsid self-assembly dynamics is still a daunting task for both theoretical and experimental virologists. One significant obstacle to computational approaches is the large number of possible intermediate species and assembly pathways, which grow exponentially with the number of assembly subunits in a complete capsid. Significant simplifications have been required by past computational models so that only subset of pathways, typically the most energetically favorable intermediate species, are considered in modeling the reaction to achieve acceptable accuracy and computational tractability (7,9). This restriction raises the question of how and under what circumstances one can limit possible pathways without appreciably affecting overall predicted assembly kinetics, an issue examined in recent simulation work (8). That is, will overall kinetics be dominated by one or a few most efficient pathways or by the enormous number of nondominant pathways available to a complex assembly system?

In this work, we examine the importance of nondominant assembly pathways to overall kinetics by focusing on one particular simplification generally used in modeling capsid assembly: the assumption that assembly intermediates do not interact with one another. This assumption is based on the lack of direct evidence of observing the interaction between intermediates, the small amount of and the slower diffusion rate of intermediates, the stricter requirement for the multiple domains of two intermediates to be able to access each other at the same time, and the computational difficulty of modeling such reactions using prevailing simulation methods. A pathway involving binding of pairs of oligomers would not be predicted to be the most efficient route to the construction of an individual capsid. But considered over an ensemble of growing capsids, such pathways might substantially influence overall assembly kinetics. We consider two possible assembly models, one allowing growth to proceed only by the accretion of individual capsomer assembly subunits, which we call the constrained binding pattern, and the other allowing the binding of sterically compatible assembly intermediates of any size, which we call the unconstrained binding pattern. Although the possible intermediate species are identical in both models, the unconstrained binding pattern involves many more pathways.

The constrained binding pattern is generally assumed in computational work to date. In a real capsid self-assembly system, the assembly pathway need not proceed through the addition of monomeric building blocks. Various sizes of stable coat protein oligomers may associate directly in capsid assembly. For example, there is evidence that assembly proceeds through the addition of monomers for bacteriophage P22 (18), dimers for hepatitis B virus (HBV) (19), pentamers for papillomavirus (20), pentamers and hexamers for bacteriophage HK97 (21), and tetrameric P1 and hexameric P4 for cystovirus phi8 (22). Although none of this evidence bears directly on the possibility of interactions between unstable intermediates, it does suggest that considerable diversity is possible in assembly mechanisms. There is evidence that interaction between transient oligomeric intermediates is required for assembly of cowpea chlorotic mottle virus (CCMV) (23). Association of partial assembly structures in low salt conditions also was observed in the phage P22 procapsid assembly (24), although little is known about the contribution of this type of association to normal P22 assembly kinetics. Furthermore, computational models of other self-assembly systems have shown analogous reactions to be important to accurately modeling overall assembly kinetics. For instance, experimentally determined length distributions of actin filaments are inconsistent with predictions from models allowing only a simple elongation and nucleation mechanism (similar to the constrained pattern) and are better fit by a model incorporating annealing and fragmentation of filaments (similar to the unconstrained pattern) (25). It is therefore important to consider whether analogous simplifications in allowed pathways for virus capsid models will affect their ability to reliably match experimental data. To address this question, we used a discrete event simulation system (15) to build two icosahedral capsid self-assembly models, one constrained and one unconstrained, and assessed the quantitative assembly behavior of each for various parameters settings. The simulation results lay the foundation for future experimental investigations of the limits on capsid assembly pathways and provide a platform for evaluating possible simplifications in future modeling efforts.

COMPUTER MODELS

Computer simulations are conducted using a discrete event simulator recently designed to allow for efficient quantitative simulation of complex biological self-assembly systems (15). This simulation model is based on local rules abstractions (10,13,17) and a fast queue-based discrete-event simulation algorithm (26). We follow Zlotnick (7,8) in exploring this problem through a simple model of the assembly of T = 1 capsids from 12 pentameric capsomer assembly subunits (shown in Fig. 1 a). Each subunit has five free binding sites, which can bind with the binding sites on other subunits to form larger assemblies. Association and dissociation reactions are assumed to occur at discrete steps. The affinities of binding sites with one another are encoded by the mean waiting times to form and break a binding interaction, T_a and T_d. Because waiting times are exponentially distributed, the means completely specify the waiting time distributions and are equal to the inverses of standard reaction rate constants. The stochastic time interval between discrete steps captures the random nature of an assembly reaction. Subunits bind to one another according to local rules derived from the geometry of the complete T = 1 capsid, forcing them to adopt the correct icosahedral symmetry (Fig. 1 b).

FIGURE 1.

Screenshots of an assembly subunit, intermediates, and complete capsid in the simulation model. (a) Assembly subunit representing a pentermeric capsomer. (b) Simplified T = 1 capsid model structure consisting of 12 subunits with structure shown in a. (c–f) Possible intermediate stages in an assembly reaction and the allowed movements between them for (c) an open linear trimer and a monomer, (d) a closed trimer and a monomer, (e) two dimers, and (f) a tetramer.

Our model differs from those in the prior work in a few respects. First, we use a discrete event model instead of a differential equation model, meaning that our simulator keeps track of discrete counts of all species present at any given time and updates these counts through single reaction events. This discrete event methodology provides an important capability: all the potential species and pathways are possible with some nonzero probability unless they are explicitly disallowed. We exploit this capability to model two different binding patterns. For the constrained binding pattern, only one capsomer is allowed to add into a growing capsid in a single reaction step. For example, to form a tetramer of capsomers (shown in Fig. 1 f), only the association of an open, linear trimer (shown in Fig. 1 c) or a closed, loop-like trimer (shown in Fig. 1 d) with a subunit is allowed, following the pathway (1) or (2) in Fig. 1. However, for the unconstrained binding pattern, the association of two species of any size is allowed provided there is no steric hindrance in the new assembled structure. For example, to form a tetramer, the unconstrained model can use pathway (4) in Fig. 1, which proceeds through the association of two dimers (shown in Fig. 1 e), in addition to the pathways (1) and (2) accessible to the constrained model.

The simulator used in this work is implemented as a set of Java classes defining a general model and algorithms for discrete event self-assembly simulation. The most recent release is available at 〈http://www.cs.cmu.edu/∼russells/software/discrete/simulation.html〉, along with documentation and some example systems. The code has been tested on Linux, Windows, and Mac OS X operating systems. At the time of this work, specific systems to be modeled must be defined in Java code specifying the local rules for a given system, which define the positions and specificities of the binding sites of all subunits as well as the on and off rates for compatible pairs of binding sites. A revised version of the simulator is in development to allow users to define new self-assembly systems through a simpler XML schema without writing new Java code. This and other future updates will be released through the same website.

The model involves some simplifying assumptions. First, during the process of assembly, all binding rate constants for any two compatible binding sites are assumed to be equal. Therefore, the reaction rate of two types of reactants is determined by the amount of these reactants and the number of compatible binding sites on each type of reactant. There is no explicitly modeled nucleation rate distinct from the subsequent elongation rate, although a slow nucleation rate is implicitly present because multiple binding interactions are required to create the first stable intermediate, a trimer in which each subunit binds the two others. Dimers will generally dissociate before incorporating the additional subunit needed for the stable nucleus, yielding an effective slow nucleation rate. Furthermore, we do not adjust rates to account for slower diffusion of larger intermediates. We further insist that coat proteins bind only with optimal bond angles, which is currently a restriction of the simulator in general. This constraint allows oligomers to form only when they are substructures of complete capsids, preventing the formation of malformed structures or inclusion bodies. We further disallow dissociation reactions involving pairs of subunits bound within a “loop”. For example, the tetramer in Fig. 1 f can only break along the pathway (3) in Fig. 1. These infinitely stable loop structures are used to compensate for the entropy benefit of binding subunits already held in the proper binding positions by other binding interactions. Simulation parameters varied in this work include the system size N, i.e., the initial number of free subunits, the association rate constant k_a and the dissociation rate constant k_d between two binding sites. Given the predefined interaction rules and simulation parameters, the simulator can output the system state (e.g., the numbers of free capsomers and complete capsids, the total number of species, etc.) at any time.

Although the stochastic method used models a single possible trajectory for a finite number of reactant molecules, the results for sufficiently large stochastic simulations will converge on those of a deterministic large-system differential equation model. The system sizes used in this work approximate those for a single bacterium infected by a phage. However, the average results from multiple simulation runs can be used to estimate the progress of an in vitro assembly system using the same concentration and rate constants but a much larger volume and total number of molecules. If A_k(t) denotes the concentration of species consisting of k subunits at time t, then the differential equations for the large-system approximation to our simulation model have the form

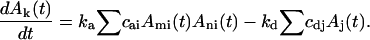The first item gives the change in A_k(t) due to association of species A_mi and A_ni, with k_a the association rate constant and c_ai the stoichiometric coefficient for possible geometrical arrangements of A_mi and A_ni. The second term gives the change due to the breaking of A_j, with k_d the dissociation rate constant and c_dj a stoichiometric coefficient counting possible sites of breaking in A_j. Therefore, a kinetic curve tracking counts of any species over time for a self-assembly reaction system with system size n × N and association rate k_a should be n times higher than that for a system with system size N and association rate n × k_a. If the ratio of k_a to k_d is fixed and the system sizes are identical, the reaction progress should be the same aside from random fluctuations and adjustment of the time scale. A given simulation can thus describe the behavior of any system for which N × k_a/k_d (a dimensionless constant that we will call ρ below) is the same, given appropriate scaling of the time and concentrations. Note that scaling N by n and simultaneously scaling k_a/k_d by 1/n does affect that variance of the results, but not their mean. Therefore, in the simulation experiments, a constant k_d = 1000 and varied k_a are used to investigate the kinetic behaviors. With the establishment of this basic scheme, the averaged simulation results from multiple runs on a small system can be extrapolated to a large system size for comparison to in vitro experimental data.

RESULTS

To investigate the average assembly behaviors for the two binding patterns, we ran the simulator with each binding pattern and with four association rate constants, k_a: 0.001, 0.01, 0.1, and 1. Each simulation was repeated 30 times. Fig. 2, a and b, shows numbers of complete capsids versus time for the range of binding rate constants with unconstrained and constrained binding patterns. For both patterns, capsid formation shows sigmoidal assembly kinetics. As we would expect, for a particular capsomer time course, the capsomer subunit concentration is reduced most quickly at the early dimerization stage due to the high concentration of available subunits. The numbers of capsomer subunits for both patterns fall off more rapidly with increasing k_a (Fig. 2, c and d). These results reflect a tradeoff in which slow binding produces slower growth but also a higher eventual yield. We attribute this increased yield to a reduction in kinetically trapped intermediates at low binding rates. As mentioned above, each simulation can also be extrapolated to the assembly behavior in a larger system with a smaller k_a. For example, the curve with parameters N = 1000, k_a = 1 in Fig. 2, b and d, would also correspond to the results expected for N = 10,000, k_a = 0.1 (tenfold higher concentration but one tenth the association rate) and have a higher degree of kinetic traps than the simulation result shown in Fig. 2, a and c, with parameters N = 1000, k_a = 0.1. This suggests that either larger association rate constants for fixed concentration or higher concentration for fixed association rate can be expected to promote the accumulation of intermediates. We conjecture that such conditions promote overly rapid nucleation relative to elongation, quickly exhausting the pool of free monomers needed to complete nascent capsids, an interpretation consistent with prior simulation (12,14) and experimental (23,27) studies. This interpretation is also supported by a more detailed examination of intermediate concentrations versus time (Fig. 3), which show the results with N = 1000, k_a = 0.001, 0.01, and 0.1 for both binding patterns. The kinetic curves of concentrations of species of each size show that increasing k_a leads to more accumulation of intermediates both transiently and in trapped states.

FIGURE 2.

Time courses of simulations with a system size N = 1000 and varied association rate constants (0.001, 0.01, 0.1, 1) and binding patterns. Error bars represent ± 1 SD derived from 30 simulation runs. (a) Complete capsid production with the unconstrained binding pattern. (b) Complete capsid production with the constrained binding pattern. (c) Capsomer concentration changes with the unconstrained binding pattern. (d) Capsomer concentration changes with constrained binding pattern. The insets in a and b are the time course with k_a = 0.001 and a longer simulation run time.

FIGURE 3.

Time courses of concentrations of species of 11 sizes (from dimer to complete capsid) from simulation runs with N = 1000. a, c, and e are for the unconstrained binding pattern with k_a = 0.001, 0.01, and 0.1. b, d, and f are for the constrained binding pattern with k_a = 0.001, 0.01, and 0.1.

Comparisons of results from the two patterns show that the unconstrained binding pattern leads to higher capsid yields and fewer kinetic traps (Figs. 2 and 3) across a broad range of k_a (0.01, 0.1, 1). Intermediate distributions are markedly different for the two binding patterns when system parameters are identical (Fig. 3, c–f). Fig. 4, a and b, illustrates the differences in intermediate distributions with screenshots of assemblies and intermediates after capsid assembly has reached its plateau from simulation runs using parameters corresponding to Fig. 3, e and f. For the unconstrained binding pattern, trapped intermediates are predominantly close in size to a complete capsid (Fig. 4 a). However, for the constrained binding pattern, there are many more small kinetically trapped species corresponding to early intermediates (Fig. 4 b). The additional pathways permitted with the unconstrained binding pattern appear to allow otherwise trapped intermediates to associate together to further advance capsid formation. However, when k_a is small, the capsid yields are similar for the two binding patterns (Fig. 2). At this low rate, neither pattern shows appreciable accumulation of intermediates, either transiently or permanently (Fig. 3, a and b). We believe that slow binding rates slow the nucleation rate relative to the elongation rate, allowing nucleated capsids enough time to go to completion before capsomers are exhausted and leading to a similar “assembly line” in both patterns. The additional pathways allowed by the unconstrained binding pattern are rarely used because intermediate concentration is low, causing no significant increases in the capsid yields for the slow binding rate.

FIGURE 4.

Screenshots of assembly products of various sizes after capsid production has reached a plateau from simulations with different binding patterns using the parameters N = 1000, ka = 0.1, and kd = 1000. (a) Unconstrained binding pattern. (b) Constrained binding pattern.

Given the indications that the two proposed binding patterns lead to divergent assembly kinetics, one immediate question is whether the true binding pattern could be inferred from the time progress of capsid yields for a real experimental system. We must separately consider two situations: growth under conditions of significant kinetic trapping and growth under conditions of no appreciable kinetic trapping. Fig. 5 a shows the comparison in a parameter domain producing kinetic trapping. The figure shows one capsid kinetic curve from a simulation with the unconstrained binding pattern with four kinetic curves from simulations with the constrained binding pattern. All systems have identical sizes and dissociation rates. Kinetic rate constants were empirically selected for the constrained simulations to approximately match the equilibrium capsid yield of the unconstrained simulation. Nonetheless, the different binding patterns produce different shapes of kinetic curves. The unconstrained binding pattern reaches the equilibrium state substantially faster than the constrained one. Given the concentration and a reasonable estimate of the ratio of the association and dissociation rates derived from the free energy of subunit-subunit binding, simulation curves of either initial rate or final yield could be matched to true in vitro data to distinguish the two models, provided the concentration is sufficiently high. Fig. 5 b shows a pair of simulations, one constrained and one unconstrained, using a parameter set that does not yield appreciable kinetic trapping. In this case, both patterns produce similar kinetic curves and it is therefore difficult to identify which binding pattern produced a given curve. The results suggest that if the reaction is performed in a domain yielding significant kinetic trapping, only one of the two binding patterns should yield a good fit to the measured data. In a domain of negligible kinetic trapping, however, the assembly behaviors in the two patterns cannot be distinguished. This further suggests that the actual binding pattern must be identified and the existence of kinetic trapping tested before an unknown rate constant could be inferred from the fitting of experimental data to time course curves from simulation runs.

FIGURE 5.

Comparison of the two binding patterns with identical initial concentrations of capsomers (N = 1000). (a) Simulations under conditions producing kinetic trapping, with capsid yields from the constrained binding pattern for k_a = 1:100, 1:90, 1:80, and 1:70 and for the unconstrained binding pattern with k_a = 1:10. (b) Simulations under conditions not producing kinetic trapping, using k_a = 0.001 for both binding patterns.

Several in vitro studies have examined the dependence of capsid assembly kinetics on initial concentrations of subunits (19). To investigate whether such dependences would allow one to distinguish the two binding patterns, we compared the capsid yields for two systems sizes (N = 500, 2000; see Fig. 6). In the simulations with the unconstrained binding pattern, for a broad range of binding rate constants (0.001, 0.01, 10⁻⁹), a fourfold increase in the initial concentrations of subunits correspondingly increases the capsid yields, whether or not there exist kinetic traps (Fig. 6, a, c, and e). However, for the constrained binding pattern, the capsid yields increase with initial concentrations of subunits only when there are no or few kinetic traps (k_a = 0.001, Fig. 6 b). With the existence of kinetic traps (when k_a ≥ 0.01, see Fig. 6, d and f), the capsid yields show no dependence on the initial subunit concentrations.

FIGURE 6.

Capsid time courses with three association rate constants (0.001, 0.01, 10⁻⁹) and two system sizes (N = 500, 2000). Left panels (a, c, e): unconstrained binding pattern. Right panels (b, d, f): constrained binding pattern.

DISCUSSION

By applying a recently developed method for fast discrete-event simulation of self-assembly, we are able to consider questions regarding the contributions of nondominant pathways to self-assembly kinetics that were inaccessible to prior simulation methods. We specifically consider the potential contributions of reactions between intermediates to the overall kinetics in a model of T = 1 capsid assembly. Our results suggest that there are reaction domains in which the two binding patterns are essentially indistinguishable as well as others in which they exhibit large quantitative differences in capsid production as a function of time. The significant differences in the assembly curves from the two models across a broad range of rate constants indicates that ignoring these additional pathways could lead to substantial errors in predictions of assembly behavior. It is thus important to establish which pattern, if either, best describes real virus capsid systems and under what conditions. The answer to this question has implications not only for the model used, but also for the simulation methods used to implement it; the discrete event methods used here were necessary to make simulations under the unconstrained model computationally tractable and such methods may need to be more widely adopted to investigate complex assembly behaviors, predict experimental results, guide new experiments, and assist in the development of new capsid-targeted antiviral drugs.

The simulation results also suggest a possible mechanism for the formation of trapped intermediates. For both binding patterns, fast reaction rates would increase the number of nuclei and leave fewer free capsomers to complete the assembly reactions. This interpretation is consistent with the kinetic changes observed in the presence of different ionic concentrations that appear to affect binding energy in P22 (24) and HBV (27) capsid assembly. It is also consistent with observations of accumulation of intermediate species during in vitro CCMV assembly at moderate concentrations, which is proposed to occur due to a similar mechanism of excessively rapid nucleation relative to elongation under those conditions (23).

The two binding patterns show similar results in low association rate/low concentration domains, indicating that the importance of intermediate-intermediate reactions to model construction depends on the specific system and conditions being modeled. Endres et al. investigated the critical intermediates with the constrained pattern by using a reaction landscape approach and found that in reaction domains without kinetic traps, there is no experimentally detectable difference between the simulations of a full model and that considering only the most energetically favorable pathway (8). This is consistent with our comparison of simulations without kinetic traps for both patterns. In this case, only “main” pathways, which could be identical for both binding patterns, may have an important effect on the assembly reactions in both patterns.

Although this work is purely theoretical, it is important to consider whether or not actual virus capsid assembly is likely to occur in domains in which oligomer/oligomer assembly pathways begin to dominate the overall kinetics. As discussed in Computer Models, any given simulation can be extrapolated to any other system for which the dimensionless constant ρ = N × k_a/k_d is the same, where N is the initial capsid subunit concentration and k_a and k_d are association and dissociation rate constants. For the simulations considered above, the transition between the low-ρ domain where the bindings patterns are indistinguishable and the high-ρ domain where they are distinguishable occurs between k_a = 10⁻³ and k_a = 10⁻², for fixed N = 1000 and k_d = 1000, yielding ρ between 10⁻³ and 10⁻². Although the binding equilibrium constant k_a/k_d will vary from virus to virus, we can derive a range of values from a low estimate of the free energy of subunit-subunit binding of −2.72 kcal/mol (7) and a high estimate of −3.5 kcal/mol (8), yielding k_a/k_d approximately between 98.9 and 369 M⁻¹. We can thus estimate that the concentration at which a true capsid assembly system would transit between the domains should fall approximately in the range 2.71–101 μM. The lower limit is well within concentrations accessible to typical in vitro assembly systems and would approximately correspond to the cellwide average concentration to be expected in a single infected phage. Should actual viruses prove to enter the high ρ-domain near the low end of the range, our results suggest it would be possible to distinguish between the two binding patterns in vitro. Given the various approximations involved in the estimates, however, it is possible the true threshold concentration for some systems will exceed feasible in vitro values. But values substantially beyond this range are plausible in vivo, particularly if mechanisms such as membrane-assisted assembly produce high local coat protein concentrations within the cell. We therefore may not be able to establish from in vitro chemistry which binding pattern a given real virus uses, nor will we necessarily know if the in vivo system operates in the high-ρ domain where the distinction between binding patterns is significant. In vitro models of capsid assembly could thus be misleading with regard to the role of oligomer/oligomer pathways in overall assembly kinetics, as high-ρ domains available within the cell might provide access to substantially different and more efficient assembly kinetics than can be observed in vitro.

There are several important issues to be dealt with in future work. More detailed models of the assembly process may lead to refinement of our results. For example, some intermediates are permanently trapped in our model because we do not allow loops to break, to account for the much higher stability of a structure in which each subunit is held in place by at least two binding interactions. In a real capsid, loops would not be infinitely stable, but should nonetheless be expected to break much more slowly than single binding interactions. It is therefore likely that real capsids would have a recovery mechanism for intermediates that is lacking from our model, although it would act on a slower timescale than other capsid assembly steps. In this work, we did not specifically differentiate the effects of intermediates of different sizes on the overall kinetics. In a real capsid assembly system, the association of larger intermediates may be limited due to their slower diffusion rate. The model could be extended to adjust binding rates to account for differential diffusion rates of larger species, as is done by Lok et al. (28). Finally, it is necessary to move beyond pure theory to identify the appropriate models and simulation parameters for real virus systems. Such parameters might be determined directly from in vitro systems as in prior experimental work (18) or assisted by computational parameter-tuning optimization procedures. Our results suggest, though, that it may prove necessary to develop new experimental methods to better monitor quantitative biochemistry in the cell or to better mimic the cellular environment in vitro to build accurate quantitative models of in vivo virus assembly dynamics.