Mechanisms of Excitation-Contraction Coupling in an Integrative Model of the Cardiac Ventricular Myocyte

Abstract

It is now well established that characteristic properties of excitation-contraction (EC) coupling in cardiac myocytes, such as high gain and graded Ca²⁺ release, arise from the interactions that occur between L-type Ca²⁺ channels (LCCs) and nearby ryanodine-sensitive Ca²⁺ release channels (RyRs) in localized microdomains. Descriptions of Ca²⁺-induced Ca²⁺ release (CICR) that account for these local mechanisms are lacking from many previous models of the cardiac action potential, and those that do include local control of CICR are able to reconstruct properties of EC coupling, but require computationally demanding stochastic simulations of ∼10⁵ individual ion channels. In this study, we generalize a recently developed analytical approach for deriving simplified mechanistic models of CICR to formulate an integrative model of the canine cardiac myocyte which is computationally efficient. The resulting model faithfully reproduces experimentally measured properties of EC coupling and whole cell phenomena. The model is used to study the role of local redundancy in L-type Ca²⁺ channel gating and the role of dyad configuration on EC coupling. Simulations suggest that the characteristic steep rise in EC coupling gain observed at hyperpolarized potentials is a result of increased functional coupling between LCCs and RyRs. We also demonstrate mechanisms by which alterations in the early repolarization phase of the action potential, resulting from reduction of the transient outward potassium current, alters properties of EC coupling.

INTRODUCTION

Myocyte contraction occurs in response to a series of events that are initiated and coordinated by the cardiac action potential (AP). Initial membrane depolarization during the upstroke of the AP activates voltage-gated L-type Ca²⁺ channels (LCCs), which provide for Ca²⁺ influx across the sarcolemma. The influx of Ca²⁺ ions triggers the release of Ca²⁺ from the junctional sarcoplasmic reticulum (SR) in the process known as Ca²⁺-induced Ca²⁺ release (CICR). CICR leads to a 10-fold increase in cytosolic Ca²⁺ concentration, and hence, provides the necessary signal to initiate mechanical shortening of the cell's contractile machinery. The elucidation of the mechanisms that underlie the process of CICR has become possible in recent years with the development of experimental techniques for simultaneous measurement of LCC currents and Ca²⁺ transients (1–3), and detection of local Ca²⁺ release events (4,5). These experimental observations gave rise to and later verified the local control theory of excitation-contraction (EC) coupling (1,6–8). The mechanism of local control predicts that within discrete regions of the dyadic cleft, the opening of an individual LCC located in the t-tubule membrane will trigger Ca²⁺ release from a small cluster of SR Ca²⁺ release channels (known as ryanodine receptors, i.e., RyRs) that reside in close proximity directly across the dyad in the junctional SR membrane. Tight regulation of CICR is achieved because LCCs and RyRs are regulated by the local dyadic Ca²⁺ signal, rather than by bulk cytosolic Ca²⁺ levels. The amplitude and profile of the whole-cell intracellular Ca²⁺ transient results from the recruitment and temporal summation of elementary Ca²⁺ release events, known as Ca²⁺ sparks, in these discrete regions (4,9). The recruitment of Ca²⁺ sparks via this mechanism allows for graded control of SR Ca²⁺ release, in which amplitude of the Ca²⁺ release flux is a smooth, continuous function of LCC Ca²⁺ influx (6,9).

Until recently, computational models of the cardiac myocyte have been unable to capture the fundamental mechanism of local control of CICR. Many recent models (10–14) can be classified as common pool models (6), in which all LCC Ca²⁺ influx and RyR release flux is directed into a common Ca²⁺ compartment, and it is this Ca²⁺ pool that controls RyR activity. Stern (6) demonstrated that in any such model exhibiting gain at or near the high level observed physiologically, the initiation of SR Ca²⁺ release will stimulate regenerative all-or-none, rather than graded, Ca²⁺ release. That is, graded release and high gain are incompatible. This limitation of common pool models has important implications for Ca²⁺-mediated LCC dynamics. An increase in local Ca²⁺ concentration will promote Ca²⁺-dependent inactivation of nearby LCCs (15). Recent experiments have shown that inactivation of LCCs is mediated primarily by a Ca²⁺-dependent process (15,16), whereas voltage-dependent inactivation is relatively slow and incomplete during the time course of the AP (15,17). We have shown that incorporation of an LCC model with this experimentally validated balance between voltage- and Ca²⁺-dependent inactivation into a common pool myocyte model destabilizes the plateau of the AP (18). In fact, recent common pool models have incorporated strong voltage-dependent inactivation of the L-type Ca²⁺ current (I_CaL) to stabilize the AP (19). For this reason, common pool models are not good candidates for the study of CICR. As an alternative to the common pool formulation, models in which Ca²⁺ release flux is represented as an explicit function of sarcolemmal Ca²⁺ influx (20–22) are able to achieve both high gain and graded Ca²⁺ release. However, because these phenomenological formulations lack mechanistic descriptions of the processes that are the underlying basis of CICR, their predictive ability is limited.

We have recently formulated a computational model of the cardiac ventricular myocyte that includes a mechanistic implementation of local control of CICR (18). The model consists of a population of Ca²⁺ release units (CaRUs), each of which represents a discrete dyadic Ca²⁺ release site at the junction of t-tubule and SR membranes. The gating of individual LCCs and RyRs within each CaRU are simulated stochastically, allowing for each CaRU to be independently modulated by its own local Ca²⁺ dynamics. Integration of this CICR model into a myocyte model describing membrane ionic and pump/exchanger currents, SR Ca²⁺ uptake, and time-varying cytosolic ion concentrations (10) yielded a model that accurately reconstructs stable APs and describes important features of CICR including graded release and voltage-dependent EC coupling gain. In addition, the stochastic model implementation has allowed for further study of the role of LCC gating noise in the generation of early after depolarizations (23). A limitation of this model, however, is that it is far more computationally demanding than its predecessors, and therefore requires significantly more computational resources. To overcome this issue, we recently introduced an approach to simplifying the local control model of CICR by applying a carefully chosen set of approximations that allow for the ensemble behavior of CaRUs to be represented by a low dimensional system of ordinary differential equations (ODEs), eliminating the need for computationally expensive stochastic simulations. This model, termed the coupled LCC-RyR model (24), retains the biophysically based description of local control of CICR, and captures its key properties including graded Ca²⁺ release and voltage-dependent EC coupling gain.

In this study, we formulate an integrative model of the canine ventricular myocyte based on the theory of local control of SR Ca²⁺ release. This is achieved by applying the method described by Hinch et al. (24) to the model of Greenstein and Winslow (18). The approach is demonstrated using a simplified CaRU model containing only a single LCC and a single RyR. We demonstrate that the resulting model faithfully reproduces features of LCC voltage- and Ca²⁺-dependent gating (8,17,25), microscopic EC coupling (1,26–29), and macroscopic whole-cell AP and Ca²⁺ cycling properties (30,31). This formulation can be considered a multiscale model because of its ability to capture details on the scale of local EC coupling events as well as on the scale of whole-cell phenomena.

Recent experiments have indicated that the quantitative features of EC coupling gain may be dependent upon local redundancy of LCC channel gating (32). Local redundancy in LCC open probability refers to the probability that multiple LCCs open simultaneously within a single release site. Manipulation of redundancy in LCC open probability (which depends upon channel-gating properties as well as the number of channels in a local cluster) is difficult to achieve experimentally. To study this phenomenon using this approach to modeling CICR, we generalize the method of Hinch et al. (24) to accommodate LCC and RyR models of arbitrary complexity, and to accommodate a CaRU containing multiple LCCs and RyRs. This is accomplished by designing a software algorithm that builds a coupled LCC-RyR model corresponding to given definitions of individual LCC and RyR models, and the numbers of each channel that resides in the CaRU. This allows for comparison of models of CICR containing different numbers of LCCs and RyRs, and therefore acts as a powerful tool for elucidating the relationship between physical RyR/LCC coupling ratio (i.e., RyR/LCC channel stoichiometry) and functional coupling ratio (i.e., the number of RyRs triggered per activated LCC, on average), and hence the underlying determinants of EC coupling gain. Simulations suggest that the steep rise in EC coupling gain at hyperpolarized potentials, as observed experimentally (1,29), is a result of increased functional coupling between LCCs and RyRs and reflects the maximal number of RyRs that can be triggered by a single LCC.

Finally, Sah et al. (33) have recently demonstrated that slowing early repolarization, in a manner consistent to that which occurs with inhibition of the transient outward K⁺ current (I_to1) in larger mammals, leads to blunted Ca²⁺ transients with slower rise times, decreased efficiency of EC coupling, and impaired contractility. Although a general mechanism by which I_to1 regulates properties of CICR has been described (18,33), we use the model presented here to demonstrate that a slowing of early repolarization of the AP via alteration in I_to1 leads to a reduction in SR Ca²⁺ release by not only a reduction of I_CaL trigger influx (18,33), but also by a loss of EC coupling gain as a result of an increase in local redundancy of LCC openings. Thus this model provides insight into the mechanisms by which alteration of a membrane current that is seemingly unrelated to EC coupling can have a significant impact on CICR and hence, contractility.

METHODS

Our recent model formulation incorporating stochastic, local control of SR Ca²⁺ release (18) was designed to capture the fundamental properties of CICR (e.g., graded Ca²⁺ release) emerging from the local interaction of LCCs and RyRs in the dyad. The basic unit of that model is the calcium release unit (CaRU), consisting of LCCs, RyRs, and the dyadic volume within which these channels communicate via the local Ca²⁺ concentration. The CaRU mimics the properties of Ca²⁺ sparks in the t-tubule/SR junction. The CaRU was formulated based on the following experimental constraints:

1. RyR/LCC stoichiometry is set to five RyRs to one LCC, based on estimates indicating that a single LCC typically triggers the opening of 4–6 RyRs (34).

2. CaRUs are simulated independently in accordance with the observation that RyR clusters (i.e., dyads) are physically separated at the ends of sarcomeres (35).

3. LCC and RyR channel models are based on previously developed and validated models (11,36,37).

The current model formulation aims to retain all of the fundamental features of our previous model (18), but to eliminate the need for computationally intensive stochastic simulation of individual ion channels. This is accomplished using a method that we have described recently (24). Briefly, LCC and RyR models composed of the minimum number of states necessary to capture fundamental dynamics of channel gating are designed and constrained based on experimental data sets. Application of a steady-state approximation for Ca²⁺ diffusion in the dyad allows the resulting CaRU to be simplified into a single Markov state model in which each state represents a unique configuration of channel states for the combined set of LCCs and RyRs in the CaRU. All parameters of this compound Markov state model are derived analytically from the parameter sets describing individual LCCs, RyRs, and CaRU Ca²⁺ fluxes. In the resulting formulation, the dynamics of a population of CaRUs can be described by a set of coupled ODEs. The computationally expensive Monte Carlo methods used for single-channel simulations in our previous model (18) are therefore not required to simulate the model presented here.

LCC and RyR channel models

The L-type Ca²⁺ channel model (Fig. 1 A) is a simplified version of the 12-state Markov model presented and validated previously (see Fig. 12 A of Greenstein and Winslow (18)), which is based on the mode-switching model developed by Jafri et al. (11). The simplified LCC model retains all of the essential features by which it has been characterized, such as:

1. Forward and reverse activation rates (α and β) based on I_CaL measured in canine midmyocardial cells (38);

2. Peak open probability in the range of 5–15% (39–41);

3. Experimentally based balance between voltage- and Ca²⁺-dependent inactivation processes (15,17,42); and

4. Channel permeability consistent with measured values of single-channel slope conductance and unitary current (39,43).

Whereas the original model contained five states in the activation pathway before the open state (18), the current model reduces the activation pathway to two states. The normal gating mode (i.e., Mode Normal) is therefore represented by states 1–3, where state 3 is the open state. Ca²⁺-dependent inactivation (CDI) occurs upon downward transitions from Mode Normal states into states 4–5 (i.e., Mode CDI). The Mode CDI open state from the original 12-state model has been excluded from this model version because its occupancy probability is nearly zero. States 6–10 represent voltage-dependent inactivation (i.e., Mode VDI) and are accessible from states 1–5, respectively. This process was previously modeled using an independent channel gate (see Fig. 12 B of Greenstein and Winslow (18)). The methods implemented here require VDI to be incorporated within the LCC Markov-state model; however, steady-state and kinetic properties of this process are identical to those in our previous LCC model description (18).

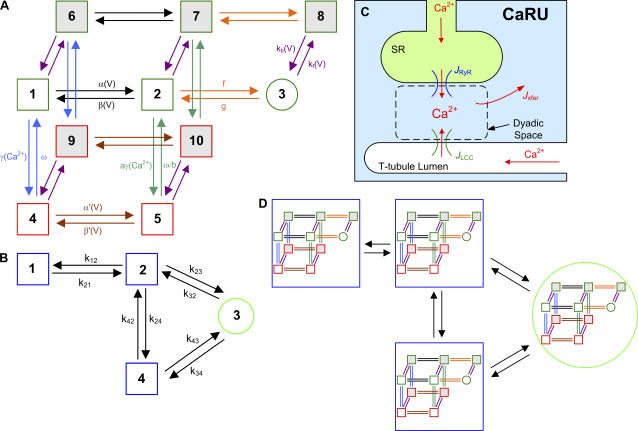
FIGURE 1.

State diagrams for the LCC and RyR Markov models and schematic diagrams of the CaRU. (A) State model of the LCC which represents a simplification of the model presented previously (see Fig. 12, A and B, of Greenstein and Winslow (18)). Upper states (green outline, states 1–3, and 6–8) encompass Mode Normal, lower states (red outline, states 4, 5, 9, and 10) encompass Mode CDI, and the backplane states (gray shading, states 6–10) encompass Mode VDI. The open state (state 3) is denoted by a circle, whereas closed states are denoted by squares. Depolarization rapidly promotes transitions from left to right, and more slowly promotes transitions into Mode VDI states, whereas downward transitions into Mode CDI states are promoted by elevation in local Ca²⁺ level. Pairs of transitions with the same arrow color share identical transition rates. (B) State model of the RyR based on a simplification described previously (see Fig. 13 C of Greenstein and Winslow (18)), where states 1 and 2 are the resting states, state 3 is the open state, and state 4 is the refractory state. Rate constants are Ca²⁺-dependent based on the assumption that four Ca²⁺ ions must bind the RyR before opening. Rate definitions for both the LCC and RyR models are provided in the Supplementary Material. (C) Schematic representation of the CaRU, which is the basis of the baseline-coupled LCC-RyR model. In the baseline model, a CaRU consists of a single LCC on the t-tubule membrane and a single RyR on the SR membrane, both facing into the dyadic space. (D) Visualization of the state diagram for the baseline-coupled LCC-RyR model. The “outer” model represents the four-state RyR model of B, and for each RyR state, there are 10 possible LCC states, shown within each RyR state as the LCC model of A. The model therefore consists of 40 states, where each state represents a unique pairing of LCC and RyR states. Each state transition of the coupled model represents a single state transition of either the LCC or the RyR. The full set of equations describing the 40-state coupled LCC-RyR model is provided in the Supplementary Material.

The free parameters of the model were determined using a Nelder-Mead simplex search algorithm (44) implemented in MatLab (The MathWorks, Cambridge, MA). The optimization algorithm was implemented using a cost function that quantified the difference in behavior of the simplified LCC model to the previous 12-state LCC model (18) based on measures of steady-state open probability and Mode Normal occupancy, peak and time-to-peak of open probability and Mode Normal occupancy in response to a depolarizing voltage-clamp, and rate of recovery from inactivation. All protocols were performed over a large range of voltages and Ca²⁺ concentrations. The number of active LCCs was chosen such that the amplitude of whole-cell I_CaL corresponds to measurements in canine myocytes (38), yielding a value of 50,000, which agrees with experimental estimates of LCC density (39,45).

The RyR is represented by a model developed by Keizer and Smith (36) and later modified by Rice et al. (37). The RyR model implemented in this study (Fig. 1 B) is identical to the reduced four-state model used in our previous local control myocyte model (see Fig. 13 C of Greenstein and Winslow (18)). It is a highly simplified model that is intended to describe Ca²⁺ release fluxes under physiologically relevant stimuli, but does not explicitly incorporate additional features such as regulation by Mg²⁺ or luminal Ca²⁺ (see Discussion). Upon influx of trigger Ca²⁺ into the dyad, RyRs will transition rapidly from state 1 through state 2 to state 3, the open state. Open channel flux is driven by the concentration gradient between SR luminal Ca²⁺ and the local dyadic Ca²⁺. Open channels will close via an inactivating transition into state 4. After local Ca²⁺ levels subside, RyRs will recover by transitioning back to state 1. RyR model parameters were constrained based on experimentally obtained properties of EC coupling (1,29), and are in agreement with the findings of Sham et al. (26) suggesting that RyR inactivation into an absolute refractory state occurs in vivo and is the primary mechanism of SR Ca²⁺ release termination. The Ca²⁺ dependence of the model state transition rates have been adjusted based on the assumption that four Ca²⁺ ions must bind to the channel before it can enter the open state (46). In most cases, it will be possible to model a small cluster of RyRs using a single model RyR. In these instances, the open channel Ca²⁺ flux rate and activation rates (transition rates between states 1 and 2) are adjusted accordingly based on the number of channels the single RyR model represents (see below).

The coupled LCC-RyR model

We have recently described a method for formulating a simplified model of the CaRU (24). Briefly, a minimal model of the CaRU (Fig. 1 C) is devised consisting of a single LCC in the sarcolemmal membrane, a single RyR in the SR membrane, and the dyadic volume within which these channels reside. The single-model RyR represents an approximation to a cluster of five RyRs (see Fig. 4 C) in agreement with estimates of RyR/LCC stoichiometry (34). This representation of the CaRU requires that the SR is considered as a single volume compartment, and no distinction is given to junctional versus network SR. This simplification can be justified by recent experimental observations that demonstrate that junctional SR Ca²⁺ is in quasiequilibrium with network SR Ca²⁺ during a Ca²⁺ release event, that is, the Ca²⁺ refilling rate from network to junctional SR is rapid relative to the release flux (47). Since the diffusion rate of Ca²⁺ between the dyad and cytosol is relatively fast compared to the gating rates of LCC and RyR channels (48,49), and because dyad volume is very small, it can be assumed that dyadic space Ca²⁺ concentration ([Ca²⁺]_ds) equilibrates very rapidly. In other words, it can be assumed that J_xfer = J_RyR + J_LCC, where J_RyR and J_LCC are the Ca²⁺ fluxes into the dyad via the RyRs and LCCs, respectively, and J_xfer is the Ca²⁺ flux from the dyad to the bulk cytosol (Fig. 1 C). Note that this assumption does not imply that [Ca²⁺]_ds = [Ca²⁺]_cyto. Rather, this assumption allows [Ca²⁺]_ds to change instantaneously upon a change in dyadic Ca²⁺ flux due to the opening or closing of an LCC or RyR. The above expression can be expanded and rearranged to yield an expression for [Ca²⁺]_ds (in terms of cytosolic and SR [Ca²⁺], and membrane potential) which can be used to evaluate [Ca²⁺]_ds in the transition rate expressions. This step transforms [Ca²⁺]_ds into a dependent variable, rather than an independent variable, in each CaRU. The LCC and RyR models can then be combined into a single coupled LCC-RyR model, in which each state represents the joint configuration of the LCC-RyR pair, and whose parameters are derived analytically from the individual LCC and RyR models (see (24) for a detailed example). The coupled LCC-RyR model of the CaRU described here consists of a 40-state Markov process (Fig. 1 D), and will be able to capture nearly all of the biophysical details of CICR associated with local control of SR Ca²⁺ release. This 40-state model will be referred to the baseline-coupled LCC-RyR model below. All equations for the baseline-coupled LCC-RyR model are provided in the Supplementary Material. The model is available for download at the Center for Cardiovascular Bioinformatics and Modeling website (www.ccbm.jhu.edu).

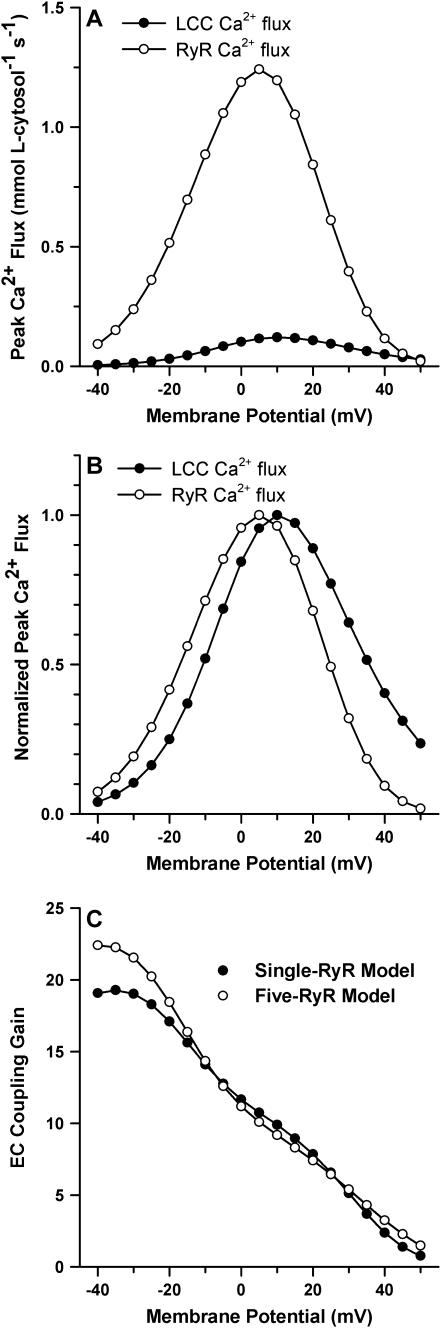
FIGURE 4.

Voltage dependence of LCC Ca²⁺ influx, RyR Ca²⁺ release flux, and EC coupling gain. (A) Peak LCC Ca²⁺ flux (solid circles) and peak RyR release flux (open circles) as a function of membrane voltage. (B) Peak Ca²⁺ fluxes (data in A) normalized by their respective maxima. (C) EC coupling gain as a function of membrane potential for the baseline-coupled LCC-RyR model (solid circles), in which a single model RyR is used to represent a cluster of five RyRs is compared to a model in which the five RyRs are each modeled individually (open circles).

The coupled LCC-RyR model lacks Ca²⁺ buffers in the dyadic space. In general, the binding/unbinding of Ca²⁺ to buffers alters the rate at which free Ca²⁺ concentration changes in any given compartment. Ca²⁺ buffers, however, do not affect the steady-state concentration of free Ca²⁺ in a compartment (i.e., at steady-state, Ca²⁺ influx equals Ca²⁺ efflux and the fraction of buffer that has Ca²⁺ bound to it remains constant). Since this model assumes that Ca²⁺ in the dyad is always at its steady-state value (i.e., rapid equilibrium with neighboring compartments), implicit in this assumption is that any Ca²⁺ buffers that may be present have fast kinetics and are not of sufficient capacity to significantly alter the rate of equilibration between the dyad and its neighboring compartments. Therefore, no dyadic Ca²⁺ buffers are explicitly included in this model.

The method described above for formulating a coupled LCC-RyR model is not limited to a dyad containing only a single LCC and single RyR. Investigation of the quantitative role of microdomain LCC-RyR signaling on CICR requires the ability to construct more complex coupled LCC-RyR gating models based on a variety of individual LCC and RyR models and/or the number and ratio of RyRs and LCCs in a CaRU. To do this, we have devised an automated method for generating a set of ODEs describing the joint behavior of all channels in a CaRU. This method is sufficiently general that it can be applied to construct a CaRU model using individual LCC and RyR models of arbitrary complexity. The generalized method is given in the Supplementary Material and is described briefly as follows. If each CaRU is composed of N_LCC LCCs, each represented by an identical M_LCC-state model, and N_RyR RyRs, each represented by an identical M_RyR-state model, then it can be shown that M_CaRU, the number of unique states in the coupled LCC-RyR model, is given by

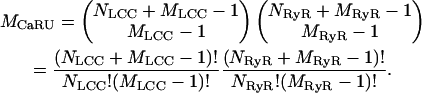A transition between any two of these states occurs as the result of a single-state transition of a single channel (either LCC or RyR) within the CaRU. Each pair of connected states in the group of M_CaRU states is identified and assigned transition rate expressions that are derived from the transition rates of the underlying channel models. Some of these rate expressions will depend upon [Ca²⁺]_ds. The value of [Ca²⁺]_ds is determined analytically based on the number of open LCCs and RyRs corresponding to each CaRU state and the assumption that Ca²⁺ flux-balance is in rapid equilibrium (as described above). A data structure is formed that stores the relevant parameters needed to correctly evaluate the rate expressions for each connected pair of states in the coupled LCC-RyR model. The velocity field of the ODEs that define the CaRU can then be evaluated within any Solver routine on a term-by-term basis where the contribution of each state pair is incrementally added to the right-hand side of the appropriate state equation. This entire process of model derivation and code implementation has been automated in software to eliminate errors in model formulation. This is a critical step, since manual derivation and implementation of models of this complexity would be tedious and error-prone. For example, using the 10-state LCC and four-state RyR models described above, evaluation of the above equation for M_CaRU shows that a CaRU containing five RyRs and one LCC will require a 560-state coupled model. Such a model can be rapidly formulated and simulated using our generalized methods. In addition, multiple model variations that differ in LCC and/or RyR number can be rapidly generated and compared, whereas a manually derived coupled LCC-RyR model must be completely reformulated upon a change in channel number.

Whole-cell simulations are performed by incorporating the coupled LCC-RyR model into the canine ventricular myocyte model described previously (18) and based on the model of Winslow et al. (10). Some membrane currents and ionic fluxes have been scaled to adjust cytosolic ionic concentrations, AP shape, and rate dependence of AP duration. All equations and parameters describing the myocyte model are provided in the Supplementary Material. The set of ODEs defining the myocyte model are solved using a trapezoidal rule algorithm (MatLab function ode23t, The MathWorks).

RESULTS

L-type Ca²⁺ current

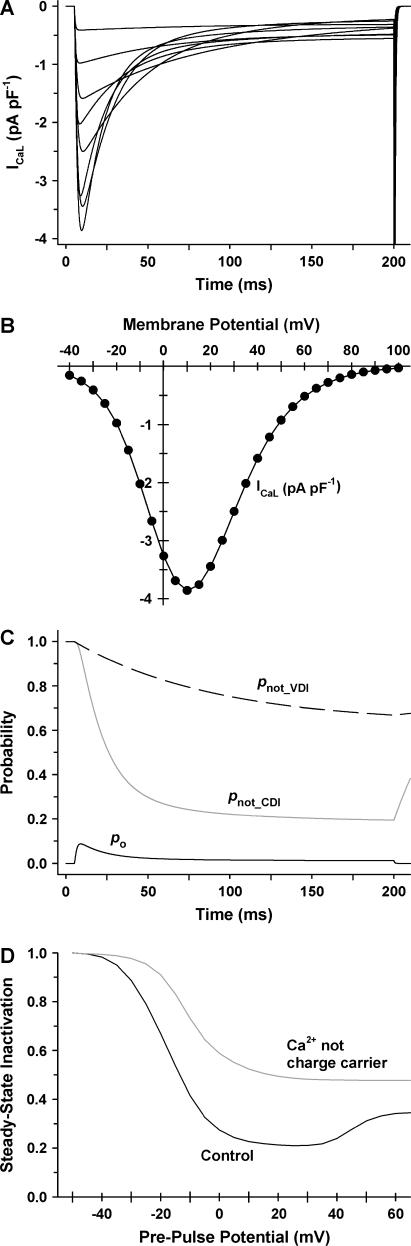
To correctly capture the strong negative feedback of SR Ca²⁺ release on the dynamics of I_CaL, the simplified LCC model presented here (Fig. 1 A) has been configured to match the kinetic properties of our previous detailed LCC model and the experimental data against which it was validated (18). Simulated whole-cell currents elicited by a family of depolarizing voltage steps from −30 mV to +40 mV in 10-mV increments are shown in Fig. 2 A. Currents activate rapidly (<8 ms) and decay over ∼100 ms. Fig. 2 B shows the LCC peak I-V relationship for I_CaL, where peak currents were determined in response to voltage steps from a holding potential of −100 mV. Maximum inward Ca²⁺ current is produced at a test potential of +10 mV. The bell-shaped peak current profile is in agreement with peak currents measured in canine (38,50,51), Guinea pig (39), and human (52) ventricular myocytes. Fig. 2 C demonstrates the underlying processes that govern the time course of I_CaL during a voltage-clamp to 0 mV. The quantities shown are LCC open probability (p_o, solid line), probability that CDI has not occurred (p_{not_CDI}, shaded line), and the probability that VDI has not occurred (p_{not_VDI}, dashed line). LCC p_o reaches a peak value of ∼0.09, consistent with studies that indicate that peak p_o with Ca²⁺ as the charge carrier is in the range of 0.05–0.15 (39,40). A comparison of the time progression of p_{not_CDI} and p_{not_VDI} clearly demonstrates that at 0 mV, Ca²⁺-mediated inactivation of I_CaL develops more rapidly and progresses more completely than voltage-dependent inactivation, consistent with recent experiments (17,53,25,15,42) and our previous model (see Fig. 3 C of Greenstein and Winslow (18)). Steady-state inactivation properties of I_CaL are measured using a standard double-pulse protocol. Normalized peak currents are shown as a function of the prepulse potential in Fig. 2 D. Simulations were performed under normal conditions (solid circles) and with subspace Ca²⁺ clamped to diastolic levels to mimic an alternative charge carrier such as a monovalent cation that would not significantly promote CDI (open circles). Under normal conditions, the I_CaL steady-state inactivation curve is U-shaped, whereas upon removal of CDI, the inactivation curve decreases monotonically with depolarization. Note that LCC inactivation is incomplete, and asymptotically approaches ∼48% at the most depolarized potentials. These features agree well with inactivation curves obtained experimentally in native myocytes (17,50,53) and demonstrate the role of graded CICR on CDI, particularly in the range of potentials that correspond to the AP plateau (–10 mV to +30 mV). The degree of inactivation attained is more than would be expected theoretically due to VDI alone (maximum of 40%, see Eq. 5 of the Supplementary Material) because there is a small degree of CDI that remains present under these conditions. Single-channel properties of the LCC model under normal physiological conditions (i.e., with EC coupling intact and 2 mM extracellular Ca²⁺) display a voltage-independent mean open time of ∼0.5 ms, an open-channel slope conductance of 8.2 pS, and a unitary current of ∼0.12 pA at 0 mV (data not shown), in agreement with experiments (39–41,54,55) and our previous model (see Fig. 2 of Greenstein and Winslow (18)).

FIGURE 2.

Properties of I_CaL. (A) Simulated whole-cell currents as a function of time in response to a family of depolarizing voltage steps from −30 mV to 40 mV in 10-mV increments. (B) Peak I-V relation for I_CaL. (C) LCC open probability (p_o, solid line), probability that Ca²⁺-dependent inactivation has not occurred (p_{not_CDI}, shaded line), and probability that voltage-dependent inactivation has not occurred (p_{not_VDI}, dashed line), in response to a voltage-clamp to 0 mV. (D) Steady-state inactivation curve obtained using a double-pulse protocol with (black line) and without (shaded line) Ca²⁺ as the charge carrier.

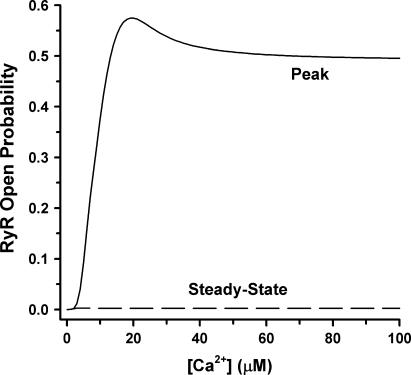
FIGURE 3.

Ca²⁺ dependence of peak (solid line) and steady-state (dashed line) RyR open probability (p_o) for simulated maintained changes in free dyadic Ca²⁺ concentration. The response at each [Ca²⁺] level was initiated from a resting [Ca²⁺] of 0.1 μM.

Fig. 3 shows the model RyR peak and steady-state open probabilities in response to a range of Ca²⁺ concentration stimuli. The peak open probability for this model is most sensitive to Ca²⁺ stimuli in the range of 1–20 μM and approaches a maximal value of ∼50% for higher Ca²⁺ concentrations. This behavior is consistent with recent experimental measurements of RyR p_o under simulated physiological conditions in the presence of 0.6 mM Mg²⁺ (56). The small overshoot in peak p_o that occurs in the range of 15–30 μM Ca²⁺ is result of model simplification. For Ca²⁺ concentrations >∼1 μM, the steady-state p_o is <1%, indicating that the process of inactivation/adaptation is nearly complete for a wide range of trigger Ca²⁺ concentrations.

Excitation-contraction coupling

Previous experiments (1,27,28,57) and mathematical models (6,18,58) have demonstrated the relationship between LCC Ca²⁺ influx and SR Ca²⁺ release flux, in which SR release is graded and there is a characteristic shift in the voltage-dependent release flux with respect to LCC trigger influx. As a result, EC coupling gain, defined as the ratio of peak SR Ca²⁺ release flux to peak LCC Ca²⁺ influx in response to a voltage-clamp step (1), decreases monotonically with increasing voltage. Fig. 4 demonstrates that the coupled LCC-RyR model captures these fundamental quantitative properties of CICR. Peak LCC trigger influx and SR release flux (solid circles and open circles, respectively, Fig. 4 A), display similar voltage dependence; however, normalization of these curves (Fig. 4 B) reveals that maximal SR release flux occurs at ∼5 mV, whereas maximal trigger influx occurs at ∼10 mV. The EC coupling-gain curve for this coupled LCC-RyR model (containing only a single LCC and a single RyR per CaRU, Fig. 4 C, solid circles) agrees with experimentally observed measurements of whole-cell Ca²⁺ measurements (1,27–29,57). As stated in Methods, this coupled LCC-RyR model contains a single LCC and a single RyR, where the RyR model is altered to approximate the behavior of a cluster of five RyRs. The validity of this approximation is demonstrated by the similarity in EC coupling gain predicted by a model in which this approximation is not applied, i.e., a model that contains one LCC and five RyRs (Fig. 4 C, open circles). Such a model requires 560 states to describe the CaRU (see Methods), and is therefore far less computationally efficient than the baseline 40-state model. The approximation of a cluster of RyRs by a single model RyR is effectively the implementation of the assumption that neighboring RyRs are functionally coupled and gate synchronously as has been observed experimentally (59). Due to the fact that Ca²⁺-release is locally regenerative in the model, the EC coupling gain curve does not depend strongly on whether RyRs are allowed to gate independently or are constrained to gate synchronously. Regardless of the number of modeled RyRs, as membrane potential decreases, EC coupling gain in the model increases approximately linearly and does not exhibit a steep rise at potentials <−10 mV as has been observed in experiments (1,29). The mechanism underlying the steep slope of the gain curve at negative potentials as observed in experimentally obtained measurements of EC coupling is addressed below. The results of Figs. 2–4 demonstrate that the baseline-coupled LCC-RyR model (i.e., the 40-state model) adequately reproduces average properties of local Ca²⁺-dynamics and can therefore reliably simulate CICR at the level of the whole myocyte.

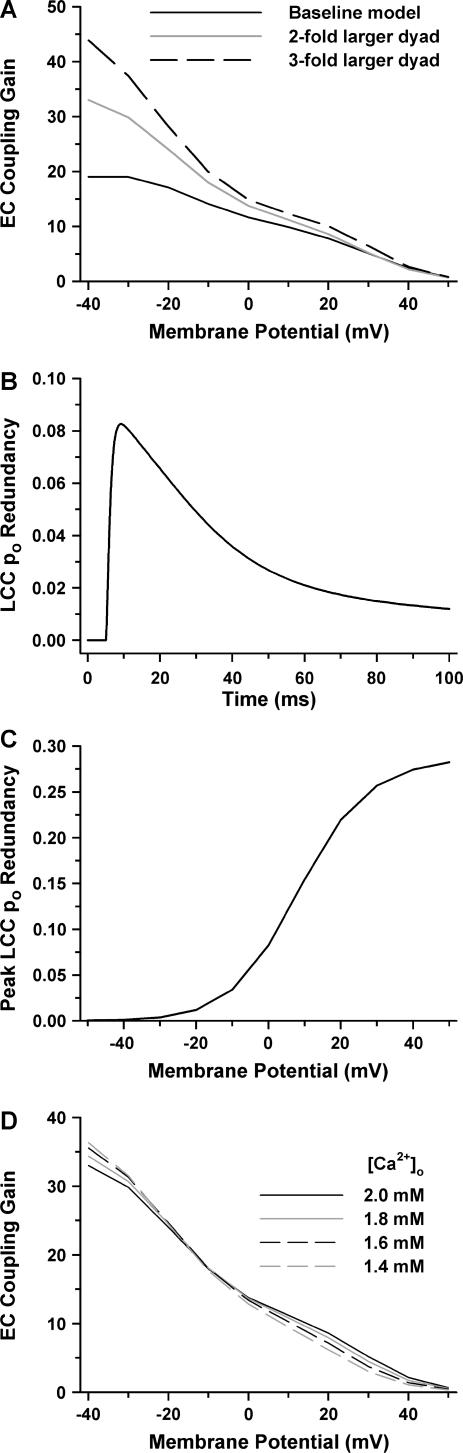
The coupled LCC-RyR model provides a unique opportunity to understand the mechanistic determinants of the shape of the EC coupling-gain curve. The effect of CaRU (i.e., dyad) size on EC coupling gain is demonstrated in Fig. 5 A. A CaRU that is n-fold larger in size than the baseline model contains an n-fold larger dyadic volume, and n-fold more LCCs and RyRs. However, regardless of CaRU size, the RyR/LCC stoichiometry of 5:1 remains unchanged. The total number of CaRUs in the cell is reduced n-fold, such that the total number of LCCs and RyRs, as well as the total aggregate dyadic volume in the whole myocyte, remains unchanged. Coupled LCC-RyR models for larger CaRUs were generated using the generalized algorithm for coupled LCC-RyR models as described in Methods. These manipulations allow for the study of the role of dyad size on EC coupling independently from the role of RyR/LCC stoichiometry. Gain for the baseline-coupled LCC-RyR model (Fig. 5 A, solid line) is compared to that for a population of CaRUs, which are twofold (shaded line) or threefold (dashed line) larger than the baseline model. The simulation results demonstrate that EC coupling gain at potentials >−10 mV increases by only a small to moderate amount with and increase in CaRU size. However, at potentials more negative than −10 mV, the increase in CaRU size yields a substantial increase in gain and, hence, the EC coupling-gain curve acquires the steep slope similar to those observed experimentally in this range of potentials (1,29). This demonstrated relationship between CaRU size and EC coupling gain arises due to the local redundancy of LCC p_o. Local redundancy of LCC p_o refers to the probability that there are multiple LCCs open simultaneously within a single CaRU. In the coupled LCC-RyR model, local redundancy of p_o is defined as the fraction of open LCCs that have at least one open neighboring LCC within the same CaRU. As shown in Fig. 5 B, in response to a voltage-clamp step to 0 mV, redundancy of p_o is a time-dependent quantity that has a peak that approximately coincides with peak trigger LCC Ca²⁺ influx (see Fig. 2). Peak redundancy of p_o as a function of voltage-clamp potential is shown in Fig. 5 C using the CaRU that is increased in size by twofold (i.e., 2 LCCs, 10 RyRs). At negative potentials, local redundancy of p_o is nearly zero due to relatively low LCC p_o. This increases the functional RyR/LCC ratio because it is likely that a single LCC opening will trigger regenerative release from all RyRs in a CaRU. The functional RyR/LCC ratio will therefore increase with an increase in CaRU size (i.e., an increase in the number of dyadic LCCs and RyRs) leading to a substantial increase in gain at negative potentials (Fig. 5 A). At more positive potentials, the local redundancy of p_o is increased significantly, and approaches 30% (note that redundancy never approaches 100% because peak LCC p_o never approaches unity). Under these conditions, the functional RyR/LCC ratio approaches the stoichiometric ratio of 5:1 due to increased likelihood of simultaneous opening of neighboring LCCs. As a result, EC coupling gain displays little dependence on CaRU size at positive potentials (Fig. 5 A). Recent experiments have demonstrated that a reduction in LCC unitary current (i_LCC), achieved via reduction of extracellular Ca²⁺ concentration ([Ca²⁺]_o), increases EC coupling gain, suggesting that the high gain at negative potentials is due to less redundancy in p_o rather than larger i_LCC (32). Fig. 5 D demonstrates model simulations in which EC coupling gain is measured as a function of [Ca²⁺]_o using the model with twofold-increased CaRU size. At negative potentials, successive decreases in [Ca²⁺]_o from 2.0 mM (solid line) to 1.4 mM (shaded dashed line) lead to successive increases in EC coupling gain, in agreement with experiments (32) suggesting that EC coupling gain relies on the redundancy of p_o rather than the magnitude of i_LCC. At higher potentials (>0 mV), however, the model predicts that the dependence of EC coupling gain on [Ca²⁺]_o reverses direction and gain declines as [Ca²⁺]_o is reduced. This suggests that the local coupling efficiency between LCCs and RyRs within a dyad becomes progressively weaker as i_LCC falls to relatively small amplitudes.

FIGURE 5.

Properties of EC coupling gain. (A) EC coupling gain as a function of membrane potential for the baseline-coupled LCC-RyR model (solid line) is compared to gain for models in which dyad size and number of channels is increased twofold (shaded line), and threefold (dashed line). The number of CaRUs in the cell is scaled such that the number of LCCs and RyRs (and total dyad volume) in the whole cell remains identical for all models. (B) Redundancy of LCC p_o as a function of time in the model with twofold increase in dyad size in response to a voltage-clamp to 0 mV. (C) Peak redundancy of LCC p_o as a function of voltage in the model with a twofold increase in dyad size. (D) EC coupling gain in the model with a twofold increase in dyad size for [Ca²⁺]_o of 2.0 mM (solid line), 1.8 mM (shaded line), 1.6 mM (black dashed line), and 1.4 mM (shaded dashed line).

Action potentials and whole-cell Ca²⁺ transients

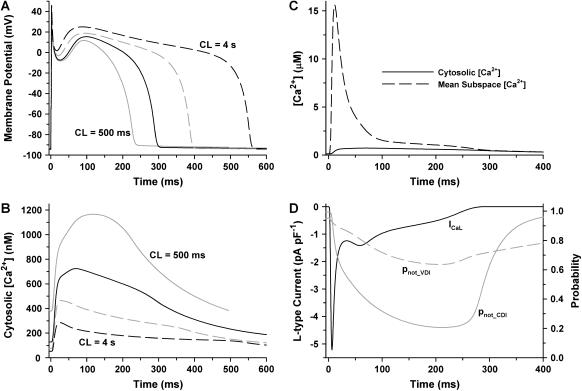
The baseline-coupled LCC-RyR model of CICR has been incorporated into a global model of the myocyte (18) and Fig. 6 demonstrates the ability of this model to reconstruct action potentials and Ca²⁺ transients of normal canine midmyocardial ventricular myocytes. Steady-state APs are shown (Fig. 6 A) for pacing cycle lengths (CL) of 500 ms, 1000 ms, 2000 ms, and 4000 ms, with the corresponding cytosolic Ca²⁺ transients (Fig. 6 B). Model AP shape and rate dependence of AP duration (APD) agree with experimental recordings obtained from isolated canine midmyocardial myocytes (31,60), and demonstrate an APD of ∼300 ms at CL of 1000 ms (30). The rate-dependence of model Ca²⁺ transient amplitude is similar to that measured in experiments (50), exhibiting peak amplitudes that increase with increasing pacing rate. Fig. 6 C compares the shape of the cytosolic Ca²⁺ transient (solid line) with the mean subspace Ca²⁺ transient (dashed line) at CL of 1000 ms. Although the cytosolic Ca²⁺ transient peaks at ∼0.73 μM, and lasts longer than the duration of the AP, Ca²⁺ in the subspace reaches a level of ∼15.5 μM on average, and after SR Ca²⁺ release, rapidly returns to near-cytosolic levels. It is important to emphasize that the [Ca²⁺]_ds signal shown in Fig. 6 C is an average over all CaRUs (including units that were not activated). Maximal [Ca²⁺]_ds in a single dyad during a release event is ∼100 μM under control conditions in this model (data not shown). Fig. 6 D shows I_CaL (solid line) corresponding to the AP at CL of 1000 ms. I_CaL peaks at ∼5.2 pA pF⁻¹ and has a sustained component of ∼0.5–1.0 pA pF⁻¹, which lasts for nearly the entire duration of the AP. The underlying LCC inactivation process is shown as p_{not_CDI} (shaded line) and p_{not_VDI} (shaded dashed line). The quantities demonstrate that, during the plateau, ∼80% of LCCs become unavailable due to Ca²⁺-dependent inactivation, whereas only ∼35% become unavailable due to voltage-dependent inactivation. This balance between voltage- and Ca²⁺-dependent inactivation is consistent with experimental data, indicating that LCC voltage-dependent inactivation is slow and incomplete, whereas Ca²⁺-mediated inactivation is strong and dominates the inactivation process (15,17,25,42), and is a key mechanism in determining how graded SR Ca²⁺ release influences AP properties and whole-cell Ca²⁺ dynamics (18). The results of Fig. 6 demonstrate that the baseline-coupled LCC-RyR model can successfully simulate CICR within a model of an AP, and retains features associated with local control of Ca²⁺ release.

FIGURE 6.

Action potentials and Ca²⁺ transients. (A) Steady-state model APs for CLs of 500 ms (shaded line), 1000 ms (solid line), 2000 ms (shaded dashed line), and 4000 ms (black dashed line). (B) Cytosolic Ca²⁺ transients corresponding to the APs of A. (C) Mean subspace (dyadic) Ca²⁺ transient (dashed line) demonstrates that microdomain Ca²⁺ levels reach significantly higher levels than that in the cytosol (solid line) during the AP at 1000 ms CL. (D) Properties of I_CaL (solid line) during the AP at 1000 ms CL, demonstrating relatively strong Ca²⁺-dependent inactivation (p_{not_CDI}, shaded line) but weak voltage-dependent inactivation (p_{not_VDI}, dashed line).

Effect of AP shape on efficiency of EC coupling

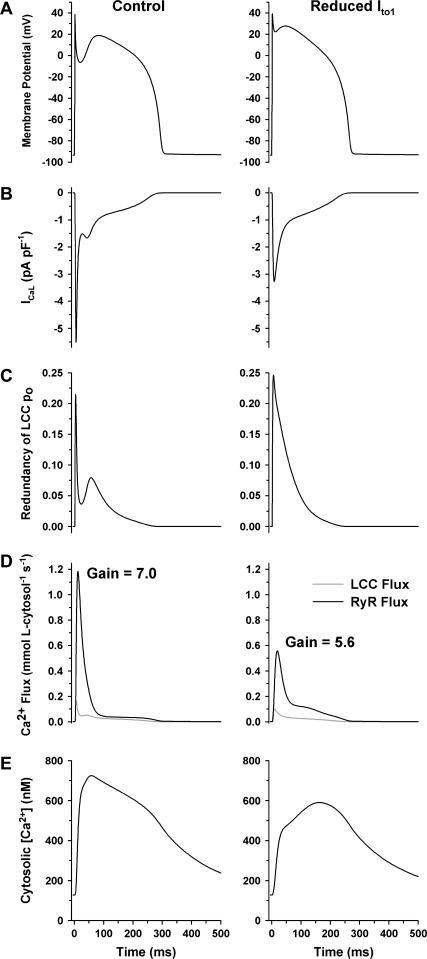
The canine myocyte model presented here provides the ability to study the mechanistic details underlying the tight coupling between AP morphology and CICR. In a previous study, we examined the role of the transient outward potassium current I_to1 in determining AP shape and duration in a canine myocyte model and showed that reductions in I_to1 lead to progressive slowing of phase-1 repolarization and elimination of the notch (61). We subsequently showed that in a model which correctly reproduces graded SR Ca²⁺ release, the loss of the notch leads to a reduction in I_CaL peak amplitude, and therefore a reduction in SR Ca²⁺ release flux (18). In agreement with these model predictions, Sah et al. (33) demonstrated that slowing early repolarization, in a manner consistent to that which occurs with I_to1 inhibition in larger mammals, leads to blunted Ca²⁺ transients with slower rise times, decreased efficiency of EC coupling, and impaired contractility. These findings have led to a number of hypotheses regarding the quantitative dependence of SR Ca²⁺ release on AP profile and I_CaL. Specifically, it has been suggested that the reduction and slowing of I_CaL in response to slowed phase-1 repolarization is associated with a reduction in local coupling efficiency at Ca²⁺ release sites and reduced synchronization of Ca²⁺ release events, indicating that in normal myocytes of large mammals (e.g., human and canine), I_to1, and the associated AP notch may be required to transiently increase I_CaL to synchronize and optimize SR Ca²⁺ release (62). Fig. 7 demonstrates the role of I_to1 amplitude on EC coupling properties in a canine myocyte model. This model incorporates the twofold larger CaRUs (i.e., containing two LCCs and 10 RyRs per dyad). Model simulations are compared in Fig. 7 under control conditions (left panels) and with a threefold reduction in I_to1 density (right panels). This degree of reduction in I_to1 is based on that observed in failing canine myocytes (51). Both simulations were run using the same set of steady-state (CL of 1000 ms) control initial conditions. Under normal conditions, the AP (Fig. 7 A) has a duration of ∼300 ms and I_to1 reduction leads to a modest shortening of APD to ∼270 ms and a less pronounced phase-1 notch, consistent with our previous findings (61). The change in AP shape due to the altered rate of early repolarization results in a 40% reduction in peak I_CaL from ∼5.5 pA pF⁻¹ to ∼3.3 pA pF⁻¹ (Fig. 7 B). The redundancy of LCC p_o displays a similar peak value in both cases (Fig. 7 C). However, in the control case, p_o redundancy is considerably reduced (by as much as fourfold) during the AP notch. The loss of the AP notch associated with reduced I_to1 results in an increased LCC p_o redundancy over this time window, suggesting an increased tendency for simultaneous openings of LCCs in the same CaRU. This effect would be expected to degrade efficiency of EC coupling and hence, reduce EC coupling gain. LCC Ca²⁺ influx (shaded line) and SR Ca²⁺ release flux (solid line, Fig. 7 D) indicate that the reduction of I_to1 leads to a 50% reduction in peak SR Ca²⁺ flux. The reduction in SR Ca²⁺ flux in Fig. 7 D occurs not only as a result of the diminished trigger influx Ca²⁺ signal, but also as a result of a reduction of EC coupling gain. EC coupling gain during the AP (i.e., the ratio of peak SR release flux to trigger influx) is reduced from 7.0 in control to 5.6 as a result of I_to1 reduction. The net effect of these changes yields a cytosolic Ca²⁺ transient (Fig. 7 E) with a dramatically slowed rise-time and an 18% reduction in peak amplitude. Such alterations would be expected to reduce contractility. The simulations of Fig. 7 demonstrate a reduction in EC coupling efficiency in the presence of identical SR Ca²⁺ load. Upon pacing the model with threefold reduction in I_to1 to steady state, the drop in I_CaL amplitude leads to a net reduction in SR Ca²⁺ load and hence, an even more pronounced reduction in SR Ca²⁺ release flux and cytosolic Ca²⁺ transient amplitude (data not shown). These data indicate that the repolarization rate during phase 1 of the AP has a marked influence on the process of CICR, and agree with the hypothesis that I_to1 plays an important role in optimizing SR Ca²⁺ release (62). The scope of these results, however, is limited to species and cell types that exhibit longer, notched AP morphologies. The role of I_to1 on CICR may in fact be reversed (i.e., reduction in I_to1 amplitude enhances SR Ca²⁺ release) in species with short triangular APs such as mouse and rat (62). In addition, some myocytes lack I_to1 completely (e.g., Guinea pig and most endocardial myocytes), which indicates that, although I_to1 plays an important role in modulating CICR, its presence is not always crucial for normal myocyte function.

FIGURE 7.

Role of I_to1 on EC coupling during the AP. Control simulations (left panels) are compared to simulations in which I_to1 density is reduced threefold (right panels). (A) AP; (B) I_CaL; (C) redundancy of LCC p_o; (D) LCC Ca²⁺ influx (shaded line) and RyR Ca²⁺ release flux (solid line); and (E) cytosolic Ca²⁺ transient.

DISCUSSION

In this study, we present a biophysically detailed model of the normal canine ventricular myocyte, which incorporates local control of EC coupling. This myocyte model is formulated by replacing a population of independent stochastically simulated CaRUs (18) with a formulation of CICR, which we refer to as a generalized coupled LCC-RyR gating model (24). The procedure for deriving the coupled LCC-RyR model has been described in detail previously (24). In this study, these methods have been generalized to allow for formulation (via automated software generation) of a coupled LCC-RyR model using any predefined LCC and RyR models and with CaRUs consisting of an arbitrary number of each of these channels. The resulting model of CICR consists of a set of ODEs that describe the state-occupancy probabilities of a population of CaRUs and retains essential properties of CICR (e.g., voltage-dependent EC coupling gain) that arise due to local control of SR Ca²⁺ release, as described in our previous model (18). This approach yields a number of advantages over previous model formulations. Ease of use is substantially increased due to the dramatically decreased computational cost and hence decreased runtime for this formulation. APs stimulated at 1-Hz can be generated two-to-threefold faster than real-time on a desktop computer. It is important to note that the runtime for this model is similar (within 20%) to that for our previous canine myocyte model, which was based on a common-pool formulation for CICR (10). An essential feature of the coupled LCC-RyR model is that it is based only on the known biological features of CICR, and does not require the introduction of any new or complex assumptions. The recent model of Bondarenko et al. (63) achieved graded Ca²⁺ release by assuming a distribution of CaRUs that contain different numbers of LCCs and RyRs. Such an assumption should not be necessary as we have demonstrated recently (24). The only assumptions used in the coupled LCC-RyR model are that [Ca²⁺]_ds is in rapid equilibrium with Ca²⁺ in its neighboring compartments (48,49), and that junctional SR Ca²⁺ is in quasiequilibrium with network SR Ca²⁺ (47), both of which are justified by experimental and theoretical considerations. Finally, parameters of a coupled LCC-RyR gating model are analytically determined from those of the underlying LCC and RyR models. Thus, there is no need for additional parameter fitting once the individual LCC and RyR model parameters have been independently constrained. The coupled LCC-RyR model is, therefore, a novel approach to simulation of EC coupling within a model of the cardiac AP, which captures the biophysical detail of CICR without requiring computationally intensive stochastic simulation of independent dyads.

The baseline-coupled LCC-RyR model of CICR presented here is a 40-state model built from the 10-state LCC model and four-state RyR model shown in Fig. 1. Each of these models are minimal-model approximations to more detailed channel models (11,36,37) where the degree of reduction in model complexity was limited to retain fundamental dynamics of channel gating that were present in the original models. In the case of the LCC, the reduced model was required to reproduce experimentally measured activation kinetics, the peak I-V relationship, and the appropriate balance between voltage- and Ca²⁺-dependent inactivation. Further simplification of this model, as was performed by Hinch et al. (24), would have sacrificed some of these critical features and therefore would not be appropriate for use in the canine myocyte model. In the case of the RyR, the model reduction has been described previously (see Fig. 13 of Greenstein and Winslow (18)), and involved reduction of a six-state model to a four-state model (Fig. 1 B) based on the difference in timescales of transition rates at higher [Ca²⁺]_ds levels. It should be noted that the simplified RyR model used in this study does not specifically account for all experimentally characterized features of RyR gating such as regulation by Mg²⁺ (56), low and high activity gating modes (64), and regulation by luminal SR Ca level (65,66). However, the RyR model is designed to operate as would be expected under physiological conditions. Fig. 3 demonstrates that the RyR model implemented here is consistent with recent measurements of open probability under simulated physiological conditions (56). The results therefore indicate that a simple RyR model that accounts for activation, inactivation and/or adaptation, and recovery is adequate to describe many features of EC coupling under both voltage-clamp (e.g., shape of the gain curve) and during an AP. Incorporation of additional mechanistic details of RyR gating would yield more complex channel models with a larger number of states, and hence would greatly amplify the complexity of the coupled LCC-RyR model (i.e., increase greatly the number of required states for the coupled model). We therefore chose to use a simplified model that has worked well for us in past studies, and left the study of the role of additional RyR gating features to future work. In the CaRU, the RyR/LCC stoichiometry was assumed to be 5:1 (34); however, the five RyRs were simulated with a single RyR model altered to approximate the behavior of a cluster of five RyRs (fivefold increase in open channel Ca²⁺ flux rate and increased Ca²⁺ sensitivity). The results of Figs. 2–4 demonstrate that a CaRU composed of a coupled LCC-RyR model based on these simplified channel models can reliably reproduce the salient features of local control of CICR which previously required a far more complex model (18).

A number of reports indicate that the Na⁺-Ca²⁺ exchanger (NCX) is primarily located within the t-tubule membrane (67,68). However, it remains unclear whether NCX actually senses the very high Ca²⁺ concentrations in the junctional space of the dyad (69). One recent study that looked specifically at the role of NCX in shaping the AP in canine myocytes (70) found from both experiments and model simulations that NCX is unlikely to sense Ca²⁺ in the dyadic cleft. This agrees with the findings of Lopez-Lopez et al. (71) that Ca²⁺ influx via reverse mode NCX current cannot alone trigger Ca²⁺ sparks. The recent experiments of Weber et al. (72) do suggest the existence of a local submembrane compartment whose Ca²⁺ is sensed by NCX; however, the experimental results of Armoundas et al. (70) are not in full agreement with these findings. Clearly, the issue regarding which pool of Ca²⁺ is sensed by NCX is not yet well understood, and may be species-dependent. We therefore chose to locate NCX outside of the dyad in this study consistent with measurements obtained in canine myocytes (70) and previous canine myocyte models (10,18).

The EC coupling gain curve for the baseline model (Fig. 4 C) does not show the steep increase in slope at hyperpolarized potentials as seen in experiments (1,29). To understand how the higher gain may arise at these potentials, we investigated the role of CaRU size on gain. Expanding the size of the CaRU (while maintaining a constant RyR/LCC stoichiometry) yields an increase in gain predominantly at hyperpolarized potentials, although it has only a small effect on gain at positive potentials (Fig. 5 A). This corresponds to an increase in slope at negative potentials by a factor similar to the increase in CaRU size. These results suggest that the slope of the EC coupling gain curve may be proportional to the functional coupling ratio between RyRs and LCCs (i.e., the number of RyRs activated per activated LCC). At depolarized membrane potentials, there is a high redundancy of LCC p_o (Fig. 5 C), indicating that many LCCs will open in a synchronous manner. Under these conditions, the functional RyR/LCC coupling ratio would be expected to approach the physical RyR/LCC stoichiometry (e.g., 5:1 in this model), and will not be affected by the size of the release unit. However, at hyperpolarized potentials, where redundancy of LCC p_o approaches zero (Fig. 5 C), only a small fraction of LCCs will be activated. The functional RyR/LCC coupling ratio will therefore be greatly enhanced, and will approach a value that represents the maximal number of RyRs that can be triggered by a single LCC (e.g., 15:1 in the model with threefold increase in CaRU size). This number can be thought of as the maximal-reach of a single trigger LCC. In the model, an increase in CaRU size translates to an increase in the maximal reach of an LCC, and results in a similar increase in the slope of the EC coupling gain curve. These results suggest that the change in slope of the EC coupling gain curve from the positive potential range to the negative potential range yields information about the relative change in the number of RyRs activated per active LCC. For example, for the CaRU increased in size by threefold (Fig. 5 A, dashed line), the slope of the gain curve in the range from −40 mV to −10 mV is −0.81 mV⁻¹, whereas the slope in the range from +10 mV to +40 mV is −0.30 mV⁻¹—and these differ by a factor of 2.7, indicating an approximately threefold change in the number of RyRs activated per LCC at negative potentials as compared to positive potentials. Unfortunately, the actual RyR/LCC stoichiometry cannot generally be derived from measures of EC coupling gain alone because the relationship between gain and stoichiometry depends upon additional unknown quantities such as single-channel Ca²⁺ flux rates and open probabilities for both LCCs and RyRs.

The above results indicate that the larger CaRU models better reproduce experimentally measured EC coupling gain curves, with steeply increasing gain at negative potentials (1,29). It is important to note that the 10 RyR to 2 LCC CaRU requires a 550-state model and that the 15 RyR to 3 LCC CaRU requires a 4400-state model. Clearly, these models will require significantly more computational resources than the 40-state baseline model, and can no longer be considered as reduced models of CICR. For this reason, the baseline model of CICR was chosen for implementation within the canine myocyte model, and should be sufficient for nearly all types of AP simulations. In cases where redundancy of LCC p_o is of interest, the CICR model can be upgraded to one containing a larger CaRU (e.g., see Fig. 7).

As in our previous canine myocyte model (18), graded SR Ca²⁺ release in this model is an emergent property based on the consideration of mechanistic details of the interaction of LCCs and RyRs in their local environment. Some other recent models have achieved graded SR Ca²⁺ release (73,74); however, this was accomplished in a phenomenological manner by formulating the RyR Ca²⁺ flux and gating kinetics as a complex function of I_CaL, rather than solely as a function of the Ca²⁺ concentrations that are in the direct vicinity of the RyRs. Although such formulations can reproduce features of CICR, they are not formulated based on the known mechanisms underlying CICR and therefore would not be appropriate for the study of the detailed interaction of EC coupling processes with whole-cell Ca²⁺ cycling and the AP. The study of heart failure serves as one example where it is critical to accurately capture the mechanisms of EC coupling because heart-failure-related defects have been identified in a number of EC coupling proteins. Single LCCs from failing myocytes exhibit increased availability and open probability compared to nonfailing myocytes (55), consistent with the observation that macroscopic I_CaL is unchanged in the face of reduced channel density (75). RyRs have been found to be hyperphosphorylated in failing hearts, resulting in increased Ca²⁺ sensitivity and open probability (76). In fact, alterations of any target protein of the β-adrenergic signaling pathway must be considered, given its heightened state of stimulation in heart failure. Finally, heart-failure-related alterations in proteins/currents not directly involved in CICR, such as I_to1, can have a significant impact on EC coupling properties as demonstrated in Fig. 7 and in experiments (62). These observations serve as a strong motivation to build mechanistic models of CICR to maximize their predictive ability in both normal and diseased states.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.