Abstract
Molecular dynamics simulations of the binding of the heterochiral tripeptide KkN to the transactivation responsive (TAR) RNA of HIV-1 is presented, using an all-atom force field with explicit water. To obtain starting structures for the TAR-KkN complex, semirigid docking calculations were performed that employ an NMR structure of free TAR RNA. The molecular dynamics simulations show that the starting structures in which KkN binds to the major groove of TAR (as it is the case for the Tat-TAR complex of HIV-1) are unstable. On the other hand, the minor-groove starting structures are found to lead to several binding modes, which are stabilized by a complex interplay of stacking, hydrogen bonding, and electrostatic interactions. Although the ligand does not occupy the binding position of Tat protein, it is shown to hinder the interhelical motion of free TAR RNA. The latter is presumably necessary to achieve the conformational change of TAR RNA to bind Tat protein. Considering the time evolution of the trajectories, the binding process is found to be ligand-induced and cooperative. That is, the conformational rearrangement only occurs in the presence of the ligand and the concerted motion of the ligand and a large part of the RNA binding site is necessary to achieve the final low-energy binding state.
INTRODUCTION
The binding of RNA and protein often involves considerable conformational changes of the molecular system (1–3). Instead of the common picture of a rigid lock-and-key docking, molecular recognition may occur via a dynamical induced-fit process, that is, a ligand-induced conformational rearrangement of local elements of RNA secondary structure, which subsequently leads to the stabilization of a defined conformation of the RNA-protein complex. Due to the high flexibility of RNA single strands, one generally expects a rugged energy landscape with multiple populated conformers. This conformational flexibility also significantly affects the affinity and specificity of RNA-protein interactions, although its biological function is not yet well understood.
Although the structures of the free and bound states of RNA and protein can be accurately described by x-ray and nuclear magnetic resonance (NMR) experiments, typically not much is known about the pathway by which the binding takes place. To investigate and understand biophysical processes in atomic detail, classical molecular dynamics (MD) simulations have proven valuable (4–7). However, so far MD studies on RNA system have focused on the free and bound states, but have not considered the dynamic binding process itself (8–17). This is because RNA-protein binding is expected to occur on a micro- to millisecond timescale, which currently is still beyond the reach of all-atom MD simulations.
A prime example for induced-fit RNA-protein binding is the interaction between the transactivation responsive (TAR) RNA and the transactivator (Tat) protein of the human immunodeficiency virus type 1 (HIV-1). A number of NMR studies of the free TAR RNA and the bound Tat-TAR complex have given a detailed picture of this highly specific and dynamic binding process (18–23). It is well established that the binding site mainly involves the trinucleotide bulge (see Fig. 1 a) and the adjacent basepairs A22–U40 and G26–C39, which undergo a substantial conformational change during the binding process. As the Tat-TAR interaction represents a crucial step in the gene expression of the virus, it has been widely studied as a possible target for anti-HIV intervention (24–26). For example, Hwang et al. (27) identified, from an encoded combinatorial library, various heterochiral tripeptides, which bind to TAR RNA with high affinity and specificity. In particular, they showed that the peptide (L)Lys-(D)Lys-(L)Asn (KkN) may suppress the transcriptional activation by Tat protein in human cells with an IC50 of ≈50 nM. Although the structure of the TAR-KkN complex was not determined in detail, their NMR studies indicate that KkN binds to the bulge region of TAR RNA.
FIGURE 1.
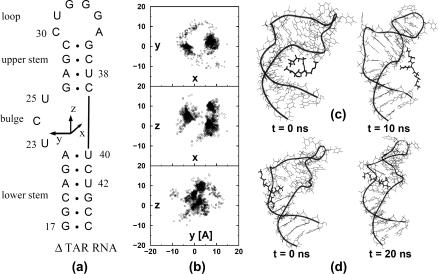
(a) Secondary structure of HIV-1 TAR RNA, indicating a local coordinate system placed at the center of mass of the A22–U40 basepair. (b) Docking results for the preferred position of the KkN ligand in TAR RNA, plotted in this coordinate system. The calculations reveal two main binding sites, which are located in the major (x > 0) and minor (x < 0) grooves of the bulge region. Choosing for both cases a representative conformation as a starting structure for a subsequent MD simulation, the right-hand-side panels show MD snapshots of the initial and final structures of (c) an unstable major-groove complex and (d) a stable minor-groove complex, respectively.
To identify possible binding modes of the TAR-KkN complex and to give a qualitative picture of the dynamics during binding, in this work we present a detailed MD study of this process, using an all-atom force field with explicit water solvent, counterions, and Ewald-sum treatment of electrostatics. Due to the (compared to the Tat protein) small size of the tripeptide, a MD description of the binding of KkN to TAR appears to be feasible, although no exhaustive sampling of the process can be expected on a timescale of some 10 ns. With this end in mind, the following strategy was employed: Starting with the NMR structure of free TAR RNA, we first used a docking method to identify the most plausible structures of the complex. Employing these results as initial structures, various 20-ns MD simulations were performed, showing that the starting structures in which KkN binds to the major groove of TAR are unstable, whereas the minor-groove starting structures are found to lead to several stable binding modes. Although the ligand does not occupy the binding position of Tat protein, it is shown to hinder the interhelical motion of free TAR RNA, which presumably is necessary to achieve the conformational change of TAR RNA to bind Tat protein (22). Considering the time evolution of the binding trajectories, the binding process is found to be ligand-induced and cooperative. Based on these findings, the importance of conformational flexibly for RNA-ligand binding is discussed in some detail.
METHODS
Docking study
We used the program AutoDoc3.0 (28), which allows for the efficient docking of a flexible ligand (i.e., the tripeptide KkN) to a rigid target (i.e., TAR RNA). Following Nifosi et al. (11), structure 2 from the NMR study (19) was taken as the starting structure of HIV-1 TAR RNA. Although the choice of the starting structure was found to hardly change the subsequent docking results, this structure exhibits low local root-mean-squared distances compared to the other NMR models and is therefore adopted as a representative starting structure for the MD simulations of free TAR RNA. The tripeptide KkN was built using the program XLEAP distributed by AMBER6 (29). To allow for flexibility of the ligand, a total of 20 active torsion angles were assigned as rotatable bonds. To be consistent with the subsequent MD studies, all partial charges of TAR and KkN were taken from the AMBER98 force field (30). Considering the van der Waals and electrostatic interactions of the TAR-KkN complex, the 10 docking structures with lowest energy were identified. These structures were analyzed in detail and served as starting structures for the subsequent MD simulations.
MD simulations
The AMBER6 program suite (29) and the force-field Amber98 (30) were used in the simulations of the free TAR RNA, the tripeptide KkN, and the TAR-KkN complex. The RNA was solvated in a rectangular box of TIP3P water (31), keeping a minimum distance of 10 Å between the solute and each face of the box. To neutralize the system, sodium counterions were added and water molecules were removed if they overlapped with the sodium ions. The final system contained 19,758 (17,224) atoms within a box dimension of 48 × 68 × 59 Å3 (49 × 67 × 51 Å3) in the case of the TAR-tripeptide complex (free TAR).
The systems were minimized and equilibrated with the same protocol, using the program SANDER. Initially, the whole system was minimized for 1000 steps and the water molecules and counterions were relaxed around the fixed solute with a 100-ps MD run. MD production runs of 20-ns duration were then performed for each system. Covalent bonds including hydrogen atoms were constrained by the SHAKE algorithm (32) with a relative geometric tolerance of 0.0001. The equation of motion was integrated by using a leapfrog algorithm with a time step of 2 fs. A cutoff of 10 Å was used for the nonbonded van der Waals interactions. The nonbonded interaction pair-list was updated every 20 fs. The solute and solvent were separately weakly coupled to external temperature baths at 300 K (33) with a temperature coupling constant of 0.1 ps (0.01 during the first 100 ps). The total system was also weakly coupled to an external pressure bath at 1 atm using a coupling constant of 0.5 ps (0.05 during the first 100 ps). Periodic boundary conditions were applied and the particle-mesh Ewald method (34) was used to treat electrostatic interactions.
Free energy analysis
The absolute free energy was estimated as the sum of the molecular mechanics energy, the solvation energy, and the entropic contribution (35). The molecular mechanics energy is given as the sum of bonded and nonbonded interactions and is directly obtained from the potential-energy function. The solvation free energy consists of electrostatic and nonpolar contributions. The electrostatic contribution was approximated by the generalized Born method (36). The nonpolar contribution Gnp was estimated from the solvent-accessible surface area (SA) of the solute using the algorithm of Sanner (37), i.e., Gnp = γSA + β, where γ = 0.00542 kcal/Å2 and β = 0.92 kcal/mol (38). To calculate the entropic contribution to the free energy, the translational, rotational and vibrational entropies are calculated using normal mode analysis tools employed in the AMBER program package (29).
The binding free energy is defined as the free energy difference between the TAR-KkN complex and the free TAR RNA and the KkN tripeptide:
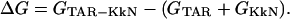 |
For simplicity, the latter two quantities are also calculated from the trajectory of the TAR-KkN complex (11). For example, to calculate GTAR from the TAR-KkN trajectory, all interactions involving the atoms of the KkN tripeptide are left out. Similarly, the atoms of TAR RNA are left out to calculate GKkN. It is noted that this approximation neglects the (presumably small) free energy difference in the bonded interactions of the complex and the two constituents.
RESULTS AND DISCUSSION
Identification of binding modes
In a first step, we have performed semirigid docking calculations to explore possible binding sites of TAR RNA for the KkN peptide. As an illustration of the thus obtained positions of the ligand, a local coordinate system of TAR RNA is introduced in Fig. 1 a, whose origin is placed at the center of mass of the A22-U40 basepair and whose x,y plane coincides with the plane of the A22–U40 basepair. The positive x-direction points toward the major groove, and the positive z-direction is parallel to the stacking direction of the bases G21 and A22. Employing these coordinates, Fig. 1 b shows the positions of the Cα atom of the middle lysine residue of KkN as obtained from the docking calculations. As may be expected, TAR RNA provides two main binding sites, which are located in the major groove (x > 0) and the minor groove (x < 0) of the bulge, respectively. From the binding energies predicted by the docking program, no superiority of the major or minor groove binding positions could be established. For this reason, we choose 10 representative low-energy structures of the KkN-TAR complex (including five minor and five major groove conformations) as initial structures for the subsequent MD study.
Upon performing several nanoseconds of MD simulation for each complex, it was found that the minor-groove structures are significantly more stable than the major-groove structures. That is, four of the major groove structures became unstable (i.e., the ligand moved far away from its initial docking position) and the fifth structure is only weakly bound. From the minor-groove structures, on the other hand, only one became unstable, while the other four assumed stable binding modes. This finding is in accord with experiment (27), which reports NMR interactions for the KkN-TAR complex that are different from known major-groove complexes. In particular, the NOESY and TOCSY resonances of only the U23 and C24 residues were shifted upon the addition of the ligand. In the calculated minor-groove structures of the KkN-TAR complex, these residues are found in direct vicinity of the ligand. Furthermore, a minor-groove binding structure was also found by NMR studies for a complex of TAR RNA and acetylpromazine (25).
As a representative example for both cases, Fig. 1 shows snapshots of the initial and final structures of an unstable major-groove complex (Fig. 1 c) and a stable minor-groove complex (Fig. 1 d). (Note that this last complex is referred to as complex 1 below.) Although in the latter case the ligand is seen to move further into the bulge to stabilize binding, in the major-groove complex the ligand clearly moves out of the binding pocket. This finding is interesting in the light of the fact that binding of the Tat-TAR complex does occur in the major groove of TAR RNA (18–20). As discussed below, the inhibition of the Tat-TAR interaction by KkN peptide can, therefore, not be explained by a simple replacement of Tat protein in the major groove of TAR RNA.
Characterization of binding modes
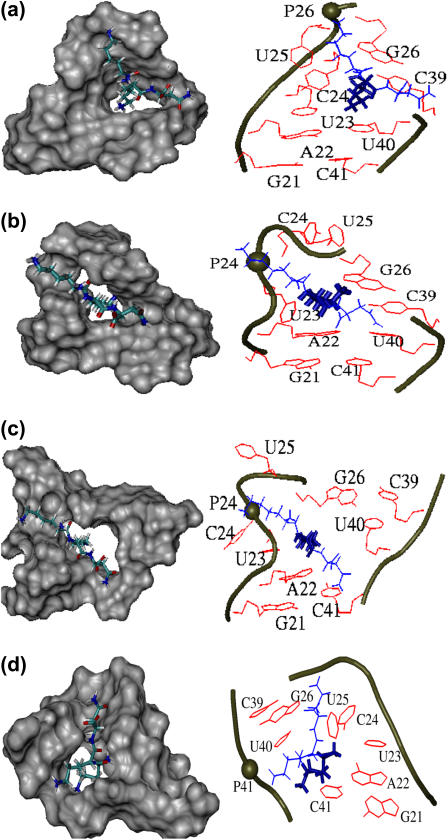
For each of the four stable binding modes identified in the above described docking/MD strategy, a 20-ns MD run was performed to characterize the structure and the binding interactions of the complex. From these simulations, Fig. 2 shows representative views of the binding sites as seen from the minor groove (for the three minor-groove complexes 1, 2, and 3) and from the major groove (for the major-groove complex 4), respectively. As a common feature of all structures, the TAR binding site is seen to exhibit a hole, which embeds the side chain of k2 for the three minor-groove complexes and the side chain of K1 in the case of the major-groove complex. The hole is caused by the imperfect stacking between the upper and lower stem due to the three unpaired nucleotides in the bulge.
FIGURE 2.
Structures (a–d) of the binding site of the TAR-KkN complex corresponding to trajectories 1–4 discussed in the text. The shaded space-filling representations on the left-hand side clearly show the binding pocket for the ligand, the right-hand-side structures reveal atomic details of TAR-KkN interactions: The ligand is drawn in blue with thick lines indicating favorable van der Waals interactions with bases. Phosphate groups involved in hydrogen bonding to the ligand are indicated by spheres.
Despite this similarity, a comparison of the various structures in Fig. 2 shows that there are quite different ways to accommodate the ligand in the binding pocket of TAR RNA. As is well known, the affinity and specificity of RNA-ligand binding is mainly achieved by stacking interactions, hydrogen bonding, and electrostatic interactions of positively charged ligand side chains and negatively charged phosphate groups of RNA (24). To obtain an impression of the overall importance of these interactions, Table 1 presents a decomposition of the enthalpic and entropic contributions to the binding free energy. The analysis shows that:
The entropy penalty for all bound structures is relatively similar.
The electrostatic and solvation energies of the complexes may differ significantly (from disfavoring binding by +6 kcal/mol in complex 1 to favoring binding by −3 kcal/mol in complex 2).
The van der Waals interactions provide, by far, the largest energetic contribution to binding, ranging from −23 to −40 kcal/mol.
TABLE 1.
Free energy analysis obtained from the four bound trajectories of the KkN-TAR complex (see Methods)
| Trajectory | ΔHvdW | ΔHel | ΔStrans | ΔSvib | ΔG |
|---|---|---|---|---|---|
| 1 | −40 (±4) | 6 (±3) | 7 (±1) | 8 (±5) | −19 (±7) |
| 2 | −38 (±3) | −3 (±3) | 9 (±1) | 9 (±4) | −23 (±5) |
| 3 | −31 (±5) | −2 (±4) | 7 (±1) | 8 (±4) | −18 (±7) |
| 4 | −23 (±5) | 1 (±4) | 7 (±1) | 7 (±4) | −8 (±7) |
The binding free energy ΔG is decomposed into the enthalpic contributions ΔHvdW and ΔHel, reflecting van der Waals as well as electrostatic and solvation energies, respectively, and into the entropic contributions ΔStrans and ΔSvib, reflecting translational and rotational as well as vibrational entropies of the solute, respectively. The (presumably small) free energy difference in the bonded interactions are neglected. All quantities are in units of kcal/mol.
Although the calculated absolute binding free energy of −19 kcal/mol is too low compared to the experimental value of −5 kcal/mol (27), we expect the relative free energies of the various binding modes as well as their decomposition to be sufficiently accurate for our purposes (35).
The above finding emphasizes the importance of stacking interactions for RNA-ligand binding. Indeed, by analyzing Fig. 2 it is found that the various binding modes can readily be characterized by their stacking interactions. In complex 1, for example, the bases of A22, U23, and C24 are tightly stacked. This pushes the ligand toward the other strand, where it prevents the stacking of the bases of C39 and U40. In complex 2, on the other hand, the bases of the other strand, C30, U40, and C41 are tightly stacked, whereas the nucleotides C24 and U25 are completely looped out. This way, the side chain of k2 is stacking to the base of A22, and to a lesser degree, to the base of U23. Complex 3 shows another possibility, in which U25 is looped out and the bases of U23 and C24 are tightly stacked. Similar to complex 2, the ligand stacks to A22, although there is no stacking of the bases of U40 and C41. Finally, there is the major-groove complex 4, which has the side chain of K1 embedded in the binding pocket of TAR RNA. Although it exhibits similar-looking stacking to complex 3, it is only weakly bound, because the van der Waals contribution ΔHvdW = −23 kcal/mol turns out to be much larger in the major groove.
As listed in Table 1, the van der Waals contribution ΔHvdW to the binding energy increases from −40 kcal/mol for complex 1 to −23 kcal/mol for complex 4, thus reflecting the decreasing degree of stacking interactions. Nevertheless, the best binding with ΔG = −23 kcal/mol is found for complex 2, which shows a slightly higher van der Waals contribution (−38 kcal/mol) but exhibits a favorable electrostatic energy of ΔHel = −3 kcal/mol. A closer analysis of the electrostatic interactions occurring in the KkN-TAR binding process reveals that the differences in ΔHel observed for the various complexes mainly reflect the number of stable hydrogen bonds maintained in the complex. Typically, strong hydrogen bonds were found to exist at both termini and at the amide hydrogens of the ligand. Efficient binding evidently requires a fine balance between van der Waals interactions and electrostatic interactions, although the latter appear to contribute only little, according to Table 1.
It is interesting to note that a minor-groove binding structure was also found by NMR studies of a complex of TAR RNA and acetylpromazine (25). In this case, the three-member ring of acetylpromazine inserts between basepairs G26–C39 and A22–U40 with the aliphatic moiety extended along the minor groove. The binding mode is therefore quite similar to the situation found for the KkN-TAR complex, where the side chain of the middle lysine is stacked between basepairs G26–C39 and A22–U40 while the two terminal residues point to the minor groove. In this respect, the two ligands employ a similar strategy to bind to the bulge region of TAR RNA, even though their structures and the type of interaction (aromatic-aromatic in the case of acetylpromazine and aliphatic-aromatic in the case of KkN peptide) are quite different. As a further difference, the acetylpromazine-TAR complex appears to occur as a single dominant binding mode (25), whereas the KkN-TAR complex exhibits pronounced conformational heterogeneity in the binding region.
Cooperative conformational transitions
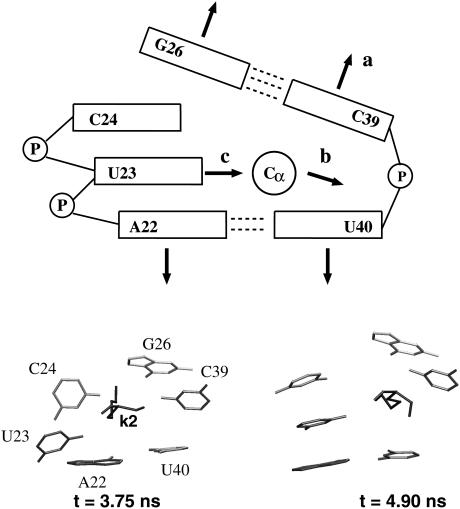
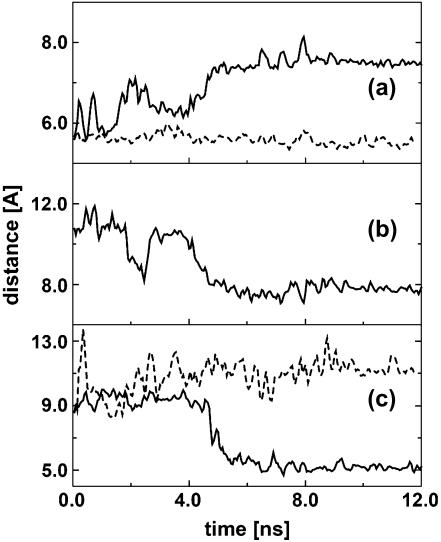
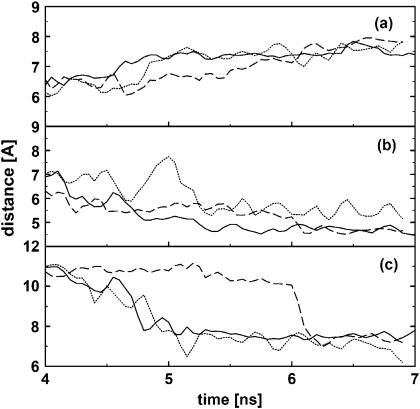
The results presented above indicate that the peptide and the nucleotides in the bulge region undergo significant conformational rearrangement to optimize the binding interface. Choosing complex 1 as a representative example, in what follows we wish to study this conformational dynamics of the binding process in some detail. The upper panel of Fig. 3 shows a simple scheme of the RNA binding site. The figure indicates several interatomic distances, which facilitate the description of the binding process of the tripeptide KkN to TAR RNA. Taking the position of the C1′ atom of U40 as a reference point, we consider the distances between this atom and the C1′ atom of U39 (Fig. 3 a), the Cα atom of k2 (Fig. 3 b), and the C1′ atom of U23 (Fig. 3 c), respectively. The time evolutions of these distances are shown in Fig. 4. Let us first consider the C39–U40 distance shown in Fig. 4 a. Initially, this distance is ∼6 Å, which reflects a close stacking of the corresponding bases. After several transient attempts to leave this stacking position, at time ≈4 ns C39 and U40 finally move apart to a distance of ∼7 Å. Interestingly, this conformational transition is followed by a rearrangement of the tripeptide in the binding pocket, which is monitored by the k2-U40 distance shown in Fig. 4 b. At ∼5 ns, this distance changes from ≈8 Å corresponding to a position between A22 and G26 to ≈5 Å, which reflects the insertion of the k2 side chain between C39 and U40. Because giving up the C39–U40 stacking in favor of the k2 insertion is energetically disfavorable, a further conformational rearrangement of the binding site is necessary to stabilize the complex. As monitored by the U23-U40 distance shown in Fig. 4 c, this rearrangement mainly consists of the motion of base U23. That is, whereas initially U23 points out of the bulge, at ≈5 ns it changes to point inside. Unlike the case of free TAR, in which the unpaired base U23 is found in a looped-out conformation due to the strong electrostatic repulsion, the positively charged side chains of the ligand reduces the repulsion and make the in-loop position of U23 favorable. To summarize the conformational dynamics shown in Figs. 3 and 4, the following simple picture emerges: (a) the binding pocket opens, (b) the ligand moves in, and (c) base U23 moves in to close the pocket. As a further illustration of the motions (a), (b), and (c), the lower panel of Fig. 3 shows the structure of the binding site directly before (left) and directly after (right) the conformational transition of the complex.
FIGURE 3.
(Upper panel) Scheme of the dynamical binding process of KkN tripeptide to TAR RNA. The nucleotides of the bulge region of TAR RNA are drawn as boxes and the position of the tripeptide is indicated by the Cα atom of k2. The arrows labeled by a, b, and c indicate the most important directions of motion: (a) the binding pocket opens, (b) the ligand moves in, and (c) base U23 moves in to close the pocket. (Lower panel) Structure of the TAR binding site and the k2 residue of the tripeptide directly before (left) and directly after (right) the conformational transition of the complex.
FIGURE 4.
Time evolution of various interatomic distances describing the cooperative binding of the tripeptide KkN to TAR RNA. Shown in full lines are (a) the distance between the C1′ atoms of U39 and U40, (b) the distance between the Cα atom of k2 and C1′ atom of U40, and (c) the distance between the C1′ atoms of U23 and U40. The dashed lines in a and c display the corresponding distances as obtained from a separate simulation of free TAR RNA.
The above discussion reveals that it takes the correlated rearrangement of the KkN ligand and several bulge nucleotides to reach the more stable binding conformation for times ∼9 ns. In other words, the binding process is cooperative. The meaning of cooperativity is nicely demonstrated by the simulation at ≈2 ns. At this time, the opening of bases C39 and U40 (Fig. 4 a) and the intercalation of k2 (Fig. 4 b) seems almost to be finished. However, the attempt fails because the necessary concerted motion of U23 does not occur at this time.
Furthermore, the conformational change of the TAR binding site is induced by the ligand, that is, induced-fit-type of binding occurs. This point is readily demonstrated by comparing the C39–U40 and U23–U40 distances obtained for bound TAR to the corresponding distances as obtained from a separate simulation of free TAR RNA (dashed lines in Fig. 4). In the absence of the ligand, clearly no specific conformational transition is observed.
Although the above results clearly show the existence of a ligand-induced cooperative conformational transition in the binding of KkN to TAR RNA, the finding, of course, raises the question on the importance of such dynamic effects on peptide-RNA binding. Analyzing the other three binding trajectories, we have found clearly cooperative rearrangements only for complex 3 (data not shown). At a time of ≈8 ns, simultaneously, the C39–U40 distance changes from 6.5 to 5.5 Å, the k2-U40 distance changes from 7.5 to 10 Å, and the U23–U40 distance changes from 11 to 13 Å, thus resulting in binding-mode 3 described above. Another way to assess the relevance of a phenomena is to study its reproducibility. To this end, we have performed additional simulations of the binding process of complex 1, in which we changed the initial conditions at time t = 4 ns, i.e., right before the conformational transition. As an example, Fig. 5 compares the original trajectory (solid lines) to a trajectory using the same initial coordinates but with completely reassigned initial velocities (dotted lines), and to a trajectory employing minor random changes of the initial coordinates and completely reassigned velocities (dashed lines). Although the three conformational transitions certainly differ in details of the time evolution, the outcome of the conformational rearrangement as well as the cooperativity is reproduced.
FIGURE 5.
Reproducibility of cooperative binding. Shown are the interatomic distances introduced in Fig. 4 obtained for three trajectories with slightly different initial conditions at t = 4 ns.
Global motion of TAR RNA
Let us finally come back to the question how a small peptide binding to the minor groove of TAR RNA may inhibit the Tat-TAR interaction, which is known to occur at the major groove of TAR RNA (18–20). With this end in mind, a separate 20-ns MD simulation of free (i.e., unbound) TAR RNA was performed and compared to the data obtained for the KkN-TAR complex. Comparing the root-mean-squared distances (RMSD) of free and bound TAR RNA (data not shown), we found, in both cases, values of ≈3 Å for the first 2 ns. Although the RMSD of the bound TAR RNA remains below 4 Å, the RMSD of free TAR increases up to 7 Å. Interestingly, a closer inspection of the trajectory reveals that all secondary elements (i.e., bulge, loop, and upper and lower stems) of TAR RNA are well maintained during the simulation. That is, the quite large RMSD observed for free TAR is mainly caused by global interhelical motion of the RNA. Interhelical hingelike motions have also been identified in MD simulations of RNA kink-turns (15,16). Furthermore, this finding is interesting in the light of recent residual dipolar couplings' NMR experiments (22), which reported strong evidence for the existence of this hinge-bending motion of TAR RNA around the bulge region.
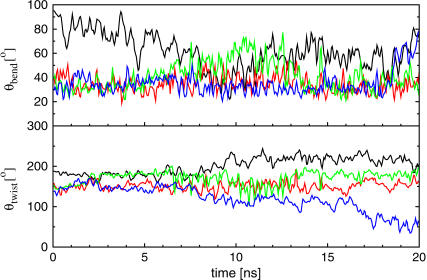
To illustrate this motion, we introduce two coordinate systems, whose origins are localized at the centers of mass of the lower stem (including the basepairs G18–C44, C19–G43, A20–U42, G21–C41) and the upper stem (including the basepairs G26–C39, A27–U38, G28–C37, and C29–G36), respectively. The z-axes are chosen orthogonal to the plane spanned (in the average) by the nucleic basepairs and therefore indicate the axial direction of the stems. The x-axes are parallel to this plane and point from the minor to the major groove. Employing these coordinates, the interhelical motion of TAR RNA can be described by two angles: The angle between the two z-axes, that is, the bending angle θbend, and the angle between the two x-axes, that is, the twisting angle θtwist. (Note: More precisely, θtwist is obtained by projecting the x-axes of the upper stem onto the x,y plane of the lower stem and calculating the angle between the projected x-axes of the upper stem and the x-axes of the lower stem in the plane.) Fig. 6 compares the time evolution of these two angles as obtained for free TAR RNA and for the three minor-grove Kkn-TAR complexes. The bending angle of free TAR is seen to vary between 20° and 100° in the 20-ns simulation, thus describing a rather slow large-amplitude motion between the two stems. The bending motion of the KkN-TAR complexes, on the other hand, is much more localized with θbend ≈ 30 ± 10°. The overall difference between free and bound TAR RNA is similar but not as prominent for the twisting motion of the RNA stems.
FIGURE 6.
Global motion of TAR RNA as revealed by the time evolution of the interstem angles θbend and θtwist. Compared are the trajectories of free TAR RNA (black) and of the three minor-groove RNA-KkN complexes 1 (red), 2 (green), and 3 (blue).
Fig. 6 clearly demonstrates that the interhelical motion of the RNA is hindered by binding small molecules in the minor-groove region. This finding also explains the observation that complexes of TAR RNA with a small ligand are significantly more stable than free TAR (11). Assuming that the interhelical motion is necessary to achieve the conformational change of TAR RNA to bind Tat protein (22,23), our results suggest that the binding of small molecules to the minor groove of TAR RNA represents a dynamical inhibition mechanism of the Tat-TAR interaction. In other words, the ligand does not occupy the binding position of Tat protein, but it prevents the conformational rearrangement of the RNA, which necessary for the binding of Tat protein.
It is instructive to compare the above findings to the residual dipolar couplings NMR experiments of Al-Hashimi et al. (22,23). Providing long-range constraints on the orientation of bond vectors, this technique has significantly enhanced the accuracy with which extended structures such as nucleic acids can be determined by NMR (39). Furthermore, the measurement of NMR residual dipolar couplings has also emerged as a powerful approach to probe the amplitudes and directions of collective motions in biomolecules. The study of TAR RNA in the free state (22) provided evidence that the two helices undergo large amplitude (46°) rigid-body collective motions about an average interhelical angle of 47°. Upon binding to argininamide, the interhelical motion of TAR RNA was found to be significantly reduced, resulting in an average interhelical angle of 11 ± 3° (23). The above reported computational results (θbend = 50 ± 40° for free TAR RNA and 30 ± 10° for the KkN-TAR complex) are in good overall agreement with experiment, thus providing a consistent picture of the flexibility change of TAR RNA upon ligand binding.
CONCLUDING REMARKS
We have employed a combination of semirigid docking and all-atom MD simulations to study the binding of a RNA-tripeptide complex in explicit water. Using free TAR RNA as the initial structure in the docking calculations, the subsequent MD study monitors the ligand-induced conformational rearrangement of the complex. Considering the wealth of intriguing data obtained by the simulation, this hybrid strategy appears to be a promising approach to study dynamical aspects of RNA-ligand binding. This is because:
The docking calculations provide an inexpensive way to identify the most plausible structures of the complex.
The much more expensive MD simulations need to be performed for only a few representative cases.
The MD study may shed light on the transition from the free to the bound conformational states of the RNA system.
It is noted that the combination of lock-and-key docking and induced-fit dynamics has also been found by NMR studies of several RNA-protein complexes (2,40). Here the initial binding mode is recognized first by flexible docking and then the binding interface is optimized by conformational rearrangements.
The MD simulations have shown that only the minor-groove starting structure leads to various stable binding modes, whereas the Tat-TAR related major-groove structures turned out to be unstable or only very weakly bound. This finding is in accord with experiment (27), which reported NMR interactions for the KkN-TAR complex that are different from known major-groove complexes. Furthermore, NMR studies for a complex of TAR RNA and acetylpromazine (25) have revealed a quite similar minor-groove binding structure. In both systems, the ligand is found between basepairs G26–C39 and A22–U40, with the minor groove accommodating the side chain of the ligand.
To characterize the stable binding modes, a detailed analysis of the enthalpic and entropic contributions to the binding free energy was given. We have found that:
The entropy penalty for all bound structures is relatively similar.
The electrostatic and solvation energies of the complexes may differ significantly (from disfavoring binding by +6 kcal/mol in complex 1 to favoring binding by −3 kcal/mol in complex 2).
The van der Waals interactions provide by far the largest energetic contribution to binding; they range from −23 to −40 kcal/mol, thus reflecting the different degree of stacking of the binding modes.
The surprisingly large conformational heterogeneity of the binding interface of the KkN-TAR complex is also reflected in the time evolution of the binding trajectories. By monitoring various interatomic distances accounting for the stacking and the hydrogen bonding during the binding process, we have identified numerous conformational rearrangements to optimize the binding interface. In particular, we have found a induced-fit-type of binding, in which the binding process is ligand-induced and cooperative. That is, the concerted motion of the ligand and a large part of the RNA binding site is necessary to achieve the final low-energy binding state. To assess the relevance of these cooperative rearrangement, its reproducibility has been checked by additional simulations with changed initial conditions. Although the resulting trajectories certainly differ in the details of their time evolution, the outcome of the conformational transition as well as the cooperativity was reproduced.
Finally, the global motions of free TAR RNA and the bound KkN-TAR complex have been investigated. We have shown that the quite large RMSD observed for free TAR is mainly caused by interhelical hinge-bending motion of the RNA. In nice agreement with residual dipolar couplings' NMR experiments of Al-Hashimi et al. (22,23), we obtain the bending angle of free TAR θbend ≈ 50 ± 40°. The bending motion of the KkN-TAR complexes, on the other hand, is much more localized, with θbend ≈ 30 ± 10°. This finding clearly demonstrates that the interhelical motion of the RNA is hindered by binding small molecules in the minor-groove region. Assuming that the interhelical motion is necessary to achieve the conformational change of TAR RNA to bind Tat protein (22), our results suggest that the binding of small molecules to the minor groove of TAR RNA represents a dynamical inhibition mechanism of the Tat-TAR interaction.
Acknowledgments
We thank Helmut Grubmüller, Harald Schwalbe, and Joseph Wachtveitl for helpful comments on the manuscript.
Financial support by the Deutsche Forschungsgemeinschaft (via SFB No. 579 “RNA-Ligand Interactions”), the National Natural Foundation of China (grant No. 90203013), the Lee Kuan Yew Fellowship, and the Fonds der Chemischen Industrie is gratefully acknowledged.
Part of the simulations were performed at the Frankfurt Center of Scientific Computing and the supercomputer of BIRC in NTU.
References
- 1.Williamson, J. R. 2000. Induced fit in RNA-protein recognition. Nat. Struct. Biol. 7:834–837. [DOI] [PubMed] [Google Scholar]
- 2.Leulliot, N., and G. Varani. 2001. Current topics in RNA-protein recognition: control of specificity and biological function through induced fit and conformational capture. Biochemistry. 40:7947–7956. [DOI] [PubMed] [Google Scholar]
- 3.Hall, K. B. 2002. RNA-protein interactions. Curr. Opin. Struct. Biol. 12:283–288. [DOI] [PubMed] [Google Scholar]
- 4.Cheatham III, T. E., and P. A. Kollman. 2000. Molecular dynamics simulation of nucleic acids. Annu. Rev. Phys. Chem. 51:435–471. [DOI] [PubMed] [Google Scholar]
- 5.Aufinger, P., and E. Westhof. 2001. RNA solvation: a molecular dynamics simulation perspective. Biopolymers. 56:266–274. [DOI] [PubMed] [Google Scholar]
- 6.Norberg, J., and L. Nilsson. 2002. Molecular dynamics applied to nucleic acids. Acc. Chem. Res. 35:465. [DOI] [PubMed] [Google Scholar]
- 7.Cheatham III, T. E. 2004. Simulation and modeling of nucleic acid structure, dynamics and interaction. Curr. Opin. Struct. Biol. 14:360–367. [DOI] [PubMed] [Google Scholar]
- 8.Hermann, T., and E. Westhof. 1998. Aminoglycoside binding to the hammerhead ribozyme: a general model for the interaction of cationic antibiotics with RNA. J. Mol. Biol. 276:903–912. [DOI] [PubMed] [Google Scholar]
- 9.Zacherias, M., and H. Sklenar. 1999. Conformational analysis of single-base bulges in A-form DNA and RNA using a hierarchical approach and energetic evaluation with a continuum solvent model. J. Mol. Biol. 289:261–275. [DOI] [PubMed] [Google Scholar]
- 10.Zacherias, M. 2000. Simulation of the structure and dynamics on nonhelical RNA motifs. Curr. Opin. Struct. Biol. 10:311–317. [DOI] [PubMed] [Google Scholar]
- 11.Nifosi, R., C. M. Reyes, and P. A. Kollman. 2000. Molecular dynamics studies of the HIV-1 TAR and its complex with argininamide. Nucleic Acids Res. 28:4944–4955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Williams, D. J., and K. B. Hall. 2000. Experimental and computational studies of the G(UUCG)C RNA tetraloop. J. Mol. Biol. 297:1045–1061. [DOI] [PubMed] [Google Scholar]
- 13.Pitici, F., D. L. Beveridge, and A. M. Baranger. 2002. Molecular dynamics simulation studies of induced fit and conformational capture in U1A-RNA binding: do molecular substates code for specificity? Biopolymers. 65:424–435. [DOI] [PubMed] [Google Scholar]
- 14.Sorin, E. J., Y. M. Rhee, and V. S. Pande. 2005. Does water play a structural role in the folding of small nucleic acids? Biophys. J. 88:2516–2524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cojocaru, V., S. Nottrott, R. Klement, and T. M. Jovin. 2005. The snRNA 15.5K protein folds its cognate K-turn RNA: a combined theoretical an biochemical study. RNA. 11:197–209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Razga, F., J. Koca, J. Sponer, and N. B. Leonitis. 2005. Hinge-like motions in RNA kink-turns: the role of the second A-minor motif and nominally unpaired bases. Biophys. J. 88:3466–3485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Koplin, J., Y. Mu, C. Richter, H. Schwalbe, and G. Stock. 2005. Structure and dynamics of an RNA tetraloop: a joint molecular-dynamics/NMR study. Structure. 13:1255–1267. [DOI] [PubMed] [Google Scholar]
- 18.Puglisi, J. D., R. Tan, B. J. Calnan, and A. D. Frankel. 1992. Conformation of the TAR RNA-arginine complex by NMR spectroscopy. Science. 257:76–80. [DOI] [PubMed] [Google Scholar]
- 19.Aboul-ela, F., J. Karn, and G. Varani. 1995. The structure of the human immunodeficiency virus type-1 TAR RNA reveals principles of RNA recognition by Tat protein. J. Mol. Biol. 253:313–332. [DOI] [PubMed] [Google Scholar]
- 20.Long, K. S., and D. M. Crothers. 1999. Characterization of the solution conformations of unbound and Tat peptide-bound forms of HIV-1 TAR RNA. Biochemistry. 38:10059–10069. [DOI] [PubMed] [Google Scholar]
- 21.Dayie, K. T., A. S. Brodsky, and J. R. Williamson. 2002. Base flexibility in HIV-2 TAR RNA mapped by solution 15N, 13C NMR relaxation. J. Mol. Biol. 317:263–278. [DOI] [PubMed] [Google Scholar]
- 22.Al-Hashimi, H. M., Y. Gosser, A. Gorin, W. Hu, A. Majumdar, and D. J. Patel. 2002. Concerted motions in HIV-1 TAR RNA may allow access to bound state conformations: RNA dynamics from NMR residual dipolar coupling. J. Mol. Biol. 315:95–102. [DOI] [PubMed] [Google Scholar]
- 23.Pitt, S. W., A. Majumdar, A. Serganov, D. J. Patel, and H. M. Al-Hashimi. 2004. Argininamide binding arrests global motions in HIV-1 TAR RNA: comparison with Mg2+-induced conformational stabilization. J. Mol. Biol. 338:7–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hermann, T. 2000. Strategies for the design of drugs targeting RNA and RNA-protein complexes. Angew. Chem. Int. Ed. Engl. 39:1891–1904. [DOI] [PubMed] [Google Scholar]
- 25.Du, Z. H., K. E. Lind, and T. L. James. 2002. Structure of TAR RNA complexed with a Tat-TAR interaction nanomolar inhibitor that was identified by computational screening. Chem. Biol. 9:707–712. [DOI] [PubMed] [Google Scholar]
- 26.Murchie, A. I. H., B. Davis, C. Isel, M. Afshar, M. J. Drysdale, J. Bower, A. J. Potter, I. D. Starkey, T. Swarbrick, S. Mirza, C. D. Prescott, P. Vaglio, F. Aboul-ela, and J. Karn. 2004. Structure-based drug design targeting an inactive RNA conformation: exploiting the flexibility of HIV-1 TAR RNA. J. Mol. Biol. 336:625–638. [DOI] [PubMed] [Google Scholar]
- 27.Hwang, S., N. Tamilarasu, K. Ryan, I. Huq, S. Richter, W. C. Still, and T. M. Rana. 1999. Inhibition of gene expression in human cells through small molecule-RNA interactions. Proc. Natl. Acad. Sci. USA. 96:12997–13002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Morris, G. M., D. S. Goodsell, R. S. Halliday, R. Huey, W. E. Hart, R. K. Belew, and A. J. Olson. 1998. Automated docking using a Lamarckian genetic algorithm and an empirical bind free energy function. J. Comput. Chem. 19:1639–1662. [Google Scholar]
- 29.P. A. Kollman et. al. 1999. AMBER6. University of California, San Francisco, CA.
- 30.Cheatham, III, T. E., P. Cieplak, and P. A. Kollman. 1999. A modified version of the Cornell et al. force field with improved sugar pucker phases and helical repeat. J. Biomol. Struct. Dyn. 16:845–862. [DOI] [PubMed] [Google Scholar]
- 31.Jorgensen, W. L., J. Chandrasekhar, J. D. Madura, R. W. Impey, and M. Klein. 1983. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
- 32.Ryckaert, J. P., G. Ciccotti, and H. J. C. Berendsen. 1977. Numerical-integration of Cartesian equations of motions of a system with constraints—molecular dynamics of n-alkanes. J. Comput. Phys. 23:327–341. [Google Scholar]
- 33.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. Dinola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
- 34.Darden, T., D. York, and L. Petersen. 1993. Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
- 35.Tsui, V., and D. A. Case. 2001. Calculations of the absolute free energies of binding between RNA and metal ions using molecular dynamics simulations and continuum electrostatics. J. Phys. Chem. B. 105:11314–11325. [Google Scholar]
- 36.Qiu, D., P. S. Shenkin, F. P. Hollinger, and W. C. Still. 1997. The GB/SA continuum model for solvation. A fast analytical method for the calculation of approximate Born radii. J. Phys. Chem. 101:3005–3011. [Google Scholar]
- 37.Sanner, M. F., A. J. Olson, and J. C. Spehner. 1996. Reduced surface: an efficient way to compute molecular surfaces. Biopolymers. 38:305–320. [DOI] [PubMed] [Google Scholar]
- 38.Sitkoff, D., K. A. Sharp, and B. Honig. 1994. Accurate calculation of hydration free energies using macroscopic solvent models. J. Phys. Chem. 98:1978–1988. [Google Scholar]
- 39.MacDonald, D., and P. Lu. 2002. Residual dipolar couplings in nucleic acid structure determination. Curr. Opin. Struct. Biol. 12:337–343. [DOI] [PubMed] [Google Scholar]
- 40.Stoldt, M., J. Wöhnert, O. Ohlenschläger, M. Görlach, and L. R. Brown. 1999. The NMR structure of the 5S rRNA E-domain-protein L25 complex shows preformed and induced recognition. EMBO J. 18:6508–6521. [DOI] [PMC free article] [PubMed] [Google Scholar]