Stimulation of Actin Polymerization by Filament Severing

Abstract

The extent and dynamics of actin polymerization in solution are calculated as functions of the filament severing rate, using a simple model of in vitro polymerization. The model is solved by both analytic theory and stochastic-growth simulation. The results show that severing essentially always enhances actin polymerization by freeing up barbed ends, if barbed-end cappers are present. Severing has much weaker effects if only pointed-end cappers are present. In the early stages of polymerization, the polymerized-actin concentration grows exponentially as a function of time. The exponential growth rate is given in terms of the severing rate, and the latter is given in terms of the maximum slope in a polymerization time course. Severing and branching are found to act synergistically.

INTRODUCTION

The motility of cells, the formation of protrusions such as filopodia and lamellipodia, and the motions of intracellular pathogens, are strongly influenced by extracellular and/or intracellular factors that regulate actin polymerization (1,2). One channel by which actin polymerization can be regulated is filament severing (2,3), which is enhanced by proteins such as those of the ADF/cofilin family, and gelsolin. These proteins accelerate actin dynamics, and this effect has often been analyzed in terms of depolymerization, resulting from severing (2) or acceleration of pointed-end dynamics (4). However, live-cell assays have shown that release of caged cofilin in MTLn3 cancer cells (5) increases the amount of polymerized actin in the cells. The interpretation of these experiments is complicated by the fact that overexpression of cofilin leads to overexpression of actin in Dictyostelium (6), suggesting that enhancement of cofilin by other means might also lead to actin overexpression. However, the localized response to cofilin release near the cell periphery found by Ghosh et al. (5) shows that the F-actin enhancement is not entirely due to actin overexpression. Since actin filaments in cells are typically capped at their rapidly growing barbed ends, the polymerization enhancement is presumably due to the creation of new free barbed ends. Analogous effects are seen in biochemical assays, which showed that polymerization of G-actin (4,7,8) or G-actin plus preexisting seed filaments (9) is accelerated by cofilin. These effects occur despite the reported ADF/cofilin-induced enhancement of the off-rate at filament pointed ends (4,10). Gelsolin can also in principle stimulate actin polymerization, but the polymerization of gelsolin-generated filaments is inhibited because gelsolin remains attached to the filament barbed end after the severing event. If the filaments can be uncapped by other agents, however, the net result can be increased polymerization (11). Gelsolin plays a major role in disassembling actin filaments; for example, studies on Listeria have shown that it is the major Ca²⁺-dependent filament recycling protein (12), whereas ADF/cofilin is Ca²⁺-independent. Although it has been shown that gelsolin-null mice have normal embryonic development and longevity (13), later studies have shown that gelsolin deficiency blocks the formation of podosomes in mouse osteoclasts and leads to abnormalities in bone structure and mass (14). On the whole, the results of this article are more relevant to proteins of the ADF/cofilin family, because their stimulation of actin polymerization does not require uncapping agents.

Another major mechanism of filament generation in cells is filament branching due to Arp2/3 complex, which creates free barbed ends. It is then natural to ask whether severing and branching act antagonistically, synergistically, or independently. Synergy between cofilin and Arp2/3 complex has been reported in both biochemical (9) and living-cell (15) studies, suggesting a synergistic interaction between severing and branching.

Previous modeling studies have addressed some of these phenomena. Du and Frieden (8) used a kinetic model based on the concentrations of actin monomers, multimers, and filaments, with a severing rate per filament, to interpret polymerization data for a solution of yeast actin and yeast cofilin. The model reproduced accurately the observed acceleration of G-actin polymerization by cofilin. Sept and collaborators (16) used a similar model, with a severing rate per subunit, to calculate the effect of spontaneous severing on the average filament length. They found that this length is independent of the starting concentration of G-actin, and is determined by a competition between severing and annealing. Edelstein-Keshet and Ermentrout (17–19) have considered the filament length distribution resulting from severing, and our underlying model of severing is very similar to theirs. They found a range of possible behaviors of the filament distribution depending on the assumptions regarding, for example, the conservation of actin and/or capping protein.

However, to our knowledge there is no quantitative analysis that gives the extent of polymerization of actin as a simple function of the severing rate and other key rate parameters such as capping rates. In a previous article (20), we have developed such an analysis for the effects of branching, and here we extend this analysis to treat severing. We treat a simple model of a model of actin polymerizing in vitro, in the presence of severing and capping proteins. Using a transformation of the severing rate into an effective uncapping rate, and a steady-state equation expressing the constancy of the number of filaments in steady state, we develop simple formulae for the critical concentration and the average filament length. We analyze the polymerization dynamics using rate equations based on the concentrations of capped and uncapped filaments, and the concentration of G-actin. Finally, to evaluate the extent of synergy between severing and branching, we extend the rate equations to include branching. The results for the critical concentration, polymerization dynamics, and synergy are bolstered by stochastic-growth simulations using a set of rate parameters (21) derived from fits to polymerization data and from previous measurements.

This work has three motivations. First, the basic understanding gained by studying the effects of severing in vitro can be used to interpret experiments on cells. Second, having simple formulae for observables such as the polymerized-actin concentration in terms of the severing rate can help in evaluating this parameter from experimental data. Finally, in analysis of whole-cell behavior using a systems approach, constitutive relations of the type developed here are crucial inputs.

MODEL

Our model describes the polymerization of actin in solution with a protein, such as ADF/cofilin, that accelerates severing. Because ADF/cofilin may act cooperatively in severing filaments, we do not give the severing rate explicitly in terms of the severing-protein concentration, but instead treat this rate as an input. In addition, most of our calculations include the effects of a capping protein, and some of them include the effects of branching induced by Arp2/3 complex. This model (without severing) has previously been used to study the dynamics of actin filament cluster sizes (22) and the effect of branching on the critical concentration and filament length of actin (20). The processes included in the model are filament polymerization/depolymerization, capping/uncapping, severing, and branching/debranching. End-to-end annealing, the inverse process of severing, is ignored. The validity of this approximation is discussed at the end of the next section.

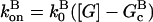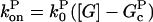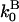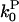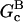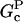Mathematically, polymerization is described by net barbed and pointed-end polymerization rates and (measured in subunits per second), where and are concentration-independent rate parameters, and are the barbed- and pointed-end critical concentrations, and [G] is the free-monomer concentration. Both 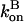and 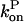will be positive in the initial stages of polymerization because [G] is high, but in later stages, 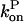will become negative as [G] drops below 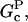and then it should be interpreted as a depolymerization rate. Capping is described by a barbed-end capping rate 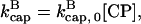where [CP] is the capping-protein concentration and 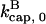is a concentration-independent rate parameter, and an uncapping rate 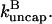The effects of capping are conveniently summarized by the parameter 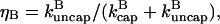which gives the equilibrium probability for a barbed end to be uncapped; the average barbed-end growth rate is then 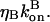Severing is described, as in Sept et al. (16) and Edelstein-Keshet and Ermentrout (17), by a severing rate k_sev per subunit. It is assumed that severing events can occur with equal probability along the length of a filament, and k_sevΔt is the (dimensionless) probability that a filament will be severed at a particular subunit during a time interval Δt. (Some other studies (8,23) have defined k_sev as a rate constant for a filament to sever; that rate constant would then exceed the present one by a factor of the filament length.) Branching is described as in Carlsson et al. (21) by a branching rate per filament subunit, 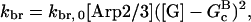where k_br,0 is a concentration-independent rate parameter, and [Arp2/3] is the concentration of activated Arp2/3 complex.

EFFECT OF SEVERING ON CRITICAL CONCENTRATION

In this section, we derive a formula for the critical concentration in terms of the severing rate, using approximations suitable for small values of the severing rate and for conditions under which most filament barbed ends are capped. This analytic formula is supplemented by stochastic-growth simulations, which are not restricted to low severing rates or high barbed-end capping. In the calculations below, variables preceded by the symbol Δ correspond to changes induced by severing. The extent of polymerization in steady state is determined by the critical concentration G_c, which is the maximum concentration of free actin that can remain unpolymerized. In the absence of capping, severing is not expected to affect the critical concentration strongly because the balance between barbed-end growth and pointed-end depolymerization is independent of the filament length. When barbed-end capping is included without severing, G_c is nearly equal to the treadmilling concentration G_tr at which polymerization of barbed ends in their equilibrium capping states is precisely balanced by depolymerization of pointed ends (20),

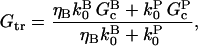(1)

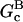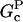where η_B is the fraction of filaments whose barbed ends are uncapped, and are the barbed- and pointed-end critical concentrations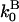, and and 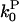are the corresponding on-rate constants.

In the presence of severing, however, the average capping state of the filament barbed ends may not be that of the equilibrium state. The new barbed end created by a severing event is uncapped. If the time for it to reach its equilibrium capping state is a sizeable fraction of the filament lifetime, the critical concentration will differ from G_tr. We account for this effect by describing severing in terms of an effective uncapping rate. To evaluate this rate, we relate the severing contribution to the time rate of change of η_B. Defining the total number of filaments to be N, and the average filament length (measured in subunits) to be 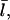the severing-induced change in the number of uncapped filaments during a time interval dt is 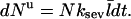This is also equal to the severing-induced change dN in the total number of filaments. A straightforward calculation shows that the time rate of change of η_B is

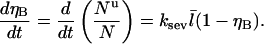(2)

A parallel calculation for uncapping filaments shows that the time rate of change of the number of uncapped filaments is 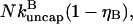where the (1 − η_B) factor is present because only capped filaments can be uncapped; the rate of change of the total number of filaments is zero. Thus the time rate of change of η_B induced by uncapping is

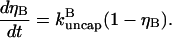(3)

Comparing Eqs. 2 and 3 shows that 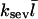operates as an additional uncapping rate, and the combined effects of severing and uncapping may be summarized by a total effective uncapping rate

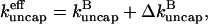(4)

where

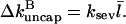(5)

The total uncapped fraction in the presence of severing will then be

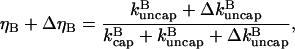(6)

where

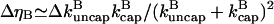(7)

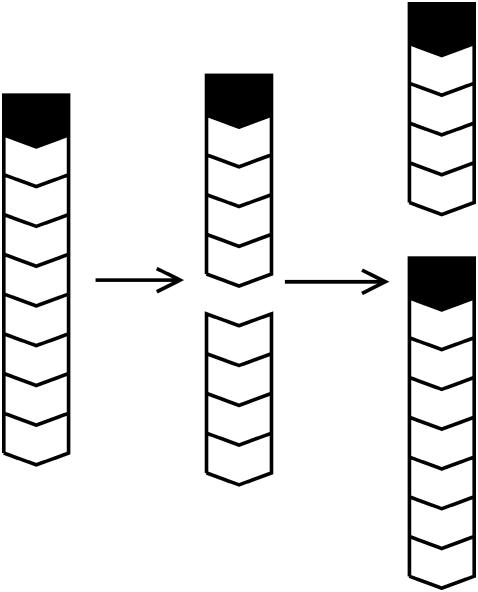
is the change in the uncapped fraction resulting from severing, and Eq. 7 holds when severing effects are small. In this view, the function of severing proteins is partly analogous to that of membrane-bound agents such as PIP₂ which cause filament uncapping (24) and thereby stimulate actin polymerization. The underlying mechanism is illustrated in Fig. 1. A capped filament is severed. The lower fragment, whose barbed end is uncapped, grows until it is capped. The end result is a net increase in the amount of polymerized actin.

FIGURE 1.

Schematic of polymerization enhancement by severing. Chevrons denote actin filament subunits, with barbed end oriented upward. Solid polygons denote capping protein.

At this point, we still need 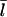to evaluate Δη_B. To calculate 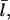we use the fact that, in steady state, filament creation and destruction balance each other. The rate of change of N is given by

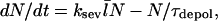(8)

where N/τ_depol is the rate of filament disappearance by depolymerization. The time τ_depol is related to the average filament lifetime, but the definition of the lifetime is ambiguous when severing is present. The steady-state condition for G_c, dN/dt=0, then implies that

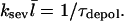(9)

The left-hand side increases with [G], because the on-rate increases, and this increases 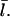The right-hand side decreases with increasing [G], since 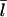increases, and the off-rate decreases, causing τ_depol to increase. Therefore, Eq. 9 uniquely determines G_c.

The [G]-dependence of τ_depol has a simple form if the distribution of filament lengths decays exponentially. In this case, the number of filaments of length l, F_tot(l), is (N/ 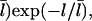where the prefactor ensures that the total number of filaments of all lengths is N. We note that 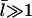and take the rate of filaments vanishing per unit time from depolymerization to be the rate of transitions from l = 2 to l = 1. Then the fact that most filaments are capped, so that only pointed-end processes contribute, means that this transition rate is very close to 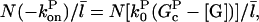where 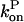is negative in steady state. Taking the rate per filament, we obtain

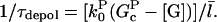(10)

A similar result was obtained by a more complete analysis treating the two distinct capping states explicitly (20). Because 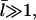the answer is not sensitive to the minimum filament length used in the definition of depolymerization.

Substituting Eq. 10 into Eq. 9 yields

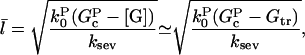(11)

where the second equality holds for small values of k_sev, for which [G] is close to G_tr. In our simulations, we find that the distribution of filament lengths is not precisely exponential; the number of very long filaments is less than expected on the basis of an exponential fit. Thus, numerical comparison of the prediction with simulation results is necessary to confirm the accuracy of our calculation.

We are now ready to calculate the effect of severing on G_c. We define the effect of severing on G_c as −ΔG, where ΔG = G_tr − G_c. By analogy with Eq. 1, we have

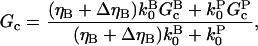(12)

so for weak severing effects (small Δη_B),

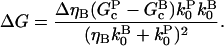(13)

Substituting Eqs. 5, 7, and 11 into Eq. 13, we obtain

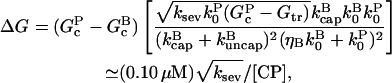(14)

where, in the second relation, [CP] is given in μM, and k_sev is given in s⁻¹. This relation is based on the rate parameters of Carlsson et al. (21), and holds approximately for the range 0.001 μM < [CP] < 0.010 μM, where 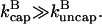In this range, the product of the other terms depending on [CP] (the ( 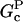− G_tr) term and the term containing η_B) varies by a factor of <2, and is replaced by the middle of its range.

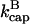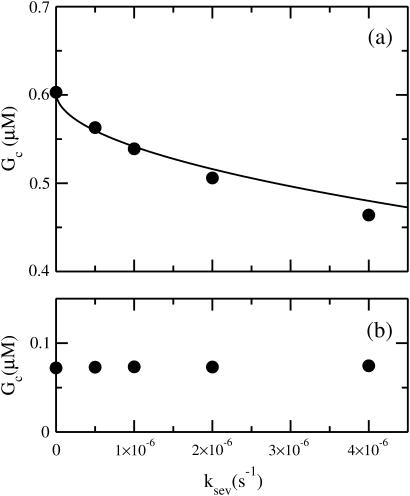
The most obvious feature of these results is that severing always lowers G_c, or enhances polymerization. Even though severing exposes pointed ends which in principle could lead to depolymerization, the larger on-rate constant at the newly exposed barbed ends always leads to net polymerization. The factor of in the k_sev term in the first equation implies that severing lowers G_c only if barbed-end capping is present. In addition, the lowering of G_c is proportional 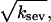which is analogous to the effects of side branching evaluated by Carlsson (20). Fig. 2 a compares the analytic result of Eq. 14 with simulation results obtained with our stochastic-growth code, using 2 μM actin and [CP] = 2 nM in a 5 μm × 5 μm × 5 μm simulation box. (This code is described in more detail in (20,22)). It gives a complete stochastic implementation of the model described above, keeping track of all filament subunits over time. Both the analytic-theory calculations and the stochastic-growth simulations use the parameter set of Carlsson et al. (21), which is a combination of previously measured values and fits to polymerization data. At this value of [CP], 97% of the barbed ends are capped in steady state. The agreement between the simulations and the analytic theory is quite close, supporting the conclusion that severing enhances polymerization when nearly all barbed ends are capped. We have also performed simulations for lower values of [CP], where roughly half of the barbed ends are capped. Here the analytic theory does not apply accurately, but the sign of the effect remains the same: severing enhances polymerization when barbed-end capping is present.

FIGURE 2.

(a) Dependence of critical concentration G_c on severing rate k_sev, for G₀ = 2 μM and [CP] = 2 nM. (Solid circles) Simulation results. (Line) Analytic theory (Eq. 14). (b) Same, but for a system containing 2 nM of a hypothetical pointed-end capper having the same rate constants for the pointed end as CP does for the barbed end.

This conclusion is also supported by an analysis of the short-time effect of suddenly turning on severing in a solution of actin filaments with capping protein. We ignore filament loss by depolymerization, because at short times after initiation of severing the filaments are still long enough to make this rate very small. The rates of change of the populations 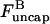and 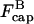of capped and uncapped filaments, and the polymerized-actin concentration P, are given by

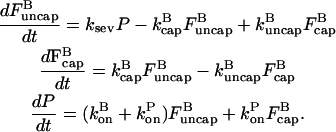(15)

Here the k_sevP term expresses the fact that the generation rate of new filaments by severing is proportional to the number density of filaments times their length, which is simply the polymerized-actin concentration; the remaining terms are straightforward. We assume that before severing is turned on, the filament populations and actin concentration are in steady state (which means that 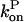is negative), so that

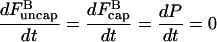(16)

at t = 0.

We evaluate the solution of these equations for short times up to second order in t, the time after severing is turned on. Over these short times, 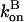and 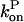can be regarded as constant. Because of Eq. 16, only the first of the expressions in Eq. 15 is non-zero immediately after severing is turned on, and its value is k_sevP(0). Therefore, to linear order in t, 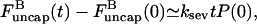and the changes of 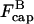and P vanish. Inserting the change of 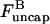into the last of the expressions in Eq. 15, we obtain

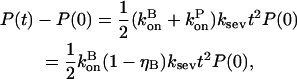(17)

where the second equality is obtained by noting that in the steady state before initiation of severing, 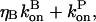the average growth rate of a filament, must vanish. In the presence of barbed-end capping, η_B < 1, so P(t) – P(0) > 0, and severing again stimulates actin polymerization. The extent of the stimulation increases with the extent of capping until η_B ≃ 0.

The above analysis ignored pointed-end capping. Severing produces both a free pointed end and a free barbed end. One might thus expect that if most of the pointed ends of the original filaments are capped, severing could increase the critical concentration by freeing up depolymerizable pointed ends. However, filament loss by depolymerization also changes the ratio of capped to uncapped pointed ends, since depolymerization occurs only at uncapped pointed ends. In fact, in the steady state, the rate of filament creation by severing equals the rate of filament loss by depolymerization. Each severing event leads to one new free pointed end, but each filament loss event by depolymerization leads to the loss of a free pointed end. Therefore, since these events occur with equal frequency, there is no net change in the capping state of the pointed ends, and there should be no change in G_c. This contention is supported by simulation results obtained by the stochastic-growth code. To see the differences between the pointed and barbed ends as clearly as possible, we consider a hypothetical pointed-end capper that has the same rate constants as CP has at the barbed end. Our results for G_c as a function of k_sev for a system containing 2 μM actin and 2 nM of this pointed-end capper are shown in Fig. 2 b. They show that the effect of severing for this system is essentially negligible. Thus for pointed-end capping, the effect of depolymerization on the ratio of capped to uncapped ends cancels the direct effect of severing. However, the depolymerization effect on the capped/uncapped ratio is small for the case of barbed-end capping treated above. Here, a depolymerizing filament will typically have its barbed end capped. Since most of the filaments are capped, depolymerization events will not greatly change the ratio of capped to uncapped filaments, and the analysis leading to Eq. 14 holds.

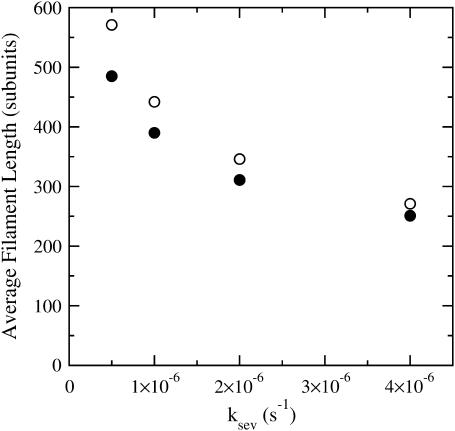
Since our analysis of the critical concentration depends on the calculation of 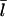according to Eq. 11, we evaluate the accuracy of this result using the stochastic-growth code. Fig. 3 shows a comparison of 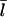values from the simulations (solid circles) with the prediction of Eq. 11 (open circles) for the conditions of Fig. 2. The theoretical prediction uses the values of [G] obtained from the simulations, to separate the errors in the 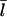calculation from those in calculation of [G]. The agreement is reasonably satisfactory, with errors <20%. We believe that these errors come from the nonexponential nature of the filament length distribution. We do not present results for this distribution because its accurate calculation would require inclusion of annealing effects absent in our model.

FIGURE 3.

Average filament length as a function of severing rate k_sev, for G₀ = 2 μM and [CP] = 2 nM. (•) Simulation results. (○) Analytic theory (Eq. 11).

Having the model results for G_c, we are now in a position to evaluate the validity of ignoring these annealing effects. On the basis of previous analysis (16), we treat filament annealing as a bimolecular diffusion-limited reaction with a rate per filament given by where k_anneal = 300 μM⁻¹ s⁻¹ 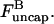Here 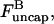the density of uncapped filaments, appears because it is assumed that two capped filaments cannot anneal with each other, the 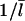dependence comes from the corresponding dependence of the filament diffusion constant, and the numerical value was obtained (16) from polymerization assays (25) and electron micrographs (26). The relative importance of annealing can be evaluated by generalizing the above steady-state analysis. Since an annealing event, like a filament loss event from depolymerization, reduces the number of filaments by one, Eq. 9 becomes

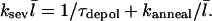(18)

Then following the steps leading to Eq. 11 gives

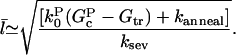(19)

Since an annealing event has the opposite effect of a severing event on the average capping state, Eq. 5 becomes

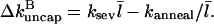(20)

Inserting Eq. 19 into 20 then shows that the ratio of 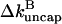with annealing to that without annealing is Using the rate parameters and concentrations of the calculations shown above in this result gives a 6% reduction in 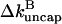from annealing at k_sev = 5 × 10⁻⁷ s⁻¹ and a 14% reduction at k_sev = 4 × 10⁻⁶ s⁻¹. Thus, the effects of annealing are noticeable but small in the range treated here. We also note that the sign of the effect of severing is not changed by annealing no matter how rapid the latter is; severing still stimulates polymerization.

ACCELERATION OF SPONTANEOUS POLYMERIZATION BY SEVERING

In the preceding section, we saw that severing can shift the steady-state critical concentration of an actin solution if barbed-end capping is present. We now consider the kinetic effects of severing actin filaments that are spontaneously nucleated from an unpolymerized solution of G-actin, without capping. Here, we do not expect a change in G_c, but rather a change in the rate of approach to G_c. We describe the polymerization dynamics using the appropriate parts of Eq. 15:

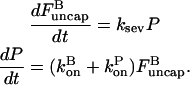(21)

One cannot obtain a complete analytic solution of these equations because the dependence of 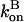and 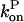on P via [G] ([G] = G₀ − P, where G₀ is the starting actin concentration) renders the equations nonlinear. However, at short times, before much polymerization has happened, [G] may reasonably be treated as constant. This leaves 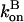and 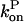constant, and makes the equations linear. The equations can be transformed into a single equation by differentiating the second equation with respect to time, and inserting the first equation into the result:

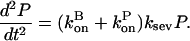(22)

This equation has the solution

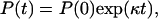(23)

where

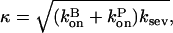(24)

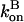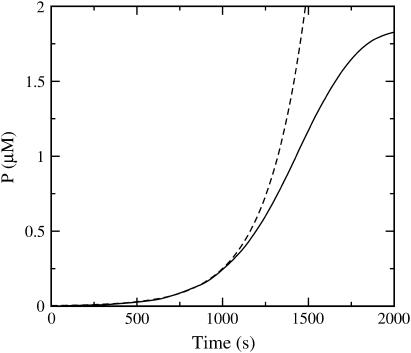
and in our approximation, and 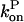are given their values at zero time. Another possible solution has a negative exponent, but the physical behavior will be dominated by the growing exponential. The functional form of Eq. 23 is compared to stochastic-growth simulations for 2 μM actin and k_sev = 10⁻⁶ s in Fig. 4. Because the initiation of polymerization in the simulations is a stochastic fluctuation event occurring at a variable time, we have shifted the time origin of the exponential curve to optimize the fit to the simulation curve. Comparison of the two curves shows that for short times, the fit is close, and the exponential form is accurate. For longer times, the simulation results drop below the exponential curve because 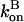and 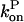drop with decreasing [G].

FIGURE 4.

Time dependence of polymerized-actin concentration P, with G₀ = 2 μM actin and k_sev = 10⁻⁶ s⁻¹. (Solid curve) Simulation result. (Dashed curve) Exponential fit with growth rate given by Eq. 24.

Since the rate parameters entering 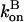and 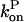are known, measurement of κ would allow evaluation of k_sev, which would be a useful counterpoint to existing estimates based on observations of filament numbers (23) and quantitative polymerization-kinetics modeling (8,16). However, measurement of κ is complicated because one must measure the small-P part of the polymerization curve, which is strongly affected by noise. Therefore, we have developed an alternative procedure, which does not involve direct measurement of κ. We consider the more easily measurable quantity

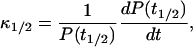(25)

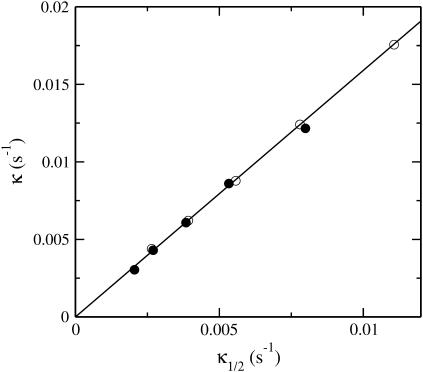
where t_1/2 is the time at which polymerization is half completed. If P(t) had an exponential time dependence, then κ_1/2 would be the exponential growth rate. Although the polymerization curves deviate from the exponential form, one would at least expect κ_1/2 to be correlated with κ. Our simulation results show that this is the case. The scatter plot in Fig. 5 compares values of κ and κ_1/2 for a range of parameter sets with k_sev ranging from 5 × 10⁻⁷ s⁻¹ to 8 × 10⁻⁶ s⁻¹, and the starting actin concentration G₀ ranging from 2 μM to 4 μM. The plot shows that there is an accurate linear relationship between the two; the relationship κ = 1.58κ_1/2 holds to a precision of ∼5%. This means that the relationship

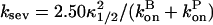(26)

is accurate to ∼10%.

FIGURE 5.

Relation of exponential growth rate κ given by Eq. 24 to effective growth rate κ_1/2 given by Eq. 25. (Solid circles) G₀ = 2 μM. (Open circles) G₀ = 4 μM. Points within each set correspond to different values of k_sev ranging from 5 × 10⁻⁷ s⁻¹ to 8 × 10⁻⁶ s⁻¹.

SYNERGY BETWEEN SEVERING AND BRANCHING

To evaluate these synergy effects, we extend the analysis of the preceding section to include branching along filament sides. Since the in vitro studies of branching-severing synergy (9) were performed in the absence of capping protein, we ignore barbed-end capping here. Because the side-branching rate, like the severing rate, is defined per subunit in a filament, the extension of Eq. 21 to include branching is

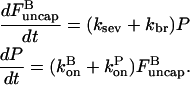(27)

Here we ignore pointed-end capping effects, which would result in some filaments growing at a rate of 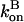instead of 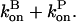This is legitimate because 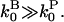The above analysis goes through, with k_sev replaced by (k_sev + k_br), so that

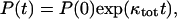(28)

where

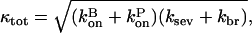(29)

and the subscript tot on κ means that it includes both severing and branching; we also define 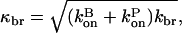the exponential growth rate for branching only.

Although k_sev and k_br appear additively in Eq. 29, the extent of the resulting actin polymerization can display strong synergy effects, because the exponential in Eq. 28 grows very rapidly as a function of its argument. Assume, for example, that k_sev = k_br, so that 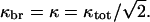Then, in the presence of either severing or branching by themselves, the induced polymerization from Eq. 23 is P(t) − P(0) = P(0)[exp(κt) − 1], and the sum of the contributions from severing and branching (the additive limit) is 2P(0)[exp(κt) − 1]. In the presence of both severing and branching, as described by Eq. 28, the induced polymerization is 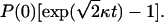Evaluation of the exponentials shows that this expression exceeds the additive limit when κt > 1.33; if κt = 3, it exceeds the additive limit by ∼80%, indicating strong synergy effects.

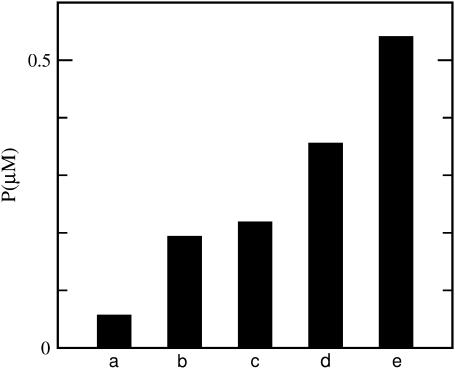
We have tested this possibility with our simulation code, using a two-step procedure inspired by the in vitro studies (9) mentioned above, which began with preformed actin filaments. First, 2 μM actin is allowed to polymerize slowly for 1000 s, in the absence of branching and severing. Then branching and severing are turned on, with k_sev = 2 × 10⁻⁶ s⁻¹ and [Arp2/3] = 1 nM, which corresponds to k_br ≃2 × 10⁻⁶ s⁻¹. The simulation is then run 400 s longer, at which point ∼25% of the actin is polymerized in the presence of both severing and branching. The simulations use the parameter set for the side-branching model of Blanchoin et al. (25), which includes pointed-end capping effects. The data, given in Fig. 6, show that the extent of polymerization resulting from both severing and branching exceeds the additive limit by ∼50%, revealing a strong synergistic interaction between branching and severing. Because of lack of input information, we are not able to simulate directly the conditions of Ichetovkin et al. (9), to see how important this effect was under the conditions of that work.

FIGURE 6.

Synergy between branching and severing. Bars represent polymerized-actin concentration P after 1400 s, in a simulation with G₀ = 2 μM. Severing (k_sev = 2 × 10⁻⁶ s⁻¹) and/or branching ([Arp2/3] = 1 nM) are turned on after 1000 s. (a) No severing or branching; (b) severing only; (c) branching only; (d) sum of severing and branching effects (additive approximation); and (e) polymerization in the presence of both severing and branching.

In Ichetovkin et al. (9), the synergy between branching and severing was attributed to an effect that we will call aging: the ability of filament subunits to form new branches decays over time. Then filaments newly grown as a result of severing provide a substrate for new branch formation. We treat the effect by an extension of the expressions in Eq. 27. Denoting the rate constant for the decay of subunits' branching ability over time by k_age, and the concentration of branching-competent filament subunits by P_br, we obtain the following rate equations:

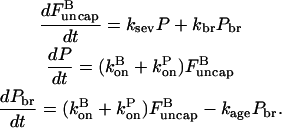(30)

At early times, where the mass of the preformed filaments greatly exceeds the mass of the newly grown filaments, the analysis of the polymerization dynamics of this model is simplified. We first assume that the preformed filaments are incapable of forming new branches, so the latter can form only on the new mass of polymerized actin generated by severing (the k_sevP term.) As in the analysis of the expressions in Eq. 15 leading to Eq. 17, the extra mass of branching-competent actin resulting from these filaments is

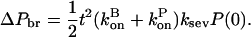(31)

Then, performing another time-integral to evaluate the number of new branches induced, one obtains

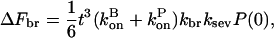(32)

and the amount of polymerized actin contained in these branches is

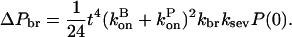(33)

Here, a synergistic interaction is apparent in the multiplication of k_br by k_sev. On the other hand, if aging effects are absent, a closely parallel calculation shows that

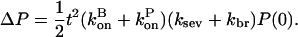(34)

Here, synergy effects are absent since the k_sev and k_br terms appear additively.

Thus, there is a strong synergy in the short-time polymerization behavior, but only if aging effects are present. Measurements of short-time polymerization dynamics could therefore be useful in establishing the importance of the aging effects.

DISCUSSION

Severing lowers the critical concentration if barbed-end capping is present

The above calculations show that severing, in the absence of changes in polymerization/depolymerization rate constants, always reduces the steady-state critical concentration if barbed-end capping is present. This conclusion is consistent with the increase in F-actin resulting from releasing caged cofilin in MTLn3 cells (5). We emphasize that this result refers to changes in the steady-state F-actin concentration. The increase in the F-actin concentration was observed for 30 min or more after the cofilin release.

In vitro testing of the prediction that severing enhances polymerization if barbed-end capping is present is complicated by the fact that severing proteins such as ADF/cofilin and gelsolin typically have other functions as well; proteins of the ADF/cofilin family can change the pointed-end rate constants and sequester actin monomers, and gelsolin caps filament barbed ends. In fact, biochemical experiments measuring the effect of ADF/cofilin proteins on the critical concentration of actin (8,10) have found increases in the critical concentration, which must be associated with monomer sequestration or an enhanced off-rate constant at the pointed end. This raises the question, why does ADF/cofilin enhance polymerization in cells, but cause depolymerization in biochemical experiments? One reason is that the biochemical experiments did not include CP, so there should be no polymerization enhancement according to the present theory. Another possibly important difference between the cell studies and the biochemical studies is the presence of profilin in the cells. This allows the maintenance of a very large pool of polymerization-competent profilin-actin complexes. Thus, a free barbed end generated by severing could grow extremely rapidly, and this might more than compensate for the acceleration in the pointed-end off-rate caused by ADF/cofilin. Finally, pointed ends in cells are partly capped by Arp2/3 complex. This will also enhance the importance of barbed end growth relative to pointed end depolymerization.

However, a human cofilin mutant (S3D) has been developed which severs filaments but activates pointed-end depolymerization only weakly (27). Measurements of G_c in the presence of this mutant and CP could test the validity of Eq. 14. All of the numerical quantities entering Eq. 14 are known or can easily be evaluated. The values of k_sev and 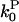can be evaluated from the number of severing events per filament and the pointed-end off-rate given in Schafer et al. (24). The values of all of the other quantities in Eq. 14 are conveniently given in Carlsson et al. (21), and have also been measured by several other workers. In tests of Eq. 14, ΔG should be measured relative to G_tr, whose value will be affected by the small changes in 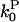caused by the S3D cofilin. We also note that recent work (10) has shown that wild-type proteins of the ADF/cofilin family form two distinct subgroups, the ADF-like ones and the cofilin-like ones. The cofilin-like ones enhance the pointed-end rate constants less than the ADF-like ones and some of them give almost no change in the pointed-end off-rate constant. The latter might be useful for testing Eq. 14.

Severing accelerates the rate of approach to the critical concentration

This phenomenon occurs in cases where the starting system, immediately before severing is initiated, is not in steady state. For the case where the starting system is G-actin, the acceleration effect has been observed by several groups (4,7,8). A closely related effect has also been observed in Ichetovkin et al. (9), which treated the case where the starting system consists of G-actin, and F-actin seeds. If the starting system consists of F-actin in a buffer without G-actin, the system will depolymerize, and the G-actin concentration will climb to reach G_c. The acceleration of this depolymerization by ADF/cofilin has also been observed by several groups (4,25,26,28,29).

Effect of severing on filament turnover

The present results indicate that severing accelerates filament turnover in the sense that it reduces the filament lifetime. Combining Eq. 9 with Eq. 11 shows that τ_depol should decrease with increasing k_sev; for small k_sev the dependence is roughly 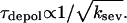Biochemical studies (4), as well as studies on Listeria (4,30), have indicated that ADF/cofilin accelerates filament turnover, and the present results show that the severing function of ADF/cofilin by itself will accelerate the turnover.

Effect of filament capping on filament lengths

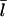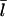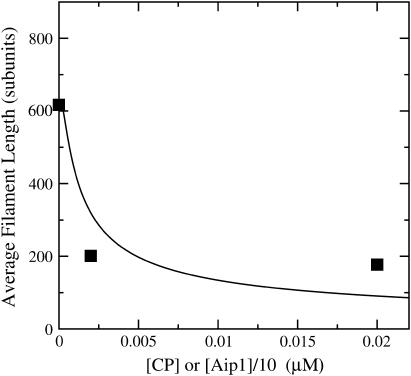
It has been reported (31,32) that the protein Aip1 caps filament barbed ends when cofilin is present. The capping reduces the average filament length (31). This is consistent with our analysis, since capping barbed ends would increase G_tr and thereby lower according to Eq. 11. We cannot accurately calculate the effect of Aip1 on because the relevant rate constants are not known. However, one might expect the general form of the dependence of 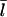on [Aip1] to be similar to that for [CP]. Fig. 7 compares the dependence of 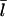on [CP], calculated using Eq. 11, to its dependence on [Aip1] measured in Okada et al. (31), with an actin concentration of 2 μM. The Aip1 concentration axis is scaled by a factor of 10 to obtain a reasonable comparison. We have used a severing rate of 2.3 × 10⁻⁶ s⁻¹, which reproduces the experimental 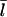at [Aip1] = 0. Although both curves show a substantial drop in 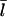due to capping, the experimental curve drops by much less than the theoretical one over the 10-fold concentration increase between 20 nM Aip1 and 200 nM Aip1. The most likely explanation of this discrepancy is a change in the distribution of Aip1 on the filaments. Okada et al. (31) showed that with increasing [Aip1], more of the Aip1 becomes distributed along the lengths of the filaments, and less of it is at the filament barbed ends. This might mean that its inhibiting effect on filament growth is weaker.

FIGURE 7.

(Solid line) Calculated average filament length from Eq. 11 as a function of [CP], for G₀ = 2 μM and k_sev = 10⁻⁶ s⁻¹. (Squares) Measured average filament length as a function of [Aip1], from Okada et al. (31).