Dynamics of Membranes Driven by Actin Polymerization

Abstract

A motile cell, when stimulated, shows a dramatic increase in the activity of its membrane, manifested by the appearance of dynamic membrane structures such as lamellipodia, filopodia, and membrane ruffles. The external stimulus turns on membrane bound activators, like Cdc42 and PIP2, which cause increased branching and polymerization of the actin cytoskeleton in their vicinity leading to a local protrusive force on the membrane. The emergence of the complex membrane structures is a result of the coupling between the dynamics of the membrane, the activators, and the protrusive forces. We present a simple model that treats the dynamics of a membrane under the action of actin polymerization forces that depend on the local density of freely diffusing activators on the membrane. We show that, depending on the spontaneous membrane curvature associated with the activators, the resulting membrane motion can be wavelike, corresponding to membrane ruffling and actin waves, or unstable, indicating the tendency of filopodia to form. Our model also quantitatively explains a variety of related experimental observations and makes several testable predictions.

INTRODUCTION

Various types of directed cell motility are driven by the polymerization of an actin network that exerts a force on the cell membrane, pushing it forward. During cell motility, the leading edge of the cell exhibits a range of dynamic structures such as lamellipodia, filopodia, and membrane ruffles (1,2). These dynamic surface patterns of moving cells are usually observed to have lengthscales in the 1-μm range, and appear in many different cell types (3). The lamellipodium is a flat, disk-like extensional structure generally occurring at the periphery of spreading cells whereas the filopodia or microspikes are actin-rich needle-like structures seen generally as extensions of the lamellipodium. To generate movement, the cells use precursor contacts found in membrane ruffles, or on the underside of filopodia, which can help form adhesive contacts. The lamellipodia are generally extruded in the direction of a strong signal such as a chemoattractant that induces cell migration. The extracellular stimulus turns on certain membrane bound activators that in turn activate a series of proteins that trigger actin branching and polymerization leading to a directed and regulated protrusive force. The interplay between the dynamics of the activators, the protrusive forces generated by the actin polymerization and the membrane dynamics results in the rich variety of dynamic structures described above. This kind of actin-based motion is ubiquitous with examples ranging from the chemotaxis of macrophages to the movement of metastatic tumor cells. Because cell motility depends so crucially on the formation of these dynamic membrane structures, it is imperative to understand the origin and dynamics of these structures.

There have been a number of theoretical approaches to the problem of cell motility driven by actin polymerization (4–7). These studies focus on the interrelationship between the dynamics of actin polymerization and the protrusive forces generated that lead to propulsion. However, one important aspect that has been neglected so far is the crucial role played by membrane bound activators (henceforth referred to simply as activators or membrane proteins), and in particular the thermal density fluctuations and the spontaneous membrane curvature associated with the activators. Activators that have been well studied include the Rho family GTPase Cdc42 and the membrane phospholipid PIP2 (8). These activators bind to, and activate, WASp/Scar family proteins by inducing a conformational change. The WASp/Scar proteins in turn activate Arp2/3, which is directly responsible for generating new branches in the actin network (8–10). Fluctuations in the density of the membrane activators can thus directly lead to fluctuations in the actin branch density and hence the protrusive force. Also important is the fact that both Cdc42 and PIP2 have been shown to induce and sense membrane curvature by binding to BAR domain proteins and epsin, respectively (11,12).

In this article we propose an approach that takes into account density fluctuations and membrane curvature associated with the membrane activators. The dynamics of the actin polymerization, and its dependence on the relative concentration of actin and supporting proteins, has been calculated by Carlsson (13). This gives us the steady-state velocity of the advancing membrane and actin gel, as a function of the branching rate, which is directly proportional to the membrane density of the activators. We therefore separate the in-cell dynamics of the actin polymerization, from the in-membrane dynamics of the activators. The diffusion and spontaneous curvature associated with these membrane activators will determine the time and lengthscales of the dynamic patterns. This allows us to write a simple model and arrive at analytical expressions, while still preserving the rich variety of dynamical behavior that is observed. The merits of such an approach, apart from the knowledge gained concerning dynamical models, lie in its quantitative and testable predictions for cell motility in vivo. Note that the effects of spontaneous curvature of membrane proteins on the shape of vesicles has been widely studied experimentally and theoretically (14,15). These works deal with a free membrane, which is different from the actin-driven membrane we deal with here.

Our work draws on previous models of instabilities in active membranes (16–20), some of which we have combined here into a simpler form. These previous analyses are different in essential ways from this study. They consider the case where the active membrane proteins are ion pumps and therefore solve for the fluid circulations, which is not necessary here. The first analysis (16) considers a system close to a phase separation transition, which is not a constraint in our work. The possibility of wave-like propagation for negative spontaneous curvature of the membrane proteins, was also not considered (16,17). The second analysis (18,19) does find propagating modes, but does not specifically relate them to the spontaneous curvature of the membrane activators. Our model is therefore an application of these previous studies to the case of actin-driven cellular motility. It allows us to describe, in a very detailed and transparent way, the physics of this system in terms of an active membrane.

MODEL

We now introduce our model for the dynamics of the coupled system consisting of the membrane, the activators, and the actin polymerization induced forces. The problem we wish to solve is shown schematically in Fig. 1. We have an average areal density of activating proteins, n₀, which induces actin polymerization such that the membrane moves forward at a velocity given by: v₀ = An₀ ∼ 1–0.1 μm/s, where A is a coefficient that depends on various factors, such as concentration of actin monomers, temperature, etc., and n₀ ∼ 2 × 10¹⁵m⁻². The time evolution of the density of these activating proteins is described by a diffusion equation (18,19)

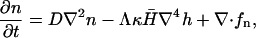(1)

where D ∼ 1 – 0.1 μm²/s is the in-membrane diffusion coefficient of the proteins, κ is the bending modulus of the membrane (typically κ ∼ 10 k_BT), Λ = D/χ is mobility of the proteins in the membrane where 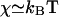is the effective in-plane compression energy of the proteins, 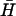is the spontaneous curvature of the membrane proteins, and the thermal noise force satisfies the following correlation: 〈f_n(r, t)f_n(r′, t′)〉 = 2n₀Λk_BTδ(r − r′)δ(t − t′). The first term describes the free diffusion of the activators on the membrane, whereas the last term captures the effect of thermal noise. Evidence for free diffusion of the membrane proteins that activate the polymerization of actin, appears in Gerisch et al. (21). The second term takes into account the coupling between the spontaneous curvature of the activators and the local curvature of the membrane. Here h refers to the coordinate that measures the normal displacement of the membrane from a flat reference plane.

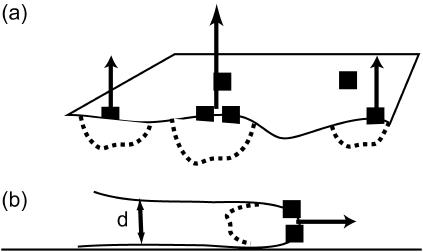
FIGURE 1.

Schematic picture of the model. (a) The Arp activating membrane proteins are symbolized by the solid squares, diffusing in the flat membrane. Where they have a high density the actin polymerization is more extensive (dashed regions) and so is the velocity of the membrane (normal arrows). (b) In the case where the polymerization is confined to a thin leading edge, the local high curvature changes the response to ω_{q, 1}.

The membrane deviation from flatness obeys the following equation of motion

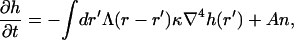(2)

for a free, flat membrane. Here the first term is simply the response of a membrane that is surrounded by a fluid, characterized by the hydrodynamic interaction kernel Λ. After Fourier transforming into q-space, the hydrodynamic interaction kernel is given by Λ(q) = 1/4ηq, and the response of the free membrane is ω_q = κq³/4η, where η is the viscosity of the surrounding fluid.

We note that if the edge of the membrane is highly curved, then the membrane response is different. We take the response in this limit to be: ω_{q, 1} ∼ κq/4ηd², where d is the local radius of curvature at the membrane edge (Fig. 1), assuming that the hydrodynamic interaction (Oseen kernel) remains the same as that for the flat membrane (22). The modified relaxation of a highly curved membrane ω_{q, 1} is obtained from adding to the curvature free energy of a flat membrane a Lagrange multiplier that constrains the membrane to have a curvature 1/d along one of its principle directions. This introduces a new term in the Hamiltonian, which to lowest order can be written as (23): 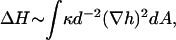which is the form of an effective surface tension. A similar form for the response of a flat membrane occurs when tension is dominant and is given by ω_{q, t} = σq/2η, where σ is the effective surface tension. This regime occurs for wavevectors: 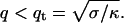In the analysis below, the results using either ω_{q, 1} or ω_{q, t} are interchangeable, by making the transformation: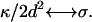

The second term in Eq. 2 describes the action of the actin polymerization induced forces, whose effect we model by the addition of a velocity to the membrane. This velocity is taken to be directly proportional to the local density of activators, with a proportionality constant, A, as described above. The two equations (Eqs. 1 and 2) form a coupled set that completely describes the dynamics of our system. We now describe, in detail, the assumptions that we make in our model.

Discussion of assumptions

In this article, we assume that the membrane proteins do not bind to the actin network, and that the diffusion coefficient (in Eq. 1) is homogeneous. The diffusion coefficient, D, may be treated as an effective value, which takes into account the average (uniform) effect of actin interactions with the membrane proteins. This is an approximation, because the diffusion coefficient is likely to decrease when the density, n, increases, due to a “crowding effect” (24). It may also depend on the actin density. Future work may include the dependence of the diffusion coefficient on the actin density, membrane curvature, and the dynamics of protein-actin binding/unbinding. The binding of the membrane proteins to the actin network that they nucleate, introduces an effective attraction between them, which may drive phase separation. An effective protein-protein interaction will introduce a term of the form: J(r − r′)n(r)n(r′), to Eq. 1. Direct and membrane-mediated protein-protein interactions are not considered in this work, for the sake of simplicity, and are deferred to future studies.

We use the term “activator proteins” in the most general sense: it stands for membrane proteins that trigger actin polymerization, branching or bundling, that produces in turn a protrusive force on the membrane. In addition to the activators mentioned above, there are, for example, the VASP membrane proteins that recruit fascin, which cross-links actin filaments into bundles. These bundles can push more effectively on the membrane, and produce filopodia (25). We consider a single species of membrane activator, which is also constantly in its “on” state. A more detailed description could allow for the kinetics of the turning-on of these activators, which is a process influenced by the presence of other proteins, such as external chemotactic signals or binding of other cellular proteins, the average density n, and membrane curvature. Nevertheless, in this article, we wish to investigate the dynamics that arise from the simplest model first.

In Eq. 2, we neglect the thermal fluctuations of the membrane, which are usually much smaller than the motion due to the actin polymerization (see Discussion). The thermal fluctuations of the membrane and the actin-induced motion described above are incoherent (decoupled), so that they simply add to the overall mean-square height fluctuations. We further expect the thermal fluctuations of the membrane to be almost eliminated when the membrane is being pushed by the actin network, because any membrane motion that is not synchronized with the actin polymerization, such as the thermal motion, will be reduced to negligible values due to the large bulk modulus Y of the actin gel, giving mean-square height fluctuations: 〈h²〉 ∝ k_BT/Y. For the same reason, membrane motion and undulations that arises in a free membrane directly due to the spontaneous curvature of the membrane proteins (16,19), is also negligible here because it too is incoherent with respect to the motion due to actin polymerization.

The membrane response, ω_q, which we used in Eq. 2, describes the dynamics of the fluid flow outside the cell (through the Oseen kernel). In this equation we therefore describe the forces that the fluid flows generate on the membrane, when it is moving. We presume here that the forces acting on the membrane are the following; due to the polymerization of actin pushing the membrane on one side, the forces due to the fluid flow on the other side and the membrane elasticity (curvature and tension). We do not treat the actin network as a viscoelastic gel in this equation, because the membrane does not move with respect to this gel, as it is being pushed actively by it. Any fluid flows on the actin side of the membrane also do not generate any significant forces, compared to the actin polymerization.

In Eq. 2 we also assume that there is a linear relation between the density of activators, n, (and therefore of activated Arp2/3 protein) and the forward velocity of the membrane. That this assumption is valid for low densities and velocities (i.e., velocities low with respect to the saturation polymerization velocity: v_p ∼1 μm/s) has been shown explicitly within the context of a model that considers an obstacle driven forward by a polymerizing actin network with a spatially homogeneous branching rate (13). Above a very small cut-off branching rate, the forward velocity increases linearly with the branching rate and saturates to a maximum at high branching rates. This behavior is generic and not crucially model dependent. One can also reach the same conclusion from a continuum perspective.

At low densities the branching of the actin gel increases linearly with the activator density (9). This means that the bulk modulus of the gel will also be a linear function of the activator density: Y ∝ n. The relation between the velocity normal to the plane of the membrane and the modulus of the pushing gel is given by Gerbal et al. (26)

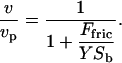(3)

At low gel densities, Eq. 3 implies: 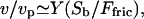where F_fric is the drag force and S_b is the local area of the membrane that is pushed by the actin gel. We assume here (26) that the friction with the surrounding fluid is negligible compared to the friction with the actin gel, so that: F_fric ∼ Γv_p, where Γ is a friction constant related to the adhesion forces between the actin filaments and the membrane. Thus we do find a linear relation between the velocity and the density n. This linear relation breaks down in the following limits: first the local density of membrane proteins cannot increase indefinitely, and is bounded due to the membrane proteins' finite size. Furthermore, at high protein densities the average membrane velocity saturates at v_p (the membrane cannot move faster than the actin is polymerizing).

Note that our description of an imposed velocity, v(n) = An in Eq. 2, due to the actin polymerization, is different from that of an imposed force condition F_actin (18,19,27). The imposed velocity condition is natural if it is determined by the dynamics of the actin polymerization in the lamellipodia. This condition also applies if there is a roughly constant drag force due to the actin gel itself (26). On the other hand, if the motion is determined by the action of the drag force of the surrounding fluid, then it is more natural to keep the imposed force condition, and substitute: 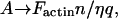in Eq. 2.

Another assumption implicit in Eq. 2 is that changes in the membrane density of the activators translates instantaneously into changes in the force with which the actin gel is pushing the membrane. This is not strictly true, and we now wish to estimate the time lag for this process. First there is the chemical time for Arp2/3 activation. This is of order 1 ms, which translates to membrane density fluctuations of lengthscale 10 nm, which, in turn, is much shorter than the typical mesh size of the actin gel (∼50 nm). So we may neglect this contribution to the time lag. There is growing evidence that the new branches are formed directly at the free barbed ends of the actin filaments, that are in contact with the membrane (10). In this case, there would be no other source of time lag. However, if the Arp2/3 can diffuse into the bulk and nucleate new branches at barbed ends further back from the leading edge, it would be another source of time lag. Experimental observations suggest that barbed ends are localized to a width of λ ∼ 100 nm from the leading edge (28). The average time for a new filament to grow and cover that distance back to the plane of the membrane, and add to the pushing force, is: t_λ = λ/v_p ∼ 100 ms. On this timescale, the membrane density fluctuations can diffuse away over lengthscales smaller than 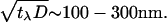This length is of the order of 2–6 unit mesh sizes of the actin gel, whereas we are interested in a continuum description that is valid over longer lengthscales. We therefore conclude that, within these limitations, for lengthscales longer than 200 nm, we can neglect the time lag.

RESULTS

We now solve for the dynamics of the system by first Fourier transforming both Eqs. 1 and 2, and using solutions of the form: e^{−i(ωt+q·r)}. This gives the following system of equations in matrix form

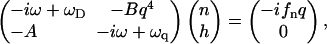(4)

where 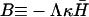and ω_D = Dq². The dispersion equation of the protein density n and membrane height h, respectively, is given by equating the determinant of the matrix in Eq. 4 to zero. The two solutions to the eigenvalue equation for ω are ω_n and ω_h, given by

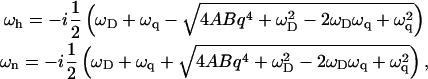(5)

where, the time-dependent response is given by (n, h)(t) ∝ exp(−iω_{n, h}t). It is to be noted that these solutions decay exponentially in time if Im[ω_{n, h}] < 0. We now discuss the results for two different cases, positive (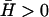) and negative (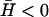) spontaneous curvature of the membrane activator proteins.

Positive spontaneous curvature

Membrane activators with positive spontaneous curvature (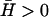) will prefer to aggregate at the locations with maximum local curvature (Fig. 2). The solution for the membrane height h, in this case, decays with time (Im[ω_h] > 0, Re[ω_h] = 0), whereas for the membrane density of the activator proteins, n, we find that there can be an instability in the form of an exponentially increasing function of time (Im[ω_n] < 0, Re[ω_n] = 0) (Fig. 3 a). Depending on the form of the membrane response we choose, we get unstable behavior for the following range of q-wavevectors

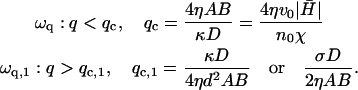(6)

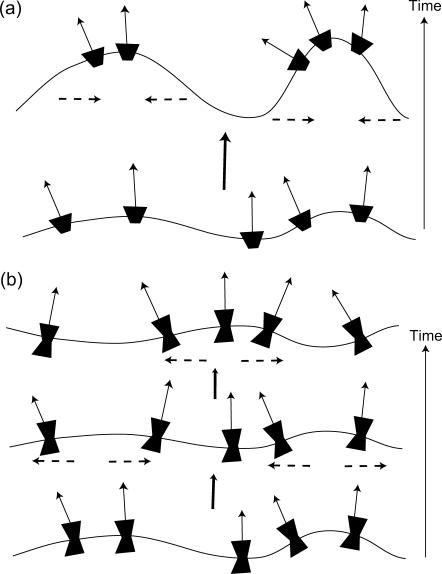
FIGURE 2.

Schematic picture of the two behaviors depending on the spontaneous curvature of the membrane proteins. (a) 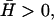fluctuations in the density of the Arp activating membrane proteins grow unstable when the proteins aggregate into the high curvature “filopodia”. (b) 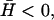wavelike propagation due to the restoring force of the curvature, breaking up high density fluctuations (dashed arrows).

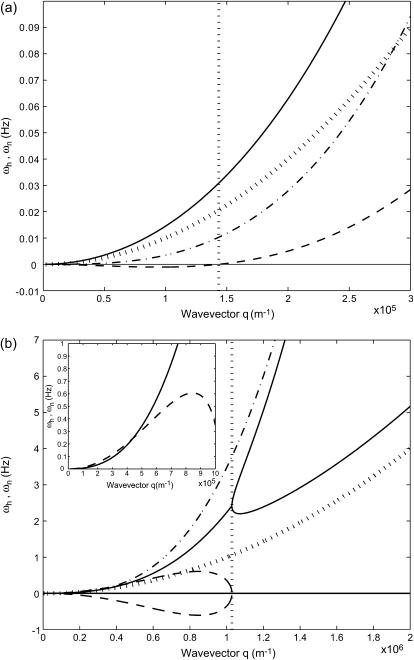
FIGURE 3.

Calculated response frequencies of the membrane protein density ω_n and membrane height undulations ω_h (using ω_q of a flat membrane, κ = 10 k_BT and v₀ = 1 μm/s). The bare diffusion rate ω_D and bare membrane response ω_q are shown by the dotted and dotted-dashed line, respectively. (a) 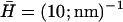: ω_n, solid line; ω_h, dashed line. The critical wavevector q_c (Eq. 6) below which the density fluctuations are unstable is indicated by the vertical dotted line. (b) 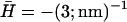: the imaginary parts are given by the solid lines whereas the real parts are given by the dashed lines. The critical wavevector q_w (Eq. 8) below which the wavelike fluctuations occur is indicated by the vertical dotted line. In the inset we show that the imaginary part can be smaller than the real part for small enough q.

That is if one uses ω_q (the free membrane form) then the instability is for q < q_c, whereas if one uses ω_{q, 1}, the instability is for q > q_{c, 1}. Note that in the second case, if q_{c, 1} turns out to be large, then terms in the free energy of higher order in the wavevector q cannot be neglected and may prevent the instability (29).

These results arise when the bare response of the protein diffusion is faster than the response of the membrane. In this case, the proteins aggregate in response to the membrane curvature fluctuations, and a density fluctuation builds up, as it responds faster (Fig. 2). Similar instabilities due to aggregation of membrane proteins with positive spontaneous curvature were described in previous studies of different active membranes (16,18,19). In Fig. 3 a we plot ω_n and ω_h as a function of q (for the case of a free tensionless membrane).

The general form of the instability criterion, q < q_c (Eq. 6), follows from comparing the timescales of membrane motion and in-membrane diffusion of the combined shape-density undulations (Fig. 2 a). These undulations combine a local increase in the membrane protein density, with the driven (active) normal motion of the membrane. The motion of these shape-density undulations can be described by an effective diffusion with a dispersion relation given by q² = ω_bump/D′, where 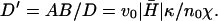We now discuss the parameters that control this motion. The membrane “bump” diffuses faster when the driving velocity produced per membrane protein, proportional to v₀/n₀, is larger. This is because, density fluctuations are converted faster into a height undulation. Larger spontaneous curvature, 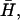causes the membrane bumps to have smaller wavelengths, which move faster. Finally, larger osmotic pressure of the membrane proteins χ results in a larger wavelength of the density fluctuations, resulting in slower motion. The unstable regime occurs for wavevectors where the membrane response, ω_q, is slower than the rate of diffusion of density bumps, ω_bump. In this regime, the aggregation of the membrane proteins can occur before membrane undulations decay away. The criterion appearing in Eq. 6 is simply a restatement of this result. It is to be noted that the final expression for q_c (Eq. 6) is independent of both the membrane bending modulus, κ, and the membrane protein diffusion coefficient, D. Quantitatively, using the parameters given before (see “Model”), we find: D′ ∼ D/2.

The instability we describe above does not lead to a real divergence, because the velocity saturates at v_p and the local density of the membrane proteins saturates due to their finite size. Note that a similar behavior of the critical wavevector of the membrane instability, was shown in Stephanou et al. (7): k_c ∝ k_a/D_a, where k_a is the rate of actin polymerization, and D_a is the bulk diffusion coefficient of actin monomers in the cell cytoplasm. Comparing to our expression for q_c (Eq. 6), we see that both results are directly proportional to the rate of actin growth (k_a or v₀) and inversely proportional to the diffusion coefficient in the plane of the membrane, which tends to smooth away the density accumulation (in Stephanou et al. (7) the actin diffusion was assumed to be confined to a submembrane layer). The details of the two models are nevertheless very different.

Negative spontaneous curvature

For negative spontaneous curvature of the membrane proteins (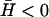), we find that there is a range of wavevectors for which the response frequencies ω_n and ω_h are real (Fig. 3 b). This corresponds to a oscillatory behavior, though still damped (or even overdamped) (Fig. 2 b). When these oscillations are not overdamped, they resemble wave-like propagation. The range of the wavevectors over which this occurs is given by the condition that the argument of the square-root term in Eq. 5 becomes negative. The criteria for these oscillatory modes are given by (note that B < 0)

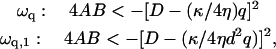(7)

which are satisfied when the wavevectors q are such that

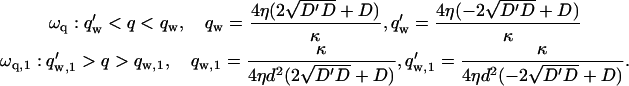(8)

However, when 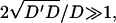as we find for real cells (see Fig. 7 and discussion in “Comparison with experiments”), both q′_w and q′_w,1 are negative. This makes the oscillatory behavior restricted to 0 < q < q_w and q_w,1 < q, for the two cases of Eq. 8.

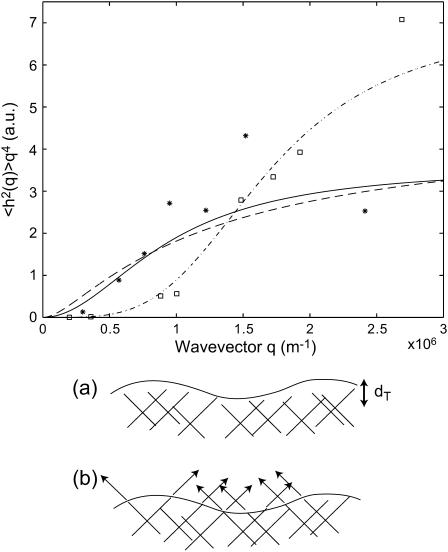
FIGURE 7.

Calculated static height correlation function 〈h²(q)〉 in the tension-dominated regime (Eq. 16) (dashed line), compared with the data (32) for normal cell (stars) and inactivated cell (squares). The solid line and dashed-dotted lines show the behavior for the thermal height fluctuations in an unconfined and confined membrane, respectively. The bottom panel shows the two cases: (a) inactivated cell with confined thermal membrane fluctuations, and (b) actin-induced fluctuations in the normal cell.

Our results are similar to those of a previous analysis (18,19), which has also yielded propagating but highly dispersive modes in an active membrane. In that system of active pumps, the q-range of the propagating solutions was explicitly given only in terms of the dependence of the pumping activity on the local membrane curvature (in combination with the protein diffusion coefficient, etc.). In our model the actin-induced force that pushes the membrane is assumed not to be dependent on the local membrane curvature, so the q-range of our propagating modes is controlled by the spontaneous curvature, through D′, for which we give an explicit expression for the first time (Eq. 8).

The real parts of the frequencies for the height function and the activator density function are in antiphase with each other (Fig. 3 b), and correspond to an effective propagation velocity v_eff = Re[ω]/q in the limit of small wavevectors ()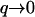

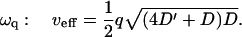(9)

The damping of these waves is given in this limit by the factor: 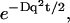coming from the membrane protein diffusion. For the tension-dominated (second case in Eq. 8), there are propagating waves in the limit of large wavevectors (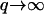), where we get

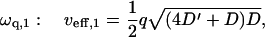(10)

and the damping of these waves is given in this limit by the factor: 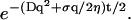The waves therefore decay over a lengthscale given by: 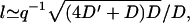which is of the order of the wavelength of the density-height perturbation.

In Fig. 3 b we plot the imaginary and real parts of ω_n and ω_h as a function of q (using ω_q of the flat and tensionless membrane). Note that for q < q_w the imaginary parts of both frequencies are equal, whereas the real parts have the same magnitude but opposite signs. For any choice of parameters, the motion of n and h changes from damped (Re[ω] > Im[ω]) to overdamped (Re[ω] < Im[ω]) wave-like propagation as q increases (see inset of Fig. 3 b). Finally, when q > q_w, we find the usual exponential decay for both functions (Re[ω] = 0, Im[ω] > 0). At the critical wavevector q_w, both the response frequencies have the value:

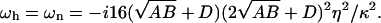In the regime of wave-like propagation q < q_w (or q > q_{w, 1}), the density fluctuations travel faster than the bare diffusion, due to the additional curvature driving force (Eqs. 9 and 10) (Fig. 3 b). The driving force for the wave-like propagation of density-curvature fluctuations is shown schematically in Fig. 2 b. A local increase in the protein density will result in increased membrane curvature there, which then drives these proteins into lower density areas due to their negative 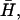in addition to the usual diffusion. This curvature-induced restoring force gives rise to the (albeit damped) oscillatory behavior.

The ratio 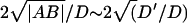is a dimensionless number called the Péclet number, that measures the relative importance of advection to diffusion in fluids. When comparing to the experimental data (see Fig. 7 and “Comparison with experiments” in Discussion section), we get a good agreement using values of D ∼ 0.1 and D′ ∼ 0.01 (in units of μ²/s), such that the corresponding Péclet number is ∼1. Because these values are of order 1, we are indeed likely to have waves of a propagative character in our system.

Protein density and membrane height correlations

So far, we have described the wavevector regimes where, depending on the sign of the spontaneous curvature of the activators, one gets either an instability or wave-like modes. We now wish to address the question of the actual amplitudes of the fluctuations that characterize the motion in these regimes. This we do by calculating the correlation functions of the membrane height and of the membrane activator density. Solving Eq. 4 we get

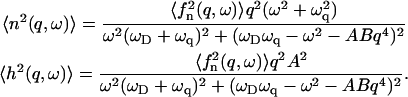(11)

Integrating these functions over ω we find the spatial (static) correlations 〈n²(q)〉, 〈h²(q)〉. We plot these functions in Fig. 4, for a free and tensionless membrane. Analytic expressions for these functions can be calculated, but are quite lengthy, so we will give them explicitly only for the limiting cases.

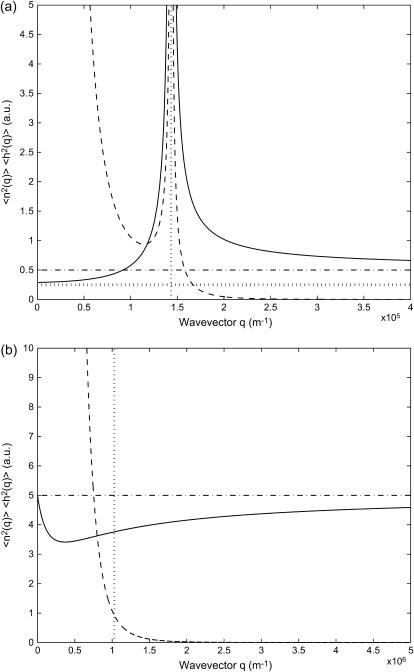
FIGURE 4.

Calculated static density and membrane height correlation functions: 〈n²(q)〉, solid line; 〈h²(q)〉, dashed line. (a) 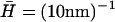: the correlations diverge at the critical wavevector q_c (Eq. 6), indicated by the vertical dotted line. The limiting values 〈n²(0)〉 (Eq. 14) and 〈n²(∞)〉 (Eq. 15) are shown by the horizontal dotted and dashed-dotted line, respectively. (b) 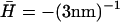: the density correlations dip for wavevectors q < q_w (Eq. 8), indicated by the vertical dotted line. The height correlations show a monotonous decay, having a crossover from 1/q⁴ to 1/q⁶ behavior around q_w. The limiting value 〈n²(∞)〉 (Eq. 15) is shown by the horizontal dashed-dotted line.

It is to be noted that the height fluctuations in our model are derived solely from thermally driven density fluctuations of the membrane proteins. This is why we get: 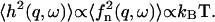These height undulations are superimposed over the average forward motion of the membrane, at average velocity v₀, determined by the average density n₀.

Another notable point is that we assumed a continuous and constant force, or driving velocity, due to the actin polymerization in Eq. 2. This is reasonable as long as we are interested in membrane motions on timescales longer than the duration of an individual actin polymerization event. More generally, we can describe the actin-induced velocity (or force) by a random shot-noise behavior (27), with a typical time τ. This amounts to replacing: 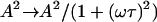in the numerator of Eq. 11 for 〈h²(q, ω)〉. This is easily calculable, and is found to change the behavior quantitatively, but not to change the value of the critical wavevector q_c, or the qualitative forms of 〈h²(q)〉 in the 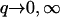limits.

We now discuss the form of the density and height correlations in various cases and limits.

For positive spontaneous curvature of the membrane proteins () (Fig. 4 a), we find a divergence of both the density and membrane height fluctuations at the critical wavevector q_c (Eq. 6). Around the critical wavevector, setting q = q_c + δ, the divergences have the form

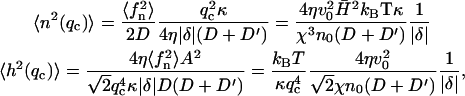(12)

where, from the last line, we can define: 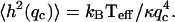The “effective temperature”: 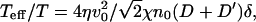diverges at the critical wavevector. This is reminiscent of the divergence in the effective temperature describing the response of active hair bundles in the hair cells of the auditory system (30) when there is a resonance with an internal driving frequency. In our case the divergence occurs when the lengthscale of the active process is in “resonance” with the lengthscale of the spontaneous curvature. Note that when the fluctuations (correlations) become very large, the validity of our linear treatment breaks down.

In the limit 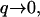the height correlations have the form: 〈h²(q)〉 = k_BT_eff/κq⁴. Here we chose to define an effective temperature, T_eff, because the power law dependence is similar to the behavior of the thermal membrane height fluctuations (31): 〈h²(q)〉_T = k_BT/κq⁴. The appearance of thermal-like correlations is not surprising, because the driving force for the height fluctuations comes from the thermal fluctuations of the membrane protein density: 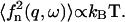Thermal-like correlations also appear for various choices of active membranes (18,19,27). The effective temperature we defined, has the following limiting forms

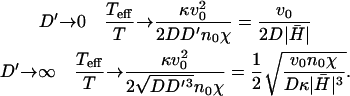(13)

The functional form of T_eff/T is very intuitive: the effective temperature increases with the pushing velocity of the actin v₀, and is inversely proportional to the diffusion coefficient of the membrane proteins, which smoothes away the density fluctuations.

In contrast, the density fluctuations are finite in the limit 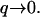Note that for the free diffusion problem, we recover the usual free diffusion: 〈n²(q)〉 = n₀q²k_BTD/2w_D ∼ n₀. In our model we find in the following limits

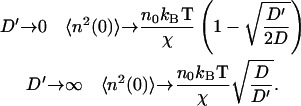(14)

The first limit shows the approach to the bare membrane diffusion in the absence of actin polymerization (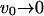). In the second limit we find that the rapid formation of membrane undulations, due to 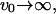effectively localizes the membrane proteins and suppresses any long wavelength density fluctuations.

In the limit 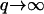the density and height fluctuations are given by

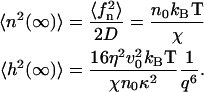(15)

The density fluctuations are finite, and approach the bare membrane diffusion result (see first part of Eq. 14). The height fluctuations decay in this limit in a nonthermal form, reminiscent of similar results for model active membranes (27).

In the case of negative spontaneous curvature of the membrane proteins (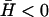), as we have already seen, no instability occurs (Fig. 4 b). For the density correlations we find that 〈n²(q)〉 is approximately a constant as a function of q (Fig. 4 b), close to the limiting value 〈n²(∞)〉 (Eq. 15) of free diffusion. There is a region of reduced correlations, that corresponds to the additional restoring curvature force, which now acts to smooth away any density fluctuations. The density correlations therefore dip for wavevectors q < q_w (Eq. 8), where there is wave-like propagation. The height correlations show a crossover from 1/q⁴ to 1/q⁶ decay around q_w.

We now consider the correlations for the tension dominated case (or thin lamellipodium edge). Here the membrane response is given by ω_{q, 1}, ω_{q, t} ∝ q. The results in the low and high q limits are

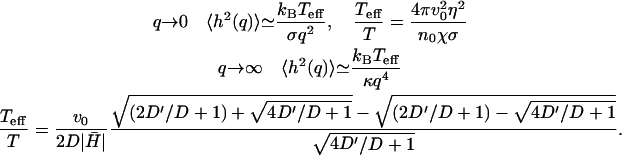(16)

The first limit has the same form as for thermal fluctuations in the tension-dominated regime, whereas the large q limit has the form of thermal fluctuations in a free and tensionless membrane, prompting us to express both in terms of an effective temperature.

One of the most striking results is that the height fluctuations increase with increasing viscosity of the surrounding fluid η (Eqs. 12–16). This is similar to the results of a previous analysis of active membranes driven by ion pumps (20). In both these cases, the active membrane proteins are allowed to have density fluctuations, while they impose a given velocity on the membrane. This is in contrast to the results of active membrane proteins that produce a fluctuating force with zero average value (shot noise), where the height fluctuations are found to decrease with increasing fluid viscosity (27). Note that if the actin imposes a force, F_actin, rather than a velocity v, on the membrane, this introduces another factor of 1/q²η² to the height correlations 〈h²(q)〉 (see discussion following Eq. 2), and the dependence on the viscosity is subsequently modified. In all of these cases the appearance of the active term in the equation of motion (Eq. 2), without a corresponding damping, allows kinetic coefficients such as the viscosity and diffusivity to determine the values of static variances of height and concentration. These are the trademarks of an out-of-equilibrium system.

The density and height fluctuations also increase when the membrane diffusion coefficient is decreased (Eqs. 12, 13, and 16): 〈h²(q)〉 ∝ 1/D. A similar result appeared in Prost et al. (20), but was limited there to the tensionless regime. We find that this behavior also appears in the tension-dominated case (Eq. 16), which seems to be more realistic for living cells (see next section). The origin of this behavior is very intuitive; slower diffusion allows fluctuations in the membrane protein density to survive longer, which in turn drive larger height undulations, due to the active term An in the equation of motion (Eq. 2).

In Eqs. 13 and 16 it seems that in the limit 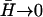the effective temperature diverges 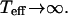This happens because the q-dependence of the correlation function changes when 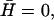and is now different from that of the thermal case. For the tensionless case (Eq. 13), in the limit of 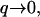we now find: 〈h²(q)〉 ∝ 1/q³, so that the effective temperature is now: T_eff ∝ 1/q, and indeed diverges in this limit. For the tension-dominated case (Eq. 16), in the limit of 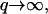we now find: 〈h²(q)〉 ∝ 1/q³, so that T_eff ∝ q, and indeed diverges in this limit.

We now examine how the height correlations depend on frequency. The power spectrum of the height fluctuations as a function of frequency can be obtained by integrating Eq. 11 over q. This gives us the temporal correlations 〈n²(ω)〉, 〈h²(ω)〉. Because the integration is not possible analytically, we do it numerically. We plot the height correlation function in Fig. 5, for the cell membrane with the elastic parameters: κ and σ. These parameters are found empirically, by fitting to the observed thermal fluctuations alone, i.e., when the actin polymerization is blocked (32) (see next section). For comparison we also plot the correlation that arises purely from thermal fluctuations. This approaches the free membrane limit at high frequencies 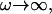where (22). At lower frequencies, in the tension-dominated regime, the thermal behavior is: ∝ ω⁻¹.

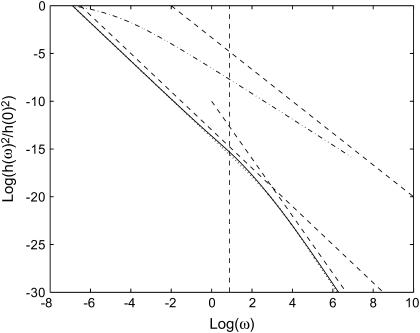
FIGURE 5.

Calculated height fluctuations as a function of the frequency ω. The dashed-dotted line is the thermal fluctuations that approach ω^−5/3 at large frequencies (asymptotic dashed line). The actin-induced fluctuations are given by the solid and dotted lines, for 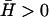and 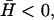respectively. The asymptotic behavior is given by the dashed straight lines: ω⁻² and ω⁻³ in the limit of small and large frequencies, respectively. The vertical dashed line represents the frequency of the crossover, roughly given by ω_h(q_w).

The active fluctuations are found to have a 〈h²(ω)〉_actin ∝ ω⁻² behavior at small 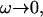and 〈h²(ω)〉_actin ∝ ω⁻³ at large 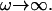The crossover occurs roughly where the frequency of the membrane bending modes equals the frequency of the effective diffusion of the membrane bumps. For the case when 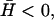the crossover corresponds to the appearance of propagating waves and occurs at the wavevector, q_w. The frequency of the height fluctuations corresponding to this wavevector, is given by ω_h, shown as the vertical dashed line in Fig. 5.

Future experiments that probe the power spectrum of the height fluctuations, should show a clear difference between the thermal and active components. The actin-induced height fluctuations are predicted to be much more confined to low frequencies than the thermal fluctuations of free membranes.

DISCUSSION

Comparison with experiments

Experimental observations of the actin-driven motion of cells and cell membranes (21,33,34) show both wave-like propagations and finger-like filopodia. Because our model predicts that both behaviors are possible, depending on the sign of the spontaneous curvature, 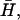of the membrane proteins, one possibility is that activators with both types of spontaneous curvature exist in vivo. There is also the possibility that the spontaneous curvature of a membrane activator is altered by a conformational change that is brought about by phosphorylation or binding to another protein (or a number of proteins), either already in the membrane or from the cytoplasm (1). Thus the cell has many options, all of which it may use to adjust the local concentration of the membrane proteins that produce either uniform growth or filopodia (25,35). We predict that these proteins (or protein complexes) have different spontaneous curvatures: 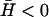for uniform growth and 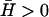for filopodia. Indeed, for filopodia growth the membrane proteins have to form specific complexes which, in light of our model, must have large spontaneous curvature (36,37). These complexes can then recruit cross-linking proteins such as fascin, which help form tight actin bundles inside the growing filopodia (25). Future extensions of our model may include the coupling of dynamical changes in the spontaneous curvature, 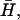to the local densities of various proteins.

Another source of experimental corroboration for our overall qualitative picture of the dynamic colocalization of activator membrane proteins and actin polymerization in high (or low) curvature regions of the leading edge, is provided by the experiments of Nalbant et al. (38). The authors visualized the dynamics of activated Cdc42 in living cells and showed that there was a strong correlation between the most recently formed protrusions and the level of active Cdc42 in its vicinity, mostly concentrated at the tips of the protrusions. They also show that the activator proteins are present only near the base regions of filopodia, consistent with our assertion that the activators form the initial seed for the filopodium by assembling an actin rich bump, whereafter the newly recruited bundling agents and normal barbed end polymerization of the actin filaments can lead to the filopodia structure. Note that a recent study (39) shows that specific lipids may serve as the initiators for the actin polymerization. In terms of our model these are treated exactly as the membrane proteins, and the dynamics of their aggregation is observed to control the inhomogeneities in the actin network.

For positive spontaneous curvature of the membrane proteins (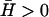), we can estimate the critical wavevectors (Eq. 6), using typical values of the various parameters (see “Model”). For the spontaneous curvature we use 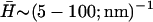(40). For the flat membrane case we find: 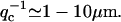For the membrane edge case we find: 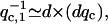where typically: d ∼ 0.5–1 μm. Our analysis predicts a specific wavevector (q_c), which becomes unstable, so that the resulting filopodia should have an average spacing given by the corresponding wavelength. This lengthscale appears to correlate well with the observed average separation between neighboring filopodia (41), of 1.5–3 μm. Note that from Eq. 6, increase in the membrane tension causes an increase in the density of filopodia (42). Increased membrane tension was found to reduce the velocity with which actin polymerization is pushing the membrane (43), so that we expect not only more numerous but also smaller filopodia under increased membrane tension.

We predict that the density and height fluctuations increase when the membrane diffusion coefficient is decreased (Eqs. 12, 13, and 16). The membrane diffusion coefficient may be changed by addition of various chemical agents, such as changing the cholesterol content (44,45). Note that changing the cholesterol level may affect the activation of the membrane proteins (46), which is a process that is not included in this work.

This prediction may explain the recently observed low membrane diffusion (high microviscosity) at the leading edge of moving cells (44). The ratio of the diffusion coefficients between the cell side and leading edge is found to be: D_trail/D_lead ∼ 3. If we correlate the root mean square height fluctuations from Eqs. 12 and 13 with the average rate of lamellipodial extension, we predict: 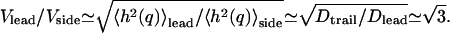This is in good agreement with the measurement (44). Our model therefore provides a natural explanation for this otherwise paradoxical observation: the membrane is stiffer (more viscous) in regions where motility is increased. Presumably larger undulations in the shape of the leading edge, help the cell overcome local friction barriers, and results in faster overall motion (47). Additionally, the membrane undulations at the moving front can provide localization points for the formation of adhesion complexes, which are important in completing the cycle of cell motility (48,49).

This result of our model may also explain the observed response of endothelial cells' motion to shear flow (50,51). In these experiments it was shown that the cells move less quickly against the direction of the flow, as compared to the perpendicular and parallel directions. Concurrent with this motion, there is an increase in the fluidity of the membrane in the front part of the cell, by as much as a factor of 2 for shear stress of 10 dyn/cm² (52,53). According to our model the amplitude of the active membrane fluctuations is therefore reduced by a factor of 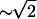compared to the rear of the cell, which is in very good agreement with the measured drop in the fluctuation amplitude in the presence of shear (54). This then results in the observed orientational motility (50,51). Such a physical response to shear flow may complement or trigger the biochemical changes that take place in the presence of shear flow (55).

The reduced amplitude of the actin-induced cell protrusions, when shear is applied, was also observed in neutrophiles (56,57). In Makino et al. (57) the projected cell area shrank by ∼0.5–0.7 in a shear stress of 5 dyn/cm². Because we expect the area to increase with the actin-induced protrusions, as: A_cell ∝ 〈h²〉_actin ∝ 1/D, the diffusion coefficient in these cells is predicted to increase by a factor of 2–1.4. These values are in agreement with the changes reported in Haidekker et al. (52) and Butler et al. (53).

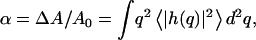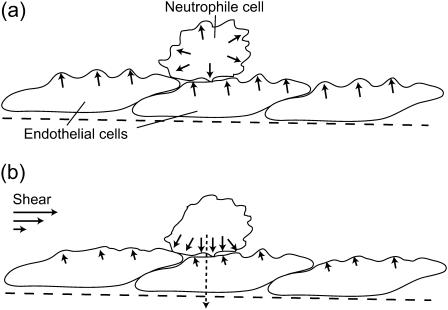
The calculated actin-driven membrane undulations result in an extra surface area ΔA, which is given by: where A₀ is the projected surface when there are no undulations (flat membrane). From the results of “Protein density and membrane height correlation” in the Results section, we find a thermal-like behavior: 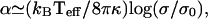where σ is the membrane tension and σ₀ is some reference tension. The excess surface area is therefore also proportional to 1/D. Because the overall amount of cortical actin layer (below the cell membrane) is proportional to the membrane area, we expect a decrease in this actin layer in the presence of shear flow. Indeed a reduction of 20–40% was observed (58). At high shear rates, there was an increase in the actin activity around the cellular nucleus, presumably as a defensive mechanism, not directly related to the cortical actin activity at the membrane. We therefore propose the following model for the shear-induced transendothelial neutrophil migration phenomenon (56). In the absence of shear (Fig. 6 a) both the neutrophile and endothelial cells have relatively active actin polymerization at their membranes. This makes the endothelial cells relatively stiff, and the neutrophile performs random motion on the endothelial surface, at most making small protrusions, but not penetration. The surface of the neutrophile will be uniformly covered by protrusions. When shear is applied (Fig. 6 b) the actin activity, in all the cell membranes that face the flow, diminishes. The entire actin activity inside the neutrophile is now concentrated at the neutrophile-endothelial junction. In the junction the membrane is “protected” from the effects of the shear flow, and the diffusion coefficient therefore does not increase there. The results of the combination of: i), softer upper endothelial surface, and ii), concentrated downward neutrophile actin activity, is the observed transendothelial neutrophil migration phenomenon (56). The neutrophile is the more active of the two cells, having much faster motility due to higher levels of actin polymerization.

FIGURE 6.

Schematic picture of the effects of shear on the actin polymerization activity at the membrane of endothelial and neutrophile cells. (a) In the absence of shear, the activity is relatively high, shown by the arrows and membrane protrusions. (b) When shear is applied, the activity is reduced in the membrane surfaces facing the flow (smaller arrows and protrusions). Consequently there is increased activity at the neutrophile-endothelial cell-cell junction, where the more active neutrophile penetrates the endothelial cell (dashed arrow).

For negative spontaneous curvature of the membrane proteins (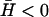), we can estimate the critical wavevector (Eq. 8) using the values of the parameters that appear above. This gives us 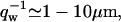which is similar to what we obtained for q_c (Eq. 6). Thus both the instabilities and the wave-like motions have the property that they occur only for membrane lengthscales larger than some critical lengthscale, ∼1 μm. Indeed, there are no long-lived actin structures smaller than this lengthscale, on the cell membrane (21,34).

For the velocity of the propagating waves, we get from Eq. 9: v_eff ∼ qD, which results in velocities of the order: v_eff ∼ 1–0.1 μm/s for wavevectors: q ∼ 1(μm)⁻¹. Actin waves with these velocities and wavelengths are indeed observed on the surface of cells and lamellipodia (21,33,34). Note that in these experiments the observed waves are on the bottom part of the cell, where the membrane is largely flat next to the glass substrate. Our analysis predicts that the actin waves correspond to small undulations on the membrane surface (Fig. 2 b). Our interpretation of these waves is therefore different from that given in Vicker (34), where the surface waves are proposed to be sections through three-dimensional spiral waves in the cell bulk. Recent experiments seem to confirm our interpretation because they suggest that the actin structures are largely confined to the cell membrane (21), and that the traveling-wave propagation is related to actin polymerization around a high density Arp2/3 complex (59). The formation and decay of these density fluctuations occurs on a timescale, t_fluct ∼ 2–3 s, which is in agreement with membrane diffusion times over the lateral size of these formations (∼1/2 μm). The slower decay as compared to the formation, ∼3.5 vs. ∼2 s, respectively, may be due to the extra distance to diffuse out of the bump (Fig. 2 b): t_fluct × v₀ ∼ 0.1 μm. Alternatively the diffusion coefficient may decrease due to the dense actin gel formation.

Another observation that supports our model, that the ruffling is a membrane phenomenon, comes from the observation of the dynamics of “microplasts” (60). These cell fragments do not contain any internal organelles, and are only ∼2 μm in diameter. Although they do not perform efficient motility, they do show the same membrane ruffling activity at their edges, as do the original intact cells.

Recently the static height correlations, 〈h²(q)〉, were measured on living cells (32). The mean-square height undulations of the active cell are found to be ∼8 times larger than for the inactive cell (32). The correlations agree with the tension-dominated behavior given in Eq. 16 (Fig. 7), if we use the same parameters as before and take the surface tension to be σ ∼ 0.5 × 10⁻⁸ J/m². In particular, cells that lack the actin-polymerization motility, display much smaller fluctuations (32) presumably of thermal origin. Indeed these fluctuations are well described by confined thermal correlations of the form (61): 〈h²(q)〉 ∝ k_BT/(κq⁴ + σq² + γ), with σ ∼ 3.7 × 10⁻⁸ J/m² and γ ∼ 2.6 × 10⁵ J/m⁴ (Fig. 7). The equivalent confinement distance: 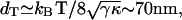is consistent with the average separation between the fibers of the actin mesh, which underlies the membrane. In a normal cell, when actin polymerization is driving the membrane fluctuations, there is no meaning to any membrane confinement. It is then possible to fit the active cell data to the thermal fluctuations of an unconfined membrane, with an “effective temperature” of T_eff/T ∼ 8 (Fig. 7). This approach though does not give us any information about the nature of the active fluctuations. From the 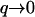limit of Eq. 16 we get an effective temperature of this magnitude if we take: σ to be smaller than the value given by the fit to the thermal fluctuations, by a factor of ∼8, n₀ ∼ (300 nm)⁻², and an effective viscosity η ∼ 100η_water. These parameters are within reasonable limits for a cell, but an exact comparison with the data awaits independent determination of these parameters.

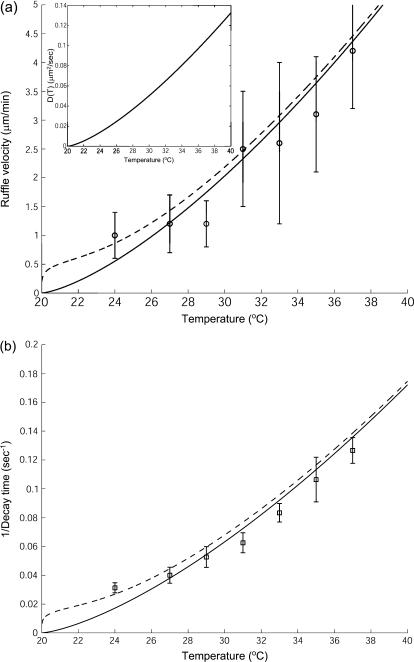
The most recent data (61) indicate that the velocity of actin-induced membrane ruffles, is strongly temperature dependent. According to our model this velocity is proportional to the membrane diffusion coefficient (Eqs. 9 and 10): 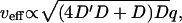where q is the inverse of the typical lengthscale of these ruffles (usually L_ruffle ∼ 1–2 μm (62)). Because the diffusion coefficient is inversely proportional to the membrane viscosity η_s (24), we expect it to vanish at the liquid-gel transition temperature T_m, where the viscosity diverges (63): D(T) ∝ k_BT/η_s(T) ∝ T|T − T_m|^1.4. Using typical values for T_m = 20°C, and 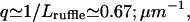we fit the overall scale of D(T) (inset of Fig. 8). We estimate the overall value of 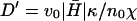to be of the order of D. Its temperature dependence is dominated by that of κ, which roughly diverges as (64): κ ∝ |T − T_m|⁻¹. The resulting velocity v_eff agrees with the observation (Fig. 8 a), using: D′ = 0.02/|T − T_m| (μm²/s). For comparison we also plot the result for D′ = 0, when 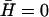for example, and v_eff ∝ Dq (Fig. 8). Similar velocities of membrane ruffles of 150–250 nm/s were also observed in Döbereiner et al. (65).

FIGURE 8.

(a) Calculated velocity of actin-induced membrane ruffles v_eff (Eqs. 9 and 10) (dashed line), where D(T) is shown in the inset and D′(T) = 0.02/|T − T_m| (μm²/s). The solid line gives v_eff in the limit D′ = 0. The experimental data (○) are from Neto et al. (61). (b) Calculated decay time of actin-induced membrane fluctuations: τ_decay ∝ 1/D(T) (solid line), compared to the experimental data (□) (61).

Furthermore, the observed decay time of smaller height fluctuations, also behaves as: τ_decay ∝ 1/v_effq, with a larger wavevector (smaller wavelength) of q = 1.15 μm⁻¹ (Fig. 8 b). We therefore predict that the slowing down of the membrane motion due to the actin polymerization, is driven by the decrease in the membrane diffusion coefficient close to the gel transition temperature.

Finally, the mean-square membrane curvature was observed not to depend on the temperature (62). The mean-square curvature: 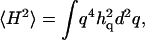is dominated by 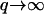modes, whereas the mean-square amplitude of height fluctuations 〈h²〉 is dominated by the 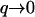modes. From our model we predict that for the tensionless membrane, the amplitude of the 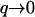modes does depend on the diffusion D (Eq. 13): 〈h²〉 ∝ 1/D(T), whereas the amplitude of the 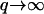modes does not (Eq. 15). This difference could explain the independence of the root mean square curvature on the temperature, except for the very weak 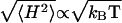dependence, which amounts to ∼2% over the observed temperature range (62).

Detailed comparisons between our model (namely 〈h²(q)〉,〈h²(ω)〉) and the experimental data (21,59), awaits more quantitative analysis of the spatial and temporal shape fluctuations in living cells (32,62,66).

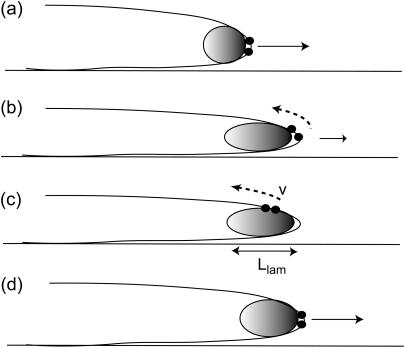
So far we have discussed the membrane dynamics at the leading edge, which is what we are modeling. However, our model can also give us insights into phenomena that occur at the cellular scale. An example of complicated, oscillatory dynamics of the bulk actin gel, is described in Giannone et al. (33). The authors find a periodic interruption (∼20 s) in the forward motion of lamellipodia that had no filopodia. One possibility for the mechanism is shown schematically in Fig. 9. The activating membrane proteins are initially concentrated at the lamellipodium edge, and because there are no filopodia we can take the spontaneous curvature to be small or negative. As the forward motion persists the leading edge thins such that the local curvature is too high for these proteins and they prefer to move to the less curved membrane on the upper surface. This causes a backward propagating wave of actin polymerization, which proceeds until the back edge of the lamellipodium. This explains why the contractions occur every t_cont ∼ L_lam/v ∼ 10–30 s, where L_lam ∼ 2 μm is the thickness of the lamellipodium (33) and v ∼ 0.1 μm/s is of the order of the calculated propagation velocity v_eff (Discussion) (Fig. 9). The membrane dynamics we considered in this model are therefore coupled in the cell to the dynamical variations affecting the entire actin layer, and this coupling remains to be described.

FIGURE 9.

Schematic description of the periodic contractions found in lamellipodia growth (33). (a) The membrane proteins initially localized at the lamellipodia's edge (•) produce a forward pushing actin network (shaded ellipse). (b,c) As the edge thins they are pushed toward less curved regions at the top of the lamellipodia, and then propagate until the back edge. (d) The forward edge is again thicker now, so these membrane proteins can localize there and forward motion resumes.

Predictions

Our model allows us to make testable and quantitative predictions. For example:

• Changing the fluid viscosity and membrane tension will shift the average density of filopodia (Eq. 6).

• The velocity of propagation of actin density fluctuations on the cell membrane is predicted to be linear in the diffusion coefficient of membrane proteins (Eq. 9).

• Similarly, the amplitude of density and height fluctuations are predicted to increase when the membrane diffusion coefficient is decreased (44) (Eqs. 12, 13, and 16). Note that the density of filopodia, given by q_c Eq. 6, is independent on D.

• In the tension-dominated regime, which seems to be applicable to most cells, the long wavelength height fluctuations increase with increasing of the fluid viscosity (Eq. 16). The same behavior is found also in the tensionless case (Eq. 13).

• Our prediction that the membrane proteins that initiate filopodia (35) have a high spontaneous curvature, has to be tested. Incorporation of these proteins into synthetic vesicles and observing the resulting shape transformations could determine this parameter.

Some of these manipulations are possible in living cells, whereas others are better tested in synthetic systems (44).

CONCLUSION

The dramatic membrane dynamics that occur at the surface of stimulated cells is a consequence, not only of the actin polymerization dynamics, but also of the interplay between the dynamics of the membrane itself and that of the activators that reside on it. Keeping this in mind, we presented a simple model that treats the dynamics of a membrane under the action of actin polymerization forces that depend on the local density of freely diffusing activators on the membrane. We took into account the thermal density fluctuations and the spontaneous curvature associated with the activators and showed that, depending on the spontaneous membrane curvature associated with the activators, the resulting membrane motion can be wavelike, corresponding to membrane ruffling and actin waves, or unstable, indicating the tendency of filopodia to form. Thus, our simple model system managed to capture the wide range of complex dynamics observed at the leading edges of motile cells both qualitatively and quantitatively indicating that the essential physics had been retained. Our model not only provides detailed estimates of the morphology and dynamics of the membrane structures, but also provides quantitative explanations for a variety of related experimental observations. These include the puzzling increase in membrane microviscosity at the leading edge of migrating cells, the response of motile cells to shear flow and the temperature dependence of the membrane ruffle velocity among others. Thus, our model offers a simple framework with which to analyze and understand experimental data and make quantitative predictions to be tested by future experiments.

We should, however, keep in mind that cell motility involves many processes that we did not take into account in our model, such as adhesion, formation of stress fibers, and the action of molecular motors. Even within the context of our model, the dynamics of the actin-driven cell motility is largely assumed to be controlled by dynamics of proteins on the cell membrane, which fails to capture the link between the dynamics of these membrane proteins and the bulk dynamics of the actin gel, occurring behind the moving front (67). Integrating all these components into a holistic picture remains a challenge. We should therefore view our model as representing the physical dynamics of the membrane-actin system, which trigger the formation of patterns in the membrane morphology that are part of the overall motility mechanism. Our model therefore provides answers to one part of the overall problem of cell motility and should be useful for any integrated approach to cellular motility.