“De Novo” Design of Peptides with Specific Lipid-Binding Properties

Abstract

In this study, we describe an in silico method to design peptides that can be made of non-natural amino acids and elicit specific membrane-interacting properties. The originality of the method holds in the capacities developed to design peptides from any non-natural amino acids as easily as from natural ones, and to test the structure stability by an angular dynamics rather than the currently-used molecular dynamics. The goal of this study was to design a non-natural tilted peptide. Tilted peptides are short protein fragments able to destabilize lipid membranes and characterized by an asymmetric distribution of hydrophobic residues along their helix structure axis. The method is based on the random generation of peptides and their selection on three main criteria: mean hydrophobicity and the presence of at least one polar residue; tilted insertion at the level of the acyl chains of lipids of a membrane; and conformational stability in that hydrophobic phase. From 10,000,000 randomly-generated peptides, four met all the criteria. One was synthesized and tested for its lipid-destabilizing properties. Biophysical assays showed that the “de novo” peptide made of non-natural amino acids is helical either in solution or into lipids as tested by Fourier transform infrared spectroscopy and is able to induce liposome fusion. These results are in agreement with the calculations and validate the theoretical approach.

INTRODUCTION

Designed peptides have been used in the last decade to improve our understanding in the structure/function relationship of proteins. This design approach notably helps us to understand the structural determinants of folds, such as those of β-sheets (1). The current methods use statistical analysis of protein-structure databank and empirical information (2–4). Rotamer analysis can also be performed to check the compatibility of side-chain packing.

Modified or non-natural amino acids are notably used to study the folding, the conformational stability, and the flexibility of peptides and proteins (5–9). Non-natural amino acids can be more resistant to protease degradation and have a decreased immunogenicity (10).

Model peptides can also be used to explore features responsible for the association of hydrophobic peptides derived from a water-soluble coiled-coil structure in membrane (11). In the same way, designed pore-forming peptides are useful models to enable us to better understand the insertion of proteins in biomembranes (12).

Peptides with antitumoral or antibacterial activity were also designed to investigate structural parameters of their lytic activity and selectivity, notably their membrane specificity (13,14).

In these cases, design of peptides with improved activity and/or selectivity might be helpful for biological and therapeutic uses.

In this study, we describe an original in silico method to design peptides with desired features, notably with specific membrane-interacting properties. We applied this method to the design of tilted peptides. The latter are short protein fragments able to destabilize membranes (15). When tilted peptides are modeled as α-helices, an asymmetric distribution of hydrophobicity is responsible for an oblique orientation at a hydrophobic/hydrophilic interface, such as a membrane (16). Tilted peptides were notably found in viral fusion proteins where they are involved in the first steps of fusion between the host cell and the virus membrane (17). They were also detected in proteins involved in lipid metabolism, in signal sequences, in toxins, etc. (18). Many among the in silico detected peptides were experimentally confirmed. Most were shown to induce liposome fusion in vitro when taken as isolated fragments (19–24). Furthermore, when the peptides were mutated to modify the hydrophobicity distribution, fusogenic properties were significantly decreased. When the same mutations were introduced in the protein, its activity was modified (23,25). Neutron diffraction experiments showed that one structural conformer of the tilted peptide from the gp32 fusion protein of simian immunodeficiency virus (SIV) is oriented at an angle of 55° in a model membrane (26). In the same way, the NMR structures of the HA2 fusion peptide from the Influenza virus were shown to be obliquely oriented in model membranes at the active pH (27).

Comparison of tilted peptides demonstrated no sequence homology (28); the only characters they shared were their mean hydrophobicity (following the Eisenberg consensus scale (29)) between 0.2 and 0.9, an asymmetric hydrophobicity gradient when helical and an insertion angle of this helix into lipids between 30° and 60°.

In this article, we report a modeling approach for the rational design of hydrophobic peptides entirely made from non-natural amino acids. The goal was to make a tilted peptide, i.e., a short 12-residue fragment with a mean hydrophobicity between 0.6 and 0.7 and a lipid-insertion angle close to 45° due to the asymmetric distribution of hydrophobic residues. One predicted sequence has been synthesized and experimentally tested for its lipid-destabilizing capacities.

MATERIALS AND METHODS

Molecular modeling materials

Egg phosphatidylcholine (PC), phosphatidylinositol (PI), phosphatidylserine (PS), cholesterol (CHOL), and sphingomyelin (SM) were purchased from Sigma (St. Louis, MO). Egg phosphatidylethanolamine (PE) is from Lipid Products (Redhill, Surrey). Octadecyl rhodamine chloride (R18) is from Molecular Probes (Eugene, OR).

The peptides were obtained from Neosystem (Strasbourg, France). They were 85% pure.

Molecular modeling methods

Orientation at the lipid-water interface (TAMMO orientation)

Each molecule structure is oriented with respect to the spatial distribution of its hydrophobicity. The line joining the hydrophilic and hydrophobic centers is set to be perpendicular to the hydrophobicity interface (30). The hydrophobic center (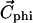) is defined by the equation

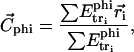(1)

in which the 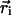values are the coordinates of the i^th atom, and E_tr(i) its transfer energy per unit of accessible surface. The hydrophobic center located in the hydrocarbon domain (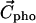) is defined by the same equation, except that the negative transfer energies are taken into account. The interface position (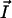) is defined by

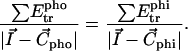(2)

Membrane insertion

We inserted peptides into an implicit bilayer integral membrane protein and lipid association (IMPALA) developed by Ducarme et al. (31). It simulates the insertion of any molecule (protein, peptide, or drug) into a bilayer by adding energy restraint functions to the usual energy description of molecules (32,33).

The lipid bilayer is defined by C_(z), which represents an empirical function describing membrane properties. This function is constant in the membrane plane (x- and y-axes) but varies along the bilayer thickness (z-axis) and more specifically, at the lipid/water interface corresponding to the transition between lipid acyl chains (no water = hydrophobic core) and the hydrophilic aqueous environment,

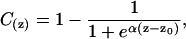(3)

where α is a constant equal to 1.99, z₀ corresponds to the middle of polar heads, and z is the position in the membrane. This function can be different for each layer according to the asymmetric composition of the membrane.

Two restraints simulate the membrane—one the bilayer hydrophobicity (E_pho), and the other, the lipid perturbation (E_lip).

The hydrophobicity of the membrane is simulated by E_pho,

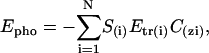(4)

where N is the total number of atoms, S_(i) the accessible surface to solvent of the i atom, E_tr(i) its transfer energy per unit of accessible surface area, and C_(z) the _zi position of atom i.

The perturbation of the bilayer by insertion of the molecule is simulated by the lipid perturbation restraint (E_lip),

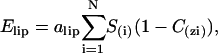(5)

where a_lip is an empirical factor fixed at 0.018 kcal.mol⁻¹ Å⁻².

The environment energy (E_env) applied on the peptide that inserts into the membrane becomes equal to

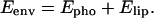(6)

Systematic analysis

A systematic procedure is performed to insert and orient the peptide into the membrane. During this process, the peptide systematically crosses the force field of the membrane from −40 to +40 Å with respect to the membrane center by steps of 1 Å. For each position along the z axis, 2000 random orientations are tested. Among these 2,000 positions, the minimal energy position is selected. At the end of the systematic analysis, the procedure selects the position and the orientation of minimum energy among all selected minima.

Angular dynamics optimization

To analyze structural variations of the peptide inserted in the membrane, we have used the angular dynamics procedure previously defined to simulate the protein folding (34).

In the simulations, the total energy (E_tot) is the sum of the intramolecular energy of the peptide (E_intra) and of the energy due to the membrane environment (E_env). E_tot is distributed at each step of the calculation on the peptide torsion k-axis as E(k). This total energy is equal to

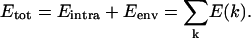(7)

The intramolecular energy E_intra is composed by E_vdw, the Van der Waals energy that represents the interaction of the electronic cloud of the atoms, and is described by the Levitt's equation (35)

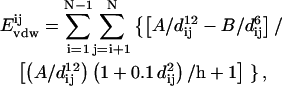(8)

where A and B are specific parameters for each atom pair and d_ij is the distance between the two nonbonded atoms i and j. The second bracket term makes the atoms soft and the parameter h is taken as 1,000 kcal/mol.

E_elec, the electrostatic energy is given by the classical Coulomb's law that takes into account the point-charge of the atoms (q_i and q_j), the dielectric constant, and the distance (d_ij) between atoms i and j,

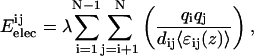(9)

where λ is the electronic density unit conversion factor and 〈ɛ_ij(z)〉 is the dielectric constant, a sigmoid function of the distance between atoms in interaction.

E_{pho_in} is the intramolecular hydrophobic energy,

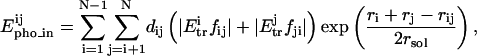(10)

where E_tr is the free energy transfer of the atoms i and j; f_ij and f_ji are the factors of atomic recovery by atom i on atom j, and conversely; r_i and r_j the Van der Waals radius of the atoms i and j; r_sol the radius of water molecule; d_ij the distance between atoms i and j; δ_ij = −1 if atoms are from the same type (hydrophobic or hydrophilic), and δ_ij = +1 if atoms are from opposite type (hydrophobic and hydrophilic).

The energy of each axis ((ΣE(k)) is supplemented by its own torsion energy (E(k)_tor),

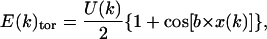(11)

where U(k) corresponds to the energy barrier in the eclipsed conformation during the rotation of the k angle, b is the periodicity of the function, and ξ(k) is the value of the torsion k angle. U(k) is equal to 48.95 kcal/mol for the C-C bond and 31.38 kcal/mol for the C-O bond.

The total energy associated with each torsion axis (E(k)) is therefore represented by the sum of 1), the torsion energy of the k axis (E(k)_tor); 2), the intramolecular interaction energies between atoms i and j, divided by the number of axes between these atoms; and 3), the energy in the membrane for the atoms i and j divided by the number of atoms of the system minus 1 (N−1) and by the number of axes between atoms i and j,

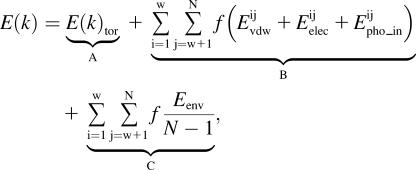, (12)

with f = 1/number of axes between i and j.

The energy E(k) allows us to calculate an angular dynamics that gives rise to an acceleration of torsion axes.

During the dynamics, the length of atomic bonds and the value of valence angles are kept constant; only the torsion angles are modified. The angular acceleration of each torsion axis is determined following Newton's equation,

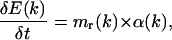(13)

where α(k) is the angular acceleration of the angle k and m_r(k) is the reduced mass calculated from the mass of the atoms on both sides of the torsion axis k,

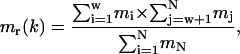(14)

where m_i, m_j are the mass of the atoms before and after the torsion axis except the atoms defining the axis, and m_N is the total mass of the molecule.

Knowing the angular acceleration of the torsion axes, the t+1 position of each torsion axis (ξ(k)^theo) can be determined following the equation derived by Verlet (36),

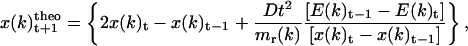(15)

where ξ(k) is the value of the torsion angle k.

At each step, E(k)_t is the energy associated to an angle k at t time and is given by Eq. 12.

During the angular dynamics, the rotation velocity v_r(k), expressed as a function of Δt is calculated according to

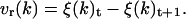(16)

In Eqs. 15 and 16, Δt = 1.

The rotation velocity v_r(k) used in our calculations is limited to 0.075°/step. It is an arbitrary empirical value that seems to be sufficient for a rapid molecule movement and slow enough to prevent molecule burst. During all the calculation, the movement quantity (Q) was kept constant,

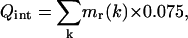(17)

with Q_int representing the initial quantity of movement.

As the velocity changes at time t+1 the theoretical movement quantity becomes Q_t+1,

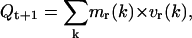(18)

where the rotational velocity (v(k)) becomes v_r*(k) to maintain the Q_int constant. This is achieved via a correcting factor f (with f = Q_int/Q_t+1),

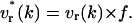(19)

This velocity variation of k is used to give the new value of ξ(k) at time t+1,

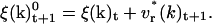(20)

A small random component (md(k)) is added to ξ(k). The final value of ξ(k)_t+1 is

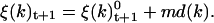(21)

This random parameter md(k) is introduced to mimic the thermal motion of the system and to enable us to bypass energy barriers during the simulations. It represents one-tenth to one-third of the initial rotation velocity.

A t = 0, the position and orientation of the peptide in the membrane are those determined from the IMPALA systematic analysis (see above). From there, an angular dynamics is performed on the peptide taking into account the mean force field of the membrane. Random rotations of 1° max and random translations of 0.1 Å max of the peptide are allowed.

Experimental materials

Calculations are performed on an Intel Pentium 4, 3.80-GHz CPU, with 4.00 Gb of RAM.

Pex2dstats files (37) are generated during the simulations and used for the analysis of each peptide. The mean gain ratio of angular versus molecular dynamics was calibrated to 1/100–1/1000 the number of calculation steps when only side chains or side chains plus backbone movements were calculated.

Experimental methods

Liposome preparation

Large unilamellar vesicles (LUV) were prepared by the extrusion technique (38) using an extruder (Lipex Biomembranes, Vancouver, Canada). In brief, dry lipid films which are mixtures in weight of 30% phosphatidylcholine (PC), 30% phosphatidylethanolamine (PE), 2.5% phosphatidylinositol (PI), 10% phosphatidylserine (PS), 5% sphingomyelin (SM), and 22.5% cholesterol were hydrated for 1 h at 37°C. The resulting suspension was submitted to five successive cycles of freezing and thawing and thereafter extruded 10 times through two stacked polycarbonate filters (pore size 0.08 μm) under a nitrogen pressure of 20 bars.

The final concentration of liposomes was determined by phosphorus analysis (39).

Lipid-mixing experiments

Mixing of liposome membranes was followed by measuring the fluorescence increase of R18, a lipid soluble probe, occurring after the fusion of labeled and unlabeled liposomes, as described (40). Labeled liposomes were obtained by incorporating R18 in the dry lipid film at a concentration 6.3% of the total lipid weight. Labeled and unlabeled liposomes were mixed at a weight ratio 1:4 and a final concentration of 50 μM in 10 mM Tris, 150 mM NaCl, 0.01% EDTA, and 1 mM NaN₃, pH 8. Fluorescence was recorded at room temperature (λ_exc, 560 nm; λ_em, 590 nm) on an LS-50B Perkin-Elmer fluorimeter (Boston, MA).

Leakage of liposome vesicle contents

The 8-hydroxypyrene-1,3,6-trisulfonic acid (HPTS)/p-xylylenebis[pyridinium] bromide (DPX) assay of Ellens et al. (41) was used to monitor vesicle leakage. The assay is based on the quenching of HPTS by DPX. HPTS and DPX are both encapsulated in the aqueous phase of the same liposomes. Leakage of vesicles was followed by measuring the dequenching of HPTS released into the medium. Fluorescence was recorded at room temperature (λ_exc, 360 nm; λ_em, 520 nm) on a LS-50B Perkin-Elmer fluorimeter.

Core-mixing experiments

The mixing of liposome contents was monitored using the core-mixing assay of Kendall and McDonald (42). Liposomes (LUV) were prepared as described above in 10 mM Tris-HCl buffer, 150 mM NaCl, and 1 mM NaN₃, pH 8.0 and containing calcein at 0.8 mM and CoCl₂ at 1.0 mM or EDTA at 20 mM. Untrapped solutes were removed by one elution on a Sephadex G-75 column (Sigma-Aldrich) with 10 mM Tris-HCl, 150 mM NaCl, and 1 mM NaN₃ buffer, pH 8.0. In a standard experiment, calcein, Co²⁺- and EDTA-containing vesicles were mixed at 1:1 molar ratio in a 10 mM Tris-HCl buffer, pH 8.0 (150 mM NaCl, 1 mM NaN₃). When peptides were added, the calcein fluorescence was monitored at room temperature (λ_exc, 490 nm; λ_em, 520 nm) as a function of time on a LS-50B Perkin-Elmer fluorimeter. Co²⁺ (0.4 mM in chelation with citrate at 1:1 mol/mol) was present in the medium to avoid fluorescence due to leakage of vesicle contents. The maximum fluorescence was determined in presence of Triton X-100, 0.5% (10 mM EDTA).

Infrared spectroscopy Fourier-transform infrared (FTIR) measurements

Attenuated total reflection (ATR) infrared spectroscopy was used to determine the secondary structure of the peptides alone and bound to lipids.

Spectra were recorded at room temperature on a Bruker Equinox 55 (Bruker AXS, Karlsruhe, Germany) equipped with a liquid nitrogen-cooled Mercury-Cadmium-Telluride detector at a resolution of 2 cm⁻¹, by averaging 512 scans. Free peptide samples (20 μg peptide) dissolved in TFE and the lipid-bound peptides (see preparation below) were spread out on a germanium ATR plate (50 × 20 × 2 mm—Aldrich Chimica, Milan, Italy—with an aperture of 45° yielding 25 internal reflections) and slowly dried under a stream of N₂. Reference spectra of a Germanium plate were automatically recorded after purge for 15 min with dry air and subtracted to the recently run sample spectra. The plate was sealed in an universal sample holder and hydrated by flushing the holder with N₂ saturated with D₂O for 3 h at room temperature.

Peptide/lipid sample preparation

A dried mixed film made of 20 μg peptide and 100 μg lipids (PC/PE 2:1 w/w) was hydrated with 100 μl of a 10 mM Tris, 150 mM NaCl, pH 8 buffer.

Phospholipid concentration was determined as mentioned above.

Secondary structure determination

Vibrational bands, especially the amide I band (1600–1700 cm⁻¹), are sensitive to the secondary structures of proteins. The C=O vibration is representative of 80% of the amide I band. This band accounts for all secondary structures which have different vibration values. The combination of resolution-enhancement methods with curve-fitting procedures allow us to assign quantitatively different secondary structures such as α-helix, β-sheets, and unordered structures. Each band was assigned according to the frequency of its maximum. The areas of all bands assigned to a given secondary structure were then summed and divided by the sum of all areas. This gives the relative ratio of each secondary structure. The bands are assigned as follows: α-helix, 1662–1645 cm⁻¹; β-sheets, 1689–1682 cm⁻¹ and 1637–1613 cm⁻¹; random, 1644.5–1637 cm⁻¹; and β-turns, 1682–1662 cm⁻¹. It should be noted that the proteins spread on the plate are deuterated to avoid an overlap of α-helix and random-coil structures, as previously described (43,44).

RESULTS

Single-letter and three-letter codes were assigned to the 14 non-natural amino acids that we used throughout the study (Table 1). These amino acids, which are commercially available, are called modified or non-natural because they have the same backbone as the 20 residues found in eukaryotic proteins but have different side chains. None of the selected amino acids contains a halogen or a potentially toxic atom.

TABLE 1.

Characteristics of the 20 classical amino acids and the modified amino acids used in this study

	One-letter symbols	Three-letter symbols	Atomic or molecule Etr (Kcal/mol)	〈H〉
Atoms
Csp2			−1.50
Csp3			−2.44
H (q=0)			−0.54
H (q/0)			1.03
O			2.83
S			−2.75
N			3.04
Natural AA
Glycine	G	Gly	7.93	0.48
Alanine	A	Ala	5.52	0.62
Valine	V	Val	1.99	1.10
Leucine	L	Leu	1.02	1.10
Methionine	M	Met	0.25	0.64
Isoleucine	I	Ile	0.91	1.40
Serine	S	Ser	11.33	−0.18
Threonine	T	Thr	8.40	−0.05
Cysteine	C	Cys	2.48	0.29
Proline	P	Pro	1.96	0.12
Asparagine	N	Asn	14.48	−0.78
Glutamine	Q	Glu	15.68	−0.85
Aspartic acid	D	Asp	14.70	−0.90
Glutamic acid	E	Glu	15.15	−0.74
Lysine	K	Lys	9.38	−1.50
Arginine	R	Arg	17.31	−2.50
Histidine	H	His	11.28	−0.40
Phenylalanine	F	Phe	−1.36	1.20
Tyrosine	Y	Tyr	5.97	0.26
Tryptophan	W	Trp	1.06	0.81
Non-natural AA
Ethanine	2	Eth	2.60	0.67
Norvaline	3	Nov	1.35	0.85
Norleucine	4	Nol	−1.68	1.28
Teurleucine	5	Ter	−0.75	1.15
Allylglycine	6	Aly	0.76	0.93
(Cyclo)hexalanine	7	Cha	−3.94	1.60
(Cyclo)hexethanine	8	Che	−5.16	1.78
Phenylethaline	9	Fet	−3.94	1.60
Naphtylalanine	B	Nap	−5.33	1.80
Methylphenylalanine	J	Mfa	−4.11	1.63
Ornithine	O	Orn	8.59	−0.18
Citrulline	U	Cit	14.10	−0.97
Parapyridine	X	Pap	3.13	0.60
Metapyridine	Z	Mep	2.38	0.70

Calculated E_tr of atoms and of natural amino acids are from Brasseur (45). The value 〈H〉 is the Eisenberg's mean hydrophobicity of the 20 classical amino acids derived from Eisenberg et al. (29). The non-natural amino acid E_tr are calculated from the atomic transfer energy and the solvent-accessible atoms of the HyperChem energy-minimized structures using the Shrake and Rupley's algorithm (51).

The structures of the 14 selected amino acids were modeled using HyperChem 5.0 (Hypercube, Gainesville, FL), starting from the backbone of alanine and optimized by the Polak-Ribiere algorithm using an AMBER force field with a gradient δ inferior to 0.1 kcal/(Å mol).

The peptide length is fixed to 12 residues. All positions can be taken by any of the 14 non-natural residues, allowing 14¹² possible sequences. Due to time constraints, we reduced the number of sequences to 10,000,000, randomly generated. Three independent runs of 10,000,000 peptides have been performed. The results from a single run were selected for presentation in this article; the two others gave similar results.

Calculation of non-natural amino acid hydrophobicity

One parameter of selection is the mean peptide hydrophobicity. This value is obtained from individual residue hydrophobicity, which is unknown for the non-natural residues.

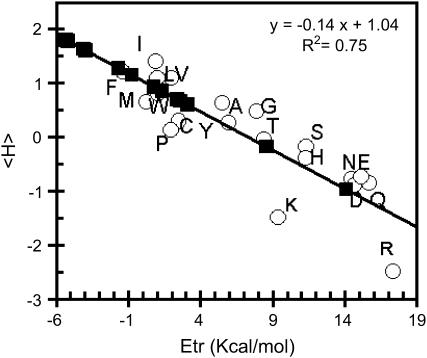
For current amino acids, we use the hydrophobicity scale of Eisenberg (29). For non-natural amino acids, we developed a method for estimating an Eisenberg-like hydrophobicity value. Hydrophobicity values are usually obtained from experimental measurements of the transfer energy (E_tr) of molecules from water to an organic phase such as octanol. Molecular transfer energy can also be calculated from atomic E_tr (Table 1) and the solvent-accessible surface of atoms in the molecule three-dimensional structures as previously described (45). Both Eisenberg's amino-acid hydrophobicity values and Brasseur's calculated E_tr values are linearly correlated with a regression coefficient of 0.75 (Fig. 1). A 75% correlation was here estimated as sufficient since hydrophobicity was used as a filter for selection. Hence from the calculated three-dimensional structures and the atomic E_tr scales, the E_tr of non-natural amino acids were calculated. The Eisenberg hydrophobicity values were then extrapolated using the linear correlation (Fig. 1). Table 1 provides all Brasseur-calculated E_tr and Eisenberg's consensus hydrophobicity values for the 20 natural amino acids and for the 14 non-natural amino acids. Hydrophobicity values of non-natural amino acids are often a bit lower or higher than those of natural amino acids. Amino acids of similar structures, such as (cyclo)hexalanine and (cyclo)hexetamine, or phenylethanine and methylphenylalanine, have very close values. For residues with increasing numbers of carbons in the lateral chain, i.e., ethanine, norvaline, allylglycine, terleucine, and norleucine, the increase in hydrophobicity values goes with the increase in the number of carbons, as expected for organic compounds (46). Two non-natural amino acids have a negative hydrophobicity: orthinine and citrulline; both are charged. Their hydrophobicity values are close to those of charged and polar natural amino acids, aspartic acid, asparagine, glutamic acid, and glutamine.

FIGURE 1.

Linear correlation between Eisenberg's mean hydrophobicity values of natural amino acids and Brasseur's calculated E_tr of those molecules (open circles). The linear regression coefficient (R²) is indicated; amino acids are named by their one-letter code. The calculated E_tr values of the 14 non-natural amino acids are also plotted (solid squares).

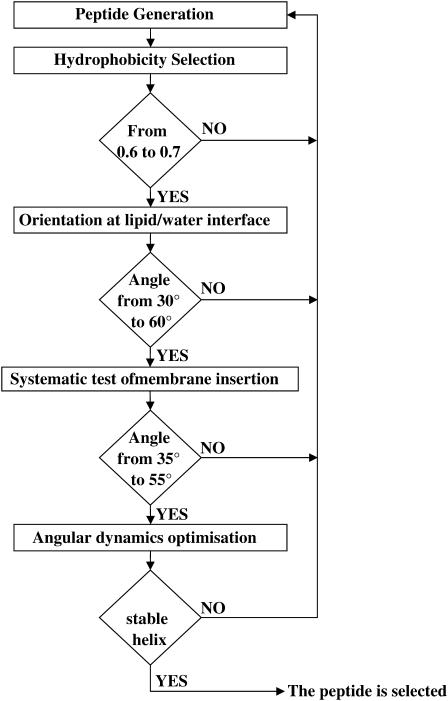
Peptide selection

The peptide selection process is based on several steps corresponding to specific criteria (Fig. 2). The first criterion is the mean hydrophobicity of the peptide. The value is calculated using the scale described above (Table 1). Sequences are kept when the mean peptide hydrophobicity is between 0.6 and 0.7 kcal/residue. This range was previously shown to correspond to tilted peptides interacting with lipids (28).

FIGURE 2.

Schematic representation of the different selection steps in the de novo generation of tilted peptides.

Sequences fulfilling this criterion were then three-dimensionally constructed as an α-helix. The distribution of hydrophobicity with respect to the helix axis was calculated by taking into account the geographic centers of hydrophobic and hydrophilic atoms. The angle between the helix axis and the molecule hydrophobicity interface of each helix structure was calculated; only those with angles between 30° and 60° were selected.

In the third step, a systematic IMPALA screening investigated the helical peptide insertion into a membrane. The optimal orientation of each helix in membrane was calculated and peptides presenting an orientation between 35° and 55° were kept. At that step a complementary criterion was introduced, which is that the position of the helix mass center had to be between 8 and 13 Å with respect to the bilayer center, i.e., near the phospholipid (PL) acyl-chain/headgroup interface. This restraint was set to choose peptides able to disturb the PL acyl-chain organization, the first step thought to induce fusion processes (16). The peptides matching the different criteria were then optimized at the interface by an angular dynamics, to analyze their conformational stability. The whole strategy is illustrated in Fig. 2.

From 10,000,000 sequences tested, a quantity of 9,109,270 were rejected by taking into account the mean sequence hydrophobicity value. Among the remaining number, 822,337 were rejected by taking into account the peptide interface orientation, and another 67,196 were rejected after the IMPALA screening, taking into account the angle and the depth of insertion. At that step, 1197 sequences were retained. To further decrease the number of candidates, one criterion was added: the peptide had to include one hydrophilic residue, i.e., citrulline or ornithine. Only 12 peptides fitted that last criterion. The angular dynamics demonstrated that four of them were conformationally stable. They correspond to sequences number 48,482; 51,208; 88,682; and 97,848 (Table 2).

TABLE 2.

Non-natural peptides fitting the criteria indicated below

Peptide number	Sequence	Insertion angle (°)	Mean hydrophobicity
22,319	U 5 U 9 4 O O 4 B 2 6 4	55	0.64
31,272	U B J 9 U 7 O U O J J 3	53	0.62
33,687	O O 2 Z 4 Z 3 O 6 5 9 X	26	0.66
48,482	O J 6 9 O 3 U 2 8 9 9 U	48	0.70
50,249	U 9 U 8 X 3 O 8 4 8 U 7	55	0.682
51,208	O U 7 8 Z X O 9 3 9 J U	35	0.67
52,230	O 3 8 O O B O 2 2 4 4 Z	52	0.69
56,571	U Z 6 J 8 5 X 7 U O X X	48	0.62
88,682	O 7 8 O 7 O 9 6 2 U Z 2	50	0.67
97,848	U 9 6 B O 9 O 6 X U 7 4	48	0.67
98,807	U O 8 7 6 O U 7 X J Z 9	53	0.68
99,721	U O 5 7 O 5 U 2 7 J 7 4	55	0.70

Mean hydrophobicity between 0.6 and 0.7, insertion angle between 35 and 55° and mass center located between 8 and 13 Å (absolute value) from the bilayer center in the IMPALA membrane, containing one ornithine or citrulline. The bold peptides are conformationally stable during angular dynamics. The boxed peptide was used in the experimental part of the study.

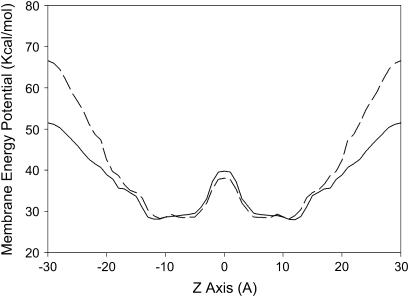
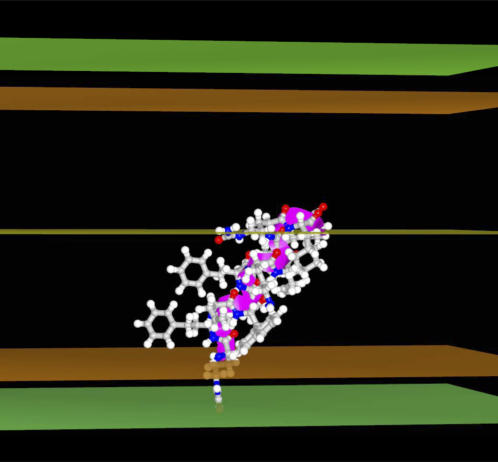
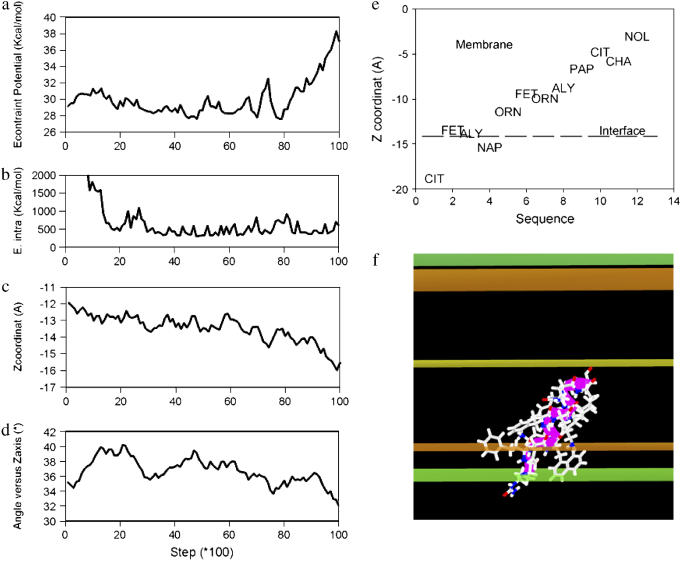
The energy minima profiles of peptide 97,484 insertion in the model membrane IMPALA (Fig. 3) demonstrates that both the pre- and post-angular dynamics structures maximally insert in a similar way—with their center of mass between 5 and 13 Å from the membrane center (i.e., at the level of phospholipid headgroup/acyl-chain interface)—and have a low energy barrier to cross the membrane. This suggests that the latter structures might have access to a wide range of membrane levels. If the angular dynamics has had little consequence on the 97,484 backbone structure supporting our conclusion of helical stability, it modified the side-chain orientation and the final structure was even more penalized in water (IMPALA energy values at z over ±20 Å) than the pre-optimized structure. This is illustrated in Fig. 3. It is also seen while comparing the best configurations in membrane for the pre- and post-angular dynamics structures (Fig. 5 as compared to Fig. 6 f) and also accounts for the increase of the IMPALA energy when the peptide is sliding toward the membrane surface after 8000 steps of dynamics (Fig. 6, a and c). After angular dynamics, side chains of naphtylalanine and phenylethaline are bent toward the phospholipid polar head interface and the citrulline polar side chain is partly protruding out of the membrane (Fig. 6, e and f).

FIGURE 3.

Best position of peptide 97,848 in the IMPALA membrane before the angular dynamics. Midplane, bilayer center (z = 0); first upper (beneath) plane; lipid acyl chain/polar headgroups interface at 13.5 Å from the center; and second upper (beneath) plane, lipid/water interface (z = 18 Å).

FIGURE 5.

Profile of the minimal IMPALA energy values (in kcal/mol) versus the mass center position (Å) of the 97,848 peptide after a systematic screening of peptide membrane traverse. Peptide 97,848 before the angular dynamics (solid line); and peptide 97,848 after the angular dynamics (dotted line).

FIGURE 6.

Angular dynamics course of peptide 97,848 in IMPALA membrane. The total number of steps is 10,000. (a) Evolution of IMPALA restraint energy (kcal/mol). (b) Evolution of peptide intramolecular energy. (c) Evolution of the peptide mass center position. (d) Evolution of the helix axis insertion angle (°). (e) Membrane position of peptide 97,848 residues in the most stable configuration of the angular dynamics simulation. The dotted line (interface) indicates where the water concentration is equal to 0.5. (f) The stick view of the most stable conformation of the angular dynamics simulation. This view is made in conditions similar to those shown in Fig. 5.

Those results suggest that the peptide 97,848 is stable in the membrane, and can move from the lipid polar head to the acyl-chain domain in that membrane. This mode of insertion generates conditions where lipid perturbation may occur and be responsible for a membrane fusion process. Peptide 97,848 was synthesized and experimentally tested for fusogenic activity and conformational analysis.

Biophysical assays

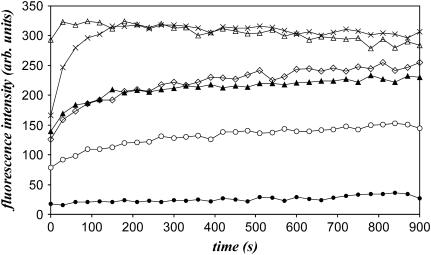
Lipid fusion (lipid and core mixing) and leakage assays were carried out. The SIV fusogenic peptide was used as a positive control, since its lipid-destabilizing properties are well known (20). The induction of vesicular lipid mixing by the different peptides is tested with PC/PE/SM/PI/PS/Chol LUVs. The R18-labeled and R18-free liposomes were mixed and the time-course increase of fluorescence intensity due to the dequenching of the probe was measured to follow-up lipid fusion. Fig. 4 clearly shows that the peptide 97,848 induces lipid mixing. The process is dose-dependent. The fusogenic activity of the peptide is further assessed by core mixing experiments (Table 3). Leakage assays confirmed the lipid-destabilizing properties of the peptide, as shown in Table 3. The process was also dependent on the peptide concentration. In three independent experiments, the 97,848 peptide appeared slightly but constantly more potent than the SIV peptide.

FIGURE 4.

Time course of lipid mixing of liposomes (LUV) induced by peptide 97,848. The peptide is added at different concentrations (from 30 μM to 600 μM corresponding to peptide to lipid molar ratio from 1:50 to 2:5) to a mixture (1:4 w/w ratio) of R18-labeled and unlabeled LUVs. Increase of the R18 relative fluorescence due to probe dilution is followed at room temperature. The SIV tilted peptide at 150 μM is used as positive control, the addition of TFE (1.6% final concentration) as negative control. TFE (blank), •; and SIV peptide at 150 μM (positive control), ⋄. Addition of peptide 97,848 at 30 μM (P/L molar ratio, 1:50), ○; 60 μM (P/L ratio 1:25), ▴; 150 μM (P/L ratio 1:10), ×; and 300 μM (P/L ratio 1:5), Δ.

TABLE 3.

Leakage of liposome contents (LUV) and core-mixing assays in the presence of increasing amounts of peptide 97,848 after 15-min incubation

Peptide concentration	TFE (blank)	SIV 150 μM	30 μM	60 μM	150 μM	300 μM
% leakage	0	60	38	44	67	83
% core-mixing	0	35	20	26	43	67

100% is established by lysing liposome vesicles with Triton X-100, 0.5% (EDTA, 10 mM). The SIV peptide is used as a positive control.

The conformation of the peptide alone and in the presence of lipids was analyzed by attenuated total reflection FTIR spectroscopy (Table 4). The peptide is mainly helical in both conditions, in agreement with our calculations. It should be noted that the purity of the peptide is 85%.

TABLE 4.

Conformation of peptide 97,848 (85% pure) alone and in presence of lipids (PC/PE 2:1 w/w) as determined by attenuated total reflection FTIR spectroscopy

	α-helix	β-sheet	β-turn	Random coil
Peptide 97,848 alone	52 ± 4%	23 ± 3%	14 ± 2%	11 ± 3%
Peptide 97,848 + lipids	60 ± 5%	21 ± 4%	9 ± 3%	9 ± 2%

The values are means ± SE from three independent experiments.

DISCUSSION

Automatic design of peptides is little described in the literature. Some computer programs, such as LUDI,were set to design protein ligands, from organic compounds to peptidomimetics (3). It was shown on inhibitors of HIV-1 protease that this algorithm essentially helps in the initial steps of the design procedure (47). Other procedures, such as DESIGNER, use a structure template, a rotamer library, and an empirical force field; this was notably applied to MHC class I binding peptides (2). Very recently, Decaffmeyer et al. (48) developed an in silico approach, called Pep Design, to design complementary peptides. The assay was used to design a partner to the C-terminal fusion domain of the Aβ peptide involved in the Alzheimer's disease. The peptide was made from natural amino acids. The leading idea was derived from the observation that the lipid-binding domain (and more specifically the C-terminal helix) of apolipoprotein E (apoE) is able to decrease the destabilizing properties of the Aβ peptide (49,50). The “de novo” peptide, derived from the apoE C-terminal helix is able to interact with the C-terminal fusogenic domain of Aβ peptide and to decrease its lipid-destabilizing properties with a higher efficiency than the apoE wild-type peptide.

In this study, we aimed to design peptides made of non-natural amino acids and eliciting peculiar lipid-interacting properties mimicking those of lipid-destabilizing tilted peptides. The in silico selection was based on several criteria common to tilted peptides (16,28). Tilted peptides are able to interact with and insert obliquely within a lipid bilayer. This behavior is notably linked to their mean hydrophobicity value (the most efficient peptides being between 0.6 and 0.7 kcal/residue according to the hydrophobicity scale of Eisenberg). Tilted peptides also present an asymmetric distribution of hydrophobic residues when helical.

A de novo peptide (12 residues long) exclusively made of non-natural amino acids was developed. Fourteen commercially available non-natural amino acids were selected. They have a normal backbone configuration but modified lateral chains such as aliphatic chains with variable number of carbon atoms, double aromatic rings, etc.

Ten million sequences were randomly generated. Taking into account the mean peptide hydrophobicity, the helix orientation toward a membrane interface, the conformational stability of the structure in membrane, and the presence of a charged residue, only four peptides met the criteria; one was synthesized.

Biophysical assays on liposomes clearly showed that the peptide is fusogenic and destabilizes lipid vesicles with an efficacy slightly superior to the SIV tilted peptide, the paradigm in the domain. Peptide 97,848 is mainly helical in water solution and in lipids, in agreement with its stability during the angular dynamics.

The systematic test of the peptide insertion in IMPALA clearly demonstrates that the peptide's center of mass might easily fluctuate between ±13 Å and ±5 Å close to the phospholipid headgroups/acyl-chain interface. This suggest that the peptide has easy access to a wide range of membrane levels and the existence of such metastable positions was already suggested for other tilted peptides (28) and should contribute to their destabilizing capacity.

The stability of the peptide was investigated by 10,000 steps of angular dynamics. The main benefit of angular versus molecular dynamics lies in its efficacy to investigate large molecular movement within a reasonable delay (34). For instance, the angular dynamics procedure required 1/100 the number of calculation steps that the molecular dynamics needed to explore the same conformational space of rotamer movements. Investigation of large movement is facilitated by the use of the Levitt's modification of Lennard Jones equation for the Van der Waals energy term. Indeed, one major problem in dynamics studies is due to the fact that all movements are discrete steps, not soft continuous movement. Hence, if steps are very short, steric clashes can be avoided, but the equilibrium will be reached after very long computations. As soon as movements are larger, steric clashes and thus, Van de Waals energy bursts, create problems in the computation of energy minimization. This is why Levitt's modification of the Van der Waals energy, which limits the energy burst of a steric clash to a value, one that we fixed to 1,000 kcal in this case, is helpful. In other experiments, the value was set to range between 100 and 10,000 kcal, according to the size of the molecule. The goal is to leave room for a balancing effect of the other energy terms for the entire course of the dynamics. The angular dynamics is interesting, because the movement is distributed in the structure, and the rotation of a φ- or ψ-angle in the middle of the structure will have more structural consequences than the rotation of an equivalent axis on the N- or the C-side or than the rotation of χ-angles of side chain. Cooperative stability of folded domains is, by this way, clearly evidenced. In the hydrophobic domain of IMPALA membrane, the peptide 97,848 backbone remains stable; φ/ψ-values are little changed while side chains are moving, creating intramolecular steric contacts that disappear after 2,000 steps—supporting the conclusion that the structure has found a local energy minimum.

Those results suggest that the peptide is stable in the membrane and that its insertion might generate conditions where lipid perturbation can occur and lead to a fusion process.

From this study, we support the idea that peptides with specific lipid-interacting properties can be de novo-designed using bioinformatic tools. The experimental tests validate the approach since a de novo peptide was able to destabilize liposomes and to adopt a stable helical conformation. By enabling the easy use of modified residues, the methods described in this article should be widely interesting even at a therapeutic design point of view. Indeed, non-natural amino acids may be more resistant to protease degradation and present a more decreased immunogenicity than natural ones (10), and specific lipid binding capacities could be useful to target virosomes and liposomes to specific cell types.