Kinetics of Cardiac Thin-Filament Activation Probed by Fluorescence Polarization of Rhodamine-Labeled Troponin C in Skinned Guinea Pig Trabeculae

Abstract

A genetically engineered cardiac TnC mutant labeled at Cys-84 with tetramethylrhodamine-5-iodoacetamide dihydroiodide was passively exchanged for the endogenous form in skinned guinea pig trabeculae. The extent of exchange averaged nearly 70%, quantified by protein microarray of individual trabeculae. The uniformity of its distribution was verified by confocal microscopy. Fluorescence polarization, giving probe angle and its dispersion relative to the fiber long axis, was monitored simultaneously with isometric tension. Probe angle reflects underlying cTnC orientation. In steady-state experiments, rigor cross-bridges and Ca²⁺ with vanadate to inhibit cross-bridge formation produce a similar change in probe orientation as that observed with cycling cross-bridges (no Vi). Changes in probe angle were found at [Ca²⁺] well below those required to generate tension. Cross-bridges increased the Ca²⁺ dependence of angle change (cooperativity). Strong cross-bridge formation enhanced Ca²⁺ sensitivity and was required for full change in probe position. At submaximal [Ca²⁺], the thin filament regulatory system may act in a coordinated fashion, with the probe orientation of Ca²⁺-bound cTnC significantly affected by Ca²⁺ binding at neighboring regulatory units. The time course of the probe angle change and tension after photolytic release [Ca²⁺] by laser photolysis of NP-EGTA was Ca²⁺ sensitive and biphasic: a rapid component ∼10 times faster than that of tension and a slower rate similar to that of tension. The fast component likely represents steps closely associated with Ca²⁺ binding to site II of cTnC, whereas the slow component may arise from cross-bridge feedback. These results suggest that the thin filament activation rate does not limit the tension time course in cardiac muscle.

INTRODUCTION

In muscle, force production is generated from the cyclic interaction between the globular heads of myosin extending from the thick filament and actin, the major component of the thin filament. This process is driven by hydrolysis of ATP and is controlled by the regulatory proteins, troponin (Tn) and tropomyosin (Tm) on the thin filament. The position of Tm is structurally coupled to the occupancy of the N-terminal, Ca²⁺ binding sites on troponin C (TnC), one of three subunits of troponin that also includes troponin I (TnI) troponin T (TnT). An individual regulatory unit comprises one Tn and Tm and seven actin monomers.

Kinetic (1,2) and structural (3) studies of thin filament activation in skeletal muscle suggest that the regulatory protein complex exists in three states. At low intracellular [Ca²⁺] in striated muscle, Tn induces an “off” blocked or B-state, in which Tm is constrained to a position on the outer domain of actin that interferes with strong cross-bridge formation. Upon activation, Ca²⁺-TnC binding results in a closed or C-state in which Tm moves toward the groove between the actin strands of the thin filament, thereby exposing binding sites for myosin. A second and further Tm displacement, further toward the groove, is promoted by myosin binding. This additional shift is thought to be required for full thin filament activation and is called the myosin-induced, “on” open, or M-state.

To be consistent with an activation process in which both Ca²⁺- and myosin-induced movements are required, the C-state or the Ca²⁺ induced is thought to sterically inhibit the binding of cross-bridges, although to a lesser extent than in the absence of Ca²⁺, the B-state (4). Thus, based on these studies, cross-bridge binding is required for full thin filament activation even at saturating [Ca²⁺]. However, such biochemical studies are technically limited to assessing only a few myosin binding states. In muscle, the constraints imposed by the concentration and arrangement of the contractile proteins in the sarcomere lead to changes in cross-bridge kinetics, especially the duration of cross-bridge attachment. Also, the mismatched periodicities of the contractile filament helices force cross-bridges to exist with wide variations in strain. Both properties could significantly affect Ca²⁺ regulation. Thus studies probing the mechanism of thin filament activation in muscle fibers are essential.

In general, muscle fiber studies have focused on the relationship between [Ca²⁺] and tension. This relation in both skeletal and cardiac muscle is much steeper than expected if tension were simply proportional to Ca²⁺ binding. Studies using direct Ca²⁺ binding (5), fluorescent (6–9) or electron paramagnetic resonance probes on TnC (10), and indirect methods involving rapid length changes of contracting muscle have indicated that thin filament Ca²⁺ sensitivity is coupled to cross-bridge attachment in cardiac muscle but less so in skeletal muscle. Possible sources for this cooperative activation process include 1), coupling between Ca²⁺-binding sites on the thin filament (11), 2), cross-bridge induced enhanced Ca²⁺-affinity or more generally thin filament Ca²⁺ sensitivity (5–9), and 3), cross-bridge-induced direct or allosteric activation of a regulatory unit (12).

It is not clear how cooperative interactions among thin filament regulatory units and cross-bridges function to augment the activation state of the thin filament in cardiac muscle, nor is it clear if thin filament activation kinetics determine the tension time course at submaximal [Ca²⁺]. At lower [Ca²⁺], the time course could be dominated by the rate of cross-bridge feedback that enhances thin filament Ca²⁺ sensitivity and promotes further cross-bridge formation. Alternatively, the rate at which conformational change is communicated among Ca²⁺ binding sites may dominate the tension time course irrespective of cross-bridge kinetics. A previous study of the activation kinetics of skinned cardiac muscle using laser photolysis of caged NP-EGTA concluded that the thin filament activation state is in rapid equilibrium with [Ca²⁺] and thus the kinetics of cross-bridge formation set the time course for the tension rise in cardiac muscle (13). However this conclusion was reached without a direct measure of the thin filament activation state. Understanding thin filament activation at submaximal Ca²⁺ levels is especially relevant for cardiac muscle, which normally functions along the steep portion of the [Ca²⁺]-tension relationship, in the range where cooperative mechanisms are most pronounced.

To address these questions, we monitored changes in TnC structure in skinned cardiac trabeculae during activation by exchanging the endogenous form with a monocysteine mutant (cTnC-C35S) labeled with tetramethylrhodamine-5-iodoacetamide dihydroiodide (5′-TMRIA, single isomer) at the remaining cysteine, Cys-84. Previous studies using dichroism to monitor TnC structure in cardiac muscle have shown this probe to be sensitive to [Ca²⁺] and cross-bridges, whereas the same probe positioned at Cys-35 (cTnC-C84S) was insensitive to both [Ca²⁺] and cross-bridges (14). In this study, fluorescence polarization (FP) was used to assess changes in the underlying cTnC conformation by monitoring changes in probe orientation, analyzed as peak angle and dispersion (15,16). Changes in probe orientation could result from changes in cTnC structure alone or as a combination of local and interregulatory unit interactions. FP was monitored simultaneously with tension during steady-state Ca²⁺ activation in the absence and presence of vanadate (Vi) to inhibit strong cross-bridge binding and thereby distinguish the effects of Ca²⁺ binding alone from those induced by cross-bridges. Finally, laser photolysis of NP-EGTA was used to vary [Ca²⁺] and determine the Ca²⁺ dependence of the tension time course simultaneously with the underlying structural changes in cTnC.

METHODS

Troponin C expression, purification, and labeling

Described in Martyn et al. (14).

Tissue preparation

Triton skinned trabeculae from the guinea pig were prepared as described in Martin and Barsotti (17) and Martin et al. (13).

cTnC exchange into trabeculae

Following a method of exchanging whole Tn into skeletal muscle by Brenner et al. (18), we adopted “passive exchange” as an alternative to extraction-reconstitution for exchanging TnC into trabeculae. Groups of trabeculae were selected and trimmed for size, then transferred to an opaque 1.5 ml conical tube containing a small volume (∼50 μl) of relaxing solution and ∼2 mg/ml bovine serum albumin (BSA) to block nonspecific binding. An equal volume of labeled protein was introduced by gentle, repetitive pipetting, resulting in a relaxing solution of ∼2.5 mM MgATP and 0.5 mg/ml of labeled protein. The tissue was incubated 48 h at 4°C during which the vial was continuously, slowly agitated. The tissue was then returned to normal storing solution, containing 50% glycerol, pinned slightly taut in a Sylgard coated dish, as when prepared initially, and kept at −20°C for no more than 5 days.

Quantitation of cTnC exchange

Following a mechanical experiment, the trabecula was removed from the apparatus, cut from the attached T-clips, and incubated in 200 μl of 6 M guanidine hydrochloride, 25 mM NaHPO₄, pH 7.6, in a small vial at 70°C for 15 min. The tissue was then sonicated for 10 min and spun at 5000 × g for 5 min, after which the supernatant containing the TnC sample was transferred into a Microcon centrifugal filter (YM-3, 3000 molecular weight cutoff, Millipore, Billerica, MA) for dialysis into spotting buffer (100 mM NaCl₂, 0.02% Tween, 25 mM NaHPO₄, pH 7.6; 1% BSA to reduce nonspecific protein binding). The Microcon tube was spun at 14,000 × g for 1 h, after which 50–100 μl remained. The sample in the Microcon was diluted in 200 μl of spotting buffer and respun, and the cycle repeated four times, with a final volume of ∼100 μl.

Purified, rhodamine-labeled and unlabeled cTnC-C35S were used as references. To ensure that quantification occurred over a linear range of the assay, tissue homogenates and standards were successively diluted into spotting buffer in a 96 well plate. Dilution series from homogenates and standards were spotted in order of increasing concentration onto an eight-pad format nitrocellulose slide (5 mm × 5 mm, Fast Slides, Schleicher & Schuell Biosciences Inc., Keene, NH), using a Q array robot (MicroGrid II, BioRobotics, Genomic Solutions, Ann Arbor, MI) equipped with 150 μm solid pins that transferred ∼1 nl per spot (19). During spotting, 50% relative humidity was maintained in the instrument. The slides were scanned for rhodamine fluorescence to determine the amount of labeled Tn subunit then placed in a light-tight box at room temperature. Fig. 1 illustrates the scan of four pads of a slide onto which two cTnC standards and six trabecular homogenates were spotted at five dilutions each.

FIGURE 1.

Detection of rhodamine-labeled cTnC exchanged into chemically skinned trabeculae of the guinea pig. Dilution series from trabecular homogenates along with standards made from labeled and unlabeled cTnC-Cys-84 were spotted onto a nitrocellulose Fast Slide as described in Methods. The figure illustrates four pads of an eight-pad slide. Each sample was spotted in triplicate from left to right and in increasing concentration from bottom row to top row. The right three columns of panel A (std in the figure) are rhodamine-labeled cTnC standards. The right three columns of panel B (std) are unlabeled cTnC standards. The top row of each pad and the first three columns of panel B were spotted with buffer (b) to estimate background fluorescence. The slide was scanned for rhodamine fluorescence (shown here), and the fluorescence of the labeled Tn subunit in the homogenate was measured directly against known concentrations of labeled protein standard. The pads were then incubated with an antibody to cTnC followed by a Cy-5-conjugated secondary antibody and scanned for Cy-5 fluorescence (not shown), providing a measure of the total (labeled plus unlabeled) cTnC in the trabecular homogenates. The extent of passive exchange of labeled cTnC-Cys-84 into guinea pig skinned trabeculae was 0.67 ± 0.01 (mean ± SE, n = 14). Panels C and D duplicate the sample dilution series of panels A and B, demonstrating the repeatability of the spotting and scanning method within the same slide.

To estimate total cTnC, the dilution series were probed with a mouse monoclonal antibody to cTnC followed by a Cy-5-conjugated secondary goat polyclonal antibody (20,21) as follows. Twelve to sixteen hours after the scan for rhodamine fluorescence, the protein microarray samples were treated with blocking buffer (6% BSA, 100 mM NaCl₂, 0.02% Tween, 25 mM NaHPO₄, pH 7.6) for 2 h at 23°C then rinsed twice for 10 min in spotting buffer. The slides were then incubated for 4 h with mouse monoclonal antibodies to human cardiac TnC (primary antibodies) at a 500-fold dilution in spotting buffer, then washed in spotting buffer four times at 10 min each. The slides were then incubated in 1000-fold dilution of a Cy-5-conjugated goat anti-mouse IgG (secondary antibodies) for 1 h and washed four times in spotting buffer, then immediately scanned for Cy-5 fluorescence. All scanning was performed on a ScanArray 4000 (Perkin Elmer Life Sciences, Boston, MA) using the same settings for all slides. Primary and secondary antibodies were purchased from Abcam (Cambridge, MA).

Spot fluorescence intensity was quantified by ScanArray Express software (Perkin Elmer Life Sciences). A fixed circle was used to locate and quantify the fluorescence intensity of each spot and its surrounding background. Spot intensity was calculated as the mean intensity of the pixels located in the spot minus the mean pixel intensity in the background mask. The dilution series for rhodamine-labeled and unlabeled cTnC standards yielded a curve of spot intensity versus cTnC concentration. The “reference ratio” of rhodamine to Cy-5 spot intensity was averaged from each concentration that fell in the linear range of the intensity versus concentration relation for the labeled standard. The same ratio was calculated for the trabecular homogenates, then normalized to the reference ratio to determine the extent of cTnC exchange. There was no significant difference in the [cTnC] to Cy-5 intensity relationship between the unlabeled and rhodamine-labeled cTnC standards, indicating no significant effect of rhodamine on Cy-5 fluorescence. In addition, “spiking” trabecular homogenates with known amounts of labeled or unlabeled cTnC yielded results similar to those from samples of cTnC alone, indicating no significant effect on label fluorescence or cTnC antibody binding from constituents of tissue homogenates.

Confocal microscopy

The microscope comprised a BioRad (Hercules, CA) MRC1024/2P imaging system fitted to an Olympus IX70 inverted microscope with a Kr/Ar-ion laser source (488 and 568 nm excitation). Images were captured using 40× UApo and 60× PlanApo objectives. Specimens were mounted in a shallow circular chamber, fashioned onto a microscope coverslip, bathed in 250 μl of relaxing solution, covered with silicone oil.

Apparatus for tissue mechanics

The apparatus to be used in these studies is described in detail in Smith and Barsotti (22).

Fluorescence polarization

The optical components were arranged as by Allen et al. (15) and Bell et al. (23). Briefly, continuous excitation of wavelength 514.5 nm was supplied by argon ion laser (∼50 mW). The beam passed through a shutter, polarizing cube, Pockels cell, and then into the epifluorescence port of a Nikon Diaphot inverted microscope. In front of the dichroic mirror, a lens of 40 mm focal length focused the collimated beam to a point in front of the objective to increase the diameter of illumination at the sample plane. The Pockels cell modulated the polarization of the exciting light from an argon laser at 25 kHz between orientations parallel and perpendicular to the sample axis. Polarized fluorescence emission passed from the objective through a Glan-Thompson prism to be split into parallel and perpendicular polarized components detected by two photomultiplier tubes (PMT) (Model 9601B, Thorn EMI, Rockaway, NJ). Fluorescence signals were digitized together with tension by a Nicolet 420 oscilloscope (Madison, WI) and stored to floppy disk. Recorded fluorescence signals were decomposed by software into four intensities, _‖I_‖, _⊥I_‖, _‖I_⊥, and _⊥I_⊥ and corrected against calibration standards as described in Bell et al. (23). Polarization ratios were calculated as Q_‖ = (_‖I_‖ − _⊥I_‖)/(_‖I_‖ + _⊥I_‖) and Q_⊥ = (_⊥I_⊥ − _‖I_⊥)/(_⊥I_⊥ + _‖I_⊥) and numerically fitted to estimate a physically reasonable orientation distribution, a Gaussian with peak angle μ and dispersion σ (15). In some experiments, a second excitation path orthogonal to that described above was used to measure a third parameter, 〈P_2d〉 (23–25), which describes nanosecond-scale motion of the probe fluorescent dipole corresponding to wobble in a cone of semiangle, δ (16).

High-frequency fluctuations in the polarized fluorescence intensities due to photon noise were compounded when mathematically combined into polarization ratios, then further compounded when fitting the Q ratios with the Gaussian model. In steady-state experiments this was improved by first averaging the intensities over many data samples taken in rapid succession, then calculating Q ratios from the averaged intensities. In time-resolved experiments, however, averaging or filtering the PMT output to “clean up” the Q ratios and calculated angles could unduly affect the temporal resolution of these parameters. According to the expressions for fluorescence provided by Irving (26), if probe angle and Gaussian dispersion change with an exponential time course, then the intensities will reflect the same exponential rate processes but with different amplitudes. We therefore adopted the approach of simultaneously fitting multiple decaying exponentials to the four time-resolved fluorescence intensities, with independent amplitudes but the same rate constants for each. The fitted exponentials were then used in subsequent calculations of time-resolved data. This approach was validated by simulating time-resolved angle data from which fluorescence intensities were calculated, then onto which random noise was superimposed. When these simulated intensities were subjected to the exponential fitting and subsequent analysis, the resulting angle data reliably reproduced the original simulation.

Solutions

Unless otherwise stated, all solutions contained 100 mM N-tris-(hydroxymethyl) methyl-2-aminoethanesulfonic acid (TES) (pH 7.1), 5 mM MgATP, 1 mM free Mg²⁺, 10 mM creatine phosphate, 1 mg/ml (∼250 units/ml) creatine kinase, and the ionic strength adjusted to 200 mM using 1,6-Diaminohexane-N,N,N′,N′-tetraacetic acid (HDTA, Aldrich Chemical Co., Milwaukee, WI). Nitrophenyl-EGTA (NP-EGTA) was synthesized as described in Ellis-Davies and Kaplan (27). Relaxing and activating solutions contained 30 mM EGTA (pCa = 9) and 30 mM Ca²⁺-EGTA (pCa 4.5), respectively. To lower the free EGTA concentration before transfer into either activating or NP-EGTA-containing solutions, the tissue was bathed in a “preactivating” solution that was identical to the relaxing solution, except that HDTA replaced all but 0.1 mM of the EGTA. The NP-EGTA solutions contained 100 mM TES, 37 mM HDTA, 10 mM creatine phosphate, 1 mg/ml creatine kinase, 10 mM glutathione, 5.5 mM ATP, 6.8 mM MgCl₂, 2 mM NP-EGTA, and ∼1.7 mM CaCl₂. To minimize photobleaching and production of oxygen-free radicals, the tissue was maintained in an oxygen-depleted solution whenever illuminated by the laser. Jets of argon gas were directed at the quartz trough on the setup and into the solution vials throughout the experiment. At commencement of each experiment, an oxygen-scavenging system of glucose, glucose oxidase, and catalase was added to each solution (28).

Protocol

T-shaped aluminum foil clips were wrapped around each end of the trabecula, which was then mounted in the mechanical apparatus while bathed in relaxing solution. For steady-state or transient activations, the tissue was incubated in preactivating solution for 2 min to lower the EGTA concentration before transfer into solutions containing either various free [Ca²⁺] or Ca²⁺-loaded NP-EGTA. For time-resolved studies, NP-EGTA was photolyzed by a 50 ns pulse of 347 nm light produced using a frequency doubled, Q-switched ruby laser (Laser Applications, Winter Park, FL) as described in detail in Martin and Barsotti (17,29) and Martin et al. (13). Initial and final [Ca²⁺] were controlled by varying the Ca²⁺ loading of NP-EGTA and/or by varying incident pulse laser energy. All experiments were performed at 21°C.

RESULTS

Exchange of labeled TnC with endogenous form in guinea pig trabeculae

The “passive exchange” method used for cTnC in these experiments represents a good alternative to extraction-reconstitution methods, in that the near-physiological conditions should better preserve structural and functional properties of the cytoskeletal and contractile apparatus. However, this approach does not allow the possibility to estimate exchange from the decrement in Ca²⁺-activated tension after the extraction of cTnC and its recovery upon the reconstitution of cTnC. We were also concerned about the specificity and uniformity of TnC binding in the contractile apparatus of the cell. To address these issues we developed an extremely sensitive and effective technique using protein microarray that allows the direct quantitation of the extent of Tn subunit exchange in single trabeculae and used confocal microscopy to determine the distribution of labeled cTnC.

Results of the exchange are shown in the accompanying confocal photomicrograph. Fig. 2 shows a confocal optical section through a trabecula in which the endogenous cTnC was exchanged for rhodamine-labeled cTnC-C35S. These images reveal no obvious “dark core” that would be indicative of incomplete labeling across the tissue, thus confirming good uniformity of radial labeling, extending from the edge of the trabecula to beyond the central axis. Fig. 3 shows the labeling pattern in another trabecula at higher magnification, in which the endogenous cTnC was exchanged passively for cTnC-Cys-84-rhodamine and then labeled for actin with fluorescein isothiocyanate (FITC)-conjugated phalloidin. The red channel (left panel) shows the TnC distribution and the green channel (right panel) shows phalloidin-actin. Note that the cTnC-Cys-84-rhodamine is confined to the area of the actin filaments. These results indicate that the fluorescence of labeled cTnC is uniform and specific to thin filaments and are in excellent agreement with the distribution of passively exchanged cTnC and actin in cardiac trabeculae recently described by Kohler et al. (30) and earlier for Tn in skeletal muscle (31).

FIGURE 2.

Confocal optical section through the core of a trabecula in which the endogenous cTnC was exchanged for rhodamine-labeled cTnC-Cys-84 as described in Methods. The trabecula was in relaxing conditions during the confocal imaging. Z-lines are indicated by arrows.

FIGURE 3.

Confocal image showing cTnC and actin in a trabecula in which the endogenous cTnC was exchanged for cTnC-Cys-84-rhodamine then labeled for actin with FITC-conjugated phalloidin. The red channel (left panel) shows the TnC distribution, and the green channel (right panel) shows phalloidin-actin. The cTnC-Cys-84-rhodamine appears to be highly colocalized with actin.

The extent of passively exchanged cTnC-C35S into guinea pig skinned trabeculae estimated using the protein microarray method described was 0.67 ± 0.01 (mean ± SE, n = 11). These results, the confocal images showing the uniform distribution of cTnC, along with the lack of any measurable decrement in isometric force/cross sectional area, indicate that labeled cTnC exchanged with native sites to form fully functional thin filament complexes.

Steady-state fluorescence polarization

The order parameter 〈P_2d〉 was measured and analyzed to yield the semiangle, δ, of the nanosecond-scale wobble of the probe fluorescent dipole (16,23,25). In relaxed conditions, δ was 37.0° ± 0.48° (mean ± SE, n = 8 fibers) with no significant difference in rigor, activating or activating + Vi conditions. This indicated that the mobility of the probe relative to the protein was not differentially affected by these biochemical conditions.

Table 1 shows the results of a series of experiments to determine the peak probe angle and dispersion under various conditions: relaxed (pCa 9), maximally activated (pCa 4.5), during rigor in the absence of Ca²⁺ (pCa 9), and in the presence of saturating Ca²⁺ (pCa 4.5). Peak probe angle decreased from 48.8° ± 0.44° (mean ± SE, n = 13) under relaxing conditions to 45.6° ± 0.67° when Ca²⁺ activated, representing a shift to a more axial orientation. Under rigor conditions, probe angle in both the absence and presence of Ca²⁺ was affected to a roughly similar extent compared to maximal Ca²⁺ activation: 46.3° ± 0.88° in rigor and 45.5° ± 1.01° in CaRigor (n = 7). There was no significant change in probe dispersion in these conditions.

TABLE 1.

Peak probe angle and dispersion

Condition (n)	pCa	Peak probe angle (degrees) mean ± SE	Dispersion (degrees) mean ± SE
Relaxed (13)	9	48.8 ± 0.44	27.6 ± 0.92
Active (13)	4.5	45.6 ± 0.67	27.4 ± 0.63
Rigor (7)	9	46.3 ± 0.88	27.5 ± 0.98
CaRigor (7)	4.5	45.5 ± 1.01	27.5 ± 0.98
Relaxed +Vi (6)	9	48.1 ± 0.25	28.6 ± 1.08
Active +Vi (6)	4.5	44.6 ± 0.56	28.2 ± 0.76

To better distinguish the effects of Ca²⁺ from cross-bridge formation in these steady-state experiments, cross-bridge formation was greatly reduced by 1 mM sodium vanadate (Vi), which reduced tension to 6.5% ± 3.0% (mean ± SE, n = 7) of maximal (see Fig. 4). In the presence of Vi, peak probe angle changed from 48.1° ± 0.25° to 44.6° ± 0.56° in the absence and presence of saturating [Ca²⁺] (pCa 4.5). These results indicate that saturating Ca²⁺ binding and cross-bridge formation produce comparable probe orientation.

FIGURE 4.

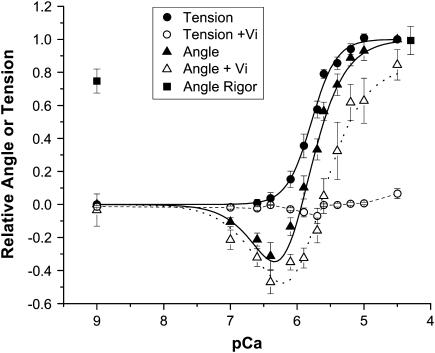
Dependence of isometric tension (circles) and cTnC-Cys-84 probe peak angle (triangles) on free [Ca²⁺] in the absence (solid symbols, solid lines) and presence of 1 mM Vi (open symbols, dashed lines) expressed as a relative change from relaxed to maximally Ca²⁺-activated. Relative angle in rigor is also shown (solid squares), with that at pCa 4.5 horizontally offset for clarity. Relative values were calculated for each trabecula before pooling the data from all trabeculae. Data at pCa 9 and 4.5 correspond to those in Table 1. The maximal isometric tension was 31 ± 2.1 (mean ± SE, n = 13). The solid curve through the tension data was generated by fitting a Hill equation to the data; the pCa₅₀ was 5.8 and the Hill coefficient was 2.4 in this series. Angular dispersion (not shown) did not significantly change from relaxed conditions across the full pCa range in the absence or presence of Vi or in rigor. The curves through the angle data were generated by fitting to the model illustrated in Fig. 8 as described in Discussion. Each point is mean ± SE of measurements in 7–13 trabeculae.

Fig. 4 shows the dependence of isometric tension and TnC-Cys-84 probe angle on free [Ca²⁺] in the absence and presence of 1 mM Vi, expressed as a relative change from relaxed (pCa 9.0) to maximally Ca²⁺ activated (pCa 4.5). Angular dispersion showed no significant change from relaxed conditions across the full range of pCa in the absence or presence of Vi or in rigor (data not shown). In the presence of Vi, saturating [Ca²⁺] alone was sufficient to cause near-maximum probe angle change, with further shift toward the maximally activated conformation in the presence of cross-bridges (absence of Vi). An interesting finding is that as the free [Ca²⁺] is increased from pCa 9.0 to ∼6.4, the probe angle changes in the direction opposite to that observed at the higher range of [Ca²⁺] (pCa 6.4–4.5).

To determine whether these changes in probe angle between pCa 7 and 6 were caused by Ca²⁺ binding to the Ca²⁺-Mg²⁺ sites of cTnC (sites III and IV), similar experiments were carried out in solutions in which the free [Mg²⁺] was changed from 1 mM to 0.5 and 3 mM with similar results (data not shown). There was a slight but insignificant shift in the probe angle-pCa relation to the left in lower and to the right in higher free [Mg²⁺], consistent with weak Mg²⁺ competition for site II.

Time-resolved fluorescence polarization

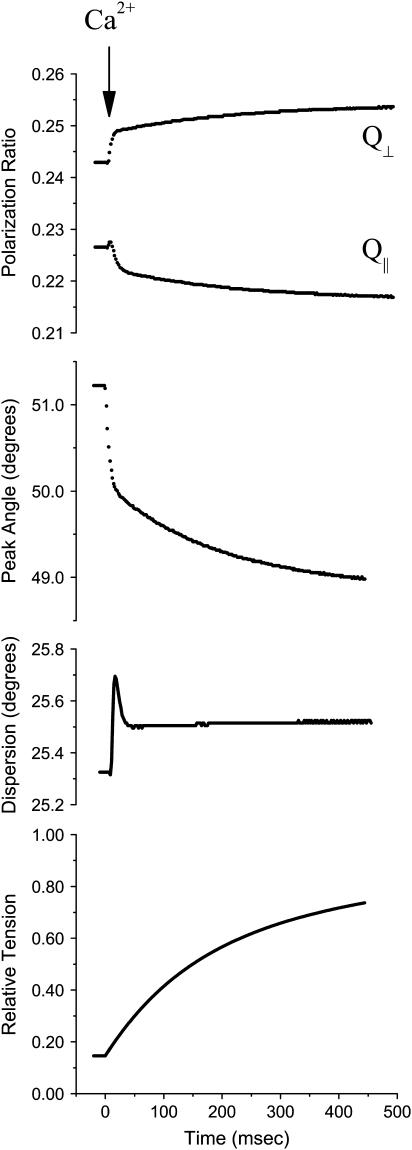
FP was monitored simultaneously with tension to investigate the structural changes in cTnC that follow rapid Ca²⁺ activation by NP-EGTA photolysis. Fig. 5 illustrates the time course of the polarization ratios, Q_‖ and Q_⊥, analyzed as peak axial angle and Gaussian dispersion along with isometric tension resulting from a step in [Ca²⁺] from approximately pCa 6.0 to 5.5 as estimated from the change in isometric tension (13). As can be seen in Fig. 5, laser photolysis of caged-Ca²⁺, which produced a jump to near saturating [Ca²⁺], resulted in a multiphasic shift in peak angle toward the filament axis: an early fast component with an ∼4 ms half time and a slower time course that appeared to closely follow the tension time course. Dispersion was relatively constant during the changes in tension and peak angle. The angle responses to elevated [Ca²⁺] and cross-bridges are in the same direction, consistent with steady-state ± Vi data of Fig. 4 where initial pCa is well to the right of the “foot” of the pCa-tension curve.

FIGURE 5.

Rapid activation of skinned trabeculae by photolysis of caged-Ca²⁺. Shown are time courses of the polarization ratios, Q_‖ and Q_⊥, analyzed as peak axial angle and Gaussian dispersion along with isometric tension resulting from a step in [Ca²⁺] from approximately pCa 5.9–5.3. The photolysis occurred at time = 0, indicated by the arrow. Data points were also taken at 2.5 s during the asymptotes of slow components in tension and polarization (not shown). Pre- and postphotolysis pCa were estimated from comparison to the steady-state pCa-tension relation (13). The halftime of the initial rapid change in probe conformation was ∼4 ms at 21°C.

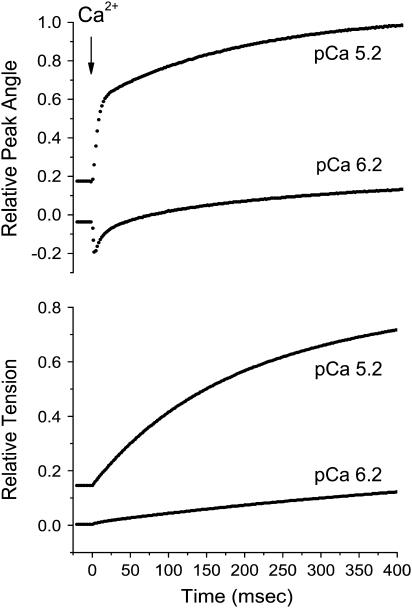
Fig. 6 shows a trabecula activated using different levels of NP-EGTA-Ca²⁺ loading to establish different preflash [Ca²⁺]. Time courses of the relative change in peak angle and relative tension are shown. These results are consistent with the steady-state probe angle data in the presence and absence of Vi shown in Fig. 4. In the caged-Ca²⁺ experiment with initial [Ca²⁺] of ∼7.5 in Fig. 6, the peak angle starts as a slight negative relative angle (less axial) compared to relaxed conditions. After the photorelease of [Ca²⁺], which generated ∼0.1 relative maximum isometric tension (pCa ∼ 6.1), the probe angle fluctuated rapidly away from and then toward the filament axis, as if following the “negative valley” of the +Vi, steady-state relative angle curve of Fig. 4. This is kinetically resolved from the apparent effects of cross-bridges, which induce an additional axial shift. At higher preflash [Ca²⁺] before photolysis, the relative probe angle is increased (more axial) above that in relaxing solution, and after the jump in [Ca²⁺], probe angle rapidly moved further axially, followed by the slow, additional axial motion. In both trials, the rapid component of relative peak angle change was significantly faster than the tension rise.

FIGURE 6.

Rapid activation of skinned trabecula at two different pre- and postflash [Ca²⁺]. Time courses of the relative change in peak probe angle (upper panel) and relative tension (lower panel) are shown. Preflash [Ca²⁺] was established by the Ca²⁺-loading level of NP-EGTA, and the magnitude of the [Ca²⁺] step varied with laser energy. Postflash pCa are indicated on the plots, estimated from comparison to the steady-state pCa-tension relation. In the trial corresponding to final pCa ≅ 5.2, initial pCa was likewise estimated at ∼6.1. In the trial corresponding to final pCa ≅ 6.2, initial tension was near zero, thus initial pCa was estimated at 7.5 from the known Ca²⁺ binding affinity of NP-EGTA under these conditions.

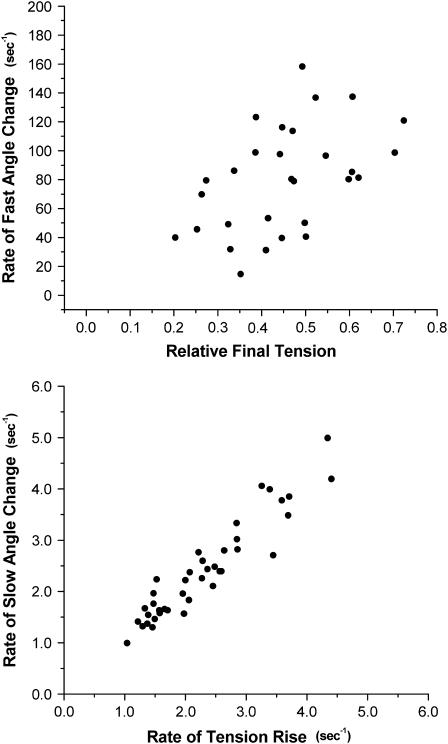
Time-resolved data for cTnC-Cys-84 were analyzed to determine the [Ca²⁺] dependence of the components of the angle change time course at Ca²⁺ loading of NP-EGTA that enabled jumps to saturating [Ca²⁺], i.e., pCa ∼ 6.0. A larger [Ca²⁺] step resulted in an increase in the rate and amplitude of the rapid or initial component of the probe angle time course. The rapid rate spanned roughly a decade in the same 10-fold change in [Ca²⁺] spanned by the tension response (Fig. 7, upper panel) and was significantly faster than the tension rise at all [Ca²⁺]. This suggests that the rate of change in probe angle is the apparent rate of Ca²⁺ binding to cTnC, or of a step controlled by the binding equilibrium; the latter would saturate as would isometric tension at pCa 4.5. A value of 5 × 10⁷ M⁻¹ s⁻¹ was estimated for the second order rate of Ca²⁺ binding. This was based on converting the relative final level of isometric tension achieved after each photolysis (upper panel in Fig. 7) to an estimated photoreleased free [Ca²⁺] using the fitted pCa-tension relation in Fig. 4.

FIGURE 7.

[Ca²⁺] dependence of components of the angle change time course for TMRIA at cTnC-Cys-84. The rate of the rapid component was plotted against relative final tension, which provides an estimate of the sensitivity of Ca²⁺-cTnC binding. The rate of the slow component of the angle change was plotted against the slow component of the tension rise to demonstrate their correlation.

The slow component of the angle change was found to track the time course of the tension rise (Fig. 7, lower panel), consistent with cross-bridge formation and/or tension generation inducing this change in probe orientation and that both Ca²⁺ binding and cross-bridges are required to achieve the final activation state.

DISCUSSION

To determine the extent and time course of structural changes in cTnC induced by Ca²⁺ activation and strong cross-bridge formation, the orientation of a fluorescent probe at Cys-84 was monitored simultaneously with tension in skinned cardiac trabeculae. A monocysteine mutant of cTnC labeled with 5′-TMRIA (single isomer) was exchanged for the endogenous form. FP, analyzed as peak axial angle and dispersion, was monitored both in steady-state and after the photoliberation of Ca²⁺ from NP-EGTA. We found that Ca²⁺ alone (in the absence of cross-bridges due to 1 mM Vi) or rigor cross-bridges alone produced a similar change in probe orientation, but that the full change required both Ca²⁺ and cross-bridges. Ca²⁺-dependent changes in probe angle were found at concentrations well below those required to generate tension. Cross-bridges increased the Ca²⁺ dependence of angle change (cooperativity). The time course of the change in angle was biphasic with a rapid component much faster than that of tension (∼10 times) and a slower component whose rate was similar to that of the tension rise.

Exchange of labeled TnC with endogenous form in guinea pig trabeculae

Previous methods of labeling TnC in rat trabeculae have involved the extraction of the endogenous form followed by reconstitution with labeled TnC (32,33), which allows fractional incorporation of labeled TnC to be estimated from the postextraction decrease in maximal isometric tension and the recovery of tension after reconstitution. Brenner et al. (18) introduced a method of exchanging whole Tn into skeletal muscle. We found that native TnC can be displaced by excess exogenous, labeled protein in relaxing conditions at 4°C. We believe this “passive exchange” represents a good alternative to extraction-reconstitution methods, with the benefit of having provided higher incorporation of labeled protein (0.67 ± 0.01, n = 11) into guinea pig trabeculae than with extraction-reconstitution (10–15% based on tension).

The specific and uniform exchange of cTnC in trabeculae was difficult to validate unequivocally by confocal imaging alone. However, the following points support specific binding resulting in functional regulatory units:

1. A characteristic of specificity is tight binding, so diffusion of weakly associated labeled protein from the tissue should lead to a decay of fluorescence during incubation in cTnC-free solution. This does not occur; in fact, after cTnC exchange, fluorescence was well maintained even after 6 months' storage in 50% glycerol, TnC-free relaxing solution at −20°C.

2. If high affinity, nonspecific sites for TnC-Tn binding were present within the contractile lattice, one would expect that over time the endogenous TnC would migrate to these sites, resulting in a dramatic drop in Ca²⁺-activated tension when the tissue is stored even for brief periods; this does not occur.

3. As revealed consistently by the data, the cTnC-Cys-84 probe angle was not only highly correlated with active force but was also sensitive to Ca²⁺ in the absence of cross-bridges (+Vi) and to both cycling and rigor cross-bridges (Fig. 4). This would be highly unlikely if the TnC were disposed at any position within the sarcomere other than its native site on the thin filament.

4. Quantitative protein microarray assay revealed no excess of either labeled or unlabeled cTnC in the exchanged tissue, as would have been expected if the tissue contained TnC bound to nonspecific sites in addition to its native site.

5. Unlike TnI and TnT which bind to actin and Tm, TnC has not been shown to bind to the thin filament outside the context of whole Tn (34). On the basis of these findings and inferences, the case for tight, specific, and uniform binding on the thin filament can be made with confidence.

Disposition of the fluorescent probe on cTnC

The fluorescent probe experiences motions that are faster than the ∼5-ns fluorescence lifetime of rhodamine and which depolarize the fluorescence (16,26). These motions are likely to be dominated by rapid movement of the probe's dipole about its linkage to the protein, since protein interdomain motions would be of a longer timescale. The wobble-in-cone equivalent for nanosecond motions of 5′-TMRIA on cTnC-Cys-84 was 37.0° ± 0.48°, higher than that measured for the C-helix of skeletal TnC in situ (25). The greater restriction observed in the skeletal TnC is explained by the bifunctional attachment of the probe in those studies. As with those studies, nanosecond probe wobble in this study was insensitive to Ca²⁺ or cross-bridges, strongly suggesting that the probe's disposition on the protein was similarly unaffected. Therefore, the rhodamine probe at Cys-84 moves in concert with the local underlying TnC structure and changes in the orientation of the probe reflecting those of the protein domain.

Steady-state fluorescence polarization

Although the changes in peak probe angle were small in absolute terms (Table 1), they were highly reproducible in trials on the same trabecula. The experimental error in absolute values represents biological variation between trabeculae arising from divergent cardiomyocyte orientations; error was therefore reduced when data for each specimen were normalized (Fig. 4).

The data summarized in Table 1 and in Fig. 4 show that the cTnC structural probe was affected by Ca²⁺ binding and rigor cross-bridges in similar ways. Peak angle was shifted to a more axial orientation at maximal Ca²⁺ activation and in rigor ±Ca²⁺. In addition, Ca²⁺ binding alone (Active + Vi) was sufficient to shift probe orientation to near-maximal levels. There was no significant change in probe dispersion in these conditions. The finding that rigor cross-bridges shift the probe orientation toward the Ca²⁺-activated conformation indicates that Ca²⁺ binding, per se, was not required, or more likely, that rigor and high [Ca²⁺] both produce the same change in cTnC structure. However, with cross-bridges inhibited by Vi, saturating [Ca²⁺] alone did not yield full probe angle change compared to maximal activation in the same trabecula. As discussed further below, these results are consistent with a graded response to fractional binding of Ca²⁺, enhanced by cross-bridges even near Ca²⁺-TnC saturation.

Our steady-state results, when expressed as linear dichroism (not shown), are consistent with those of Martyn et al. from rat trabeculae (14). However, since dichroism cannot resolve between probe axial angle and angular dispersion, it was not certain from Martyn et al. (14) whether the changes in TnC structure induced by Ca²⁺ and cross-bridges were similar. The results in this study suggest that the Ca²⁺-induced conformational change was similar to that induced by cross-bridges: a shift in probe angle toward the thin filament axis with little change in dispersion.

In skeletal fibers, the angle between the C helix of sTnC and actin increases 32° (more perpendicular to fiber axis) upon Ca²⁺ activation (25). Also upon activation, the D helix undergoes a 40° torsion and an axial shift from 102° to 82°, both consistent with the angular shift we observed for our probe on Cys-84 at the C-terminal end of the D helix, under the reasonable assumption that our probe was arrayed at some angle relative to the D helix. They also reported that the angular dispersion of bifunctional probes on the N-terminal lobe of TnC was ∼28° and changed little in going from relaxed to active or rigor, similar to our finding for the monofunctional Cys-84 probe (see Table 1). The relative insensitivity of probe dispersion to biochemical state in these two studies suggests that the N-terminal lobe of TnC is stabilized by multiple, Ca²⁺-insensitive interactions in situ, in contrast to the Ca²⁺-sensitive mobility observed for the same moiety in isolated Tn (35).

The similarities in the relative tension and peak angle versus pCa curves in Fig. 4 strongly suggest that they arose from common processes underlying thin filament activation. An interesting finding is that as the free [Ca²⁺] is increased from pCa 7.0 to ∼6.0, the probe angle changes in the opposite direction from that observed at the higher range of [Ca²⁺] (pCa 6.0–4.5). Is this the result of Ca²⁺ binding at sites III-IV, the “Ca²⁺-Mg²⁺ sites” of cTnC? At pCa 7.0, nearly 85% of sites III-IV are bound with Ca²⁺ based on the binding affinities for the cTnC sites from Kobayashi and Solaro (36): K_Ca = 7.4 × 10⁷ M⁻¹, K_Mg = 0.9 × 10³ M⁻¹ for sites III-IV and for site II, K_Ca = 1.2 × 10⁶ M⁻¹, K_Mg = 1.1 × 10² M⁻¹. Thus the majority of Ca²⁺ for Mg²⁺ exchange at sites III-IV occurs between pCa 9 and 7, yet the largest relative drop in probe angle occurs between pCa 7 and 6. Hence, the angle change between pCa 7 and 6 is unlikely to arise from Ca²⁺ binding or the exchange of Mg²⁺ for Ca²⁺ at sites III-IV. This was further verified by the similar results obtained from steady-state experiments carried out in solutions containing 0.1 and 3 mM free [Mg²⁺].

The finding that probe orientation changed in the opposite direction between pCa 9 and 6.4 compared to that between 6.4 and 4.5 is strong evidence that the conformation of the regulatory system ensemble is not a simple linear combination of cTnC in Ca²⁺-free, “off states” and Ca²⁺-bound, “on states”. Instead these results suggest that the conformation attained by some or all of the cTnC at intermediate pCa is different from that in either the full off or on state. If the 30–40% change in relative angle observed at pCa 6.4 were the result of a small fraction of Ca²⁺-bound cTnCs, the probe orientation in these units would have to be quite different from the Ca²⁺-free units. This is hard to reconcile with the finding that dispersion does not significantly increase at intermediate pCa, as would be expected from an ensemble comprising a multiplicity of states. The results instead suggest that cTnC structure changes in concert with neighboring units in a graded response to Ca²⁺ binding as suggested by previous studies of skeletal fibers (37).

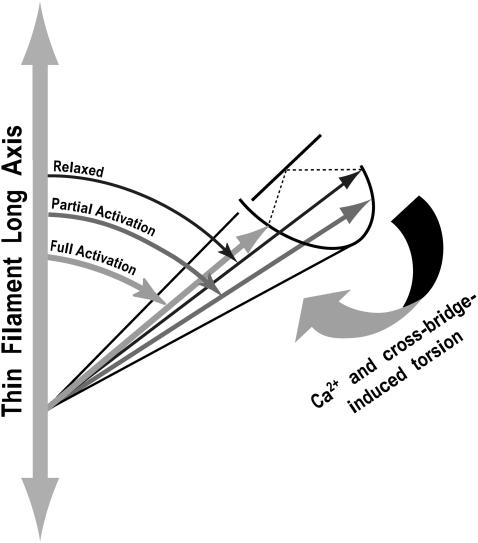
To fit the structural changes represented by probe angle versus pCa data in Fig. 4, a model was developed which exhibits an apparent reversal of axial angle at intermediate pCa. In this model, the probe's fluorescent transition dipole is disposed at some angle with respect to cTnC to which it is attached. Fig. 8 shows the probe tracking the rotation of cTnC about a local torsional axis to positions corresponding to relaxed, partially and fully activated thin filament states (discussed further below). The probe undergoes a graded rotation in proportion to Ca²⁺ binding, which exhibits cooperativity and cross-bridge feedback according to the Hill equation. Because of the geometry, this rotation is detected as an initial increase then a decrease in the dipole's angle with respect to the thin filament axis. The model is reasonable because it includes an azimuthal/torsional component of Tn motion which may correspond to the azimuthal motion reported for Tm in multiple structural studies, e.g., Vibert et al. (4) and/or the torsion at the N-terminal end of the D helix of skeletal TnC reported by Ferguson et al. (25).

FIGURE 8.

Model to assist in the interpretation of the observed pCa-tension relation of TMRIA at cTnC-Cys-84. The probe's fluorescent transition dipole is disposed at some angle with respect to a torsional axis of the protein (cTnC) to which it is attached. In response to increasing Ca²⁺ binding or cross-bridge formation, cTnC undergoes a rotation about its local axis, swinging the dipole first away from (less axial, labeled “partial activation”), and then at higher activation levels, closer to the long axis of the thin filament. FP reports these changes as an increase and then a decrease in the dipole's angle with respect to the filament axis.

Three-state models of thin filament activation include a Ca²⁺-free B or blocked state, a Ca²⁺-induced or closed C state, and the requirement that cross-bridges induce the fully active, M or open state (1–4). Our data are consistent with these models with the refinement that at Cys-84 of cTnC, the activation state induced by Ca²⁺ alone may in fact comprise several Ca²⁺-dependent substates. For instance, from pCa 9 to 6.4, cTnC-Cys84 probe orientation shifts away from axial to one of the C-substates, C_LO, but the regulatory unit remains closed and thus strong cross-bridge formation remains inhibited (as does force). From pCa 6.4 to 4.5, increased Ca²⁺ binding allows population of the C_HI state which is characterized by the probe having shifted more axially. In the absence of Vi, this state allows cross-bridge formation and subsequent induction of the M state by strong binding bridges, which impels the probe to its “maximally active” orientation. The exact correspondence of states we observed for cTnC-Cys-84 to the B, C, and M states deduced from kinetic and structural studies of other parts of the regulatory system remains speculative pending further investigation.

Rigor cross-bridges have been shown to maximally activate the regulatory system in the absence of Ca²⁺, as inferred from actomyosin ATPase activity (38–40) or fluorescence of IANBD-modified TnI in reconstituted filaments at low ionic strength (41). In this study, the maximally active configuration at cTnC-Cys-84 is attained only in the presence of cross-bridges and Ca²⁺ (see Fig. 4, rigor at pCa 4.5 versus rigor or relaxed at pCa 9), consistent with TnI-IANBD fluorescence in filaments at low ionic strength (42) and in skeletal fibers at physiological ionic strength (18), and consistent with the Ca²⁺ sensitivity of force in cardiac myocytes being maintained in the presence of “rigor-like” N-ethylmaleimide-modified myosin subfragment 1 (NEM-S1) cross-bridges (43). Because functional activation of the thin filament by strong cross-bridges is likely to be “downstream” of the probed site, it is reasonable that complete propagation from cross-bridge binding upstream to cTnC conformation would be incomplete without Ca²⁺. When Ca²⁺ is bound to the regulatory site (site II) of TnC, the amphiphilic H3 helix of TnI interacts with the hydrophobic cleft on the N lobe of TnC and induces the detachment of the inhibitory region of TnI-I from actin (44–47). Because Cys-84 of cTnC is near this area of TnC-TnI interaction, the sensitivity of our probe to Ca²⁺ in rigor conditions may elucidate conformational states of both TnC and TnI in these conditions: Ca²⁺ binding at site II may be required for the interaction to be complete. A similar argument could be made for the requirement for cross-bridge feedback to complete the interaction at saturating [Ca²⁺].

It is clear from the results shown in Fig. 4 that cTnC structural changes occur at [Ca²⁺] below that required for tension development, consistent with those of Putkey et al. (48) and Hannon et al. (8), who showed that the fluorescence from 2-(4′-iodoacetamidoanilo)naphthalene-6-sulfonic acid (IAANS)-labeled cTnC was enhanced at lower [Ca²⁺] than tension in skinned rat cardiac fibers. Interestingly, the Hill coefficient for tension in Fig. 4 was 2.34, whereas the Ca²⁺ dependence of the probe angle spans two pCa units with a Hill coefficient of only 1.13 in the presence of Vi when fitted by the model in Fig. 8, increasing to 1.56 in the absence of Vi. This appears inconsistent with the cooperativity observed on isolated cardiac thin filaments in the absence of cross-bridges (11). However, our results suggest that ∼30% of cTnC had already bound Ca²⁺ before tension was observed at pCa 6.4 (Fig. 4). It is possible that Ca²⁺ binding to individual cTnC may be sufficient to induce a localized, measurable shift in cTnC conformation (i.e., the mean probe angle seen at pCa 6.4 when Tn is fractionally Ca²⁺ occupied), but the unit is restrained from transitioning to the “on” state until one or more adjacent unit also binds Ca²⁺. The tension response to such nonlinear thin filament activation would appear cooperative without requiring cooperative Ca²⁺ binding per se. If this same “apparently cooperative” off-to-on transition underlies the cTnC-IAANS fluorescence change of Tobacman and Sawyer (49), then the Ca²⁺ dependence of fluorescence should also appear cooperative in the absence of cross-bridges, as they observed. Greene and Eisenberg (50) have also explained their Tn fluorescence data by invoking Ca²⁺ binding to adjacent TnC. When interaction between adjacent regulatory units along the thin filament is interrupted, cTnC-IAANS fluorescence increases at lower [Ca²⁺] and with a Hill coefficient ∼1, consistent with the disruption having removed the aforementioned restraint of a Ca²⁺-free unit on its neighbor. In any event, this scheme maintains the trait that cross-bridge formation causes further cooperative enhancement of thin filament activation and increased affinity for Ca²⁺, consistent with our data and those of numerous others.

Time-resolved fluorescence polarization

One of the goals of the proposed studies was to ascertain the relative roles of the regulatory system and cross-bridge kinetics in controlling the rate of cardiac muscle tension production. Possible mechanisms underlying the Ca²⁺-dependent rate of tension generation are 1), the rate of Ca²⁺ binding and activation of the regulatory units, 2), the rate of propagation of the activation state among neighboring regulatory units, and 3), cross-bridge kinetics, i.e., the rate of binding and force generation.

To date, it has been difficult to measure directly the kinetics of thin filament activation in situ. In studies of the structural changes using time-resolved x-ray diffraction pattern during electrical stimulation of frog skeletal muscle, Kress et al. (51) found that the position of Tm changed before cross-bridges moved toward the thin filament. Baylor et al. (52) concluded that in frog skeletal fibers at 16°C, the Ca²⁺ transient reaches its peak ∼10 ms after stimulation and Ca²⁺-Tn binding reached saturation ∼14 ms after stimulation. This Ca²⁺-TnC binding time course correlates well with a t_1/2 of 8 ms for Tm movement reported by Kress et al. at a similar temperature. These results imply that at least during maximal activation, thin filament structural changes result from a rapid Ca²⁺ binding equilibrium that is too rapid to limit cross-bridge formation.

In previous studies of the kinetics of cardiac muscle activation, we reported that there was no [Ca²⁺]-dependent lag in the rise of tension and stiffness in fibers after a step [Ca²⁺] increase (13). We hypothesized that thin filament transitions leading to activation were too rapid to be rate limiting for tension generation in situ and that the onset of cross-bridge formation was controlled instead by a rapid equilibrium between [Ca²⁺] that set the number of available myosin binding sites on the thin filament. Our results here are consistent with these premises and are also supported by the results from studies by Brenner and Chalovich (31) in which thin filament activation state in skeletal muscle fibers was directly probed using a fluorescent tag on TnI during a k_tr protocol at varying [Ca²⁺]. The authors concluded that equilibration among different states of the thin filament with [Ca²⁺] is rapid, and as a result, k_tr was not rate limited by changes in the thin filament activation state that may have been induced by the isotonic contraction before tension redevelopment.

In experiments with fluorescently labeled, isolated cardiac TnC, Cheung and co-workers (53,54) observed structural changes whose rates (∼20 s⁻¹) were similar to those of tension transients reported in the above studies, suggesting that Ca²⁺-induced changes in TnC limit the rate of tension development. However, recent studies using time-resolved fluorescence resonance energy transfer have shown that structural rearrangements within Tn occur rapidly with Ca²⁺ binding: ∼5 ms half time at 20°C (55,56), too fast to limit cross-bridge formation. These latter results are also consistent with previous stopped-flow studies using fluorescently labeled skeletal TnC and TnI on regulated actin (41,57). Thus transient kinetics studies of isolated cardiac and skeletal TnC and on reconstituted thin filaments indicate relatively rapid thin filament activation upon Ca²⁺-TnC binding.

If the tension time course of cardiac muscle were determined by the rate of Ca²⁺ thin filament activation, then the structural changes of cTnC and the tension rise should follow similar time courses. As shown in Figs. 5 and 6, upon the photorelease of Ca²⁺ from NP-EGTA, the probe on cTnC-Cys-84 responded with a multiphasic change in peak angle: an early fast component, and a slower time course that closely tracked to the tension time course. The rapid component at ∼100 s⁻¹ near full activation was too fast to limit tension development and likely reflects either the elementary Ca²⁺-binding step or a step closely associated with Ca²⁺ binding. These data were analyzed to determine the [Ca²⁺] dependence of the components' time course of the change in angle. A larger [Ca²⁺] step resulted in an increase in the rate and amplitude of the rapid (initial) component of the probe angle change. The rate of the rapid component varied over a 10-fold range similar to the change in [Ca²⁺] spanned by the tension response (Fig. 7, upper panel). This suggests that the rapid change in probe orientation reflects the apparent rate of Ca²⁺ binding to cTnC or of a step controlled by the binding equilibrium. Ca²⁺ binding along with tension would be expected to saturate at pCa 4.5.

In the trial shown in Fig. 6, the jump to near-saturating [Ca²⁺] quickly brought the angle toward its C_HI conformation (pCa < 5 in Fig. 4), and the slow component reflects an additional conformational change at cTnC-Cys-84, perhaps in transitioning from C_HI to the M thin filament states. In the [Ca²⁺] jump experiments of Figs. 5 and 6, the initial (rapid) angular deflection precedes significant formation of cross-bridges and thus corresponds to the steady-state angle of the cTnC-Cys-84 probe in the presence of Vi shown in Fig. 4. The slow time course parallels cross-bridge formation, with the asymptote corresponding to the steady state in the absence of Vi. Because initial pCa in these transients was near or to the right of the “foot” in the pCa-tension curve (pCa ≤ 6.4 in Fig. 4), cTnC was already near or beyond C_LO with cross-bridges further impelling the probe in the axial direction, as seen in the difference between the probe angles with and without cross-bridges in Fig. 4. For the initial and postphotolysis [Ca²⁺] attained in these transients, the angle response to elevated [Ca²⁺] and cross-bridges are thus in the same direction, consistent with the steady-state ± Vi data. In some transients, beginning from a lower initial [Ca²⁺] and jumping to final [Ca²⁺] that yielded little active tension, “opposite going” less axial rapid angle changes were detected followed by slow recovery to a near-relaxed angle (see Fig. 6). This response was consistent with the “negative” +Vi angle curve in Fig. 4, transitioning to the −Vi curve as cross-bridges form. In discussion of the steady-state data, it was suggested that cTnC operates as an ensemble in a graded coordinated manner to achieve the negative relative angle. The finding shown in Fig. 6 that the negative-going part of probe angle transient is faster than the tension rise would thus suggest that the rate of communication among regulatory units is rapid. However, it is not known whether this change is the actual activation step or simply an “upstream” cTnC structural transition that precedes activation. Future experiments will probe alternate sites in the Tn-Tm complex to map the fundamental interactions on the activation pathway.

The rate of the slow component of the angle change was found to track that of tension at all [Ca²⁺] (Fig. 7, lower panel). At lower [Ca²⁺] the relative amplitude of the slow component was larger than that observed at near saturating [Ca²⁺], suggesting that at intermediate activation levels cross-bridges greatly influence the final activation state. Because the Cys-84 probe responds independently to both Ca²⁺ and cross-bridges, the slow time course may reflect a direct effect of cross-bridge binding or additional Ca²⁺ binding in response to cross-bridge induced increase in cTnC affinity. Since a similar probe orientation occurs with saturating [Ca²⁺] and Vi as in rigor and pCa 9.0, increased Ca²⁺-cTnC binding may not be required for the conformational change.

In a study that compared k_tr to k_Ca, the rate of tension rise after step increases in [Ca²⁺], it was found that k_tr was twofold faster than k_Ca in rat trabeculae (58), presumably because k_tr bypasses rate-limiting steps in thin filament activation. This work does not rule out the possibility that the slow component of the angle change reflects a thin filament activation rate that limits the rate of tension rise. Future experiments are planned in which kinetics of either myosin or TnC-Ca²⁺ binding are altered inhibited to test whether the slow angle change is cross-bridge mediated or an intrinsic part of thin filament activation.