Conformational Changes in Single-Strand DNA as a Function of Temperature by SANS

Abstract

Small-angle neutron scattering (SANS) measurements were performed on a solution of single-strand DNA, 5′-ATGCTGATGC-3′, in sodium phosphate buffer solution at 10°C temperature increments from 25°C to 80°C. Cylindrical, helical, and random coil shape models were fitted to the SANS measurements at each temperature. All the shapes exhibited an expansion in the diameter direction causing a slightly shortened pitch from 25°C to 43°C, an expansion in the pitch direction with a slight decrease in the diameter from 43°C to 53°C, and finally a dramatic increase in the pitch and diameter from 53°C to 80°C. Differential scanning calorimeter scans of the sequence in solution exhibited a reversible two-state transition profile with a transition temperature of 47.5 ± 0.5°C, the midpoint of the conformational changes observed in the SANS measurements, and a calorimetric transition enthalpy of 60 ± 3 kJ mol⁻¹ that indicates a broad transition as is observed in the SANS measurements. A transition temperature of 47 ± 1°C was also obtained from ultraviolet optical density measurements of strand melting scans of the single-strand DNA. This transition corresponds to unstacking of the bases of the sequence and is responsible for the thermodynamic discrepancy between its binding stability to its complementary sequence determined directly at ambient temperatures and determined from extrapolated values of the melting of the duplex at high temperature.

INTRODUCTION

DNA duplexes undergo dissociation into single strands at high temperature that can be monitored by changes in the UV absorption spectrum at 260 nm. The temperature where 50% dissociation occurs is termed the melting temperature, T_m, which is commonly used as a measure of the binding affinity between the two complementary strands of the duplex or its thermodynamic stability. This measure of stability of the duplex is commonly used at all temperatures since it is based on the assumption that the duplex dissociates into the same single-strand DNA (sDNA) random coil conformations at all temperatures. Furthermore, this assumption has been used as the basis for nearest-neighbor estimation schemes on the association thermodynamics of the DNA duplex (1). These estimation schemes assign a thermodynamic parameter for every two nearest-neighbor basepair in the duplex that is derived solely from the dissociation thermodynamics of the duplex at its melting temperature. A simple summation of the thermodynamic values assigned to each of the two nearest-neighbor basepairs in the duplex is used to determine the thermodynamic stability of the DNA duplex. Early results from calorimetric studies on the dissociation of a 13-mer DNA duplex have shown, however, that the conformation of the single complementary sDNA does depend on temperature (2). This was evident in the absolute difference between the heat of dissociation of a 13-mer DNA duplex of 490 kJ mol⁻¹ determined at 74°C determined from differential scanning calorimeter (DSC) measurements and the heat of association of the duplex of −236 kJ mol⁻¹ directly determined at 25°C from batch calorimetry measurements (2). This difference was attributed to the additional thermodynamic contributions from conformational changes in the complementary single strands implied from UV absorption changes upon heating solutions of each of the complementary strands from 25°C to 74°C. In addition, a conformational transition of one of the strands was observed in DSC measurements at 40°C (2). More recent results also show a large disparity between the free energies of the dissociation of 10-mer duplexes extrapolated from DSC measurements at high temperature to 25°C and the free energies determined directly from isothermal titration calorimetry measurements on the binding of the single strands of the duplex at this temperature (3). This was again attributed to free energy contributions of the change in the single-strand random coil conformations as the temperature increased from 25°C to the melting temperature of the duplex (3). UV measurements on the single strands did indeed show the presence of a transition for each of the strands that accounted for this disparity (3). A conformational transition was also observed in DSC scans of 5′-GCGTCATACAGTGC-3′ and its complementary strand but these transitions were attributed to unfolding of a hairpin conformation involving the two terminal GC basepairs of DNA (4). It is not known how pervasive these conformational changes occur in sDNA, particularly in the absence of hairpin loop formation. In addition, the structural nature of these conformational changes has yet to be determined. The implication that the structural change involves an unstacking of the purine and pyrimidine bases with increase in temperature has been based solely on the observed increases in the UV optical density of sDNA at 260 nm with increase in temperature (5).

In the present investigation, small-angle neutron scattering (SANS) measurements were performed on a 10-base single strand of the sequence 5′-ATGCTGATGC-3′ as a function of temperature from 25°C to 80°C to determine the structural nature of the reversible conformational change of this sequence over this temperature range. The buffer solution was 10 mM sodium phosphate buffer with 0.1 M NaCl and 0.1 mM ethylenediaminetetraacetate at pH = 7.0 as was used in the earlier study (3). In addition to the possibility of a stacking conformation at ambient temperature there is also a possibility for the hairpin loop conformation for 5′-ATGCTGATGC-3′ with G3 interacting with C10 and C4 interacting with G9, but a calculation on its stability shows that it is highly unstable with a ΔG = 5.6 kJ mol⁻¹ (private communication from Oligo Etc., Wilsonville, OR). The SANS data are fitted using the recently published LORES program (6) to various geometrical models that mimic a base-stacking conformation to determine if indeed this is the nature of this conformation of 5′-ATGCTGATGC-3′ at low temperature. Differential scanning calorimetry and ultraviolet melting measurements were performed on the strand to determine the thermodynamics of the conformational change observed in the SANS measurements.

METHODS

Materials

The 10-mer single-strand DNA sequence 5′-ATGCTGATGC-3′ was purchased purified to HPLC Level I (90–95 mol %) from Oligos, Etc. (Wilsonville, OR). For SANS measurements, the sDNA was rehydrated from powder in a H₂O-based 10 mM sodium phosphate buffer, pH 7.0, containing 0.1 M sodium chloride and 0.1 mM ethylenediaminetetraacetate, to a final concentration of 3.8 mg/ml. The concentration of the sDNA was determined from UV absorption measurements at 260 nm using an extinction coefficient of 9.5 × 10⁴ M⁻¹ cm⁻¹ (7). The concentration of the complementary DNA strand, cDNA, was also determined from UV absorption measurements at 260 nm using an extinction coefficient of 9.7 × 10⁴ M⁻¹ cm⁻¹ (7). All materials were research grade from Sigma-Aldrich Chemical (St. Louis, MO).

SANS measurements

The SANS measurements were performed on the NG3 30m SANS instrument at the National Institute of Standards and Technology Center for Neutron Research in Gaithersburg, MD (8). A neutron wavelength of λ = 5 Å with a wavelength spread, Δλ/λ of 0.15, was used for the measurements. The source and sample apertures were 5.0 cm and 1.27 cm, respectively. Neutrons were detected on a 64.0 cm × 64.0 cm two-dimensional position-sensitive detector with 1.0-cm resolution. A sample-to-detector distance of 1.5 m and a source-to-sample distance of 5.47 m were used. The center of the detector was offset by 20.0 cm to obtain a range of momentum transfer, Q, values between 0.035 Å⁻¹ and 0.35 Å⁻¹, where Q = 4πsin(θ)/λ and 2θ is the scattering angle. The 10-mer sDNA solution was measured in the phosphate buffer at ∼10°C temperature increments from 25°C to 80°C. After heating, the sDNA solution was cooled back down to 25°C and measured one final time for comparison to the original 25°C measurement to determine if changes in the single-strand conformation were reversible. Attempts to scan solutions of the sDNA strand in D₂O to reduce the background scatter were unsuccessful since the sDNA tended to aggregate in the D₂O buffer at the high concentrations necessary for the SANS measurements.

The SANS data were normalized to a common monitor count and corrected for empty cell counts, ambient room background counts, and nonuniform detector response. Data were placed on an absolute scale by normalizing the scattered intensity to the incident beam flux. The two-dimensional data were then radially averaged to produce I(Q) vs. Q curves. The one-dimensional scattered intensities from the samples were then corrected for buffer scattering and incoherent scattering from hydrogen in the samples. The uncertainty in the values of R_g were estimated as the geometrical mean of the estimated 3% uncertainty in the concentration of sDNA and the 10% average standard deviation of the SANS measurements.

Analysis using the LORES computational algorithm

To study the changing geometry of the 10-mer sDNA structure as the temperature of the experiment was increased from 25°C to 80°C, we utilized the low-resolution shape optimization program, LORES (6). Briefly, LORES is an extension of the original work of S. Hansen (9) and S. Henderson (10), whereby macromolecular structures are determined from an optimization of specific geometric shapes that best fit the inputted experimental small-angle scattering data. The LORES program will allow for the optimization of macromolecular structures which can be defined as spheres, cylinders, ellipsoidal, hollow, and semihollow cylinders, shells, semi-spheres, semi-ellipsoids, rectangles, and helices (single and double, left and right). In the current study, we optimized the experimental data for two possible candidate shapes, cylindrical and single helix. For each model, at each temperature studied, LORES calculated a corresponding radius of gyration, R_g, scattering profile, χ² and R² values (Tables 2 and 3).

TABLE 2.

Comparison of the experimental R_g values with the calculated sDNA fitted parameters as a function of temperature using the helical structural model

	Diameter (Å)	Length (Å)	Rg (Å)	χ2, R2 (goodness-of-fit)	3D model from LORES
25°C	11.6 ± 0.5*	26.4 ± 0.8	8.5 ± 0.2 (9 ± 1)	0.09318, 0.6859
35°C	19.3 ± 2.3	24.2 ± 1.5	9.7 ± 0.2 (10 ± 1)	0.1482, 0.4739
43°C	24.8 ± 3.4	22.1 ± 2.6	10.8 ± 0.3 (11 ± 1)	0.2147, 0.4727
53°C	18.2 ± 1.8	26.5 ± 1.5	10.2 ± 0.2 (10 ± 1)	0.2250, 0.2392
71°C	32.5 ± 3.2	54.0 ± 3.4	19.0 ± 0.6 (19 ± 2)	0.1553, 0.6240
80°C	35.9 ± 5.4	72.5 ± 6.7	24.1 ± 2.0 (24 ± 2)	0.1716, 0.5689

^*The deviation is calculated from running LORES 15 times with same criteria. The values in parentheses are the experimental R_g values.

TABLE 3.

Comparison of the experimental R_g with the calculated sDNA fitted parameters as a function of temperature using the cylindrical structural model

	Diameter (Å)	Length (Å)	Rg (Å)	X2, R2	3D model from LORES
25°C	6.1 ± 0.1*	29.8 ± 0.5	8.8 ± 0.1 (9 ± 1)	0.09319, 0.6965
34°C	14.9 ± 0.4	28.3 ± 0.9	9.6 ± 0.1 (10 ± 1)	0.1482, 0.4752
43°C	23.0 ± 0.5	21.9 ± 0.8	10.3 ± 0.1 (11 ± 1)	0.2148, 0.4749
53°C	14.7 ± 0.5	30.5 ± 1.0	10.1 ± 0.1 (10 ± 1)	0.2251, 0.2391
71°C	25.4 ± 0.7	68.2 ± 1.5	21.7 ± 0.4 (19 ± 2)	0.1381, 0.6727
80°C	22.5 ± 0.6	78.3 ± 1.0	24.3 ± 0.3 (24 ± 2)	0.1686, 0.5884

^*The deviation is calculated from running LORES 15 times with same criteria. The values in parentheses are the experimental R_g values.

To model the experimental scattering profile of the intensity versus the momentum transfer (I(Q) vs. Q), the scattering intensity was calculated by considering a randomly oriented molecule in solution and using the following simplified scattering equation (11,12):

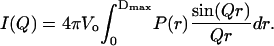(1)

Here, 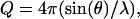where λ is the neutron wavelength, 2θ is the scattering angle, V_o is the volume of the scatterer, and P(r) is defined as the distance distribution function. The integral is carried out to a value D_max, defined as the maximum diameter beyond which there is no significant scattering mass of the sample. In this case, the solvent is treated as a uniform scatterer.

The calculation of the scattering profile in Eq. 1 relies on the computation of the distance distribution function, P(r). To calculate the P(r) function, the LORES program will automatically generate a uniform distribution of scattering points within the specific volume to be optimized, which in this case is cylindrical and helical. The distance distribution function is then relatively straightforward to calculate and is accomplished by simply making a histogram representation of all possible distances between all pairs of scattering points within the given structure, weighted according to the product of the neutron scattering lengths for each point. Details of the LORES program as well as specific examples for protein and nucleic acid optimization can be found in Zhou et al. (6). (The program is freely available to download from the Computer Physics Communications Program Library at http://www.cpc.cs.qub.ac.uk.)

UV melting measurements

The temperature dependence of the optical density of the 5′-ATGCTGATGC-3′ strand in solution was monitored at 260 nm by a Perkin-Elmer Lambda 4B Spectrophotometer (Boston, MA) equipped with a PTP-1 Peltier System for temperature scanning. The UV absorption cell containing the sample was heated up at a rate of 1 K min⁻¹, and the reference cell containing just the buffer solution was maintained at room temperature. The resulting increase in the optical density of the sample solution was recorded every 30 s over the temperature range from 20°C to 90°C. The increase in the optical density of the sDNA solution was analyzed by using the EXAM software program (13), which normalized the optical densities to the total optical density change and fitted the normalized data to a two-state A↔B transition model. The extent of change in state of the sDNA, α(T), is, thus, the normalized optical density at the temperature T. The temperature at the midpoint of the transition where α(T_m) = 0.5 is the transition temperature T_m and the van't Hoff enthalpy for the transition, ΔH_v, is

(2)

where dα(T_m)/dT is the slope of the normalized optical density versus temperature curve at T_m.

There is a random uncertainty in the optical density measurements which was determined from several ultraviolet optical density measurements of strand melting (UVM) scans of the sample and estimated systematic uncertainties of 0.003 ΔH_v from uncertainty in the temperature of the sample (0.1°C), and of 0.001 ΔH_v from uncertainty in the optical density reading. The random and estimated systematic uncertainties were combined in a quadrature to yield a combined standard uncertainty in the values for ΔH_v.

DSC measurements

DSC measurements were performed on solutions of the sDNA by using a VP-DSC Microcalorimeter from Microcal (Northampton, MA). The DSC consists of a matched pair of 0.511 mL sample and reference vessels. In a series of DSC scans, both vessels were first loaded with buffer solution, equilibrated at 5°C for 15 min scanned up to 105°C at a preset scan rate of 60°C h⁻¹. The buffer/buffer scan was repeated once after the cooling of the second scan, the sample vessel was emptied and loaded with the DNA solution by means of a syringe and before the 15-min equilibration period at 5°C. The scan was repeated several times to show that the transition was reversible. After completion of a set of scans, the second buffer/buffer scan was used as the baseline scan and subtracted from each of the sDNA solution/buffer scans before analysis. The net solution/buffer scan was converted to a heat capacity/temperature scan and analyzed in terms of an A↔B thermodynamic transition model by using the EXAM software program (13). The program determines the transition peak area and the transition temperature, the temperature where the transition peak area is half of the total area. A sigmoidal baseline, which followed the profile of the transition peak, was used to extrapolate the pre- and post-transitional baselines under the transition peak in the determination of the transition peak area. The ratio of the transition peak area to the amount of sDNA in the sample cell yielded values for the transition enthalpy. The uncertainties in T_m and the van't Hoff enthalpies were determined from the least-squares fit of the two-state transition model to the experimental excess heat capacity measurements. The uncertainty in the calorimetric enthalpies was estimated as the geometric mean of the 3% uncertainty in the sDNA concentrations and the estimated 5% in the total endothermic heat absorbed under the transition profile.

RESULTS

SANS results

Typical SANS results are shown in Figs. 1–3 where the neutron scattering curve in terms of I(Q) is plotted as a function of the momentum transfer, Q, for samples at different temperatures. Also presented in each of the figures are the calculated SANS scattering curves from the LORES optimization program for a single-strand helical shape at 25°C in Fig. 1 and at 71°C in Fig. 2 and for a random coil shape at 71°C in Fig. 3. More detailed information on changes in the cylindrical, helical, and random coil shapes that best fit the SANS data as a function of temperature are presented in Tables 1–4. The parameter space in terms of the diameter and length that was searched for the cylindrical and helical models is presented for each temperature in Table 1. The calculated parameters of the diameter and length of the cylindrical model are presented in Table 2. The calculated parameters of the diameter and length of pitch of the helical model are presented in Table 3. The diameters and lengths of each model were used to calculate the R_g values in each Table for comparison with the experimental R_g values at each temperature. Only the calculated R_g values at each temperature are presented for the random coil model in Table 4. A comparison of the values for the R_g calculated from the different models are summarized in Table 5 and again compared to the experimental R_g values. As shown in Table 5, the calculated R_g values are the same for the different models used in the LORES optimization program.

FIGURE 1.

The experimental neutron scattering data, I(Q) vs. Q (•), of sDNA fitted by the scattering curve of a single-strand helical shape (solid line with error bar) at 25°C. The error bars on the experimental data have been omitted for clarity. The scatter in the data accurately reflects these errors.

FIGURE 2.

The experimental neutron scattering data, I(Q) vs. Q (•), of sDNA fitted by the scattering curve of a single-strand helical shape (solid line with error bar) at 71°C. The error bars on the experimental data have been omitted for clarity. The scatter in the data accurately reflects these errors.

FIGURE 3.

The experimental neutron scattering I(Q) vs. Q (♦), of sDNA fitted by the scattering curve of a random coil shape (• with error bar) at 71°C. The error bars on the experimental data have been omitted for clarity. The scatter in the data accurately reflects these errors.

TABLE 1.

The parameter space searched as a function of temperature for the cylindrical and helical structural models

	Helix (Å)*		Cylinder (Å)
25°C	Diameter	15 ± 4	Diameter	10 ± 8
	Length	27 ± 10	Length	30 ± 10
34°C	Diameter	15 ± 7	Diameter	14 ± 8
	Length	27 ± 10	Length	30 ± 10
43°C	Diameter	23 ± 8	Diameter	18 ± 8
	Length	33 ± 15	Length	30 ± 10
53°C	Diameter	23 ± 8	Diameter	18 ± 10
	Length	33 ± 15	Length	30 ± 10
71°C	Diameter	26 ± 12	Diameter	24 ± 10
	Length	50 ± 10	Length	50 ± 20
80°C	Diameter	32 ± 12	Diameter	24 ± 10
	Length	65 ± 20	Length	70 ± 20

^*The diameter of the helix = r1 + MR where r1 is the elliptical radius and MR is the major radius.

TABLE 4.

Comparison of the experimental R_g values with the sDNA fitted parameters as a function of temperature using the random coil structural model

	Rg (Å)	Scale
25°C	8.1 ± 0.6 (9 ± 1)	0.0115 ± 0.0004
34°C	9.6 ± 0.7 (10 ± 1)	0.0099 ± 0.0003
43°C	11 ± 1 (11 ± 1)	0.0083 ± 0.0004
53°C	10 ± 1 (10 ± 1)	0.0077 ± 0.0004
63°C	14 ± 2	0.007 ± 0.001
71°C	19 ± 3 (19 ± 2)	0.007 ± 0.001
80°C	28 ± 7 (24 ± 2)	0.008 ± 0.002
Cooled to 25°C	9.2 ± 0.9	0.0114 ± 0.0006

The values in parentheses are the experimental R_g values.

TABLE 5.

R_g variations of experimental sDNA, with increasing temperature for the different structural models

	25°C	34°C	43°C	53°C	71°C	80°C
Experiment (Å)	9 ± 1	10 ± 1	11 ± 1	10 ± 1	19 ± 2	24 ± 2
Cylinder (Å)	8.8 ± 0.1	9.6 ± 0.1	10.3 ± 0.1	10.1 ± 0.1	21.7 ± 0.4	24.3 ± 0.3
Helix (Å)	8.5 ± 0.2	9.7 ± 0.2	10.8 ± 0.3	10.2 ± 0.2	19.0 ± 0.6	24.1 ± 1.9
Random coil (Å)	8.1 ± 0.6	9.6 ± 0.7	11 ± 1	10 ± 1	14 ± 2	28 ± 7

The optimized results for the LORES modeling of the SANS data to the cylindrical and helical shapes are plotted as a function of temperature with regard to changes of the diameters in Fig. 4 and to changes of the lengths in Fig. 5. These plots show that the diameter of the sDNA increases from 25°C to 43°C whereas the length decreases slightly. Then the length increases from 43°C to 53°C whereas the diameter decreases. Both the diameter and pitch increase from 53°C to 80°C.

FIGURE 4.

Change in the sDNA diameter as a function of temperature using the cylindrical (∇) and helical (Δ) DNA models.

FIGURE 5.

Change in the sDNA length as a function of temperature using the cylindrical (∇) and helical (Δ) DNA models.

After the 10-mer sDNA was heated up to 80°C, it was cooled down slowly to 25°C. The results of heating up the sDNA and cooling it down are presented in Table 6. As shown in Table 6, the parameters, which describe the shape of the sDNA that was cooled down after heating, are the same as the parameters that describe the shape of the sDNA before heating it up, indicating that the conformational changes evident in the SANS temperature measurements on the sDNA are reversible.

TABLE 6.

Comparison between the original sDNA and cooled sDNA

	Diameter (Å)	Length (Å)	Rg (Å)
25°C (original)	11.6 ± 0.5	26.4 ± 0.8	8.5 ± 0.1
25°C (cooled)	11.7 ± 0.5	24.8 ± 0.4	8.0 ± 0.1

UVM results

A UVM scan of the melting of a 2-μM sDNA solution is shown in Fig. 6 along with a fit of the two-state A↔B transition model to the data. The optical density at 260 nm increases with temperature, which indicates increasing exposure to the solvent as the bases are unstacking. The fit of the two-state transition model to the data is very close as shown in Fig. 6. The temperature midpoint of the transition is 47 ± 1°C and the van't Hoff enthalpy determined from Eq. 2 is 68 ± 4 kJ mol⁻¹.

FIGURE 6.

Normalized UVM scan of a 2-μM sDNA solution. The solid line is the least-squares fit of a two-state, A↔B transition model to the data points. The broken horizontal lines are the extrapolated pre- and post-transitional base lines and the broken vertical line indicates the temperature at the midpoint of the transition.

DSC results

A typical DSC scan of a 0.124 mM solution of the sDNA in the phosphate buffer is shown in Fig. 7 along with a rescan of the solution. A fit of a two-state transition model to the data, as shown in Fig. 7, yields a transition temperature of 47.5 ± 0.5°C and a van't Hoff enthalpy of 90 ± 5 kJ mol⁻¹. The calorimetric enthalpy determined from the transition peak area is 30 ± 3 kJ mol⁻¹. The transition temperature is close to 47 ± 1°C determined from the UVM measurements. However, the van't Hoff enthalpy is larger than the van't Hoff enthalpy of 68 ± 4 kJ mol⁻¹determined from the UVM measurements. Part of this discrepancy in the van't Hoff transition values can be attributed to the broadness of the transition so that the van't Hoff enthalpy becomes critically dependent upon the limits set for the transition. For example, with limits from 15°C to 95°C, the van't Hoff enthalpy is 80 kJ mol⁻¹ and with limits from 17°C to 81°C, the van't Hoff enthalpy is 100 kJ mol⁻¹. The thermodynamic data from additional DSC scans of the DNA strand are summarized in Table 7. As shown in Table 7, the transition temperature and enthalpies are independent of the strand concentration and the sodium chloride concentration. The average transition temperature is 47.2 ± 0.7°C, the average van't Hoff enthalpy is 93 ± 3 kJ mol⁻¹, and the average calorimetric enthalpy is 32 ± 1 kJ mol⁻¹. The average transition cooperativity, Δ_trsH/Δ_vHH, is 0.34 ± 0.06, much lower than the ideal 1.00 for a two-state transition. Similar results were obtained with the cDNA solution (not shown). A fit of a two-state transition model to the cDNA transition data yields a higher transition temperature of 57.3 ± 0.5°C, a van't Hoff enthalpy of 120 kJ mol⁻¹, and a calorimetric enthalpy of 30 kJ mol⁻¹.

FIGURE 7.

First and second DSC scans of a 0.124-mM solution of sDNA in the phosphate buffer (upper curves) and a fit of the A↔B transition model to the first scan with the transition temperature marked by the broken vertical line (lower curve).

TABLE 7.

Thermodynamics quantities from DSC measurements on the thermal unstacking transition of sDNA

Conc. (mM)	[NaCl]		ΔvHH	ΔtrsH
mM	M	Tm°C	kJ/mol	kJ/mol	ΔtrsH/ΔvHH
1.29	0.100	47.8 ± 0.4	96 ± 5	22 ± 2	0.23 ± 0.03
0.41	0.100	47.3 ± 0.5	95 ± 5	32 ± 3	0.34 ± 0.04
0.124	0.100	47.5 ± 0.5	90 ± 5	30 ± 3	0.33 ± 0.03
0.21	0.020	46.1 ± 0.5	92 ± 5	33 ± 2	0.36 ± 0.04

DISCUSSION

The helical, cylindrical, and random coil models exhibit the same dimensional changes with temperature. The overview of the three-dimensional changes of the sDNA in solution from these three models is that it undergoes an expansion in the diameter direction that causes a slightly shortened length as the temperature increases from 25°C to 43°C. Then, as the temperature increases further from 43°C to 53°C, it expands in the length direction as the diameter decreases. Finally, the sDNA increases dramatically both in length and diameter as the temperature is further increased from 53°C to 80°C. The midpoint of 47°C where these changes occur corresponds to the transition temperature of 47.5 ± 0.5°C for the conformational change determined from the UVM and DSC measurements. Furthermore, the low calorimetric enthalpy corresponds to a transition occurring over a very broad temperature range. These conformational changes correspond to the unstacking of the A and G purines as well as the T and C pyrimidines in 5′-ATGCTGATGC-3′ as the temperature is increased. The unstacking is manifested in molecular motion of the nucleotides in and out of the cylindrical axis (an increase in diameter) and in the stretching of the helix or cylinder (increase in pitch). The increase in the optical density upon melting of the single-strand substantiates the SANS results since the optical density changes indicate exposure of the purine and pyrimidine bases to a more polar (water) environment. The stacking is the result of hydrophobic interactions between the purines and pyrimidines that is enthalpically driven so that in the DSC scan, the unstacking transition occurs as an endothermic transition. The stacking enthalpies of single-stranded ribonucleic acid sequences, poly A and poly C, are, respectively, −33 kJ mol⁻¹ (14) and −33 ± 4 kJ mol⁻¹ (15) and are the same as the average calorimetric enthalpy of −30 ± 3 kJ mol⁻¹ for 5′-ATGCTGATGC-3′.

The melting temperature of a DNA duplex is usually used as an index of the stability of the duplex at ambient temperatures. This is based on the assumption that the melting or dissociation of the duplex yields the same final thermodynamic (random coil state) at both high and ambient temperatures. However, as shown from the SANS, UVM, and DSC results, this is not the case since the final random coil state at the duplex melting temperature becomes stacked as the temperature is decreased to ambient temperatures. Just how this affects the extrapolation of the high temperature results to low temperature and the use of the melting temperature as an index of the stability of the duplex is shown in the thermal cycle below,

where T_m is the melting temperature of the duplex, and T_s and T_c are the coil/stack transition temperatures for the sDNA and cDNA strands, respectively. The free energy change for association of the two strands to form a duplex is then related to the dissociation of the duplex at high temperature through

(3a)

If the single-strand products are in the same random coil conformation at T and T_m, then Eq. 3a becomes simply

(3b)

where Δ_aC is the heat capacity change for the association reaction. Neglecting Δ_aC, Eq. 3b simplifies to

(3c)

In the actual case with both strands undergoing a stacking/coil transition as the temperature is increased, the actual Δ_assG(T) at any value of T is a composite of the four possible types of reactions, as

(4a)

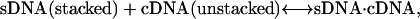(4b)

(4c)

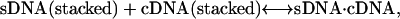(4d)

with Reaction 4a at the high temperature limit, Reaction 4d at the low temperature limit, and the distribution of each reaction's contribution to the actual Δ_assG(T) depending on the temperature. Reaction 4a corresponds to the temperature dependence given by Eq. 3b. However, if Δ_aC for the heat capacity of the other reactions is also neglected, then the temperature dependence of Δ_assG(T) becomes

(5)

For example, the use of Eq. 3b alone yielded an extrapolated DSC value of 46 ± 2 kJ mol⁻¹ for melting of the duplex sDNA · cDNA at 23.4°C, which is not in agreement with 37.5 ± 0.5 kJ mol⁻¹, the reverse of the association process measured by isothermal titration calorimetry at 23.4°C (3). The difference of 8.5 kJ mol⁻¹ between the two values at 23.4°C, however, can be accounted for by Δ_trsH(Ts){1 − T/T_s}= 4.6 ± 0.5 kJ mol⁻¹ obtained for the stacking transition of sDNA and by Δ_trsH(Tc){1 − T/T_c}= 2.65 ± 0.2 kJ mol⁻¹ obtained for the stacking transition of cDNA. Clearly, in this case, without taking the thermodynamics of the conformational change of the sDNA strands into consideration, the extrapolation of the melting duplex thermodynamics to ambient temperatures can lead to incorrect results.

Many biological processes in the cell such as transcription of genes into messenger RNA by RNA polymerase involve DNA duplex separation into single-stranded DNA, and predominant stacking of the separated DNA may promote the transcription process. The stacking conformation would also enhance the thermodynamic stability of single-stranded DNA in the cell. Interestingly, the transition temperatures for the single-stranded DNA also depends on sequence since the transition temperature is 47.5 ± 0.5°C for 5′-ATGCTGATGC-3′ and 57.3 ± 0.5°C for its complementary sequence 5′-GCATCAGCAT-3′. This dependence of the conformational change in single-stranded DNA on the sequence warrants further study of the conformational change in other DNA sequences. It is also not known as to how the single-strand transition depends on the length of the strand. Finally, the geometrical changes described by the SANS results would permit calculations of changes in the solvent-accessible surface areas as the DNA transforms from a stacked to an unstacked conformation and, in analogy to the unfolding of proteins, such changes have been linearly, albeit empirically, related to the thermodynamic parameters of the unfolding heat capacity change and unfolding enthalpy change for the protein (16,17). It is possible such an approach may be employed here but first the unstacking thermodynamic parameters of a large number of DNA sequences must be experimentally determined to yield and test such an empirical relationship.