Frequency Modulation Atomic Force Microscopy Reveals Individual Intermediates Associated with each Unfolded I27 Titin Domain

Abstract

In this study, we apply a dynamic atomic force microscopy (AFM) technique, frequency modulation (FM) detection, to the mechanical unfolding of single titin I27 domains and make comparisons with measurements made using the AFM contact or static mode method. Static mode measurements revealed the well-known force transition occurring at 100–120 pN in the first unfolding peak, which was less clear, or more often absent, in the subsequent unfolding peaks. In contrast, some FM-AFM curves clearly resolved a force transition associated with each of the unfolding peaks irrespective of the number of observed unfolded domains. As expected for FM-AFM, the frequency shift response of the main unfolding peaks and their intermediates could only be detected when the oscillation amplitudes used were smaller than the interaction lengths being measured. It was also shown that the forces measured for the dynamical interaction of the FM-AFM technique were significantly lower than those measured using the static mode. This study highlights the potential for using dynamic AFM for investigating biological interactions, including protein unfolding and the detection of novel unfolding intermediates.

INTRODUCTION

The reversible unfolding of immunoglobulin (Ig) domains in the I-band region of the modular protein titin is believed to function for the passive elasticity of muscle. Along with other proteins (e.g., barnase) (1), the mechanical unfolding of the well-defined tertiary structure of the wild-type titin Ig 27 domain (I27) has been studied extensively using atomic force microscopy (AFM) in the static mode (i.e., the DC-deflection of a nonoscillating cantilever is measured) (2–6). By stretching recombinant proteins consisting of multiple repeats of a single domain using AFM, a suite of information on protein folding has been revealed, including the mechanical unfolding forces of individual domains, kinetic parameters for both unfolding and refolding pathways, determination of unfolding intermediates, and comparison of forced unfolding with physiological or chemical denaturant unfolding (for reviews, see Best and Clarke (7) and Fisher et al. (8)). Related to this study, an unfolding intermediate due to the disruption of hydrogen bonds between A and B β-strands of the I27 domain was initially indicated using steered molecular dynamic (SMD) simulations (9) and later confirmed in AFM measurements (3).

More recently, two major types of dynamic AFM (where the cantilever is oscillated), amplitude modulated (AM) and frequency modulated (FM), have been used to study various biological force interactions, including ligand-receptor interactions (10,11), polysaccharides elasticity (12–14), nucleic acids/peptides (15,16), and proteins (17–19). These techniques typically involve oscillating the cantilever well below, or at, the resonance frequency to detect changes in the amplitude, phase, and/or resonance frequency that occur in response to changes in the interaction force. Attempts are then made to quantify the force, though this can be complex in most cases. In relation to protein unfolding, Okajima et al. (18) were able to detect a suggested refolding response of the hydrophobic core in a single monomeric globular protein, and Janovjak et al. (19) revealed novel unfolding peaks in the unfolding of bacteriorhodopsin protein from native purple membrane. Pertinent to this study, Forbes and Wang (20) used AM-AFM to measure the unfolding response of native titin from skeletal muscle myofibrils. These authors revealed the typical periodic sawtooth pattern, though they also detected additional peaks in the stiffness measurements that were suggested to correspond to structural transitions or intermediates during unfolding. Due to the heterogeneity of the ≈300 globular domains in the native titin and apparent lack of correlation between the peaks in the simultaneous stiffness and force measurements, the assignment of the additional peaks to specific unfolding intermediates was not feasible. However, the study importantly highlighted the ability of the dynamic technique to detect transitions that could not easily be detected in the force measurements alone. The recent advance toward polymer pulling experiments using dynamic methods is due to this possibility of achieving a greater force resolution and ability to obtain additional information on the dissipative components of the force.

In contrast, for this study, we use FM detection to investigate the unfolding of tandem repeats of the I27 domain and make comparisons to static measurements that are also performed in the study. As mentioned above, an intermediate in the first unfolded peak has previously been observed using static mode AFM (3), though the transition in the force due to the intermediate becomes very unclear, or is more often absent, with subsequent unfolded domains. By performing dynamic measurements on a well-defined modular protein, such as titin I27, that has a known intermediate, we were able to detect corresponding individual unfolding intermediates for each peak in the force-extension curves. In addition, the intermediate could clearly be observed in the final unfolded domain (eighth peak) for an I27 construct with eight domains. This highlights the potential of dynamic techniques for future studies on protein folding, including the detection of novel unfolding intermediates.

MATERIAL AND METHODS

Construction of wild-type TI I27 multimer

Recombinant methods used to express and synthesize direct tandem repeats of wild-type TI I27 consisting of eight individual modules or domains were performed according to the recent study by Steward et al. (21).

Static mode force measurements on titin protein

Cleaved round 1 cm mica surfaces on Teflon were coated with titin protein by pipetting 100 μL of 30 μg/ml protein suspension in phosphate-buffered saline (PBS) buffer onto the mica surface. The mica surface was immersed for 15 min to allow for sufficient adsorption of the protein and then washed by exchanging the protein solution (three times) with fresh PBS buffer. The protein-coated mica surface was then mounted on the AFM sample stage and static mode force measurements performed using an Asylum Research MFP-3D AFM (Santa Barbara, CA). Force measurements were taken using Mikromasch silicon nitride cantilevers that were calibrated using the plan view method and had measured spring constants 40–100 pN/nm. Force measurements were taken with a piezo velocity of 1 μm/s and numerous force curves obtained on different positions on the protein substrate. Analysis of the force curves, including worm-like chain model (WLC) fitting to the elastic response of the extended protein, was performed using the Asylum Research AFM IGOR Pro software (Wavemetrics, Lake Oswego, OR).

Frequency modulation detection (dynamic) measurements on titin protein

Preparation of cantilevers for magnetic activation

First, a nanosensor silicon cantilever was calibrated as above and had a measured spring constant of 1.2 N/m. A glass encapsulated NdBFe (neodymium/boron/iron) particle was then glued (Epotek 41) onto the back of the cantilever, directly behind the tip, with the aid of an optical microscope and micromanipulator. The particle was then magnetized using an impulse magnetizer (ASC Scientific, (Carlsbad, CA), Model IM-IO-ZO) by positioning the cantilever at an angle of 12° from the normal surface (i.e., tip angle in AFM holder) and applying a charging voltage of 300 V, corresponding to a magnetic field strength of 37.3 kG, for 30 s.

Modification of AFM for frequency modulation detection

Force measurements were taken using a modified Asylum Research MFP-3D to enable frequency modulation (FM) detection in liquid. This was achieved by implementing magnetic activation dynamic (MAD) mode (22–24), whereby the cantilever with attached magnetic particle was oscillated by applying an external magnetic field via a solenoid positioned underneath the sample stage. For this setup, the voltage to the coil was amplified using a homemade ‘coil driver’, and the solenoid replaced the position of the objective lens in the AFM base. To regulate the FM detection scheme, we used a Nanosurf (Liestal, Switzerland) Phase-Loop-Lock controller/detector (PLL). The PLL used two feedback systems to control the dynamic force measurements. One feedback system kept the oscillation amplitude of the cantilever constant by varying the driving voltage to the coil. A second feedback system shifted the phase signal of the lever response to 90°, which was then used as the excitation signal to keep the lever oscillating at its fundamental eigenfrequency. By monitoring changes in the resonance frequency and excitation amplitude required to keep a constant oscillation amplitude, we were able to measure frequency shift and dissipation caused by the tip sample interaction. The AFM was controlled using a modified version of the Asylum Research software (IGOR Pro, Wavemetrics).

In contrast to previous dynamical techniques (12–14), a DC-deflection signal was not acquired simultaneously with the frequency shift and dissipation. This was because the FM-AFM technique in liquid required the use of stiffer levers (i.e., 1.2 N/m) with higher resonant frequencies to reduce frequency noise and maintain a stable cantilever oscillation. Thus, the increase in the cantilever stiffness dramatically reduced the DC deflection sensitivity and made obtaining simultaneous DC measurements difficult. More importantly, by using relatively large oscillation amplitudes (i.e., 4.5 nm, 6.2 nm, 11.5 nm, 26.5 nm), the DC deflection probes the average force experienced by the tip during one oscillation cycle, leading to complexity in its interpretation and comparison to standard DC measurements.

Frequency modulation measurements on titin and data analysis

Titin protein-coated mica surfaces were prepared for AFM, as above. Before taking measurements, the resonance frequency of the cantilever (18.47 kHz) in PBS buffer, with attached magnetic, was obtained by performing a thermal power spectrum. Frequency shift curves were taken with a piezo velocity of 1 μm/s and varying oscillation amplitudes of 4.5 nm, 6.2 nm, 11.5 nm, and 26.5 nm. Importantly, physisorption of the protein to the cantilever tip could be achieved only when the tip was set to dwell for 3–5 s during intermittent contact with the mica surface before retraction.

Frequency shift (volts) versus extension (nanometer) curves were obtained and converted to frequency shift (hertz) curves using the sensitivity value (73.4 Hz/V) of the PLL. To convert the observed frequency shift into an interaction force 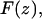the formulation recently proposed by Sader and Jarvis (25) was used,

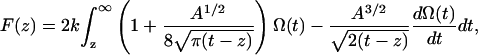(1)

where k is the spring constant, A is the oscillation amplitude of the tip, 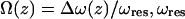is the natural resonant frequency of the cantilever in the absence of an interaction force, and z is the distance of closest approach between the tip and the surface. Note that 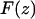is the conservative component of the interaction force between tip and sample and does not include any contribution due to dissipative effects. This formula is valid for any A and requires that the interaction force be continuous throughout the measurement. However, our curves contained an apparent discontinuity in the interaction force at the moment of unfolding of each I27 domain (i.e., peak-to-trough transition). To satisfy the requirement of the formula, we investigated only the region where the force was continuous, which corresponded to the elastic response of the unfolded polypeptide. Equation 1 also required that the force decay to zero as the tip-surface distance approaches infinity, which is not the case in our measurements, i.e., the interaction force increases with increasing separation, with the maximum attractive force experienced by the tip being on the retract portion of the oscillation cycle. To address this, we effectively treated the elastic response of the unfolded region as we would for a repulsive interaction that is experienced during an approach to the surface. In doing so, the data to be analyzed were reversed so that the peak maximum of the unfolding event corresponded to the origin of a hypothetical surface. The effect of frequency noise, exacerbated by a derivative step in the force conversion, was eliminated by using a polynomial fit of the unfolding region for the analysis.

It is noted that this technique relies on measuring the change in resonance frequency of the cantilever upon application of an interaction force. Equation 1 unifies previously established theoretical work (26) by allowing for the unequivocal determination of the interaction force, for any oscillation amplitude. The constant-amplitude approach implicitly decouples the influence of conservative and dissipative force. Equation 1 thus gives a direct connection between the change in frequency and the true interaction force, with no ambiguity, and is a dynamic analogy of Hooke's law for FM-AFM constant amplitude measurements. The above analysis procedure has been explained in detail previously (11) and used to calculate unbinding forces of single ligand receptors interactions using a flexible linker.

RESULTS

Static mode force curves revealing protein unfolding and force transitions

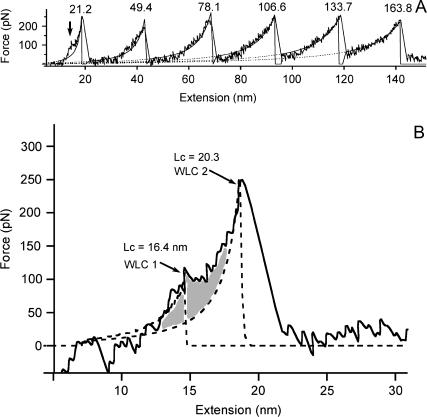
Static mode measurements performed to explain the principle of force-induced modular protein unfolding, and for comparison with FM detection, revealed that the protein had sufficiently adsorbed to both the cantilever tip and mica to enable the unfolding of the I27 domains during extension. Typical force-extension curves for the protein were observed (Fig. 1 A), whereby the sawtooth pattern with periodic spacing between adjacent peaks indicated the sequential unfolding of modular domains (six domains in this case) within the polymer construct. The mean spacing between peaks was found to be 25.4 nm ± 2.56 nm (mean ± SD, n = 52), indicating the nonfully extended length of the unfolded polypeptide. The error in the spacing may be due to the measurements being taken on a mica surface compared to a gold surface that is typically used to promote good binding. A reduction in the binding on the mica would lower the probability of observing an idealized protein unfolding curve (many curves are convoluted by multiple protein interactions) and thus may increase the measured error. WLC fitting to the elastic response of the unfolded polypeptide regions in Fig. 1, using the persistence length p as an adjustable parameter, gave an average p of 0.29 nm and change in contour length ΔL of 28.5 nm for each unfolding event. It is noted that the elastic response in the first peak does not represent an unfolded polypeptide, but the elastic properties of the polymer construct with fully folded domains (i.e., no domains have yet unfolded). The p and ΔL were in agreement with the stretching of a single titin I27 molecule and were consistent throughout all curves that showed similar force-extension profiles. The average peak force was measured to be 208 ± 43 pN (n = 93), which was in the range for unfolding forces previously measured at similar tip velocities. As previously reported, the elastic response of the first unfolding peak was not well described by the WLC due to a known force transition, observed as a ‘hump’, occurring at ∼100 pN (Fig. 1, A and B). This force transition was regularly observed in the first peak (Fig. 1 A) but became less clear, or was mostly absent, with increasing peak number (data not shown). For the force curve shown in Fig. 1 A, the transition could not be observed past the first peak. Fig. 1 B shows an expanded image of the first unfolding peak from Fig. 1 A, which consists of two WLC fits, one to the elastic response of the fully folded polymer construct before the force transition (WLC 1) and after the transition (WLC 2). With p set at 0.4 nm (3), ΔL between both fits was measured to be 3.9 nm.

FIGURE 1.

(A) Typical force-extension curve for the unfolding of repeating titin I27 domains in recombinant protein. The sawtooth pattern with periodic spacing of 25.4 nm ± 2.56 nm for all recorded peaks (n = 52) indicated the sequential unfolding of modular domains. WLC fitting to the elastic response of the unfolded polypeptide region (with the exception of the first peak) of each peak in the figure gave a mean persistence length of 0.29 ± 0.04 nm and change in the contour length of 28.5 ± 1.1 nm. The first peak (leftmost peak beginning at zero extension) was not fitted well by the WLC due to the force transition (arrow) occurring at a force of ∼100 pN. The force transition was not observed in the subsequent unfolded domains. (B) Expanded image of the first unfolded peak from A clearly showing the occurrence of the force transition. WLC fitting, with the persistence length set at 0.4 nm, to the elastic response of the polymer construct with fully folded domains before the transition (WLC 1) and after the transition region (WLC 2) gave contour lengths of 16.4 nm and 20.3 nm, respectively. A previous relationship shows that the ΔL for these two WLC fits to the first unfolded peak increases with an increase in the observed number of unfolded domains. A ΔL of 3.9 nm for the WLC fits in the figure agrees with the described relationship for the observed unfolding of six domains, as in A.

The analysis of the intermediate using two WLC fits was performed according to previous work first describing the intermediate (3), and the ΔL value obtained is used to describe the accumulated lengthening of the folded domains in their native state during extension. Our ΔL value fell on the linear regression slope for the previously observed relationship between ΔL in the first unfolding peak and number of unfolded domains observed in the force-extension curve (3). A full statistical analysis is still required to make a comparison with the previous work mentioned, as the first peak is known to be convoluted by the effects of various protein-surface and protein-protein adhesive interactions. For the purpose of this work, we give only an example of this WLC fitting procedure to provide background detail on the intermediate.

Frequency modulation detection revealing individual force transitions of each module

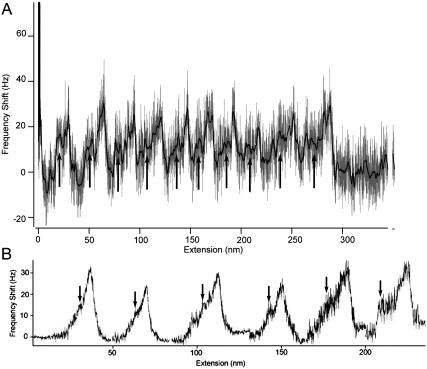
FM detection measurements revealed sawtooth patterns in the frequency shift curves, indicating that the dynamic technique was also able to detect the sequential unfolding of domains in the I27 protein construct (Fig. 2 A, light gray trace). The mean spacing between adjacent peaks in curves for A values of 4.5 nm, 6.2 nm, and 11.5 nm was found to be 25.2 ± 2.9 nm (n = 35), 25. 3 ± 3.4 nm (n = 61), and 24.6 ± 3.1 nm (n = 13), respectively. Thus, irrespective of A, the mean spacing agreed with the nonfully extended length of the unfolded polypeptide region measured in the static force measurements. In addition to the main frequency peaks representing the onset of an unfolded domain, a second smaller peak was also observed to be associated with each of the main unfolding peaks (Fig. 2 A). These secondary peaks were very difficult to observe in the raw frequency shift curves due to the significant noise level. A smoothed curve of the frequency shift (dark line) also revealed the secondary peaks, which appeared as a small increase in the frequency shift to ∼15–18 Hz to form a discontinuity in the initial frequency shift (Fig. 2 A, arrows), followed by a further increase in the frequency shift corresponding to the main unfolding peak. This discontinuity in the frequency shift of the main unfolding peaks appeared to indicate the presence of a force transition, presumably that observed in the static measurements. However, we stress that the secondary peaks observed in the smoothed frequency curve do not represent the true structure of the transition and must be further validated, as the binominal smoothing process applied consists of both the feature of the transition and frequency noise. To validate the true presence and structure of the transition for the different unfolded domain numbers, we performed an averaging process for all measured peaks obtained for A of values 4.5 nm and 6.2 nm and according to their unfolding number (Fig. 2 B). This is possible because the frequency noise had a mean of zero and is additive to the true signal (26). This property enabled the noise to be minimized by averaging multiple measurements of the same interaction to leave the underlying true signal undistorted. The averaged frequency shifts for the different folded domains are shown in Fig. 2 B. We emphasize that these measurements were highly reproducible and independent of the number of averages taken. In addition, averaging a greater number of peaks reduced the noise level without distorting the underlying curve and thus demonstrated the validity of this procedure. Fig. 2 B revealed that the intricate structure of the transition appeared to be hump-like or a plateau that occurred at a consistent frequency shift of ∼15–18 Hz and had a slight tendency to increase in length with an increase in the unfolding number. In some curves, the intermediate was not always present for every unfolded domain in the frequency shift curves, as highlighted in the first few peaks for the top curve (4.5 nm) in Fig. 3 A. The absence of the intermediate may have been due to a reduction in the signal because of the apparent frequency noise highlighted in Fig. 2 A. Interestingly, the intermediate was always clearly resolved in the final unfolded domain for the I27₈ construct.

FIGURE 2.

(A) Frequency shift versus extension curve (light gray trace) for the sequential unfolding of titin I27 domains taken using a resonance frequency f of 18.5 kHz and oscillation amplitude A of 6.5 nm. The mean spacing for A values of 4.5 nm, 6.5 nm, and 11.5 nm were 25.2 ± 2.9 (n = 35), 25.3 ± 3.4 (n = 61), and 24.6 ± 6 (n = 13), respectively, indicating the successful unfolding modular domains using this dynamic technique. The curve shows 10 peaks with each peak recording a positive frequency shift of ≈25 Hz. The first two peaks, which are slightly greater in magnitude than the remaining eight, may be due to multiple binding of proteins (i.e., the peaks correspond to an additional protein molecule on the tip). During extension, the increasing stiffness of the unfolded polypeptide region restricts the cantilever movement, causing an increase in the effective spring constant k_c of the cantilever. Thus, an increase in k_c causes a direct increase in the cantilever resonance frequency, which is observed as a positive frequency shift in the unfolding peaks. A smoothed curve (dark line) clearly shows a discontinuity (arrows) in the positive frequency shift of the main unfolding peak, indicating the unfolding intermediate. (B) Graph showing averaging of all peaks showing intermediates (from A = 4.5 nm and 6.5 nm) and according to their unfolded domain number, which was done by superimposing and aligning each peak at their peak maximum. The distance between peaks is negligible, and the noise in each peak increases with the unfolded domain number due to the fewer numbers of samples averaged. The distance from the beginning of the force transition (arrow) to the peak maximum showed a slight increase with an increase in the unfolded domain number. These distances were calculated to be 5.6 nm (peak 1), 6.6 nm (peak 2), 7.9 nm (peak 3), 8.1 nm (peak 4), 10.9 nm (peak 5), and 14.4 nm (peak 6).

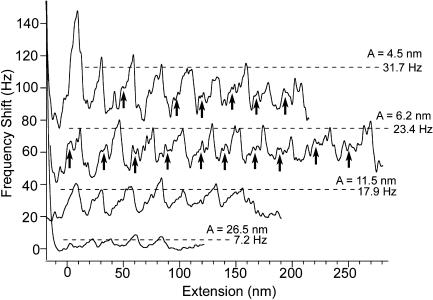
FIGURE 3.

Comparison of unfolding peaks obtained using a range of oscillation amplitudes. Peaks for A = 4.2 nm and 6.2 nm mostly show a clear unfolding intermediate (arrows) in the frequency shift (the intermediate is not clear for three peaks in A = 4.2 nm, no arrows) compared to A = 11.5 nm. For A = 26.5 nm, the peaks do not correspond to a specific unfolded domain number, as measurements for this amplitude showed irregularities in the peak spacing. The frequency shift of the peaks increases with a decrease in A according to Δf ≈ ΔF/A^1.5, as given in Eq. 1.

In comparison to smaller A values of 4.5 nm and 6.2 nm, force transitions were not observed in the unfolding peaks, or were albeit very unclear, for the A of 11.5 nm (Fig. 3), whereas only some irregular peaks were observed for the A of 26.5 nm (Fig. 3). In addition, frequency shifts were greater for smaller amplitudes, which was expected due to Δf ≈ ΔF/A^1.5, as given in Eq. 1 (Fig. 3). Conversion of the frequency shift curves into an interaction force, as outlined in the Material and Methods section and shown in Fig. 4, A and B, surprisingly resulted in much lower unfolding forces compared to static mode measurements (Fig. 4 B). Average peak unfolding forces were found to be 75 ± 19.9 pN (n = 37), 63.1 ± 20.2 pN (n = 54), and 63.9 ± 7.9 (n = 14) pN for A values of 4.5 nm, 6.2 nm, and 11.5 nm, respectively, indicating that the same force law was recovered irrespective of the oscillation amplitude used.

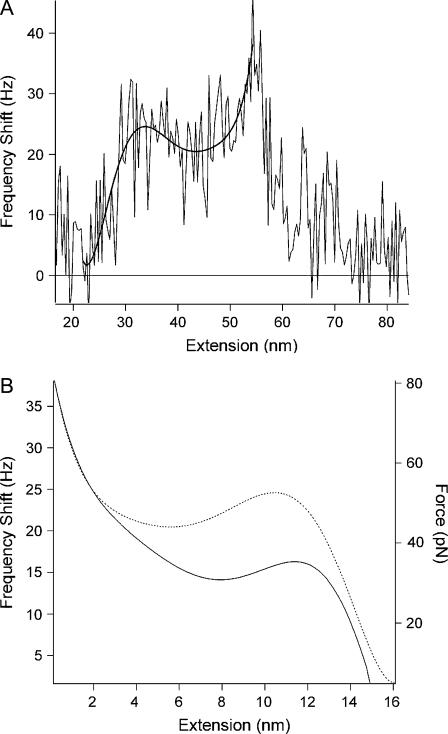
FIGURE 4.

(A) Diagram showing method for the conversion of the frequency shift curves to a force. The elastic response of the unfolded polypeptide region in the frequency shift curves was fit to a polynomial (smooth trace), which was then reversed so that the peak maximum occurred at zero extension distance that corresponded to the origin of a hypothetical surface. (B) The force (solid line) was then calculated from values of the fit using Eq. 1. The mean forces were 75 ± 19.9 pN (n = 37), 63.1 ± 20.2 pN (n = 54), and 63.9 ± 7.9 (n = 14) pN for A values of 4.5 nm, 6.2 nm, and 11.5 nm, respectively. The intermediate unfolding forces were typically half, or just below half, of the unfolding force, as observed in the force curve. The corresponding reversed frequency shift curve (dotted line) is plotted for comparison and shown to reflect the force profile.

DISCUSSION

The Ig I27 domain in native titin or as tandem repeats in recombinant polypeptides is unique compared to other modular proteins in that individual domains unfold via an intermediate when under an applied force. SMD simulations (9) show that this intermediate results from the rupture of two hydrogen bonds bridging the A and B β-strands, which is expected to proceed before the detachment of the A′ and G strands. The latter process presumably renders the C- and N-terminal free to unravel, causing the domain to completely unfold. This intermediate has been directly observed previously using AFM (3) with similar results repeated in this study for comparison with dynamic techniques. In these static mode AFM studies, the intermediate is observed as a prominent ‘hump’ or force transition in the first unfolding peak occurring at ≈100–120 pN that subsides, or is not present, in subsequent unfolding events. Data showing an increase in the change of contour length in the first unfolding peak, as described in Fig. 1 B, as a function of an increase in the number of observed unfolded domains are used to explain a 15% lengthening or 6.6 Å extension of a resting domain during the force transition (3), which agrees with previous SMD observations (9). It is suggested that the force transition in the first peak corresponds to the accumulation transitional lengthening of all the folded domains, whereas the reappearance of smaller transitions in subsequent peaks describes the process as being reversible before the next unfolding event takes place. However, the latter point is still vague, as a review of the literature reveals that it is very difficult to discern the transition past the second unfolding peak, or third peak at most, even when many domains are observed to have unfolded. This observation is also apparent in the static mode curves measured in this study. To address this issue, we have shown here that FM detection is able to detect individual transitions associated with each domain regardless of the number observed in the force-extension profile. This is perhaps in most part due to the FM detection technique being more sensitive to the force in the z direction compared to the static mode. The transition cannot be explained due to refolding due to the following: partial refolding (i.e., the entire domain is not relaxed) would only be possible on the downswing of an oscillation cycle and where the cantilever spends most of its time at the bottom of the cycle. However, the time period for a complete oscillation cycle (1/f = 54 μs) is much smaller than the time required for domain refolding (5). In addition, a greater opportunity for refolding should be the case for the larger amplitude of 11.5 nm due to sampling farther back (i.e., during the downswing of an oscillation) along the refolding pathway, though these measurements showed only peaks corresponding to the unfolding of the domains, indicating that refolding was not evident.

The ability to detect both discrete unfolding events and their intermediate in titin I27 is dependent on the size of the A being smaller than the length scale of the interactions intended for measurement. In this case, the predominant length scales for an individual unfolding event and its intermediate are ∼25 nm and 10–15 nm, respectively. For amplitudes much greater than these length scales, such as the 26.5 nm used here, it is apparent that the detected frequency shifts become smaller and less clear. This decrease in the frequency shift is expected as the interaction force of a single unfolding domain is averaged over a larger distance in comparison to smaller amplitude measurements, i.e., a shorter portion of the oscillation cycle experiences the interaction force for larger amplitudes. Furthermore, in the case of modular proteins, a single oscillation cycle with large amplitude may contain different components of the unfolding force profile, including unfolding one domain while stretching another. This can lead to discontinuities in the force and make interpretation of the data difficult. For an A value of 11.5 nm, discrete frequency shifts can be detected for each unfolded domain, though the intermediate is smoothed out due to a decrease in the frequency shift when sampling this comparable length scale. In contrast, both of the smaller A values (4.5 nm and 6.2 nm) are most sensitive to both the length scales in question. Due to the complexity of protein structure and composition, the length scales of interactions determining unfolding pathways will be highly variable and be protein specific. Therefore, the ideal situation for these types of measurements would be to use the smallest achievable amplitude to account for all possible interactions. Here in this study, the use of smaller amplitudes was limited due to the stability of the oscillation and size of the frequency noise, though further AFM modifications are being made in an attempt to reduce amplitudes to subnanometer values.

As predicted by Eq. 1, similar unfolding peak forces were obtained, irrespective of A, which supports the validity of the approach. Thus, it remains unclear why the measured forces (≈70 pN) are significantly lower than the forces obtained in static force measurements (≈208 pN). This observation is in contrast to previous dynamic studies where measured forces are comparable to the statically measured forces of the same system. For example, two different dynamic approaches were able to measure the chair-to-boat transition forces (700–1000 pN) of single dextran polysaccharides (12,14), which were comparable to those measured independently in earlier static mode studies (27). For the latter dynamic studies, the forces were obtained by filtering out the dynamic signal to obtain the static deflection of the cantilever. In contrast, here, the force is determined directly from the dynamic signal (frequency shift). We now discuss possible reasons for the lower forces observed with our dynamic technique. Errors in the measured frequency shift may arise if the interaction response of the molecule occurs on a shorter timescale than the time constant of the PLL. In which case, a positive frequency shift would be underestimated (as too the force) due to the delayed response of the PLL not being able to track the frequency shift increase. However, for the measurements here, the 400 Hz bandwidth of the PLL is sufficient to correctly track significantly larger frequency shifts during the ≈35 ms timescale of the elastic response of the unfolded polypeptide. Therefore, the frequency shifts recorded here would pertain to being real. The converted forces were obtained using a recently developed arbitrary amplitude formula (Eq. 1) (25) that unifies two previous well-established formulas that describe the relationship between the frequency shift and force (26,28,29). The fact that the unfolding forces scale correctly with respect to A validates the unification of the two previous formulas within Eq. 1. This arbitrary amplitude formula has also been experimentally validated by quantifying the structural forces of liquids whereby the forces scaled appropriately with A and, importantly, agreed with the forces previously measured for the same liquid using a different technique (i.e., surface force apparatus) (30). Without any previous constant amplitude FM measurements on modular proteins for comparison, we speculate that the lower unfolding forces may relate to the discontinuity in the force interaction during a single oscillation cycle of the tip as the domain unfolds (e.g., during the intermediate). This discontinuity in the force may occur if bonds are broken during the upswing of an oscillation cycle and are unable to reform on the timescale of the cantilever oscillation, even when the domains are allowed to relax during the downswing. As a result, the oscillating cantilever would be repeatedly sampling through the force interaction of already unfolded domain regions, with the effective averaging of the force resulting in potentially lower values. In addition, the potential for the force to vary as a function of the measurement technique has also recently been observed for the folding and refolding of individual proteins (31). To alleviate possible discontinuities in the force, appropriate modifications to the force analysis have been outlined in the Material and Methods section and other studies (11), though further investigation is required to assess the possible additional effects due to the disruption of hydrogen bonds during the intermediate.

As mentioned, previous dynamic AFM studies have shown that extended single polysaccharide chains also display force transitions that are comparable to those previously observed in static mode measurements (12–14), and novel transitions and intermediates have also been reported in recent experiments on proteins. Both Mitsui et al. (17) and Okajima et al. (18) measured an out-of-phase response in the cantilever deflection signal for a partially unfolded protein and attributed the response to refolding. Recently, Janovjak et al. (19) dynamically unfolded single bacteriorhodopsin proteins from native purple membranes to reveal novel force peaks that were ascribed to an intermediate involving kinks in the α-helices, though the possibility of refolding due to relaxation was noted.

CONCLUSION

The aim of this study was to investigate the possibility of detecting unfolding intermediates in I27 domains using FM detection, as the dynamic technique was proposed to be more sensitive in regions where tip instabilities normally occur for typical static mode measurements and to changes in the force gradient along the force-extension profile. Although the protein unfolding response in dynamic measurements was more complex compared to static measurements, it was clearly shown that the unfolding intermediate could be observed for each unfolded domain. Thus, this approach opens up the possibility of detecting novel unfolding intermediates in similar protein studies. Future work is ongoing to make a full statistical analysis of the effects of the oscillation amplitude and resonance frequency on the unfolding response of the protein. In addition, the implementation of subangstrom oscillation amplitude measurements is currently being developed and modified for operation in the liquid environment.