Detection of Forces and Displacements along the Axial Direction in an Optical Trap

Abstract

We present measurements of the forces on, and displacements of, an optically trapped bead along the propagation direction of the trapping laser beam (the axial direction). In a typical experimental configuration, the bead is trapped in an aqueous solution using an oil-immersion, high-numerical-aperture objective. This refractive index mismatch complicates axial calibrations due to both a shift of the trap center along the axial direction and spherical aberrations. In this work, a known DNA template was unzipped along the axial direction and its characteristic unzipping force-extension data were used to determine 1), the location of the trap center along the axial direction; 2), the axial displacement of the bead from the trap center; and 3), the axial force exerted on the bead. These axial calibrations were obtained for trap center locations up to ∼4 μm into the aqueous solution and with axial bead displacements up to ∼600 nm from the trap center. In particular, the axial trap stiffness decreased substantially when the trap was located further into the aqueous solution. This approach, together with conventional lateral calibrations, results in a more versatile optical trapping instrument that is accurately calibrated in all three dimensions.

INTRODUCTION

In the past two decades, optical trapping techniques have helped to revolutionize mechanical studies of single biological molecules. When a biological molecule is attached to an optically trapped bead, forces exerted by, and displacements of, the biological molecule can be detected via those of the trapped bead. Essential to these techniques are accurate force and displacement calibrations of the optical trapping system. Calibration methods for lateral directions (perpendicular to the laser propagation) have been well established (for a review, see Svoboda and Block (1)). However, those for the axial direction (laser propagation direction) have proved to be much more challenging.

In general, both lateral and axial calibrations are desirable for an accurate measurement. When the motion to be detected is only along the lateral directions, lateral calibrations are generally sufficient (for representative examples, see Svoboda et al. (2), Molloy et al. (3), Smith and Bustamante (4), Wuite et al. (5), deCastro et al. (6), Liphardt et al. (7), and Shaevitz et al. (8)). However, in many other experimental configurations, the motion to be detected has both a lateral and an axial component. For example, in studies of the RNA polymerase motor (9–12), the polymerase is attached to the surface of a microscope coverglass while one end of the DNA to be transcribed is attached to a trapped bead (or vice versa). Translocation of the polymerase produces both a lateral and an axial motion of the trapped bead. Axial contributions start to dominate the signal for a short DNA tether between the trapped bead and the polymerase. Besides studies of RNA polymerase, a number of other single-molecule studies adopt a similar experimental configuration (13–17). In fact, for DNA tethers shorter than the radius of the bead, it would be advantageous to operate solely along the axial direction to avoid having to deal with a complicated geometry. For these experimental configurations, it becomes imperative to accurately calibrate axial forces and displacements.

In a typical single-molecule experimental configuration, the bead is trapped near the laser focus in an aqueous solution across a microscope coverglass from an oil-immersion, high-numerical-aperture (NA) objective. The refractive index mismatch between the aqueous solution (index of refraction 1.33) and coverglass (index of refraction 1.52) produces a shift of the laser focus from its nominal focus along the axial direction and distorts the laser-beam profile (spherical aberrations). These effects are more evident for a system with a large numerical aperture objective, an overfilling laser beam at the back focal plane of the objective, and a deep focusing of the objective into the aqueous solution. Furthermore, the trap center and the laser focus along the axial direction do not coincide due to the presence of the scattering force. This results in the trap center being located down-beam of the laser focus.

Therefore, three parameters must be established by axial calibrations. First, the location of the axial trap center relative to the coverglass surface (trap height) (see Fig. 1 A) needs to be accurately determined. Second, the axial displacement of, and, third, the axial force on, the trapped bead need to be calibrated against an axial detection signal. Theoretical work has shown that the latter two calibrations depend on the trap height due to spherical aberrations (18,19) and therefore they should be established experimentally at various trap heights.

FIGURE 1.

Experimental configuration. (A) Cartoon of the unzipping configuration. A DNA molecule is unzipped axially by moving the coverglass away from an optically trapped bead. The coordinate system (z) is fixed with respect to a stationary microscope objective. The left-hand cartoon shows that is defined as the position where the upper surface of the coverglass () just makes contact with a trapped bead. The right-hand cartoon shows that the DNA molecule is progressively unzipped as the coverglass is lowered at a constant velocity An index of refraction mismatch between the aqueous solution and the coverglass brings the laser focus closer to the objective as the coverglass is lowered. is the axial trap center location. is the axial bead center location. is the axial displacement of the bead center from the trap center. is the position of the upper surface of the coverglass. is the trap height defined as the axial distance between and (B) Schematic of the DNA molecule used for pattern matching (not to scale) (see text). The sequence of the ligation region is shown. The locations of the digoxigenin and biotin labels, and the nick are also indicated. (C) Axial detection resolution. A bead was fixed to the coverglass surface and positioned in the trap center. The coverglass position was moved axially in a 1-nm square-wave pattern (upper graph) while the normalized axial detector signal was recorded (lower graph). The 1-nm steps are clearly resolved by the axial detector.

Some aspects of these axial calibrations have been investigated experimentally. Trap height has been measured using two methods (20,21). One method measures the corner frequency of a trapped bead at different coverglass positions relative to a fixed objective. The relation between trap height and coverglass position is obtained by using the known relation of viscous drag coefficient versus trap height. This method requires the assumption that trap stiffness is independent of trap height and this assumption necessarily introduces some uncertainties in this conversion. A more accurate method takes advantage of an oscillatory axial signal that is observed as the coverglass is moved away from a trapped bead. The oscillations arise from interference between the beam and its reflection from the trapped bead. They are more evident with a less focused laser beam. Therefore, to make this method more feasible, a separate laser beam for detection is desirable.

In addition, the relation of axial displacement versus axial signal has been estimated (20–25). By moving the coverglass with a fixed or freely trapped bead through the trapping laser beam, the axial signal is detected as a function of the coverglass position. It is worth noting that this relation cannot be readily converted to bead displacement from the trap center versus axial signal, unless the relation of trap height versus coverslip position has been previously established. No calibrations of axial bead displacement versus axial signal have been established for trap heights away from the coverglass surface. Finally, the relation of axial force versus axial signal has only been measured for small bead displacements near the trap center (21).

In this work, we introduce a novel method that allows calibrations of all three parameters. By unzipping a single DNA molecule, the characteristic unzipping force-extension data were used as a reference signal for calibrations. The trap height was determined with exceptional accuracy without the need for a second laser beam for detection. The axial bead displacement and force versus axial signal were also calibrated for large ranges of bead displacement (up to ∼600 nm) and trap heights (up to ∼4 μm). We tested the accuracy of our calibrations by unzipping a known DNA template that was not used for calibrations and by stretching a known double-stranded DNA (dsDNA) along the axial direction.

MATERIALS AND METHODS

The experimental configuration for unzipping a single DNA molecule is shown in Fig. 1 A. One strand of a dsDNA molecule to be unzipped was attached to the surface of a microscope coverglass while the other strand was attached to a polystyrene bead. To unzip the dsDNA, the two strands of the DNA molecule were pulled apart by lowering the coverglass at a fixed rate while the bead was held in an optical trap.

As shown in Fig. 1 A, our coordinate system (z) is fixed with respect to the stationary microscope objective. The positive z direction is opposite to that of the laser propagation. We define 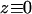to be the position of the upper surface of the coverglass when a trapped bead just barely makes contact with it. For experiments, the coverglass is generally moved closer to the objective and its position is denoted by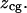 is the axial trap center position, defined as the equilibrium position for a trapped bead. is the position of the bead center. is the axial displacement of the bead center from its equilibrium position. The trap height is the axial distance of the trap center from the upper surface of the coverglass.

Biochemical materials

Three unzipping DNA constructs were made using methods similar to those previously described (17). Fig. 1 B shows a schematic of one of these constructs. One end of each DNA molecule was labeled with a digoxigenin (dig) for attachment to a coverslip via anti-digoxigenin (Roche Molecular Biochemicals, Indianapolis, IN). A nick in one of the strands was located 1.1 kb distant from the dig-labeled end. This strand was labeled with a biotin at 6 bp away from the nick for attachment to a streptavidin-coated bead with a radius R = 240 ± 4 nm (Bangs Laboratories, Fishers, IN). Each unzipping DNA construct was generated by ligation of an anchoring segment containing the dig label and a variable-length unzipping segment containing the biotin label.

The anchoring double-stranded segment (1.1 kbp) was derived from pRL574 (kindly provided by R. Landick; template 5 in Shafer et al. (26)). The dig label was a result of polymerase chain reaction (PCR) with a dig-labeled primer. After PCR, the segment was digested with BstXI (New England Biolabs, Beverly, MA), gel extracted, and ligated to the 3′ATCG overhang of an unzipping segment.

Unzipping segments of 0.6 kbp, 3.7 kbp, and 4.1 kbp were derived from the p601 plasmid (kindly provided by J. Widom (27)), the pBR322 plasmid (Invitrogen, Carlsbad, CA), and the pCP681 plasmid (kindly provided by C. L. Peterson (16)), respectively. The biotin label was a result of PCR with a biotin-labeled primer. The PCR product was digested with BstXI (New England Biolabs) and gel extracted, and the 5′ phosphate was removed with calf intestinal phosphatase (New England Biolabs) before ligation to the anchoring segment. The 0.6-kbp unzipping segment was also capped with a 33-bp hairpin at the distal end.

As discussed below, unzipping constructs with unzipping segments of 0.6 kbp, 3.7 kbp, and 4.1 kbp were used for determination of single-stranded DNA (ssDNA) elasticity parameters and estimation of basepairing thermodynamic parameters, for axial calibrations, and for verification of axial calibration results, respectively.

Another 3.7-kbp entirely dsDNA construct for verification of the axial calibration results was obtained by PCR from pCP681 as previously described (16).

Experiments were performed at room temperature (23°C) in a buffer containing 10 mM Tris, pH 7.5, 1 mM EDTA, 150 mM NaCl, 100 μg/ml BSA, 3% glycerol (v/v), and 1 mM DTT.

Instrumentation and lateral calibrations

Measurements were obtained using a single-beam optical trap produced by a linearly polarized TEM00 1064-nm laser (T40-8ss-NSI, Spectra-Physics, Mountain View, CA). The laser beam was coupled into a polarization-preserving single-mode fiber (Oz Optics, Carp, ON) and then passed through an acousto-optic deflector (NEOS Technologies, Melbourne, FL). A beam sampler reflected 10% of the light onto a photo detector (Thorlabs, Newton, NJ) that was used to record the power of the laser before its entrance into an objective. The beam was focused at the sample plane using a 100×, 1.4-NA, oil immersion objective on an Eclipse TE200 DIC microscope (Nikon USA, Melville, NY). After interacting with a trapped bead, the laser light was collected by a 1.4-NA oil immersion condenser and projected onto a quadrant photodiode (S5981, Hamamatsu, Bridgewater, NJ). In our setup, the overfilling ratio (the ratio of the beam diameter to the back aperture diameter of the objective at its back focal plane) was 1.2. The quad photodetector was used to determine x and y bead displacements from the trap center as well as the total laser power. Photocurrents from each quadrant of the detector were amplified and converted to voltage signals using an amplifier (On-Trak Photonics, Lake Forest, CA). The optical trap was always held stationary, whereas the coverglass position was adjusted with a servocontrolled 3-D piezoelectric stage (Physik Instrumente, Waldbronn, Germany). Calibration and data conversion methods along lateral directions were adapted from those used by Wang et al. (9,13).

Axial detection method

Axial detection was performed using the trapping laser via back-focal-plane interferometry, which exploits the Gouy phase anomaly of a focused beam. After the beam interacts with a trapped bead, the forward scattered light from the trapped bead interferes with unscattered light, resulting in a change in the total light intensity (28). The axial displacement of the bead from the trap center determines the extent of constructive or destructive interference, and therefore the light intensity signal serves as an indicator of the axial position of the bead in the trap. The sensitivity of the intensity signal to bead displacement can be optimized by adjustment of the condenser aperture diaphragm before the light reaches the detector (25). In our setup, this corresponded to an aperture size with a half capture angle of 36.8°.

In our apparatus, a raw axial detection signal measured the total laser power incident on the quadrant photodetector. To eliminate noise caused by laser power fluctuations that were unrelated to axial bead displacements, this raw signal was normalized against the laser power signal recorded from the beam sampler photodetector. The beam sampler's gain was adjusted so that 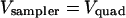when a bead was located at the trap center. We defined the normalized axial detector signal because axial displacements of the bead are related to changes in the laser intensity. Thus, when a bead was located in the trap center.

Fig. 1 C shows that this axial detection method offers excellent axial position resolution. A bead that was fixed to the coverglass surface was centered in the laser focus, and then the coverglass was moved piezoelectrically in a 1-nm, ∼2.5-Hz square wave along the axial direction. The 1-nm steps were readily detectable in the normalized axial detector signal.

Preliminary axial displacement and force calibrations

We carried out preliminary calibrations of axial displacement and force as a function of coverglass position using a Brownian motion method. Axial detector signal ζ from Brownian motion of an untethered, trapped bead was measured at various coverglass positions These measurements and the corresponding power spectra were then used to obtain the conversion from ζ to axial bead displacement and force using a method similar to that of Wang et al. (13). These measurements were performed at low laser powers that corresponded to sub-kHz corner frequencies to avoid possible filtering effects (29) due to the detector itself or its electronics. This conversion requires a knowledge of the trap height to determine the correct axial viscous drag coefficient (30,31). Before an accurate determination of the trap height, we estimated it from the coverglass position based on a paraxial ray approximation (18,32): at a water-coverglass interface.

Since these calibrations were obtained from small amplitude Brownian motions, they should only be used to estimate data from small bead displacements from the trap center. In this limit, the normalized axial detector signal can be assumed to be linearly related to both the bead displacement and the force.

DNA stretching data acquisition

There were three steps involved in the acquisition of DNA stretching data. First, the DNA tether was positioned to the trap center laterally. The lateral trap center was located by stretching the tether along x and y directions piezoelectrically at low force (<5 pN) using a method similar to that previously described (9,13). Second, the origin of coverglass position () was established as follows (33). The coverglass was raised piezoelectrically, so that the trapped bead contacted the coverglass and subsequently was pushed upward axially away from the trap center by the coverglass. The contact point () was determined by observing an abrupt change in the axial signal ζ as the bead transitioned from an effectively “free” state to an effectively “stuck” state. Third, the coverglass was lowered at a constant velocity so that the DNA tether was stretched. Analog voltage signals from the quadrant detector and the beam sampler were digitized at 1 kHz using a multiplexed analog to digital conversion PCI board (National Instruments, Austin, TX), and boxcar-averaged to 50 Hz.

Theoretical force-extension relations

Calculations of the force-extension relations for both dsDNA and ssDNA require knowledge of the elasticity parameters of dsDNA and ssDNA as well as DNA basepairing energies.

The elasticity parameters of dsDNA based on an extensible wormlike-chain model (34) were obtained from Wang et al. (13): contour length per basepair of 0.338 nm, persistence length of 43.1 nm, and stretch modulus of 1205 pN.

To obtain the elasticity parameters of ssDNA, we used the method of Koch et al. (17). In brief, the unzipping construct with 0.6-kbp unzipping segment and a capped distal end was completely unzipped (forces 11–18 pN) by moving the coverglass along the x direction, resulting in a DNA molecule that contained dsDNA and ssDNA in series. This resulting molecule was then stretched to 55 pN to obtain a force-extension curve, which reflected elastic contributions from both the dsDNA and ssDNA. Given the elasticity parameters of dsDNA, this curve allowed the determination of the elastic properties of ssDNA as described by an extensible freely jointed chain model (4): contour length per base of 0.559 nm, persistence length of 0.799 nm, and stretch modulus of 597 pN.

The DNA basepairing energies, together with ss- and dsDNA elasticity parameters, determine the sequence-dependent equilibrium unzipping forces (35,36). To determine these energies under our buffer conditions, the unzipping construct with 0.6-kbp unzipping segment was unzipped by moving the coverglass along the x direction at 100 nm/s while recording the forces required for unzipping. The unzipping rate used here was slow enough that the measured force-extension curve should approach that of the equilibrium curve (37). The resulting force-extension curve was used to obtain basepairing energies of 4.37 and 1.33 for G-C and A-T bonds, respectively, where is the thermal energy.

The DNA elasticity parameters and basepairing energies presented above were combined to produce a theoretical force versus extension relationship for unzipping the construct with the 3.7 kbp unzipping segment. The force-extension relation was also measured by using the conventional technique of moving the coverglass along the x direction at a constant rate of 100 nm/s (17). The measured curve in Fig. 2 represents an average of five unzipping traces. The close agreement between the theoretical and measured curves indicates that the theoretical curve provides an accurate description of the force-extension relation. Thus, the theoretical curve was used as a reference curve in subsequent axial calibrations.

FIGURE 2.

Unzipping force-extension curves. The characteristic force-extension curves for the DNA construct shown in Fig. 1 B are calculated theoretically (black) and verified by conventional lateral unzipping (blue). Note that the unzipping patterns are sequence-dependent.

RESULTS AND DISCUSSION

The overall goals of this work are to establish 1), the trap height as a function of the coverglass position, ; 2), the axial bead displacement as a function of the normalized axial signal and the coverglass position, ; and 3), the force exerted on the bead as a function of the normalized axial signal and the coverglass position,

Determination of the trap height: h_trap(z_cg)

For axial stretching applications, it is critical to have knowledge of the trap height As discussed in Materials and Methods, when a trapped bead barely makes contact with the coverglass (). If there were no index of refraction mismatch, the axial trap center would stay stationary as the coverglass moves away from the trapped bead, and the change in trap height would simply be the change in the coverslip position, since However, due to the aforementioned index-of-refraction mismatch between the aqueous solution and the coverglass, the axial trap center does not stay stationary. In fact, the trap center is expected to move toward the objective (Fig. 1 A). Therefore, the change in trap height is less than the change in the coverglass position, and the trap height must be directly determined experimentally.

We present a novel method for measuring versus by taking advantage of the well characterized force-extension relation for unzipping a DNA molecule of known sequence. A DNA molecule containing the 3.7-kbp unzipping segment (see Materials and Methods) was unzipped axially by moving the coverglass away from the trapped bead piezoelectrically, and the normalized axial detector signal ζ was monitored as a function of the coverglass position (Fig. 3 A). The resulting unzipping force was expected to fluctuate between 11 and 18 pN (Fig. 2; Materials and Methods), producing corresponding fluctuations in ζ. The characteristic patterns in the ζ versus curve strongly resembled the theoretical force F versus extension curve established in Fig. 2. By pattern-matching the two curves, we mapped to Since was also related to this in turn allowed mapping of to The details of this method are discussed below.

FIGURE 3.

Method of trap height calibration. (A) Axial unzipping of a DNA molecule at high laser power. A DNA molecule was unzipped axially with a laser power of 725 mW (before laser entrance into the objective). Plotted are normalized axial detector signal ζ versus the coverglass position (red) and the corresponding theoretical force versus extension curve (black). Notice the similarity in the unzipping patterns in the two curves. (B) A comparison of normalized axial detector signal ζ versus extension (red) and theoretical force versus extension (black) curves. A cross-correlation method (see text) allowed conversion from the ζ versus curve to the ζ versus 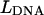curve to extract the trap height versus coverglass position relation (see Fig. 4). After this procedure, unzipping features of both curves had nearly identical alignment with respect to the extension axis.

As shown in Fig. 1 A, is determined by and the bead displacement from the trap center :

(1)

We assumed that was related to via a function that was yet to be determined. We found that this function was well approximated by a second-order polynomial:

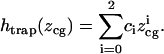(2)

Therefore,

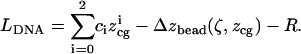(3)

To obtain {c_i}, needed to be known, i.e., the normalized axial detector signal ζ needed to be converted to axial bead displacement at a given coverglass position Since was yet to be accurately calibrated, we used preliminary calibrations (see Materials and Methods). To minimize possible errors introduced by these preliminary data, unzipping experiments were conducted at a rather high trapping power (∼725 mW measured before laser entrance into the microscope objective) so that the maximum was typically 75 nm but no more than 130 nm.

To facilitate the pattern matching, linear fits were performed on the measured ζ versus and the theoretical F versus curves and the results were used to remove offsets and tilts of these curves. These line fits, and 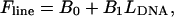were respectively subtracted from ζ and F before pattern matching:

(4)

and

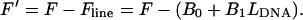(5)

The measured ζ versus curve was then converted to a versus curve using Eqs. 3 and 4. Pattern-matching was accomplished by cross correlating the versus curve with the theoretical versus curve as a function of We define a generalized cross-correlation function as a function of as:

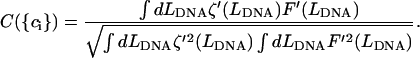(6)

The best values of corresponded to the coordinates of the maximum peak of the cross-correlation function. The height of the maximum peak measures the extent of correlation. Its value can be from −1 to +1, with +1 being perfect correlation, −1 being perfect anticorrelation, and 0 being no correlation. The average peak value for the correlation among all measurements was 0.67. The average peak value for the correlation did not improve by using higher-order polynomials with n > 2 for Eq. 2. A linear estimate of the versus (assuming n = 1 in Eq. 2) resulted in a significantly lower average peak value of 0.53. Fig. 3 B shows that, after the optimal correlation was located, the resulting ζ and F versus curves aligned nicely along the horizontal axis.

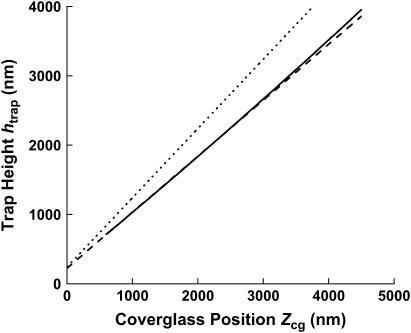
Fig. 4 shows the versus relation from this calibration (solid curve). For comparison, two other curves are also shown. One is a simple linear relation with a slope of 1, which would be the case if there were no index of refraction mismatch (dotted curve). The other is the linear estimate of the versus relation using n = 1 in Eq. 2, yielding a slope of 0.808 ± 0.005 (dashed curve). Additionally, as expected, the measured coefficient is in agreement with the known radius of the trapped bead (240 ± 4 nm).

FIGURE 4.

Results of trap height calibration. Three curves are shown for the versus relation: measured relation (solid curve), a linear estimate of the relation (dashed curve), and a line with a slope of exactly 1, which would result if there were no index of refraction mismatch (dotted curve). The polynomial coefficients of the measured versus relation (Eq. 2) are and 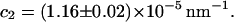Errors are standard errors of the means obtained from six measurements. The linear estimate of the versus relation was obtained by assuming n = 1 in Eq. 2, yielding a slope of 0.808 ± 0.005.

This calibration provides an accurate measure of the relation between the trap height and the coverglass position, and is valid for trap heights up to ∼4 μm, limited only by the length of the unzipping segment used here. Although the relation is dominated by a strong linear component with a slope of 0.808, a nonlinear contribution that accounts for ±0.8% over the range of the trap height is also evident. Thus, this method has sufficient accuracy and precision to reveal this higher-order correction in the calibration. It is possible that some of the nonlinearity could be due to nonlinearity from the piezo stage. However, this is rather unlikely considering that the factory specifications for our stage quote nonlinearities <0.02% over a 20-μm range. We have also performed tests to further exclude the piezo stage as a culprit (data not shown). The existence of some nonlinearity in the versus should not be too surprising. The trap center location is determined by a balance between the gradient and scattering forces, and these forces may have a different dependence on the trap height.

The linear component with a slope of 0.808 ± 0.005 is significantly smaller than what would be expected from a simply paraxial ray approximation (a slope of 0.878). This trend is consistent with the fact that larger angle rays focus closer to the coverglass than paraxial rays. We can also compare this calibration with other previously measured values. However, this is nontrivial since each optical trapping apparatus may have a different objective, laser overfilling factor, etc., and thus a versus relation should be separately established for each apparatus. Nonetheless this slope is in line with those measured by Neuman and Block (20): 0.82 ± 0.02 using the viscous drag method, and 0.799 ± 0.002 using the interference method. In addition, this slope is significantly less than the theoretically predicted focal shift (not trap-center shift) ratio which is in the range of 0.65–0.73 (19,38).

Determination of axial bead displacement and force at various trap heights: Δz_bead(ζ, z_cg) and F(ζ, z_cg)

Once the trap height was accurately determined for a given coverglass position and could be established using a method that also involved axially unzipping a DNA molecule of known sequence. The DNA construct and the overall experimental design were the same as those used for trap-height calibration. Again, the normalized axial detector signal ζ was monitored as a function of the coverglass position However, the measurements were performed with one significant difference: the laser power (and therefore trap stiffness) was lowered to allow the bead to displace further away from the trap center, and ζ versus measurements were obtained at different laser powers (160–725 mW before laser entrance into the microscope objective). Fig. 5 A shows an example of such a curve measured at one laser power. Since the unzipping force was rather constant over the DNA sequence, with a mean of 14 pN and a standard deviation of 1 pN, the laser power thus controlled the range of the axial bead displacement. When DNA was unzipped at lower laser power, the bead was further away from the trap center.

FIGURE 5.

Method of axial bead displacement and force calibrations. (A) Axial unzipping of a DNA molecule at lower laser power. This is a similar measurement to that shown in Fig. 3 A, except that the unzipping was performed at a laser power of 225 mW (before laser entrance into the objective). Plotted are ζ versus (red) and the corresponding theoretical force versus extension curve (black). (B) A comparison of normalized axial detector signal ζ versus extension (red) and theoretical force versus extension (black) curves. A cross-correlation method allowed conversion from the ζ versus curve to the ζ versus curve to extract and relations (see Fig. 6). After this procedure, unzipping features of both curves have nearly identical alignment with respect to the extension axis. (C) A comparison of measured (red) and theoretical (black) force versus extension curves. Normalized axial detector signal in Fig.5 B was converted into force after the cross correlation. The resulting measured force-extension curve (red) is identical to that of the theoretical curve (black).

We developed a method similar to that used in the trap-height determination, to calibrate and Each ζ versus curve at a given laser power was converted to a versus curve using Eqs. 3 and 4. The versus curve was then cross correlated with the theoretical versus curve. The cross-correlation process was facilitated by approximating with a defined plausible function. Since the unzipping force fluctuated ∼1 pN around a mean of 14 pN, this generated an estimated axial bead displacement fluctuation of ∼5%. Thus, at a given trapping laser power the bead displacement fluctuations were small enough that the versus ζ relation could be well described by a linear relation. The slope and offset may be functions of which we found could be well described by second-order polynomials. Therefore,

(7)

and, from Eq. 3,

(8)

where have already been established. We define another generalized cross-correlation function as a function of as:

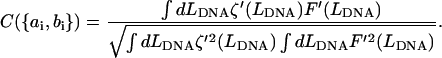(9)

The best values of corresponded to the coordinates of the maximum peak of the cross-correlation function. The average peak value for the correlation among all measurements was 0.69. Fig. 5 B shows that, after the optimal correlation was located, the resulting ζ and F versus curves aligned nicely along the horizontal axis. This procedure also allowed mapping of ζ to F along the vertical axis (Fig. 5 C). For each laser power, the cross-correlation procedure resulted in a set of values, which established and for a small range of ζ. This procedure was then repeated for a wide range of laser powers for calibrations over a wide range of ζ.

Since for given values of ζ and force is proportional to the trapping laser power, we present the force calibrations as force F normalized by the laser power (measured immediately before the laser entrance to the objective): The resulting calibrations of 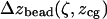and 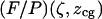are surface plots in a two-dimensional space. Note that these calibrations yielded values over a virtually continuous range of and therefore from 0.7–4 μm. In Fig. 6, for clarity, we summarize these data as versus ζ (Fig. 6 A), versus ζ (Fig. 6 C), and versus (Fig. 6 E) plots at six representative trap heights (corresponding to six values). Some general features are evident from these curves. First, all these relations are predominantly linear, even for bead displacement up to 600 nm. Second, the normalized detector signal ζ becomes a less sensitive measure of bead displacement but a more sensitive measure of force at deep trap heights. Third, trap stiffness decreases with trap height. Fourth, Fig. 6 E shows that the maximum axial trapping force is at least ∼0.09 pN/mW for up to 4 μm of trap height.

FIGURE 6.

Results of axial bead displacement and force calibrations. Data were obtained from 50 unzipping measurements performed at 160–725 mW of laser power (before laser entrance into the objective). For clarity, results are only presented at six different trap heights. A, C, and E show versus ζ, normalized force versus ζ, and versus relations, respectively. Line fits through their respective origins are also shown. B, D, and F summarize data from A, C, and E, respectively, as position sensitivity, normalized force sensitivity, and normalized trap stiffness as functions of trap height. Error bars are obtained from uncertainties in the slopes of the line fits in A, C, and E. For comparison, calibrations from a Brownian motion method are also shown. Error bars are standard errors of the means from 12 measurements.

These calibrations are further summarized in Fig. 6, B, D, and F. versus ζ, versus ζ, and versus from Fig. 6, A, C, and E, respectively, were fit with lines that pass through their respective origins (fits with offsets resulted in nearly identical slopes). Their slopes were used to obtain position sensitivity (normalized detector signal nm⁻¹), normalized force sensitivity (normalized detector signal pN⁻¹ mW⁻¹), and normalized trap stiffness (pN nm⁻¹ mW⁻¹), in Fig. 6, B, D, and F, respectively. Position and force sensitivities here are parameters used to measure how sensitive or responsive the detector is to changes in position and force, respectively. These parameters are plotted as functions of trap height. For comparison, also plotted are the corresponding parameters obtained using the Brownian motion calibrations (see Materials and Methods) after incorporating the calibrated trap heights. Parameters obtained from the unzipping calibrations and the Brownian motion calibrations are entirely consistent. All these plots show rather linear relations with trap height. The position sensitivity, normalized force sensitivity, and normalized trap stiffness vary with every micron increase in trap height by ∼−14%, +13%, and −17%, respectively.

These trends in the calibrations likely originated from an increase in spherical aberration with trap height. Our calibrations clearly show that the normalized detector signal ζ became less sensitive to the axial bead displacement with an increase in trap height. This trend is expected since the beam becomes more broadened along the axial direction with an increase in trap height due to spherical aberration. Considering that the axial signal is a result of the Gouy phase shift, an increase in the axial beam width decreases the phase sensitivity and therefore the detector's position sensitivity. Furthermore, a broadened laser beam corresponds to a weaker trap so that trap stiffness decreases with an increase in trap height. Our results show that trap stiffness decreases faster with trap height than position sensitivity. Consequently, force sensitivity shows an increase with an increase in trap height.

Verification of calibration results

The calibration results were verified with two axial experiments using DNA constructs not used for calibrations. First, a DNA construct with the 4.1-kbp unzipping segment (see Materials and Methods) was unzipped. The resulting ζ versus curve was then converted to a force-extension curve using the calibrations established above (Fig. 7 A). For comparison, a theoretical curve, and a measured curve obtained by moving the coverglass laterally, are also shown. All these curves show good agreement with each other. Second, a 3.7-kbp dsDNA molecule was stretched axially and data were similarly converted. Fig. 7 B shows the measured force-extension curve as compared with the corresponding theoretical curve. Again, there is a good agreement between these two curves. These verifications demonstrate that our axial calibrations for trap height, bead displacement, and force have sufficient accuracy for axial stretching experiments of biological molecules.

FIGURE 7.

Verification of calibration results. DNA constructs not used for calibrations were stretched axially and data were converted to force-extension curves using the newly established calibrations. (A) Measured force-extension curve for axial unzipping of a DNA molecule of known sequence (red). For comparison, also shown are the corresponding theoretical curve (black) and measured curve from lateral unzipping (blue). Only data within the range of our calibrations are shown. (B) Axial stretching of a dsDNA molecule (red) and its comparison with the theoretical curve (black).

Other considerations

The refractive-index mismatch effects that necessitate the trap-height calibration technique discussed in this work could be avoided by using a water-immersion objective for trapping. However, such an approach has been less popular in optical trapping applications due to the rapid rate of water evaporation, which severely limits the possible duration of an experiment. In any case, the axial bead displacement and force calibrations still need to be established.

The calibrations established here are specific to our optical trapping design, buffer, temperature, and bead type and size. If these conditions were to change, calibrations would have to be reestablished. This consideration, however, is not unique to our methods of calibration, and is shared by other more conventional methods. Our calibrations also require the use of unzipping DNA constructs. With the advent of modern molecular biological techniques, generation of such constructs is rather straightforward. Even if unzipping DNA constructs are not readily available, because we have shown that the axial bead displacement and force are linear functions of the normalized detector signal over a broad range of bead displacements, these calibrations can still be established using the conventional Brownian motion method, assuming that the trap height can be estimated.

SUMMARY AND CONCLUSIONS

The techniques presented here are novel and general tools for generating axial calibration curves for trap center location, bead displacement, and force. Utilizing the techniques outlined in this article, an optical trap can be calibrated for use with an axial geometry at trapping depths up to several micrometers. When all these calibrations are properly performed, measurements along the axial direction become as accurate and precise as those along either of the two lateral directions. We anticipate that incorporation of refractive-index mismatch effects into instrument calibrations will produce a more reliable optical trapping instrument that improves the accuracy of traditional single-molecule biophysics experiments. In addition, new experiments that utilize extremely short DNA tethers in an axial geometry are now possible.