Quantification and Correction of Systematic Errors Due to Detector Time-Averaging in Single-Molecule Tracking Experiments

Abstract

Single-molecule tracking is a powerful way to look at the dynamic organization of plasma membranes. However, there are some limitations to its use. For example, it was recently observed, using numerical simulation, that time-averaging effects inherent to the exposure time of detectors are likely to bias the apparent motion of molecules confined in microdomains. Here, we solve this apparently limiting issue analytically. We explore this phenomenon by calculating its effects on the observed diffusion coefficients and domain sizes. We demonstrate that the real parameters can be easily recovered from the measured apparent ones. Interestingly, we find that single-molecule tracking can be used to explore events occurring at a timescale smaller than the exposure time.

It has been pointed out (1) that time-averaging, due to the exposure time of detectors in single-molecule tracking experiments, can have dramatic effects. This is particularly important in measures of the apparent motion of tracked molecules (proteins or lipids) at the cell surface when they are confined in small regions of the membrane, such as rafts, synapses, or other signaling platforms. Diffusion coefficients and size of confining domains can be significantly underestimated. However, the arguments used relied on numerical simulation (1) and it seems important to validate them by analytical calculation. The work presented here addresses this issue and also enables the prediction of the range of experimental parameters within which this detector time-averaging effect perturbs the observations. Using systematic quantification of the time-averaging effects in the ranges of parameters of experimental relevance, we demonstrate that the values of diffusion coefficients or domain sizes are not significantly affected in a broad range of parameters. In addition, we show that these effects can be easily corrected and that real parameters can be recovered from those measured using simple formulas.

Consider a molecule diffusing in the membrane with diffusion coefficient D. Its displacements are followed by single-molecule tracking by means of a detector with exposure time T. R_m(t) denotes the measured position of the molecule at time t (multiple of T). The measured mean-square deviation MSD_m(t) is

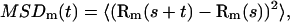(1)

where the brackets denote a discrete average over frames s. We further suppose that the diffusion is restricted to a square domain of side L. The usual experimental procedure to extract information from MSD_m(t) is to fit it with the expected generic expression 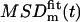for a confined diffusion:

(2)

from which one extracts the measured (or apparent) domain size L_m and equilibriation time τ_m. The measured diffusion coefficient D_m is given by

The real time-dependent positions of the molecule (as opposed to those measured) are denoted by r(t). Because the molecule is confined, they are correlated. The real equilibriation time τ in the box is the typical decay time of the following two-time correlator C(t) where averages are over times s:

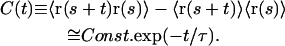(3)

In practice, there are several timescales because the different modes of the diffusion operator do not decay at the same rate in the square box (2). The slowest mode decays exponentially with a decay time τ₀ = L² / (π²D) and the next modes have decay times τ₀/(2k + 1)² with k an integer. Keeping the first-order term in the exact expansion of C(t) (2)

(4)

leads to the approximation

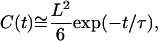(5)

as C(0), the variance of r(t), equals L²/6. To restore the fact that C(t) − C(0) =1/2 〈(r(s + t) − r(s))²〉 = 2 D t at small t for a diffusing molecule, we need to set

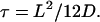(6)

Note that Eqs. 5 and 6 remain valid if the confining domain is not a square, but a disk, an ellipse or any more complex shape. In such cases, τ still represents the equilibriation time and L is the typical domain size. For example, if the domain is a circle, its diameter is related to L by d = (2/√3) L. For a quadratic confining potential, U(r) = 1/2Kr², Eq. 5 is even exact (3) and L is the typical width of the trap at temperature θ given by L² = 6k_Bθ/K.

The measured position R_m(t) is related to the real one by

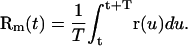(7)

After replacing R_m(t) using Eq. 7, the expansion of Eq. 1 leads to four correlators. Approximating them with Eq. 5 and setting x = τ / T gives

(8)

This exact expression of the measured MSD_m(t) in the case of a detector time-averaging is valid only if t ≥ T. If t < T, MSD_m(t) is still calculable but this is beyond the scope of this letter.

We extract the measured parameters from MSD_m(t) as described above and compare them to the real ones. The domain size L_m is obtained by equaling the large t limits of Eqs. 8 and 2:

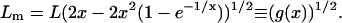(9)

From Eq. 2, we get τ_m via the simple relation

(10)

We have checked that within the range of parameters studied here, the so-obtained value of τ_m is the same as the one deduced from the fit of MSD_m(t) by Eq. 2. If we set f(x) = x² (exp(1/x) + exp(−1/x) − 2), Eqs. 10 and 8 give

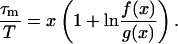(11)

When x is large, or τ ≫ T, the previous equation reads at the first order in 1/x. We have checked that this approximation remains excellent as long as x ≥ 1/3. For any x < 1/3, as for instance in the case of a very large diffusion coefficient D (see, for example, Ritchie et al. (1)), we have checked by numerical simulation that τ_m < 2T/3. Thus, any measured τ_m ≥ 2T/3 ensures that x ≥ 1/3 and that the real corrected τ ≥ T/3 is given by

(12)

which is of immediate practical interest to extract equilibriation times from measured ones. The real L is then calculated using Eq. 9, which reads

(13)

and the real D can now be recovered from Eq. 6. The corrected parameters are thus simply determined using Eqs. 13 and 6. In the case of an exposure (or averaging) time T smaller than the time T′ between two successive frames, the calculation leading to Eq. 8 is unchanged as well as its consequences. In particular, Eqs. 12 and 13 still hold. If the confinement geometry is more complex than a square, the whole analysis, based on the correlator in Eq. 5 itself independent of geometry, remains valid. The only difference is that L does then not measure the side of a square but a typical domain size.

To summarize, we have quantified how time-averaging affects observables of biological interest. However, if τ is large compared to the exposure time T, then τ, L, and D remain essentially unmodified. This point is illustrated in both Table 1 and in the following example.

TABLE 1.

Comparison of apparent analytically and numerically calculated L and D, and corrected ones, to their real values for different temporal regimes

τ/T	Lm/L	Lm,s/L	Lc/L	Dm/D	Dm,s/D	Dc/D
10	0.984	0.984	1.000	0.936	0.933	0.996
6.4	0.975	0.958*	ND	0.903	ND	ND
2	0.923	0.924	1.000	0.730	0.721	0.983
1	0.858	0.859	0.998	0.552	0.542	0.967
0.5	0.753	0.755	1.002	0.341	0.342	1.002
0.333	0.675	0.676	1.026	0.228	0.235	1.136
0.0048	0.10	0.13*	ND	0.010	ND	ND

τ is the equilibriation time and T the detector exposure time. Parameters without index are real ones. The index “m” denotes an analytically calculated apparent parameter; “m,s” a numerically calculated one. The index “c” denotes a corrected value (ideally equal to the real one) obtained from the numerically calculated one using Eqs. 12, 13, and 6. ND, not determined (because D_2-4 measured in Ritchie et al. (1) cannot be used in this framework).

^*Data from Figs. 2 and 3 C of Ritchie et al. (1).

The cases of domain-to-domain jumps or other mechanisms leading to slow long-term diffusion (with coefficient D_MAC) superimposed to confined short-term diffusion (4) deserve attention (1). We consider, as an example, the movement of the μ-opioid receptor at the surface of a normal rat kidney fibroblast cell from Daumas et al. (5). We calculate MSD_m(t) from one trajectory acquired at common video rate, i.e., T = 40 ms (see Fig. 1).

FIGURE 1 .

Experimental trajectory (120 s) of a μ-opioid receptor at the surface of a normal rat kidney cell (5), truncated in successive 20-s segments shown in different colors (indigo, cyan, green, yellow, orange, red) to highlight the displacement of the confining domain of size L ≅ 500 nm, in which the receptor diffuses rapidly. The black trajectory shows the slow diffusion of the barycenter of this domain calculated on sliding 4-s intervals.

Fitting this MSD_m(t) with the generic form:

(14)

we find τ_m = 192 ms and L_m = 483 nm. We deduce τ = 178 ms (from Eq. 12), L = 501 nm (from Eq. 13), and finally D = 0.117 μm²s⁻¹ whereas D_m = 0.101 μm²s⁻¹ (from Eq. 6). The influence of time-averaging is weak in this case, as well as in all the trajectories of Daumas et al. (5), because T ≪ τ_m. This validates a posteriori the measures in Daumas et al. (5). By contrast if τ_m is smaller than a few T, the corrections to τ and L must imperatively be taken into account. In addition to the existing numerical data from Ritchie et al. (1), we have performed numerical simulations in all relevant ranges of the parameters (τ ≥ T/3). The agreement with our analytical predictions is excellent (see Table 1). Our formulas allow us to recover accurately the real L and D from those measured within a few percents.

To conclude, we have demonstrated that the drawbacks of single-molecule tracking techniques due to time-averaging are limited. In the case of confined diffusion in membrane domains, we have proposed simple formulas to recover the real domain sizes and diffusion coefficients from those measured. The accuracy remains excellent for confinements with characteristic diffusion times down to τ = T/3 where T is the exposure time, i.e., τ is of the order of 10 ms at common video rates. Interestingly, this work has shown that events occurring at a timescale smaller than the exposure time can be explored by single-molecule tracking.