Transition in the Temperature-Dependence of GFP Fluorescence: From Proton Wires to Proton Exit

Abstract

In green fluorescent protein, photo-excitation leads to excited-state proton transfer from its chromophore, leaving behind a strongly fluorescing anion, while the proton is commonly thought to migrate internally to Glu-222. X-ray data show that the protein contains more extended hydrogen-bonded networks that can support proton migration (i.e., proton wires). Here we study the temperature-dependence of the transient fluorescence from both the acid and anionic forms up to 15 ns. At low temperatures, we find that the (lifetime-corrected) fluorescence of the acidic form decays asymptotically as t^−1/2, following quantitatively the solution of a one-dimensional diffusion equation for reversible geminate recombination with quenching. This indicates proton migration along the internal proton wires. A small degree of geminate proton quenching is attributed to the formation of the zwitterion by proton migration on a side-branch of the proton wire. Above 230 K, the fluorescence kinetics undergo a transition, exhibiting an asymptotic t^−3/2 decay, and the quenching effect disappears. We interpret these findings as evidence for a conformational change enabling the rotation of Thr-203, which eventually allows the proton to escape to the exterior solution.

INTRODUCTION

The green fluorescent protein (GFP) of the jellyfish Aequorea victoria has attracted great interest as a biological fluorescent marker and as one of the few examples of excited-state proton transfer (ESPT) in nature (1–4). Formation of the wild-type chromophore (p-hydroxybenzylidene-imidazolidinone) occurs via post-translational cyclization followed by auto-oxidation within a tripeptide unit (Ser-65, Tyr-66, Gly-67) of the 238 amino-acid sequence. X-ray diffraction (5,6) revealed that the chromophore (Cro) is protectively housed along a coaxial helix threaded through the center of an 11-stranded β-barrel. It is covalently anchored and effectively secluded from the aqueous solvent surrounding the protein. Additional noncovalent coupling of the Cro to the protein backbone is facilitated via an extended hydrogen-bond (HB) network.

At room temperature (RT), wild-type (wt) GFP exhibits two main absorption peaks with maxima at 398 nm (band A) and 478 nm (band B). The ratio of the absorption bands depends weakly on the pH. As the pH increases, the B-band gets stronger while maintaining an isosbestic point indicative of two-state kinetics. At RT there are two emission peaks in the steady-state fluorescence spectrum, a very weak band at 460 nm and a very strong band at 510 nm. Time-resolved emission showed a decrease in the 460-nm emission concomitant with a rise in the 510-nm emission. This has been interpreted (7,8) as evidence for ESPT from the hydroxyl of Tyr-66 (R*OH form, A-state, 460 nm), resulting in the green fluorescence of the anion (R*O⁻ form, 510 nm).

Previous time-resolved studies of excited GFP focused on the complex decay of the emission at short times up to 150 ps (7–10). Leiderman et al. (11) have extended the fluorescence measurements to long-times (up to 10 ns), because this time regime can reveal important facets of the recombination reaction between the conjugate base and the diffusing proton. Our experience with ESPT in homogeneous solutions (water, alcohols, dimethylsulfoxide) shows that this reaction is reversible in the excited state (ES), and thus it is possible to monitor the probability that the dissociated and solvated proton, which diffuses with a diffusion constant D, will recombine geminately with the deprotonated base (12,13). The theoretical formulation for this process in d-dimensions leads to the asymptotic (∼) long-time behavior of the normalized fluorescence signal, I_f (t;λ), at the wavelength λ characteristic of the protonated Cro:

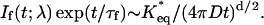(1)

Here K*_eq is the ES equilibrium constant for the protonation reaction whereas τ_f is the fluorescence lifetime of the deprotonated form.

In solution, one consistently finds t^−3/2 asymptotics (13), which is commensurate with the three-dimensional character of the homogeneous solution (d = 3 in Eq. 1). A surprising finding of Leiderman et al. (11) was that a similar behavior is observed for wt-GFP at RT. This was unexpected from the prevailing model (14,15) of irreversible proton migration along a short HB network connecting Tyr-66, via a water molecule and the hydroxyl of Ser-205, to the carboxylate of Glu-222. In Leiderman et al. (11), the t^−3/2 decay was interpreted as evidence for three-dimensional proton diffusion. Since there was no effect of proton scavengers on the kinetics, it was concluded that the diffusion occurs inside the protein. These proton scavengers can be relatively high concentrations (0.4 M) of fluoride or acetate anions, which are added to the buffer solution.

A more detailed examination of the x-ray data (5,6) was consequently initiated (16). It was not possible to find three-dimensional HB arrays, which could support three-dimensional proton diffusion inside the GFP barrel. However, linear chains of HBs (i.e., proton wires) were found to be more prevalent within the GFP than previously reported. These proton wires involve a few crystallographic water molecules plus mainly oxygen atoms on amino-acid side chains as well as backbone carbonyls.

Two functionally relevant proton wires were observed:

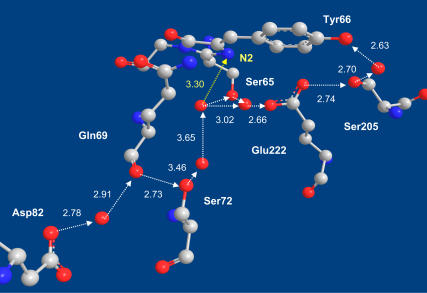
1. A rather long proton wire continues from Glu-222 via the buried Asp-82 to Glu-5, which is located on the bottom of the β-barrel (Fig. 1). Except for one water molecule along this pathway, all of the HB lengths are below 3 Å. This unique arrangement should facilitate proton migration along this pathway even at low temperatures.

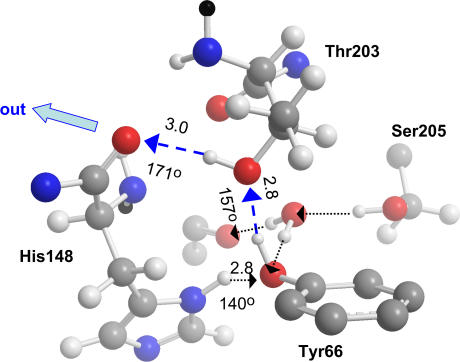
2. In addition, it was found that the rotation of the Thr-203 side chain establishes an HB net from the OH of Tyr-66 to the backbone carbonyl of His-148, from which the proton can easily hop outside (Fig. 2).

The various possibilities for proton migration in GFP can be explored by monitoring its transient fluorescence as a function of temperature. Here we extend the transient fluorescence work (11) from RT to a wide temperature range, 87–291 K. Interestingly, we find a transition from the t^−3/2 decay at RT to a t^−1/2 behavior below ∼230 K. The implications are that at low temperatures the proton migrates within the protein, possibly along the one-dimensional HB chain of Fig. 1. The transition at higher temperatures is ascribed to a conformational change within the protein, which allows proton exit possibly via the threonine gateway of Fig. 2.

FIGURE 1.

A proton pathway in GFP (16) leads from Glu-5 on the bottom of the β-barrel (not shown), via an inward-pointing aspartate (Asp-82), the backbone carbonyl of Gln-69, the hydroxyl of Ser-72, the buried Glu-222, and Ser-205 to the hydroxyl of Tyr-66 on the GFP Cro. A short side-branch of the HB pathway (yellow) connects to the N2 atom of the imidazolidinone ring, whose protonation leads to zwitterion formation. Atomic coordinates from Protein DataBank file 1GFL (5) with the HB O–O distances in Å. (Color code: Carbon atoms, gray; oxygens, red; nitrogens, blue.) Hydrogens are not depicted, since they are unobservable in the x-ray structure.

FIGURE 2.

Rotation of the Thr-203 side chain in wt-GFP (Protein DataBank file 1GFL (5)) by 120° establishes a transient proton escape route (blue) connecting the OH of Tyr-66 to the backbone carbonyl of His-148 (its side chain was rotated by 13°). Adapted from Fig. 5 of Agmon (16). Other notations are as in Fig. 1.

MATERIALS AND EXPERIMENTAL METHODS

Sample preparation and characterization

wt-GFP samples are a gift from Prof. S. J. Remington, University of Oregon. The stock solution of 10 mg/ml included 0.3 M NaCl, and was stored under refrigeration. Glycerol (purchased from Fluka, Buchs, Switzerland) was added to the solution to prepare 12%, 30%, and 60% (by volume) glycerol-water mixtures. Glycerol is habitually used to protect the sample under cryogenic conditions. The pH of the sample was 7.9.

Samples were placed in a 1-mm optical path-length quartz cell. The temperature of the irradiated sample was controlled by placing it in a liquid nitrogen cryostat with thermal stability of ∼±1 K. The absorbance at 397 nm was typically 0.1 OD. Steady-state fluorescence spectra at low temperature were taken using CVI SM-240 spectrometer (CVI Spectral Products, Putnam, CT) with ∼2 nm resolution.

Time-resolved measurements

Time-resolved fluorescence was acquired using the time-correlated single-photon counting (TCSPC) technique, the method of choice when sensitivity, large dynamic range, and low intensity illumination are important criteria in fluorescence decay measurements. For excitation we used a cavity-dumped Ti:sapphire femtosecond laser (Mira, Coherent, Santa Clara, CA), which provides short pulses (80 fs), operating at the second harmonic generation frequency (spectral range of 380–400 nm) and a relatively low repetition rate (500 kHz). A low rate might be important to ensure that the GFP is fully relaxed before re-excitation. The excitation pulse energy was reduced by neutral density filters to ∼1 pJ. We checked the sample before and after time-resolved measurements, not finding noticeable irradiation-induced changes in the absorption spectra or the transient emission decay. We conclude that, under our irradiation conditions, no sample deterioration could be detected.

The TCSPC detection system is based on a Hamamatsu 3809U photomultiplier (Hamamatsu City, Japan) and an Edinburgh Instruments TC900 computer module (West Lothian, United Kingdom) for TCSPC. The overall instrumental response function (IRF) was ∼40 ps (full-width half-maximum). The large dynamic range of the TCSPC system (more than four decades) enables us to accurately determine the non-exponential photoluminescence decay profiles of wt-GFP fluorescence. Measurements were taken at 10-nm spectral width at two frequencies: λ = 450–455 nm (R*OH kinetics) and λ = 505–525 nm (R*O⁻ kinetics), as well as at λ = 485 nm (stabilized RO⁻, see below). The latter was used to determine the ES lifetime, τ_f = 1/k_f. The lifetime-corrected signals, I_f(t;λ) exp(t/τ_f), when measured at the frequencies of the acid and the anion and normalized, are denoted below by P(t) and 1 – P(t), respectively.

THEORY

The diffusion model

We utilize a mathematical model for the description of the coupled geminate reactions

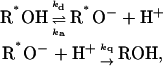(2)

depicting reversible proton binding/unbinding in the ES and proton-induced quenching. All other channels of the ES decay are lumped into the fluorescence lifetime τ_f, which is assumed to be identical for both R*OH and R*O⁻. The effect of ES decay in this case is simply to multiply the calculated kinetics without decay by exp(−t/τ_f). Thus, we need to solve the kinetics of Eqs. 2 without the ES decay.

Since the reaction under consideration is inherently fast, it is not possible to neglect the diffusive transport of the proton, which couples to the reactions under consideration. In the diffusion model (12,13), one assumes that the proton can execute spherically symmetric diffusive motion in a d-dimensional space. At the contact distance, r = a, it may associate with the excited base with a rate coefficient k_a or dissociate from it with a rate coefficient k_d. The competing irreversible quenching reaction (rate coefficient k_q) is assumed, for simplicity, to occur at the same contact distance a. The potential V(r) (in units of the thermal energy, k_BT) describes the proton-anion interaction as a function of their separation, r. In solution-phase studies (13), a Coulomb (or screened Coulomb) potential was used but, as we shall see below, this is inapplicable for the protein interior. The association (equilibrium) constant is given by K*_eq = k_a e^−V(a)/k_d, which includes the effect of the potential at the contact distance.

The mathematical depiction of this problem utilizes the d-dimensional spherically symmetric Smoluchowski equation

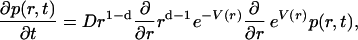(3)

for the probability density, p(r, t), of the geminate proton to be separated by a distance r from the Cro by time t after excitation. This partial differential equation is coupled to a kinetic equation (i.e., an ordinary differential equation) for the binding probability, P(t), of the Cro and the proton,

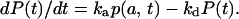(4)

Note that the quenching reaction does not enter here because it leads exclusively to the ground-state, whereas P(t) represents the R*OH population. The initial conditions for the two equations are those of a bound pair,

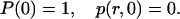(5)

The boundary condition (17) for p(r, t) at r = a couples the reversible and irreversible reactions:

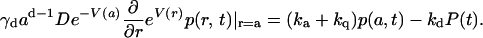(6)

At the boundary, the (excited) Cro population is depleted by both association and quenching reactions. The geometric factor γ_d = 1, 2π, and 4π for d = 1, 2, and 3, respectively. Some limiting cases of this equation can be solved analytically (see below). However, for arbitrary times and potentials one needs to solve Eq. 3 numerically, and this is conveniently done using the Windows application (18) for solving the Spherically Symmetric Diffusion Problem (SSDP, Ver. 2.65). Its graphical interface allows one to convolute the theoretical solution with the IRF and compare with the time-resolved experimental data.

Analytic solution

A central result of the present analysis is that, below a critical temperature (of 230 K), the fluorescence signal from the excited GFP Cro behaves as if the proton diffuses in one dimension—namely, d = 1 in Eqs. 3 and 6. In this case, the above equations admit an analytic solution in several limiting cases. The simplest case is that of no potential (unbiased diffusion) and no quenching, V(r) = 0 and k_q = 0. This problem has been solved two decades ago (17). Interestingly, we will see that this simple case almost suffices to describe our low temperature results.

We present this solution below, mainly to show (19) that from the time dependence of P(t) it is possible to determine only two combinations of the three parameters, k_d, k_a, and D. These combinations are k_d and 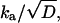both having units of 1/time. It is not possible to determine k_a and D independently, because these two parameters depend also on the units of r, whereas our data depends only on time. Thus, although diffusion is indispensable in explaining the data, the diffusion constant itself can be determined only from measurements that sample the spatial distribution, p(r, t).

The analytic solution can be conveniently obtained (17) by the Laplace transform method. It depends on two roots of a quadratic equation

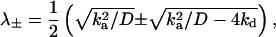(7)

which may be either real or complex conjugated. The binding probability is then given by

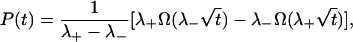(8)

where the function Ω(z) is defined by

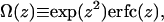(9)

and erfc(z) is the complementary error function of a complex variable, z. From a fit to Eq. 8 one could determine λ_±, and from their product and sum,

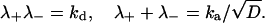(10)

Thus, the solution depends only on k_d and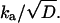

The long-time asymptotic behavior of P(t) can be obtained directly from that of erfc(z); see Abramowitz and Stegun (20). This can be worked out even when V(r) ≠ 0, provided that V(r) → 0 as r → ∞ (21, 22). It leads to Eq. 1 with K*_eq = k_a e^−V(a)/k_d. Thus, when only the long-time asymptotics is measured, its slope allows us to determine only a single parameter, which is the ratio of the two parameters in Eq. 10.

More general cases with k_q ≠ 0 and/or a linear potential, V(r) = αr, can also be worked out analytically (23, 24, 25), though the solution becomes more complicated. In these cases the additional parameters that could possibly be determined from fits to the complete time-dependence of P(t) are 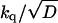and

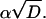
RESULTS

Anion fluorescence

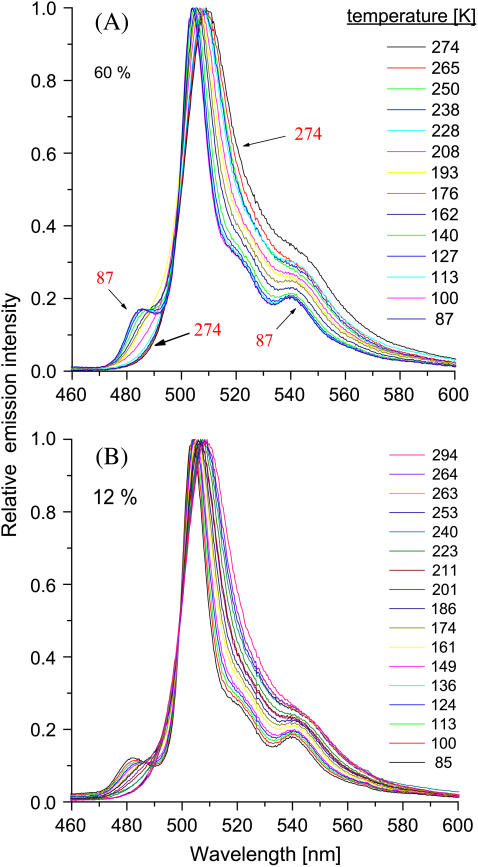
Most of the fluorescence intensity in GFP is due to its anionic form. Fig. 3 shows the steady-state emission of wt-GFP dissolved in aqueous solutions containing different amounts of glycerol and excited at the 396-nm ROH absorption maximum. Qualitatively, the spectrum is similar for both solutions. It consists of a strong and narrow band, located at ∼510 nm at RT and blue-shifting by ∼5 nm at the lowest T. This is attributed to R*O⁻ formed by the photodissociation of R*OH. Separated from it by an iso-emissive point, a smaller band at 485 nm grows with decreasing temperature. This band has previously been observed at 77 K (7). Now we see that it appears rather abruptly below ∼230 K.

FIGURE 3.

Steady-state emission from wt-GFP in a (A) 60% (v/v) and (B) 12% (v/v) glycerol-water solution at different temperatures (indicated), after irradiation at 396 nm.

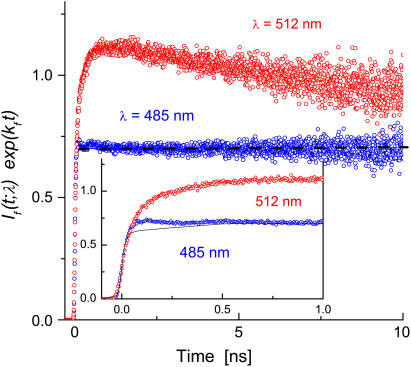
The transient fluorescence decay at these two frequencies and at low temperatures is shown in Fig. 4. The data were corrected for the ES decay using the radiative decay rate constant, k_f = 0.35 ns⁻¹, as determined at 485 nm for T < 230 K (when this band is observed). Both traces in Fig. 4 increase initially with the IRF (inset). However, the signal at 485 nm soon flattens off (meaning that it exhibits a pure exponential decay, exp(−k_ft)), whereas that at 512 nm exhibits an extended rise that tracks the decay of the ROH signal at 460 nm (see below). Moreover, its decay at long-times is slightly faster than that of the 450-nm band, resulting in the small maximum seen in the figure.

FIGURE 4.

Transient TCSPC fluorescence at 485 nm (87 K or 151 K) and 512 nm (110 K) in a 60% (v/v) glycerol-water solution. Data corrected for ES decay using k_f = 0.352 ns⁻¹. Dashed straight line to guide the eye. Inset shows the data on an expanded scale with the line representing the IRF convoluted with a constant.

These observations indicate that the two bands represent two types of R*O⁻ populations:

1. The decay at 485 nm arises from a species that does not undergo an ES reaction, and thus its fluorescence rises with the IRF and decays with the ES lifetime. Because the excitation spectrum at this frequency follows the absorption spectrum of RO⁻ rather closely (see Fig. 3 B in (8)), one concludes that it is due to direct excitation of ground-state RO⁻. Possibly the protein conformation of this species, or the absence of an available proton within the protein, prevent its conversion to ground-state ROH, which characterizes the majority of the protein molecules in the sample.

2. The 510-nm band represents the species that exists as ROH in the ground-state and converts from R*OH to R*O⁻ in the ES. Therefore its fluorescence signal rises with a delay, which is determined by the magnitude of k_d. At long-times it decays slightly faster than the 485-nm band. We attribute this to quenching of the excited Cro by the geminate proton, a familiar effect for excited bases formed by ESPT (13). In contrast, the protein molecules emitting at 485 nm do not contain an available proton within their barrel structure that could interact with the Cro.

Interestingly, the 485-nm peak appears rather abruptly as T is lowered below ∼230 K. This transition could indicate the onset of a protein conformational change. The blue shift, and its enhancement at low T, suggests ground-state stabilization of the anionic species. Because the transient signal at 485 nm is a pure exponential, the population emitting at 510 nm does not convert to the 485-nm population during the ES lifetime, so that the conformational change must occur on a longer timescale in the ground-state. Hence, this population is decoupled from the low-T ES acid-base reaction, and could thus be ignored in the treatment of the ES kinetics. In contrast, the main 510-nm band continues shifting and widening to the red also above 230 K. Thus its broadening could involve less localized protein modes with a wider distribution of barrier heights.

Acid fluorescence

The ROH emission occurs around 460 nm. It is barely seen in the steady-state spectrum (Fig. 3) because it is ∼500 times weaker than the anion emission. Nevertheless, its intensity is sufficient for TCSPC measurements. The central result of the present work is the temperature-dependence of the time-resolved fluorescence for wt-GFP (Fig. 5). Here we present results in 30% glycerol-water (v/v) solutions, although we have obtained qualitatively similar data for other glycerol contents (12% and 60%). The data are multiplied by exp(k_ft), where k_f = 0.35 ns⁻¹ was determined from the pure exponential decay of the emission from the directly excited anion at 485 nm. For the acid form it is not possible to measure k_f directly due to its rapid decay, so we apply the same value, assuming that (like the 485-nm band) it has no temperature-dependence.

FIGURE 5.

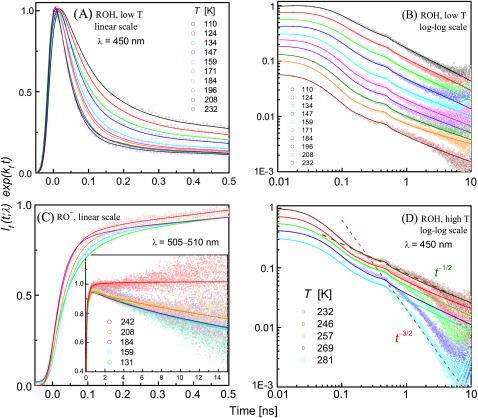
Time-resolved emission from wt-GFP in a 30% (v/v) glycerol-water solution at the different indicated temperatures (in K). Circles are TCSPC data corrected for the ES lifetime. Lines are fits to the diffusion model in Eqs. 3–6 using the SSDP software (18) with the parameters in Table 1. The calculated P(t) was convoluted with the measured IRF. (A) Low temperature ROH fluorescence at 450 nm on a linear 500-ps timescale, normalized to unity at the peak. (B) Same data on a 10-ns time window and a log-log scale, with curves shifted each by ∼0.12 log units along the intensity scale for clearer visibility of the long-time tails. (C) Anion (RO⁻) fluorescence, measured at 505–510 nm, depicted on both short and long (inset) timescales. (D) Same as B, above the transition temperature. The two dashed lines depict t^−1/2 and t^−3/2 decay, illustrating the transition.

Interestingly, the transient R*OH emission (450 nm) exhibits a transition at ∼230 K. (Note that this temperature is close to the transition temperature of the 485-nm band in Fig. 3). The data below this temperature are presented in Fig. 5, A and B. Fig. 5 A gives the short time behavior on a linear scale, whereas Fig. 5 B shows the long-time behavior on a log-log scale (with data shifted vertically for clarity). It exhibits a power law asymptotic decay as in solution-phase ESPT (13), except that the power is t^−1/2 rather than t^−3/2. This strongly suggests that the proton is migrating along one-dimensional proton wires within the protein.

To check this hypothesis, we have fitted the data to the one-dimensional diffusion model, solving Eq. 3 numerically for d = 1 to obtain P(t) (lines). The same calculation is used to compare 1 – P(t) with the RO⁻ kinetics, as measured in the 505–510 nm range (Fig. 5 C). The parameters, collected in Table 1, correspond in a first approximation to free diffusion (V(r) ≈ 0) with the simplest reversible boundary condition (i.e., k_q ≈ 0). As shown in the Theory section and in Agmon (19), the transient traces in this limit allow one to determine k_d and 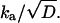It is not possible, from an experiment containing only temporal information, to determine independently the two spatially dependent parameters, k_a and D. In liquid solutions D is known from mobility measurements, but within the protein D is unknown.

TABLE 1.

Parameters for fitting the time-resolved fluorescence in Fig. 5 to the one-dimensional diffusion model (d = 1) in Eqs. 3–6; temperature-independent parameter: k_f = 0.35 ns⁻¹

Temperature (K)	kd (ns−1)		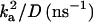kq/ka	αka (ns−1)
86.8	21	34	0.06	0.42
110.1	21	9.6	0.04	0.42
124	22.3	7.2	0.04	0.42
134	26	7.2	0.04	0.42
147	28	5.3	0.04	0.42
159	29	3.2	0.04	0.42
171	33	2.9	0.04	0.42
184	35	2.4	0.04	0.42
196	41	2.9	0.04	0.54
208	49	2.6	0.02	0.35
223	52	3.6	0.02	0.60
232	58	5.8	0	0.17
246	55	4.8	0	0.17
257	50	5.8	0	0
269	38	4.8	0	0
281	40	6.4	0	0

To achieve a global fit, which agrees simultaneously with the kinetics at both acid and base wavelengths, we have introduced two additional effects. First, we included a small proton quenching effect with a rate coefficient, k_q, which is typically 4% of k_a. It accounts for the decrease in the R*O⁻ signal at long-times (Fig. 5 C, inset). Such a decrease can also be explained by increasing k_f, but in our case k_f has been determined independently from the decay of the 485-nm peak, and was found to be temperature-independent (below 230 K). Note that our depiction of the quenching reaction is least accurate at short times, because Eq. 6 assumes that it occurs at the same contact distance as dissociation and recombination, whereas it probably takes place at a site on the back ring of the Cro (on atom N2 in Fig. 1). However, at longer times the proton migrates sufficiently far that the difference in distance to the two sites becomes relatively small.

The second effect is a weak linear attractive potential (in one dimension), V(r) = αr. It enhances the tail of the R*OH signal, which is otherwise diminished by the quenching effect. We find that the attracting Coulomb potential traditionally used for ESPT in solution (13) is inadequate, as it leads to excessive recombination at short and intermediate times, even if a much larger dielectric constant is used for the interior of the protein than commonly assumed. The success of electrostatic considerations on nanometric scales is contrasted with their inadequacy on the molecular scale.

By fitting the time-resolved kinetics, one can determine at most five parameters: k_f, k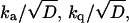_d, and 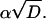The radiative decay rate constant, k_f, was kept constant throughout the whole temperature range at the value obtained for the 485-nm band below 230 K. This leaves us with four adjustable parameters, 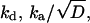k_q/k_a, and αk_a (Table 1). The last two parameters were found to be temperature-independent below 200 K. Above it, they decrease to zero over a rather small temperature range. Thus, below 200 K we adjust only two parameters at each temperature. The good fits obtained simultaneously to both ROH and RO⁻ kinetics on all timescales lend credibility to the one-dimensional diffusion model below 230 K.

Above this temperature, the one-dimensional model deteriorates with increasing T (Fig. 5 D). There is a switchover to steeper decay occurring at earlier times with increasing T. Above 270 K, the long-time tail seems to approach the t^−3/2 asymptotic behavior (dashed line) as previously reported (11). This could indicate that, on these timescales (say, t > 300 ps at RT), the proton is exiting from the protein (16) either irreversibly or reversibly, after executing three-dimensional diffusion in the external solution. Commensurate with the proton exit event, the proton-quenching process is eliminated (see red curve in Fig. 5 C, inset), and k_q decreases to zero.

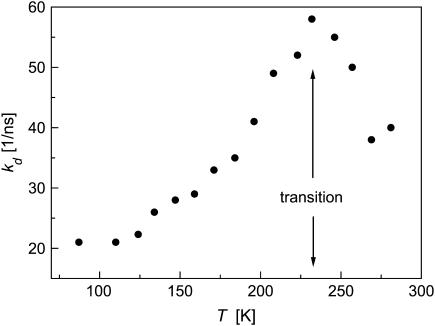
Another signal of the transition temperature is seen in the temperature-dependence of the dissociation rate constant in Fig. 6. At very low T, k_d is nearly constant, suggesting the involvement of a quantum tunneling effect. Then k_d increases with increasing T up to 230 K, where it reaches a maximum. Possibly the conformational change occurring near the transition temperature modifies the HB network around the Cro in a way that slows the dissociation process at higher T. At this stage, however, we do not analyze this temperature-dependence quantitatively, because an IRF of 40 ps can distort the fast dissociation process.

FIGURE 6.

Temperature-dependence of the proton dissociation rate constant from excited wt-GFP obtained by the present diffusion model fitting (see Table 1).

DISCUSSION

GFP is a protein that is attracting considerable interest, and thus its fluorescence has been rather intensively studied. Almost invariably the focus was on the R*O⁻ band, which is important for biotechnology (2). The weaker R*OH band was studied at short times (≈100 ps) to demonstrate the ESPT phenomenon (7–10), but its long-time behavior remained unexplored until recently (11). In addition, there were no systematic studies of the temperature-dependence. Here we presented a first report of the temperature-dependence of the transient fluorescence from wt-GFP, with particular emphasis on the R*OH band up to t > 10 ns.

We find that the transient fluorescence kinetics exhibit a transition around 230 K. Below it, there is t^−1/2 asymptotic decay, with the whole time-dependence fitting quantitatively to a one-dimensional diffusion model for a geminate reversible reaction, indicating that the proton is migrating along one-dimensional proton wires within the protein. Above 230 K, the long-time behavior switches to a steeper t^−3/2 decay, suggesting a conformational change that allows the proton to escape to a region from which its probability of return to the active site is much more limited.

Proton wires

It is commonly assumed that proton conduction within proteins occurs along proton wires, which are specialized HB networks for transporting protons within proteins. Such wires are used to conduct protons to, from, or between active sites in enzymes or across the cell membrane in proton pumps (26,27). Evidence for proton wires is typically obtained from x-ray structures and mutagenesis work. However, we are not aware that proton motion along such networks has ever been recorded in real-time.

Below 230 K, wt-GFP seems to be frozen into two major conformations in its ground electronic state. The minority is locked in the anionic state, giving rise to the 485-nm fluorescence band. When excited, it decays mono-exponentially with a rate constant k_f = 0.35 ns⁻¹, which is independent of temperature in this range, allowing us to obtain a reliable value for the ES lifetime, τ_f = 1/k_f.

The majority of the population is in the ROH state, in which the OH of Tyr-66 is connected to a rather rigid HB network. Its fluorescence shows a remarkably slow decay with the ubiquitous t^−1/2 tail characteristic of reversible proton migration in one dimension. The anion shows a small excess decay (over that of the directly-excited minority form at 485 nm), suggesting a small degree of quenching by the dissociated proton. This interpretation is corroborated by fits to a one-dimensional diffusion model for reversible dissociation-association with quenching (Fig. 5 B). Rigorously speaking, the t^−1/2 asymptotics should hold only in the absence of quenching and for potentials that decay to zero at infinity. For a linear potential (as employed here), the asymptotic behavior shows transitions between various forms, such as t^−3/2, t^−1/2 and exponential (23–25). In the present case, however, the competing quenching reaction is minimal (k_q/k_a ≈ 0.04). It affects the long-time behavior only marginally in our observation time-window, causing minor deviations from the t^−1/2 behavior.

Thus, in accordance with the prevailing mechanism for proton migration in GFP (14,15), the proton is transferred in the ES from Tyr-66 to Glu-222. However, this transfer is reversible and probably continues beyond Glu-222. The pathway up to Glu-222 involves only two intermediate proton acceptors: water and Ser-205. Irreversible transfer along this route should result in biexponential kinetics. Conceivably, longer HB chains are required to allow the diffusional power-law to evolve, such as the one continuing from Glu-222 to Asp-82 (Fig. 1 and (16)).

Our measurements, devoid of a characteristic length-scale, cannot determine how far within the protein the proton migrates. This fundamental question might, however, be addressed in combination with mutagenetic work. If the proton-wire could be bisected at points progressively closer to the proton release point, the power law should terminate by a flat plateau at progressively shorter times. Alternatively, blocking of proton entry might lock the Cro in its RO⁻ state indefinitely, precluding the observation of ESPT altogether.

The possibility that proton migration is not limited to a single linear pathway follows from the observation of proton quenching. Quantum chemistry calculations (28) suggest that the GFP Cro is actually a bifunctional compound (29), with the N2 nitrogen on the imidazolidinone enhancing its basicity in the ES. Attack of the geminate proton on this site will form the zwitterion (30), which decays rapidly via conical intersection to the ground-state (31). Indeed, Fig. 1 shows an HB connecting a water molecule along the Asp-82–Glu-222 pathway to N2 (yellow), and this could allow the formation of the dark zwitterion as manifested in the quenching kinetics.

The possibility of seeing proton-wires using ESPT could potentially be utilized to map out conjectured pathways in other proteins, by artificially tailoring an ESPT Cro at a location where connection to the HB pathway could be made. The formation of the desired connection could be verified by x ray, and proton migration along the pathway could then be studied by time-resolved fluorescence.

Proton exit

As the temperature is increased above 230 K, the probability of the geminate proton to return to the dissociation site on Tyr-66 and rebind diminishes, and then the fluorescence signal from the protonated Cro drops below the t^−1/2 behavior observed for T < 230 K (Fig. 5 D). This could result from a conformational transition occurring within the protein, one which is also connected to the disappearance of the 485-nm band in Fig. 3. This conformational change does not occur instantly upon excitation, but rather with some delay, which is manifested in the residual t^−1/2 kinetics observed at intermediate times before the conformational change. The delay time increases with decreasing T, until it eventually becomes infinite below 230 K. Clearly, in a complex protein structure many different conformational changes may occur. Here we focus on one such change that has been noted in comparing the x-ray structures of the protonated and deprotonated forms of wt-GFP (14).

It is known that the side chain of Thr-203 can assume two conformations in wt-GFP. In the ROH form, Thr-203 points its OH group away from that of Tyr-66. In the RO⁻ form, the Thr-203 side chain is rotated by 120°, so that its OH forms a HB to the phenoxide, RO⁻···HO. This is demonstrated in Fig. 2. If this rotational motion freezes below 230 K, there would be a fraction of the population which is trapped indefinitely in the RO⁻ state, giving rise to the 485-nm band. Moreover, it has been noticed (16) that the rotated Thr-203 forms a short HB-network leading from Tyr-66 to the backbone carbonyl of His-148, as seen in Fig. 2. This group is already on the surface of the protein, which should allow for facile proton escape to solution. In the ground-state, the majority of the population is in the ROH state. Below 230 K, the threonine switch does not open after photoexcitation, so that the ROH releases its proton to the long proton wire of Fig. 1. Above 230 K, the switch opens (with a delay of a few 100 ps), and then the proton hops across the short HB connection seen in Fig. 2 to the external solution.

As noted before (11), the steeper decay at the higher temperatures shows a t^−3/2 dependence, which could be indicative of proton diffusion in three-dimensional space with reversible recombination (13). Diffusion is now taking place outside the protein, with occasional reentry and rebinding to the excited Cro (16). However, this reversible exit scenario is at odds with the experimental finding of essentially zero effect for relatively high concentrations of external proton scavengers (11).

An alternative interpretation may be that proton exit is irreversible, because it is difficult for it to find its way back into the small hole on the protein surface. Indeed, pH jump experiments (32,33) suggest that proton entry from bulk solution occurs on the 100-μs timescale. Thus, in this scenario, after the proton escapes it can no longer affect the Cro fluorescence. The subsequent non-exponential decay might then arise from a different effect, such as an inhomogeneous distribution in the Thr-203 side-chain angle which determines the exit rate.

An independent evidence for proton exit comes from the observation of cessation of geminate quenching above 230 K (Fig. 5 C, inset). The dissociated proton outside the protein cannot reach the N2 site at the back side of the Cro, where the quenching occurs. The lifetime of the R*O⁻ formed by protic dissociation (510-nm band) then increases, coinciding with that of the directly excited RO⁻ population (485-nm band).

These conclusions do not contradict the transient IR measurements of Stoner-Ma et al. (34), which indicate that Glu-222 gets (partially) protonated in deuterated GFP at RT on a 300-ps timescale. Until the Thr-203 switch opens, the proton wanders along the internal proton wire(s), in accordance with the fact that the one-dimensional diffusion model still fits the data at short times in Fig. 5 D. At 281 K we observe the transition to the t^−3/2 decay at 300 ps, while for deuterated GFP this should occur even at later times. Thus we expect the transient IR signal to start decreasing at longer times.

The 230 K transition

An interesting observation is the transition in GFP steady-state and transient fluorescence around 230 K. It is manifested at three different characteristic wavelengths:

485 nm

The emission at 485 nm is attributed to anionic GFP, which does not get reprotonated even after long residence times in the ground-state. This small peak in the emission spectrum (Fig. 3) disappears abruptly near 230 K.

510 nm

Emission at this wavelength is attributed to the GFP anion, which is formed in the ES from the acidic R*OH form. Unlike the 485 K population, its fluorescence signal at short-times grows with a delay. At long-times and above 230 K, the decay at both wavelengths is exponential with a time constant of ∼2.9 ns. Below 230 K, the emission at this wavelength decays faster, which we attribute to quenching by the geminate proton. Thus the quenching reaction in Eq. 2 bears evidence to the 230 K transition.

450 nm

The weak emission at 460 nm is attributed to excited GFP in its R*OH form. The transient kinetics show two signatures of the 230 K transition:

1. At short-times, the dissociation reaction is enhanced as the temperature is lowered from RT to 230 K, but it slows down again upon further decrease in T. This results in the maximum in k_d depicted in Fig. 6. (This maximum may nevertheless be an artifact of the finite-width IRF.)

2. At long-times, we observe the switchover from the t^−3/2 decay above 230 K to the t^−1/2 behavior below it, as discussed in detail above.

The accumulation of several different experimental evidences for the transition temperature indicates that there might be an observable change in the protein structure around T = 230 K. It may therefore be interesting to re-measure the x-ray diffraction of a wt-GFP sample above and below this temperature to check this possibility.

Proton re-entry

Our fluorescence measurements, which follow the ES on a 20-ns timescale, do not probe the proton reentry process. Here, two types of measurements are relevant. By monitoring the transient absorption of the ROH band, one can follow its ground-state recovery after the ES deprotonation process. It was found to proceed nearly in parallel to ES decay, with a time-constant of 3–4 ns (35). In contrast, pH-jump experiments (33) indicate that proton entry into anionic GFP mutants occurs on the much slower 100-μs timescale. It could be that the two kinds of experiments track different GFP populations. If the R*O⁻ decays before proton exit has occurred, reprotonation by the geminate proton can be very fast. However, for those GFP molecules that have lost their proton, reprotonation requires proton entry from solution, which is a much slower process.

Two proton wires connecting the Tyr-66 OH with the protein surface are depicted in Figs. 1 and 2. As discussed in Agmon (16), the protein surfaces near their end-points have completely different characteristics. The short pathway in Fig. 2 ends on a hydrophobic surface patch, which should not be attractive to protons. The long pathway in Fig. 1 ends at Glu-5 on the bottom surface of the GFP barrel. This face contains many Glu and Asp residues, which could serve to collect protons from solution. The structure of this pathway is analogous to that of the D-pathway in cytochrome-c oxidase, which serves to conduct protons into the active site of that protein. By homology, proton reentry into GFP from solution at RT could proceed mainly along the long pathway in Fig. 1.

CONCLUSION

The robust GFP barrel structure seems unique in maintaining an extended network of internal proton wires, without the need for slower water entry to complete these chains. Commensurate with these structural features, our kinetic results suggest that the proton migrates along such wires at low temperatures on the nanosecond timescale. At higher temperatures it might escape to the external solution after a delayed conformational change (16), or become distributed over so many proton-wires that its behavior appears three-dimensional (11). The unique combination of proton wires with an ESPT Cro within the same protein allows one to follow these proton migration processes in real-time using transient fluorescence, which was not achieved in studies of other proteins thus far.

Our findings are consistent with the mechanism suggested in Agmon (16), where GFP under normal conditions acts as a proton pump. In this scenario, photo-excitation induces rotation of the Thr-203 side chain leading to proton ejection to solution (Fig. 2). The proton is then replenished in the ground-state from another face of the protein via the long internal proton wire of Fig. 1. From this viewpoint, GFP has similar features to those of bacteriorhodopsin (br), for example, which makes it an efficient proton pump. Both proteins have a Cro that utilizes light energy to induce proton transfer: ESPT in GFP and ground-state PT in br. Both proteins couple PT and conformational change to ensure the directionality of the transfer process. The isomerization occurs within the Cro in br or right next to it (Thr-203) in GFP. Both have postulated exit and entry paths for the proton along intraprotein proton wires. These wires are not clearly visible in br, which has many labile water molecules. Remarkably, in the rigid GFP barrel these proton conduction pathways are much more stable, so that they could be inferred (16) directly from the x-ray structure (Figs. 1 and 2). The combination of more stable proton wires, with the faster PT occurring in the ES, could actually make the proton-pumping cycle in GFP faster than that of br.

If these conjectures can be corroborated, GFP mutants might have a new line of applications, because proton pumping proteins are candidates for devices capable of direct light conversion into proton gradients (36). GFP is considerably more rigid than known membrane proton pumping proteins, so that it may be expected to exhibit higher stability in such devices.

In marine biology, bioluminescence (which derives its excitation energy from a chemical reaction) is actually a much more prevalent phenomenon than biofluorescence. It has recently been suggested that ESPT plays a role also in bioluminescence, e.g., from aequorin and coelenterazine-based photoproteins in general (37). Thus, the detailed study of ESPT in photoproteins may be essential also for understanding bioluminescence phenomena on the molecular level.