Abstract
The kinetics of insulin-based amyloid gel formation has been studied using extinction and fluorescence detection. The process is treated as autocatalytic, and the kinetic profiles are fit using a nonconventional analysis involving a time-dependent rate constant (factor): k(t) = ko + kc(kct)n. The dependence of the kinetic parameters on initial solution conditions of concentration, pH, and ionic strength has been investigated. A mechanism is proposed in which the rate-determining step involves the activation of insulin solute species into partially unfolded, structurally modified monomers, which then aggregate. The influence of added metalloporphyrins on the rate and extent of gel formation is described. Metal derivatives of tetrakis(4-sulfonatophenyl)porphine prove effective at inhibiting the aggregation of insulin via pathways that depend on concentration and identity of the incorporated metal.
INTRODUCTION
The current intense interest in protein misfolding and aggregation is linked in large part to the role these processes play in human and animal diseases (1–4). In general for prion diseases, a conversion from the correctly folded native state of the protein to a structure rich in β-sheets is involved in the production of pathological forms (4,5). The population of structurally converted protein molecules recruits and induces conversion of other molecules, which then aggregate to form insoluble plaques (6). Deposits of these plaques in the brain are the hallmark of scrapie, Alzheimer's disease, Creutzfeld-Jakob disease, and bovine spongiform encephalopathy. The plaques, though composed of different proteins depending on the disease, share a common general structure, termed “amyloid”.
It has recently been shown that amyloid formation is not a phenomenon restricted to a select group of proteins but that many (if not all (7)) naturally occurring polypeptides can form such oriented assemblies under conditions that destabilize the native structure but still favor noncovalent interactions. This requirement is met when bovine pancreatic insulin is heated under acidic conditions (8,9). Although insulin is not directly involved in amyloid-based pathogenesis, it provides several advantages when used as a source for investigations of amyloid-type aggregate formation. First, insulin is inexpensive and readily available commercially. Second, it is a well-characterized peptide whose structure, sequence, and properties are well known. Third, insulin β-amyloid-type aggregates can be produced in a standard laboratory setting without the use of specialized equipment (9). Fourth, insulin β-amyloids behave chemically much like β-amyloids derived from proteins implicated in various disease states as evidenced by gel structure and interactions with Congo red (CR) and Thioflavin T (Thio T) (10–12). Thio T and CR provide unique spectral features when bound to Aβ arrays (fibrils), interactions that depend upon aggregate morphology and the regularity of the cross-β-structure characteristic of these species. Absorption and fluorescence results suggest very similar structures for insulin gels and Aβ fibrils (supplementary Fig. S1); electron micrographs and x-ray diffraction studies confirm this conclusion (13).
Insulin is a 51-residue protein consisting in its native state of two peptide chains linked by two disulfide bridges. Crystalline insulin is a hexamer, with three insulin dimers coordinated to two Zn2+ ions, although the number of zinc ions per hexamer has been reported as ranging from two to four (14). Conformational studies have shown insulin to be rich in α-helical motifs but acid causes dissociation of the insulin hexamer with subsequent change in conformation at elevated temperatures to enable aggregates to form (13–17). The putative series of events leading to the formation of amyloid-type gels begins, therefore, with acidification of insulin; at pH ∼ 2 in HCl, the peptide is largely dimeric (15). The dimer dissociates at high temperature producing a partially unfolded monomer (18,19), which aggregates to form thermodynamically favorable protofilaments (protofibrils) (20,21). These protofibrils have been reported as being short, rather flexible species, generally 4–10 nm in diameter and up to ∼200 nm in length (22). Protofibrils are in turn precursors of the longer, more rigid, amyloid-type fibrils of the type generally associated with Alzheimer's disease (14,20–22).
The motivation for this study is: i), to examine the kinetics and mechanism of fibril formation; ii), to determine the impact of changes in solution conditions on the rate of the process; and iii), to examine various substances as potential catalysts or inhibitors of β-amyloid formation. For this analysis we have applied an autocatalytic kinetic model (23–25) that has been developed for assembly processes in which an array surface catalyzes the rate-determining formation of a critical “nucleus” or “seed”, comprised of m reactant units. The distinctive feature of this model is a time-dependent rate constant (“rate factor”) that reflects catalysis by a growing surface (in this instance, the protein assembly):
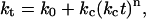 |
(1) |
where ko and kc are time-independent constants (both having units of s−1) for the uncatalyzed and catalyzed aggregation, respectively. The time-dependence parameter n is related to the growth rate of the activating surface. The integrated rate law for this model is given by:
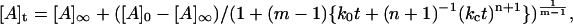 |
(2) |
where [A] represents the aggregated or assembled insulin units and m ≠ 1. For the special case in which m = 1 (which corresponds to activation of the unassembled, initial solute species by the array surface as the rate-determining step), the equation takes on a more familiar form referred to as a “stretched exponential” (24):
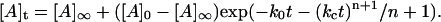 |
(3) |
(Notice that for n = 0, Eq. 3 reverts to a simple exponential form).
The autocatalytic model (Eq. 2) has been applied with considerable success to porphyrin-assembly kinetic data (23–25), and it proves effective at fitting literature data for a number of biological/pathological growth processes including the polymerization of actin (23,24); the aggregation of hemin to produce the malaria pigment, hemozoin (26); and the formation of β-amyloids by fragments of the OsmB protein. However, the kinetic study for this last system (27) does not provide closely spaced data points, and therefore, conclusions based on these data are at best tentative. In particular, from the preliminary analysis, the autocatalytic model predicts that the seed size for OsmB aggregation is very small, approaching unity. It is clear that if more definitive mechanistic arguments concerning amyloid formation are to be made, precise data are needed. Studying the mechanism of protein aggregation with model systems can, in principle, contribute to a better understanding of the molecular mechanisms involved in the disease state (28,29) and, with this goal in mind, we embarked on this kinetic study involving bovine pancreatic insulin. This report includes the results of that investigation along with our findings on the influence of pH and metal ion concentration on the rate of aggregation, and also includes the effect of several water-soluble metalloporphyins on insulin gel formation.
EXPERIMENTAL
Materials
Crystalline bovine pancreatic insulin was obtained from Sigma (St. Louis, MO), stored with a dessicant below 0°C, and used without further purification. Concentrations of insulin solutions were determined using a molar absorptivity of 6040 M−1cm−1 at 278 nm (30). Thio T and CR obtained from Sigma were used to prepare stock solutions on the day of use. The free base porphyrins, tetrakis(N-methylpyridinium-4-yl)porphine (H2T44+) and tetrakis(4-sulfonatophenyl)porphine (H2TPPS4−) were purchased from MidCentury Chemical (Posen, IL) as the chloride and sodium salts, respectively. Metalloporphyrin derivatives were synthesized by literature methods (see Table 1 references, below). Their concentrations were determined using molar absorptivity values available in the literature. All other reagents were of the highest purity available from Fisher Scientific (Hampton, NH) and Sigma/Aldrich. Solutions were prepared using ultrapurified water that had been passed through a 0.2-mm Nalgene filter and degassed.
TABLE 1.
Molar absorptivities of porphyrin derivatives
| Ligand Derivative | T4 λmax (nm) | ɛλ (× 10−5 M−1cm−1) | TPPS λmax (nm) | ɛλ (× 10−5 M−1cm−1) |
|---|---|---|---|---|
| Cu(II) | 425 | 2.31 | 412 | 4.16 |
| Ni(II) | 420 | 1.49 | 409 | ∼2 |
| Fe(III) | 401 | 1.02 | 394 | 1.52 |
| Mn(III) | 462 | 0.92 | 467 | 0.95 |
| Co(III) | 434 | 2.14 | 425 | 2.38 |
| Au(III) | 404 | 2.82 | 405 | 4.37 |
Instruments
Extinction measurements and absorbance spectra were recorded with Jasco (Easton, MD) V-550 and V-560 ultraviolet-visible (UV-Vis) spectrophotometers. Fluorescence and some scattering measurements were conducted with a Spex Fluorolog 3 fluorimeter. Simultaneous extinction and fluorescence measurements were made using a modified QuantaMaster fluorescence system from Photon Technology (Birmingham, NJ). An additional photodetector was installed in line with the excitation beam to allow for intensity measurements. Because there is no second monochromator in the forward direction, narrow-band-pass filters (394 nm maximum, 10 nm full width half-maximum) were placed before and after the sample in the direction of the excitation beam to eliminate the effect of fluorescence at longer wavelengths on the extinction measurements. Also, a neutral density filter (Edmund Optics, Barrington, NJ) was placed in front of the additional photodetector to decrease the light intensity reaching it, thereby allowing slits to be opened to a convenient size. The optical configuration of this instrument involves a focused rather than collimated beam for extinction measurements.
Methods: insulin gel preparation
The method of Burke and Rougvie was used to prepare large quantities of amyloid-type insulin gels (9). The amyloid nature of the gels was confirmed using criteria previously established involving interactions with Thio T and CR (10–12). Recent work has shown that a combination of heating and freezing steps yields a great diversity of fibrils with different structures and spacings. In contrast, when an insulin sample is simply heated to ∼60°C near pH 2 (as in the protocol described below) only a single type of compact fibril forms (21).
Standard kinetics protocol
Details of preparation and treatment of reactant solutions need to be documented to permit direct comparisons of experimental results from different laboratories. In the procedure used here, a reaction mixture containing the desired concentrations of reagents other than insulin was prepared in a disposable methacrylate cuvette. The resulting solution was thermally equilibrated at a preselected temperature (generally 67.4°C) in the cuvette block of a spectrophotometer or fluorimeter. The precise temperature was determined using a Thermolyne thermocouple. A fresh stock solution of ∼3 mM insulin in 0.056 M HCl was prepared daily. A small volume of this stock was added to the thermally equilibrated reaction mixture to produce the target insulin concentration and pH, with a total volume of 3 mL. The cuvette was capped, inverted twice, and returned to the cuvette block for data collection. Because the stock insulin was at room temperature when added to the thermally equilibrated solution, this mixing method gives a slight uncertainty in the initial temperature. However, the volume delivered was relatively small and the transfer was done very quickly, generally within 3 s.
The rate of the aggregation process proves to be dependent not only on the preparation and mixing protocol but on size and shape of foreign objects, e.g., magnetic stir bars, included in the reactor. In addition, stirring speed, and cuvette topology have an impact on the kinetics of gel formation as reported in a previously published study in which the rate of fibril formation was significantly increased by stirring (31). To avoid some of these complications, we employed a vortex mixer to agitate the reaction mixture. The sample was vigorously agitated for a very brief period every 200 s so as not to interfere with data collection. The timescale for the reaction profile for this experiment involving periodic, thorough mixing of reagents and that of an experiment in which there was no stirring of the reagents are virtually identical. The kc, m, and n values (see Introduction) each agreed to within 10%. The major difference between the two profiles is the total turbidity of the mixture at the end of the reaction, with the vortexing method producing the more turbid sample (supplementary Fig. S2). Although the final extinction values differ, the close agreement of the kinetic parameters led us to employ as a standard protocol one in which the reagents are mixed to initiate the experiment (as described above) and then allowed to react unstirred. This protocol provided the most self-consistent results of the various methods attempted and avoids the potential difficulties inherent in mechanical agitation of the forming gel and surface effects arising from the presence of a stirrer. It also avoids the necessity of scrupulously cleaning stir bars to avoid contamination by inadvertent “seeding” of reaction mixtures.
Data analysis
A minimum of 98% of the total extinction change for each kinetics experiment was fit using the model described in the Introduction. The data for some runs were truncated to 98% to avoid complications arising from multiple, forward scattering of highly turbid samples (vide infra) or settling of the gel. Data were fit to either Eq. 2 or Eq. 3 given above, depending upon the value of the nucleus size parameter m. We also attempted to fit our kinetic data using an alternative model proposed by Sabaté et al. for aggregation of the amyloid protein Aβ (32). We found that in most cases the Sabaté model provided a fit equivalent to that of this model. However, autocatalytic profiles that were recorded at low pH or concentration, or that have seed sizes >1–1.5 (23–25) are better fit with this model, and, therefore, because of its broader applicability, the kinetic approach described here was used consistently for all kinetic runs.
Two detection modes were employed for kinetic studies of insulin gelation. In one, the time dependence of scattering of the system was determined (usually at a 0° detection angle although a few studies were conducted at 90° for comparison). Alternatively, fluorescence detection was used, which takes advantage of the enhanced quantum efficiency for Thioflavin T emission when interacting with amyloid structures (12). These two detection modes complement one another in that Thio T fluorescence enhancement occurs as the fluorophore recognizes protofibril species that are formed en route to the final aggregation product (22) whereas scattering is sensitive not only to the number density of the scatterer but also the size of the object. Hence, this latter method is biased toward the largest objects (fibrils) that form.
Using extinction at a nonresonance wavelength to follow kinetic events is not as straightforward as are most commonly employed detection methods. Scattering intensity depends on the size and shape of the scattering object (angle dependent) as well as its number density and, in a kinetic process these features will change with time. However, extinction measurements at 0° provide, in effect, information on the total scattering at all angles (other than in the forward direction) through a single measurement. Therefore, this would appear to be the optimum angle for such kinetic studies. This choice needs to be tested for each system and instrument—the cone angle of photon detection is finite, and forward scattering could change appreciably during the course of the reaction. We performed a number of experiments to test whether such scattering measurements are reliable for this system under the conditions used. To assess the limits of applicability of these measurements, two aspects of the Beer-Lambert law were considered. In one, a serial dilution of vortexed, preformed gel (9) was carried out and the extinction in the visible range was determined. Extinction in this wavelength range is due to scattering only because there is no absorbance component. Plots of extinction versus volume of added gel proved linear up to an extinction of ∼1 (supplementary Fig. S3 a). The Beer-Lambert law also predicts that extinction will vary linearly with pathlength, although appreciable multiple and/or forward scattering could result in deviations from linearity. The extinction of an insulin gel suspension was recorded in cuvettes with pathlengths varying from 1 to 10 mm; there is no significant deviation from linearity in the plot (supplementary Fig. S3 b). Therefore, we conclude that any time-dependent change in forward scattering is of little significance for this system under the conditions of our experiments, and that extinction measurements on a UV-Vis spectrophotometer—where the detection angle is near 0°—are appropriate for kinetic analyses of gel formation. To investigate the possibility that time-dependent scattering profiles and, therefore kinetic parameters, may vary with detection angle, extinction measurements were made for insulin aggregation using a UV-Vis spectrophotometer and a fluorimeter, detecting at 0° and 90° to the incident light, respectively. The analysis of the kinetic profiles yielded kinetic parameters in good agreement but the signal/noise ratio was considerably more favorable for the spectrophotometric measurements. The close agreement between the two sets of rate constants in these experiments conducted at different detection angles is a result of considerable importance for studies to be described below in the Results section.
RESULTS
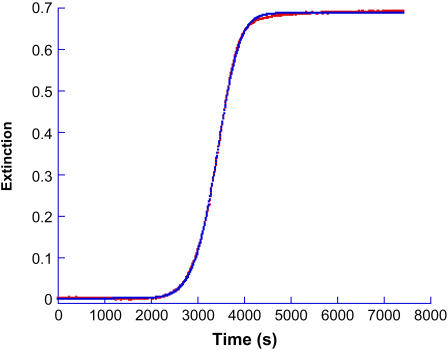
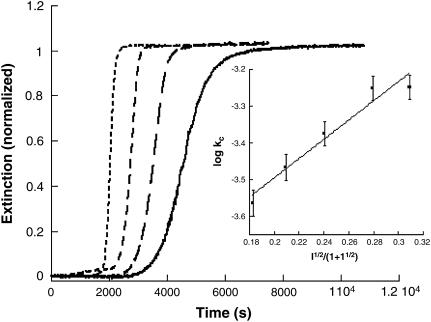
A kinetic profile for insulin gel formation involving extinction measurements at 488 nm is shown in Fig. 1. None of the reaction components absorb light at this wavelength so the increase in signal with time corresponds to enhanced light scattering by the sample. The initial conditions were 200 μM insulin at pH 1.37, 67°C. The profile is shown in Fig. 1 along with the fit obtained by application of the autocatalytic model, Eq. 2. Because of the insignificant slope of the initial portion of the kinetic profile, a reliable value of ko could not be estimated but kc = 3.8 × 10−4 s−1; n = 11 and m = 1.4.
FIGURE 1.
Kinetic profile for insulin gelation and the fit provided by Eq. 2. Extinction was measured at 488 nm on a standard spectrophotometer for a solution whose initial conditions were [Insulin] = 200 μM, pH 1.37 at 67°C. The best fit was obtained for ko ∼ 0; kc = 3.8 × 10−4 s−1; n = 11 and m = 1.4.
A second method of detection for insulin gel formation involves monitoring the fluorescence of added Thioflavin T with time. An isosbestic point for Thio T when free in solution and when gel-bound was determined at 395 ± 3 nm, the wavelength used for excitation of the fluorophore. Our preliminary experiments focused on whether the addition of 10 μM Thio T to the reaction mixture has an impact on the aggregation kinetics as detected via extinction measurements. The agreement among kinetic parameters for gelling with and without added Thio T was within experimental error, and no systematic variation of these parameters was found in multiple runs. We conclude that under the conditions of our experiments, the presence of low concentrations of Thio T does not affect the kinetics of the gelling process, consistent with previous results on insulin aggregation (31). Next, an experiment was conducted under identical conditions to those described above, using an instrument specially designed to allow simultaneous detection of fluorescence and scattering from a single sample, thus relieving any uncertainties arising from attempts to prepare two identical reaction mixtures. The values for the kinetic parameters were in excellent agreement for the two detection modes. For fluorescence monitoring, kc = 3.6x10−4 s−1; n = 11 and m = 1.6. A comparison of the two sets of kinetic parameters—one for extinction and the one for fluorescence monitoring—leads us to conclude that the kinetic profile and measured rates for insulin gelling are the same regardless of which detection mode is used to monitor the reaction.
Dependence on initial conditions
Insulin concentration
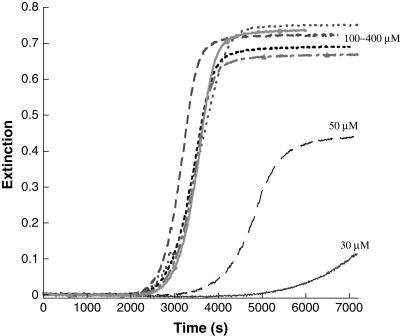
Kinetics of gelation was studied over a range of insulin concentrations between 30 and 400 μM (Fig. 2). At the lower end of the range, the final extinction values scale with insulin concentration. However, the final extinction value does not change appreciably above ∼100 μM insulin, even with a fourfold increase in peptide concentration. Apparently, aspects of the size, shape, and number density of the insulin aggregates offset one another to produce final mixtures of comparable extinction. Selected gel samples throughout the concentration range, when treated with Congo red and/or Thioflavin T show the spectral changes characteristic of β-amyloid assemblies. Complete kinetic analyses of these data indicate that for all solutions, m ∼ 1, n = 10 ± 1, and above ∼50 μM insulin there is no dependence of the catalytic rate constant on the initial insulin concentration; kc ∼ 3.5 × 10−4 s−1. Kinetic studies for subsequent experiments were generally conducted at or near 200 μM insulin, chosen for convenience.
FIGURE 2.
Kinetic profiles of gel formation for insulin concentrations between 30 and 400 μM. Equation 3 was adequate to fit these data (m = 1) and n = 10 ± 1. For [Insulin] = 30 μM, kc = 2.0 × 10−4 s−1; [Insulin] = 50 μM, kc = 2.5 × 10−4 s−1 and for all higher concentrations, kc = 3.5 × 10−4 s−1.
pH dependence
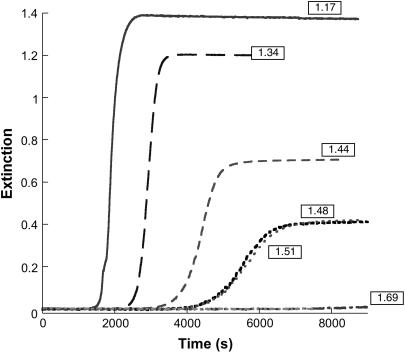
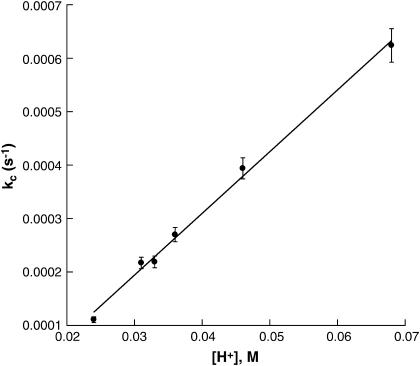
Gelation kinetics were studied at 67° and 200 μM insulin in a pH range between 1.17 and 1.69 (Fig. 3). As may be seen in the figure: i), only very small increases in extinction were observed over a 2-h period when the pH was above ∼1.65; and ii), the lag time decreases with decreasing pH from ∼4200 s at higher pH to ∼1400 s. Kinetic profiles retain their sigmoidal form throughout the pH range studied, but the sloped portion of the profiles become increasingly steep with decreasing pH. Upon analysis using Eq. 2, the kinetic parameters m and n show practically no dependence on pH (m ∼ 1.0–1.5; n ∼ 11 ± 1) but the catalytic rate constant (kc) increases with increasing [H+], as shown in Fig. 4. That the pH of the reaction mixture has a large effect on aggregation kinetics is an important factor in experimental design. We have found that different lots of crystalline insulin have differing buffering capacities, and therefore careful adjustment of pH is required to obtain reproducible results.
FIGURE 3.
Kinetic profiles for insulin gel formation at various pH values (200 μM insulin, 67°). As the pH decreases, the rate of aggregation and final extinction values increase, whereas the apparent lag time decreases.
FIGURE 4.
Plot of the catalytic rate constant, kc versus [H+] for the insulin gelation reactions shown in Fig. 3. The slope of the line is 0.012 M−1s−1.
Ionic strength
The ionic strength dependence of the gelation rate was determined by the addition of NaCl in a concentration range between 0.011 and 0.16 M at a fixed pH. For these studies, a value of pH ∼ 1.62 proved convenient because the speed and magnitude of the extinction increase markedly with ionic strength. The experimentally determined value of kc under these pH conditions in the absence of NaCl is 1.1 × 10−4 s−1. The kinetic profiles all have a similar form throughout the NaCl concentration range, with a shortened delay period up to [NaCl] = 0.10 M (Fig. 5). A plot of log kc versus I1/2/(1 + I1/2) is linear with a slope of +2.6 ± 0.3.
FIGURE 5.
Overlay of normalized representative kinetic profiles for insulin gelation at various ionic strengths (NaCl). Shown in the figure (from right to left) are [NaCl] = 0.050, 0.070, 0.10, and 0.15.The conditions were 200 μM insulin, pH 1.62, 67°C. (Inset) Plot of log kc versus I1/2/(1 + I1/2) for insulin gelation in the presence of NaCl. The slope of the line is +2.6 ± 0.3, indicating interaction between two species of like charge type.
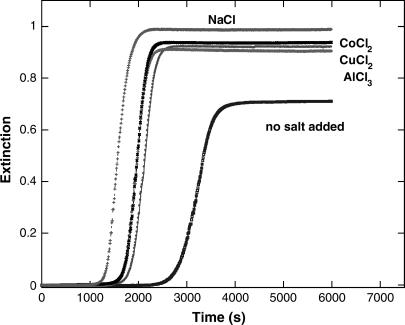
A series of experiments were conducted in which various electrolytes were added to the reaction mixture to determine their impact on the kinetics at fixed pH. Each of CuCl2, CoCl2, and AlCl3 were tested. The concentrations of these species were adjusted so as to produce a constant ionic strength (0.060 M) in the reaction mixture. The results are shown in Fig. 6; the presence of electrolytes enhances the rate of gel formation. However, under constant ionic strength conditions, these several electrolytes are nearly indistinguishable, but somewhat less effective at promoting the aggregation than the 1:1 NaCl electrolyte at the same ionic strength.
FIGURE 6.
Effect of added electrolytes on kinetics of insulin gelation. Each of the salts (NaCl, CuCl2, CoCl2, and AlCl3) is added so as to make the final ionic strength 0.060 M. The kinetics of gelation is always faster than for a solution to which no electrolyte was added but the difference among electrolytes is minor.
Influence of added porphyrins
Previous studies have indicated that a number of hydrophobic aromatic ring-containing drugs, including several porphyrins and phthalocyanines, are effective at inhibiting prion protein formation both in vitro and in vivo (33,34). This observation encouraged us to test water-soluble metalloporphyrin derivatives for possible inhibitory effects on the kinetics of insulin gelation. A range of concentrations of the Cu2+, Ni2+, Fe3+, Mn3+, Co3+, and Au3+ derivatives of the cationic tetrakis(N-methylpyridinium-4-yl)porphine (MT4) and anionic tetrakis(4-sulfonatophenyl)porphine (MTPPS) were included in the reaction mixture and the extinction was monitored at 620 nm where metalloporphyrin absorption does not contribute appreciably. A marked dependence of inhibitory influence on charge type of the metalloporphyrin was observed. Whereas the MT4 cationic porphyrins have no significant impact on the kinetics of gelation of insulin regardless of the metal derivative used, all MTPPS metalloporphyrins show inhibitory effects, with the efficiency and mechanism of inhibition dependent on metal derivative and concentration.
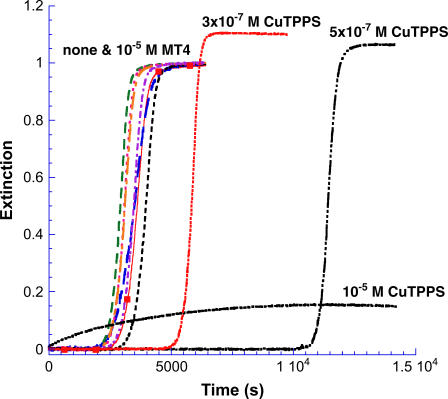
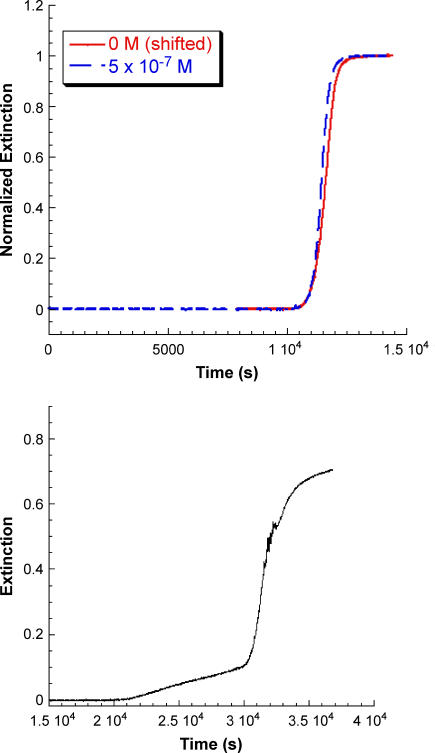
For all of FeT4, MnT4, CoT4, AuT4, and NiT4 at a concentration of 1 × 10−5 M, the values of the critical kinetic parameters were m ∼ 1; n = 12 ± 1; kc = 3.6 ± 0.6 × 10−4 s−1 as compared to n = 11 and kc = 3.4 × 10−4 s−1 for the porphyrin-free solution, as run in this series of experiments (Fig. 7). Results for CuTPPS at several concentrations are included in the figure for comparison. At concentrations below 10−6 M CuTPPS, reaction profiles retain the lag period/growth burst form similar to the control profile (no porphyrin), although the onset of the rapid growth phase is shifted to longer times. To determine whether the growth portion of the profile is affected by the presence of CuTPPS in this submicromolar concentration range, the control profile was moved through a time increment equivalent to the extension of the delay period as shown in Fig. 8 A for 5 × 10−7 M metalloporphyrin. After shifting the control (in this case by some 8000 s), the normalized profile is nearly identical to that obtained in the presence of porphyrin. Apparently the growth phase is essentially unaltered by the presence of low concentrations of CuTPPS, whereas the lag period is significantly prolonged.
FIGURE 7.
Insulin gelation kinetics in the presence of added metalloporphyrins. None of the metal derivatives of H2T4 influenced either the lag time or growth rate appreciably. An experiment conducted under the same conditions but without added metalloporphyrin is shown for comparison (▪). In contrast, the copper(II) derivative of H2TPPS has a marked influence on the kinetic profile that depends on CuTPPS concentration.
FIGURE 8.
(A) The kinetic profile for insulin gelation in the absence of metalloporphyrin is shifted by 8000 s to compare to the profile in the presence of 5 × 10−7 M CuTPPS. The growth phase of the profile is unaffected by the presence of the metalloporphyrin. (B) Kinetic profile for insulin gelation in the presence of 1 × 10−6 M CuTPPS. The lag period is now extended to some 20,000 s after which two successive growth patterns are observed; one characteristic of high CuTPPS concentrations followed by the low-concentration growth profile.
We attempted experiments that would demonstrate whether the rapid growth process can be postponed, reversed, or eliminated by timely incremental additions of CuTPPS. Kinetic runs were conducted in which the concentration of CuTPPS (initially at 3 × 10−7 M) was doubled during the rapid rise in extinction or during the delay period. Doubling the CuTPPS concentration during the growth phase had no effect on the continuation of that part of the process. Likewise, rapid growth was unaffected when the CuTPPS concentration was doubled during the delay period. However, the delay period itself was shortened to ∼2500 s when the CuTPPS concentration was doubled during this phase; this shortening of the “lag time” was shown to be a result of agitating the reaction mixture to insure thorough mixing as additional CuTPPS was added. This effect was further probed by vortexing a mixture that, unperturbed, would have had a greatly extended lag time. At 3 × 10−7 and 5 × 10−7 M CuTPPS, the delay periods were shortened to approximately that of a control profile (∼2500–3000 s) when the reaction was subjected to vortexing at periodic intervals. Thus, at low concentrations of CuTPPS the lag time is prolonged through an interaction that can be disrupted by mechanical agitation of the reaction mixture. It is worth noting, however, that this delay period at low concentrations of CuTPPS is never shortened to less than that of a control profile.
Above a concentration of 3 × 10−6 M CuTPPS, a very different set of observations is made (Type II behavior). First, very little gel forms as indicated by the relatively low values of the extinction obtained after hours (or days) of waiting. Very small quantities of gel can be separated upon centrifugation. Second, as can be seen in Fig. 7 for [CuTPPS] = 1 × 10−5 M, a scattering signal—albeit small—is observed beginning at t = 0; i.e., there is no delay period. The profile appears very simple and, in fact, is fit satisfactorily as a first-order process with a rate constant, k′ ∼ (2.5–3.0) × 10−4 s−1, a value that is comparable to the rate constant obtained from autocatalytic fits under these conditions of pH and temperature. A concentration of 1 × 10−6 M CuTPPS seems to represent a transition between the low and high concentration mechanisms (see Fig. 8 B). After an incubation period of >20,000 s, the initial rise in extinction is slow but at ∼30,000 s, rapid growth begins. The profile shown in Fig. 8 B appears to be the result of two (or more) reaction pathways.
Emission by Thioflavin T was used for detection in a set of kinetic experiments in both the low and high CuTPPS concentration regimes. Recall that monitoring Thio T emission over time can provide insight as to the rate-determining step of the reaction because Thio T reports the presence of protofibrils, thus allowing detection of intermediates in the overall gelation process. At low concentrations of CuTPPS, the profile was the same as that measured by extinction. The same observation was made at higher concentration but very little gel was produced and, therefore, little fluorescent enhancement was observed. The amyloid nature of the gel at high CuTPPS concentration was confirmed by testing an accumulated product of several runs with Thio T and CR. The characteristic enhancement and maxima shifts were observed and, therefore, the gels formed with 10−5 M CuTPPS are amyloid in nature. In summary, two types of behavior are observed for kinetic studies of insulin aggregation in the presence of CuTPPS. At low concentration of CuTPPS, the delay period is extended and the final extinction is increased, but the slope of the growth phase is similar to that of a control profile. At high CuTPPS concentration, the kinetic profiles have a first-order dependence on time with a rate constant that is of the order of the catalytic rate constants of an insulin control experiment, fit with the autocatalytic model. The transition concentration for these two types of behavior is ∼10−6 M.
Other metal derivatives
The iron(III) derivative of TPPS is also inhibitory but exhibits somewhat different behavior from that of CuTPPS. In general, FeTPPS is a less efficient inhibitor than is CuTPPS. At 10−6 M FeTPPS, the delay period is extended from that of the control profile by ∼2800–3000 s (see Table 2), compared to >15,000 s for a reaction mixture containing 10−6 M CuTPPS. At concentrations >10−6 M FeTPPS, the lag and rapid growth phases are still observed, with delay periods extended to somewhat longer times. Type II behavior, seen with high concentrations of CuTPPS, is not observed at or below 10−5 M FeTPPS. To determine if the growth phase of FeTPPS-containing reaction mixtures are significantly different from the growth phase of a control profile, overlays of a shifted control were made with the 1 × 10−6 and 3 × 10−6 M FeTPPS profiles. As for CuTPPS the profiles are almost identical. When a reaction mixture containing 10−6 M FeTPPS was vigorously agitated on a vortex mixer, practically no change is observed in the lag time of the profile. Unlike the situation for CuTPPS vigorous agitation does not affect the inhibitory effects of FeTPPS on fibril formation.
TABLE 2.
Comparison of delay times for several metalloderivatives of tetrakis(4-sulfonatophenyl)porphine
| Delay period (s)
|
|||
|---|---|---|---|
| Concentration (μM) | CuTPPS | FeTPPS | AuTPPS |
| 0 | 2000–2500 | 2000–2500 | 2000–2500 |
| 0.1 | 2400 | — | — |
| 0.3 | 5000 | — | — |
| 0.5 | 10,000 | — | — |
| 1.0 | 20,000 | 5,100 | 7,600 |
| 3.0 | Type II | 35,000 | >48,000 |
| 10 | Type II | >50,000 | — |
Preliminary experiments were conducted with other metalloderivatives of TPPS; Au(III), Co(III), Ni(II), and Mn(III)TPPS were all tested for their inhibitory effects. The concentration dependence of AuTPPS is similar to that of FeTPPS, though as shown in Table 2, AuTPPS is slightly more efficient than the iron derivative at extending the delay period. Kinetic profiles were recorded for AuTPPS concentrations between 10−6 and 10−5 M. At 10−6 M, the delay period is extended to ∼7600 s and the final extinction is greater than for a control profile. At 3 × 10−6 M AuTPPS, the delay period is >48,000 s. This pattern is similar to that of FeTPPS, in that all of the profiles indicate lag period/growth burst kinetics rather than Type II behavior observed at higher concentrations of CuTPPS. A vortexing experiment shows that AuTPPS has a weak interaction with intermediates similar to that of CuTPPS, but unlike FeTPPS. The delay period of a 10−6 M AuTPPS reaction mixture that was vortexed every 500 s is ∼4000 s, compared with 7600 s for an unvortexed reaction mixture. This decrease in delay period is not as dramatic as for CuTPPS, for which agitation consistently lowers the lag time to that of a control profile. The disruption of inhibition by vortexing of AuTPPS and CuTPPS—but not the FeTPPS—suggests that axial ligation (typical of the iron(III) derivative) may contribute to the gel-binding or general interference ability of the metalloporphyrin. Limited concentration studies on CoTPPS, NiTPPS, and MnTPPS indicate that each porphyrin has a similar inhibitory effect as either CuTPPS or FeTPPS, though the efficiency of the inhibition varies with the metal. Additional studies are required before a correlation can be made between specific porphyrin properties and their influence on gel formation.
DISCUSSION
Conversion of soluble insulin into insoluble amyloid-type gels is a multistep process involving alteration of the peptide's secondary structure (13) and aggregation, first into protofibrils and then into fibrils (18). At acidic pH at room temperature, insulin exists as small oligomers of native-like α-helical molecules (14) containing disulfide bridges that are retained in the product fibrils (19). The predominant solute species at pH ∼ 2 (HCl) at room temperature is reported to be the dimer (15). At high temperature, the dimer dissociates in the presence of acid and undergoes a structural change, resulting in the formation of assemblies of a nonnative insulin structure (rich in β-sheets) (13). The process involves a partial unfolding of the peptide monomer leading to the exposure of nonpolar side chains to the solvent, which promotes self-assembly (18).
Experimental results presented here make apparent—even without the application of a kinetic model—that the rate-determining step in this overall pathway comes early in the process. Kinetic profiles obtained via extinction detection are virtually identical to those measured by fluorescence enhancement of added Thioflavin T. Because the Thio T fluorophore recognizes and reports the presence of protofibrils, the slow step in the mechanism must precede fibril formation. In fact, our results suggest that the rate-determining step occurs at a still earlier stage in the reaction pathway. The nonconventional autocatalytic model of Eqs. 1–3 has been successfully applied to the kinetic data for insulin gel formation (Fig. 1). In this approach, the surface of the aggregated product is proposed to catalyze the rate-determining step for the conversion of the soluble insulin reactant into the insoluble amyloid-type fibril. The value of the m parameter (which in the model defines the total number of insulin reactant species participating in the rate-determining step) approaches unity in our experiments. This result parallels the conclusion reached earlier that application of this kinetic model to data for the gelation of OsmB protein provides a “seed size” of about one, and is consistent with the empirical finding by Shinozaki et al. that data for the formation of amyloid fibrils formed by amyloid-β-proteins can be fit with a stretched exponential (Eq. 3) (35). A value of m = 1 implies that the rate-determining step is the activation of the reactant rather than its assembly into a critical nucleus or seed. Certainly, molecular assembly is involved in the gelling process but, according to our kinetic results (and therefore subject to the applicability of the model), the rate-determining step precedes an aggregation process, even of small arrays. Studies on the in vitro conversion of mammalian prion protein into fibrils have also been interpreted as involving a rate-limiting conformational rearrangement of polypeptides (36).
In summary, a suggested sequence for insulin gelling begins with the insulin dimer (D), which is reported as the stable form of the peptide in acidic solution (HCl) at room temperature (15):
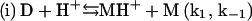 |
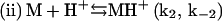 |
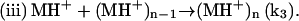 |
Upon heating, the dimer dissociates into monomers with the involvement of a proton (Fig. 4) that perhaps serves to interfere with hydrogen bonding or other weak interactions between the monomeric units. In this step (i), MH+ represents a partially unfolded, structurally modified protonated insulin monomer that aggregates (step (iii)). The free monomer (M) that also forms in step (i) becomes protonated to yield MH+ (step (ii)). This three-step mechanism is consistent with the proposal that insulin fibril formation proceeds through a monomeric form (31,37). If included in this mechanistic argument is catalysis of step (i) by the gel surface, the result is a rate-determining step involving an autocatalyzed activation of insulin solute species. A key event in the aggregation process is the attack of a proton on the cationic peptide dimer, a reaction whose rate is expected to increase with increasing ionic strength, as shown in Fig. 5.
Because the gelation of peptides in general is likely to involve charged species, it is important to consider ionic strength effects when evaluating the kinetic impact of added metal salts. For this system CoCl2, CuCl2, and AlCl3 are nearly indistinguishable when present at the same ionic strength, and just slightly less effective at promoting aggregation than is NaCl (Fig. 6). However, considerable evidence exists that when considering authentic prion protein aggregation, specific electrolyte effects exist for these and similar salts (38). Our result points out a limitation of using insulin gelation at low pH as a model system for the formation of amyloid fibrils in vivo. The low pH conditions used here likely interfere with the binding of these metal ions to side chains of amino acid moieties, and thus the metal salt influence is restricted to a general electrolyte effect arising from the partial neutralization of like-charged interacting species. However, this result underscores the necessity of considering general electrolyte effects as well as specific interactions when studying the influence of metal ions on the aggregation rates of authentic prion proteins. We are currently investigating specific anion effects for the insulin system, and especially as a consequence of our findings with metalloporphyrins.
The effect of added metalloporphyrins on the rate of gelation can be considered in the context of the proposed mechanism described above. None of the tested cationic porphyrins showed any significant influence on the reaction kinetics, and this we believe is due largely to Coulombic effects. The aggregating peptide is cationic and the large positive charge on the MT4 species effectively prevents any direct interaction with the fully protonated insulin molecule. That is not to say that these metalloporphyrins may not be effective inhibitors for other protein aggregations, but apparently not when the peptide is carrying a large positive charge. On the other hand, all the anionic MTPPS species tested influence insulin gelling kinetics.
The copper(II) derivative, CuTPPS, shows two types of inhibitory behavior depending on concentration. In the lower concentration range, CuTPPS extends the lag time before the growth phase of the aggregation process, but has no effect on the rate of the growth phase itself. Furthermore, the inhibition by CuTPPS can be disrupted by agitation when the metalloporphyrin is present at low concentration (<10−6 M). It is likely that there is a weak interaction between CuTPPS and small fibril intermediates preventing the formation of a clean, catalytic surface for additional monomerization/conformational change of insulin. However, eventually the CuTPPS supply is exhausted and the amyloid formation process continues as if no CuTPPS were present, albeit at a later time; the delay timescales with metalloporphyrin concentration. The small, precursor catalytic structure (small enough not to scatter light appreciably) is thus “poisoned” by the metalloporphyrin. However, upon agitation, previously interior peptide molecules create new surfaces that then lead to the structures responsible for catalysis. All of the MTPPS derivatives tested show this behavior with varying efficiency and precursor stability, depending upon the metal incorporated into the porphine structure. Interestingly, the diacid form of TPPS (H4TPPS2−) at this concentration level has no effect on either delay time or growth rate. Again, Coulombic effects may be playing a role; the porphyrin diacid involves a buildup of positive charge at the core of the porphine unit. However, the presence of the metal-free derivative at high concentration (∼10−5 M) does have a profound impact on the morphology of the formed aggregate; for this derivative the insulin gel (now green with adsorbed porphyrin diacid) settles out almost completely without any need for centrifugation.
CuTPPS shows a second type of behavior at higher concentrations shared by only a small number of the metalloderivatives. A sufficiently high concentration of CuTPPS markedly decreases the amount of gel produced. CuTPPS self-aggregates to form dimers (as does NiTPPS) in this higher concentration range, and it is possible that this dimeric porphyrin structure serves as a catalyst for gel formation. The lag time disappears at these metalloporphyrin concentrations and the rate constant is comparable to kc but under these conditions, the product gel is sufficiently contaminated that even on agitation there is no tendency for the peptide to undergo the explosive growth phase characteristic of the reaction profile in the absence of inhibitors. At an intermediate concentration of CuTPPS both behaviors are observed for a single sample providing a reaction profile of considerable complexity.
In summary, we suggest that the rate-determining step for the formation of amyloid-type gels of insulin involves the activation of the solute species of the peptide rather than “seed” formation. This process, which can be modeled effectively as being catalyzed by insulin aggregates, has marked temperature and ionic strength dependences. Metalloporphyrins hold considerable promise as inhibitors of assembly kinetics, and in vitro studies can be helpful in determining the particular derivatives and concentration conditions needed to maximize their impact. Our results indicate that the overall charge of the porphyrin as well as the oxidation state and ligand-binding tendencies of the incorporated metal all play a role in tuning the efficiency of inhibition.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Supplementary Material
Acknowledgments
The authors gratefully acknowledge support from the National Institutes of Health (AG 19302, R.F.P.), the Howard Hughes Medical Institute (Swarthmore College), as well as summer research funds from Goucher College. We benefited from useful input from Peter Collings, Nile Chang, and Emily Ullman of Swarthmore College.
References
- 1.Kelly, J. W. 1998. The alternative conformations of amyloidogenic proteins and their multi-step assembly pathways. Curr. Opin. Struct. Biol. 8:101–106. [DOI] [PubMed] [Google Scholar]
- 2.Dobson, C. M. 2004. Principles of protein folding, misfolding and aggregation. Semin. Cell Dev. Biol. 15:3–16. [DOI] [PubMed] [Google Scholar]
- 3.Prusiner, S. B. 1998. Prions. Proc. Natl. Acad. Sci. USA. 95:13363–13383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pan, K.-M., M. Baldwin, J. Nguyen, M. Gasset, A. Serban, D. Groth, I. Mehlhorn, Z. Huang, R. J. Fletterick, F. E. Cohen, and S. B. Prusiner. 1993. Conversion of α-helices into β-sheets features in the formation of scrapie prion proteins. Proc. Natl. Acad. Sci. USA. 90:10962–10966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sunde, M., and C. C. F. Blake. 1998. From the globular to the fibrous state: protein structure and structural conversion in amyloid formation. Q. Rev. Biophys. 31:1–39. [DOI] [PubMed] [Google Scholar]
- 6.Tompa, P., G. E. Tusnady, P. Friedrick, and I. Simon. 2002. The role of dimerization in prion replication. Biophys. J. 82:1711–1718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gazit, E. 2002. The “correctly folded” state of proteins: is it a metastable state. Angew. Chem. Int. Ed. Engl. 41:257–259. [DOI] [PubMed] [Google Scholar]
- 8.Waugh, D. F. 1946. A fibrous modification of insulin. I. The heat precipitate of insulin. J. Am. Chem. Soc. 68:247–250. [Google Scholar]
- 9.Burke, M. J., and M. A. Rougvie. 1972. Cross-β- protein structure. I. Insulin fibrils. Biochemistry. 11:2435–2438. [DOI] [PubMed] [Google Scholar]
- 10.Klunk, W., J. Pettegrew, and D. J. Abraham. 1989. Quantitative evaluation of congo red binding to amyloid-like proteins with a beta-pleated sheet conformation. J. Histochem. Cytochem. 37:1273–1281. [DOI] [PubMed] [Google Scholar]
- 11.Klunk, W. E., R. F. Jacob, and R. P. Mason. 1999. Quantifying amyloid β-peptide (Aβ) aggregation using congo red (CR-Aβ) spectrophotometric assay. Anal. Biochem. 266:66–76. [DOI] [PubMed] [Google Scholar]
- 12.LeVine, H. 1993. Thioflavin T interaction with synthetic Alzheimer's disease beta-amyloid peptides: detection of amyloid aggregation in solution. Protein Sci. 2:404–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bouchard, M., J. Zurdo, J. Nettleton, C. M. Dobson, and C. V. Robinson. 2000. Formation of insulin fibrils followed by FTIR simultaneous with CD and electron microscopy. Protein Sci. 9:1960–1967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Nettleton, E. J., P. Tito, M. Sunde, M. Bouchard, C. M. Dobson, and C. V. Robinson. 2000. Characterization of the oligomeric states of insulin in self-assembly and amyloid fibril formation by mass spectrometry. Biophys. J. 79:1053–1065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Whittingham, J. J., D. J. Scott, K. Chance, A. Wilson, J. Finch, J. Brange, and G. G. Dodson. 2002. Insulin at pH 2: structural analysis of the conditions promoting insulin fibre formation. J. Mol. Biol. 318:479–490. [DOI] [PubMed] [Google Scholar]
- 16.Ahmad, A., M. Millet, D. Doniach, S. Uversky, and A. L. Fink. 2003. Partially folded intermediates in insulin fibrillation. Biochemistry. 42:11404–11416. [DOI] [PubMed] [Google Scholar]
- 17.Brange, J., G. G. Dodson, D. J. Edwards, P. H. Holden, and J. L. Whittingham. 1997. A model of insulin fibrils derived from the x-ray crystal structures of a monomeric insulin (despentapeptide insulin). Proteins. 27:507–516. [PubMed] [Google Scholar]
- 18.Hua, Q., and M. A. Weiss. 2004. Mechanism of insulin fibrillation. J. Biol. Chem. 279:21449–21460. [DOI] [PubMed] [Google Scholar]
- 19.Brange, J., L. Anderson, E. Laursen, G. Meyn, and E. Rasmussen. 1997. Toward understanding insulin fibrillation. J. Pharm. Sci. 86:517–525. [DOI] [PubMed] [Google Scholar]
- 20.Harper, J. D., S. S. Wong, C. Lieber, and P. T. Lansbury, Jr. 1999. Assembly of Aβ amyloid protofibrils: an in vitro model for a possible early event in Alzheimer's disease. Biochemistry. 38:8972–8980. [DOI] [PubMed] [Google Scholar]
- 21.Jimenez, J., E. J. Nettleton, M. Couchard, C. V. Robinson, C. Dobson, and H. R. Saibil. 2002. The protofilament structure of insulin amyloid fibrils. Proc. Natl. Acad. Sci. USA. 99:9196–9201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Walsh, D. M., D. M. Hartley, Y. Kusumoto, Y. Fezoui, M. M. Condron, A. Lomakin, G. B. Benedek, D. J. Selkoe, and D. B. Teplow. 1999. Amyloid β-protein fibrillogenesis. Structure and biological activity of protofibrillar intermediates. J. Biol. Chem. 274:25945–25952. [DOI] [PubMed] [Google Scholar]
- 23.Pasternack, R. F., E. J. Gibbs, P. J. Collings, J. C. dePaula, L. C. Turzo, and A. Terracina. 1998. A non-conventional approach to supramolecular formation dynamics. The kinetics of assembly of DNA-bound porphyrins. J. Am. Chem. Soc. 120:5873–5878. [Google Scholar]
- 24.Pasternack, R. F., C. Fleming, S. Herring, P. J. Collings, J. C. dePaula, G. DeCastro, and E. J. Gibbs. 2000. Aggregation kinetics of extended porphyrin and cyanine dye assemblies. Biophys. J. 79:550–560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Pasternack, R. F., S. Ewen, A. Rao, A. S. Meyer, M. A. Freedman, P. J. Collings, S. L. Frey, M. Ranen, and J. C. dePaula. 2001. Interactions of copper(II) porphyrins with DNA. Inorg. Chim. Acta. 317:59–71. [Google Scholar]
- 26.Egan, T. J., W. W. Mavuso, and K. K. Ncokazi. 2001. The mechanism of β-hematin formation in acetate solution. Parallels between hemozoin formation and biomineralization processes. Biochemistry. 40:204–213. [DOI] [PubMed] [Google Scholar]
- 27.Jarrett, J. T., and P. T. Lansbury, Jr. 1992. Amyloid fibril formation requires a chemically discriminating nucleation event: studies of an amyloidogenic sequence from the bacterial protein OsmB. Biochemistry. 31:12345–12352. [DOI] [PubMed] [Google Scholar]
- 28.Bucciantini, M., E. Giannoni, F. Chiti, F. Baroni, L. Formigli, J. Zurds, N. Taddei, G. Ramponi, C. Dobson, and M. Stefani. 2002. Inherent toxicity of aggregates implies a common mechanism for protein misfolding diseases. Nature. 416:507–511. [DOI] [PubMed] [Google Scholar]
- 29.Jansen, R., W. Dzwolak, and R. Winter. 2005. Amyloidogenic self-assembly of insulin aggregates probed by high resolution atomic force microscopy. Biophys. J. 88:1344–1353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Frank, B. H., A. J. Veros, and A. H. Pekar. 1972. Physical studies on proinsulin. A comparison of the titration behavior for the tyrosine residue in insulin and proinsulin. Biochemistry. 11:4926–4931. [DOI] [PubMed] [Google Scholar]
- 31.Nielsen, L., S. Frokjaer, J. Brane, N. Uversky, and A. L. Fink. 2001. Probing the mechanism of insulin fibril formation with insulin mutants. Biochemistry. 40:8397–8409. [DOI] [PubMed] [Google Scholar]
- 32.Sabate, R., M. Gallardo, and J. Estelrich. 2003. An autocatalytic reaction as a model for the kinetics of the aggregation of β-amyloid. Biopolymers. 71:190–195. [DOI] [PubMed] [Google Scholar]
- 33.Caughey, W. S., L. D. Raymond, M. Horiuchi, and B. Caughey. 1998. Inhibition of protease-resistant prion protein formation by porphyrins and phthalocyanines. Proc. Natl. Acad. Sci. USA. 95:12117–12122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Priola, S. A., A. Raines, and W. S. Caughey. 2000. Porphyrin and phthalocyanine anti-scrapie compounds. Science. 287:1503–1506. [DOI] [PubMed] [Google Scholar]
- 35.Shinozaki, K., T. Konakahara, H. Okuno, and M. Kodaka. 2003. Analysis of fibril formation of amyloid-β-protein by stretched exponential function. Protein Pept. Lett. 10:569–574. [DOI] [PubMed] [Google Scholar]
- 36.Baskakov, I. V., and O. V. Bocharova. 2005. In vitro conversion of mammalian prion protein into amyloid fibrils displays unusual features. Biochemistry. 44:2339–2348. [DOI] [PubMed] [Google Scholar]
- 37.Ahmad, A., M. Millet, D. Doniach, S. Uversky, and A. L. Fink. 2004. Stimulation of insulin fibrillation by urea-induced intermediates. J. Biol. Chem. 279:14999–15013. [DOI] [PubMed] [Google Scholar]
- 38.Bush, A. I. 2003. The metallobiology of Alzheimer's disease. Trends Neurosci. 26:207–214. [DOI] [PubMed] [Google Scholar]
- 39.Pasternack, R. F., L. Francesconi, D. Raff, and E. Spiro. 1973. Aggregation of nickel(II), copper(II), and zinc(II) derivatives of water-soluble porphyrins. Inorg. Chem. 12:2606–2611. [Google Scholar]
- 40.Gibbs, E., W. R. Skowronek, Jr., W. T. Morgan, and U. J. Muller-Eberhard. 1980. Reactions of water-soluble metalloporphyrins with the serum protein, hemopexin. J. Am. Chem. Soc. 102:3939–3944. [Google Scholar]
- 41.Pasternack, R. F., E. G. Spiro, and M. J. Teach. 1974. Solution properties of nickel(II)tetra(4-N-methylpyridyl)porphine and the influence of acetone, pyridine and imidazole. J. Inorg. Nucl. Chem. 36:599–606. [Google Scholar]
- 42.Pasternack, R. F., H. Lee, P. Malek, and C. J. Spencer. 1977. Solution properties of tetrakis-(4-N-methyl)pyridylporphineiron(III). J. Inorg. Nucl. Chem. 39:1865–1870. [Google Scholar]
- 43.Fleischer, E. B., J. M. Palmer, T. S. Srivastava, and A. J. Chatterjee. 1971. Thermodynamic and kinetic properties of an iron-porphyrin system. J. Am. Chem. Soc. 93:3162–3167. [DOI] [PubMed] [Google Scholar]
- 44.Harriman, A., and G. J. Porter. 1979. Photochemistry of manganese porphyrins. Chem. Soc. Farad. Trans. 2. 75:1532–1542. [Google Scholar]
- 45.Pasternack, R. F., and M. A. Cobb. 1973. The substitution reactions of a water soluble cobalt(III) porphyrin with thiocyanate as a function of pH. J. Inorg. Nucl. Chem. 35:4327–4339. [Google Scholar]
- 46.Ashley, K. R., and J. G. Leipoldt. 1981. Kinetic and equilibrium study of the reaction of (meso-tetrakis(p-sulfonatophenyl)porphinatodiaquacobaltate(III) with pyridine in aqueous solution. Inorg. Chem. 20:2326–2333. [Google Scholar]
- 47.Abou-Gamra, Z., and A. J. Harriman. 1986. Redox chemistry of gold(III) porphyrins in water. Chem. Soc. Farad. Trans. 2. 82:2337–2350. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.