Cell Population Dynamics Modulate the Rates of Tissue Growth Processes

Abstract

The development and testing of a discrete model describing the dynamic process of tissue growth in three-dimensional scaffolds is presented. The model considers populations of cells that execute persistent random walks on the computational grid, collide, and proliferate until they reach confluence. To isolate the effect of population dynamics on tissue growth, the model assumes that nutrient and growth factor concentrations remain constant in space and time. Simulations start either by distributing the seed cells uniformly and randomly throughout the scaffold, or from an initial condition designed to simulate the migration and cell proliferation phase of wound healing. Simulations with uniform seeding show that cell migration enhances tissue growth by counterbalancing the adverse effects of contact inhibition. This beneficial effect, however, diminishes and disappears completely for large migration speeds. By contrast, simulations with the “wound” seeding mode show a continual enhancement of tissue regeneration rates with increasing cell migration speeds. We conclude that cell locomotory parameters and the spatial distribution of seed cells can have profound effects on the dynamics of the process and, consequently, on the pattern and rates of tissue growth. These results can guide the design of experiments for testing the effectiveness of biomimetic modifications for stimulating tissue growth.

INTRODUCTION

Tissue engineering applies the knowledge gained in biology, biochemistry, medical sciences, and engineering to develop bioartificial implants or to induce tissue remodeling to replace, repair, or enhance the function of a particular tissue or organ (1,2). Tissue growth is a complex process whose rate and pattern are affected by many factors such as the cell phenotype, the density and spatial distribution of seed cells, and the culture conditions (3). These factors affect tissue growth by directly or indirectly modulating basic cell functions including adhesion, migration, proliferation, and differentiation. Recent advances in biomaterials research have made it possible for us to manipulate cellular functions (like adhesion and migration) through special fabrication techniques (4) or biomimetic modification of biomaterial scaffolds (5–9). However, theoretical guidance on how altered cell-level properties may affect the process of tissue growth is still lacking. As a result, the development of tissue substitutes is still in an early stage, based almost exclusively on empirical approaches that require many expensive and time-consuming experiments.

The lack of comprehensive models for tissue growth processes can be attributed mainly to the complexity of biological systems consisting of entire cell populations. The numerous components of a biosystem participate in countless and tightly coupled processes occurring at the molecular, cellular, cell population, and tissue levels. Cell population heterogeneity plays an important role in determining the complexity of biological behavior and function (10–12). The intricate population dynamics resulting from cell-cell and cell-biomaterial interactions constitute another very important (and yet often neglected) factor in determining the growth rate and structure of developing tissues. The division of most anchorage-dependent mammalian cells is contact inhibited, a phenomenon observed both on flat surfaces (13–17) and in three-dimensional scaffolds (18–21). Contact inhibition has significant adverse effects on tissue growth. These effects, however, can be compensated (at least partially) by cell migration. Enhanced cell motility increases the probability that a cell will move away from its immediate neighbors and will have room to divide at the end of its cycle. Several studies found that the enhancement of cell proliferation rates resulting from the addition of growth factors to the culture media was actually caused by the stimulating effect of the growth factors on cell migration (22,23). The migration process, however, can be slowed down by cell-cell collisions that may cause a pause in cell movement or the formation of an aggregate. Fibroblasts, for example, will stop for ∼25 min after a collision before breaking away from each other to resume their migration (24). Similar behavior has been observed with bovine pulmonary artery endothelium cells (25). Epithelial cells, on the other hand, adhere to each other irreversibly when they collide. Subsequent collisions lead to the creation of small colonies that grow until a contiguous sheet of cells is formed. This process is essential for wound healing (24,26).

To capture the dynamics of tissue growth, one must accurately describe the competing processes of contact inhibition and cell migration. The first attempts to model cell population dynamics considered the limiting cases of nonmotile cells proliferating on two-dimensional (2D) surfaces (27,28) or microcarriers (29,30). By neglecting migration, however, these models could not offset the adverse effects of contact inhibition on cell proliferation. Frame and Hu (31) used an empirical approach to describe the reduction in growth rates caused by contact inhibition, whereas Ruann and co-workers (32) attempted to describe the beneficial effects of cell locomotion by assuming that the daughter cells were quickly separated by a certain distance after every division event. Lee and co-workers (25) were the first to directly quantify the competing effects of migration and contact inhibition without simplifying assumptions. Their model considered individual cells that executed persistent random walks on a 2D grid, collided, and proliferated to build a new tissue. Key parameters of this model could be easily obtained from long-term tracking and analysis of cell locomotion and division (33,34). Simulation results agreed well with experimental data on the expansion of keratinocyte megacolonies (22), the growth of endothelium (25), and the expansion of marrow stromal osteoblast megacolonies on biomimetic hydrogels (35). Cell migration speeds and the spatial distribution of seed cells were found to be crucial factors in determining proliferation rates. Because of the significant advantage they have in describing cell population dynamics, discrete models were also used in several recent studies to address the two-dimensional problems involving the aggregation and self-organization of Dictyostelium discoideum (36–38) and the interactions between extracellular matrix and fibroblasts (39).

The modeling approaches described in the previous paragraph, however, have not been extended to three-dimensional (3D) tissue growth processes. Chang and co-workers (40) developed a 3D discrete model for the growth of biofilms, but the division of bacterial cells was not contact inhibited and cell migration was not considered. Kansal and co-workers developed a 3D model based on cellular automata (41) to simulate brain tumor growth dynamics. However, each automaton of this model represented 100–10⁶ real cells. Although greatly reducing the computational requirements, this approach did not provide a detailed description of cell population dynamics.

This study will present a significant extension of our earlier 2D work (25) to asynchronous cell populations that migrate, collide, and proliferate to build a tissue inside a 3D scaffold. Our objective is to characterize the dynamics of the tissue growth process and to identify the key system parameters that affect the structure and growth rate of the developing tissue. Simulating the growth of 3D tissues with substantial size requires large grids to handle the locomotion and interactions of individual cells, as well as small time steps to accurately describe the population dynamics. For this reason, our tissue growth algorithm was parallelized for execution on distributed-memory multicomputers.

MODEL DEVELOPMENT

Tissue growth dynamics

The growth of bioartificial tissues is a highly dynamic and complex process. A small tissue sample is harvested from the patient or donor. Cells from this tissue are isolated, cultured, and seeded into a 3D scaffold with the proper structure and surface properties. We will consider here highly porous scaffolds that allow cells to migrate freely in all directions. Such scaffolds are formed, for example, from entangled fibers made of polymers or natural proteins like collagen. The inoculated scaffold is then immersed into a liquid tissue culture medium containing the necessary nutrients for cell growth (in vitro tissue culture). Growth factors, that is soluble proteins serving as intercellular chemical messengers, are also necessary for normal tissue development. These proteins bind to specific receptors on the surface of target cells and modulate key cellular processes (like migration or proliferation) by inducing or directing the action of specific genes. As nutrients and growth factors diffuse into the 3D scaffold, the seeded cells migrate in all directions and proliferate to populate the scaffold and form the new tissue. Migration is slowed down by cell-cell collisions and proliferation stops when cells are completely surrounded.

Our model will focus on the key processes of migration, cell-cell collision, and proliferation. The competing processes of migration and contact inhibition will be analyzed for homogeneous cell populations and under a variety of conditions that may appear in tissue engineering applications. To simplify the analysis, we will not consider at this stage the coupling of cell population dynamics with the transport of nutrients or other molecules that modulate cellular functions like migration and proliferation. Instead, we will assume that the parameters necessary to describe the locomotory and proliferative behavior of the cells are known for the given culture conditions. This does not necessarily mean that the culture environment has to be uniform. In fact, we will see that the discrete model presented here is capable of describing biased cell movement under conditions that lead to chemotaxis. We will finally assume that the process of tissue growth takes place over a relatively short time (few consecutive cell divisions). Thus, cell apoptosis can be neglected.

Several studies have shown that cells execute persistent random walks when allowed to migrate in uniform 2D or 3D environments (42–44). This motion is usually described with two parameters: migration speed S and persistence time t_p, the average (or expected) time between significant directional changes (45–47). Breaks in the migratory patterns of cells are often observed as they enter stationary phases of variable duration and frequency (44). When cells collide, they also enter a stationary phase whose duration depends on the cell type (34,48). Clearly, breaks in the persistent random walks and cell collisions will slow down the movement of cells. As a result, the effective speed of migration S_e computed from data obtained from a “dense” cell population will be lower than the true migration (or swimming) speed. Even when the swimming speed S is time invariant, the effective speed S_e will decrease as the density of a cell population increases and cell collisions are more frequent.

We can now summarize the key steps of the tissue growth process as follows:

1. Each cell in the population moves in one direction for a certain length of time (persistence time). At the end of this interval, the cell stops and turns to continue its migration in another direction. Fig. 1 shows the simulated trajectory (solid arrows) of a typical cell. If the cell does not collide with another cell, this persistent random movement will continue until it is time for the cell to divide. Although all cells move with the same “swimming” speed, their effective (or observed) speed will be lower due to breaks in their motion that are either spontaneous or caused by collisions with other cells.

2. At the end of its cycle, the cell stops to divide. The length of the cell cycle (or division time) will be considered as a random variable whose probability density function is characteristic of each cell type and can be measured experimentally (33,34). When the mitosis phase is over, the two daughter cells move away from each other and resume their persistent random movement (dashed and dotted arrows of Fig. 1).

3. When two cells collide, they stop for some time before resuming their migration. The time interval of adherence will be another parameter of our model because it varies widely among cell types (33,34,48).

4. This process is repeated until confluence has been reached, that is until the scaffold is filled and the cells cannot migrate or divide any further.

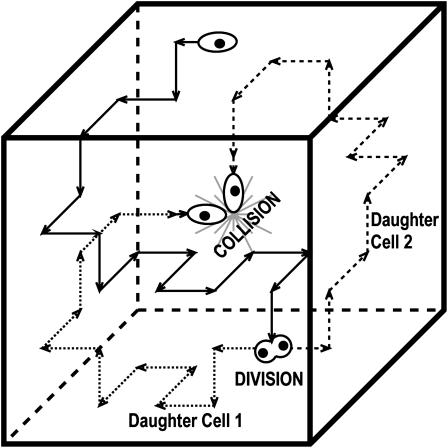
FIGURE 1.

Schematic showing the persistent random walk (solid arrows) of a cell during its division cycle. The two daughter cells move away from each other and resume their persistent random movement (dotted and dashed arrows). Cells may also collide.

The model developed in the following sections will be referred to as the CPMC/S/A model for cell proliferation, migration, and collision model of a single, asynchronous population of cells that move with the same speed and persistence.

Discrete model for tissue growth

To model the previously described dynamics of tissue growth, we will consider cellular automata (49,50) consisting of 3D grids with 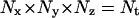cubic computational sites. Each site of our cellular array is a finite automaton that can exist at one of a finite number of states at each time interval. That is, a site may be either: 1), empty and available for a cell to move in; or 2), occupied by a cell that is at some point in its mitotic cycle and either moves in a certain direction or is stationary. The model assumes that each site can contain at most one cell.

Every automaton is “connected” to a set of “neighbors” and its state evolves at discrete time steps 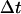through interactions with neighboring automata. In our algorithm, the neighborhood of every automaton consists of the six cubic sites that share a face with it and are located to the east, north, west, south, below and above the considered automaton (von Neumann neighborhood). Let us assume now that the i-th automaton contains a cell at time t^r. Its state 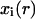is specified by a vector of integers with the following components:

• Migration index m_i: If m_i = 1,2,…,6, then the cell is migrating in one of the six directions (1 = east, 2 = north, 3 = west, 4 = south, 5 = down, 6 = up). If m_i = 0 or m_i = 7, the cell is in one of two stationary states that will be defined below.

• Division counter k_d,i: The time that must elapse before the cell divides is equal to 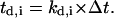This counter is decremented by one at each time step, and the cell divides when 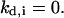The cell division times of the seed cells are assigned using a probability density function that can be determined from experimental data (11). Thus, the cell population evolves in an asynchronous fashion. The same density function is used to assign division times to the two daughter cells after each mitosis event.

• Persistence counter k_p,i: The time that must elapse before the cell changes its direction of movement is equal to 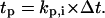This counter is decremented by one at each time step, and the cell turns when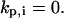

The migration speed S of a homogeneous cell population is set when we specify the iteration interval 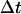and assume that the time required for a cell to move from one site to an adjacent one is 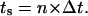Given that the side of a cubic computational site is fixed and equal to h, the migration speed S becomes:

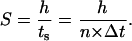(1)

The following model parameters must also be specified:

• Waiting times E(T_j) of migration states: These are the average times that a cell will: a), keep moving in a specific direction (j = 1, 2,…, 6); or b), stay at the same location after entering the stationary state (j = 0). These parameters characterize the persistence of cell migration and can be measured using the procedure established by Noble and Levine (33,51).

• Transition probabilities 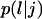: These are the probabilities with which cells switch their direction of movement from j (j = 0, 1, 2, …,6) to l (l = 1, 2, …, 6 and j ≠ l). These parameters characterize the cells' turning behavior and can be experimentally determined (33,51).

Let us assume that a cell i is in state j when its persistence counter k_p,i reaches zero. If there are empty sites in its immediate neighborhood, the cell will select one of them as its next location using a random algorithm based on the probabilities 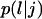of the possible transitions. If a cell is completely surrounded when k_p,i reaches zero, it cannot move. Instead, it enters the stationary state j = 0 and we set:

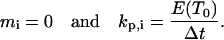Cell divisions are handled in a similar fashion. When the division counter reaches zero and there is at least one empty neighboring site, the cell will divide. One daughter cell will stay in the current site while the second one will be placed in a randomly selected neighboring site. All free neighboring sites have equal probabilities of being selected. The two daughter cells are set to migrate in randomly selected directions and are assigned new division counters that are computed using the experimentally determined probability density function of cell division times. If a cell finds itself completely surrounded when its division counter reaches zero, however, it cannot divide. Instead, it enters the stationary phase.

When cells migrate in a uniform environment, the transition probabilities 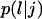are equal to each other for j, l = 1,2,…,6 (33). The same is also true for the waiting times of all the migration states E(T_j), for j = 1,2,…,6. Thus, in the absence of chemotactic gradients or other nonuniformities in the cellular microenvironment:

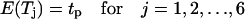(2)

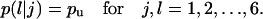(3)

However, factors such as substrate surface patterns or the presence of chemoattractants can induce biased cell movement, significantly altering the values of transition probabilities (or waiting times) in one or more directional states.

Cell-cell collisions

To account for the “slowdown” caused by cell-cell collisions, our model has a second stationary state j = 7. Cells enter this state after a collision and will stay in the same location for a period of time equal to E(T₇) before resuming their migration. The magnitude of E(T₇) is a measure of the “stickiness” of cells, that is their tendency to form multicellular aggregates.

When two cells collide, their migration indices are changed to 7 and their persistence counters are reset to 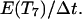If one of the colliding cells is already in state 7, its persistence counter is reset to 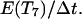When the waiting time E(T₇) has expired, the two cells move away from each other in directions that are randomly selected using equal transition probabilities:

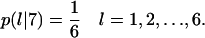(4)

Our model also assumes that the division clock continues to run while the cells are in this stationary state.

Initial conditions (seeding modes)

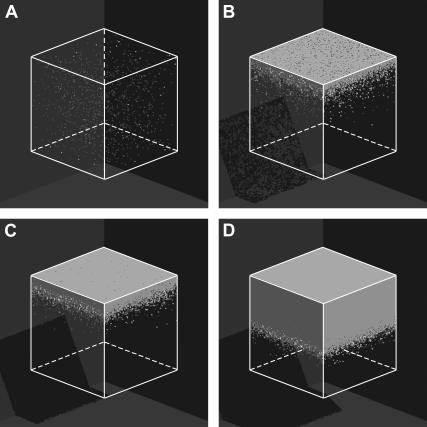
Two initial conditions or seeding modes will be considered in this study to demonstrate the significant effect of the initial spatial distribution of cells on tissue growth rates. The first mode distributes 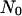seed cells randomly and uniformly throughout the computational grid. This “uniform” seeding mode is shown in Fig. 2 A, where the sites occupied by the seed cells are depicted as small white cubes. To facilitate the visualization of this seeding mode, the empty cells of the grid of Fig. 2 A are transparent. The uniform mode is the most common seeding employed for in vitro culture of bioartificial tissues. Vunjak-Novakovic and co-workers (52) used dynamic methods to seed bovine articular chondrocytes into polyglycolic acid scaffolds. Using data from this study, we estimated that the seeding density (or cell volume fraction) was in the range of 0.367–1.33%. Similar seeding densities have been reported for various combinations of cell type and scaffold material (53–60).

FIGURE 2.

Initial configuration (A) and temporal evolution of a 100 × 100 × 100 cellular array simulating the growth of a homogeneous tissue in a 3D scaffold. The initial cell volume fraction for this run is 0.001 (A). Panels B–D correspond to 0.01, 0.1, and 0.5 cell volume fraction, respectively. Other run parameters are: cell migration speed = 60 μm/h; persistence time = 2 h; aggregation time = 1 h; uniform transition probabilities; average division time = 20 h. The horizontal arrows in panels A and C identify the vertical scale corresponding to each curve. (A) Iteration = 0, t = 0.0 days, κ(t) = 0.001. (B) Iteration = 388, t = 3.23 days, κ(t) = 0.01. (C) Iteration = 719, t = 5.99 days, κ(t) = 0.1. (D) Iteration = 949, t = 7.90 days, κ(t) = 0.5.

As we will see later, however, the uniform seeding mode may not be the most appropriate initial condition for studying the effect of surface modification on tissue growth rates. This is particularly true for scaffolds that are developed to promote wound healing to repair damaged bone or guide nerve regeneration. To demonstrate the importance on initial conditions and, at the same time, show how our model can be used to optimize wound healing therapies, we will consider a second seeding mode. In this mode, the seed cells occupy every site surrounding a cylindrical “wound” located in the center of the computational grid (see Fig. 8 A). We will assume that this wound is filled again with a highly porous scaffold that allows cells to migrate freely in all directions. When the simulation starts, cells detach from the confluent tissue around the wound, migrate into the scaffold, and proliferate to fill (or “heal”) the cylindrical wound. We must emphasize here that our model does not attempt to describe all the steps of the complicated wound healing process (61). The model is only appropriate for the phases characterized by migration of fixed cells into the natural or artificial scaffold that fills a wound (2). These phases follow the initial hemostasis, inflammation, and scab formation steps that characterize the typical wound healing processes (61).

FIGURE 8.

Images showing the tissue growth patterns for two runs that started with the same wound seeding mode but widely different cell migration speeds: S = 1 μm/h (A–C) and S = 60 μm/h (A, D, and E). The black line indicates the initial boundary of the wound. Run parameters are: size of the cellular array = 200 × 200 × 200; diameter of cylindrical “wound” = 100 pixels. All other parameters are the same as in Fig. 2. (A) Iteration = 0, t = 0.0 days, κ_w(t) = 0.0. (B) S = 1 μm/h; t = 2.32 days; κ_w(t) = 0.1. (C) S = 1 μm/h; t = 10.19 days; κ_w(t) = 0.5. (D) S = 60 μm/h; t = 0.58 days, κ_w(t) = 0.1. (E) S = 60 μm/h; t = 1.83 days; κ_w(t) = 0.5.

Cell population dynamics

For every automaton i (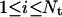), the application of the rules described in the previous subsections define a local transition function that specifies the state 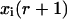of the automaton at 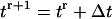as a function of the state 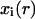at 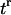and the states of its six neighbors. The simultaneous application of the local transition functions to all the automata defines a global transition function F that transforms a configuration 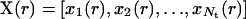of the cellular automaton to the next one:

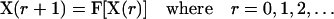(5)

Starting with the initial configuration 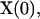the global transition function F transforms the cellular array to simulate the dynamic process of tissue growth. At some time t after the start of the simulation, 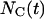sites of the cellular automaton are occupied by cells and the cell volume fraction 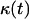for runs starting with uniform seeding is defined as:

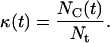(6)

For wound healing runs, we are interested in determining how fast the sites belonging to the cylindrical wound (equal to 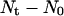) are filled with cells. For these runs, the cell volume fraction 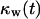is defined by a slightly different formula:

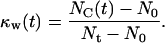(7)

The simulation continues until all sites are occupied by cells, that is until 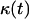or 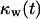equals one. As previously mentioned, breaks in the persistent random walks and cell collisions will slow down the movement of cells. Thus, only a fraction of the cells 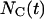will move in the time interval 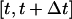and the effective speed of migration S_e can be calculated as:

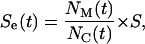(8)

where 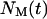refers to the number of cells that were moving in the time interval 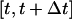and S is the cell “swimming” speed. For wound healing runs, we first count the total number of cells 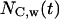and the number of migrating cells 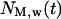located inside the cylindrical wound. The effective speed of migration 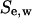is then calculated as:

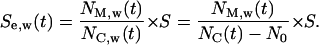(9)

In both cases, the effective speed of a migration is a population-average quantity and is affected by: a), the frequency and duration E(T₀) of random breaks in cell movement, b), the frequency 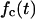of cell-cell collisions and the magnitude of E(T₇), and c), the fraction 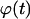of cells that are completely surrounded and, therefore, cannot move or divide. The frequency and duration of migration breaks depend on the cell phenotype and the presence of soluble growth factors or ligands that modulate cell behavior. The frequency of collisions and the fraction of surrounded cells, however, depend primarily on the dynamics of the cell population. If we let 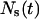denote the number of completely surrounded cells in the time interval 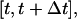these two quantities can be computed as follows:

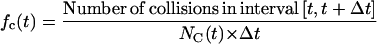(10)

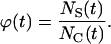(11)

For wound healing runs again, the frequency of collisions and the fraction of completely surrounded cells are found by considering only the “wound” sites for counting cell-cell collisions and completely surrounded cells.

Computer implementation

Simulating the growth of tissues with substantial size is a computationally challenging problem requiring large grids to handle the populations of discrete cells and small time steps to accurately describe the cell population dynamics. For this reason, our tissue growth algorithm was parallelized using the MPI standard for interprocessor communication. Simulations were carried out on a Beowulf cluster (Evolocity, Linux Networx, Sandy, UT) with 41 computational nodes. Each node had two 1.7-GHz Pentium 4 Xeon processors (Myricom, Arcadia, CA) and 2 GB of DDR memory. The nodes were connected with a switched 1.2 GB/s Myrinet (Arcadia, CA) network. Several model parameters affect the CPU time required to run a simulation. In addition to the size of the grid, these parameters include the initial seeding density, cell division time, migration speed, and persistence time. A typical simulation on a 120 × 120 × 120 grid takes 722 s to run on a single node and 201 s on 10 nodes. This grid represents a cubical section of tissue whose side is only equal to 2.4 mm. For the same model parameters and a 300 × 300 × 300 grid, we need 13,112 s to run a simulation on a single node and 2,153 s to run it on 10 nodes.

RESULTS AND DISCUSSION

Uniform seeding mode

Fig. 2 shows the temporal evolution of a cellular array that simulates the growth of a homogeneous cell population. This simulation starts by randomly placing cells in 0.1% of the sites of the 100 × 100 × 100 cellular array. The occupied sites are shown as small white cubes in Fig. 2 A. The cells are then allowed to migrate, interact, and proliferate. After 388, 719, and 949 iterations, the cell population occupies 1, 10, and 50% of the computational sites, respectively (Fig. 2, B–D).

A systematic parametric study was carried out to investigate how key model parameters affect the rates of tissue growth. First, we looked at the effect of speed and persistence of cell locomotion. The magnitude of swimming speed S and persistence time t_p depends on both cell type and extracellular environment. Reported values from 2D migration studies range from S = 30 μm/h and t_p = 4–5 h for human microvessel endothelial cells and smooth muscle cells (62,63) to S = 600 μm/h and t_p = 4 min for rabbit neutrophils (64). Recent 3D studies report speeds of 8–15 μm/h for adenocarcinoma and prostate cancer cell lines in collagen (44) and speeds of 20–40 μm/h for melanoma cells migrating in collagen matrices modified with RGD peptides (42).

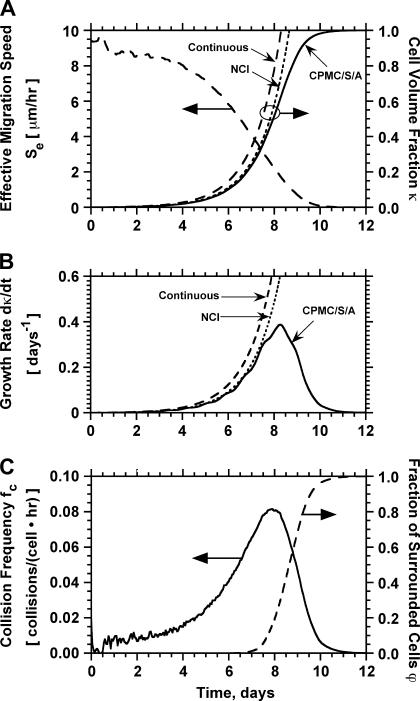
Fig. 3 presents the simulation results for a population of cells with swimming speed equal to 10 μm/h and persistence equal to 0.4 h, values that are within the range reported in the previously mentioned studies. This run started with uniform seeding and 0.001 initial cell volume fraction. Cells had to remain stationary for 1 h after a collision and had a distribution of division times with average equal to 20 h. The simulation results show that the tissue grows in a uniform spatial pattern (see Fig. 2, B and C). After an initial lag phase, the tissue enters a stage of rapid growth reaching confluence after ∼10 days (Fig. 3 A). Fig. 3 A also shows that the effective speed of migration S_e decreases with increasing cell density. The rate at which S_e falls becomes more pronounced as the cell volume fraction goes above the 0.1 level. This is primarily due to the increasing frequency of cell-cell collisions (Fig. 3 C), events that force the colliding cells to enter a stationary state. The collision frequency reaches a peak at ∼8 days when 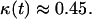As the cell density increases beyond this level, we see a rapid increase in the fraction of completely surrounded cells that leads to a sharp drop in the frequency of actual cell-cell collisions (Fig. 3 C).

FIGURE 3.

Temporal evolution of cell volume fraction 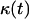and its relation to the other variables that quantify the dynamics of cell population: effective speed of migration (A), tissue growth rate (B), average frequency of cell-cell collisions (C), and fraction of surrounded cells (C). Panels A and B present predictions from three models: the continuous model of Eq. 14, the discrete NCI model that ignores contact inhibition, and the comprehensive CPMC/S/A model described in “Model development”. Panel C presents predictions from the CPMC/S/A model. Run parameters are: uniform seeding mode; cell migration speed = 10 μm/h; persistence time = 0.4 h. The other parameters are the same as in Fig. 2.

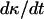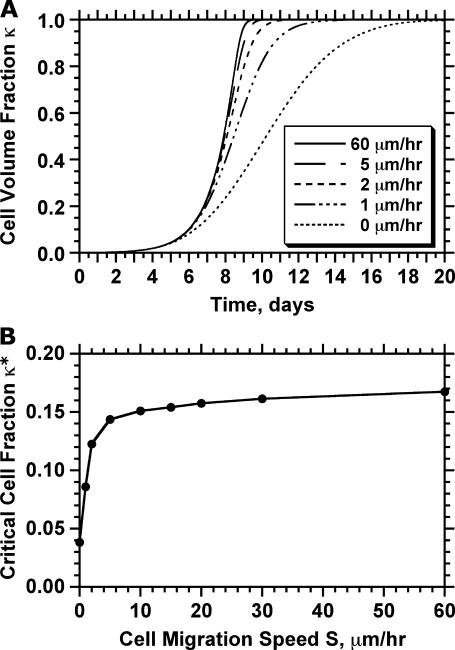
It is important to note here that the tissue growth rate continues to increase even when the effective migration speed of the cell population falls to one-quarter of its maximum value (Fig. 3 B). Only when the fraction of surrounded cells becomes significant (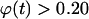), we see a decrease in the tissue growth rate. This is a strong indication that even low migration speeds may be enough to overcome the adverse effects of contact inhibition on tissue growth. Fig. 4 shows the temporal evolution of cell volume fractions obtained with nonmotile and motile cells with a wide range of migration speeds. All the simulations shown in Fig. 4 started with uniform seeding of cells in the scaffold. In the case of nonmotile cells, 3D clumps of cells formed after a few divisions. Because of contact inhibition, only the cells located on the outside of these clumps could divide and the tissue grew very slowly reaching confluence only after 20 days. Even very low migration speeds, however, are enough to overcome the contact inhibition effects. The tissue grows much faster for cell migration speeds equal to 1, 2, and 5 μm/h, and confluence is reached after ∼14, 11, and 10 days, respectively. However, the beneficial effect of increasing cell migration speeds diminishes rapidly for speeds >5 μm/h. As shown in Fig. 4 A, the predicted growth patterns for S = 60 μm/h is virtually indistinguishable from that obtained for S = 5 μm/h. When cells are uniformly dispersed in a 3D scaffold, high migration speeds offer no advantage in overcoming contact inhibition. The separation distance between neighboring cells is the same everywhere and decreases as the cell density increases. To overcome contact inhibition, cells only need to move far enough from each other so that they can divide again at the end of their cycle. Because the size of the cells and the computational sites considered here are of the order of 10 μm, speeds of the order of 1–2 μm/h are enough to maintain near-maximal growth rates for division times around 15–20 h. Higher migration speeds would be required to overcome contact inhibition if the cell division times were shorter.

FIGURE 4.

Effect of cell migration speed S on the temporal evolution of cell volume fraction (A) and the value of critical cell volume fraction (B). The other parameters are the same as in Fig. 2.

The ability of motile cells to overcome contact inhibition raises an interesting question: How accurately can a simpler continuous model predict the growth rate of tissues when we start with uniform cell seeding? For cell suspension cultures, the following exponential model is often used to describe the dynamics of population growth:

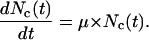(12)

Here, N_c is the numbers of cells present in the reactor at time t and μ is a constant given by:

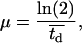(13)

where 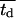is the average division time of the cultured cells. If we normalize the number of cells N_c by the total number of cells at confluence N_t, Eq. 12 becomes:

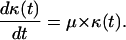(14)

The simple continuous model of Eq. 14 assumes an “average” division time for all cells and predicts that cells will start proliferating as soon as they are dispersed in the scaffold. Experimental studies have shown, however, that a significant time interval passes by before cells seeded on surfaces or in scaffolds will start proliferating (11,28). To account for this initial delay, we have also developed a simple stochastic model that allows a population of cells to proliferate with the same distribution of division times used in our comprehensive CPMC/S/A model. The simple stochastic model does not account for migration or cell-cell collisions, and assumes that all cells can divide freely up to the point where the population reaches confluence. Clearly, this model ignores contact inhibition effects and we will refer to it as the no-contact-inhibition (NCI) model.

Fig. 3, A and B, compare the cell fractions and growth rates predicted by the comprehensive model to those predicted by the continuous model of Eq. 14 and the NCI discrete model. Contact inhibition effects appear very early and become pronounced when the cell fraction rises above 0.2. Although both the continuous and discrete NCI model predict continuously increasing growth rates until the population reaches confluence, the comprehensive CPMC/S/A model reveals that contact inhibition effects force 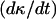to pass through a maximum. To quantify the onset of significant contact inhibition effects, we will introduce the critical cell fraction 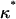as the cell fraction above which the predictions of the CPMC/S/A and NCI models differ by >5%. Specifically, if 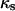and 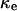are the cell fractions predicted by the CPMC/S/A and NCI models, respectively, the critical cell fraction is defined by the following condition:

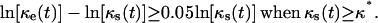(15)

Fig. 4 B shows how the critical cell fraction is affected by the cell migration speed. For an initial cell fraction of 0.001, nonmotile cells reach the critical threshold at 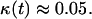At this point, cell “clumps” appear leading to a rapid decrease of the fraction of proliferating cells. Even low migration speeds are enough to overcome the contact inhibition effects in this case, however, and the critical cell fraction rises rapidly with increasing migration speeds. However, the beneficial effects of cell migration diminish as S increases beyond 5 μm/h, and the critical cell fraction reaches a plateau at levels higher than 0.8.

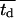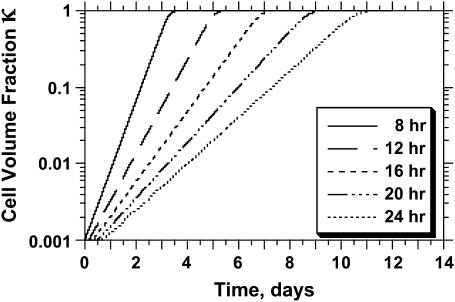
As mentioned earlier, the CPMC/S/A model described here assigns to each cell a division time that is randomly selected from a normal distribution with mean and variance 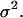Fig. 5 presents on a semilog plot of the temporal evolution of cell fractions for several runs where the mean division time 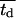ranged from 8 to 24 h with σ² fixed at 2 h. For all these runs, a large cell migration speed (S = 60 μm/h) was used to minimize the effect of contact inhibition. Fig. 5 shows that the average cell division time is a key factor in determining tissue growth rates. The time required to reach confluence increased from 3.5 days for 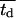= 8 h to 11 days for 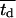= 24 h. Higher values of 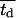prolong the initial delay in the growth curves (see Fig. 5) because they shift the entire distribution of cell division times to the right. Changes in the variance 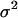of the distribution of division time did not significantly affect the predicted results as long as the mean division time of the population was kept constant.

FIGURE 5.

Effect of average cell division time on tissue growth. Cell division times were normally distributed with mean 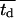(shown in inset) and variance σ² = 2 h. The other parameters are the same as in Fig. 2. Cell volume fractions are shown using a semilog scale.

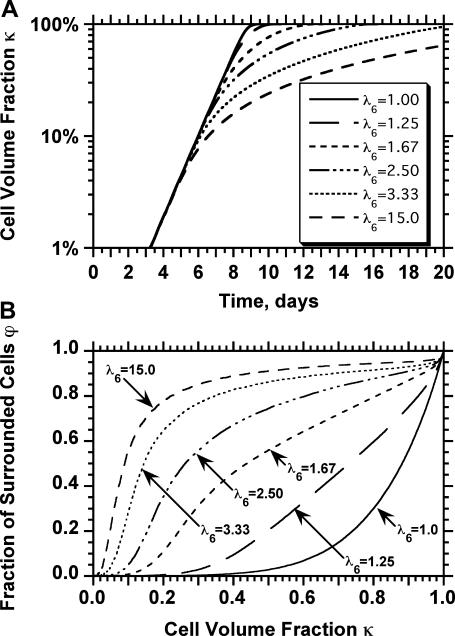
For the simulation runs discussed until now, we assumed that 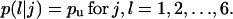However, the transition probabilities can be unequal to simulate the biased cell movement observed under conditions that lead to chemotaxis (65–68). Such a biased cell movement dramatically changes not only the tissue growth rates, but also the pattern of tissue growth. Fig. 6 shows the anisotropic growth of the tissue when cells move with a higher probability toward the top surface of the scaffold (migration state j = 6) due to the presence, for example, of a chemotactic gradient. 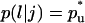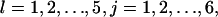For this run for and 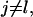while 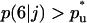for 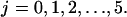A dense layer of cells forms quickly in the upper part of the scaffold, leading to severe contact inhibition effects. Tissue growth is now limited to the cells that form the “diffuse front” in the bottom part of the developing tissue shown in Fig. 6, C and D. The dramatic effects of contact inhibition are quantified in Fig. 7, A and B. Fig. 7 A shows increasing and significant slowdowns of tissue growth with increasing magnitude of the cell movement bias that can be expressed as the ratio 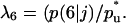Deviations from the case of uniform transition probabilities appear at cell fractions that may be lower than 0.05 (see Fig. 7 A). Fig. 7 B quantifies the changes in the growth pattern by showing the evolution of the fraction 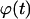of completely surrounded cells versus the cell fraction 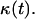We see here a qualitative shift from the convex 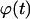curve observed for uniform transition probabilities to a concave curve for large values of 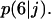In the latter case, the sharp increase of 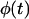observed in the early stages of tissue growth signifies the formation of the dense cell layer formed at the top part of the scaffold and shown in Fig. 6, B and C.

FIGURE 6.

Anisotropic patterns of tissue growth are observed when cells move preferentially toward the upper boundary of the computational domain. This run began with the same initial condition (uniform seeding) as the one used for the run of Fig. 2. Here, however, the ratio of transition probabilities 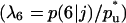is equal to 5. All other parameters are the same as in Fig. 2. (A) 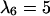: t = 0.0 days, κ(t) = 0.001. (B) 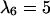: t = 3.25 days, κ(t) = 0.01. (C) 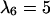: t = 6.57 days, κ(t) = 0.1. (D) 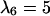: t = 16.41 days, κ(t) = 0.5.

FIGURE 7.

Biased cell migration affects both the rate (A) and the pattern of tissue growth (B). These simulation runs started with uniform cell seeding and had the indicated values of the ratio of transition probabilities 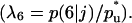All other parameters were the same as in Fig. 2. Cell volume fractions are shown in panel A using a semilog scale.

Wound seeding mode

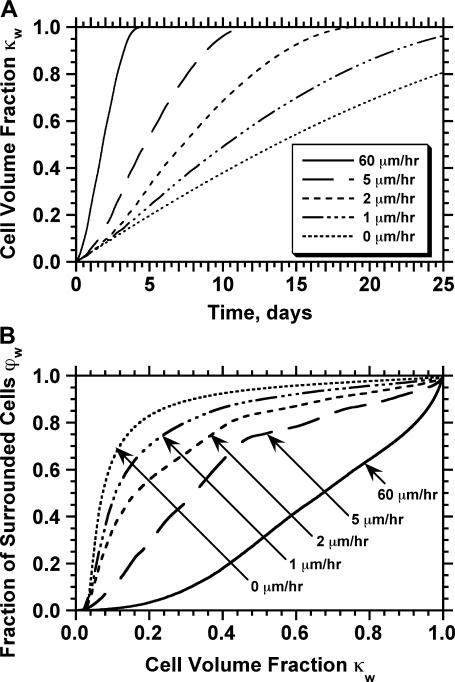
Fig. 8 shows the tissue growth pattern for two runs that started with the “wound” seeding mode, but had widely different cell migration speeds (1 and 60 μm/h, respectively). As soon as the simulation starts, cells begin to infiltrate the cylindrical wound area that has been filled with the scaffold (Fig. 8 A). When the migration speed is low (S = 1 μm/h), cells infiltrate the wound as a front that has a thin rim of proliferating cells in front of it (Fig. 8, B and C). This front moves slowly toward the center to “heal” the wound. Clearly, only the cells located in a shallow proliferating rim will divide in this case. When the migration speed is raised to 60 μm/h, however, we do not observe the formation of a front. Instead, the wound is infiltrated by cells that are rapidly scattered throughout the domain (see Fig. 8, D and E). This migration-driven dispersion delays the onset of contact inhibition effects until the cell density reaches high levels.

Fig. 9 A quantifies the effect of cell migration speed on tissue growth. Although nonmotile cells need almost 42 days to “heal” a wound of this size, cells moving at the relatively slow speeds of 1 and 2 μm/h heal the wound in only 29 and 19 days, respectively. In contrast to what was observed with the uniform seeding mode, however, the beneficial effect of cell migration does not disappear at higher speeds. Cells migrating at 20, 30, and 60 μm/h need only 6.5, 5.6, and 4.4 days, respectively, to completely fill the cylindrical wound with new tissue. Contact inhibition effects again provide the explanation for the observed behavior. Nonmotile or slow-moving cells (S = 1–2 μm/h) infiltrate the wound in the form of a sharp front. After only a short period of time, the majority of cells located in the wound will be completely surrounded and unable to divide. This is clearly shown by the concave 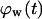vs. 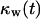curves of Fig. 9 B for nonmotile and slow-moving cells. The fraction 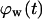of surrounded cells in the wound is 0.65 for nonmotile cells and 0.50 when S = 1 μm/h, even at the low cell fraction value of 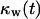= 0.1. The onset of contact inhibition effects is delayed as S increases. Speeds >10 μm/h, however, lead to a very good dispersion of the migrating cells into the wound, minimizing the contact inhibition effects and changing the 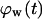vs. 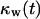curves from concave to convex (Fig. 9 B). The fast and almost uniform dispersion of cells observed for high cell speeds is consistent with the persistent random walk model (46,47). According to this model, the diffusion coefficient (or random motility coefficient) of cells moving into an open space is proportional to the square of the migration speed S. The curve for S = 60 μm/h on Fig. 9 B shows the three distinct phases of the tissue growth process. The fraction 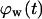stays at virtually zero until the fast-moving cells reach the center of the wound and then grows slowly as cell density increases throughout the wound. The final phase is characterized by an accelerating growth of 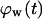as cell density increases beyond a critical threshold.

FIGURE 9.

Effect of cell migration speed S (shown in inset) on (A) the temporal evolution of cell volume fraction and (B) the 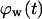vs. 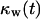tissue growth pattern. These runs started with the wound mode of cell seeding, and all other run parameters are the same as in Fig. 8.

These results indicate that we can always accelerate the process of tissue growth if we increase the cell migration speed on materials used to fill the wound. This is consistent with experimental studies on natural wound healing that have revealed dramatic enhancements of the migration speed of cells surrounding the wound. Using time-lapse video microscopy, Chan and co-workers (69) monitored the migration and proliferation of rabbit corneal epithelial cells during in vitro wound healing. The average migration speed of cells at wound edge was 104 μm/h, significantly higher than its normal value of 30–40 μm/h (70). A similar phenomenon has been observed by Zahm and co-workers (71) on the healing process of a wound created in a collagen I matrix cultured with human respiratory epithelial cells. The simulations also provide us with invaluable guidance for the design of experiments (72) that can test the efficacy of surface modifications designed to enhance cell migration speeds.

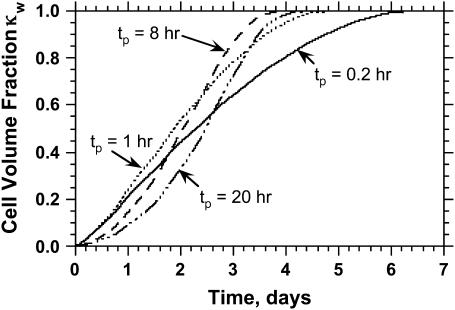
The persistence of cell movement plays an important role on tissue regeneration for wound healing. This is in contrast to what we observed with simulations that started with a uniform dispersion of cells in the scaffold (uniform seeding mode). Fig. 10 shows the temporal evolution of cell fraction 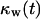for cells migrating with S = 60 μm/h and persistence times 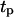ranging from 0.2 to 20 h. The simulation results indicate that there is an optimal value of 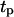at which the tissue regeneration is fastest. For the runs of Fig. 10, the time required to fill the wound (or “healing time”) decreases from ∼6.5 days for 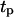= 0.2 h to 4.1 days when 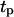= 8 h, and then increases again slowly to 4.5 days when 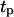reaches 20 h. A careful analysis of tissue growth patterns provided an explanation for these results. Short persistence time forces the cells to turn frequently, offsetting the beneficial effects of high migration speeds and reducing the ability of the cells to disperse in the wound. Even when they move with swimming speeds as high as 60 μm/h, cells cannot move far away from their neighbors and form a front with a proliferating rim that advances toward the center of the wound. The growth pattern looks similar to that shown on Fig. 8, B and C. When the persistence time increases, the cells can penetrate deeper into the wound before they have to turn. This leads to fewer collisions, better cell dispersion into the wound, and faster tissue regeneration rates. The tissue growth patterns observed in such cases are very similar to that shown in Fig. 8, D and E. However, when the persistence time is very long and the distance 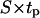is comparable to the size of the wound, cells may immediately start to collide with cells moving from the opposite direction. This will enhance the adverse effects of contact inhibition and will slow down the rate of tissue growth.

FIGURE 10.

Effect of persistence time (shown in text) on the temporal evolution of cell volume fraction. These runs started with the wound mode of cell seeding, and all other run parameters are the same as in Fig. 8.

This analysis shows that the effect of persistence time on tissue regeneration rates is not as pronounced as that of migration speeds. Nevertheless, this effect is significant and a direct consequence of the initial condition or seeding mode. In addition, the trends revealed by the simulations are consistent with experimental data. Lepekhin and co-workers (73) found that the different rates and patterns of wound healing in two-dimensional cultures of buccal, periodontal, and skin fibroblasts were due to variations of migration speed and persistence time among the different types of cells. Weimann and co-workers (74) studied the effect of Ca D-pantothenate on the healing of wounds created in cultures of human dermal fibroblasts and reported that Ca D-pantothenate accelerated the healing process by 1.2 ∼ 1.6-fold by increasing cell migration speed and persistence time. We should note, however, that most experimental studies use assays that do not allow us to clearly distinguish between the effects of persistence and speed of cell movement.

Finally, we carried out several simulations to determine how tissue regeneration rates are affected by the tendency of cells to form aggregates when they collide. The key parameter here is the waiting time E(T₇) that provides a measure of tendency of cells to form multicellular aggregates when they collide. Our simulations showed that long waiting times E(T₇) can significantly slow down tissue regeneration rates for runs that started with a wound seeding mode. For runs with a cell migration speed of 60 μm/h, the healing times increased from 4.5 days for E(T₇) = 1 h to 6.8 days for E(T₇) = 10 h, but appeared to reach a plateau for waiting times longer that 60 h. Simulations with uniform seeding mode revealed a similar effect of E(T₇) on tissue growth rates. These results are not presented in any of the figures.

CONCLUSIONS

To demonstrate the potential of computational models for tissue engineering, we have developed a discrete model that describes the dynamic process of tissue growth in 3D scaffolds. The model considers a population of cells that execute persistent random walks on the computational grid, collide with each other, and proliferate until they reach confluence. A major advantage of our discrete modeling approach is its ability to describe the competing processes of contact inhibition and migration without resorting to empirical assumptions like earlier models. In addition, all the key system parameters can be easily adjusted to reflect the influence of external stimuli.

For uniform cell seeding, our simulations showed that increasing migration speeds initially enhanced tissue growth rates. As cell speeds increased >5 μm/h, however, this beneficial effect diminished and disappeared completely for large migration speeds. Simulations with the “wound” seeding mode, however, predicted that we could always accelerate the process of tissue regeneration if we increased the cell migration speed on the biomaterial used to fill the wound. These results point out that the locomotory parameters of a cell population and the initial condition can have profound effects on the dynamics of the process and, consequently, on the pattern and rates of tissue growth. The speed and persistence of cell locomotion modulate the rates of tissue regeneration by controlling the effects of contact inhibition. However, the magnitude of this modulation strongly depends on the spatial distribution of seed cells. This conclusion has significant implications for the design of experiments that can test the efficacy of surface modifications designed to enhance cell migration speeds. To study how surface modifications and the resulting changes of migration speeds affect tissue growth rates, assays based on the “wound” seeding mode (72) must be adopted. Experiments that begin by uniformly distributing seed cells in modified scaffolds may not be sensitive enough to elucidate these effects.