Compartment Volume Influences Microtubule Dynamic Instability: A Model Study

Abstract

Microtubules (MTs) are cytoskeletal polymers that exhibit dynamic instability, the random alternation between growth and shrinkage. MT dynamic instability plays an essential role in cell development, division, and motility. To investigate dynamic instability, simulation models have been widely used. However, conditions under which the concentration of free tubulin fluctuates as a result of growing or shrinking MTs have not been studied before. Such conditions can arise, for example, in small compartments, such as neuronal growth cones. Here we investigate by means of computational modeling how concentration fluctuations caused by growing and shrinking MTs affect dynamic instability. We show that these fluctuations shorten MT growth and shrinkage times and change their distributions from exponential to non-exponential, gamma-like. Gamma-like distributions of MT growth and shrinkage times, which allow optimal stochastic searching by MTs, have been observed in various cell types and are believed to require structural changes in the MT during growth or shrinkage. Our results, however, show that these distributions can already arise as a result of fluctuations in the concentration of free tubulin due to growing and shrinking MTs. Such fluctuations are possible not only in small compartments but also when tubulin diffusion is slow or when many MTs (de)polymerize synchronously. Volume and all other factors that influence these fluctuations can affect MT dynamic instability and, consequently, the processes that depend on it, such as neuronal growth cone behavior and cell motility in general.

INTRODUCTION

Microtubules (MTs) are long, polar polymers of tubulin dimers that are found in almost all eukaryotic cells. They are part of the structural scaffold of the cell and serve as tracks along which organelles, vesicles, and large molecules are transported (1,2). MTs exhibit dynamic instability, the random alternation between phases of MT growth (net polymerization of tubulin at the ends of a MT) and shrinkage (depolymerization) (see Fig. 1) (3).

FIGURE 1.

A schematic view of the dynamic instability of a MT. The MT randomly switches between phases of growth and shrinkage. In addition to growth and shrinkage rates and catastrophe and rescue frequencies, the distributions of growth and shrinkage times are important characteristics of MT dynamic instability.

Dynamic instability of MTs is essential in a number of fundamental cellular processes, including development, division, and motility (1,4). In developing cells, dynamic instability allows MTs to explore the intracellular space for specific targets or favorable regions of cytoplasm (5). When the right targets are found, MTs stabilize at them, leading to a long-term rearrangement of the spatial organization of MTs and thus to morphological changes of the cell. In motile cells, dynamic MTs are involved in the regulation of cellular movements by affecting both the actin cytoskeleton and myosin, which play a central role in generating the force for movements (6). Interestingly, growth and shrinkage phases of MTs have differential effects on cell motility by activating different Rho GTPases, which each have distinct effects on the dynamic behavior of the actin cytoskeleton (6–8).

Dynamic MTs are also part of the cytoskeleton of the growth cone, a motile structure at the tip of a growing neurite that senses the extracellular environment, steers the neurite, and mediates neurite elongation and branching. Dynamic MTs explore the peripheral domain of the growth cone (which contains actin) and often enter into the filopodia (usually one MT per filopodium), the finger-like protrusions of the growth cone (8), which constantly extend and retract to sense the environment and steer the growth cone (9). If the dynamics of the MTs within the growth cone is blocked with specific drugs, neurites lose their ability to turn (10,11) and to branch (12).

In addition to the average times that MTs spend in growth and shrinkage phases, an important aspect of MT dynamic instability is the distribution of growth and shrinkage times. In vitro and in vivo (including neuronal growth cones), growth and shrinkage times have been found to be non-exponentially, gamma-like distributed (13–15). Since in contrast to an exponential distribution, a gamma distribution has relatively fewer very short and very long growth or shrinkage times, it allows MTs to optimally search the intracellular space for targets at a certain distance away, without wasting energy on very small and very large length excursions (13,16).

Simulation models have been widely used to investigate MT dynamic instability (e.g., 17,18). Modeling studies have shown that for a gamma or gamma-like distribution of MT growth and shrinkage times to arise, the probabilities of catastrophe (transition from growth to shrinkage) and rescue (transition from shrinkage to growth) have to increase during an individual growth or shrinkage phase, respectively (13). This implies that the value of the catastrophe or rescue probability of a MT contains information of—and thus can viewed as a form of memory for—the time that the MT has been growing or shrinking in that particular growth or shrinkage phase (13). Several proposals have been put forward to explain how this MT memory can arise. One possibility is that several consecutive transitions at the MT tip are required for a catastrophe or rescue to occur (13,16,19). Another possibility is that the catastrophe and rescue probabilities depend on MT length ((20); thoroughly discussed in (21))—for example, because of the accumulating strain in the MT lattice (20)—so that longer MTs have a higher catastrophe probability and a lower rescue probability than shorter MTs. Currently, neither of these possibilities have strong experimental support.

So far, all models that study the properties of dynamic instability assume a constant concentration of free tubulin in the medium. However, for small compartments with a relatively small amount of free tubulin, this may not be a valid assumption. Growth and shrinkage of MTs decreases and increases, respectively, the amount of free tubulin, so that in a small compartment dynamic MTs can cause fluctuations in the concentration of free tubulin. The volumes of neuronal growth cones, for example, are so small (1–200 μm³) (9) that such fluctuations may indeed occur. Because most properties of dynamic instability depend on tubulin concentration (22), these fluctuations in tubulin concentration could greatly affect MT dynamics.

Here we investigate by means of a simulation model how compartment volume, via its influence on the fluctuations in the concentration of free tubulin, affects MT dynamics. We find that compartment volume affects both the lengths and distributions of MT growth and shrinkage times. Our results show that fluctuations in the concentration of free tubulin caused by dynamic MTs in small compartments are already capable of providing the MT memory that is required for non-exponential, gamma-like distributions of growth and shrinkage times to arise. This suggests that the volume of cells or cellular compartments could be an important factor in determining the properties of MT dynamic instability and, consequently, the processes that depend on it, such as cell motility.

MODEL AND METHODS

We study the influence of compartment volume on MT length changes, fluctuations in the concentration of free tubulin, and the averages and distributions of growth and shrinkage times. The variables of our model are the lengths of the MTs, the states of the MTs (growth or shrinkage), and the concentration of free tubulin in the compartment. First, we consider the dynamics of a single MT in compartments ranging from 1 to 100 μm³. Then, we investigate how changing the number of MTs, to up to 10 MTs in a compartment, affects MT dynamics.

We model only the dynamics of the plus end of a MT, because in vivo the minus ends of MTs are often attached to centrosomes or otherwise stabilized (23–25). Further, we do not distinguish between GTP-tubulin and GDP-tubulin. In vivo and in vitro, GTP-tubulin associates with the MT in the growth phase and later hydrolyzes into GDP-tubulin; in the shrinkage phase, GDP-tubulin dissociates from the MT and then regenerates into GTP-tubulin (1). In the model, we consider the regeneration of free GTP-tubulin from free GDP-tubulin to be a fast process on the timescale of MT dynamic instability (26), so that all free tubulin can be taken to be GTP-tubulin. There is no influx or efflux of tubulin, so the total amount of tubulin, i.e., free tubulin plus tubulin bound in MTs, is constant. We take the concentration of free tubulin to be homogeneous within the compartment; i.e., diffusion of tubulin is assumed to be fast enough (27,28) that no local concentration differences can arise (see also Discussion). We use the same initial concentration of free tubulin in compartments of all volumes; consequently, a smaller compartment contains a smaller amount of free tubulin and is therefore expected to have larger concentration fluctuations caused by dynamic MTs. Apart from responding to the same concentration of free tubulin, the MTs do not otherwise interact with each other.

To model MT dynamics, we use a Monte Carlo event-based approach (17,18,29,30). In this approach, one event takes place per iteration of the simulation. An event is, for example, the association of a tubulin dimer to a particular MT. For an event that should occur with frequency f (s⁻¹), the waiting time to the next occurrence of the event is sampled from an exponential distribution with mean 1/f. If more than one event is possible (e.g., association or dissociation of a tubulin dimer at a particular MT, or association of a tubulin dimer to either of several MTs), then the waiting time of each event has to be sampled and the event with the shortest waiting time be implemented (17,29,30).

The frequencies of tubulin association and dissociation events are derived from a differential-equation description of the length changes of a MT (22):

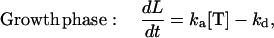(1)

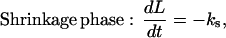(2)

where L is the length of a MT (in number of dimers), [T] is the concentration of free tubulin, k_a is the association rate constant of tubulin in the growth phase, k_d is the rate of dissociation in the growth phase, and k_s is the rate of dissociation in the shrinkage phase (see Table 1 for parameter values). Eq. 1 shows that the growth phase of a MT consists of two separate processes: the association of tubulin, which is dependent on the concentration of free tubulin (represented by k_a[T] in Eq. 1), and the dissociation of tubulin, which is independent of the concentration of free tubulin (k_d in Eq. 1), because dissociation rate is determined only by the structure of the tip of the MT. Similarly, the dissociation of tubulin in the shrinkage phase is also independent of the concentration of free tubulin (k_s in Eq. 2), but it occurs at a much faster rate than in the growth phase. So, based on Eqs. 1 and 2, the frequency of tubulin association to a MT (in number of dimers per second, s⁻¹) in a Monte Carlo event-based approach is f_a = k_a[T]; the frequency of tubulin dissociation from a MT in the growth phase is f_d = k_d; and the frequency of tubulin dissociation from a MT in the shrinkage phase is f_s = k_s.

TABLE 1.

Parameter values as used in the simulations (see Eqs. 1–4)

Constant	Aspect of MT dynamic instability	Value
ka	Association of tubulin in the growth phase	8.9 μM−1 s−1
kd	Dissociation of tubulin in the growth phase	44 s−1
ks	Dissociation of tubulin in the shrinkage phase	733 s−1
ac	Catastrophe	−0.00058 μM−1 s−1
bc	Catastrophe	0.0092 s−1
ar	Rescue	0.005 μM−1 s−1
br	Rescue	−0.03 s−1

All the values of the constants were taken from (22) (a_c, b_c, a_r, b_r were measured from that article's Figs. 7 and 8).

Random switches of MTs from growth to shrinkage phase (catastrophes) and from shrinkage to growth phase (rescues) are characterized by catastrophe and rescue frequencies (1). The catastrophe frequency f_c (the average number of catastrophes per unit of time of MT growth, or the reciprocal of the average growth time) and rescue frequency f_r (the average number of rescues per unit of time of MT shrinkage, or the reciprocal of the average shrinkage time) depend on the concentration of free tubulin (22):

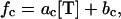(3)

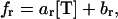(4)

where a_c, b_c, a_r, and b_r are constants (with a_c < 0 and a_r > 0; see Table 1 for parameter values). Thus, the catastrophe frequency decreases with increasing concentration of free tubulin, whereas the rescue frequency increases with increasing concentration of free tubulin. Equations 3 and 4 were determined empirically (22), but the biophysical mechanisms underlying these relationships are not fully known. However, such relationships can in part be expected from what we know about the mechanisms of MT dynamic instability. A dynamic MT is mostly composed of GDP tubulin and is capped at its tip by GTP tubulin, which associates to the MT in the growth phase. It is believed that when this cap is lost due to hydrolysis of GTP tubulin, a catastrophe occurs, whereas regaining the cap due to association of GTP tubulin at the MT tip results in a rescue (1). We can therefore expect that a higher concentration of GTP-tubulin, and consequently a faster association of GTP tubulin to the MT tip (Eq. 1), would make the loss of the GTP cap less likely and thus the catastrophe frequency lower (Eq. 3). Likewise, a higher concentration of GTP tubulin, and consequently a higher likelihood that GTP tubulin will associate to the MT tip, would make the restart of MT growth more likely and thus the rescue probability higher (Eq. 4).

At the start of a simulation, the MTs are set in the growth phase. The length of a MT is expressed relative to its initial length, which is arbitrarily set to zero. The steady-state concentration of free tubulin—i.e., the concentration at which MT growth in the growth phase is on average balanced by MT shrinkage in the shrinkage phase, so that on average there is no net length change of the MT—is used as the initial concentration for all compartment volumes. The steady-state concentration [T]_ss can be determined as follows. At steady state, there is on average no length change of a MT per oscillation cycle, so (22)

(5)

where v_g = k_a[T]_ss − k_d is the growth rate at the steady-state concentration of free tubulin (Eq. 1), v_s = −k_s is the shrinkage rate (Eq. 2), t_g = (a_c[T]_ss + b_c)⁻¹ is the growth time (the reciprocal of f_c; see Eq. 3), and t_s = (a_r[T]_ss + b_r)⁻¹ is the shrinkage time (the reciprocal of f_r; see Eq. 4). Solving this equation yields an expression for [T]_ss. Using the parameter values from Table 1, we obtain [T]_ss = 11.76 μM.

Each iteration of the simulation procedure then consists of the following steps:

1. Making a list of all possible events. For a system of two MTs (MT1 and MT2), for example, where MT1 is in the growth phase and MT2 is in the shrinkage phase, the list of all possible events is: (i) association of a tubulin dimer to MT1, and consequently an increase in MT1 length by one tubulin dimer and a decrease in the concentration of free tubulin in the compartment; (ii) dissociation of a tubulin dimer from MT1, and consequently a decrease in MT1 length and an increase in the concentration of free tubulin; (iii) catastrophe of MT1, i.e., a change in the state of MT1 to the shrinkage phase; (iv) dissociation of a tubulin dimer from MT2, and consequently a decrease in MT2 length and an increase in the concentration of free tubulin; and (v) rescue of MT2, i.e., a change in the state of MT2 to the growth phase.

2. Calculating the frequency f (s⁻¹) of each event.

3. Sampling the waiting time for each event from an exponential distribution with a mean μ = 1/f. The probability density function of an exponential distribution of waiting times t with mean μ is p(t) = μ⁻¹ exp(−μ⁻¹t). The mean waiting time μ for a catastrophe event, for example, is 1/f_c.

4. Implementing the event with the smallest waiting time. For the example given under step 1 with two MTs in the compartment, only one of the five possible events is implemented per iteration.

A simulation ends after 10⁸ events have been implemented.

The distributions of MT growth and shrinkage times as observed in the model or in neuronal growth cones were compared to an exponential distribution using the χ² test (e.g., (31)), whereby the mean of an observed distribution was used as the mean of the fitted exponential distribution. To compare the shapes of the distributions of MT growth times in our model with those in neural growth cones, a χ² two-sample test was used (32).

To quantify the extent of concentration fluctuations in free tubulin, the weighted standard deviation of the tubulin concentration, S, was calculated using

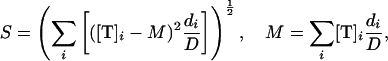(6)

where M is the weighted mean of the concentration of free tubulin, [T]_i is the concentration of free tubulin at iteration i, d_i is the duration (in seconds) of the iteration, and D is the duration of the whole simulation. Note that further on in the text, the phrases “concentration of free tubulin” and “concentration of tubulin” are used interchangeably.

The following procedure was used to fit analytical functions to the observed dependencies of average MT growth time, average MT shrinkage time, and tubulin concentration fluctuations on compartment volume and number of MTs in the compartment (Fig. 6). As an example, we explain how we fitted an exponential function to the average MT growth times in Fig. 6. First, the exponential function G(V) = a + be^cV (where G is average MT growth time, V is volume, and a, b, and c are coefficients) was applied to fit the dependence of average growth time on compartment volume for each number of MTs separately (1, 2, 5, or 10 MTs; see Fig. 6), using an optimization procedure based on the Levenberg-Marquardt algorithm (32). This produced four sets of coefficients: one set for a compartment with 1 MT (a₁, b₁, c₁), one for a compartment with 2 MTs (a₂, b₂, c₂), one for a compartment with 5 MTs (a₃, b₃, c₃), and one for a compartment with 10 MTs (a₄, b₄, c₄). Second, for each coefficient (e.g., a), the four values (a₁, a₂, a_3, a₄) were fitted with a linear function to obtain a relationship between each coefficient and MT number (i.e., a(N) = e + fN, where N is number of MTs and e and f are coefficients). Finally, a relationship between average growth time and both compartment volume and number of MTs was obtained by inserting these linear functions (e.g., a(N)) into function G(V). Using the same procedure, we also fitted a power function (i.e., G(V) = a + b(V – c)^d) to the data on average growth time, and exponential and power functions to the data on average shrinkage time and tubulin concentration fluctuations.

FIGURE 6.

For compartments of different volumes and for different numbers of MTs, the fluctuations in the concentration of free tubulin (weighted standard deviation S; see Model and Methods) and the average growth and shrinking times of the MTs. For the models with more than one MT, the growth and shrinkage times of all MTs are pooled. As the compartment volume gets smaller or the number of MTs in it decreases, the fluctuations in the concentration of free tubulin increase and the average growth and shrinkage times become shorter.

RESULTS

We find that MT dynamics in small compartments is markedly different from MT dynamics in large compartments, with respect to MT length changes and the averages and distributions of growth and shrinkage times.

Dynamics of MT length and concentration of free tubulin

Fig. 2 shows the dynamics of MT length and concentration of free tubulin for a single MT in compartments of different volumes. We observe that decreasing the volume of the compartment from 100 μm³ to 1 μm³ increases the fluctuations in tubulin concentration in the compartment, makes the growth of the MT more nonlinear, and decreases the length excursions and the average growth and shrinkage times of the MT (see also Fig. 6).

FIGURE 2.

For compartments of different volumes, the dynamics of MT length and concentration of free tubulin in the model with a single MT. To express the length of a MT in micrometers, we assume that there are 1625 tubulin dimers per 1 μm of a MT.

In the compartment of 100 μm³, the concentration of free tubulin over time is almost constant (Fig. 2, 100 μm³). This is a consequence of the fact that the amount of free tubulin is large in a large compartment, so that a growing and shrinking MT can hardly change the concentration of tubulin. For the compartment of 100 μm³, we also observe a nearly constant growth rate of the MT over time (Fig. 2, 100 μm³). This is simply explained by the growth rate of a MT being dependent only on the concentration of free tubulin (Eq. 1), which is nearly constant.

As the volume of the compartment gets smaller, the fluctuations in the concentration of free tubulin increase (Fig. 2: 10 μm³, 5 μm³, and 1 μm³; see also Fig. 6). Because the initial concentration of free tubulin is the same for all compartment volumes (see Model and Methods), as the compartment gets smaller, the amount of free tubulin in the compartment decreases, and assembly and disassembly of tubulin during MT growth and shrinkage have a bigger effect on the concentration of free tubulin. Furthermore, in small compartments, the growth rate of the MT decreases over time in a single growth excursion, i.e., MT growth is nonlinear (Fig. 2: 10 μm³, 5 μm³, and 1 μm³). The decrease of the growth rate is caused by the decrease in the concentration of free tubulin during MT growth (Eq. 1). The shrinkage rate, however, is constant over time for all compartment volumes (i.e., MT shrinkage is linear), because it does not depend on the concentration of free tubulin (Eq. 2).

As the volume of the compartment gets smaller, the average growth and shrinkage times and the length excursions of the MT decrease (Fig. 2; see also Fig. 6). In addition, in a small compartment, MT length oscillates around its initial value with relatively small deviations (Fig. 2, 1 μm³). The changing concentration of free tubulin during MT growth and shrinkage is again responsible for these effects. As the MT grows and takes away free tubulin, the catastrophe probability rises (Eq. 3). Thus the longer the MT becomes relative to its initial length, the more likely it is that a catastrophe occurs and the MT starts shrinking. This decreases the average growth time and the length excursion of the MT. As the MT shrinks, the increasing rescue probability, as a result of the increasing concentration of tubulin (see Eq. 4), in a similar fashion decreases the average shrinkage times and the length excursions due to shrinkage. Thus, a small compartment stabilizes a MT against large deviations from its initial length.

Non-exponential distributions of growth and shrinkage times

Fig. 3 shows the distributions of growth and shrinkage times for a single MT in compartments of different volumes. For the compartment of 100 μm³ (and larger, results not shown), the distributions are exponential. As the volume of the compartment decreases, the distributions of growth and shrinkage times become non-exponential and gradually change into a gamma-like distribution (Fig. 3: 10 μm³, 5 μm³, and 1 μm³). In contrast to an exponential distribution, a gamma distribution has relatively fewer very short and very long growth and shrinkage times.

FIGURE 3.

For compartments of different volumes, the distributions of growth and shrinkage times in the model with a single MT. P-values show the goodness of fit between the observed distributions and an exponential distribution (see Model and Methods). For large volumes (100 μm³) the exponential distribution fits well, but for small volumes the hypothesis that the growth and shrinkage times are exponentially distributed is rejected (P ≪ 0.001).

Why are the distributions in small compartments different from those in large compartments? As explained earlier, in a large compartment the concentration of free tubulin is nearly constant (Fig. 2, 100 μm³), which means that the probabilities of catastrophe and rescue are constant over time as well (Eqs. 3 and 4; Fig. 4, 100 μm³). Constant probabilities of catastrophe and rescue can be regarded as describing stationary Poisson processes, which yield an exponential distribution of growth and shrinkage times (33).

FIGURE 4.

The dynamics of catastrophe frequency (left) and rescue frequency (right) in the average growth and the average shrinkage phase, respectively, of a single MT in compartments of different volumes. The dynamics of the catastrophe frequency was determined by calculating at each time point the average concentration of tubulin over all different growth phases in the simulation (aligned at time zero), and inserting this concentration in Eq. 3 to obtain the catastrophe frequency. The dynamics of the shrinkage frequency was calculated similarly, by considering all shrinkage phases and inserting the average tubulin concentrations into Eq. 4 to obtain the rescue frequencies. In small compartments (1 μm³, 5 μm³, and 10 μm³), the catastrophe and rescue frequencies at the initial stages of the average growth or shrinkage phase are low; they then increase and become larger than the respective frequencies of catastrophe and rescue at the initial, steady-state concentration of tubulin (dashed line). In a large compartment (100 μm³), the frequencies hardly deviate from the frequencies at the initial, steady-state concentration of tubulin. For 1 μm³, the catastrophe frequency is initially zero because, according to Eq. 3, for high tubulin concentration the catastrophe frequency becomes negative and is therefore set to zero. (Note that the time axes are different for different compartment volumes because the average growth and shrinkage times are different.)

In a small compartment, the tubulin concentration changes as the MT grows and shrinks, which implies that the probabilities of catastrophe and rescue also change. To understand what this means for growth and shrinkage times, let us consider a single growth phase. Because the growth of the MT usually starts at a length smaller than the initial length (see Fig. 2, 1 μm³), the tubulin concentration at the initial stage of MT growth is relatively high, so that the catastrophe probability is low (Eq. 3; Fig. 4, 1 μm³, 5 μm³, and 10 μm³). A low probability of catastrophe at the beginning of MT growth means that the growth phase has little chance of becoming very short. As the MT grows, the tubulin concentration decreases and the probability of catastrophe becomes high. As a result, the growth phase has little chance of becoming very long, because a catastrophe will very likely have occurred at some earlier point in time. So, compared to a MT in a large compartment, both very short and very long growth times are less likely to occur. Similarly, the modulation of the rescue probability by the changing concentration of tubulin results in a low number of very short and very long shrinkage times (Eq. 4; Fig. 4, 1 μm³, 5 μm³, and 10 μm³).

Thus, in small compartments, the modulation of the catastrophe and rescue probabilities by the changing concentration of free tubulin results in a distribution that has relatively fewer very short and very long growth and shrinkage times, i.e., a gamma-like distribution. Interestingly, at the level of individual growth and shrinkage phases, the system can be regarded as having a form of memory of the time that the MT has been growing or shrinking, because this time is reflected in the catastrophe and rescue probabilities of a MT (see Eqs. 3 and 4). Note that this memory occurs within an individual growth or shrinkage phase and does not extend over multiple growth or shrinkage phases.

Increasing the number of MTs in a compartment

Fig. 5 shows how the distribution of growth times gradually changes from non-exponential to exponential as the number of MTs increases in a compartment of 1 μm³. The distribution of shrinkage times, however, remains non-exponential even for 10 MTs in the compartment. In addition, the average growth and shrinkage times increase with the number of MTs in the compartment. Thus, increasing the number of MTs has similar effects on the distributions and lengths of MT growth and shrinkage times as increasing the volume of the compartment.

FIGURE 5.

For different number of MTs in the compartment, the distributions of MT growth and shrinkage times in the compartment of 1 μm³. For the models with more than one MT, the growth and shrinkage times of all MTs are pooled. P-values show the goodness of fit between the observed distributions and an exponential distribution. For the growth times in the models with 5 and 10 MTs the exponential distribution fits well, but for all other cases the hypothesis that the growth and shrinkage times are exponentially distributed is rejected (P ≪ 0.001).

Like increasing the volume of the compartment, increasing the number of MTs in the compartment reduces the fluctuations in the concentration of free tubulin (Fig. 6). In both cases, the ability of a single dynamic MT to change the concentration of free tubulin is reduced. In the first case, the concentration fluctuations become smaller because the total amount of tubulin in the compartment is increased. In the second case, with more MTs in the compartment, the fluctuations become smaller because the decrease of tubulin due to growing MTs can be compensated for by the increase of tubulin due to shrinking MTs (and vice versa), so that the net changes in the concentration of free tubulin are smaller and not well correlated with the dynamics of any single MT. However, even for 10 MTs in a compartment as large as 10 μm³ (see Figs. 6 and 8), the growth and shrinkage times of the MTs are still, respectively, 6% and 11% shorter than in a compartment of 100 μm³.

FIGURE 8.

For compartments of different volumes, the distributions of growth and shrinkage times in the model with 10 MTs (the growth and shrinkage times of all MTs are pooled). P-values show the goodness of fit between the observed distributions and an exponential distribution. The hypothesis that the observed distribution is an exponential distribution is rejected only for MT shrinkage times in small volumes (P ≪ 0.001).

To find general expressions for the observed dependencies of average MT growth time, average MT shrinkage time, and tubulin concentration fluctuations on compartment volume and number of MT, we fitted several analytical functions to the data of Fig. 6. We find that the dependence of tubulin concentration fluctuations on compartment volume can best be described by a power function (Fig. 7). A power function for concentration fluctuations is to be expected, since concentration by definition is inversely proportional to volume. The dependence of average MT growth time on compartment volume, and the dependence of average shrinkage time on compartment volume, can best be described by exponential functions.

FIGURE 7.

For different number of MTs, the function fits for the dependencies of average MT growth time, average MT shrinkage time, and tubulin concentration fluctuations on compartment volume and number of MTs. The data points (squares) are the outcomes of the model simulations, and the continuous curves are the functions that best fitted these points (for the procedure we used, see Model and Methods). For the tubulin concentration fluctuations, a power function best describes the data, whereas for the growth and shrinkage times, exponential functions fit best. The relationship between the tubulin concentration fluctuations, S (see Model and Methods), and compartment volume V is S(V) = a + b(V – c)^d, where a, b, c, and d are coefficients that depend linearly on microtubule number N: a(N) = 0.204 – 0.0547N, b(N) = 9.77 – 0.272N, c(N) = −0.476 – 0.136N, and d(N) = −0.575 + 0.0184N. For the average growth time G, the relationship is G(V) = a + be^cV, where a(N) = 411 – 0.0816N, b(N) = −205 + 11.2N, and c(N) = −0.233 + 0.0052N. For the average shrinkage time H, the relationship is H(V) = a + be^cV, where a(N) = 33.5 + 0.0194N, b(N) = −22.7 + 1.25N, and c(N) = −0.237 + 0.00608N.

Fig. 8 shows the distributions of growth and shrinkage times for 10 MTs in compartments of different volumes. As the volume of the compartment decreases, the distribution of growth times changes little and remains exponential. The distribution of shrinkage times, however, gradually changes from exponential to gamma-like. Both Figs. 5 and 8 show that, if there is more than one MT in the compartment, the distribution of shrinkage times is more gamma-like than the distribution of growth times. This can be explained by the fact that, at the steady-state concentration of free tubulin, the growth rate is ∼12 times smaller than the shrinkage rate (see Eqs. 1 and 2 and Table 1), so that the ratio of growing to shrinking MTs is 12:1. Because more MTs are available to switch from growth to shrinkage than vice versa, the ability to compensate for a decrease in tubulin concentration (as a result of MT growth) by switching to shrinkage is better than the ability to compensate for an increase in tubulin concentration (as a result of MT shrinkage).

DISCUSSION

By means of computational modeling, we have shown that the volume of the compartment in which dynamic MTs are located and the number of MTs in the compartment can affect both the lengths and distributions of MT growth and shrinkage times. Smaller compartments, and compartments with fewer MTs, have larger concentration fluctuations in tubulin and, as a result, have shorter growth and shrinkage times that are non-exponentially distributed. We have shown that MT dynamics in compartments smaller than 100 μm³ markedly differ from MT dynamics in a large compartment with a nearly constant concentration of free tubulin. Although the difference is largest with a single MT in the compartment, even for 10 MTs in a compartment as large as 10 μm³ (see Fig. 8) the growth and shrinkage times of the MTs are still markedly shorter, while the distribution of shrinkage times is non-exponential.

Non-exponential, gamma-like distributions of MT growth and shrinkage times that we find in our model have also been observed in vivo (14,15). Theoretical analysis shows that for non-exponential, gamma-like distributions to arise, the probabilities of catastrophe and rescue of a MT have to increase during an individual growth and shrinkage phase, respectively (13). In other words, a MT needs to have some sort of memory of the time that it has been growing or shrinking in a particular growth or shrinkage phase (see Introduction). Several, though not experimentally tested, proposals have been put forward to explain the origin of MT memory, such as the existence of several transitional states at the MT tip (13,16) or the dependence of catastrophe and rescue probabilities on MT length (20,21). Our results show that non-exponential distributions of growth and shrinkage times can already arise as a result of fluctuations in the concentration of free tubulin caused by dynamic MTs in a small compartment. In our system, the required MT memory arises because catastrophe and rescue probabilities of a MT depend on the concentration of free tubulin, which is decreasing or increasing as the MT grows or shrinks, respectively. Therefore, within an individual growth or shrinkage phase, the concentration of free tubulin reflects the time that the MT has been growing or shrinking in that particular phase.

Our results show that the volume of cells or cellular compartments, and the number of MTs they contain, could be an important factor in determining the properties of MT dynamic instability. One such compartment where MT dynamics is expected to be influenced by compartment volume is the neuronal growth cone. From data in Tanaka and Sabry (9), we estimate that the volumes of neuronal growth cones are in the range of 1–200 μm³. Further, we estimate that the number of dynamic MTs in the growth cone, i.e., the ones that could contribute to changes in the concentration of free tubulin, is <10. This estimate is based on the observation that the total number of MTs in a growth cone is ∼10–40 (9) and that MTs in the central domain of the growth cone are nondynamic and only MTs in the peripheral domain of the growth cone show marked growth or shrinkage (34). Furthermore, the diffusion rate of tubulin in cytoplasm and the diameter of an axon are such that, on the timescale of MT dynamic instability, the exchange of tubulin between the growth cone and the rest of the cell is limited. Several diffusion constants (D) of tubulin in cytoplasm have been reported: 1.3–1.6 μm²/s (35), 5.9 μm²/s (27), and 8.591 μm²/s (36). Using an average value of D = 5.3 μm²/s, a terminal axon diameter of 0.5 μm (37) and Fick's law, we estimate that the amount of tubulin that is taken up by a MT during an average growth phase in a compartment of 100 μm³ is at least 15 times bigger than the amount of tubulin that during the same period can diffuse from the axon into the growth cone. In addition, the timescale of tubulin diffusion inside the cell can be estimated by the Einstein-Smoluchowski relation, 〈d²〉 = 2nDt, where 〈d²〉 is the mean-square displacement of a tubulin dimer, t is time, and n is the spatial dimension of the system. Using this relation with n = 1, we find that the time needed for a tubulin dimer to cover the length of an axon (millimeters to centimeters) by diffusion is on the order of days to months (see also (38)). In contrast, the time needed for a tubulin dimer to move a distance of 10 μm, i.e., the diameter of a large neural growth cone, is on the order of 3 s (obtained using n = 3). Thus, on the timescale of MT dynamic instability (minutes), the diffusion of tubulin is fast enough to equilibrate the concentration of tubulin within the growth cone, but too slow for a significant exchange of tubulin with the rest of the cell. Taken together, the volume of the growth cone, the number of dynamic MTs it contains and the diffusion of tubulin are such that growing and shrinking MTs can cause fluctuations in tubulin concentration that will result in non-exponentially distributed growth and shrinkage times. We analyzed MT growth times observed in neuronal growth cones (15) and found that they are indeed not exponentially distributed (χ² test, P = 0.0025). Moreover, the shape of the distribution of MT growth times in neuronal growth cones does not differ from the shapes of the non-exponential distributions that we observe in our model (χ² two-sample test, P-values range from 0.08 to 0.63).

The filopodia of a growth cone are much smaller (0.1–4 μm³) (9) than the growth cone itself and are usually invaded by a single dynamic MT (8,9). The shape of a filopodium is such that the exchange of tubulin with the rest of the growth cone may be limited, so a filopodium may be viewed as a small compartment with a single MT. Interestingly, the times of extension of filopodia show a gamma-like distribution too (39), just like MT growth and shrinkage times, raising the possibility that this distribution may be a direct result of MT dynamic instability with fluctuating concentrations of free tubulin. Our model also predicts that when a MT from the central domain of a growth cone enters the much smaller volume of a filopodium, a change in MT dynamics will occur.

In motile cells, MT growth promotes local activity of Rho GTPase Rac1, which drives actin polymerization and lamellipodial protrusion and is thought to mediate growth cone attraction (4,7,40,41). MT shrinkage activates Rho GTPase RhoA, which drives the formation of contractile actomyosin bundles and is thought to mediate growth cone repulsion (6,42). In studies on fibroblasts, it has also been found that the time spent by MTs in the growth phase is positively correlated with the rate of cell movement and the area of lamellipodia (43). Because our model predicts that the volume of neuronal growth cones influences MT growth and shrinkage times, we also expect, on the basis of the above, that growth cone volume could affect lamellipodial protrusions, contractility of actin, and the rate of growth cone movements.

It should be stressed that even small changes in MT dynamics may be relevant for cell motility. MTs not only regulate the activity of Rho GTPases, but they can also be regulated themselves by Rho GTPases (reviewed in (6)). For example, MT growth activates Rho GTPase Rac1, which in turn not only drives actin polymerization and lamellipodial protrusion, but also stimulates MT growth by inactivating the MT catastrophe-promoting protein Op18/stathmin (44,45). Similarly, RhoA activity induced by MT shrinkage contributes to MT destabilization via phosphorylation of the MT-associated protein tau (46). These positive feedback loops could amplify small changes in MT growth or shrinkage (as we predict would occur as a result of changes in volume) so that they become big enough to influence cell motility and growth cone behavior.

To assess the contribution of small volume on MT dynamic instability experimentally, one has to monitor, over time, the dynamics of MTs and the concentration of free tubulin (e.g., using fluorescent proteins as markers for tubulin) (47) in filopodia, growth cones, or small cells or cellular compartments, and to determine whether the observed fluctuations in tubulin concentration relate to changes in the amount of MT polymer. Also artificial membrane compartments with dynamic MTs inside (48,49) can be used to investigate whether compartment volume affects the lengths and distributions of MT growth and shrinkage times as predicted by our model.

In our model, dynamic MTs cause concentration fluctuations because the volume of the compartment is small. Marked fluctuations in the concentration of free tubulin as a result of dynamic MTs are also possible in several other situations. One such situation would be if the diffusion of tubulin is so slow that a growing or shrinking MT creates a gradient of free tubulin near its tip. These local fluctuations in the concentration of free tubulin around the tip of a MT would be similar to those caused by a single MT in a small compartment, with similar effects on MT growth and shrinkage times. Since the diffusion coefficient of the same protein in different cell types can vary greatly (up to 90-fold) (27), the possibility of slow diffusion of tubulin and tubulin gradients around MT tips should be explored experimentally.

Another situation where dynamic MTs could cause fluctuations in the concentration of free tubulin, even in compartments much larger than 100 μm³, is when many MTs would (de)polymerize in concert. In our model, MTs appear to behave independently of each other. Thus, increasing the number of MTs in the compartment reduces the fluctuations in the concentration of tubulin (and consequently reduces the effects of compartment volume on MT dynamics) because a decrease in free tubulin due to growing MTs is compensated for by an increase in free tubulin due to shrinking MTs. If the MTs were not independent of each other and polymerized or depolymerized synchronously, the whole population of MTs could be viewed as a single MT that takes up or releases a large amount of tubulin. Such concerted MT (de)polymerization would cause marked fluctuations in tubulin concentration even in relatively large volumes (larger than 100 μm³), and this would then result in the change in MT dynamics that is observed in our model. Interestingly, under certain conditions in vitro, MTs can show synchronized polymerization and depolymerization (50–54), which is associated with marked fluctuations in GTP-tubulin concentration. Unfortunately, the distributions of MT growth and shrinkage times were not measured in these studies. Conversely, non-exponential, gamma-like distributions of MT growth and shrinkage times have been observed in one in vitro study (13), but it was not reported whether or not the MTs (de)polymerized synchronously. Whether concerted oscillations in MT growth and shrinkage can also occur in vivo, is an open question. However, during the anaphase of a dividing cell, kinetochore MTs (i.e., the MTs that are attached to chromosomes) depolymerize in concert to separate the chromosomes (55). Since there can be several hundreds of synchronously depolymerizing kinetochore MTs (56), the influence of compartment volume on MT dynamics could, in principle, take place in volumes up to several hundreds of times larger than 100 μm³. Many eukaryotic cells have volumes smaller than that, which means that during anaphase, the influence of compartment volume on MT dynamics could be considerable in those cells.

In conclusion, although we do not rule out that structural changes in the MT during growth or shrinkage can contribute to the generation of non-exponential distributions of MT growth and shrinkage times, our study suggests that when the volumes of cells or cellular compartments are small, when diffusion of tubulin is slow, or when many MTs (de)polymerize in concert, the growing and shrinking MTs cause fluctuations in the (local) concentration of free tubulin that are already enough for non-exponential distributions of MT growth and shrinkage times to arise. These fluctuations, and the factors that influence them (e.g., volume), are expected to affect all the processes that depend on MT dynamic instability, such as neuronal growth cone behavior and cell motility in general.