Calculation of Absolute Protein-Ligand Binding Affinity Using Path and Endpoint Approaches

Abstract

A comparative analysis is provided of rigorous and approximate methods for calculating absolute binding affinities of two protein-ligand complexes: the FKBP protein bound with small molecules 4-hydroxy-2-butanone and FK506. Our rigorous approach is an umbrella sampling technique where a potential of mean force is determined by pulling the ligand out of the protein active site over several simulation windows. The results of this approach agree well with experimentally observed binding affinities. Also assessed is a commonly used approximate endpoint approach, which separately estimates enthalpy, solvation free energy, and entropy. We show that this endpoint approach has numerous variations, all of which are prone to critical shortcomings. For example, conventional harmonic and quasiharmonic entropy estimation procedures produce disparate results for the relatively simple protein-ligand systems studied in this work.

INTRODUCTION

The accurate calculation of absolute binding affinities of protein-ligand complexes is an important goal for the study of biomolecular recognition (1) and computational drug design (2). However, currently available computational methods often require some knowledge of experimental binding affinities to calibrate parameters for a particular protein target (3). Free-energy techniques, known as double decoupling methods (4–6), have been developed to calculate the absolute binding affinities of complexes without a priori experimental information. The methods involve calculating the free-energy cycle for decoupling the protein and ligand, and then reintroducing the ligand to the bulk solvent. This rigorous technique has only been used for very small ligands (4) or with simplistic implicit solvent models (6). One of the difficulties involved in this approach is that the ligand must be decoupled slowly enough from the binding pocket such that the mechanical work associated with the process can be performed reversibly. New techniques have been developed that can obtain free energies from repeated nonequilibrium simulations (7,8) and may help make double decoupling applications more efficient. Using a different strategy, Chang et al. enumerated the configuration integrals of the bound and unbound state of simple host-guest complexes to calculate the free energy of association (9).

Any alchemical pathway between bound and unbound states can, in principle, be used to obtain free energies of complex formation. One of the most obvious pathways is to simply pull out the ligand from the active site of the protein by a potential of mean force (PMF) approach. The PMF approach has existed since the early days of molecular mechanics and is well grounded in the statistical mechanics of liquids. The exponential improvements in computer hardware as well as enhanced molecular dynamics algorithms make the PMF approach a reality for protein-ligand systems. Nevertheless, the computational requirements are still quite demanding. Izrailev et al. (10) have been using pulling methods for over a decade to study the nature of molecular recognition in protein-protein complexes. Fukunishi et al. (11) devised an approach to estimate the free energy of binding in protein-ligand complexes utilizing a self-avoiding random walk procedure. Also, in the last year, Woo and Roux (12) successfully applied a PMF approach to the calculation of the equilibrium binding constant of the phosphotyrosine peptide pYEEI to the Src homology 2 domain of human Lck.

A commonly used approximate method for the calculation of absolute binding affinities is the so-called molecular mechanics-Poisson-Boltzmann-surface area (MM/PB-SA) method (13,14). In this approach, an explicit solvent simulation of the bound state is carried out. Then the simulation is postprocessed to determine the enthalpic differences between the bound and unbound solute states. The solvation free energy of binding is obtained from a Poisson-based solvation model (15). Separately, the binding entropy is estimated by harmonic analysis using a simple r-dielectric function to approximate solvent screening of charge-charge interactions.

There are a few variations to this method in the literature as seen in Table 1. One idea is to use the faster generalized Born (GB) solvent model to score structures versus the Poisson method, also known as MM/GB-SA (16). Also, the simulations can be run with explicit solvent or GB. Another method requires running both bound and unbound simulations. A further choice is that the vibrational entropy can be calculated using either the normal mode approach or the quasiharmonic approximation. Moreover, the quasiharmonic entropy calculation can be performed in two ways: one method is analogous to the normal mode entropy calculation, which uses an ideal gas correction and the other involves separation of the ligand translational and rotational degrees of freedom from the other coordinates (17).

TABLE 1.

Variations of techniques for the MM/PB(GB)-SA method (54)

Decision	Options
Solvation model for ensemble generation and/or harmonic entropy	1. Explicit solvent
	2. GB-SA
	3. r-dielectric
Number of simulations	1. One-state, complex only
	2. Two-state, complex/free protein and ligand
Electrostatic solvation free energy	1. Explicit solvent charging free energy(36)*
	2. Poisson Boltzmann
	3. Generalized Born
Nonpolar solvation free energy	1. Single surface-area term of cavitation and nonpolar
	2. Surface-area term of cavitation, Born-like term for nonpolar(53)*
Entropy	1. Harmonic approximation + ideal gas R/T correction
	2. Quasiharmonic + ideal gas R/T correction
	3. Quasiharmonic vibration + rigid body rotation and translation

^*Option was not evaluated in this work.

In this study, we tested several variations of the MM/GB-SA method on two protein-ligand systems and compared them to the more rigorous PMF method and experimental results. The outline of the article is the following. We first describe the general theory and computational methods that were used in this study. We then present our results followed by a discussion and summary of conclusions.

THEORY

The theoretical derivation of expressions that can be used for the calculation of absolute binding affinities of a protein-ligand complex from computer simulations has been expounded elsewhere (5,18). We will outline some of the key points pertaining to the issues that are addressed in this work. For reference, Table 2 lists some of the terms and acronyms used in this work. The chemical reaction of a simple two-state binary protein-ligand complex formation in an aqueous environment (aq) is

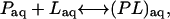(1)

where the left-hand side corresponds to the unbound state (U), and the right-hand side corresponds to the bound state (B) of the protein, P, and the ligand, L. The dissociation constant for this reaction is

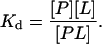(2)

TABLE 2.

Glossary of some of the abbreviations and terms used in this work

Abbreviation/term	Definition
BUQ	1-hydroxybutanone
COM	Center-of-mass
COG	Center-of-geometry
cpx	Complex
FKBP	FK506-binding protein
GBMV2	Generalized Born molecular volume method (34)
GB-SA	Generalized Born plus a surface-area-based nonpolar term
Hybrid	Hybrid explicit/implicit solvent method that has a fixed boundary but a uniform water layer surrounding the solute (35)
lig	Ligand
NM	Normal mode vibrational entropy analysis
prot	Protein
QH	Quasiharmonic vibrational entropy analysis
QH1	Standard quasiharmonic vibrational entropy analysis
QH2	Quasiharmonic vibrational entropy analysis where ligand translations and rotations are calculated independently
RBT	Rigid-body translation of the ligand
RBR	Rigid-body rotation of the ligand
RD4	Distance-dependent dielectric with a prefactor of 4
SASA-1	Solvent-accessible surface-area method for estimating nonpolar solvation free energy (34)

Experimentally, K_d is the molar concentration of ligand necessary to make a 50:50 mixture of bound and unbound protein. The free energy of binding in the standard state (1 M) is defined in terms of the dissociation constant,

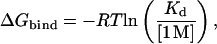(3)

where R is the universal gas constant and T is the absolute temperature. A general expression for calculating 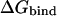from a computer simulation is (5)

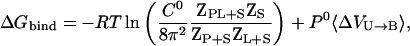(4)

where C⁰ is 1 M (∼1 mol/1660 ų), Z corresponds to the configuration integral over the subscripted coordinates, and S corresponds to solvent degrees of freedom. The second term in Eq. 4, which corresponds to the work associated with the volume difference between the bound and unbound states, is negligible in water and can be safely omitted (19). No kinetic energy component is present in Eq. 4 because these terms cancel out in the classical thermodynamic limit (5). For implicit solvent simulations, Eq. 4 reduces to (5)

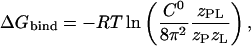(5)

where represents configuration integrals in the case that the solvent degrees of freedom are embedded in an external potential acting on the complex and unbound states.

It is convenient to separate out the six coordinates associated with the relative position and orientation of the ligand with respect to the protein, namely, 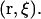The determination of ΔG_bind via simulation can then be formulated in terms of a binding zone, B, that covers a range of these six coordinates,

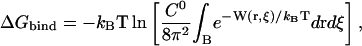(6)

where 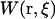is the work necessary to bring the center-of-mass (COM) of the ligand from infinity to a point 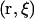relative to the COM and orientation of the protein, and k_B is the Boltzmann constant. Equation 6 can be reduced further by integrating over the orientational degrees of freedom of the ligand in the reference frame of the protein,

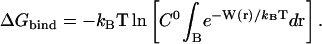(7)

The work function, 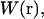can be obtained from the probability, 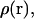of finding a ligand in a given position relative to the protein,

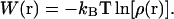(8)

A difficulty arises in how one should numerically define the bound state. In principle, the bound state should mimic the experimental zone whereby a “signal” is detected corresponding to binding. However, this zone is theoretically unknown. This issue is most critical for weakly bound complexes (19) where the integrands of the configuration integrals in Eqs. 6 and 7 are significant over a relatively large range of space. One practical suggestion (19), called an “exclusion zone”, is to define the binding zone as the states of a ligand for which no second ligand can have a more favorable interaction with the protein (19). For this work, we will approximate the binding zone as the range of coordinates for the ligand COM associated with a computer simulation of the unrestrained complex. This definition, albeit imperfect, is the basis behind other absolute binding free-energy methods in the literature such as the double decoupling methods (4,6).

Potential of mean force approach

Most rigorous free-energy methods (e.g., free-energy perturbation and thermodynamic integration) determine the free-energy difference between two states of a system through the use of an arbitrarily defined path. For absolute binding-affinity calculations, the two states are the bound complex and the unbound protein and ligand. In this work, the pathway between these two endpoints was chosen as the pulling of the ligand out of the complex into the bulk solvent along a straight line (12). A curvilinear pathway would be necessary for certain types of protein-ligand complexes, especially when the protein atoms are held rigid (20). We define a unit-vector pulling direction, 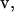and a coordinate, λ, which measures the progress along the pathway from bound to unbound. Assuming the center-of-mass and orientation of the protein is fixed, the center-of-geometry (COG) of the ligand can be pulled out of the binding groove with a translation vector,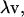

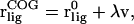(9)

where 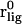is the initial bound position. In this work, we used umbrella sampling to visit overlapping regions along the path. We then calculate the PMF along this reaction coordinate by combining the probability distributions of each sampling window. The protein is restrained to be in a standard frame of reference and the COG of the ligand is restrained for window j at spatial point, 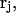along the pathway in Eq. 8, using a biasing potential, 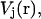of the form

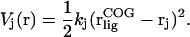(10)

Also, an unrestrained complex simulation is performed to determine the bound state and to increase sampling of the complex. The distributions in three-dimensional space of the separate simulation windows are merged by using the weighted histogram method (WHAM) (21,22) to form a single unweighted distribution, 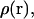that spans the two states of interest. Because we are only sampling over a small fraction of the total translational space, we choose to integrate 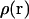over the two directions perpendicular to the pulling coordinate, thus yielding 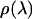and subsequently 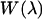via analogy to Eq. 8. We also make the assumption that the work function is effectively quadratic in the binding groove. The binding free energy then can be calculated from 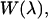as well as an equilibrium simulation of the complex via (17)

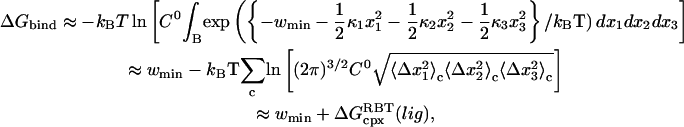(11)

where 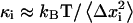based on the classical harmonic oscillator approximation (17), w_min is the discrete minimum value of 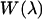when the asymptotic value of 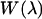at large 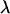is shifted to zero, and the summed term, 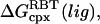is defined as the free energy of rigid-body translation (RBT) of the ligand in the complex compared to confinement in a 1660-ų volume. The rigid-body translation term and the ligand center-of-geometry fluctuation eigenvectors, 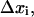for each cluster, c, are obtained using a prescription described in the next section (17). We used a combination of two criteria to determine the location of the unbound endpoint of the PMF. First, one can look for the PMF to flatten out over several angstroms and assume this to be the asymptote. Second, the nonbonded cutoffs provide an approximate estimate of the distance such that the ligand and protein no longer directly interact with each other.

Endpoint approaches

In an endpoint approach representing MM/GB-SA models, the basic formula for the binding free energy involves the sum of the enthalpic, entropic, and free-energy differences between the bound and unbound states,

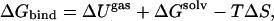(12)

where ΔS is the entropy difference between the two states either in the gas or aqueous phase, and ΔG^solv reflects the solvation free-energy difference. The term ΔU^gas is the difference in gas phase enthalpies defined as

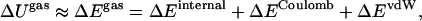(13)

where the terms ΔE^internal, ΔE^Coulomb, and ΔE^vdW correspond to differences in internal energy, electrostatic energy, and van der Waals (vdW) dispersion energy, respectively.

In the two-state version of the MM/GB-SA model, simulations of the complex, and free protein and ligand are performed. Changes in energy terms of component X (e.g., X = Coulomb) are obtained by independently averaging over bound and unbound simulations,

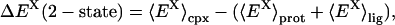(14)

where the subscript “cpx” of the thermal average, 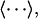denotes the complex, and similarly for the free protein (prot) and free ligand (lig). The two-state model, although admirable in its simplicity, is actually very difficult to pursue in practice, because of at least two critical issues. First, it is difficult to pinpoint the average energy of an ensemble of protein or complex structures, because the system may jump from macrostate to macrostate over time periods larger than what is currently feasible to simulate by today's computing resources (23). Second, the statistical uncertainty is quite large for taking the difference between average enthalpies of bound and unbound ensembles (16,17).

Often researchers revert to an one-endpoint simulation method where only the complex is simulated and the energy components for binding are determined by subtracting the average complex energy from the average protein and ligand energies obtained by effectively pulling the species infinitely far apart,

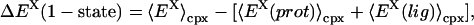(15)

where 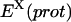is evaluated over the complex trajectory with the ligand deleted, and 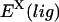is evaluated over the complex trajectory with the protein deleted. This method leads to significantly lower statistical uncertainty but completely neglects the enthalpies of protein and ligand reorganization proceeding from the bound to the unbound state, which, in many cases, may not be negligible.

The general approach to normal mode (NM) and standard quasiharmonic entropy (denoted here as QH1) methods involves computation of the vibrational (vib) and ideal gas entropies in the bound and unbound states,

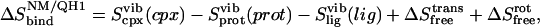(16)

where S_bind denotes absolute entropy, the simulation type is in subscript, the evaluated degrees of freedom are in parentheses, and the ideal gas entropy components, 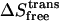and 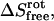are described below. Quasiharmonic entropy methods are based on either classical or quantum harmonic oscillator theory (18,24). Both quantum and classical forms produce roughly the same result when differences in entropy are taken (results not shown). We employ the quantum model in this work. All quasiharmonic methods involve the formation of a covariance fluctuation matrix, C (24),

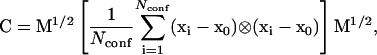(17)

where x_i is the conformation of snapshot i, x₀ is the average structure over the entire set of conformations, N_conf is the number of conformations, ⊗ denotes the outer product, and M is a diagonal matrix of the atomic masses (24). Each conformation used in Eq. 17 is rotated and translated to best fit the average structure. Finally, the C matrix is diagonalized to obtain eigenvalues, ɛ_i. These eigenvalues are converted to frequencies (24),

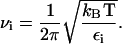(18)

Normal mode entropy methods differ in that the C matrix is calculated as the mass-normalized second derivative matrix (24),

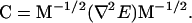(19)

The C matrix is diagonalized to yield eigenvalues. The frequencies are then calculated as the square root of the eigenvalues. The frequencies from either harmonic or quasiharmonic methods are substituted into the vibrational entropy formula for a noninteracting collection of quantum harmonic oscillators (24),

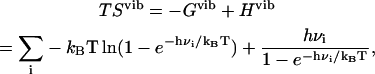(20)

where h is Planck's constant. In harmonic entropy and standard quasiharmonic binding entropy calculations, the ideal gas entropy terms for translation (trans) and rotation (rot) are used to account for the six degrees of freedom of the free ligand and free protein at 1 M (C⁰) concentration in solution (25):

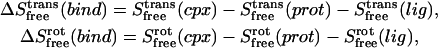where

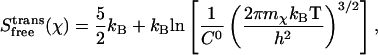(21)

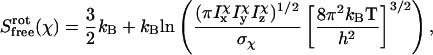(22)

an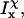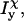d and 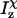are the moments of inertia of species χ (χ = cpx, prot, or lig), 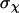is the symmetry factor of χ, which is set to 1 for this work. An alternative method for calculating quasiharmonic entropy, dubbed here as QH2, involves a complete decoupling of the RBT and rigid-body rotations (RBR) of the ligand from the complex (17),

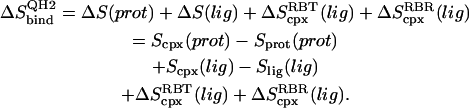(23)

The benefit of this approach is that one can directly estimate 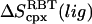and 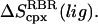The drawback of this procedure is that coupled motions between the RBT and RBR of the ligand and the protein are neglected and thus the binding entropy may be underestimated. Also, it should be noted that we use rigid-body entropy terms rather than free energy terms as in Swanson et al. (17) to avoid double-counting the rigid-body enthalpy. The rigid-body translational entropy term, 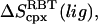is (17)

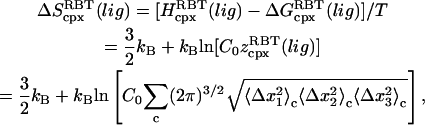(24)

where 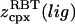is the same integral as in Eq. 11 with w_min = 0, and the eigenvalues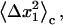 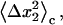and 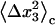are calculated by diagonalizing the covariance matrices of clustered sets of snapshots, indexed as c, of the COM of the ligand. Clustering was performed in three-dimensional space using a standard hierarchical agglomeration algorithm (26). Clustering was used to ensure that quasiharmonic basins were found such that Eq. 24 is appropriate. We arbitrarily selected the hierarchical level so that there were five clusters. Results varied little with larger numbers of clusters. The rotational term is calculated through histogram binning of the spherical-polar angles, 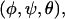which are necessary to orient each ligand conformation into the standard reference frame (27),

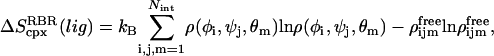(25)

where

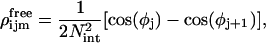(26)

such that each of the angles are divided into N_int equally spaced intervals, and 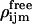is the probability of finding the ligand in a certain bin assuming it can rotate freely. There are no precise criteria for how to choose the number of intervals to achieve the best entropy estimate. Based on empirical observations, we chose N_int = 15, but also looked at values of 10 and 20 to calculate errors associated with binning.

Accurately calculating entropy is a nontrivial task. For example, there can be a significant source of error due to the above-stated problem of inadequate sampling of macrostates. In addition, the standard methods used to evaluate entropy make sweeping assumptions of ideal harmonic behavior, which may be inadequate for flexible proteins (28). For instance, the quasiharmonic entropy method assumes that the protein is vibrating in a 3N_atom − 6 dimensional harmonic well. A simple illustration of nonideal harmonic behavior would be a freely rotating side chain on the surface of a protein. Also, harmonic and quasiharmonic methods assume that each mode is uncoupled to all other modes such that the entropy of each mode is additive (28). This only seems to be a reasonable assumption when sampling a single local minimum.

METHODS

The two protein-ligand complexes that were evaluated in this work were FK506-binding protein/4-hydroxy-2-butanone (FKBP-BUQ) (Protein Data Bank (PDB) identifier, 1D7J) (29), and FKBP-FK506 (PDB identifier, 1FKF) (30). FKBP contains 107 residues, BUQ consists of six heavy atoms, and FK506 consists of 57 heavy atoms. For the FKBP-BUQ simulations, the protein atoms were simulated with the PARAM22 force field (31), and the ligand parameters were derived from the analogous functional groups already available in the PARAM22 and PARAM27 parameter files. For the FKBP-FK506 simulations, the CHARMm MSI force field was used and the parameters were obtained directly from the ligand-protein database (LPDB) of Roche et al. (32). The FKBP-BUQ test case was selected mainly because it was the subject of a previous work where the MM/PB-SA method was used (17), and therefore, various energy terms could be compared. The FKBP-FK506 system was chosen because FK506 is significantly larger than BUQ and is an appreciably more favorable binder to FKBP ( 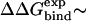−8 kcal/mol). Also the force-field parameters were readily available from the LPDB (32).

All single-point simulations were run for a total of 2 ns where the first 0.5 ns of trajectory was considered equilibration and the last 1.5 ns was used for production. Snapshots were saved every 0.1 ps for a total of 15,000 structures per simulation. The high frequency of snapshot storage was selected to ensure convergence of the quasiharmonic vibrational entropy methods. Energy averages were made only over 1-ps intervals for a total of 1500 snapshots. Likewise, the rigid-body translation/rotational entropies of the ligand in the complex were estimated using these 1500 snapshots. The SHAKE algorithm was used for all hydrogens, and the time step of the simulation was set to 2 fs. A Nose-Hoover thermostat (33) with a thermal inertia parameter of 10 was used to keep the simulation temperature constant at 298 K.

All implicit solvent simulations were run with the GB electrostatic solvation potential GBMV2 (34). Nonpolar (np) solvation was modeled as proportional to the solvent-accessible surface area (SASA), 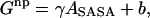where A_SASA is the solvent-accessible surface area using a water probe of 1.4 Šand the SASA-1 algorithm (34), 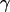is the surface tension parameter and was set to 5.42 cal/(mol Ų), and b was set to 0.92 kcal/mol. Note that for simulating two molecules such as a complex, the constant b term needs to be treated carefully. When the protein and ligand are spatially separated from each other but part of the same simulation as in the PMF simulations, a second b term must be added to account for the two distinct cavitation points.

Explicit solvent simulations were performed with the hybrid explicit/implicit solvent method (35) using an explicit solvent layer width of 10 Å. The hybrid solvent model (35) involves encapsulating a biological solute by a layer of water molecules. Outside this layer, a GB-based implicit solvent reaction field is used to model the bulk water continuum. The hybrid solvent method has been shown to be significantly less computationally expensive than conventional Ewald approaches, primarily because less explicit solvent molecules are required. However, some minor deviations to the conventional methods are to be expected (35) because of surface boundary artifacts. Details on the theory and implementation of the hybrid method can be found elsewhere (35,36). The pairwise multigrid method (35,37) was used to approximate the long-range electrostatic and GB terms. The short-range nonbonded cutoff was set to 12 Å. The Lennard-Jones interactions were truncated at this short range with no long-range correction. The center-of-mass and rotational moments of inertia of the protein were harmonically restrained (35) with force constants of 500 kcal/(mol Ų) and 500 kcal/(mol rad²), respectively, to prevent the protein from moving out of its fixed shell of water molecules.

The umbrella-sampling procedure involved restraining the protein as above and holding the COG of the ligand at various points along a linear pathway. In the standard molecular orientation frame of reference of the FKBP protein, the pathway unit vector (in Å), 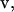for BUQ was visually chosen to be [−0.5243, 0.1068, 0.8448] using the visual molecular dynamics (VMD) molecular graphics software (38). For the FKBP-FK506 complex, the unit vector was chosen to be the z axis. The initial bound ligand position, 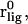was simply the COG of the ligand in x-ray crystal structure. In the FKBP calculations, 15 simulations were performed independently with the 1 kcal/mol Ų COG restraint potentials at points defined by Eq. 8, where 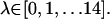In the FK506 simulation windows were in the range, 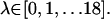Due to insufficiently sampled regions, which pertained to barriers in the PMF along the pathway in the FK506 cases, certain simulation windows were added in the GB and hybrid simulations. For the FK506/GB simulations, simulation windows were added at 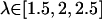with 4 kcal/mol Ų COG restraints. For the FK506/hybrid simulations, windows at 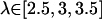were added with 4 kcal/mol Ų COG restraints and 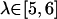with 2 kcal/mol Ų COG restraints. A more elegant solution to this problem might involve an automated adaptive umbrella sampling method (39). Also, for the FK506/hybrid simulations, we added 8 Å more water layer (for a total of 18 Å) to the ligand in the range, 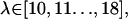to avoid small but cumulative surface artifacts (35). Because of the extra computational effort, lack of protein-ligand interactions, and ultimate flatness of the PMF curve at this range, we limited our production time to 500 ps per window. WHAM analysis on the resulting three-dimensional probability distributions was performed with an in-house program using a histogram bin size of 0.5 Å to obtain the unweighted composite probability distribution, 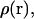as required in Eq. 8. A one-dimensional probability distribution along the pulling coordinate, 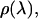was generated by summing 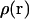over the plane perpendicular to the pulling direction. Finally, the one-dimensional work function, 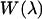was obtained from 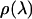in analogy to Eq. 8.

In the all of the hybrid solvent simulations, before the dynamics run, explicit solvent molecules were added. For the PMF runs, this was performed after the ligand had been shifted to the center of its restraint potential. Water molecules in the x-ray structures were preserved. The additional explicit solvent molecules were put into place using a prescription outlined elsewhere (35).

In the endpoint studies, the hybrid simulations were rescored with the implicit solvent model to estimate binding free energies. Snapshots at 1-ps intervals starting from 500 ps (1500 structures) were processed by deleting the explicit water molecules and evaluating, with infinite nonbonded cutoffs, the molecular mechanics energy plus GBMV2 and SASA-1. For comparison in the FKBP-BUQ endpoint study, molecular surface-based Poisson solvation energies were also obtained at 0.5-Å grid resolution using the PBEQ module in CHARMM (40).

Normal mode analysis of the two complexes was performed on 16 complex structures extracted at equally spaced intervals covering the entire production run. Two implicit solvent models were employed: distance-based dielectric (r-dielectric) with a prefactor of 4 and GBMV2/SASA-1. Each structure was minimized using the adopted-basis Newton-Raphson method for 6000 steps or until a gradient tolerance of 10⁻⁶ was reached. Second derivatives were calculated using analytical formulas for the r-dielectric runs and finite difference with a step size of 10⁻⁶ Å for the GBMV2/SASA-1 runs.

RESULTS

PMF calculations

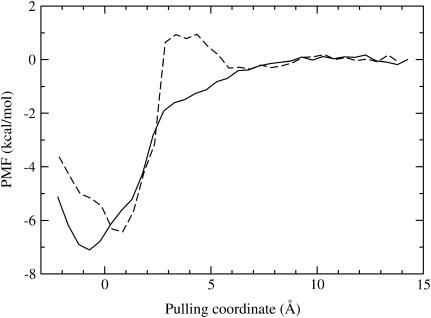
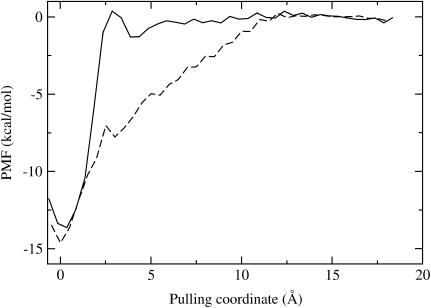
The one-dimensional profiles of the PMF results are presented in Figs. 1 and 2. In Fig. 1, the most favorable position of the center of the ligand for the BUQ/GB simulations is roughly 1.5 Å distance from the most likely spot for the hybrid calculation. Also the BUQ/GB simulations result in generating a 1 kcal/mol barrier while pulling the ligand out of the pocket. Because this barrier is not present in the BUQ/hybrid results, it is likely a result of the physics of the GB-SA implicit solvent model. In Fig. 2, the locations of the binding minima are roughly the same, but the decays of the interactions are different. The FK506/hybrid PMF levels out at 10 Å. The FK506/GB PMF decays comparatively slower until it flattens out at ∼12.5 Å. In general, one would expect that a PMF would flatten out when the corresponding protein-ligand interaction energy decays to zero because of nonbonded cutoffs. The fluctuations in Figs. 1 and 2 at larger values of the pulling coordinate are likely due to lack of statistical convergence. Based on comparisons with a PMF derived from half of the production simulation length, the errors at any given bin are between 0.1 and 0.5 kcal/mol.

FIGURE 1.

One-dimensional potential of mean force for pulling BUQ out of the FKBP binding pocket using GB-SA and hybrid explicit/implicit solvent models. See Theory and Methods sections for simulation details. Solid line indicates a hybrid solvent and dashed line signifies GB-SA implicit solvent. Arbitrary vertical shifts of each curve were manually adjusted so that the perceived asymptotic values of the PMF are located near 0.

FIGURE 2.

One-dimensional potential of mean force for pulling FK506 out of the FKBP binding pocket using GB-SA and hybrid solvent models. See Fig. 1 for legend and details.

Table 3 summarizes the free-energy results for all of the PMF calculations. The BUQ results for both solvent models are very close to the experimentally determined values. The FK506 results are systematically too large by roughly 1–3 kcal/mol. The 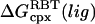terms are very similar in both solvent models. The statistical error associated with the accumulation of errors in the PMF is estimated to be ∼0.5 kcal/mol, based on the above analysis. Also, in general, errors will be better or worse depending on the height of the barriers in the PMF, which is, in turn, a function of the pulling direction. In addition, we should note that it is nearly impossible to determine what errors, if any, are caused by not sampling the lowest free-energy states of the force field at each window.

TABLE 3.

Summary of results for PMF calculations (kcal/mol) of the two protein-ligand complexes studied in this work

Ligand	Solvent model	wmin*		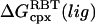ΔGnp (correction)†	ΔGbind (calculation)	ΔGbind (experimental)
BUQ	GB-SA	−6.4 (0.5)	3.5 (0.3)	−0.9	−3.8 (0.6)	−4.5‡
BUQ	Hybrid	−7.2 (0.5)	2.9 (0.3)	–	−4.3 (0.6)	−4.5‡
FK506	GB-SA	−14.6 (0.5)	4.2 (0.3)	−0.9	−11.3 (0.6)	−12.3§, −12.8¶
FK506	Hybrid	−13.6 (0.5)	3.8 (0.3)	–	−9.8 (0.6)	−12.3§, −12.8¶

^*Error estimates in parentheses.

^†Correction term in GB-SA simulations accounts for second cavitation point in unbound state.

^‡Derived from experimentally measured K_i (29).

^§Bierer et al. (55).

^¶Bierer et al. (56).

As pointed out in the Methods section, the simple overlay of equally spaced windows was not sufficient for broad sampling of the FK506 landscape for either solvent model. The primary reason for this was that the pulling direction that was chosen led to mild steric clashes of the ligand with the protein active site. It would certainly be desirable to have complete automation in a PMF simulation. One could envision using an adaptive umbrella-sampling procedure (39) whereby the histograms of the original equally spaced window simulations are automatically analyzed to determine where there are deficits in sampling. Then, new simulations would be issued to fill in the gaps (11). Nevertheless, as for computational timings, the GB-SA simulations for both systems required 8 CPU-days per simulation window, whereas the hybrid simulations used ∼20 CPU-days per window. These timings were obtained from simulations run on a cluster of 32 AMD Athlon MP 2200+ processors (AMD, Sunnyvale, CA).

Endpoint calculations

In comparison to the PMF calculations, energy components are extracted from endpoint simulations and combined with entropy estimates to form approximate binding free energies. The enthalpy of complex formation for the two systems, which for simplicity includes the solvation free energy, is broken down into components (41) in Tables 4 and 5. As expected, the two-state energy differences have a much higher degree of uncertainty than the one-state models. The mean ± SEs in the one-state model are quite small at around a few tenths of a kcal/mol, and thus, the one-state model is more advantageous even though it neglects the enthalpy of structural reorganization (14,16).

TABLE 4.

Average energies (kcal/mol) for the different components of the one- and two-state MM/GB-SA simulations of the FKBP-BUQ complex

Component*	GB-SA one-state	GB-SA two-state	Hybrid one-state	Hybrid two-state
ΔUinternal	0.0	−5.8	0.0	−11.3
ΔUvdW	−9.0	−13.3	−11.0	−3.2
ΔUCoulomb	−12.7	−63.4	−9.5	−26.7
ΔGGB	10.0	67.6	13.1	19.3
ΔGnp	−2.6	−3.2	−2.8	−2.2
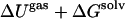	−14.3	−18.1	−10.1	−24.1

^*Mean ± SEs for the one-state models are on the order of a few tenths of a kcal/mol, whereas errors for the two-state models are ∼10 kcal/mol except for the nonpolar term, which is in error by ∼1 kcal/mol.

TABLE 5.

Average energies (kcal/mol) for the different components of the one- and two-state MM/GB-SA simulations of the FKBP-FK506 complex

Component*	GB-SA one-state	GB-SA two-state	Hybrid one-state	Hybrid two-state
ΔUinternal	0.0	2.7	0.0	11.2
ΔUvdW	−48.9	−50.1	−50.2	−47.8
ΔUCoulomb	−15.3	−46.3	−17.3	5.9
ΔGGB	28.4	52.3	38.1	7.8
ΔGnp	−6.0	−6.9	−6.3	−6.2
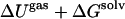	−41.8	−48.4	−35.7	−29.1

^*Error estimates discussed in Table 4.

Another observation is that the Coulomb and GB terms are numerically large, though nearly compensatory. Their sum, often denoted as the electrostatics of binding, plays an important role in the free-energy difference (16). The nonpolar surface area terms are uniform among different protocols. The vdW terms are quite large, especially in the FK506 system. It would appear that these terms must be predominantly compensated by solute entropy in the final free-energy estimation (9,41). The total enthalpy estimates for the different methods are quite varied. Some variations between one- and two-state models were expected, given that the protein and ligand are allowed to relax in the two-state model.

It seems quite unusual that the change in enthalpies become more favorable for most cases when relaxation is included. To understand this phenomenon, we extended the GB-SA simulation times of the FKBP-BUQ system to 7 ns in both the complexed and unbound states. After 7 ns, 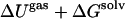rose to −6.3 kcal/mol, which is higher than the one-state model (−14.3 kcal/mol). The enthalpy of the complex varied little from the 2-ns value. However, the protein energy declined by ∼14 kcal/mol. This additional calculation agrees with those of other studies (16) in showing that 2-ns simulations are too short to obtain converged 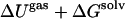values for two-state models.

Because we used a GB-SA solvent model rather than the conventional PB in our rescoring of explicit solvent simulations, we employed the CHARMM PBEQ module (see, e.g., Feig et al. (40) for calculation details) to rescore the 1500 structures in each of the one-state hybrid simulation sets. In the BUQ set, the PB model obtained an average binding ΔG^PB = 14.1 kcal/mol, which is 1.0 kcal/mol higher than the GB-SA model's result. In the FK506 set, the binding ΔG^PB = 42.4 kcal/mol, which is 4.3 kcal/mol higher than ΔG^GB. Note that at the 0.5-Å grid resolution used in the calculation, the PBEQ Poisson model is only slightly more accurate than GBMV2 compared to a benchmark 0.25-Å resolution PBEQ Poisson model (40). Also, the GB-SA PMF results were in reasonable agreement with the explicit solvent results. For this reason, we attributed discrepancies with Poisson results as simply contributions to overall error.

By way of the endpoint approach, there are two primary methods for estimating entropy values: normal mode and quasiharmonic (QH). Normal mode analysis was performed for two potential energy functions as shown in Table 6. As one might expect, there are significant discrepancies between the entropy values using the conventional r-dielectric (RD4) versus GB-SA. Although one can criticize the validity of the entropy values based on r-dielectric, because it is a crude treatment of solvation, the GB-SA entropy terms are not without reproach. For example, the GBMV2 potential that we employed has rotational variance because of the fixed-orientation angular integration grid used in calculating the Born radii (34). This means that there are broad energy wells corresponding to rigid-body rotations of each chemical species. We tried to limit the effect of this issue, by applying orientational restraints to the system (35), which were intended to contaminate the low-frequency rotational modes with high-frequency restraint modes. The r-dielectric modes, in contrast, were summed into the entropy by removing the lowest six eigenvalues in each entropy calculation, which roughly correspond to the rotational and translation degrees of freedom. Another related problem is that strong minimization with the GBMV2 potential can lead to artificially low minima that are rotationally dependent. Moreover, the structures may distort slightly due to grid artifacts. These last two problems are probably somewhat muted by error cancellation in taking the difference between two entropy terms.

TABLE 6.

Normal mode-derived vibrational entropy components (kcal/mol) for different systems averaged over 16 equally spaced snapshots of the 1.5-ns production run

	BUQ		FK506
Component*	GB-SA†	RD4‡	GB-SA†	RD4‡
TScpx(cpx)	884.3 (1.3)	1218.1 (0.9)	973.0 (1.4)	1260.8 (1.5)
TScpx(prot)	876.8 (1.2)	1205.9 (1.0)	907.6 (1.5)	1189.7 (0.9)
TScpx(lig)	5.6 (0.1)	5.4 (0.0)	78.0 (1.0)	73.4 (0.0)
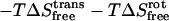	17.1	17.1	21.2	21.2
−TΔSbind	15.2 (1.8)	10.3 (1.4)	33.8 (2.3)	23.5 (1.7)

^*Mean ± SEs are shown in parentheses.

^†GB calculations were run with translational and rotational restraints. Zero and negative eigenvalues were omitted (see Results section for details).

^‡In the RD4 calculations, the lowest six vibrational modes were omitted.

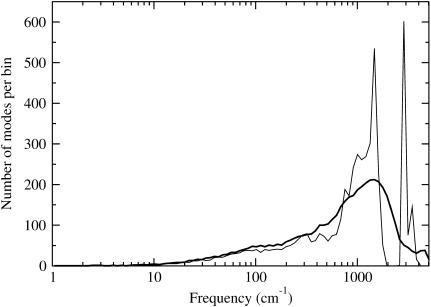
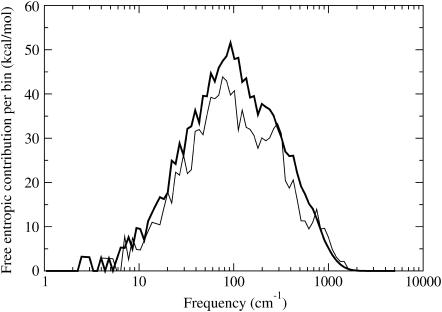
Large differences in absolute entropy estimates exist between NM and QH1 (Table 7) for the individual species. Fig. 3 shows that NM has more fine structure compared to QH1 (42). In Fig. 4, one can see that over a wide range of frequencies, the QH1 modes provide larger entropy contributions than NM. It might have been expected that the QH1 method would have more low-frequency modes than NM as seen in Fig. 3, as multiple basins along the energy landscape are explored over the MD simulation run. However, higher frequency modes (∼100–1000 cm⁻¹) also seem to contribute to higher entropy values as seen in Fig. 4. One should keep in mind that the QH1 method is void of the high-frequency covalent hydrogen bond stretching and bending modes because of the SHAKE constraints imposed on the system. These high-frequency modes, nonetheless, are not expected to make any noticeable contribution to the entropy estimate.

TABLE 7.

Quasiharmonic entropy components (kcal/mol) for the different simulations

	BUQ		FK506
Component*	GB-SA	Hybrid	GB-SA	Hybrid
TScpx(cpx)	1470.4	1487.3	1579.3	1567.2
TScpx(prot)	1445.7	1460.6	1495.8	1472.2
TScpx(lig)	15.3	14.5	82.6	102.6
TSprot(prot)	1489.0	1424.3	1526.1	1484.0
TSlig(lig)	11.7	17.0	93.4	114.7
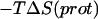	43.3	−36.3	30.3	11.8
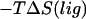	−3.6	2.5	10.8	12.1
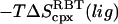	2.6 (0.3)	2.0 (0.3)	3.3 (0.3)	2.9 (0.3)
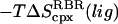	1.6 (0.2)	1.2 (0.3)	4.0 (0.4)	3.8 (0.4)
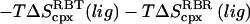	4.2 (0.4)	3.2 (0.4)	7.3 (0.5)	6.7 (0.5)
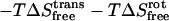	17.1	17.1	21.2	21.2
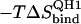	47.4	−28.9	61.4	52.7
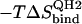	43.9	−30.6	48.4	30.6

^*Trajectory snapshots were taken every 0.1 ps. Mean ± SEs are shown in parentheses.

FIGURE 3.

Distribution of modes for normal mode and quasiharmonic vibration calculations for the FKBP-BUQ complex. Harmonic modes (thin line) are shown for one complex structure from the RD4 calculation. Quasiharmonic modes (thick line) were obtained from the 1.5-ns production run of the GB-SA complex simulation. Frequency bins start at 1 cm⁻¹ and exponentially increase with a multiplier of 1.1.

FIGURE 4.

Contribution to free entropy values from harmonic/quasiharmonic modes. See Fig. 3 for legend and details.

The results of the alternative quasiharmonic analysis technique, QH2, are also presented in Table 7. The results for the two variants of QH are in good agreement with each other in the case of the BUQ complex given a particular choice of solvent model. In contrast, the QH variants differ quite substantially in the FK506 complex. One possibility is that FK506 is coupled quite closely with the protein and therefore the separation of degrees of freedom between the protein and ligand in the complex (17) may be too strong of an approximation. The QH results for BUQ with hybrid solvent are inconsistent with the results obtained by other entropy approaches. Once again, separation of degrees of freedom of the solute and water molecules may be an important factor, although, this factor alone may not be sufficient to explain such disagreements.

When the enthalpic and entropic components are combined, a wide range of free-energy estimates emerges as seen in Table 8. Some of the possible combinations of one- and two-state enthalpies and NM, QH1, and QH2 provide good absolute and relative values. Unfortunately, it is not immediately obvious how one would choose a priori a particular protocol. Two protocols deserve some comment. First, the GB-SA one-state ensemble/GB-SA normal mode is arguably self-consistent and reasonably statistically reliable. On the downside, this protocol lacks an estimate of the configuration entropy associated with the multiplicity of basins, and the relaxation enthalpy and entropy of the free protein and ligand. Although the relative free-energy estimate is the best of all of the protocols, the absolute free energies are too high by ∼5 kcal/mol. The other notable protocol is the one closest to that recommended in the article by Kollman and co-workers (14): the hybrid one-state ensemble using RD4 normal mode entropy. This procedure succeeds in predicting the binding free energy of FK506, but overestimates the free energy of BUQ. Confirming the results of Gohlke and Case (16), none of the quasiharmonic entropy-based free energies of binding reported in Table 8 are close to the experimentally observed values. The best relative free energy is obtained with the one-state GB-SA simulation using QH1 entropy.

TABLE 8.

Free energies of binding (kcal/mol) for various protocols

	BUQ		FK506		ΔΔbind
Simulation Entropy	GB-SA	Hybrid	GB-SA	Hybrid	GB-SA	Hybrid
NMRD* 1-pt	−4.0	0.2	−18.3	−12.2	−14.3	−12.4
NMRD 2-pt	−7.8	−13.8	−24.9	−5.6	−17.1	8.2
NMGB† 1-pt	0.9	5.1	−8.0	−1.9	−8.9	−7.0
NMGB 2-pt	−2.9	−8.9	−14.6	4.7	−11.7	13.6
QH1‡ 1-pt	33.1	−39.0	19.6	17.0	−13.5	56.0
QH1 2-pt	29.3	−53.0	13.0	23.6	−16.3	76.6
QH2 1-pt	29.6	−40.7	6.6	−5.1	−23.0	35.6
QH2 2-pt	25.8	−54.7	0.0	1.5	−25.8	56.2

^*NMRD, normal mode entropy obtained using r-dielectric potential.

^†NMGB, normal mode entropy obtained using GB potential.

^‡QH, quasiharmonic entropy (see Theory section and Table 1).

Some of our results can be compared directly to the work of Swanson et al. (17), where the FKBP-BUQ system was studied using the AMBER 7.0 program (force-field version was not specified). Swanson et al. performed the explicit simulation one-state ensemble method with the QH2 entropy protocol, but did not present their vibrational entropy calculations. As we have seen in our work and as was discussed by them, the QH2 vibrational entropy leads to an erroneous absolute binding-affinity prediction. Without corrections for relaxation and vibrational entropy, they predicted a free energy of −7.8 kcal/mol, whereas we obtained a value of −7.2 kcal/mol [ 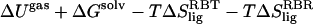]. As to be expected from using different force fields, our molecular mechanics (i.e., gas-phase) energies differ by ∼5 kcal/mol with their prediction of −13.4 kcal/mol. Our GB and SA terms are in good agreement with their values of 13.6 kcal/mol (obtained from PB) and −2.3 kcal/mol, respectively. Our rotational free-energy term is in line with their value of 1.1 kcal/mol. They predicted a ligand translational free energy of 4.1 kcal/mol, whereas we obtained a value of 2.9 kcal/mol. Some of the discrepancy here can be explained by the fact that we employed clustering, which increases the calculated volume of space accorded by the center-of-geometry of the ligand and thus reduces the ligand translational free-energy estimate. It is important to point out that a neglect of relaxation and vibrational entropy may lead to a reasonable estimate of binding affinity for BUQ, but it does not lead to good prediction for the larger ligand, FK506 (−29.0 kcal/mol).

DISCUSSION

Path-based free-energy approaches

The PMF method we have detailed here provides explicit information about the work function of pulling a ligand out of an active site pocket into bulk solvent. The path we selected for both ligands was arbitrary and manually determined by visual inspection using VMD (38). Our method is similar in spirit to the recent work of Woo and Roux (12). One major difference between their method and the one presented in this work is that they separately computed the free energy of ligand rotation and then held the ligand with an orientational restraint as it was pulled out of the binding pocket. Although this procedure certainly reduces the space the ligand has to sample, it could cause larger barriers if the ligand is occluded by parts of the binding pocket and is unable to rotate out.

Although few methods in the field of absolute-binding affinity calculations are truly “black box”, it might be desired to have a general method that does not require a user-specified path. Fukunishi et al. (11) have detailed such a method. In their approach, the sampled COM coordinates of the ligand are used to dynamically install barrier potentials, which prevent the ligand from revisiting to the same spots. Eventually, the ligand is sufficiently far away from the target that one defines the ligand's current location as the unbound endpoint. Fukunishi et al. obtained excellent correspondence to experimental binding free energies for the ligands that they studied. However, in their analysis of the absolute binding free energy, this group did not include the correction to standard state, which would perhaps shift their predicted free energies upwards by 2–4 kcal/mol. It is likely though, that in their determination of relative-binding free energies, the standard-state corrections would cancel, leading to their apparent agreement with experiment.

The alternative double decoupling method involves the free-energy calculation of the disappearance of the ligand inside the active site, and the reappearance of the ligand in the bulk solvent (4–6). These methods have some very salient properties. For example, the paths between endpoints can be defined automatically without user specifications. Also, one can study components of the free energy to some extent, because one energy term at a time can be turned on and off (12). On the other hand, there are a few drawbacks to these approaches. First, the definition of the bound state is inevitably determined to be the configurational space of the unrestrained complex simulation. This might be an issue for weak binders where the experimentally observed bound state may in fact require a broader definition such as an exclusion zone (19). The other potential problem with this method is that the disappearance of a large ligand in an explicit solvent simulation may require a large number of simulation windows such that there is sufficient configurational space overlap between successive windows. Grand canonical sampling, which would involve the addition/deletion of water molecules during a simulation might improve statistics in this case (20). Woo and Roux also point out in their work (12) that decoupling a highly charged ligand in the protein and solvent environments may lead to large opposing energies, the sum of which could result in considerable statistical errors.

Although the PMF method we used in this work is purported to be more accurate than the endpoint methods, there is still a significant deviation (∼3 kcal/mol) from experimental binding affinities for the FK506 complex using the hybrid solvent model. Certainly, our method introduced certain approximations that could be removed by an even more costly computational study. For example, the PMF over a larger three-dimensional landscape could be mapped out and integrated (43). Also, a more accurate definition of the bound state, such as an exclusion zone definition (19), might improve correspondence to experiment. Furthermore, as discussed below, a truly explicit solvent model with periodic boundary conditions could be employed. Finally, there are inevitable errors associated with the classical force field we employed. Investigation of force fields that incorporate charge polarization is warranted for future studies (44).

It is interesting to note the difference between the PMF curves of the GB-SA and hybrid models in the FK506 case. The hybrid approach, which we assume to provide a more rigorous physical picture, suggests a very steep funnel toward binding and a strong screening of charge-charge protein-ligand interactions from water molecules at distances >6 Å. The diffusing ligand would have to make a relatively close approach to the binding pocket in order for it to be brought into association. In contrast, the GB-SA model provides a smooth long-range funnel toward the bound state, indicating a weaker solvent descreening of charge-charge interactions. The exponential behavior of the GB-SA PMF is likely due to the analytical form of the GB descreening term (34).

In trying to understand why the minimum of the GB-SA PMF differed in position from the hybrid PMF for the BUQ complex, we found that the x-ray structure, hybrid, and GB-SA each propose different protein-ligand hydrogen bond interactions. In the x-ray structure, the backbone amine of Ile-56 forms a hydrogen bond with the carbonyl oxygen of BUQ. In the hybrid simulations, one of the side-chain carboxylic oxygens of Asp-37 forms a hydrogen bond with the hydroxyl of BUQ. Finally, in the GB-SA simulations, the hydroxyl of Tyr-82 is a hydrogen bond donor to the BUQ hydroxyl. Although one can argue that the GB-SA simulation distorted the complex and changed the key polar protein-ligand interaction, one must also acknowledge that the hybrid solvent method may have also predicted the wrong polar interactions. Somewhat fortuitously, the free energy of binding was still predicted well in both cases.

Endpoint methods

Calculation of absolute binding affinities requires the evaluation of the work definition, Eq. 6, which is without doubt a computationally intensive task for a protein-ligand system regardless of the path between the endpoints chosen. In comparison, two-state methods are difficult because the configuration integrals over all of the degrees of freedom must be estimated in each state. Straightforward evaluation of the bound and unbound state configuration integrals for all of the degrees of freedom of the protein-ligand complex is a truly monumental task given today's computing resources. What is required is a complete sampling of all of the local energy minima of the bound and unbound systems, and a complete characterization of each energy basin (41). For small host-guest systems, this analysis is feasible and can provide good agreement with experimental binding affinities (9). Gilson and co-workers have shown (28) that the quadratic assumption for a single potential breaks down for the first few lowest frequency modes of a particular minimum. This problem can be alleviated by scanning the potential along these low-frequency modes in a bond-angle-torsional coordinate system (28). However, even with this fundamental improvement, one is still left with the task of enumerating every low-energy local minimum in the molecules' potential energy functions for both the bound and unbound states of the protein-ligand complex. Chang et al. conduct an enumeration of conformations of small host-guest complexes through a technique that combines second derivative information and searching along internal coordinates (28). Suppose instead one were to use a naïve MD approach to explore conformational space through relatively short independent multiple MD trajectories? It is likely that one would not achieve complete enumeration of the low-energy local minima for each endpoint. Lacking convergence, the errors in the free-energy estimates of the bound and unbound states might not cancel each other.

An alternative to enumerating configuration integrals, is to calculate the average enthalpy and entropy of each endpoint, as is done in the MM/PB(GB)-SA method (14). The average enthalpy calculation seems to be relatively convergent if one assumes no relaxation upon unbinding and uses the one-state approach (14,16). Calculating relaxation is difficult because it is directly related to the incomplete enumeration problem mentioned above. The independent simulations of the bound and unbound state in a two-state model are likely to randomly walk to different parts of the configurational space and incompletely span the complete space within a finite-time simulation. Relaxation estimation can be done reliably if one resorts to path-based free-energy approaches. For example, Warshel and co-workers evaluated the free energies associated with placing structural restraints to hold the unbound protein receptor to its bound-state configuration (45).

Efficient entropy estimation for molecules the size of proteins is also an unsolved problem. One of the simplest and most stable entropy methods is to estimate the configurational entropy as the average harmonic vibrational entropy of an arbitrary selection of molecular-dynamics trajectory snapshots. This approach is commonly employed in the MM/PB(GB)-SA (14,16) method. This approximation neglects the entropy associated with the multiplicity of energy basins, i.e., configurational entropy. In addition, the MM/PB-SA entropy term is lacking in other respects. First, the implicit solvent model often used to calculate normal mode entropy is a simple r-based dielectric function (14). This model is inadequate as shown above in reproducing the more accurate GB-SA model. Most likely, this model is still commonly used because the second derivatives are easy to analytically formulate and the computational procedure is efficient compared with other implicit solvent functions. Furthermore, another approximation often employed in the entropy calculation is that the system is truncated around the active site of the protein (14). This approximation likely causes distortions because no adequate boundary conditions are imposed on the remaining fragment. Additionally, the lowest vibrational modes of the complex and protein may be removed upon truncation. These modes make the largest contribution to the absolute entropy estimate. Perhaps, though, the entropy differences between the complex and protein benefit from a cancellation of errors.

Another approximation built into the MM/PB(GB)-SA method is the rescoring of explicit solvent trajectories with either Poisson or GB implicit solvent models. In principle, this is the only way one can derive solvation energies for each snapshot without costly explicit solvent charging studies, as has been done elsewhere (36). The subtle problem with rescoring protocols (46) is that the structures generated by one energy function are likely on the wall of the potential energy surface of other energy functions. As was seen in this study, significant errors can result that are not necessarily compensated by energy differences. One solution might be to minimize each snapshot a small amount by using the rescoring energy function. A drawback with this strategy is that the optimized structures will lose their correspondence to a constant-temperature 298 K ensemble. Also, this approach is not feasible for the conventional molecular surface Poisson model, as analytic derivatives are not well defined. Other Poisson solvation models that do have analytical definitions, such as the smooth boundary (47), appear to be less accurate compared to explicit solvent results (36). Generalized Born models are perhaps best suited to this task because they are analytically formulated and can nearly reproduce molecular surface Poisson calculations (40). Furthermore, most current implicit solvent models, including Poisson and GB, are still deficient in treating residues with formal charges (36,48).

Simulation protocol issues

There are a few approximations inherent to our simulation protocol. For instance, we utilized a hybrid explicit/implicit solvent scheme rather than a pure periodic box Ewald simulation. There are drawbacks to both Ewald and hybrid methods. The hybrid method will tend to give different electrostatic solvation energies compared to Ewald, because in the hybrid method there are water dipoles at the explicit/implicit solvent interface even when the solute is neutral (35). Although there is still some controversy as to whether the interface should have a net dipole (49), it is possible that such discrepancies are diminished for a net-neutral system (36). The Ewald method includes artificial real-virtual charge-charge interactions that could cause errors in the computed binding affinity or artifacts in the PMF surface. On the other hand, the hybrid solvent model has a surface boundary that may cause structural distortions of the solute and water molecules especially for small water layer widths.

Another related problem that also concerns conventional Ewald calculations is the distance cutoff used in the vdW term. Certainly, long-range corrections to the vdW term can be used (50). The drawback with these types of corrections is that the long-range vdW spheres are assumed to have a density of bulk water, thus not appropriately accounting for long-range solute-solute interactions. We performed some tests with large boundaries and large vdW cutoffs and found that our layer size (10 Å) and cutoff ranges (11–12 Å) were sufficient in estimating the change in vdW interaction energy of the ligand with the protein and solvent between bound and unbound states. Errors associated with not using a larger layer or vdW cutoff were found to be ∼0.1 kcal/mol (results not shown).

More approximate than a hybrid explicit/implicit solvent treatment, the fully implicit GB model is expected to cause some structural distortions in simulated systems (51) and be less accurate in calculating free energies versus explicit solvent (35). In this study, the GB-SA model was unable to properly simulate a loop region near the binding site (containing residues 82–97), because two structural waters had been deleted. In the hybrid simulations, these two water molecules remained as scaffolds in this region during the entire simulation. The α-carbon root mean square deviation for this loop compared to the x-ray structures was ∼2.5 Å for the GB-SA simulations and 1.7 Å for the hybrid simulations. Mezei et al. noted similar issues with regards to simulating β-strand regions with implicit solvent models where single water molecules are thought to stabilize the strand (52).

In this work, we see that the surface-area term appears to have a strong influence on the PMF results. Nevertheless, it is unclear whether the standard coefficient of 5.42 cal/(mol Å)² is general for applications besides this one. Levy and co-workers (53) have suggested an alternative nonpolar solvation model based on both surface area and Born radii. The surface-area component accounts for the free energy of cavitation, and the Born radii term accounts for the enthalpy of attractive dispersion between the solute and bulk solvent. This model may turn out to be more accurate for binding free-energy calculations.

CONCLUSION

We have used two contrasting techniques to calculate the binding affinities of two ligands for the FK506 protein receptor. In the PMF method, we estimated the absolute binding affinity by calculating the free energy necessary to pull the ligand out of the complex and obtained reasonable correspondence with experiment. Although the actual shapes of the potentials of mean force were different between hybrid and implicit solvent models, the resultant free energies were roughly the same. Using a more approximate endpoint method, MM/GB-SA, which actually had several variations, we found greater statistical uncertainty and inferior absolute correspondence with experiment. The least reliable results were those obtained by the quasiharmonic approximation and the two-point methods, where the bound and unbound states were both simulated. Finally, we introduced generalized Born normal mode analysis as perhaps a more accurate alternative to the simpler r-dielectric-based approach.