Abstract
We present a computational particle method for the simulation of isotropic and anisotropic diffusion on curved biological surfaces that have been reconstructed from image data. The method is capable of handling surfaces of high curvature and complex shape, which are often encountered in biology. The method is validated on simple benchmark problems and is shown to be second-order accurate in space and time and of high parallel efficiency. It is applied to simulations of diffusion on the membrane of endoplasmic reticula (ER) in live cells. Diffusion simulations are conducted on geometries reconstructed from real ER samples and are compared to fluorescence recovery after photobleaching experiments in the same ER samples using the transmembrane protein tsO45-VSV-G, C-terminally tagged with green fluorescent protein. Such comparisons allow derivation of geometry-corrected molecular diffusion constants for membrane components from fluorescence recovery after photobleaching data. The results of the simulations indicate that the diffusion behavior of molecules in the ER membrane differs significantly from the volumetric diffusion of soluble molecules in the lumen of the same ER. The apparent speed of recovery differs by a factor of ∼4, even when the molecular diffusion constants of the two molecules are identical. In addition, the specific shape of the membrane affects the recovery half-time, which is found to vary by a factor of ∼2 in different ER samples.
INTRODUCTION
The lateral mobility of components of biological membranes is vital for numerous cellular processes. These include exo- and endocytosis, signal transduction, cell motility, and growth. The technique of fluorescence recovery after photobleaching (FRAP) (1,2) is frequently used to study lateral diffusion of membrane components.
In the past, FRAP on biological surfaces has mostly used planar diffusion models. For FRAP and the related continuous fluorescence microphotolysis, calculations exist for planar membranes (3), for spherical membranes (4), and singly-connected periodically curved membranes (cosine surfaces) (5). Several real biological membranes are, however, much more complex. They can contain tubular networks, holes, and large curvature variations, and are usually not singly-connected. Moreover, diffusion in biological membranes can appear anisotropic even though it is molecularly isotropic in all observed instances (6). The apparent anisotropy in FRAP experiments is due to different membrane curvatures is different spatial directions (7). Taking the exact surface geometry into account is thus mandatory for isotropic FRAP models. Numerical simulations of diffusion on realistic membrane surfaces are needed, both to investigate the influences of geometry and to derive corrected molecular diffusion constants.
In computational science, a number of techniques have been proposed to solve the diffusion equation on surfaces, requiring rectangular grids (8) or surface triangulations (9). These explicit techniques allow a piecewise linear representation of the surface and encounter severe difficulties in tracking large surface deformations. Monte Carlo techniques (11) for the simulation of diffusion processes suffer from slow convergence rates and they are not competitive with their deterministic counterparts for simulations of diffusion in realistic geometries (12,13).
The simulation of diffusion on surfaces has received considerable attention in the area of computer graphics. We take advantage of recent advances developed for image and video imprinting (14) by representing biological surfaces reconstructed from image data as implicit surfaces using particle level set techniques (15). The key concept amounts to considering the biological surface as a level set of a higher-dimensional function. The resulting governing equations are solved in a Cartesian coordinate system spanning a region consisting of all points close to the surface. We note here that this technique has been recently employed for the simulation of isotropic diffusion on the plasma membrane of hl-60 cells (10).
In the present work, simulations on complex curved surfaces are enabled by the use of particle methods developed for simulations of diffusion in complex geometries (13). This method relies on a particle representation of the implicit surfaces, is second-order accurate in space and time, and is shown to be an efficiently parallelizable method for simulating (an) isotropic diffusion process on realistic biological surfaces as they are reconstructed from micrographs.
The simulations are applied to determine geometry-corrected molecular diffusion constants from FRAP data in the probably most complex biological surface, the membrane of the endoplasmic reticulum (ER). Although this particular application requires only the simulation of isotropic diffusion on the membrane, we present the method in its general form, which also allows for anisotropic and inhomogeneous diffusion. The results of the simulations indicate that the diffusion behavior of molecules in the ER membrane differs significantly from the volumetric diffusion of soluble molecules in the lumen of the same ER. The apparent speed of recovery differs by a factor of ∼4, even if the molecular diffusion constants of the two molecules are identical. In addition, the specific shape of the membrane affects the recovery half-times to vary by a factor of ∼2 for different ER samples.
THEORY
Governing equation for diffusion on curved surfaces
We consider diffusion of a scalar quantity u on a surface 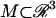 in three dimensions as governed by the equation
in three dimensions as governed by the equation
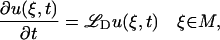 |
(1) |
where the intrinsic diffusion operator on M is defined as
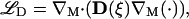 |
(2) |
where ∇M is the intrinsic gradient operator on the surface M, and D(ξ) is the anisotropic diffusion tensor (in the case of isotropic diffusion D = Dℐ). The surface is closed and finite, such that no boundary conditions are required. As shown by Bertalmio et al. (14), the diffusion equation (Eq. 1, above) on the surface M can be transformed into a partial differential equation for generalized anisotropic diffusion in the surrounding ℛ3. This is achieved by embedding the surface in a small annular domain (i.e., the band), consisting of all points close to the original surface. By virtue of this embedding, the differential operators in Eq. 1 are transformed into equivalent operators in ℛ3, which are in turn discretized in the complex domains using particle methods (12,15).
The surface is represented as the zero level of a function ψ : ℛ3→ℛ, thus M = {x:ψ(x) = 0}. The fluxes are constrained in the tangential direction using the projection map
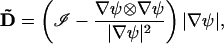 |
(3) |
where ∇ is the gradient operator in space. The initial condition u(ξ, t = 0) is only known on M. It is extended to the band around M by solving to steady-state the partial differential equation
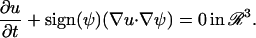 |
(4) |
This enforces that the direction of the diffusive flux ∇u is orthogonal to the normal on M, ∇ψ, and the extension is neutral with respect to above mapping operator. The embedded governing equation for anisotropic diffusion on the surface thus becomes
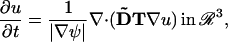 |
(5) |
where ∇ is the regular Nabla operator in ℛ3 and the tensor T(x) is obtained from the diffusion tensor D(ξ) on the surface by extending it with an arbitrary radial component (invariant under the projection map).
Formulation of the numerical scheme
We implement particle methods for the discretization of the governing equations and for the representation of the surfaces as they are reconstructed from image data. Particle methods replace implicit functions and differential operators by equivalent integral representations that are in turn discretized using particle locations as quadrature points. These particle-quadrature points do not require a regular grid and thus avoid the difficulties associated with grid-based techniques in the presence of complex boundaries. In this particle framework, we discretize both the solution u and the level function ψ onto the same set of N computational particles. Each particle pi, i = 1, …, N supports a property vector qi = (ui, ψi) at position xi, such that
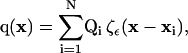 |
(6) |
where Qi is the local volume integral of the quantities being discretized, ζε is a mollification kernel whose properties determine the accuracy of the representation (12), and ε is the size of the discretizing particles.
Discretization of the embedded Eq. 5 is done for an arbitrary, space-dependent tensor 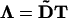 by using Lagrange interpolation polynomials for both u and Λ (element-wise). These continuous functions are then used to analytically compute the right-hand side of Eq. 5. Evaluating the resulting expression at particle locations xi yields the final discretized form of the operator. We are using a second-order polynomial basis, leading to a second-order-accurate discretization of the embedded diffusion operator. The discretized operator has a compact support consisting of 27 particles, corresponding to an interaction radius of σ = 1h, where h is the interparticle distance.
by using Lagrange interpolation polynomials for both u and Λ (element-wise). These continuous functions are then used to analytically compute the right-hand side of Eq. 5. Evaluating the resulting expression at particle locations xi yields the final discretized form of the operator. We are using a second-order polynomial basis, leading to a second-order-accurate discretization of the embedded diffusion operator. The discretized operator has a compact support consisting of 27 particles, corresponding to an interaction radius of σ = 1h, where h is the interparticle distance.
Orthogonal extension of the solution
When the discrete operator is evaluated at locations closer than σ to the boundary of the band, the solution will be inaccurate, since particles outside the band are absent, resulting in an inaccurate representation of the corresponding integral operators (12). Discretization errors at the boundary would eventually propagate into the band and destroy the whole solution. To remedy this situation, the solution u is reinitialized after each time step, enforcing ∇u · ∇ψ = 0 inside the band. Since the band is finite, this procedure requires an extrapolating method such as the fast-marching method (FMM) (16).
The original FMM is, however, only first-order accurate, and requires the particles to be sorted according to their distance to the surface. The latter property prohibits a parallel implementation on distributed computer systems and renders the method inherently sequential. We are using the second-order-accurate interface-locating algorithm of Chopp (17) using tri-cubic interpolation near the interface. Sorting in the marching method is avoided by using the marching Eikonal solver of Kim (18), called the group-marching method (GMM). It advances several particles per iteration and can therefore be employed on parallel computers. Avoiding the global sorting also reduces the computational cost of the method from 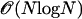 to
to 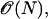 where N is the total number of particles. To avoid the intrinsic instabilities of the GMM for higher-order upwind differences, the backward computation (18) is done r times with r being the order of the upwind differences. Moreover, centered differences are used to compute ∇ψ, since ψ is known in the whole band. The combination of centered differences for ψ and upwind differences for u leads to smoother errors. This second-order extension scheme is used both to construct the initial condition in the band and to reinitialize the solution in a σ-neighborhood of the band boundary at each time step.
where N is the total number of particles. To avoid the intrinsic instabilities of the GMM for higher-order upwind differences, the backward computation (18) is done r times with r being the order of the upwind differences. Moreover, centered differences are used to compute ∇ψ, since ψ is known in the whole band. The combination of centered differences for ψ and upwind differences for u leads to smoother errors. This second-order extension scheme is used both to construct the initial condition in the band and to reinitialize the solution in a σ-neighborhood of the band boundary at each time step.
METHODS
Cell line, DNA construct, and expression of VSVG-GFP
Vero cells were maintained in MEM (plus Earle's plus GlutaMAXI; Gibco BRL, San Diego) supplemented with 10% fetal calf serum and non-essential amino acids (Gibco BRL) at 37°C/5% CO2. The cDNA plasmid VSVG3-SP-GFP (19) encoding GFP-tagged temperature sensitive vesicular stomatitis virus glycoprotein (tsO45-VSV-G) was kindly provided by Dr. Kai Simons. Cells on 18-mm glass coverslips at 80–90% confluence were transfected with 0.5 μg plasmid DNA per coverslip using FuGENE 6 Transfection Reagent (Roche Diagnostics, Indianapolis, IN) and incubated for 12–14 h at the nonpermissive temperature (40°C), at which VSVG-GFP is incompletely folded and retained in the ER (20).
Live cell microscopy and FRAP analyses
For live cell microscopy, transfected cells on 18-mm glass coverslips were transferred to a custom-built metal microscope coverslip chamber in CO2-independent medium, supplemented with 10% FCS (Gibco BRL). FRAP analyses were performed at 40°C on an inverted Zeiss LSM510 confocal microscope (Oberköchen, Germany) equipped with a temperature-controlled stage and a 100× 1.4 NA objective. A defined region of interest (ROI, 4 × 4 μm) was bleached using the 488-nm line of a 30-mW Argon laser at high laser intensity (100% power, 100% transmission) and fluorescence recovery was recorded by scanning at low laser intensity (100% power, 10% transmission). Images were acquired as 12-bit LSM files at 512 × 512 pixels/frame and 0.09-μm/pixel lateral resolution. Image series with little or no apparent motion of ER structures within the ROIs were selected and imported into ImageJ 1.34 (http://rsb.info.nih.gov/ij/) for processing. The average fluorescence intensity of the ROI was determined after background subtraction and normalization according to Phair and Misteli (21).
Z-sectioning and three-dimensional reconstruction of ER surfaces
ER geometries were imaged and reconstructed as described (13). Immediately before FRAP analysis, 0.1-μm optical z-sections of the cell to be bleached were collected with a lateral resolution of 0.09-μm/pixel. Imaging noise was removed in Imaris 4.1.1 (BitPlane, Zürich, Switzerland) using a Gaussian filter of half-width 200 nm. Reconstruction was done in Imaris 4.1.1 (BitPlane) using the same number of voxels as pixels, a voxel size of 0.09 μm, and the optimal threshold settings as described (13). The resulting triangulated surfaces were checked to be closed, connected, and orientable—and, on average, consisted of 500,000 triangles. Note that the triangulation of the surface is not an inherent feature of this method and it represents only the format available from the image reconstruction software. The surfaces do not remain piecewise linear in our simulations, as smooth particles are used to represent the surfaces implicitly (see Theory, above).
Simulation of FRAP experiments
The in silico FRAP experiments were performed using the above-described algorithm, implemented in Fortran 90 and parallelized using the PPM library (I. F. Sbalzarini, J. H. Walther, M. Bergdorf, S. E. Hieber, E. M. Kotsalis, and P. Koumoutsakos. PPM–A highly efficient parallel particle-mesh library for the simulation of continuum systems. J. Comput. Phys., accepted). The triangulated surfaces from the three-dimensional reconstruction were converted to level sets using the second-order GMM reinitialization scheme as described above. All simulations used a computational diffusion constant of Dsim = 1.0 μm2/s, a band half-width of k = 3h (h between 0.042 and 0.047 μm), and employed between 800,000 and 2,000,000 particles concentrated in a 14 × 14 μm neighborhood around the ROI. Time integration was done using a nine-step STS scheme (22) with an elementary Euler time step of 1 × 10−4 s. The concentration was initially set to 1 everywhere outside the bleached ROI, where it was set to 0. The total mass of fluorescent molecules in the ROI was determined at each simulation time step by linearly interpolating the strengths of adjacent particles along interparticle lines that cross the membrane. Before analysis, all FRAP curves were normalized by their steady-state value to make them comparable (13).
Fitting of simulated FRAP curves to experimental data and derivation of molecular diffusion constants
The FRAP curves obtained from simulations were fitted to experimental datapoints using MATLAB 7.0.4 (The MathWorks, Natick, MA) and a Nelder-Mead simplex scheme to minimize the L2 error of the fit. Fitting was only done in time and the FRAP values were left unchanged (13). All L2 residuals were <1%. The effective molecular diffusion constant Deff was then computed from the computational diffusion constant Dsim, the time-stretching factor ts determined in the fit, and the ratio ξ = (voxel size)/(lateral resolution [μm/pixel]) as
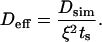 |
(7) |
RESULTS
Accuracy and convergence of the numerical method
As a test case with known analytic solution, we consider isotropic diffusion on the surface of the sphere S2(R) with center (0, 0, 0) and radius R = 1,
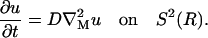 |
(8) |
The analytic solution in spherical coordinates (defined according to Bronstein et al. (23)) is obtained by expansion to spherical harmonics 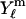 as
as
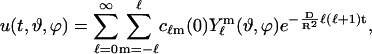 |
(9) |
with
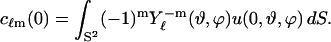 |
(10) |
To study convergence without the effects of series truncation, we use the special initial condition
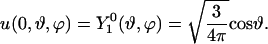 |
(11) |
For this initial condition, the analytic solution simplifies, due to the orthogonality of the spherical harmonics, to
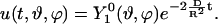 |
(12) |
Embedding is done using as level-function ψ the signed distance to the surface, 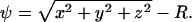 Particles are only present in a band of half-width k around the interface, thus |ψ| < k. In this band, ∇ψ is computed using representations equivalent to second-order upwind differences, thus avoiding boundary errors, and the tensors
Particles are only present in a band of half-width k around the interface, thus |ψ| < k. In this band, ∇ψ is computed using representations equivalent to second-order upwind differences, thus avoiding boundary errors, and the tensors 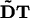 at all particle locations are determined according to Eq. 3. The right-hand side of Eq. 8 is computed in an inner band of half-width |ψ| < κ < k. The region between κ and k serves as a ghost-layer and is reinitialized after each time step using the orthogonal extension GMM (see Theory) to enforce ∇ψ × ∇u = 0 (no radial flux).
at all particle locations are determined according to Eq. 3. The right-hand side of Eq. 8 is computed in an inner band of half-width |ψ| < κ < k. The region between κ and k serves as a ghost-layer and is reinitialized after each time step using the orthogonal extension GMM (see Theory) to enforce ∇ψ × ∇u = 0 (no radial flux).
To assess the accuracy of the interface-locating interpolation, we use it for all particles in the inner band to determine the approximate distance 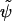 to the surface of the sphere. From the pointwise errors
to the surface of the sphere. From the pointwise errors 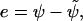 the following error norms are computed for different interparticle spacings h:
the following error norms are computed for different interparticle spacings h:
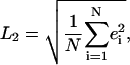 |
(13) |
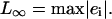 |
(14) |
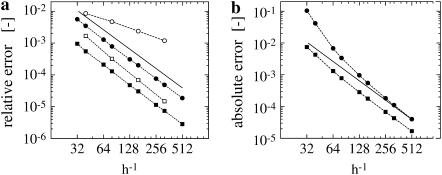
For relative errors, they are normalized with 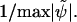 Fig. 1 a shows the result for the tri-cubic procedure of Chopp (17).
Fig. 1 a shows the result for the tri-cubic procedure of Chopp (17).
FIGURE 1.
Convergence of the level set algorithms. (a) Convergence of the second-order interface locating algorithm by Chopp (17). A signed distance function, defined in a band of half-width 3h around a sphere, is reinitialized. The relative L2 (squares) and L∞ (circles) errors of the present implementation (solid symbols) are compared to the numbers published by Chopp (17) (open symbols) and the theoretical second-order scaling (solid line). The errors are computed from all points immediately adjacent to the interface. (b) Convergence of the second-order orthogonal extension. The spherical harmonic 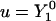 (Eq. 11) is initialized in a band of half-width 3h and orthogonally extended outwards to a 9h band. This is done over the exact signed distance function ψ, initialized in a 12h band (centered differences are used for ∇ψ in the extension). To compute the error, ∇u is computed using fourth-order centered differences in the band 3h < |ψ| < 6h, and ∇ψ is known analytically. The error
(Eq. 11) is initialized in a band of half-width 3h and orthogonally extended outwards to a 9h band. This is done over the exact signed distance function ψ, initialized in a 12h band (centered differences are used for ∇ψ in the extension). To compute the error, ∇u is computed using fourth-order centered differences in the band 3h < |ψ| < 6h, and ∇ψ is known analytically. The error 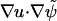 is computed and the absolute L2 (squares) and L∞ (circles) norms are reported.
is computed and the absolute L2 (squares) and L∞ (circles) norms are reported.
To test the orthogonal extension with the parallel GMM method (see Theory), the initial condition given in Eq. 11 is extrapolated from an inner band of half-width 3h to a band of half-width 9h. The error is computed for 3h < |ψ| < 9h using the exact signed distance function and a fourth-order approximation to ∇u. Fig. 1 b shows the resulting convergence curve of second-order accuracy.
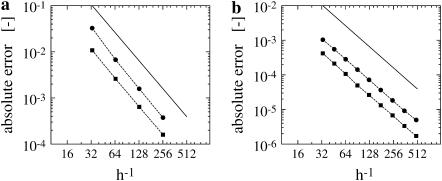
The accuracy of the discretization of the anisotropic diffusion operator is assessed by comparing the right-hand side of Eq. 8 to the one computed analytically (Fig. 2 a). The compact discrete operator is evaluated in an inner band of half-width κ = 1h with a ghost layer of 1h, thus only a k = 2h neighborhood around the surface is populated with particles. Compactness of the operator is an important aspect of this method as it allows us to resolve thin surface protrusions.
FIGURE 2.
Convergence of the discretization and the overall method. (a) Convergence of the discretization of the anisotropic diffusion operator. The approximate operator is evaluated on the initial condition and compared to the exact (analytic) right-hand side in a band of half-width 1h. The operator is evaluated in a narrow band of half-width κ = 1h with an additional ghost layer of 1 grid point, thus k = 2h. (b) Convergence for diffusion on a sphere of radius 1 and intrinsic diffusion constant D = 1. The diffusion operator is evaluated on a support of 3 × 3 × 3 particles in a narrow-band of half-width κ = 3h and extended to a larger band of k = 4.5h after each time step, using the second-order GMM extension method. A second-order TVD Runge-Kutta scheme is used with a time step of δt = 10−5 until final time 10−4. The straight line indicates convergence order 2.
Fig. 2 b shows the overall convergence of the complete simulation algorithm after 10 time steps. The solid line indicates convergence of order 2. To reconstruct the solution on the interface, we use linear interpolation along all interparticle lines that cross the interface. It can be seen that the method is second-order accurate for all particle spacings tested. The single-processor and the parallel version of the code yield exactly the same results.
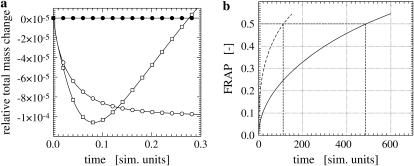
Conservation of mass
If no transport to/from the membrane occurs, the total mass of the surfactant, integrated over the implicit surface, should remain constant. Spurious radial fluxes of the discretized diffusion operator as well as errors in the GMM extension of the solution, however, lead to mass drift. Using a global rescaling method (24), conservation of mass is enforced. The surface integrals are evaluated using linear interpolation along interparticle lines across the interface and the rectangular quadrature rule. Fig. 3 a shows the evolution of the total mass over time for the sphere test case with initial condition
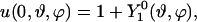 |
(15) |
since the rescaling method is only applicable for non-negative concentration fields. If no orthogonal extension is applied between time steps, the mass grows linearly. Even after the solution has reached its steady state and gradients are no longer present, the mass continues to grow, which eventually leads to instabilities. Using extension, but no rescaling, the mass approaches an asymptotic level as the solution reaches its steady state. Using both extension and rescaling, the mass remains constant to machine precision for all times.
FIGURE 3.
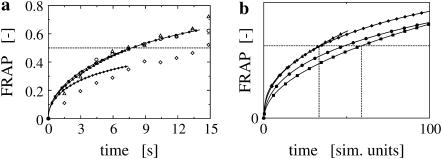
(a) Conservation of mass. Evolution of the total surfactant mass on a sphere of radius 1 and intrinsic diffusion constant D = 1. The diffusion operator is evaluated on a support of 3 × 3 × 3 particles in a narrow band of half-width κ = 3h. For the cases marked by circles, the solution is extended to a larger band of k = 4.5h after each time step, using the second-order GMM extension method. No extension was applied to the squares case. A Euler scheme is used with a time step of δt = 10−4 until final time 0.3. The open symbols mark the cases of no rescaling, and the solid symbols indicate the rescaled solution at each time step (see main text). (b) Comparison of FRAP in the ER lumen and on the membrane. Comparison of FRAP curves in the lumen (dashed) and on the membrane (solid) of the same ER sample (compare to Fig. 4). Both curves correspond to the same diffusion constant Dsim = 1.0 and are normalized by their prebleach value. The recovery half-time (in simulation time units) is 111 for the luminal protein and 485 for the membrane protein, indicating that recovery in the lumen is significantly faster than recovery on the membrane. All curves are normalized by their asymptotic value to allow comparison.
Simulation of diffusion of membrane proteins in the endoplasmic reticulum
The simulation method presented so far is used to simulate diffusion in the complex-shaped membrane of the ER corresponding to experiments described in Methods. The initial condition consists of a uniform concentration on the ER membrane with the exception of the bleached region, where the concentration is set to zero. More accurate initial conditions (25,26) can easily be used if they are experimentally available. The obtained simulated fluorescence recovery curve is then used to determine geometry-corrected molecular diffusion constants of membrane molecules (see Methods, this article, and (13)). Fig. 3 b shows the simulated FRAP curves in the lumen and on the membrane of the same ER sample for the same computational diffusion constant. The recovery half-times are 111 for the luminal protein and 485 for the membrane-bound protein.
The narrow-band level set method imposes a scale constraint on the geometry that can be resolved: The bands from two opposite sides of the surface must never overlap, i.e., the smallest feature of the surface must be at least 2k in diameter. In the present simulations, this amounts to 2k = 6h = 300 nm, which is more than 10 times larger than the curvature radius limit for biological membranes. To avoid underresolved regions, the level function ψ is thus low-pass filtered before the simulations. This makes sense as the wavelength of the light used to record the geometry is larger (488 nm; see Methods).
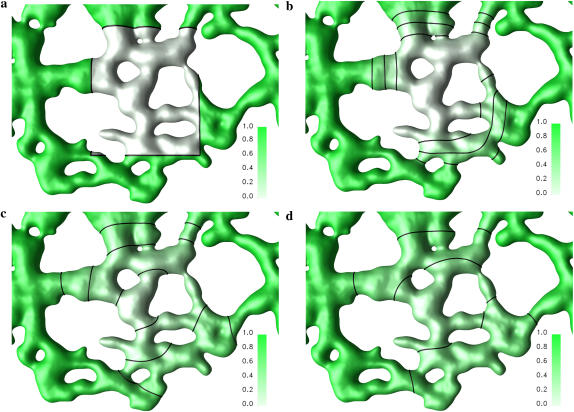
Since only the geometry in the vicinity of the bleached ROI influences the fluorescence recovery, an ER cut-out around the bleached region is considered in the simulations. The finite reservoir of the rest of the ER is modeled using Dirichlet boundary conditions. Fig. 4 shows the visualized concentration field from a sample simulation at different times after bleaching.
FIGURE 4.
Simulation of diffusion in the ER membrane. Solution on the membrane of an in vivo ER geometry at times t = 0 (a), t = 36 (b), t = 216 (c), and t = 441 (d). The computational diffusion constant is Dsim = 1.0 and the diffusion operator is supported on 3 × 3 × 3 particles in a narrow band of half-width κ = 2h and extended to a larger band of k = 3h every time step, using the second-order GMM extension method. An Euler scheme with a time step of 0.025 is used for the first 20 time steps, then a nine-step STS with a time step of 0.45 is used until the final time 600.0 (simulation time units). The membrane and the concentration field are discretized using 1.7 million particles. The concentration on the membrane is recovered from the adjacent particles using linear interpolation along interparticle lines and visualized as a green surface color density. The three lines indicate the 25%, 50%, and 75% recovery iso-lines.
The influence of membrane geometry on FRAP experiments
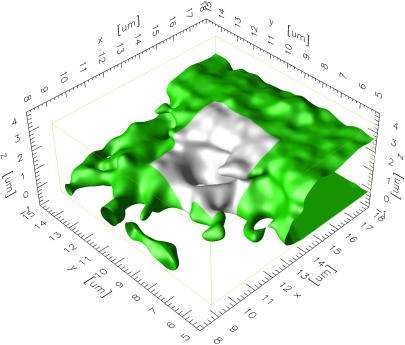
The simulations are validated by comparing them to FRAP experiments in the same ER shapes. The molecular diffusion constant of GFP-labeled tsO45-VSV-G is determined in Vero cells as outlined in Methods. From four samples we find Deff = 0.16 ± 0.07 μm2/s at 40°C. This is a factor of 2.7 lower than the previously published value of 0.45 ± 0.03 μm2/s (27), which was obtained in COS-7 cells without shape correction. Fig. 5 a shows three fits of simulated FRAP curves to experimental data. Clearly, the simulation fails to explain the data in one of the cases. Looking at the membrane geometry of this sample reveals an overhanging membrane section (Fig. 6). At early times, lateral recovery could thus be occluded in the experiment, whereas the simulation always integrates the concentration over the whole membrane surface. In addition, the biochemistry could be different in this more lamellar part of the ER membrane.
FIGURE 5.
(a) Comparison of simulations and experiments. The computer simulations are done using the method outlined in Theory. The experiment is a standard FRAP experiment, preceded by the recording of a stack of serial sections used for the reconstruction of the geometry. The simulated FRAP curves (lines with solid symbols) are stretched in time to fit the experimental data (corresponding open symbols). As time and diffusion constants are inversely proportional, this allows us to estimate the molecular diffusion constant while fully taking the specific geometry into account. For the three examples shown, the molecular diffusion constants are determined to be 0.13 μm2/s (circles), 0.24 μm2/s (triangles), and 0.12 μm2/s (diamonds). All curves are normalized by their asymptotic value to allow comparison. In the case of the diamonds, the simulation clearly fails to fit the data well. This can be explained by looking at the specific geometry of this sample. As shown in Fig. 6, there is an overhanging piece of membrane in the region of interest. This causes occlusion in the experiment, but not in the simulation, where the concentration is integrated over the entire membrane surface. At early times, the experimental data are thus expected to show slower recovery than the simulation. (b) The influence of ER membrane geometry. All simulations are done using the same computational diffusion constant of Dsim = 1.0 and the same simulation parameter settings. All curves are normalized by their asymptotic value to allow comparison. The variation observed in the FRAP curves is therefore only caused by the different geometries of the ER samples. The recovery half-times scatter in the interval [32…60] (simulation time units). This factor of 1.8 is less than the factor of 2.5 observed for the luminal case in the same four ER samples (13).
FIGURE 6.
Visualization of an ER piece with overhanging regions. The visualization is done in the computer from the reconstructed ER membrane surface. A 9 × 9 μm neighborhood around the bleached region of interest (indicated in light gray) is shown. The overhanging membrane piece causes a discrepancy between the simulation and the experiment (compare to Fig. 5).
To estimate the geometry-induced uncertainty in FRAP experiments, we perform simulations in the membrane of ER samples reconstructed from different cells. The same computational diffusion constant of Dsim = 1.0 is used in all instances, and all simulation parameters are kept constant. The only source of variation are the geometrical differences in the membranes. As shown in Fig. 5 b, the recovery half-times vary by a factor of 1.8, which can be explained by membrane curvature effects (5).
DISCUSSION
We have presented a deterministic particle method to simulate anisotropic, inhomogeneous diffusion on complex surfaces. We have demonstrated the method to be second-order accurate in space and time, and have successfully applied it to simulations of diffusion of an integral membrane protein in the ER membrane of live cells after confocal microscopy and three-dimensional reconstruction (13). The method is efficiently parallelized with linear computational cost and is well-suited for biological applications such as the analysis of FRAP data.
The present implicit formulation of the complex ER membrane surface as a level set, and its discretization using particles, has many advantages over traditional grid-based methods. It can handle surfaces of arbitrary complexity at constant computational cost. Furthermore, it allows us to use the embedding approach (14) with the usual discretization schemes and particle interaction algorithms, because the metric of the surface is completely contained in the mapped operator.
Our approach is limited by the resolution of light microscopy and the computational resolution limit imposed by the banded level set formulation. The latter limitation can be addressed using multiresolution particle methods developed for convection-diffusion equations (28). Future work involves extensions of these methods to surfaces of complex shape. The microscopy resolution limit implies that sufficiently detailed ER geometries can only be obtained in peripheral regions of the cell, where the ER is relatively sparse. The bleached ROI of any FRAP experiment to be evaluated must be located in well-resolved areas of the organelle. A further limitation of the method is that it cannot be applied if the organelle moves or deforms inside the ROI during the time of a FRAP experiment or between recording the z-stack and performing the FRAP experiment. Ongoing work is concerned with extending the simulation method to cases of moving surfaces.
The presented simulations of FRAP in different ER membranes have shown that diffusion of membrane molecules is significantly different from diffusion of soluble components in the ER lumen. We find that the recovery half-times differ by a factor of ∼4, if the same ER shape and the same molecular diffusion constant are used for both cases. Moreover, the geometry-induced variation in recovery half-times is a factor of 1.8. As expected, this is less than the factor of 2.5 found for soluble molecules in the ER lumen (13). Using the present method, a geometry-corrected molecular diffusion constant of 0.16 ± 0.07 μm2/s is found for tsO45-VSV-G at the nonpermissive temperature of 40°C.
What do these findings mean? First, we demonstrated that FRAP models derived for planar membranes will yield incorrect molecular diffusion constants if applied to curved membranes. The factor of ∼2 can be explained by purely geometric effects. Moreover, diffusion will appear anisotropic if the membrane has different curvatures in different directions (7). Isotropic models are thus only valid when one takes the real membrane geometry in the ROI into account. Membrane FRAP models should not be applied to luminal proteins and vice versa, as the apparent diffusion constants differ by a factor of ∼4.
We envision that the present computational technique will find applicability in several other areas of cell biology for studies of diffusion on curved surfaces. In this context, the software developed in this work is freely available from the authors.
Acknowledgments
The authors gratefully acknowledge many enlightening discussions with Michael Bergdorf, Institute of Computational Science, ETH Zürich.
References
- 1.Axelrod, D., D. E. Koppel, J. Schlessinger, E. Elson, and W. W. Webb. 1976. Mobility measurement by analysis of fluorescence photobleaching recovery kinetics. Biophys. J. 16:1055–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lippincott-Schwartz, J., E. Snapp, and A. Kenworthy. 2001. Studying protein dynamics in living cells. Nat. Rev. Mol. Cell Biol. 2:444–456. [DOI] [PubMed] [Google Scholar]
- 3.Peters, R., A. Brünger, and K. Schulten. 1981. Continuous fluorescence microphotolysis: a sensitive method for study of diffusion processes in single cells. Proc. Natl. Acad. Sci. USA. 78:962–966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Brünger, A., R. Peters, and K. Schulten. 1985. Continuous fluorescence microphotolysis to observe lateral diffusion in membranes. Theoretical methods and applications. J. Chem. Phys. 82:2147–2160. [Google Scholar]
- 5.Aizenbud, B. M., and N. D. Gershon. 1982. Diffusion of molecules on biological membranes of nonplanar form—a theoretical study. Biophys. J. 38:287–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Jacobson, K., A. Ishihara, and R. Inman. 1987. Lateral diffusion of proteins in membranes. Annu. Rev. Physiol. 49:163–175. [DOI] [PubMed] [Google Scholar]
- 7.Aizenbud, B. M., and N. D. Gershon. 1985. Diffusion of molecules on biological membranes of nonplanar form. II. Diffusion anisotropy. Biophys. J. 48:543–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Abarbanel, S., and A. Ditkowski. 1997. Asymptotically stable fourth-order accurate schemes for the diffusion equation on complex shapes. J. Comput. Phys. 133:279–288. [Google Scholar]
- 9.Abdulle, A., and C. Schwab. 2005. Heterogeneous multiscale FEM for diffusion problems on rough surfaces. Multiscale Model. Simul. 3:195–220. [Google Scholar]
- 10.Schwartz, P., D. Adalsteinsson, P. Colella, A. P. Arkin, and M. Onsum. 2005. Numerical computation of diffusion on a surface. Proc. Natl. Acad. Sci. USA. 102:11151–11156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Christensen, M. 2004. How to simulate anisotropic diffusion processes on curved surfaces. J. Comput. Phys. 201:421–438. [Google Scholar]
- 12.Koumoutsakos, P. 2005. Multiscale flow simulations using particles. Annu. Rev. Fluid Mech. 37:457–487. [Google Scholar]
- 13.Sbalzarini, I. F., A. Mezzacasa, A. Helenius, and P. Koumoutsakos. 2005. Effects of organelle shape on fluorescence recovery after photobleaching. Biophys. J. 89:1482–1492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bertalmio, M., L. T. Cheng, S. Osher, and G. Sapiro. 2001. Variational problems and partial differential equations on implicit surfaces. J. Comput. Phys. 174:759–780. [Google Scholar]
- 15.Hieber, S. E., and P. Koumoutsakos. 2005. A Lagrangian particle level set method. J. Comput. Phys. 210:342–367. [Google Scholar]
- 16.Sethian, J. A. 1996. A fast marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. USA. 93:1591–1595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chopp, D. L. 2001. Some improvements on the fast marching method. SIAM J. Sci. Comput. 23:230–244. [Google Scholar]
-
18.Kim, S. 2001. An
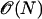 level set method for Eikonal equations. SIAM J. Sci. Comput. 22:2178–2193. [Google Scholar]
level set method for Eikonal equations. SIAM J. Sci. Comput. 22:2178–2193. [Google Scholar] - 19.Keller, P., D. Toomre, E. Diaz, J. White, and K. Simons. 2001. Multicolour imaging of post-Golgi sorting and trafficking in live cells. Nat. Cell Biol. 3:140–149. [DOI] [PubMed] [Google Scholar]
- 20.Gallione, C. J., and J. K. Rose. 1985. A single amino acid substitution in a hydrophobic domain causes temperature-sensitive cell-surface transport of a mutant viral glycoprotein. J. Virol. 54:374–382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Phair, R. D., and T. Misteli. 2000. High mobility of proteins in the mammalian cell nucleus. Nature. 404:604–609. [DOI] [PubMed] [Google Scholar]
- 22.Alexiades, V., G. Amiez, and P.-A. Gremaud. 1996. Super-time-stepping acceleration of explicit schemes for parabolic problems. Commun. Num. Meth. Eng. 12:31–42. [Google Scholar]
- 23.Bronstein, I. N., and K. A. Semendyayev. 1991. Handbook of Mathematics, 20th Ed. Van Nostrand Reinhold, New York.
- 24.Xu, J.-J., Z. Li, J. Lowengrub, and H. Zhao. 2005. A level set method for interfacial flows with surfactant. J. Comp. Phys. To appear.
- 25.Braga, J., J. M. P. Desterro, and M. Carmo-Fonseca. 2004. Intracellular macromolecular mobility measured by fluorescence recovery after photobleaching with confocal laser scanning microscopes. Mol. Biol. Cell. 15:4749–4760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Weiss, M. 2004. Challenges and artifacts in quantitative photobleaching experiments. Traffic. 5:662–671. [DOI] [PubMed] [Google Scholar]
- 27.Nehls, S., E. L. Snapp, N. B. Cole, K. J. M. Zaal, A. K. Kenworthy, T. H. Roberts, J. Ellenberg, J. F. Presley, E. Siggia, and J. Lippincott-Schwartz. 2000. Dynamics and retention of misfolded proteins in native ER membranes. Nat. Cell Biol. 2:288–295. [DOI] [PubMed] [Google Scholar]
- 28.Bergdorf, M., G.-H. Cottet, and P. Koumoutsakos. 2005. Multilevel adaptive particle methods for convection-diffusion equations. Multiscale Model. Simul. 4:328–357. [Google Scholar]