Single Channel Analysis Reveals Different Modes of Kv1.5 Gating Behavior Regulated by Changes of External pH

Abstract

In the voltage-gated potassium channel Kv1.5, extracellular acidification decreases the peak macroscopic conductance and accelerates slow inactivation. To better understand the mechanistic basis for these two effects, we recorded unitary currents of Kv1.5 expressed in a mouse cell line (ltk⁻) using the voltage clamp technique both in cell-attached and excised outside-out patches. Single channel current amplitude at 100 mV (1.7 ± 0.2 pA at pH 7.4, 1.7 ± 0.2 pA at pH 6.4) and the single channel conductance between 0 and 100 mV (11.8 ± 0.6 pS at pH 7.4 and 11.3 ± 0.8 pS at pH 6.4) did not change significantly with pH. External acidification significantly decreased the number of active sweeps, and this reduction in channel availability accounted for most of the reduction of the peak macroscopic current. The results of runs analyses suggested the null sweeps occur in clusters, and the rate constants for the transition between clusters of null and active sweeps at pH 6.4 were slow (0.12 and 0.18 s⁻¹, to and from the active clusters, respectively). We propose that low pH facilitates a shift from an available mode (mode A) into an unavailable mode of gating (mode U). In addition to promoting mode U gating, external acidification accelerates depolarization-induced inactivation, which is manifest at the single channel level as a reduction of the mean burst length and an apparent increase of the interburst interval. These effects of external acidification, which are thought to reflect the protonation of a histidine residue in the turret (H-463), point to an important role for the turret in the regulation of channel availability and inactivation.

INTRODUCTION

Kv1.5 is a Shaker-related, voltage-gated potassium channel encoded by the gene KCNA5. In the human heart it mediates the ultrarapid delayed rectifier current (I_Kur) involved in repolarizing the atrial action potential (1,2). In a previous study, we reported that low external pH inhibits macroscopic Kv1.5 currents and causes a depolarizing shift of the conductance-voltage (g-V) relationship without substantially affecting activation kinetics (3). Based on structure-function analyses, a histidine residue (H-463) in the pore turret (S5-P linker) has been suggested to form part of the site to which external protons bind to produce these effects. Current inhibition by external protons can be attenuated either by raising the external [K⁺] or by mutating an arginine residue near the outer pore mouth to valine (Kv1.5 R-487V) (3), which is equivalent to the T-449V mutation in Shaker. These latter manipulations also influence an inactivation process involving the selectivity filter, which is best characterized in Shaker channels where it is known as slow, P/C-type inactivation (4) but is often referred to below as outer pore inactivation. Together with the observation that the inactivation rate of residual currents increases in a pH-dependent manner with a K_D similar to that for the current inhibition (5,6), these findings suggested a possible link between the proton-induced inhibition of Kv1.5 and outer pore inactivation. Pore occlusion as the basis for the effect has been considered but deemed unlikely given that Na⁺ currents, reflecting ion flux through the inactivated pore, are little affected by decreasing pH (7).

To get a clearer picture of the mechanistic basis for the current inhibition by external protons in Kv1.5, currents through single Kv1.5 channels were studied. Our results show that single channel current (i) is not affected by changing the extracellular pH and indicate that a change of P_o is the basis for the effect. Consistent with the acceleration of inactivation of residual macroscopic currents at low pH, there was, in sweeps showing channel activity, a decrease of the mean burst duration and an increase of the mean interburst duration, suggesting a stabilization of inactivation. Within bursts, channel gating between the open state and closed states outside of the activation pathway was only slightly affected, if at all. The main cause of the pH-induced current inhibition of Kv1.5 was an increased probability of a gating mode where the channel was unavailable for activation.

MATERIALS AND METHODS

Cell preparation

A stable mouse cell line, ltk⁻, expressing hKv1.5 channels at a low density was generated by transfection with the cDNA of the human potassium channel Kv1.5 (hKv1.5) subcloned in the gentamicin-resistant gene-containing pcDNA3 vector using methods described previously (8). Cells were maintained in minimum essential medium supplemented with 10% fetal bovine serum, 1% penicillin-streptomycin, and 1% gentamicin and incubated at 37°C in an atmosphere of 5% CO₂ in air. Cells were dissociated and plated onto coverslips for experimental use within 1–3 days. All tissue culture supplies were obtained from Invitrogen (Burlington, Ontario, Canada).

Electrophysiology

Single channel current (i) and whole-cell current (I) were recorded in either the cell-attached or, in experiments where responses at two different pHs were compared, the outside-out patch configuration. For cell-attached recordings, the bath solution was assumed to depolarize the cell to 0 mV; it contained (in millimolar) 140 KCl, 3.5 NaCl, 2 CaCl₂, 1 MgCl₂, 5 glucose, 10 HEPES and was adjusted to pH 7.4 with NaOH; the patch pipette (external) solution contained 140 NaCl, 3.5 KCl, 2 CaCl₂, 1 MgCl₂, 5 glucose and was adjusted either to pH 7.4 with 10 HEPES/NaOH or to pH 6.4 with 10 MES/NaOH. For recordings from an outside-out patch or in the whole-cell configuration, the bath (external) solution contained 140 NaCl, 3.5 KCl, 2 CaCl₂, 1 MgCl₂, 5 glucose and was adjusted to pH 7.4 (10 HEPES/NaOH), 6.4 (10 MES/NaOH), or 5.9 (10 MES/NaOH); the patch pipette (internal) solution contained 130 KCl, 10 EGTA, 10 HEPES, 4.75 CaCl₂, 1.38 MgCl₂ and was adjusted to pH 7.4 with KOH. The free [Ca²⁺] and [Mg²⁺] were calculated to be 50 nM and 1 mM, respectively, using the MaxChelator program (Stanford University, Stanford, CA). In subsequent text the reference to pH means the extracellular pH. All chemicals were purchased from Sigma-Aldrich (Mississauga, ON, Canada).

Voltage commands and current measurements were made with an EPC-7 patch clamp amplifier connected to an ITC-18 digital interface (Instrutech, Port Washington, NY) and controlled by Pulse software (HEKA Electronik, Lambrecht, Germany). Patch electrodes pulled from thin-walled borosilicate glass (World Precision Instruments, Sarasota, FL) had a resistance measured with recording solutions of 8–25 MΩ. Current signals were low-pass filtered at 3 kHz (−3dB, 8-pole Bessel, NPI Electronics, Tamm, Germany) and digitized at 10 kHz with a 16-bit A/D converter. Cells were held at −80 mV at rest. A junction potential of −4 mV was compensated in the voltage measurements in the outside-out patch configuration; no junction potential correction was made for data acquired in the cell-attached recording mode.

Data analysis

Outside-out recordings were made at room temperature (20–25°C) and involved exclusively one-channel patches identified as such by the absence of overlapping open events in pH 7.4 solution at a potential, usually 100 mV, where the open probability was high. In cell-attached recordings it was not possible to change the pH of the solution in the recording electrode, and although patches containing one channel could be identified unequivocally at pH 7.4 this was not the case at pH 6.4 where the open probability was lower. Single channel records were analyzed with TAC and TACFit software (Bruxton, Seattle, WA) after digital filtering at 1 kHz. Capacitive currents were removed by subtracting the average of sweeps obtained at the same voltage that showed no channel activity (i.e., blank or “null” sweeps). Given a combined analog and digital filter frequency of 950 Hz, the dead time of the system was calculated to be 0.3 ms using the formula 0.253/f, where f represents the overall combined analog and digital filter cutoff frequency in Hz (9). Half-amplitude threshold analysis, with a rise time of 0.3 ms, was used to detect events and generate idealized records from which dwell time histograms and ensemble time courses were constructed. Events with durations shorter than the dead time were censored. Although there was evidence for a conductance substate in some traces (e.g., Fig. 1), this phenomenon was not analyzed in detail due to its relatively infrequent occurrence. For the analysis of gating kinetics a burst was defined as a group of brief open and closed events followed by a closed interval of 20 ms or more. There was no correction for missed events in the analysis of dwell time histograms that were fitted to exponential functions. The choice of the number of components used for fitting was based on a maximum likelihood technique, in which the least number of components with a significant improvement was used (10). A value of twice the difference in log likelihood (i.e., 2|LL₁ – LL₂|) being greater than the χ² value with a given degrees of freedom (ν) is considered significant. The number of degrees of freedom is equal to the difference in free parameters between the models (10). Averaged results are expressed as the mean ± SE unless otherwise stated. Results for fitting histograms and the Hill equation are given as the mean ± SD. Statistical tests (Student's t-test, ANOVA) were performed with Jmp In Software (SAS Institute, Cary, NC). A probability of <0.05 was considered significant.

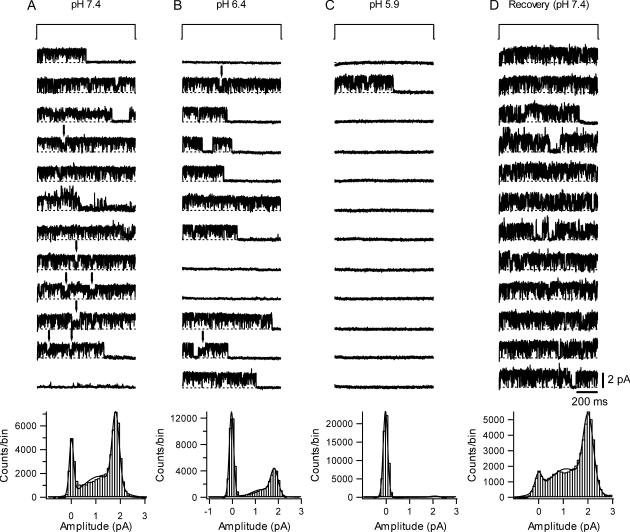
FIGURE 1.

The single channel current amplitude of Kv1.5 does not change between pH 7.4, 6.4, and 5.9. (A) Representative unitary current through a one-channel, outside-out patch at pH 7.4. Current traces were evoked by 1-s depolarizing pulses at 100 mV from a holding potential of −80 mV every 15 s. Kv1.5 unitary currents show flickering behavior. The failure of the channel to open (e.g., last trace in pH 7.4 column) was an infrequent observation at this pH. The corresponding cumulative all-points histogram based on traces in panel A is shown at the bottom of the panel. Fitting the histogram to a three-component Gaussian function gave a value of 1.7 pA for the major conducting level. (B) Unitary current from the same outside-out patch using the same voltage protocol after switching to external solution at pH 6.4. The open channel current does not change but there are more null sweeps. The all-points amplitude histogram shown at the bottom gave a single channel current of 1.7 pA for the major conducting level. The higher proportion of the nonconducting points reflects the higher proportion of null sweeps and the more frequent termination of active sweeps by a long-lived nonconducting state. (C) Unitary current from a different outside-out patch using the same voltage protocol as in panel A but with an external solution at pH 5.9. Channel activity is observed in only one of the 12 sweeps. This dramatic decrease of channel activity was not due to the loss of the channel from the patch since recovery of activity was obtained after returning to pH 7.4 solution (D). The all-points histograms at the bottom of panels C and D give a value of 2.0 pA for the mean open channel current.

A “runs analysis” was performed (11) to check the randomness of the occurrence of sweeps in which the channel was available or unavailable (12). Data were obtained from one-channel cell-attached patches stepped to 100 mV for 150 ms with a cycle length of 3, 5, 10, or 15 s. A run (R) is defined as a sequence of sweeps showing similar gating behavior which, for the purposes of this work, means either a sequence of null sweeps in which the channel was in the unavailable mode (U) or a sequence of active (A) sweeps in which at least one open event was detected. When the number of trials is >40, a normalized statistical value (Z) can be calculated by the equation,

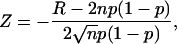(1)

where R is the number of runs, n is the number of trials or sweeps, and p is the probability of the event.

The expected number of runs is 2np(1 − p). A smaller than expected number of runs implies clustering and generates values of Z > 0. Conversely, a value of Z < 0 indicates a tendency to alternate between null and active sweeps (13). The value of Z was compared to the normal distribution to determine the statistical significance; a value >1.64 indicated behavior that was nonrandom and clustered (p < 0.05, one-tail test (14,15)).

Contingency tables (2 × 2) were constructed to determine whether, at pH 6.4, there was a correlation between a sweep ending in an inactivated or noninactivated state and the following sweep being active or null. χ² analyses were performed using the equation

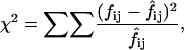(2)

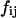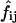where and represent, respectively, the experimental and expected frequency for row i and column j (16). A χ² value >3.841 is considered significant (p < 0.05, ν = 1).

RESULTS

Representative, consecutive unitary current traces recorded at pH 7.4 from an outside-out patch during 1-s depolarizing pulses at 100 mV with 3.5 mM 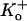are shown in Fig. 1 A. As noted above, Kv1.5 exhibits conductance substate behavior (marked by arrows) but these were not systematically analyzed. As with ShakerIR (inactivation-removed) channels (9,17), at this voltage and pH the latency to first opening was consistently very brief (<1 ms) and the channel rapidly flickered between short-lived open and closed states. Save for a few traces in which the channel entered a long-lived closed state presumed to be due to outer pore inactivation, the open probability was high for the duration of the depolarization. At pH 7.4, null sweeps occurred rarely, e.g., Fig. 4 A. Fitting the all-points amplitude histogram (Fig. 1 A, bottom panel) with a three-component Gaussian function gave a single channel current of 1.7 ± 0.2 pA for the main conductance state, which is comparable to previously published results for hKv1.5 (1). The intermediate component is due to a conductance substate and incomplete opening/closing events.

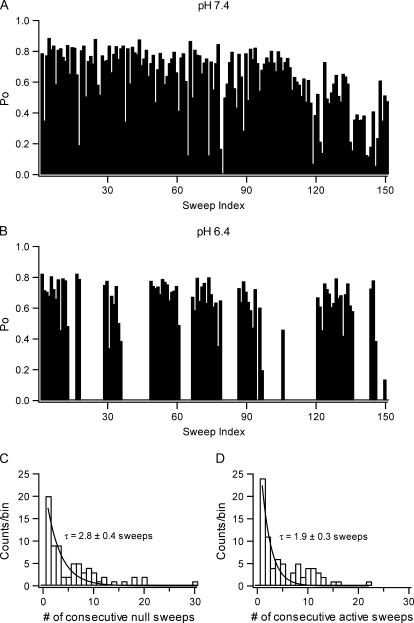
FIGURE 4.

Modal gating of Kv1.5 at different pHs. (A) A diary plot of Kv1.5 constructed by plotting the open probability per sweep for 150 consecutive sweeps depolarized at 100 mV for 150 ms every 3 s at pH 7.4 with a cell-attached patch. In this example, only one sweep (No. 79) shows mode U gating. (B) Diary plot from another cell-attached patch using an identical protocol but at pH 6.4. Mode A (available) and mode U (unavailable) gating appear in clusters, as suggested by runs analyses (see text). (C) Frequency histogram of the number of consecutive sweeps showing mode U gating at pH 6.4. The length of runs with mode U gating was pooled from seven patches, and the resulting histogram was fitted to a single exponential distribution to give a time constant of 2.8 sweeps (8.4 s). (D) Frequency histogram of the number of consecutive sweeps with mode A gating at pH 6.4. Fitting the histogram to a single exponential distribution gave a time constant of 1.9 sweeps (5.7 s).

Fig. 1 B shows unitary currents from the same patch as in Fig. 1 A using the identical voltage protocol but after switching to pH 6.4. As at pH 7.4, flickery channel behavior and conductance substates (arrows) were observed. There was no obvious difference in the probability of substates at pH 7.4 and 6.4. However, more sweeps showed the channel entering a long-lived closed state before the end of the voltage step, and the proportion of null sweeps was higher. Fitting of the all-points amplitude histogram at pH 6.4 gave a single channel current of 1.7 ± 0.2 pA.

Fig. 1, C and D, shows representative current traces recorded from another outside-out patch at pH 5.9 and after recovery at pH 7.4 using the same voltage protocol as in Fig. 1 A. At pH 5.9, the number of null sweeps was even higher; there was no evidence of channel activity in 11 of the 12 sweeps shown. The absence of activity in the first sweep suggests that depolarization-induced inactivation is unlikely to account for the null sweeps. In addition, the series of 10 consecutive null sweeps observed over a period of ∼150 s is not likely to be due to a failure to recover from depolarization-induced inactivation since the recovery of residual macroscopic currents from inactivation at pH 5.4 with 3.5 mM 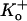is ≈ 4 s (18). This long period of inactivity is not likely to be due to entry into a defunct state since K⁺ was present in both the intracellular and extracellular solution and recovery did not require a long depolarizing pulse (19). Recovery responses were obtained after switching the bath solution back to pH 7.4, demonstrating that the dramatic decrease of channel availability at pH 5.9 was also not due to the spontaneous loss of the channel from the patch. Furthermore, the single channel current (i) did not change between pH 5.9 and pH 7.4 (Fig. 1, C and D). Similar results were observed in two other patches. Together, these results show that decreasing external pH decreases the availability but not the single channel current of Kv1.5.

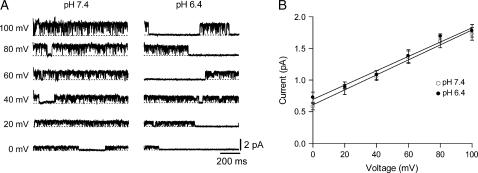
Analysis of single channel currents over a range of voltages confirmed that the single channel conductance is not affected by changing pH. Representative unitary currents recorded at 0–100 mV in 20 mV increments at pH 7.4 or 6.4 from different outside-out patches are shown in Fig. 2 A. The graph in panel B shows the i-V relationship based on data from three cells, derived from all-points histograms as described for Fig. 1, at pH 7.4 (open circles) and pH 6.4 (solid circles). A line fitted to the data gave a slope conductance (γ; mean ± SD) of 11.8 ± 0.6 pS at pH 7.4 and 11.3 ± 0.8 pS at pH 6.4, which were not significantly different. This finding, together with the data of Fig. 1, allowed us to reject the hypothesis that the reduction in macroscopic current by acidification is due to the reduction of the single channel conductance arising either by a change of the permeation pathway or by occlusion of the pore. Instead, the results of Figs. 1 and 2 indicate: 1), that the low pH-induced decrease of macroscopic current must arise solely by an effect on channel gating, and 2), that depolarization-induced inactivation is unlikely to play a significant role in the mechanism responsible for the null sweeps.

FIGURE 2.

Open channel current-voltage relationship showing the single channel conductance does not change with pH. (A) Representative unitary currents at voltages between 0 and 100 mV in 20 mV increments at pH 7.4 and 6.4. All traces shown were digitally filtered at 1 kHz. (B) Fitting a line to the i-V relationship at pH 7.4 (○) and pH 6.4 (•) gave a slope conductance (mean ± SD) of 11.8 ± 0.6 pS and 11.3 ± 0.8 pS, respectively. These values for the slope conductance were not significantly different.

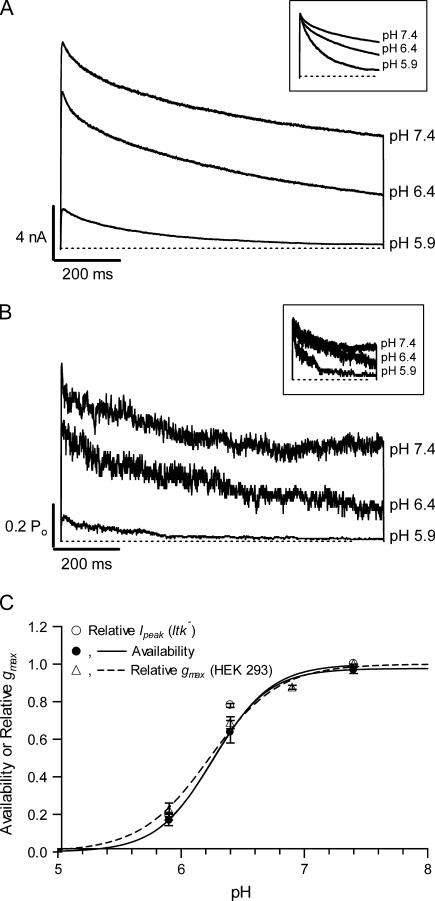
Macroscopic currents and the ensemble current behavior generated from idealized records, obtained in each case from channels expressed in ltk⁻ cells, are shown for comparison in Fig. 3, A and B, respectively. Macroscopic currents evoked by a 1 s pulse to 100 mV at pH 7.4, 6.4, and 5.9 showed a pH-dependent decrease of the peak current along with an increased rate of inactivation (Fig. 3 A; see inset of normalized currents and figure legend for numerical values) as reported previously (3). The reductions in peak currents are comparable to the reduction in macroscopic conductance measured from Kv1.5 expressed in HEK293 cells with similar recording conditions (5 mM 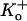; Fig. 3 of Kehl et al. (3)) and that measured from the ensemble current (Fig. 3 B; see figure legend for details). Furthermore, the time courses of inactivation measured in the whole-cell configuration at different pH also agreed well with those measured from the ensemble currents. This correlation shows that a change of P_o nicely accounts for the effect of pH on the amplitude and kinetics of macroscopic currents. Inspection of the single channel responses reveals that this low pH-induced decrease of P_o arises for two reasons: 1), channel availability decreases, and 2), the burst duration decreases. Of these two actions, the influence of pH on channel availability was much greater and is considered first.

FIGURE 3.

Current behavior at the macroscopic level and the ensemble average of unitary current of Kv1.5 at pH 7.4, 6.4, and 5.9 are qualitatively similar. (A) Representative, superimposed macroscopic currents at pH 7.4 (top trace), pH 6.4 (middle trace), and pH 5.9 (bottom trace) evoked with a 1 s depolarizing pulse to 100 mV from a holding potential of –80 mV. Peak current was reduced by ∼22% at pH 6.4 and 81% at pH 5.9. Fitting the currents at pH 7.4, 6.4, and 5.9 to a single exponential function gave mean inactivation time constants of 558 ± 75 ms, 556 ± 61 ms, and 346 ± 46 ms, respectively. Normalized currents are shown in the inset to better illustrate the acceleration of inactivation. (B) Ensemble open probability generated from idealized single channel records at pH 7.4, 6.4, and 5.9. The ensemble behavior reproduces the changes of the peak amplitude and kinetics observed in the macroscopic currents. Compared to that at pH 7.4, the peak ensemble current was reduced by 34% at pH 6.4 and 82% at pH 5.9. A single exponential fitted to the ensembles gave time constants of 548, 401, and 197 ms for pH 7.4, 6.4, and 5.9, respectively. Normalized ensembles are shown in the inset. (C) A reduction in channel availability accounts for the reduction of peak macroscopic current by external H⁺. Channel availability (•) agrees well with the normalized relative g_max recorded in HEK293 cells (▵) or the normalized peak macroscopic current in ltk⁻ (○). Availability is defined as the proportion of sweeps with one or more open events. Data from HEK293 cells were obtained from our previous study (3). Briefly, whole-cell currents were recorded from a series of 300-ms depolarizing steps at −50 to +60 mV, and the instantaneous tail currents at −50 mV were analyzed to give the relative g_max values at different pHs. The composition of the bath and pipette solutions were identical to that listed in Materials and Methods except the bath solution contained 5 mM K⁺ and 138.5 Na⁺. Fitting the whole-cell data to the Hill equation gave a pK_H of 6.2 ± 0.2 with a Hill coefficient of 1.6 ± 0.4 (dashed line) for the reduction in relative g_max. Fitting channel availability to the Hill equation (solid line) gave a pK_H of 6.4 ± 0.2 with a Hill coefficient of 1.9 ± 0.2.

pH affects channel availability

Fig. 3 C shows a plot of channel availability, defined as the proportion of sweeps with at least one open event, against pH (solid circles). Availability changed from 0.97 ± 0.02 at pH 7.4, to 0.64 ± 0.6 at pH 6.4 and to 0.17 ± 0.03 at pH 5.9 (n = 3–12 patches). Included for comparison in Fig. 3 C is the relationship between pH and either the normalized macroscopic peak current at 100 mV for Kv1.5 expressed in ltk⁻ cells (open circles) or the relative macroscopic conductance data taken from our study using Kv1.5 in HEK293 cells (open triangles; (3)). The similarity of these three relationships indicates that a change of availability is the primary cause of the inhibition of Kv1.5 currents by extracellular protons and is consistent with our previous conclusion (3) that the pH-induced increase of the depolarization-induced inactivation rate alone is an insufficient explanation.

The decrease in availability may result from an increase in the number of random null sweeps or from a modal gating scheme in which the null (or active) sweeps are clustered together. To determine if gating was modal, unitary currents through cell-attached patches were recorded using a pipette solution buffered to pH 7.4 or 6.4, and the voltage protocol consisted of a 150 ms pulse at 100 mV applied at an interval of 3 s. The attached cell was depolarized by a high [K⁺] bath solution and its resting potential was assumed to be 0 mV. It was also assumed that the absence of more than one (main conductance) open level indicated that the patch contained just one channel. A representative diary plot of P_o per trace at pH 7.4 (panel A) and 6.4 (panel B) is shown in Fig. 4. At pH 6.4, the diary plot indicates a clear tendency for alternating periods of null and active traces, and for that reason a runs analysis was done (see Materials and Methods) to determine if sweeps showing similar channel behavior were clustered, i.e., that gating was modal. Sweeps were labeled as either unavailable (U) for null traces or available (A) for traces showing one or more openings of the channel. Using Eq. 1, the Z values were calculated to be 5.0 ± 1.3 (range 1.77–19.6; n = 6) at pH 7.4 and 6.3 ± 1.0 (range 2.85–9.17; n = 7) at pH 6.4. Both values indicate a significant clustering (p < 0.001) of active and null sweeps.

To estimate the average lifetimes of epochs of U and A sweeps, histograms were constructed from the numbers of consecutive sweeps with either type of gating. Data at pH 7.4 or 6.4 were combined from six and seven one-channel, cell-attached patches, respectively (14), and represent a total of 1502 sweeps (1308 A sweeps, 194 U sweeps) at pH 7.4 and 843 sweeps (385 A sweeps, 458 U sweeps) at pH 6.4. Despite the large number of sweeps recorded at pH 7.4, there were only 93 runs (49 in mode A, 44 in mode U), and the histogram for mode A was inconclusive due to a large proportion of very long runs (not shown). Fitting the histogram for mode U to a single exponential gave a time constant of 0.76 ± 0.06 sweeps (or 2.3 ± 0.2 s given a stimulus period of 3 s; not shown). On the other hand, 385 runs (194 in mode A, 191 in mode U) were recorded with pH 6.4, and histograms for mode U and mode A are shown in Fig. 4, C and D, respectively. A log likelihood test revealed the distribution was better fitted by a single exponential function (difference in log likelihood <0.2, not significant, ν = 2) with a time constant of 2.8 ± 0.4 sweeps (8.4 ± 1.2 s) for mode U and 1.9 ± 0.3 sweeps (5.7 ± 0.9 s) for mode A. Together, these results suggest decreasing pH promotes mode U gating whereas increasing pH favors mode A gating.

If, for simplicity, we assume that the transition between the two modes is first order, i.e.,

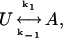then k₁ and k₋₁ are equal to the reciprocal to the mean lifetime of U and A, respectively. At pH 6.4, the estimates for k₁ and k₋₁ were 0.12 s⁻¹ and 0.18 s⁻¹, respectively. These numbers translate to a probability for A of 0.4 at pH 6.4. This analysis was based on the assumptions that: 1), a channel could make at most one transition during a 3 s period, and 2), the probability of switching between the two gating modes during a 150 ms pulse to 100 mV was negligible. The first assumption is probably valid since changing the interpulse interval to either 5 or 10 s did not alter the outcome of the runs analysis; however, when the interpulse interval changed to 15 s the grouping of U and A sweeps showed no statistical tendency to cluster (not shown). The second assumption seems valid for the transition from U to A because very few traces (<1%) had a latency to first opening longer than a few ms. However, the long-lived closure sometimes observed before the end of a voltage pulse could be due to either a depolarization-induced inactivation or a transition to mode U.

An important question regarding mode U is whether it simply reflects depolarization-induced inactivation. With a 1 s depolarization to 100 mV at pH 6.4 there was, compared to pH 7.4, a higher probability of entering a long-lived closed state (Fig. 1 B), but this was not invariably linked to the channel being unavailable on the next sweep evoked 15 s later. In Fig. 1 B, for example, five of 11 active sweeps terminate in a long-lived closed state, which is presumed to reflect depolarization-induced inactivation, and four of those five sweeps are followed by an active sweep. Statistical analysis of a 2 × 2 contingency table (sweep ending in inactivation versus sweep active at end) × (next sweep null versus next sweep active) showed there was no correlation between a pulse ending in an inactivated state and the next sweep being blank (27 pairs, χ² value = 2.41, p > 0.1). With shorter depolarizations (150 ms), such as those used for Fig. 4 B, the probability of inactivating before the end of the pulse was low, as indicated by the similarity of the P_o per active trace at either pH, but clustering of null sweeps persisted. Similarly, runs analysis at pH 6.4 with 20 ms depolarizing pulses to 100 mV delivered at 0.33 Hz (not shown) showed clustering of null sweeps (Z = 12.0 ± 3.5; n = 6; not shown). These results indicate that mode U gating is not simply due to depolarization-induced inactivation. This is consistent with our previous finding that decreasing external pH has no effect on the maximum gating charge (Q_max) mobilized during activation (3) and in contrast to what is expected were the channels in the depolarization-induced C-type inactivated state. The gating charge data also imply that mode U gating includes voltage-sensitive transitions between several nonconducting states. However, the data do not allow us to say whether transitions between mode U and the depolarization-induced inactivated state are possible.

pH does not substantially affect intraburst behavior

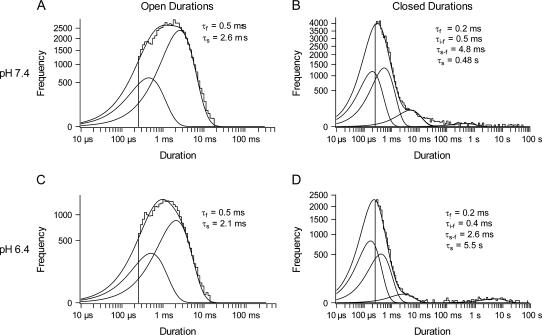
As noted above, inspection of channel behavior during active sweeps at either pH 7.4 or 6.4 revealed bursts comprised of brief closures and brief openings. Dwell time histograms of open (conducting) and closed (nonconducting) events within bursts at pH 7.4 and pH 6.4 are shown (see Fig. 6) and are based on depolarizations lasting for up to 180 s (Fig. 5) to prevent the censoring of a long-lived, nonconducting state that usually occurred with 1 s depolarizations to 100 mV, particularly at pH 6.4 (e.g., Fig. 1 B). The open duration histogram at pH 7.4 (Fig. 6 A) was fitted by the sum of two exponentials. The slower component of the frequency distribution had a mean open time (τ_s) of 1.5 ± 0.1 ms (n = 8 patches) and represented the more frequently observed open event (a_s = 0.70 ± 0.04). The faster component of the distribution represented 0.3 ± 0.04 of the open events and had a mean duration (τ_f) of 0.34 ± 0.02 ms, which is probably an underestimate, given the limited frequency response of the system. At pH 6.4 the open duration histogram was also biexponential (Fig. 6 C). The slower component had a longer mean open time (τ_s) of 1.4 ± 0.1 ms and represented ∼0.80 ± 0.04 of the events. The less frequent (a_f = 0.20 ± 0.04), faster component had a mean dwell time (τ_f) of 0.35 ± 0.05 ms (n = 7 patches). Neither the mean dwell times nor the proportion of time spent in these two open states changed significantly between pH 7.4 and 6.4 (p > 0.05; ANOVA).

FIGURE 6.

Extracellular acidification does not significantly affect gating transitions within bursts. Unitary current from cell-attached patches recorded at pH 7.4 and 6.4 with 2- or 3-min depolarizing pulses to 100 mV were idealized using a half-amplitude method. (A) The open duration histogram obtained from the current trace shown in Fig. 5 A was fitted to a biexponential distribution to give time constants of 0.5 and 2.6 ms, and an area of 0.30 and 0.70, respectively. (B) The closed duration histogram obtained at pH 7.4 was fitted to a four-component exponential distribution, and the fastest three time constants were 0.2, 0.5, and 4.8 ms, with a respective area of 0.63, 0.36, and 0.02. The slowest component (time constant 0.48 s) is thought to represent one or more inactivated states. It has a relative area <1% of the total closed events. (C) The open duration histogram generated from the current trace shown in Fig. 5 B at pH 6.4. The fast and slow time constants are 0.5 and 2.1 ms with an area of 0.2 and 0.8, respectively. (D) The closed duration histogram at pH 6.4 was fitted to a four-component exponential distribution. The three fastest components have time constants 0.2, 0.4, and 2.6 ms and an area 0.81, 0.18, and 0.01, respectively. The slowest component (time constant 5.5 s) represents <1% of the total nonconducting events.

FIGURE 5.

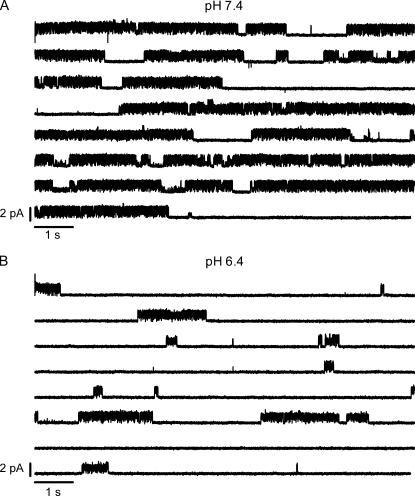
Decreasing external pH to 6.4 decreases the mean burst length and increases the apparent interburst duration. (A) Representative unitary currents at pH 7.4 in a cell-attached patch. High 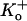bath solution was assumed to depolarize the cell to 0 mV; the pipette solution contained 3.5 mM K⁺. Contiguous traces of the first 80 s of activity at 100 mV are shown. Bursts of flickering channel behavior were bracketed by gaps longer than 20 ms (see Materials and Methods). (B) Representative contiguous traces from another cell-attached patch but at pH 6.4. The within-burst behavior was only slightly changed, the mean burst duration was decreased, and the apparent interburst duration was increased. Both traces were digitally filtered at 1 kHz.

Panels B and D of Fig. 6 plot, at pH 7.4 and 6.4, respectively, the frequency distribution of the closed events during a long depolarization to 100 mV. At pH 7.4 the closed duration histogram was fitted to the sum of four exponentials, but we focus initially on the three fastest components that largely reflect gating behavior within a burst. A critical time of 20 ms was used as the minimum gap length that signified the end of a burst (defined below). The time constants (and amplitudes) for the fastest, intermediate-fast and slow-fast components were 0.22 ± 0.1 ms (a_f = 0.63 ± 0.02), 0.42 ± 0.03 ms (a_i–f = 0.35 ± 0.02), and 2.6 ± 0.2 ms (a_s–f = 0.02 ± 0.003) (n = 8 patches). The corresponding values at pH 6.4 were 0.17 ± 0.04 ms (a_f = 0.81 ± 0.03), 0.45 ± 0.05 ms (a_i–f = 0.18 ± 0.03), and 2.4 ± 0.3 ms (a_s–f = 0.01 ± 0.002) (n = 7 patches). The fastest closed component had a time constant shorter than the dead time of our system and consequently its mean lifetime should be taken as a rough estimate only. Although the mean dwell time of each of the three fastest components of the closed duration histograms did not change significantly between pH 7.4 and pH 6.4 (p > 0.05; ANOVA), their relative proportions did change. Compared to that at pH 7.4, the relative proportion of the fastest component increased significantly (p < 0.01) at pH 6.4, whereas the intermediate-fast component decreased significantly (p < 0.01) at pH 6.4; however, the slow-fast component was unchanged (p > 0.1). These results showed that intraburst gating behavior was not dramatically affected by changing pH from 7.4 to 6.4.

pH affects the burst- and interburst duration

A burst of openings is conventionally defined as a series of openings separated by gaps that are less than a critical length (t_crit) (20). A value for t_crit was determined by numerically solving the equation, exp(−t_crit/τ_s–f) = 1− exp(−t_crit/τ_s) where τ_s–f is the time constant for the slow-fast component during a burst and τ_s is the time constant for the slowest component in the closed duration histogram (Fig. 6). Using conservative estimates for τ_s–f and τ_s of 3.5 and 500 ms, respectively, t_crit was set to 20 ms for either pH. Despite pooling the data from patches at pH 7.4 (n = 8) or pH 6.4 (n = 7), the frequency of events remained low and therefore it was not possible to obtain a reliable estimate of the number of interburst nonconducting states. Additionally, at pH 6.4 the P_o was low and, although overlapping channel openings were never observed in the data that were analyzed, it was not possible to be certain that there was only one channel in the patch, thus making a meaningful analysis of the interburst data problematic. An analysis of the mean burst duration was more straightforward because overlapping openings were never observed during bursts at either pH. By dividing the accumulated burst length by the number of bursts observed, the mean burst duration was determined to be 1.7 s at pH 7.4 and 0.73 s at pH 6.4. The data of Fig. 5 also show that the slow, nonconducting state at either pH is nonabsorbing. Compared to the pH 7.4 data, the probability of the slow, nonconducting state was higher at pH 6.4 and it is more stable.

DISCUSSION

Whether Kv1.5 channels are expressed in HEK293 cells (3) or in ltk⁻ cells, as in this study, extracellular acidification has two major effects on Kv1.5 macroscopic current: 1), the peak current amplitude decreases, and 2), the inactivation rate of residual currents increases. Macroscopic current, I, is equal to NP_oi or, in an expanded form, NP_oγ(V-E_K) where N is the channel density, P_o is the open probability which has voltage and time dependence, γ is the single channel conductance, and E_K is the reversal potential. Analysis of one-channel patches showed that decreasing pH did not affect i at pHs between 7.4 and 5.9 and over a range of voltages (Figs. 1 and 2), indicating that γ had not changed. This provided direct evidence that the decline of macroscopic currents is not due to occlusion of the open pore or a change of the permeation pathway. A similar conclusion has been reached for the effect of external protons on macroscopic ShakerIR current (21).

Ensemble data constructed from idealized traces (Fig. 3 B) replicated the main features of macroscopic currents, indicating that the observed changes of single channel behavior can account for most of the previously reported effects. One effect of low pH, a rightward shift of the g-V relationship (3) that is presumably due to screening and/or binding to surface charges (22), was not apparent at the single channel level because of the strong depolarization that was typically used. The main effect of acidification was to decrease P_o: 1), by decreasing channel availability as shown by an increased proportion of blank or null sweeps, and 2), by decreasing the average burst duration during active sweeps. Of these two changes, the decrease of channel availability was the primary cause of the decrease of the peak macroscopic conductance. This was illustrated by the overlap of the availability-pH curve derived from single channel analysis and the g_max-pH curves derived from the analysis of macroscopic currents (Fig. 3 C). Diary plots and the outcome of runs analyses of the channel behavior at pH 6.4 (Fig. 4) showed that null and active sweeps were clustered and consequently that the behavior likely represented different sets or modes of gating. The three criteria typically used to define modal gating were met (15). First, the two distinct kinetic behaviors were consistently observed in one-channel patches, thus ruling out the possibility of two populations of channels. Second, the probability of a given gating mode could be experimentally manipulated, in this case by changing pH. And, third, the rate for the transition between the two modes was slow, as shown by clustering in diary plots and by the absence of clear evidence of a switch from mode U to mode A during 1-s depolarizations. Active sweeps at pH 6.4 and 5.9 frequently ended with a long, censored closed state (Fig. 1 B) that we assume is due primarily to depolarization-induced inactivation, but we cannot preclude the possibility of transitions to mode U.

Three lines of evidence lead us to reject a model in which depolarization-induced inactivation accounted for the null sweeps. These are, first, that mode U gating observed at low pH is not dependent on prior channel opening (first sweeps in Fig. 1, B and C). The mean burst length, which is a reflection of the rate of depolarization-induced inactivation, is much longer than the dead time of our system so that a failure to detect very brief open events is an unlikely explanation for the null sweeps. Second, clustering of null sweeps was observed even with very brief (20 ms) depolarizations where the probability of depolarization-induced inactivation was very low. Third, in a previous study of macroscopic currents the decline of the peak current was evident on the first sweep after a 2 min period in which the potential was held continuously at −80 mV while the pH was changed (3). These observations are inconsistent with a model in which null sweeps resulted from the occupancy of a long-lived inactivated state entered during a depolarizing pulse.

The lumping together of two distinct gating behaviors into U and A modes and the assignment of a first order reaction scheme for transitions between these two modes is very likely an oversimplification of a more complex gating behavior. The details of states and the kinetics of transitions within a gating mode, as well as the exact connectivity between states in the two modes, will be required to develop a full understanding of the kinetic processes involved. A more detailed scheme of mode A would include several closed states, closed-inactivated states, an inactivated state, an open state as well as closed states outside of the activation pathway (23–25). Much less is known about the states traversed in mode U. However, save for a rightward shift of the Q-V curve, gating currents are unchanged at low pH, indicating that voltage sensor movement is more or less intact in channels gating in mode U.

Analysis of active sweeps at pH 7.4 or pH 6.4 suggests that in mode A the opening and closing transitions within a burst were largely pH insensitive (Fig. 6). At either pH, Kv1.5 channel activity is characterized by rapid flickering that, especially at 100 mV, most likely reflects transitions between short-lived open and closed (i.e., noninactivated) states outside of the normal activation pathway (26,27). There was evidence for two states in the open duration histogram, but the faster of these two was near the dead time of the system and is therefore equivocal. Aside from this second open state, channel gating within a burst, including the existence of the three fastest components in the closed duration histogram, is very much as described for ShakerIR channels (26).

The slowest component of the closed duration histogram represented a state that terminated a burst and was attributed to inactivation. However, because of the relatively small number of these long nonconducting events, we cannot be certain of either the number of inactivated states or their mean dwell times. To address the simpler question of how a change of pH affected the equilibrium between bursting behavior and gaps between bursts, channel activity was studied during minutes-long depolarizations to 100 mV (Fig. 5). Decreasing pH from 7.4 to 6.4 decreased the burst duration and appeared to increase the interburst interval, which can account for the faster inactivation rate of macroscopic and ensemble currents (Fig. 3, A and B) as well as the slower rate of recovery from inactivation at low pH (18).

Extracellular protons increase the depolarization-induced inactivation rate in ShakerIR (21), N-terminal deleted Kv1.4 (28), rat Kv1.5 (6), and human Kv1.5 (5). This enhancement of the inactivation rate is attenuated by the T-449V mutation in ShakerIR and by the homologous mutation, R-487V, in Kv1.5 and as such is consistent with a connection to outer pore inactivation. However, despite the fact that depolarization-induced inactivation both in ShakerIR and Kv1.5 is accelerated by decreasing pH, there are several important, unexplained differences in the response of these two structurally related channels to extracellular acidification. Protonation of H-463 appears to be the primary event that triggers both a change of availability and the acceleration of depolarization-induced inactivation in Kv1.5 since both effects are substantially reduced in Kv1.5 H-463Q (3). In contrast, in ShakerIR the acceleration of depolarization-induced inactivation has been provisionally attributed to protonation of the aspartate residue in the GYGD sequence of the selectivity filter. The most striking disparity is that acidification decreases channel availability (increases mode U gating) in Kv1.5 but not in ShakerIR or Kv1.4. Interestingly, however, mutations of the threonine residue at position 449 in Shaker (4) or its positional equivalent in Kv1.4 (29) can produce currents that collapse in K⁺-free external medium, an effect that has been attributed to a change of availability due to closed-state inactivation (29). We have not yet assessed the consequences of mutations of R-487 on channel availability at pH 7.4 in Kv1.5 but have found that mutations of residues at or near the putative proton-binding site (H-463) in the pore turret can produce currents at pH 7.4 that show fast inactivation and have a 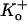sensitivity similar to that observed both for ShakerIR mutants and for wild-type (wt) Kv1.5 channels at low pH_o (3,30). Although a faster rate of depolarization-induced inactivation is associated with a 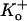-sensitive change of availability in ShakerIR T449 mutants, this is not a consistent correlation. For example, with wt ShakerIR decreasing the external pH can dramatically speed inactivation but does not appear to affect channel availability (21), and, conversely, the inhibition of Kv1.5 current by divalent cations such as Ni²⁺, Co²⁺, and Zn²⁺ is correlated with a substantial decrease of channel availability that is associated with relatively small changes of depolarization-induced inactivation rate (18). This indicates that “closed-state inactivation” and “open-state inactivation” do not always show parallel changes.

An important question that remains to be answered is whether the decreased availability or mode U gating we observe at low pH in Kv1.5 is due to a constriction of the outer pore mouth, as has been proposed for P/C type inactivation. Typically, P/C type inactivation is assumed to be strongly coupled to channel activation such that it occurs from the open state or perhaps from one or more closed states accessed outside of the activation pathway. If, as suggested by the effects of 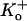and the R-487V mutation on the inhibition of Kv1.5 current at low pH, the decreased channel availability does indeed reflect outer pore inactivation, this would mean that this process becomes uncoupled from activation. Evidence obtained from the nonconducting mutant ShakerIR W^434F for “permanent” or resting P-type inactivation provides some support for this idea (31).