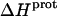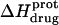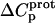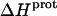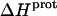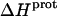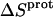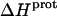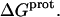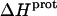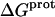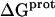Abstract
The binding of aminoglycoside antibiotics to a broad range of macromolecular targets is coupled to protonation of one or more of the amino groups that typify this class of drugs. Determining how and to what extent this linkage influences the energetics of the aminoglycoside-macromolecule binding reaction requires a detailed understanding of the thermodynamics associated with the protonation equilibria of the aminoglycoside amino groups. In recognition of this need, a calorimetric- and NMR-based approach for obtaining the requisite thermodynamic information is presented using paromomycin as the model aminoglycoside. Temperature- and pH-dependent 15N NMR studies provide pKa values for the five paromomycin amino groups, as well as the temperature dependence of these pKa values. These studies also indicate that the observed pKa values associated with the free base form of paromomycin are lower in magnitude than the corresponding values associated with the sulfate salt form of the drug. This difference in pKa is due to drug interactions with the sulfate counterions at the high drug concentrations (≥812 mM) used in the 15N NMR studies. Isothermal titration calorimetry studies conducted at drug concentrations ≤45 μM reveal that the extent of paromomycin protonation linked to the binding of the drug to its pharmacologically relevant target, the 16 S rRNA A-site, is consistent with the pKa values of the free base and not the sulfate salt form of the drug. Temperature- and pH-dependent isothermal titration calorimetry studies yield exothermic enthalpy changes (ΔH) for protonation of the five paromomycin amino groups, as well as positive heat capacity changes (ΔCp) for three of the five amino groups. Regarded as a whole, the results presented here represent an important first step toward establishing a thermodynamic database that can be used to predict how aminoglycoside-macromolecule binding energetics will be influenced by conditions such as temperature, pH, and ionic strength. Such a predictive capability is a critical component of any drug design strategy.
INTRODUCTION
2-Deoxystreptamine (2-DOS)-containing aminoglycosides are archetypical rRNA-directed antibiotics (1). In addition to their pharmacologically relevant target, the 16 S rRNA A-site, 2-DOS aminoglycosides have also been shown to bind to a broad range of other nucleic acid structures that adopt A-like conformations, including DNA and RNA triplexes (2–4), DNA·RNA hybrid duplexes (3–6), and a number of different RNA structures that function as aptamers (7–17), ribozymes (18–24), and protein binding sites (25–33). The interacting macromolecular partners of 2-DOS aminoglycosides are not restricted to nucleic acids. They also include proteins. In this connection, the primary mechanism by which bacteria develop resistance to 2-DOS aminoglycosides is through the expression of enzymes that bind to and covalently modify the drugs (34,35). These aminoglycoside-modifying enzymes include phosphotransferases, acetyltransferases, and nucleotidyltransferases.
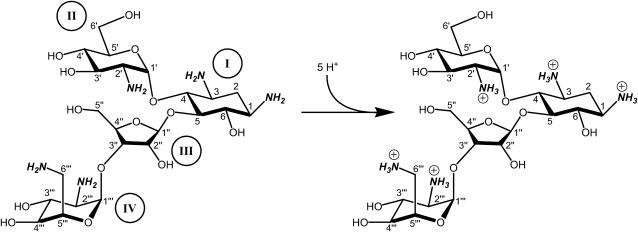
Aminoglycosides are typified by the presence of multiple primary amine functionalities, which exist in pH-dependent equilibria between noncharged NH2 and positively charged  states. A common theme that has emerged from the structural and biophysical characterizations of aminoglycoside-macromolecule interactions that have been reported to date is the central role that the drug amino groups play in target recognition. In several instances, aminoglycoside binding was found to be linked to protonation of at least one drug amino group (5,33,36–41). Furthermore, this linkage had a profound influence on the energetics of the binding reactions. In other words, the energetics of aminoglycoside-macromolecule interactions are influenced by the basicities of the drug amino groups. Determining the nature and magnitude of this influence requires a detailed thermodynamic understanding of the protonation equilibrium associated with each aminoglycoside amino group, which varies in number from four to six depending on the drug. Toward this end, the pKa values for the amino groups of a number of different aminoglycosides have been characterized at a single temperature (38–40,42–47). However, a rigorous thermodynamic characterization (including ΔH, ΔS, ΔG, ΔCp, and ΔpKa/°C) of the protonation equilibria associated with the multiple amino groups of any aminoglycoside has yet to be reported. Here, we describe an approach for obtaining the requisite thermodynamic information using paromomycin, a 2-DOS aminoglycoside that contains five amino groups (see structure in Fig. 1), as our model drug. Significantly, this approach, which employs a combination of natural abundance 15N NMR and isothermal titration calorimetry (ITC) techniques to derive the relevant information, can be applied to the characterization of any biomolecule that contains multiple ionizable amine functionalities.
states. A common theme that has emerged from the structural and biophysical characterizations of aminoglycoside-macromolecule interactions that have been reported to date is the central role that the drug amino groups play in target recognition. In several instances, aminoglycoside binding was found to be linked to protonation of at least one drug amino group (5,33,36–41). Furthermore, this linkage had a profound influence on the energetics of the binding reactions. In other words, the energetics of aminoglycoside-macromolecule interactions are influenced by the basicities of the drug amino groups. Determining the nature and magnitude of this influence requires a detailed thermodynamic understanding of the protonation equilibrium associated with each aminoglycoside amino group, which varies in number from four to six depending on the drug. Toward this end, the pKa values for the amino groups of a number of different aminoglycosides have been characterized at a single temperature (38–40,42–47). However, a rigorous thermodynamic characterization (including ΔH, ΔS, ΔG, ΔCp, and ΔpKa/°C) of the protonation equilibria associated with the multiple amino groups of any aminoglycoside has yet to be reported. Here, we describe an approach for obtaining the requisite thermodynamic information using paromomycin, a 2-DOS aminoglycoside that contains five amino groups (see structure in Fig. 1), as our model drug. Significantly, this approach, which employs a combination of natural abundance 15N NMR and isothermal titration calorimetry (ITC) techniques to derive the relevant information, can be applied to the characterization of any biomolecule that contains multiple ionizable amine functionalities.
FIGURE 1.
Structure of paromomycin highlighting (in bold and italics) the five titratable amino groups. The atomic and ring numbering systems are denoted in Arabic and Roman numerals, respectively. Ring I of this structure is 2-deoxystreptamine.
MATERIALS AND METHODS
RNA and chemicals
The 27-mer RNA oligonucleotide used in this study was obtained in its PAGE-purified sodium salt form from Dharmacon Research (Lafayette, CO). Paromomycin·H2SO4 was obtained from Fluka (Milwaukee, WI) and further treated as described in the next section. The OH form of Amberlite IRA-400 resin was obtained from Supelco (Bellefonte, PA), whereas the 1.0-N HCl volumetric standard solution used in the calorimetric experiments was obtained from Aldrich (St. Louis, MO). The 1 M [15N]urea standard in DMSO was obtained from Isotec (Miamisburg, OH).
Preparation of the free base form of paromomycin
Amberlite IRA-400 resin in its OH form (70 mL) was washed with 350 mL of water. The washed resin was placed in a glass column 2.5 cm in diameter and 30 cm in length, and washed with 50 mL of water. A 1.0-mL solution of 0.5 M paromomycin·H2SO4 was loaded onto the column. The paromomycin was then eluted from the column with 200 mL of water at a flow rate of 1 mL/min, and 30-mL fractions were collected. The pH of each fraction was measured, with the first three fractions having a pH > 9.0. These three fractions were pooled, lyophilized, and stored in their dry state at −20°C until used in the NMR and calorimetric studies described below.
Natural abundance 15N NMR spectroscopy
15N NMR spectra were acquired at 30.4 MHz and a temperature of either 25, 35, or 45°C on a Varian Unity 300 spectrometer (Palo Alto, CA) using a recycle delay of 1 s. All 15N chemical shifts are reported relative to NH3 using 1 M [15N]urea in DMSO as an external reference, with the 15N chemical shift of the reference set to 77.0 ppm. The experimental NMR solutions were prepared by dissolving at least 300 mg of the lyophilized paromomycin free base in 600 μL of 85% H2O/15% D2O. The pH of the NMR samples was adjusted by addition of either HCl or KOH in 85% H2O/15% D2O. All pH measurements of NMR samples were acquired using a Corning 430 pH meter (Corning, NY) interfaced with a microstem glass/calomel combination electrode (Mettler Toledo, Columbus, OH). The assignments of the 15N resonances for paromomycin were based on those previously reported (38,43).
Isothermal titration calorimetry
All isothermal calorimetric measurements were conducted on a MicroCal VP-ITC (MicroCal, Northampton, MA). In the drug protonation experiments (conducted at either 25 or 45°C), three 10 μL aliquots of a solution containing 1 mM HCl and 100 mM KCl were injected from a 250-μL rotating syringe (300 rpm) into a sample chamber containing 1.42 mL of a solution containing 2 mM paromomycin in its free base form and 100 mM KCl (at pH values ranging from 5.53 to 9.40). Each experiment of this type was accompanied by the corresponding control experiment in which 10 μL aliquots of 100 mM KCl alone were injected into the relevant solution of paromomycin and KCl. After three HCl injections, the total change in solution pH was ≤0.05 units. Note that all the solutions containing HCl and KCl were freshly prepared before each experiment using a 1.0-N HCL volumetric standard solution. The delay between each injection was 420 s, with the duration of each injection being 10 s. The initial delay before the first injection was 60 s. Each injection generated a heat burst curve (μcal/s versus s). The area under each heat burst curve was determined by integration (using the Origin version 7.0 software (MicroCal)) to obtain a measure of the heat associated with that injection. At any given pH, the heat associated with each injection of KCl into the drug-KCl mixture was subtracted from the corresponding heat associated with each injection of HCl-KCl into drug-KCl to yield the heat of protonation for that injection. The resulting corrected heats corresponding to the second and third injections were averaged to yield the observed enthalpy of drug protonation at that pH.
In the RNA binding experiments (conducted at 25°C), 10 μL aliquots of 250 μM paromomycin sulfate were sequentially injected into an RNA solution that was 10 μM in duplex. Each experiment of this type was accompanied by the corresponding control experiment in which 10 μL aliquots of the drug were injected into a solution of buffer alone. The duration of each injection was 10 s and the initial delay before the first injection was 60 s. The delay between injections was 300 s. The heat associated with each drug-buffer injection was subtracted from the corresponding heat associated with each drug-RNA injection to yield the heat of drug binding for that injection. The resulting corrected injection heats were plotted as a function of the [drug]/[duplex] ratio and fit with a model for two independent sets of binding sites. Buffer solutions contained either 10 mM sodium cacodylate (pH 6.8) or 10 mM TES (pH 6.8), 0.1 mM EDTA, and sufficient NaCl to bring the total Na+ concentration to 150 mM.
In the sulfate binding experiment (conducted at 25°C), 5 μL aliquots of 125 mM paromomycin in its free base form (preadjusted to pH 7.0 by addition of HCl) were sequentially injected into a 10-mM sodium sulfate solution. This experiment was accompanied by the corresponding control experiment in which 5 μL aliquots of the drug were injected into water alone. The duration of each injection was 5 s and the initial delay before the first injection was 60 s. The delay between injections was 900 s. The heat associated with each drug-water injection was subtracted from the corresponding heat associated with each drug-sulfate injection to yield the heat of drug binding for that injection. The resulting corrected injection heats were plotted as a function of the [drug]/[sulfate] ratio and fit with a model for one set of binding sites.
Analysis of the pH dependence of the ITC-derived enthalpy of drug protonation
At any given value of pH, the fraction (fj) of a given drug amino group (j) of known pKa that exists in the deprotonated (NH2) state is given by the Henderson-Hasselbalch relationship:
 |
(1) |
The extent (qj) to which the jth amino group becomes protonated as a result of an HCl injection at a given pH can be described by the derivative of Eq. 1 with respect to pH:
 |
(2) |
Paromomycin has five ionizable amino groups with differing pKa values. Thus, the extent of drug protonation (qdrug) that results from an HCl injection is given by
 |
(3) |
The observed enthalpy of drug protonation (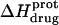 ) at a given pH can be described by the following equation:
) at a given pH can be described by the following equation:
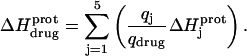 |
(4) |
In this equation, 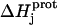 is the enthalpy for protonation of the jth amino group. The pH-dependent protonation enthalpy data obtained by ITC were fit with Eq. 4 using the Origin version 7.0 software suite.
is the enthalpy for protonation of the jth amino group. The pH-dependent protonation enthalpy data obtained by ITC were fit with Eq. 4 using the Origin version 7.0 software suite.
RESULTS AND DISCUSSION
Temperature and pH-dependent 15N NMR characterizations of paromomycin in its free base form
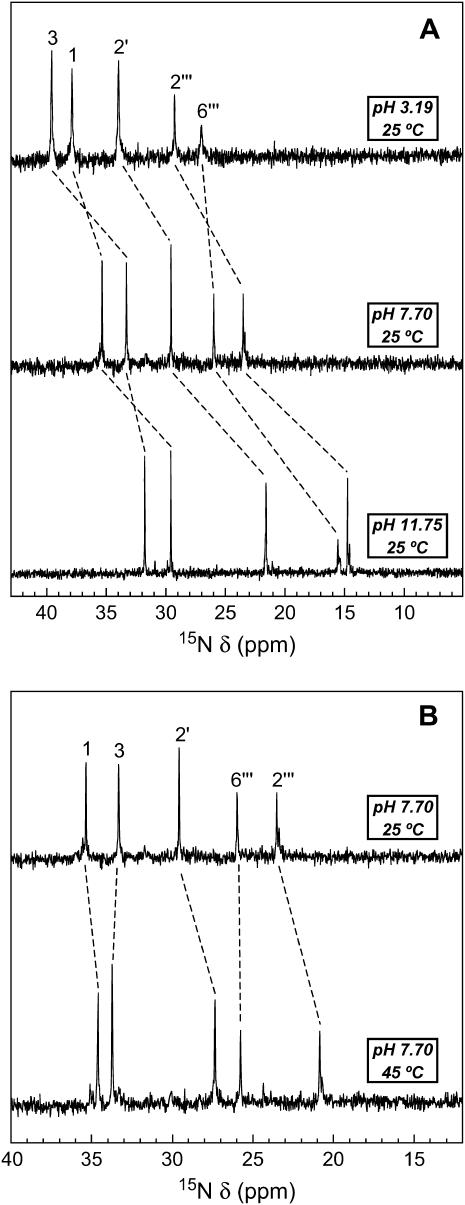
We monitored the 15N NMR spectrum of paromomycin base as a function of pH and temperature. Fig. 2 A shows the 15N NMR spectra of paromomycin base at 25°C and three representative pH values (3.19, 7.70, and 11.75). The spectrum at pH 3.19 reflects that of the fully protonated form of paromomycin, with the spectrum at pH 11.75 reflecting that of the fully deprotonated form of the drug. Note that each amino nitrogen peak shifts upfield with increasing pH, an observation indicating that each NH2 nitrogen resonates at a lower frequency than the corresponding NH3 nitrogen. Such pH-induced upfield shifts of amino nitrogen resonance frequencies have been previously observed for a number of different aminoglycosides, including neomycin, lividomycin, tobramycin, gentamicin, kanamycin B, and amikacin (38,42–45,47). Between pH 3.19 and 7.70, the peaks corresponding to the 1-, 3-, 2′-, and 2‴-nitrogens shift further upfield than the peak corresponding to the 6‴-nitrogen, with the reverse being true between pH 7.70 and 11.75. Thus, the 6‴-amino group is more basic than the other four amino groups, an observation consistent with it being the only alkyl amine among the five amino groups.
FIGURE 2.
Temperature and pH dependence of the 15N NMR spectrum of the free base form of paromomycin. The resonances corresponding to the five amino nitrogens are indicated, with the pH- and temperature-induced shifts of these resonances being denoted by the dashed lines. The 15N chemical shifts (δ) are reported relative to NH3 using 1 M [15N]urea in DMSO as an external standard, with the 15N chemical shift of the reference set to 77.0 ppm. (A) 15N NMR spectra of the free base form of paromomycin at 25°C and pH values of 3.19 (top), 7.70 (middle), and 11.75 (bottom). (B) 15N NMR spectra of the free base form of paromomycin at pH 7.70 and temperatures of 25°C (top) and 45°C (bottom).
Fig. 2 B shows the 15N NMR spectra of paromomycin base at pH 7.70 and temperatures of either 25 or 45°C. Note that the peaks corresponding to the 1-, 2′-, and 2‴-nitrogens shift upfield with increasing temperature. These temperature-induced upfield shifts are indicative of decreased protonation (i.e., decreased basicity) of the 1-, 2′-, and 2‴-amino groups with increasing temperature at pH 7.70, a conclusion verified by our temperature-dependent pKa analyses described in the next section. In contrast to the 1-, 2′-, and 2‴-nitrogen peaks at pH 7.70, the 3- and 6‴-nitrogen peaks do not undergo a shift with increasing temperature. One possible interpretation of this observation is that the basicities of the 3- and 6‴-amino groups are not temperature dependent. An alternative explanation is that the effects of temperature on the basicities of the 3- and 6‴-amino groups are not detectable at pH 7.70 over the temperature range of 25–45°C. As discussed below, our temperature-dependent pKa analyses support the latter interpretation.
The pKa values of the five paromomycin amino groups decrease with increasing temperature
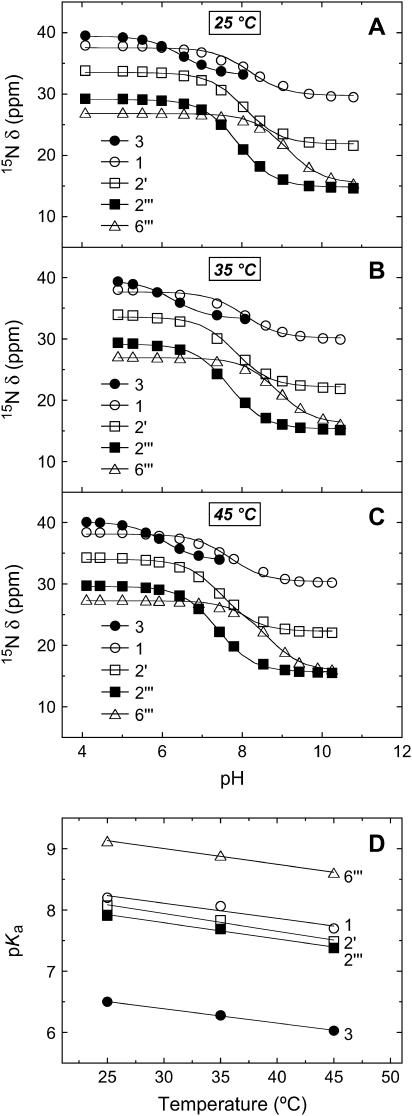
We monitored the pH dependencies of the 15N chemical shifts (δ) of the five amino nitrogens of paromomycin base at 25, 35, and 45°C, with the resulting pH profiles being shown in Fig. 3, A–C, respectively. Estimates of the pKa values for the drug amino groups were derived from nonlinear least squares fits (depicted as solid lines in Fig. 3, A–C) of the pH profiles with the following relationship:
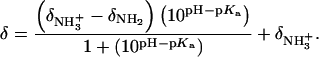 |
(5) |
FIGURE 3.
pH dependence of the 15N chemical shifts (δ) of the free base form of paromomycin at 25°C (A), 35°C (B), and 45°C (C). The 15N chemical shifts are reported as described in the legend to Fig. 2. The continuous lines reflect the calculated fits of the experimental data using Eq. 5. (D) Temperature dependence of the pKa values for the five paromomycin amino groups. The experimental data points were fit by linear regression to yield the solid lines.
In this relationship, 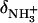 and
and 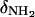 are the 15N chemical shifts of the amino nitrogens in their
are the 15N chemical shifts of the amino nitrogens in their 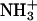 and NH2 states, respectively. The pKa values to emerge from the fits of the pH profiles shown in Fig. 3, A–C, are listed in Table 1. The corresponding values of
and NH2 states, respectively. The pKa values to emerge from the fits of the pH profiles shown in Fig. 3, A–C, are listed in Table 1. The corresponding values of 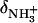 and δNH2 to emerge from these fits are summarized in Table S1 of the Supplementary Material.
and δNH2 to emerge from these fits are summarized in Table S1 of the Supplementary Material.
TABLE 1.
15N NMR-derived pKa values for the amino groups of paromomycin free base at 25, 35, and 45°C
| Amino group* | 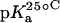 |
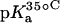 |
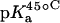 |
ΔpKa/°C† |
|---|---|---|---|---|
| 1 | 8.20 ± 0.07 | 8.06 ± 0.07 | 7.70 ± 0.06 | −0.025 ± 0.006 |
| 3 | 6.50 ± 0.03 | 6.21 ± 0.06 | 6.04 ± 0.02 | −0.023 ± 0.001 |
| 2′ | 8.07 ± 0.04 | 7.83 ± 0.06 | 7.49 ± 0.04 | −0.029 ± 0.003 |
| 2‴ | 7.91 ± 0.02 | 7.69 ± 0.03 | 7.38 ± 0.02 | −0.027 ± 0.003 |
| 6‴ | 9.13 ± 0.03 | 8.89 ± 0.04 | 8.61 ± 0.03 | −0.026 ± 0.001 |
pKa values were derived from fits of the pH-dependent 15N chemical shift data shown in Fig. 3 using Eq. 5. The indicated uncertainties reflect the standard deviations of the experimental data from the fitted curves (depicted as solid lines in Fig. 3).
Values of ΔpKa/°C were determined by linear regression analyses of the pKa versus temperature plots shown in Fig. 3 D. The indicated uncertainties reflect the standard deviations of the experimental data from the fitted lines.
Inspection of the data in Table 1 reveals that the pKa values for all of the amino groups of paromomycin in its free base form decrease with increasing temperature. Fig. 3 D graphically depicts these temperature dependencies in the form of pKa versus temperature plots, which are linear in nature. The slopes of these linear plots provide quantitative estimates of ΔpKa/°C for the drug amino groups. Linear regression analyses of these plots (depicted as solid lines in Fig. 3 D) yields ΔpKa/°C values that range from −0.023 to −0.029 for the five amino groups (see Table 1). In other words, the pKa values of the paromomycin amino groups decrease by an average of 0.026 pH units per increase in temperature of 1°C. This temperature dependence of pKa for the paromomycin amino groups implies that the charged state of paromomycin can vary significantly with temperature. As an illustrative example, the pKa values at 25°C predict an average charge of +3.41 for paromomycin base at pH 7.5, with the predicted average charge at 45°C being only +2.50 at the same pH value.
The 15N NMR-derived pKa values associated with the free base form of paromomycin are lower in magnitude than the corresponding values associated with the sulfate salt form of the drug
At 25°C, the pKa values of paromomycin base range from 6.50 to 9.13 (see Table 1). We have previously reported (38) the following 15N NMR-derived pKa values for the sulfate salt form of paromomycin at 25°C: 7.07 for the 3-amino group, 8.25 for the 2‴-amino group, 8.35 for the 2′-amino group, 8.65 for the 1-amino group, and 9.46 for the 6‴-amino group. Note that these pKa values are 0.26–0.57 pH units higher than the corresponding values for the free base form of the drug reported here in Table 1, with the difference in pKa between the two forms of the drug being smallest for the 2′-amino group and largest for the 3-amino group. We have observed a similar trend when comparing the 15N NMR-derived pKa values for the sulfate salt and free base forms of the aminoglycosides neomycin and kanamycin B (not shown). Taken together, these results indicate that the presence of sulfate counterions increases apparent aminoglycoside pKa values determined by natural abundance 15N NMR. It is likely that this effect is not limited to sulfate counterions, although the magnitude of the effect may depend on the identity of the counterion.
Calorimetric detection and characterization of interactions between sulfate ions and the free base form of paromomycin
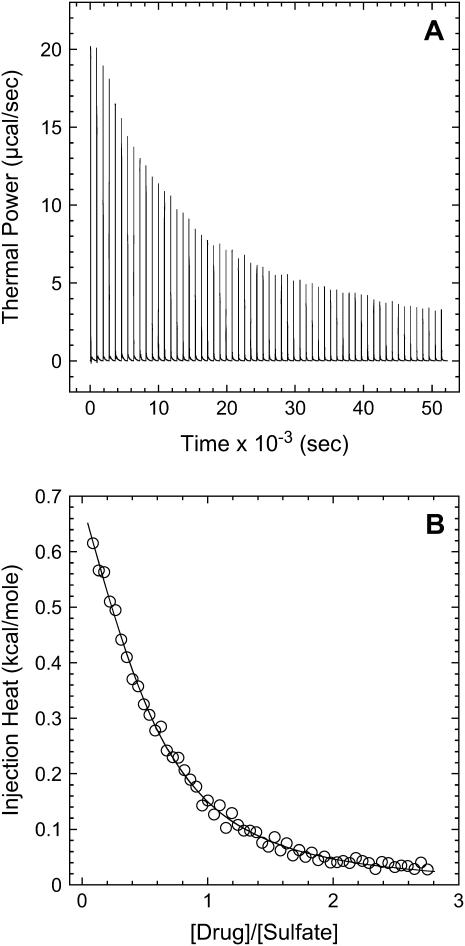
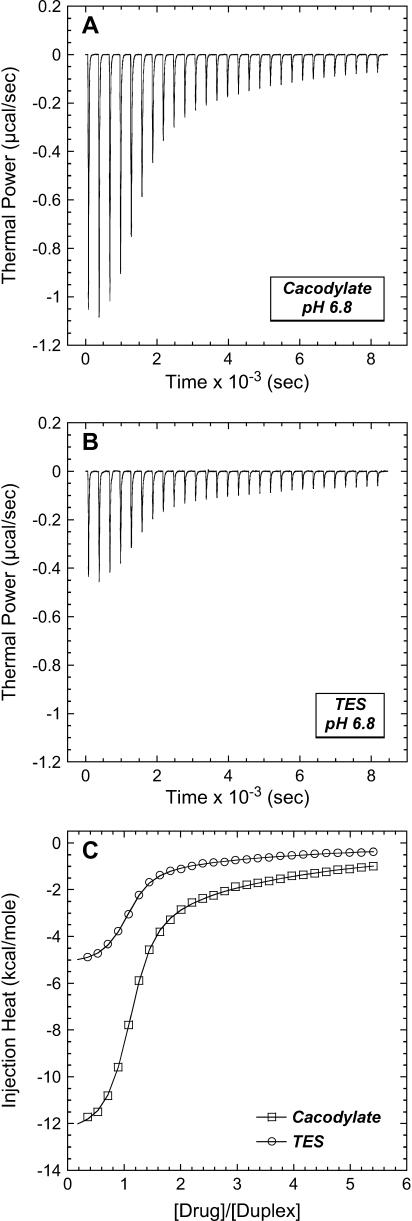
One potential explanation for the sulfate-induced increase of the 15N NMR-derived pKa values is the stabilization of the cationic (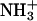 ) forms of the drug amino groups through electrostatically driven interactions with the sulfate anions. Such interactions are likely to be weak, but would be favored at the high drug concentrations (≥812 mM) used in the 15N NMR studies. We probed for such interactions using ITC. Specifically, we monitored the observed heat associated with sequential injection of 125 mM paromomycin (in its free base form) into a solution of 10 mM sodium sulfate at 25°C. The resulting ITC profile is shown in Fig. 4. Each of the heat burst curves in panel A of Fig. 4 corresponds to a single paromomycin injection. Note the nonlinearly decreasing nature of the heat burst curve peak heights, an observation consistent with an interaction between the injected drug and the sulfate ions. The heats derived from integration of the heat burst curves in Fig. 4 A were corrected for drug dilution effects as described in the Materials and Methods, with the resulting corrected injection heats being shown in Fig. 4 B. These corrected injection heats were fit with a model for one set of binding sites (depicted as a solid line in Fig. 4 B). This fit yielded a binding stoichiometry (N) of 0.44 ± 0.02 drug molecules per sulfate ion. In other words, approximately two sulfate ions bind to a single drug molecule. Note that each divalent sulfate anion is capable of interacting with more than one cationic drug amino group. A second binding parameter to emerge from the fit of the corrected injection heat profile shown in Fig. 4 B was a binding enthalpy (ΔHbind) of +1.2 ± 0.1 kcal/mol. This endothermic (unfavorable) binding enthalpy indicates that the paromomycin-sulfate interaction is entropically driven at 25°C, a driving force that may reflect desolvation of the drug and sulfate ions upon complex formation. A third binding parameter to emerge from the fit of the injection heat profile shown in Fig. 4 B was an association constant (Ka) of 266 ± 15 M−1. This affinity explains why the presence of sulfate counterions increases the pKa values determined by 15N NMR, because virtually every drug molecule is bound by at least one sulfate ion at the drug concentrations (≥812 mM) used in the NMR studies.
) forms of the drug amino groups through electrostatically driven interactions with the sulfate anions. Such interactions are likely to be weak, but would be favored at the high drug concentrations (≥812 mM) used in the 15N NMR studies. We probed for such interactions using ITC. Specifically, we monitored the observed heat associated with sequential injection of 125 mM paromomycin (in its free base form) into a solution of 10 mM sodium sulfate at 25°C. The resulting ITC profile is shown in Fig. 4. Each of the heat burst curves in panel A of Fig. 4 corresponds to a single paromomycin injection. Note the nonlinearly decreasing nature of the heat burst curve peak heights, an observation consistent with an interaction between the injected drug and the sulfate ions. The heats derived from integration of the heat burst curves in Fig. 4 A were corrected for drug dilution effects as described in the Materials and Methods, with the resulting corrected injection heats being shown in Fig. 4 B. These corrected injection heats were fit with a model for one set of binding sites (depicted as a solid line in Fig. 4 B). This fit yielded a binding stoichiometry (N) of 0.44 ± 0.02 drug molecules per sulfate ion. In other words, approximately two sulfate ions bind to a single drug molecule. Note that each divalent sulfate anion is capable of interacting with more than one cationic drug amino group. A second binding parameter to emerge from the fit of the corrected injection heat profile shown in Fig. 4 B was a binding enthalpy (ΔHbind) of +1.2 ± 0.1 kcal/mol. This endothermic (unfavorable) binding enthalpy indicates that the paromomycin-sulfate interaction is entropically driven at 25°C, a driving force that may reflect desolvation of the drug and sulfate ions upon complex formation. A third binding parameter to emerge from the fit of the injection heat profile shown in Fig. 4 B was an association constant (Ka) of 266 ± 15 M−1. This affinity explains why the presence of sulfate counterions increases the pKa values determined by 15N NMR, because virtually every drug molecule is bound by at least one sulfate ion at the drug concentrations (≥812 mM) used in the NMR studies.
FIGURE 4.
ITC profile (acquired at 25°C and pH 7.0) for the titration of the free base form of paromomycin into a sodium sulfate solution. Each of the heat burst curves in panel A is the result of a 5-μL injection of 125 mM paromomycin, with the sodium sulfate concentration being 10 mM. The corrected injection heats shown in panel B were derived by integration of the heat burst curves in panel A, followed by subtraction of the corresponding dilution heats resulting from control titrations of drug into water alone. The data points in panel B reflect the corrected injection heats, while the continuous line reflects the calculated fit of the data using a model for one set of binding sites.
Paromomycin binding to its pharmacologically relevant target (the 16 S rRNA A-site) is coupled to drug protonation, with the extent of binding-linked protonation being consistent with the pKa values determined for the free base and not the sulfate salt form of the drug
We have previously demonstrated that the binding of 2-DOS aminoglycosides (including paromomycin) to their pharmacologically relevant target, the 16 S rRNA A-site, is linked to drug protonation (37–40). Given the differences between the pKa values of the free base and sulfate salt forms of paromomycin noted above, it is of interest to determine which set of pKa values is consistent with the observed extent of RNA binding-linked drug protonation. Toward this end, we used ITC to determine the observed enthalpies (ΔHobs) that accompany the injection of paromomycin sulfate into a solution containing an E. coli 16 S rRNA A-site model oligonucleotide (schematically depicted in Fig. 5) at pH 6.8 in the presence of two different buffers (cacodylate and TES) that exhibit differing heats of ionization (ΔHion). The number of drug protons (Δndrug) linked to RNA binding at this pH can be determined by simultaneous solution of the following two equations (48,49):
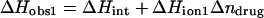 |
(6a) |
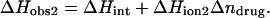 |
(6b) |
FIGURE 5.
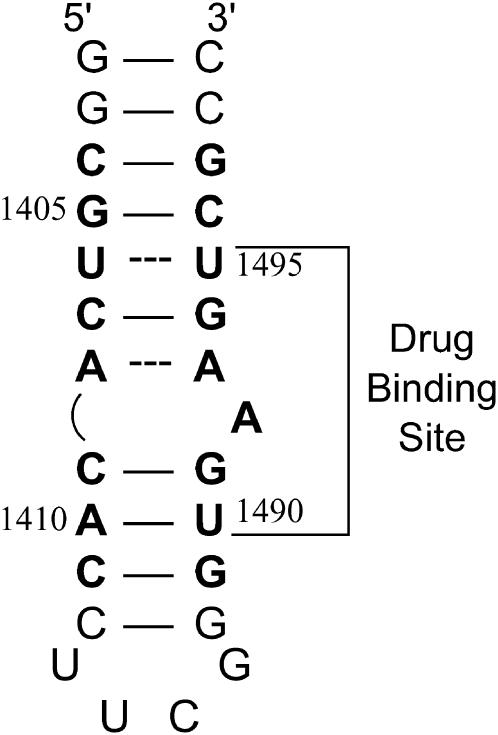
NMR-derived (53–55) secondary structure of the E. coli 16 S rRNA A-site model oligonucleotide used in this study. Watson-Crick basepairs are denoted by solid lines, whereas mismatched basepairs are denoted by dashed lines. Bases present in E. coli 16 S rRNA are depicted in bold face, and are numbered as they are in 16 S rRNA. The paromomycin binding site, as revealed by NMR and footprinting studies (53,54,56), is indicated.
In these equations, the numerical subscripts refer to the different buffers and ΔHint is the intrinsic enthalpy, which differs from ΔHobs in that it excludes contributions from buffer ionization. Although the value of ΔHint is independent of buffer ionization effects, it includes contributions from both intrinsic drug-RNA interactions and drug-protonation reactions.
The profiles resulting from our buffer-dependent ITC characterizations are shown in Fig. 6. Each of the heat burst curves in panels A and B of Fig. 6 corresponds to a single paromomycin injection. The heats derived from integration of these heat burst curves were corrected for drug dilution effects as described in the Materials and Methods, with the resulting corrected injection heats being shown in Fig. 6 C. Note that the magnitude of the exothermic signal is substantially greater in cacodylate buffer (ΔHion = −0.47 kcal/mol) than in TES buffer (ΔHion = +7.83 kcal/mol). This observation is indicative of binding-linked drug protonation, consistent with our previous results demonstrating such behavior at pH values >5.5 (37,38). Table 2 lists the ΔHobs values derived from fits of the injection heat profiles shown in Fig. 6 C, as well as the corresponding values of Δndrug and ΔHint calculated using Eqs. 6a and 6b. Inspection of these data reveals a Δndrug value of 0.88, indicating that paromomycin binding is linked to the uptake of 0.88 protons at pH 6.8. Table 2 also summarizes the protonation states of paromomycin (expressed as fdrug = fraction of drug amino groups in their NH2 states) at pH 6.8 predicted by the NMR-derived pKa values for the free base and sulfate salt forms of the drug. Note that the pKa values for the sulfate salt predict that 0.43 out of 5.00 amino groups are deprotonated at pH 6.8. By contrast, the pKa values for the free base form of the drug predict that 0.83 out of 5.00 amino groups are deprotonated at this pH. The observed Δndrug value of 0.88 at pH 6.8 is indicative of at least that number of amino groups being deprotonated in the unbound (RNA-free) state of the drug. This state of deprotonation is inconsistent with that predicted by the pKa values of the sulfate salt. In other words, the observed value of Δndrug for the paromomycin-RNA interaction is consistent with the pKa values of the free base and not the sulfate salt form of the drug, even though the sulfate salt form of the drug was used in the RNA binding ITC experiments. Recall that the 15N NMR-derived pKa values for the sulfate salt form of paromomycin were higher than the corresponding values for the free base form of the drug due to interactions between the sulfate ions and the drug amino groups. In addition, these interactions were associated with a Ka value of 266 M−1. Note that the concentration of paromomycin sulfate used in the RNA binding ITC experiments ranged from 0 to 45 μM, a range of concentrations at least 18,000-fold lower than that used in the 15N NMR experiments. Over the range of paromomycin sulfate concentrations used in the ITC studies, the drug molecules are essentially free of sulfate interactions (given the Ka value of 266 M−1 we observed for the sulfate-drug interactions), and thus behave like the free base. It is also important to note that the RNA binding ITC studies were conducted in the presence of 150 mM Na+, as compared to 20 mM Na+ in the sulfate binding ITC study. With the reasonable assumption that the binding of paromomycin to sulfate ions is electrostatically driven and therefore salt sensitive, the Ka value for the sulfate-drug interactions in the presence of 150 mM Na+ should be <266 M−1. This reduction in Ka would serve to further reduce the already low degree of sulfate-drug interactions that occur over the range of drug concentrations used in the RNA binding ITC studies.
FIGURE 6.
ITC profiles (acquired at 25°C and pH 6.8) for the titration of paromomycin sulfate into a solution containing the E. coli 16 S rRNA A-site model oligonucleotide in cacodylate (A) and TES (B) buffer. Each of the heat burst curves in panels A and B is the result of a 10-μL injection of 250-μM paromomycin sulfate, with the RNA concentration being 10-μM in duplex. The corrected injection heats shown in panel C were derived by integration of the heat burst curves in panels A and B, followed by subtraction of the corresponding dilution heats resulting from control titrations of drug into buffer alone. The data points in panel C reflect the corrected injection heats, whereas the continuous lines reflect the calculated fits of the data using a model for two sets of binding sites. Each experimental solution contained 10 mM buffer, 0.1 mM EDTA, and sufficient NaCl to bring the total Na+ concentration to 150 mM.
TABLE 2.
Number of protons linked to the binding of paromomycin to the E. coli 16 S rRNA A-site model oligonucleotide at pH 6.8
| Buffer (10 mM) | ΔHion* (kcal/mol) | ΔHobs† (kcal/mol) | ΔHint‡ (kcal/mol) | Δndrug‡ | fdrug§ (Sulfate salt) | fdrug§ (Free base) |
|---|---|---|---|---|---|---|
| Cacodylate | −0.47 | −12.5 ± 0.1 | −12.1 ± 0.1 | 0.88 ± 0.03 | 0.43 ± 0.01 | 0.83 ± 0.03 |
| TES | +7.83 | −5.2 ± 0.1 |
Ionization heats (ΔHion) at 25°C for the indicated buffers were taken from Fukada and Takahashi (52).
ΔHobs values were derived from fits of the ITC profiles shown in Fig. 6 C, with the indicated uncertainties reflecting the standard deviations of the experimental data from the fitted curves.
Values of ΔHint and Δndrug were determined using Eqs. 6a and 6b, with the indicated uncertainties reflecting the maximum errors in ΔHobs as propagated through these equations.
Values of fdrug were calculated from the 15N NMR-derived pKa values for the sulfate salt and free base forms of paromomycin using the Henderson-Hasselbalch relationship: 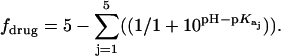 In this relationship,
In this relationship, 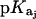 is the pKa value for the jth amino group. The indicated uncertainties in fdrug reflect the maximum errors in the NMR-derived pKa values as propagated through the above relationship.
is the pKa value for the jth amino group. The indicated uncertainties in fdrug reflect the maximum errors in the NMR-derived pKa values as propagated through the above relationship.
The observed enthalpy of paromomycin protonation varies with pH
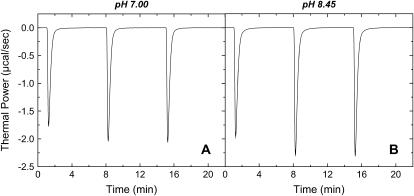
We used ITC to determine the enthalpy of paromomycin protonation. Fig. 7 shows representative ITC data obtained at 25°C for three sequential 10-μL injections of 1 mM HCl into a 1-mM solution of paromomycin base at either pH 7.00 (panel A) or pH 8.45 (panel B). Each heat burst curve in Fig. 7 corresponds to a single HCl injection. Inspection of these ITC data reveals the following significant features: i), the heat burst curves at both values of pH are exothermic in nature, an observation indicating that at least one drug amino group has an exothermic protonation enthalpy ( ) at 25°C. ii), At each pH value, the intensity of the exothermic signal corresponding to the first injection is smaller in magnitude than the signals corresponding to the second and third injections. The comparatively small magnitude of the signal corresponding to the first injection is a commonly observed phenomenon in ITC experiments, and is instrumental in origin. iii), At each pH value, the intensities of the exothermic signals corresponding to the second and third injections are similar in magnitude. This observation is consistent with all the protons from the injected HCl binding to the drug under the conditions employed. iv), The magnitudes of the exothermic signals are greater at pH 8.45 than at pH 7.00. This result implies that the value of
) at 25°C. ii), At each pH value, the intensity of the exothermic signal corresponding to the first injection is smaller in magnitude than the signals corresponding to the second and third injections. The comparatively small magnitude of the signal corresponding to the first injection is a commonly observed phenomenon in ITC experiments, and is instrumental in origin. iii), At each pH value, the intensities of the exothermic signals corresponding to the second and third injections are similar in magnitude. This observation is consistent with all the protons from the injected HCl binding to the drug under the conditions employed. iv), The magnitudes of the exothermic signals are greater at pH 8.45 than at pH 7.00. This result implies that the value of 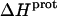 for one or more of the drug amino groups differs in magnitude from the corresponding values of
for one or more of the drug amino groups differs in magnitude from the corresponding values of 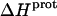 for the other amino groups. In other words, the pH-induced change in the observed heat of drug protonation reflects proton binding to two or more amino groups with differing protonation enthalpies.
for the other amino groups. In other words, the pH-induced change in the observed heat of drug protonation reflects proton binding to two or more amino groups with differing protonation enthalpies.
FIGURE 7.
ITC heat burst curves resulting from 10 μL injections of 1 mM HCl into a solution containing 2 mM of paromomycin in its free base form at 25°C and pH values of 7.00 (A) and 8.45 (B). All experiments were conducted in the presence of 100 mM KCl.
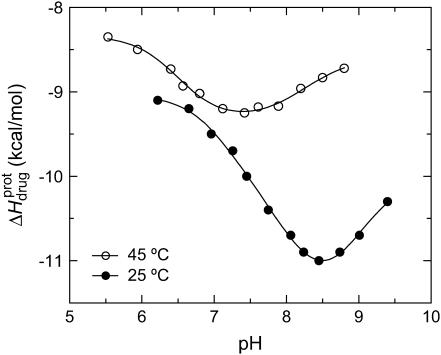
The ITC data shown in Fig. 7, as well as corresponding data (not shown) acquired at 25°C and other values of pH (ranging from 6.22 to 9.40), were analyzed as described in the Materials and Methods to yield the observed enthalpies of drug protonation (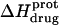 ) depicted by the solid circles in Fig. 8. In addition, Fig. 8 also shows the corresponding pH dependence of
) depicted by the solid circles in Fig. 8. In addition, Fig. 8 also shows the corresponding pH dependence of 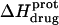 at 45°C (depicted by the open circles). At both temperatures, increasing pH results in an initial decrease in
at 45°C (depicted by the open circles). At both temperatures, increasing pH results in an initial decrease in 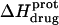 followed by an increase. Note that the pH at which
followed by an increase. Note that the pH at which 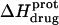 reaches a minimum is ∼1 unit lower at 45°C than at 25°C. This observation is consistent with our temperature-dependent 15N NMR results, which revealed an inverse relationship between temperature and the pKa of each paromomycin amino group (see Fig. 3 and Table 1). Further note that, at any given pH, the value of
reaches a minimum is ∼1 unit lower at 45°C than at 25°C. This observation is consistent with our temperature-dependent 15N NMR results, which revealed an inverse relationship between temperature and the pKa of each paromomycin amino group (see Fig. 3 and Table 1). Further note that, at any given pH, the value of 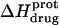 at 45°C is less exothermic than the corresponding value of
at 45°C is less exothermic than the corresponding value of 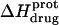 at 25°C. This result implies that the
at 25°C. This result implies that the 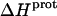 value of at least one drug amino group is temperature dependent, with increasing temperature resulting in a less exothermic value of
value of at least one drug amino group is temperature dependent, with increasing temperature resulting in a less exothermic value of 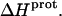 In this connection, our heat capacity change determinations discussed below reveal that three paromomycin amino groups exhibit such a behavior.
In this connection, our heat capacity change determinations discussed below reveal that three paromomycin amino groups exhibit such a behavior.
FIGURE 8.
pH dependence of the observed protonation enthalpy of paromomycin (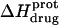 ) in its free base form acquired at 25°C (•) and 45°C (○). Values of
) in its free base form acquired at 25°C (•) and 45°C (○). Values of 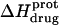 were derived from ITC experiments similar to and including those shown in Fig. 7 using an approach detailed in Materials and Methods. The continuous lines reflect the calculated fits of the data using Eq. 4.
were derived from ITC experiments similar to and including those shown in Fig. 7 using an approach detailed in Materials and Methods. The continuous lines reflect the calculated fits of the data using Eq. 4.
Protonation of the five paromomycin amino groups is associated with an exothermic enthalpy change, the magnitude of which is not correlated with pKa
The pH-dependent 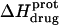 profiles shown in Fig. 8 were fit with Eq. 4 to yield quantitative estimates of the
profiles shown in Fig. 8 were fit with Eq. 4 to yield quantitative estimates of the 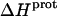 values for the five paromomycin amino groups. The resulting values of
values for the five paromomycin amino groups. The resulting values of 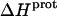 are listed in Table 3. Note that protonation of all five amino groups is exothermic, with
are listed in Table 3. Note that protonation of all five amino groups is exothermic, with 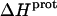 values at 25°C ranging from −5.4 kcal/mol (for the 2‴-amino group) to −15.8 kcal/mol (for the 1-amino group). This range of
values at 25°C ranging from −5.4 kcal/mol (for the 2‴-amino group) to −15.8 kcal/mol (for the 1-amino group). This range of 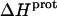 values is consistent with the range of previously reported protonation enthalpies for the amino groups of numerous different types of amine derivatives, including glucosamines, alkylamines, phenylamines, and amino acids (50). Further note that the uncertainties (which range from ∼18 to 43%) associated with the
values is consistent with the range of previously reported protonation enthalpies for the amino groups of numerous different types of amine derivatives, including glucosamines, alkylamines, phenylamines, and amino acids (50). Further note that the uncertainties (which range from ∼18 to 43%) associated with the 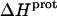 values of the 1-, 2′-, and 2‴-amino groups are substantively greater than the corresponding uncertainties (of ∼1%) associated with the
values of the 1-, 2′-, and 2‴-amino groups are substantively greater than the corresponding uncertainties (of ∼1%) associated with the 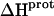 values of the 3- and 6‴-amino groups. The comparatively large uncertainties associated with the
values of the 3- and 6‴-amino groups. The comparatively large uncertainties associated with the 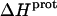 values of the 1-, 2′-, and 2‴-amino groups stem from the similar pKa values of these three groups, which are all within ∼0.3 pH units of each other. A comparison of the
values of the 1-, 2′-, and 2‴-amino groups stem from the similar pKa values of these three groups, which are all within ∼0.3 pH units of each other. A comparison of the 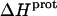 data in Table 3 with the corresponding pKa data in Table 1 reveals that the magnitude of
data in Table 3 with the corresponding pKa data in Table 1 reveals that the magnitude of 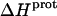 does not correlate with the basicity (i.e., pKa) of the amino group. As an illustrative example, the
does not correlate with the basicity (i.e., pKa) of the amino group. As an illustrative example, the 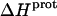 values of the 6‴- and 3-amino groups at 25°C are similar (−9.4 and −9.0 kcal/mol, respectively). By contrast, the pKa values of these two groups at 25°C differ markedly from one another (9.13 for the 6‴-amino group versus 6.50 for the 3-amino group).
values of the 6‴- and 3-amino groups at 25°C are similar (−9.4 and −9.0 kcal/mol, respectively). By contrast, the pKa values of these two groups at 25°C differ markedly from one another (9.13 for the 6‴-amino group versus 6.50 for the 3-amino group).
TABLE 3.
Temperature dependent enthalpy and corresponding heat capacity changes for protonation of the five paromomycin amino groups
| Amino group |
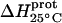 * (kcal/mol) * (kcal/mol) |
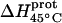 * (kcal/mol) * (kcal/mol) |
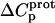 † (cal/mol K) † (cal/mol K) |
|---|---|---|---|
| 1 | −15.8 ± 3.4 | −7.9 ± 1.4 | +392 ± 244 |
| 3 | −9.0 ± 0.1 | −8.2 ± 0.1 | +38 ± 4 |
| 2′ | −11.5 ± 5.0 | −12.7 ± 3.6 | −58 ± 430 |
| 2‴ | −5.4 ± 1.7 | −7.3 ± 2.2 | −93 ± 199 |
| 6‴ | −9.4 ± 0.1 | −8.4 ± 0.1 | +48 ± 12 |
Defining the heat capacity changes for protonation of the paromomycin amino groups
The heat capacity change associated with a protonation reaction (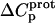 ) can be determined from the temperature dependence of the protonation enthalpy. To this end, the values of
) can be determined from the temperature dependence of the protonation enthalpy. To this end, the values of 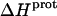 determined at 25 and 45°C enabled us to determine
determined at 25 and 45°C enabled us to determine 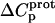 for the five paromomycin amino groups using the following standard relationship:
for the five paromomycin amino groups using the following standard relationship:
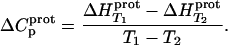 |
(7) |
The resulting values of 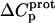 are listed in Table 3. Inspection of these data reveals that the heat capacity changes for protonation of the 1-, 3-, and 6‴-amino groups are positive and range from 38 ± 4 cal/mol K (for protonation of the 3-amino group) to 392 ± 244 (for protonation of the 1-amino group). The positive
are listed in Table 3. Inspection of these data reveals that the heat capacity changes for protonation of the 1-, 3-, and 6‴-amino groups are positive and range from 38 ± 4 cal/mol K (for protonation of the 3-amino group) to 392 ± 244 (for protonation of the 1-amino group). The positive 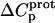 values for these three amino groups account for the less exothermic nature of the
values for these three amino groups account for the less exothermic nature of the 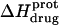 versus pH profile acquired at 45°C relative to that acquired at 25°C (see Fig. 8). Furthermore, the signs and magnitudes of these
versus pH profile acquired at 45°C relative to that acquired at 25°C (see Fig. 8). Furthermore, the signs and magnitudes of these 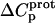 values are consistent with those predicted for charge-transfer (e.g., protonation) reactions based on the Poisson-Boltzmann equation (51). Note that the observed
values are consistent with those predicted for charge-transfer (e.g., protonation) reactions based on the Poisson-Boltzmann equation (51). Note that the observed 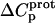 values for the 2′- and 2‴-amino groups are negative. However, the magnitudes of these values are sufficiently small so as to fall within the experimental uncertainty. Thus, the uncertainty of our data does not permit us to accurately define the
values for the 2′- and 2‴-amino groups are negative. However, the magnitudes of these values are sufficiently small so as to fall within the experimental uncertainty. Thus, the uncertainty of our data does not permit us to accurately define the 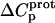 values for the 2′- and 2‴-amino groups, even though these values, like those for the 1-, 3-, and 6‴-amino groups, may be nonzero.
values for the 2′- and 2‴-amino groups, even though these values, like those for the 1-, 3-, and 6‴-amino groups, may be nonzero.
Completing the thermodynamic profiles for protonation of the paromomycin amino groups
Armed with the NMR-derived pKa values listed in Table 1, we calculated the corresponding free energies of protonation (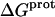 ) using the following relationship:
) using the following relationship:
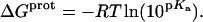 |
(8) |
These protonation free energies, coupled with the ITC-derived protonation enthalpies listed in Table 3, allowed us to calculate the corresponding protonation entropies (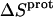 ) using the standard relationship
) using the standard relationship
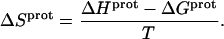 |
(9) |
Application of Eqs. 8 and 9 enabled us to generate complete thermodynamic profiles for protonation of the five paromomycin amino groups, with the resulting profiles at 25°C being listed in Table 4. Protonation of all five amino groups is enthalpically favorable (i.e., all five 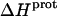 values are exothermic). However, the nature and magnitude of the entropic forces associated with protonation depend on the identity of the amino group. For the 3- and 2′-amino groups, the protonation entropies are essentially zero, with the differences between the determined values of
values are exothermic). However, the nature and magnitude of the entropic forces associated with protonation depend on the identity of the amino group. For the 3- and 2′-amino groups, the protonation entropies are essentially zero, with the differences between the determined values of 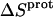 and zero being within the experimental uncertainty. In other words, protonation of these two amino groups is entropically neutral. In contrast to the values of
and zero being within the experimental uncertainty. In other words, protonation of these two amino groups is entropically neutral. In contrast to the values of 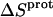 for the 3- and 2′-amino groups, the corresponding values for the 1-, 2‴-, and 6‴-amino groups are nonzero, with
for the 3- and 2′-amino groups, the corresponding values for the 1-, 2‴-, and 6‴-amino groups are nonzero, with 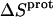 being negative for the 1-amino group and positive for the 2‴- and 6‴-amino groups. Thus, protonation of the 1-amino group is entropically unfavorable, while being entropically favorable for the 2‴- and 6‴-amino groups. Regarded as a whole, these observations indicate that protonation of the 1-, 3-, and 2′-amino groups is driven by enthalpic forces, which overcome neutral or unfavorable entropic forces. By contrast, protonation of the 2‴- and 6‴-amino groups is driven by positive contributions from both enthalpic and entropic forces, with the relative contributions being ∼50% enthalpic/50% entropic for the 2‴-amino group and 75% enthalpic/25% entropic for the 6‴-amino group.
being negative for the 1-amino group and positive for the 2‴- and 6‴-amino groups. Thus, protonation of the 1-amino group is entropically unfavorable, while being entropically favorable for the 2‴- and 6‴-amino groups. Regarded as a whole, these observations indicate that protonation of the 1-, 3-, and 2′-amino groups is driven by enthalpic forces, which overcome neutral or unfavorable entropic forces. By contrast, protonation of the 2‴- and 6‴-amino groups is driven by positive contributions from both enthalpic and entropic forces, with the relative contributions being ∼50% enthalpic/50% entropic for the 2‴-amino group and 75% enthalpic/25% entropic for the 6‴-amino group.
TABLE 4.
Thermodynamic profiles for protonation of the five paromomycin amino groups at 25°C
| Amino group |
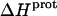 * (kcal/mol) * (kcal/mol) |
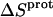 † (cal/mol K) † (cal/mol K) |
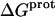 ‡ (kcal/mol) ‡ (kcal/mol) |
|---|---|---|---|
| 1 | −15.8 ± 3.4 | −15.4 ± −11.7 | −11.2 ± 0.1 |
| 3 | −9.0 ± 0.1 | +0.3 ± 1.0 | −8.9 ± 0.1 |
| 2′ | −11.5 ± 5.0 | −1.7 ± 17.1 | −11.0 ± 0.1 |
| 2‴ | −5.4 ± 1.7 | +18.1 ± 6.0 | −10.8 ± 0.1 |
| 6‴ | −9.4 ± 0.1 | +10.4 ± 0.7 | −12.5 ± 0.1 |
Validation of our calorimetrically derived values ΔHprot for the five paromomycin amino groups at 25 and 45°C
As noted in a previous section, the similar pKa values of the 1-, 2′-, and 2‴-amino groups cause our calorimetrically derived values of 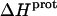 for these amino groups at 25 and 45°C to be associated with a greater of degree of uncertainty than the corresponding
for these amino groups at 25 and 45°C to be associated with a greater of degree of uncertainty than the corresponding 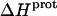 values for the 3- and 6‴-amino groups. These differential uncertainties in
values for the 3- and 6‴-amino groups. These differential uncertainties in 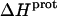 were conferred upon our calculated values of
were conferred upon our calculated values of 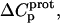 because the
because the 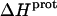 values acquired at 25 and 45°C were used to calculate
values acquired at 25 and 45°C were used to calculate 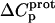 via Eq. 7. Given these uncertainties, we sought to validate our experimental values of
via Eq. 7. Given these uncertainties, we sought to validate our experimental values of 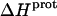 (and thus
(and thus 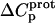 as well) by using them to calculate theoretical pKa values at 35°C, and subsequently comparing these calculated pKa values with our corresponding NMR-derived values. To this end, we used the calorimetrically derived
as well) by using them to calculate theoretical pKa values at 35°C, and subsequently comparing these calculated pKa values with our corresponding NMR-derived values. To this end, we used the calorimetrically derived 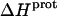 and
and 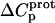 values listed in Table 3, coupled with the NMR-derived pKa values at 25°C listed in Table 1, to calculate theoretical pKa values at 35°C for the five paromomycin amino groups utilizing the following expression:
values listed in Table 3, coupled with the NMR-derived pKa values at 25°C listed in Table 1, to calculate theoretical pKa values at 35°C for the five paromomycin amino groups utilizing the following expression:
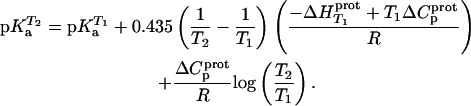 |
(10) |
In our application of this expression, T1 = 25°C (298.15 K) and T2 = 35°C (308.15 K). The resulting calculations yielded the following pKa values at 35°C: 7.87 ± 0.11 for the 1-amino group; 6.29 ± 0.01 for the 3-amino group; 7.79 ± 0.17 for the 2′-amino group; 7.77 ± 0.06 for the 2‴-amino group; and 8.91 ± 0.01 for the 6‴-amino group. These calculated pKa values at 35°C are in good agreement with the corresponding NMR-derived values listed in Table 1, the differences being within the collective uncertainties. This gratifying concordance validates not only our calorimetrically derived values of 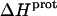 and
and 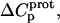 but also our delineation of the thermodynamic forces that govern the drug protonation reactions.
but also our delineation of the thermodynamic forces that govern the drug protonation reactions.
CONCLUDING REMARKS
We have used natural abundance 15N NMR and ITC to determine complete thermodynamic profiles (ΔH, ΔS, ΔG, ΔCp, pKa, and ΔpKa/°C) for the five protonation equilibria of the 2-DOS aminoglycoside paromomycin. To the best of our knowledge, this study represents the first such thermodynamic characterization of the pH and temperature-dependent properties of an aminoglycoside antibiotic. Significantly, the approach presented here can be applied to the characterization of any compound or biomolecule that contains multiple ionizable groups.
The linkage of drug protonation reactions to the interactions between drugs and macromolecules can have a profound effect on the observed binding thermodynamics. The affinities of aminoglycosides for a broad range of nucleic acid targets have been shown to decrease with increasing pH (5,33,36–38). In addition, this pH dependence of the binding energetics was shown to result from the linkage of drug protonation reactions to formation of the drug-nucleic acid complexes. Note that aminoglycoside protonation reactions are not only linked to the interactions between these drugs and nucleic acids, but also to the interactions of the drugs with modifying enzymes, which confer resistance to the microbes that carry them. In this connection, the Serpersu group has demonstrated that drug protonation reactions are linked to the binding of aminoglycosides to a phosphotransferase enzyme (41).
The type of pKa and thermodynamic information presented here is essential for understanding the nature of the linkage between drug-macromolecule binding and drug protonation, as well as the thermodynamic consequences of that linkage. In particular, such information enables one to: i), identify the specific amino groups whose protonation is linked to the binding interaction; ii), define the contributions that the relevant protonation reactions make to the observed binding thermodynamics; and iii), predict how the binding energetics will be affected by environmental conditions, such as temperature, pH, and ionic strength. Such capabilities are important elements of any rational drug design strategy.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Supplementary Material
Acknowledgments
This work was supported in part by National Institutes of Health grant CA097123. C.M.B. was supported by a National Institutes of Health training grant (5T32 GM08319) in Molecular Biophysics.
References
- 1.Puglisi, J. D., S. C. Blanchard, K. D. Dahlquist, R. G. Eason, D. Fourmy, S. R. Lynch, M. I. Recht, and S. Yoshizawa. 2000. Aminoglycoside antibiotics and decoding. In The Ribosome: Structure, Function, Antibiotics, and Cellular Interactions. R. A. Garrett, S. R. Douthwaite, A. Liljas, A. T. Matheson, P. B. Moore, and H. F. Noller, editors. ASM Press, Washington, DC. 419–429.
- 2.Arya, D. P., R. L. Coffee, Jr., B. Willis, and A. I. Abramovitch. 2001. Aminoglycoside-nucleic acid interactions: remarkable stabilization of DNA and RNA triple helicies by neomycin. J. Am. Chem. Soc. 123:5385–5395. [DOI] [PubMed] [Google Scholar]
- 3.Arya, D. P., R. L. Coffee Jr., and I. Charles. 2001. Neomycin-induced hybrid triplex formation. J. Am. Chem. Soc. 123:11093–11094. [DOI] [PubMed] [Google Scholar]
- 4.Arya, D. P., L. Xue, and B. Willis. 2003. Aminoglycoside (neomycin) preference is for A-form nucleic acids, not just RNA: results from a competition dialysis study. J. Am. Chem. Soc. 125:10148–10149. [DOI] [PubMed] [Google Scholar]
- 5.Barbieri, C. M., T.-K. Li, S. Guo, G. Wang, A. J. Shallop, W. Pan, G. Yang, B. L. Gaffney, R. A. Jones, and D. S. Pilch. 2003. Aminoglycoside complexation with a DNA·RNA hybrid duplex: the thermodynamics of recognition and inhibition of RNA processing enzymes. J. Am. Chem. Soc. 125:6469–6477. [DOI] [PubMed] [Google Scholar]
- 6.Li, T.-K., C. M. Barbieri, H.-C. Lin, A. B. Rabson, G. Yang, Y. Fan, B. L. Gaffney, R. A. Jones, and D. S. Pilch. 2004. Drug targeting of HIV-1 RNA·DNA hybrid structures: thermodynamics of recognition and impact of reverse transcriptase-mediated ribonuclease H activity and viral replication. Biochemistry. 43:9732–9742. [DOI] [PubMed] [Google Scholar]
- 7.Wallis, M. G., U. von Ahsen, R. Schroeder, and M. Famulok. 1995. A novel RNA motif for neomycin recognition. Chem. Biol. 2:543–552. [DOI] [PubMed] [Google Scholar]
- 8.Wang, Y., J. Killian, K. Hamasaki, and R. R. Rando. 1996. RNA molecules that specifically and stoichiometrically bind aminoglycoside antibiotics with high affinities. Biochemistry. 35:12328–12346. [DOI] [PubMed] [Google Scholar]
- 9.Lato, S. M., and A. D. Ellington. 1996. Screening chemical libraries for nucleic acid binding drugs by in vitro selection: a test case with lividomycin. Mol. Divers. 2:103–110. [DOI] [PubMed] [Google Scholar]
- 10.Jiang, L., A. K. Suri, R. Fiala, and D. J. Patel. 1997. Saccharide-RNA recognition in an aminoglycoside antibiotic-RNA aptamer complex. Chem. Biol. 4:35–50. [DOI] [PubMed] [Google Scholar]
- 11.Werstuck, G., and M. R. Green. 1998. Controlling gene expression in living cells through small molecule-RNA interactions. Science. 282:296–298. [DOI] [PubMed] [Google Scholar]
- 12.Jiang, L., and D. J. Patel. 1998. Solution structure of the tobramycin-RNA aptamer complex. Nat. Struct. Biol. 5:769–774. [DOI] [PubMed] [Google Scholar]
- 13.Patel, D. J., A. K. Suri, F. Jiang, L. Jiang, P. Fan, R. A. Kumar, and S. Nonin. 1997. Structure, recognition and adaptive binding in RNA aptamer complexes. J. Mol. Biol. 272:645–664. [DOI] [PubMed] [Google Scholar]
- 14.Jiang, L., A. Majumdar, W. Hu, T. J. Jaishree, W. Xu, and D. J. Patel. 1999. Saccharide-RNA recognition in a complex formed between neomycin B and an RNA aptamer. Structure. 7:817–827. [DOI] [PubMed] [Google Scholar]
- 15.Patel, D. J., and A. K. Suri. 2000. Structure, recognition and discrimination in RNA aptamer complexes with cofactors, amino acids, drugs and aminoglycoside antibiotics. J. Biotechnol. 74:39–60. [DOI] [PubMed] [Google Scholar]
- 16.Cowan, J. A., T. Ohyama, D. Wang, and K. Natarajan. 2000. Recognition of a cognate RNA aptamer by neomycin B: quantitative evaluation of hydrogen bonding and electrostatic interactions. Nucleic Acids Res. 28:2935–2942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kwon, M., S.-M. Chun, S. Jeong, and J. Yu. 2001. In vitro selection of RNA against kanamycin B. Mol. Cells. 11:303–311. [PubMed] [Google Scholar]
- 18.von Ahsen, U., J. Davies, and R. Schroeder. 1991. Antibiotic inhibition of group I ribozyme function. Nature. 353:368–370. [DOI] [PubMed] [Google Scholar]
- 19.von Ahsen, U., and H. F. Noller. 1993. Footprinting the sites of interaction of antibiotics with catalytic group I intron RNA. Science. 260:1500–1503. [DOI] [PubMed] [Google Scholar]
- 20.Stage, T. K., K. J. Hertel, and O. C. Uhlenbeck. 1995. Inhibition of the hammerhead ribozyme by neomycin. RNA. 1:95–101. [PMC free article] [PubMed] [Google Scholar]
- 21.Rogers, J., A. H. Chang, U. von Ahsen, R. Schroeder, and J. Davies. 1996. Inhibition of the self-cleavage reaction of the human hepatitis delta virus ribozyme by antibiotics. J. Mol. Biol. 259:916–925. [DOI] [PubMed] [Google Scholar]
- 22.Waldsich, C., K. Semrad, and R. Schroeder. 1998. Neomycin B inhibits splicing of the td intron indirectly by interfering with translation and enhances missplicing in vivo. RNA. 4:1653–1663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hermann, T., and E. Westhof. 1998. Aminoglycoside binding to the hammerhead ribozyme: a general model for the interaction of cationic antibiotics with RNA. J. Mol. Biol. 276:903–912. [DOI] [PubMed] [Google Scholar]
- 24.Wang, H., and Y. Tor. 1998. RNA-Aminoglycoside interactions: design, synthesis, and binding of “amino-aminoglycosides” to RNA. Angew. Chem. Int. Ed. Engl. 37:109–111. [Google Scholar]
- 25.Hendrix, M., E. S. Priestly, G. F. Joyce, and C. Wong. 1997. Direct observation of aminoglycoside-RNA interactions by surface plasmon resonance. J. Am. Chem. Soc. 119:3641–3648. [DOI] [PubMed] [Google Scholar]
- 26.Hamy, F., V. Brondani, A. Flörsheimer, W. Stark, M. J. J. Blommers, and T. Klimkait. 1998. A new class of HIV-1 Tat antagonist acting through Tat-TAR inhibition. Biochemistry. 37:5086–5095. [DOI] [PubMed] [Google Scholar]
- 27.Wang, S., P. W. Huber, M. Cui, A. W. Czarnik, and H.-Y. Mei. 1998. Binding of neomycin to the TAR element of HIV-1 RNA induces dissociation of the Tat protein by an allosteric mechanism. Biochemistry. 37:5549–5557. [DOI] [PubMed] [Google Scholar]
- 28.Mei, H.-Y., M. Cui, A. Heldsinger, S. M. Lemrow, J. A. Loo, K. A. Sannes-Lowry, L. Sharmeen, and A. W. Czarnik. 1998. Inhibitors of protein-RNA complexation that target the RNA: specific recognition of human immunodeficiency virus type I TAR RNA by small organic molecules. Biochemistry. 37:14204–14212. [DOI] [PubMed] [Google Scholar]
- 29.Faber, C., H. Sticht, K. Schweimer, and P. Rösch. 2000. Structural rearrangements of HIV-1 Tat-responsive RNA upon binding of neomycin B. J. Biol. Chem. 275:20660–20666. [DOI] [PubMed] [Google Scholar]
- 30.Kirk, S. R., N. W. Luedtke, and Y. Tor. 2000. Neomycin-acridine conjugate: a potent inhibitor of Rev-RRE binding. J. Am. Chem. Soc. 122:980–981. [Google Scholar]
- 31.Baker, T. J., N. W. Luedtke, Y. Tor, and M. Goodman. 2000. Synthesis and anti-HIV activity of guanidinoglycosides. J. Org. Chem. 65:9054–9058. [DOI] [PubMed] [Google Scholar]
- 32.Luedtke, N. W., Q. Liu, and Y. Tor. 2003. RNA-ligand interactions: affinity and specificity of aminoglycoside dimers and acridine conjugates to the HIV-1 Rev response element. Biochemistry. 42:11391–11403. [DOI] [PubMed] [Google Scholar]
- 33.Blount, K. F., F. Zhao, T. Hermann, and Y. Tor. 2005. Conformational constraint as a means for understanding RNA-aminoglycoside specificity. J. Am. Chem. Soc. 127:9818–9829. [DOI] [PubMed] [Google Scholar]
- 34.Kotra, L. P., J. Haddad, and S. Mobashery. 2000. Aminoglycosides: perspectives on mechanisms of action and resistance and strategies to counter resistance. Antimicrob. Agents Chemother. 44:3249–3256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chambers, H. F. 2004. Aminoglycosides and spectinomycin. In Basic and Clinical Pharmacology, 9th Ed. B. G. Katzung, editor. McGraw-Hill, New York. 764–772.
- 36.Jin, E., V. Katritch, W. K. Olson, M. Kharatisvili, R. Abagyan, and D. S. Pilch. 2000. Aminoglycoside binding in the major groove of duplex RNA: the thermodynamic and electrostatic forces that govern recognition. J. Mol. Biol. 298:95–110. [DOI] [PubMed] [Google Scholar]
- 37.Kaul, M., and D. S. Pilch. 2002. Thermodynamics of aminoglycoside-rRNA recognition: the binding of neomycin-class aminoglycosides to the A Site of 16S rRNA. Biochemistry. 41:7695–7706. [DOI] [PubMed] [Google Scholar]
- 38.Kaul, M., C. M. Barbieri, J. E. Kerrigan, and D. S. Pilch. 2003. Coupling of drug protonation to the specific binding of aminoglycosides to the A site of 16 S rRNA: elucidation of the number of drug amino groups involved and their identities. J. Mol. Biol. 326:1373–1387. [DOI] [PubMed] [Google Scholar]
- 39.Pilch, D. S., M. Kaul, C. M. Barbieri, and J. E. Kerrigan. 2003. Thermodynamics of aminoglycoside-rRNA recognition. Biopolymers. 70:58–79. [DOI] [PubMed] [Google Scholar]
- 40.Pilch, D. S., M. Kaul, and C. M. Barbieri. 2005. Ribosomal RNA recognition by aminoglycoside antibiotics. Top. Curr. Chem. 253:179–204. [Google Scholar]
- 41.Özen, C., and E. H. Serpersu. 2004. Thermodynamics of aminoglycoside binding to aminoglycoside-3′-phosphotransferase IIIa studied by isothermal titration calorimetry. Biochemistry. 43:14667–14675. [DOI] [PubMed] [Google Scholar]
- 42.Dorman, D. E., J. W. Paschal, and K. E. Merkel. 1976. 15N nuclear magnetic resonance spectroscopy. The nebramycin aminoglycosides. J. Am. Chem. Soc. 98:6885–6888. [DOI] [PubMed] [Google Scholar]
- 43.Botto, R. E., and B. Coxon. 1983. Nitrogen-15 nuclear magnetic resonance spectroscopy of neomycin B and related aminoglycosides. J. Am. Chem. Soc. 105:1021–1028. [Google Scholar]
- 44.Gaggelli, E., N. Gaggelli, A. Maccotta, G. Valensin, D. Marini, M. E. Di Cocco, and M. Delfini. 1995. Determination of intramolecular hydrogen bonds in amikacin in water solution by NMR spectroscopy. Spectrochim. Acta A Mol. Biomol. Spectrosc. 51:1959–1963. [Google Scholar]
- 45.Cox, J. R., and E. H. Serpersu. 1997. Biologically important conformations of aminoglycoside antibiotics bound to an aminoglycoside 3′-phosphotransferase as determined by transferred nuclear Overhauser effect spectroscopy. Biochemistry. 36:2353–2359. [DOI] [PubMed] [Google Scholar]
- 46.Kane, R. S., P. T. Glink, R. G. Chapman, J. C. McDonald, P. K. Jensen, H. Gao, L. Pasa-Tolíc, R. D. Smith, and G. M. Whiteside. 2001. Basicity of the amino groups of the aminoglycoside amikacin using capillary electrophoresis and coupled CE-MS-MS techniques. Anal. Chem. 73:4028–4036. [DOI] [PubMed] [Google Scholar]
- 47.Lesniak, W., J. McLaren, W. R. Harris, V. L. Pecoraro, and J. Schacht. 2003. An isocratic separation of underivatized gentamicin components, 1H NMR assignment and protonation pattern. Carbohydr. Res. 338:2853–2862. [DOI] [PubMed] [Google Scholar]
- 48.Doyle, M. L., G. Louie, P. R. Dal Monte, and T. D. Sokoloski. 1995. Tight binding affinities determined from thermodynamic linkage to protons by titration calorimetry. Methods Enzymol. 259:183–194. [DOI] [PubMed] [Google Scholar]
- 49.Kozlov, A. G., and T. M. Lohman. 2000. Large contributions of coupled protonation equilibria to the observed enthalpy and heat capacity changes for ssDNA binding to Escherichia coli SSB protein. Proteins: Struct., Funct. For. Genet. 41:8–22. [DOI] [PubMed] [Google Scholar]
- 50.Christensen, J. J., L. D. Hansen, and R. M. Izatt. 1976. Handbook of Proton Ionization Heats. John Wiley & Sons, New York.
- 51.Sharp, K. A. 2000. Electrostatic interactions in proteins and nucleic acids: theory and applications. In Thermodynamics in Biology. E. Di Cera, editor. Oxford University Press, New York. 113–130.
- 52.Fukada, H., and K. Takahashi. 1998. Enthalpy and heat capacity changes for the proton dissociation of various buffer components in 0.1 M potassium chloride. Proteins. 33:159–166. [PubMed] [Google Scholar]
- 53.Recht, M. I., D. Fourmy, S. C. Blanchard, K. D. Dahlquist, and J. D. Puglisi. 1996. RNA sequence determinants for aminoglycoside binding to an A-Site rRNA model oligonucleotide. J. Mol. Biol. 262:421–436. [DOI] [PubMed] [Google Scholar]
- 54.Fourmy, D., M. I. Recht, S. C. Blanchard, and J. D. Puglisi. 1996. Structure of the A Site of Escherichia coli 16S ribosomal RNA complexed with an aminoglycoside antibiotic. Science. 274:1367–1371. [DOI] [PubMed] [Google Scholar]
- 55.Fourmy, D., S. Yoshizawa, and J. D. Puglisi. 1998. Paromomycin binding induces a local conformational change in the A-Site of 16 S rRNA. J. Mol. Biol. 277:333–345. [DOI] [PubMed] [Google Scholar]
- 56.Recht, M. I., S. Douthwaite, K. D. Dahlquist, and J. D. Puglisi. 1999. Effect of mutations in the A-site of 16 S rRNA on aminoglycoside antibiotic-ribosome interaction. J. Mol. Biol. 286:33–43. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.