Glycolytic Enzyme Interactions with Yeast and Skeletal Muscle F-Actin

Abstract

Interaction of glycolytic enzymes with F-actin is suggested to be a mechanism for compartmentation of the glycolytic pathway. Earlier work demonstrates that muscle F-actin strongly binds glycolytic enzymes, allowing for the general conclusion that “actin binds enzymes”, which may be a generalized phenomenon. By taking actin from a lower form, such as yeast, which is more deviant from muscle actin than other higher animal forms, the generality of glycolytic enzyme interactions with actin and the cytoskeleton can be tested and compared with higher eukaryotes, e.g., rabbit muscle. Cosedimentation of rabbit skeletal muscle and yeast F-actin with muscle fructose-1,6-bisphosphate aldolase (aldolase) and glyceraldehyde-3-phosphate dehydrogenase (GAPDH) followed by Scatchard analysis revealed a biphasic binding, indicating high- and low-affinity domains. Muscle aldolase and GAPDH showed low-affinity for binding yeast F-actin, presumably because of fewer acidic residues at the N-terminus of yeast actin; this difference in affinity is also seen in Brownian dynamics computer simulations. Yeast GAPDH and aldolase showed low-affinity binding to yeast actin, which suggests that actin-glycolytic enzyme interactions may also occur in yeast although with lower affinity than in higher eukaryotes. The cosedimentation results were supported by viscometry results that revealed significant cross-linking at lower concentrations of rabbit muscle enzymes than yeast enzymes. Brownian dynamics simulations of yeast and muscle aldolase and GAPDH with yeast and muscle actin compared the relative association free energy. Yeast aldolase did not specifically bind to either yeast or muscle actin. Yeast GAPDH did bind to yeast actin although with a much lower affinity than when binding muscle actin. The binding of yeast enzymes to yeast actin was much less site specific and showed much lower affinities than in the case with muscle enzymes and muscle actin.

INTRODUCTION

Eukaryotic cell cytoplasm is observed by electron microscopists to be an anastemosing three-dimensional network (1,2) in which most or all proteins of the cell participate (2–4). This organization is proposed to orient around the structural proteins that constitute the cytoskeleton (5). Actin is a highly conserved eukaryotic protein that exists either as globular actin (G-actin) or as filamentous actin (F-actin), which is the polymerized form of actin. Actin filaments are 5–7 nm in diameter and consist of two linear chains of quasispherical subunits wound into a double helix with a repeating structure of ∼13 subunits as evident from x-ray studies (6,7). Actin is known to be involved in a variety of cell functions that include contractility, cytokinesis, maintenance of cell shape, cell locomotion, and organelle transport (8). In addition, glycolytic enzymes colocalize in muscle cells with actin filaments (9–11); this interaction of glycolytic enzymes with F-actin may be one mechanism for compartmentation of the glycolytic pathway in cells. Compartmentation of the enzymes together on a cytoskeletal structure may allow the glycolytic substrates to move much shorter distances from one enzyme to another instead of being forced to search the entire cytoplasm for an enzyme. Fructose-1,6-bisphosphate aldolase (aldolase), glyceraldehyde-3-phosphate dehydrogenase (GAPDH), pyruvate kinase, glucose phosphate isomerase, and muscle lactate dehydrogenase interact with muscle microfilaments via direct enzyme-actin interactions (12–15). Other glycolytic enzymes such as triose phosphate isomerase (14,16) and phosphoglycerate mutase (14) only associate indirectly through interactions with other enzymes that do bind to actin. This indirect binding is referred to as enzyme-enzyme-actin or piggy-back interaction. Furthermore, the glycolytic enzymes, aldolase and GAPDH, have also been shown to compete against one another for binding sites (17). Muscle actin-enzyme interactions have been shown to be electrostatic in nature, owing to their dependence on factors such as ionic strength (14,15). Polyethylene glycol (PEG), which functions to cause volume exclusion referred to as molecular crowding (18,19), enhances binding (20).

Thus, it is clear from earlier work that muscle F-actin strongly binds glycolytic enzymes. This allows the general conclusion that “actin binds enzymes”, and it has been speculated that the phenomenon is generalized. Muscle actin is only one form of actin. The general statement can be tested by investigating actin-glycolytic enzyme interactions from different species. By taking actin from a lower form, such as yeast, which is more deviant from muscle actin than other higher animal forms, the generality of glycolytic enzyme interactions with actin and the cytoskeleton can be tested.

Skeletal muscle actin (α–actin) and yeast actin monomers consist of 375 amino acid residues. Saccharomyces cerevisiae contains a single actin gene, ACT1, which is 87% identical to skeletal muscle actin. Unlike muscle actin, yeast actin does not undergo the typical posttranslational modification of removing the N-terminal methionine because it lacks an actin-specific-processing enzyme (21); therefore, the initial methionine is acetylated and the first four residues are acetyl-Met-Asp-Ser-Glu. In contrast, the N-terminus of skeletal muscle actin consists of acetyl-Asp-Glu-Asp-Glu. This difference in N-terminus composition accounts for the greatest degree of variability between skeletal muscle and yeast actin. The N-terminal acidic residues of actin have been shown to interact with a variety of actin-binding proteins such as myosin, depactin, fragmin, and cofilin (22).

Studies show that when the N-terminal acidic residues of yeast actin are completely eliminated, actin bundling increases, myosin S-1 ATPase activity decreases, and the sliding of actin filaments over myosin is completely inhibited (23). If the number of acidic residues is increased from 2 to 4 (versus two neutral and two acidic residues), a threefold increase in the catalytic efficiency of actin activation of myosin results (24). These results indicate the importance of the negatively charged N-terminal residues of actin for protein-protein interactions.

The tertiary structures of many glycolytic enzymes, e.g., aldolase and GAPDH from rabbit and human muscle, have been solved by x-ray crystallography and are available from the RCSB Protein Data Bank (PDB) (25). The x-ray structure of the actin monomer (G-actin) from rabbit muscle is available (26) (accession code 1ATN). Holmes and co-workers (6) solved the structure of actin filaments (F-actin) using x-ray diffraction of phalloidin-stabilized actin filaments. Their resulting atomic model resembles the actin filament structure obtained from electron microscopy based on three-dimensional reconstruction of frozen hydrated (27) as well as negatively stained F-actin filaments (28). The knowledge of atomic structure of actin filaments and glycolytic enzymes allows for the study of the binding between them using computational approaches.

The Brownian dynamics (BD) method has been developed to simulate the relative translational and rotational diffusive motion of whole macromolecules under the influence of complicated electrostatic and excluded volume interactions present in solution. The electrostatic potential around molecules in solution can be calculated if the atomic structure of the molecule is known. From these potentials the deterministic forces acting on molecules in solution can be calculated. These forces in combination with solute-solvent interaction (modeled as random force) and volume-exclusion effects (accounted for by using the real shape of molecules) cause the steered diffusion of macromolecules relative to each other. If two molecules attract each other, their binding in solution can be simulated. From BD simulations one can calculate the potential of mean force (effective attractive potential) between molecules and determine the free energy of binding. The two main advantages of the BD method are the realistic presentation of electrostatic potential around macromolecules and the possibility of running very long simulations (e.g., a single trajectory can last up to a second). In our previous work we investigated the interactions of aldolase (29) and GAPDH (30) with G/F-actin from rabbit muscle using the BD method. We determined the binding modes between these molecules and identified the residues involved in intermolecular contacts. Our results suggested that it is the quaternary structure, rather than the tertiary structure, of aldolase and F-actin that is important for binding (29). Further studies with dimers and peptide segments of aldolase and GAPDH also supported the observation of the importance of quaternary structure for binding actin (31).

Skeletal muscle actin-glycolytic enzyme interactions have been known for several years and are often assumed to be transferred to other tissues and phylogenetic forms. Whether glycolytic enzymes associate with actin in other tissues or organisms with the same affinity as they associate with muscle actin has yet to be investigated. We postulate that actin-enzyme interactions may occur in lower eukaryotes, e.g., yeast, and that the strength of the interactions will be driven by electrostatics as it was for high eukaryotes. We further postulate that the composition of the N-terminus has a substantial effect on the actin-enzyme interaction. In this study, the binding of muscle and yeast glycolytic enzymes to both muscle and yeast actin is investigated. The binding interactions for each cell type in vitro are described. The application of BD simulations has allowed for the calculation of the free energy profiles for aldolase and GAPDH binding to F-actin (rabbit muscle and yeast).

MATERIALS AND METHODS

Reagents

All chemicals and both rabbit muscle and yeast forms of the glycolytic enzymes (lyophilized powders or ammonium sulfate suspensions) were purchased from Sigma Chemical Co. (St. Louis, MO). Yeast extract and bactopeptone, both Difco Brand, were purchased from Fisher Scientific (Fair Lawn, NJ). DABS amino acid kit and DABS ODS HPLC columns were purchased from Beckman (Palo Alto, CA). Distilled and Millipore-filtered water and analytical or HPLC grade reagents were used in all experiments.

Preparation of actin

Extraction and purification of rabbit muscle actin was conducted according to Katz et al. (32). Purification of yeast actin was modified from Nefsky and Bretcher (33) and Kron et al. (34) to increase the yield of actin. Wild-type S. cerevisiae (yeast) cells were grown to log phase in YPD medium (1% yeast extract, 2% bactopeptone, and 2% dextrose) and isolated by centrifugation for 5 min at 4°C and 5000 rpm. The cells were washed with distilled water and centrifuged under the same conditions. The cells (∼100 g) were resuspended in 150 mL of 10 mM imidazole, pH 7.5, 0.75 mM β-mercaptoethanol, 0.5 mM ATP, 0.1 mM CaCl₂, 10 mM EDTA, 10 EGTA, and 0.3 PMSF and disrupted with 0.5 mm glass beads (∼100 g) using a Bead Beater. Homogenization of the cells was performed with five 30 s blasts of the Bead Beater, with each blast interrupted by a 1 min rest and followed by two 1 min blasts each interrupted by 30 s rests. The homogenate was centrifuged for 20 min at 4°C and 14,000 rpm. The crude supernatant was saved, and 2.5% streptomycin sulfate was added and centrifuged for 105 min at 4°C and 40,000 rpm. The supernatant was put through six layers of cheesecloth to remove lipid and other debris; the pH was adjusted to 7.5 with 10 N KOH and stored on ice overnight.

The supernatant was passed through a 9 mL DNase I affinity column preequilibrated with G-buffer (10 mM imidazole, pH 7.5, 0.2 mM ATP, 0.2 mM CaCl₂, and 0.1 mM DTT). The column effluent was directly passed to a 20 mL DEAE-Sephacel column also preequilibrated with G-buffer. The columns were washed with several volumes of G-buffer to remove nonadsorbing proteins. Then both columns were washed with G-buffer containing 50% formamide to elute the G-actin (35). The coupling of the columns (36) allowed for elution of the actin from the affinity column directly onto the DEAE-Sephacel column with the least time of contact, with formamide minimizing the denaturation of the actin and significantly increasing the yield. The columns were disconnected, and the DEAE-Sephacel column was washed with G-buffer, followed by G-buffer containing 500 mM KCl. The fractions containing the pure actin were combined and dialyzed with several changes of pH (2.5 mM imidazole, pH 7.0, 0.5 mM ATP, and 0.5 mM CaCl₂) overnight in the cold box. The actin was concentrated by placing a dialysis bag containing the G-actin over dry PEG (PEG removed water), dialyzed again, and then polymerized using 50 mM KCl, 3 mM MgCl₂, 0.3 mM EDTA, and 0.2 mol/mol phalloidin in a 37°C water bath for 1.5 h. Actin was purified to a single band on SDS-PAGE with a yield of 7–8 mg per 100 g of yeast cells, and it was then stored on ice for use within 2 days.

Cosedimentation assays

Rabbit muscle and yeast F-actin and the rabbit and yeast forms of aldolase and GAPDH were dialyzed in two changes of IKMD buffer (10 mM imidazole, pH 6.5, 0.5 mM DTT, 1.5 mM MgCl₂, and 40 mM KCl) before each experiment. The actins were incubated for 30 min in a 37°C water bath and sheared using a Genie vortex set on 4 for 10 s. IKMD buffer, water, 25 mM actin, and varying amounts of enzyme were all placed into Beckman TL-100 ultracentrifuge tubes and mixed. The samples were incubated for 30 min at 37°C followed by centrifugation for 35 min at 37°C and 100,000 rpm. The supernatant was removed and placed into Eppendorf tubes and KCl adjusted to 0.3 M so that the supernatant and pellet fraction contained equal concentrations of KCl. After careful washing with water, the pellets were resuspended in IKMD buffer with 0.3 M KCl. The pellet and supernatant fractions were assayed for enzyme activity to verify the measurement of enzyme concentration. All controls were treated in the same manner as described above.

The actin concentrations were determined according to the Bradford (37) method. The enzyme concentrations were determined by spectrophotometry at 280 nm, using absorption coefficients (A₂₈₀, 1 mg/mL) of 0.91 for rabbit muscle aldolase, 1.00 for rabbit muscle GAPDH, 1.02 for yeast aldolase, and 1.03 for yeast GAPDH.

Scatchard analysis of cosedimentation plots

When a ligand A (actin) binds to an enzyme E to form a complex EA_n (where n is the number of ligands bound per each enzyme molecule), the equilibrium constant is expressed as

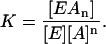(1)

This high-power equation can be simplified by breaking [A]ⁿ into [A]ⁿ⁻¹ [A] (thus assuming that the binding of A on all n sites is equally strong). Then since the concentration of [A] is much larger than [E], it can be assumed that the change in concentration of [A]ⁿ⁻¹ can be neglected and only the change of the concentration of [A] needs to be considered. This way, we assume that [A]ⁿ⁻¹ = 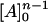and, thus, 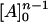can be included in the value of the equilibrium constant:

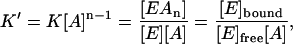(2)

because, out of stoichiometry (one enzyme molecule binds n ligand molecules), [EA_n] can be replaced with [E]_bound in Eq. 2, since

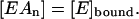(3)

The classical Scatchard analysis (38) in which the molar balance on [E] was used to introduce the stoichiometry of binding into the equation has been followed to this point. The specific feature of the current system is that both [E]_bound and [E]_free are measured. So, to find both the binding constant and stoichiometric enzyme/actin ratio, the molar balance on [A] should be considered instead:

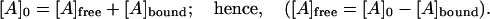(4)

Plugging Eq. 4 into Eq. 2, we obtain

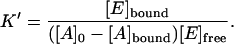(5)

[A]_bound is replaced with [E]_bound since [E], and not [A], is measured. Since, according to the stoichiometric Eq. 3, [E]_bound = 1/n [A]_bound, or, otherwise, [A]_bound = n [E]_bound, Eq. 5 can be adjusted to

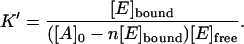(6)

Multiplying both parts of this equation by the denominator of the right part, we obtain

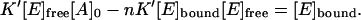(7)

Now we divide all the terms by [E]_free [A]₀:

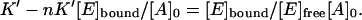(8)

Note that Eq. 8 can be transformed into the classical Scatchard equation by consistently replacing A with E and vice versa. The resulting modified plot may have the same axes as the Scatchard plot. This becomes clear when it is rearranged to leave [E]_bound/[E]_free and [E]_bound as y and x of a straight line equation:

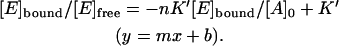(9)

The values of 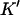and n, however, can be found from the y- and x-intercepts in a different way:

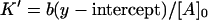(10a)

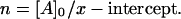(10b)

In biochemistry, dissociation constants are used more often than binding constants:

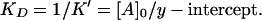(10c)

This value corresponds to binding of one enzyme molecule to one actin subunit, because actin concentration is measured as that of the subunits.

Viscosity measurements

Falling ball viscometry was performed using the procedure of Wang et al. (39) in their studies of interaction of various forms of aldolase with muscle F-actin.

Protein models

Aldolase

The x-ray structure of rabbit muscle aldolase (40,41) was obtained from the RCSB PDB (accession code 1ADO). Yeast aldolase, a class II dimeric aldolase with one Zn⁺² associated with each subunit, was built by homology modeling. The yeast (S. cervisiae) aldolase sequence was obtained from the SWISS-PROT Sequence Data Bank (entry P14540). The primary sequence of Escherichia coli aldolase, also a class II aldolase, had 48% sequence identity with the yeast enzyme (Fig. 1). An additional 24% of the residues was strongly similar: sequence identity above 40% is usually considered strong evidence of homology (42–44). The three crystal structures for E. coli aldolase in the PDB were 1B57 (45), 1DOS (46), and 1ZEN (47). 1DOS was used as the reference structure because it was the most complete; the B subunit was chosen over the A subunit because the A subunit had a large loop whose location was different from those in the other E. coli aldolase structures. This loop had high temperature factors in both subunits; the difference in location between subunits was due to crystal packing. The sequence alignment obtained in the Homology module of InsightII was confirmed by reproducing the sequence alignment using VectorNTI Suite (Frederick, MD). After performing the sequence alignment, four boxes indicating regions of high sequence similarity were identified and used for building the homology model (Fig. 1): Ser¹ to Lys⁷² in the E. coli enzyme (versus Val² to Lys⁷² of yeast); Val⁷⁷ to Gly²²⁷ of E. coli (versus Glu⁷⁷ to Gly²²⁷ of yeast); Asn²³³ to Leu²⁵⁴ of E. coli (Asp²³² to Cys²⁵³ of yeast); and Leu²⁵⁹ to Leu³⁵⁸ of E. coli (versus Leu²⁵⁹ to Leu³⁵⁸ of yeast). Boundaries for the boxes were determined by the positions of the three single residue gaps from the sequence alignment. Coordinates for the three short loops between the boxes were assigned using the “generate loop” option of the Homology module of InsightII (Accelyrs, San Diego, CA); the initial version of the model was completed using the “end repair” option. After assignment of coordinates within the Homology module of InsightII, energy minimizations using the CVFF force field and a dielectric constant of 78.54 with a maximum of 10,000 conjugate gradient iterations were performed using the InsightII Discover module to eliminate overlaps. The first minimizations were only performed on the loops and ends; further minimizations were performed leaving the backbone constrained but allowing all side chains to move except those involved in binding zinc ions. The complete dimer was formed by superimposing copies of the model subunit on the two subunits of 1DOS and converting them into an assembly. Zinc ions were reintroduced into the minimized structure by superimposing them onto the homology model. The residues critical for binding Zn⁺² (His¹¹⁰, Glu¹⁷⁴, His²²⁶, and His²⁶⁴) (46) and those proposed by Hall et al. (45) to be involved in the reaction mechanism (Asp¹⁰⁹, Glu¹⁸², and Arg³³¹) were found to be in the same relative locations in the homology model as in the crystal structure (root mean square deviation (RMSD) for the trace atoms: 0.00001 Å), thus providing partial confirmation of the validity of the model structure. Using DaliLite (48) the RMSD for the α-carbons of the yeast model versus subunit B of 1DOS was 0.6 Å and the Z-score was 60.4. Z-scores (a measure of the quality of the alignment) that are above 20 are considered to mean two structures are definitely homologous. The superimposed structures with side chains displayed (Fig. 2 a) that are involved in binding Zn²⁺ (His¹¹⁰, Glu¹⁷⁴, His²²⁶, His²⁶⁴) (46), or involved in catalysis (Asp¹⁰⁹, Glu¹⁸², Arg³³¹) (45) showed that all these critical residues were conserved. Hall et al. (45) identified ∼16 additional residues of interest (for ion binding, catalysis, substrate or inhibitor binding, etc.) in E. coli aldolase; all are conserved in the yeast enzyme. The loops showed the greatest differences between the structures where the three gaps in the sequence alignment were located; two of these loops had high temperature factors in the E. coli aldolase crystal structure.

FIGURE 1.

Sequence alignment of E. coli and yeast aldolases. Identical residues are indicated by solid lines; strongly similar residues, by dashed lines. The alignment and designation of strongly similar residues were performed using the Homology module of InsightII. The four boxes are those used for homology modeling to predict the structure of yeast aldolase.

FIGURE 2.

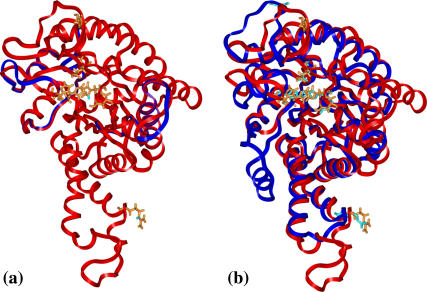
(a) Ribbon structure for a single subunit of E. coli aldolase (blue) superimposed on the yeast aldolase model (red). The side chains (cyan for E. coli; orange for yeast) displayed are those of critical residues listed in the text; there is nearly complete overlap of the side chains. The two proteins have 48% sequence identity; the RMSD for these structures was 0.6 Å. (b) Ribbon structure for a single subunit of the yeast aldolase model (red) superimposed on a subunit of T. aquaticus aldolase (blue). The two proteins have 28% sequence identity; the RMSD for these structures was 2.0 Å. Although these polypeptides have only 28% sequence identity and are different in length (358 vs. 305 residues), the basic (α/β)₈ barrel structures are highly similar. The side chains (cyan for T. aquaticus; orange for yeast) displayed are those of critical residues listed in the text; the RMSD for the trace atoms of these residues is 0.5 Å except for Glu¹⁸², which is located on a loop which undergoes a conformational change on binding ligand.

Recently structures of another Class II aldolase, an extreme thermophile Thermis aquaticus (49), were added to the PDB (accession codes 1RV8 and 1RVG). This enzyme had only 305 residues per chain, used cobalt(II) instead of zinc ions, and was a tetramer rather than a dimer; also, the sequence identity with yeast aldolase was only 28%. Since the T. aquaticus aldolase has considerable differences from the yeast enzyme, the model was not modified using the T. aquaticus structure. In Fig. 2 b, however, the (α/β)₈ barrel structure of T. aquaticus aldolase was highly similar to that of the yeast model aldolase. The RMSD for the α-carbons of these structures was 2.0 Å, and the Z-score is 30.1 (results from DaliLite (48)). Izard and Sygusch (49) reported an RMSD between E. coli and T. aquaticus aldolases of 1.33 Å for the 221 α-carbons in common. Although the yeast and T. aquaticus enzymes have only 28% sequence identity, all seven critical residues discussed above (Fig. 2) were conserved and superimposing these residues (except Glu¹⁸²) gave an RMSD of 0.5 Å for the trace atoms; the additional residues discussed by Hall et al. (45) are also nearly all conserved. Glu¹⁸² was in a loop that shows a large conformational change on binding ligands (49). The similarity in spatial locations of critical residues in the model structure and in the distantly related T. aquaticus enzyme is strong evidence of the validity of the essential features of the model.

Although they act by entirely different mechanisms and may have low sequence identities, class I and II aldolase structures all contain the (α/β)₈ barrel triosephosphate isomerase fold. Even the archaeal class I aldolase from the hyperthermophile Thermoproteus tenax (PDB code 1OJX) shares this fold; Lorentzen et al. (50) reported only 13% sequence identity between this protein and human aldolase but an RMSD of 1.9 Å for the structurally equivalent residues.

GAPDH

Based on the 91% sequence identity between rabbit and human GAPDH, the tertiary structure for rabbit GAPDH was built by homology modeling as described elsewhere (30).

Similarly, the structure of yeast GAPDH was constructed as a homology model based on a reference frame consisting of three crystal structures: human (3GDP (51)), American lobster (4GPD (52)), and South China sea lobster (1CRW (53)), which showed 66–70% sequence identity with yeast. The primary sequence of yeast GAPDH was obtained from the SWISS-PROT Sequence Data Bank (entry P00360 (42–44)). NAD⁺ and PO₄³⁻ groups and their atomic coordinates were copied into the yeast structure from the PDB structure of human GAPDH. The complete tetramer of yeast GAPDH was obtained by superimposing the monomer onto the four subunits of the human tetramer. The complete tetramer was then energy minimized using the Discover module of InsightII by 1,000 steps of conjugate gradient using the AMBER force field.

Actin

The x-ray structure of yeast G-actin (54) was obtained from the PDB (1YAG). According to the classification of Kabsch et al. (26), G-actin can be schematically subdivided into four subdomains: subdomain I (residues 1–32, 70–144, 338–375), subdomain II (residues 32–69), subdomain III (residues 145–180, 270–337), and subdomain IV (residues 181–269) (26). Yeast actin is more similar to mammalian β-actin than to α-actin in sequence and function and has been shown by Belmont et al. (55) to exist predominantly in an open conformation. The sequences of yeast and α-actin are 87% identical, whereas the sequences of yeast and β-actin are 89% identical. The β-actins have the same number of residues as the yeast actin, but the α-actins have two more residues before posttranslational modification; after translation, the first two residues, Met-Cys on the N-terminus, were clipped off before the α-actin became active in the muscle. The molecule was stripped of the complexed human gelsolin segment, and the missing N-terminal residues (Ace-Met-Asp-Ser) were added. This was accomplished by using the Biopolymer module in InsightII to build the acetylated tripeptide, which was then attached to the rest of the protein through a partial double bond linking the carboxyl group of the serine to the amino-group of residue number 4 (glutamate). Other missing side-chain atoms were also added, using the residue replace command in the biopolymer module to modify the desired residues (His⁴⁰, Gln⁴¹, Ile⁴³, Val⁴⁵) and then readjusting the coordinates to match those from the PDB file. The resulting structure was subjected to 200 steps of conjugate gradient energy minimization in the AMBER force field. Six copies of the monomer were superimposed onto each of the six subunits of the Holmes model for rabbit F-actin built previously (29). The six yeast subunits were merged to create a hexamer model of yeast F-actin, which was then energy minimized using the Discover_3 module in InsightII.

Protein charge and electrostatic potential calculations

Using the atomic coordinates for each protein, the charges of the titratable amino acids were calculated and assigned by applying the Tanford-Kirkwood method with static accessibility modification (55–59); this method, which included the solvent environment implicitly by solving the linearized Poisson-Boltzmann equation, used the atomic coordinates of each model to determine the location and degree of exposure in the protein of each titratable amino acid residue. Thus, each residue was assigned a net charge based on its protein environment, pH, ionic strength, and temperature. At or near neutral pH, as was used in this study, lysines and arginines are fully protonated and carboxylates are fully dissociated (i.e., they carry a full formal charge). The more ambiguous assignments of the charges for the N-termini and the histidines depended on the environment and were estimated by the Tanford-Kirkwood calculation. These charges are often fractional because the pKa is near enough to the pH that the equilibrium state contains significant amounts the protonated and deprotonated states. The MacroDox charge set (60) was used to assign charges at pH 7.0, ionic strength 0.05 M, and a temperature of 298 K. The calculated charges for all species can be found in Table 1.

TABLE 1.

Calculated charges for actin subunits and free energies of binding glycolytic enzymes to different forms of F-actin at pH 7.0, ionic strength 0.05 M, and temperature 298 K

	Proteins: calculated charges		Interacting components: energies
Protein	Enzyme charge (e)	Actin charge (e)	Radial binding energy (kcal/mol)	Specific energy (kcal/mol)
RM_actin/RM_aldolase	+15.9	−9.7	−1.91 ± 0.08	−13.56 ± 1.2
RM_actin/RM_GAPDH	+17.8	−9.7	−0.8 ± 0.1	−11.4 ± 0.9
Y_actin/Y_aldolase	−11.2	−9.4	+0.4 ± 0.1*	−9.1 ± 0.6
Y_actin/Y_GAPDH	+14.9	−9.4	−0.51 ± 0.02	−13.7 ± 9.0
RM_actin/Y_aldolase	−11.2	−9.7	+0.4 ± 0.1*	−6.4 ± 1.4
RM_actin/Y_GAPDH	+14.9	−9.7	−1.00 ± 0.06	−8.1 ± 0.3
Y_actin/RM_aldolase	+15.9	−9.4	−1.00 ± 0.05	−9.4 ± 0.5
Y_actin/RM_GAPDH	+15.9	−9.4	−0.03 ± 0.01	−5.4 ± 1.8

Specific electrostatic energies for complexes found are also shown. The specific energy is the average potential energy using the Poisson-Boltzmann grid for the complex. The radial binding energy is the orientationally averaged free energy as the enzyme tumbles into the electrostatic field of F-actin. The charge for actin is reported as the charge of a single subunit in F-actin.

^*When the interaction was weak, the energy at reaction coordinate 82 Å (corresponding to the minimum for muscle actin/muscle aldolase) is quoted.

After charge assignments, the electrostatic fields around the proteins were determined by numerically solving the linearized Poisson-Boltzmann equation as implemented in the program MacroDox (algorithm overviewed in Northup et al. (61)). For all proteins, the electrostatic field was determined on two cubic lattices—an outer grid with 4.125-Å resolution and an inner grid with a resolution of 1.375 Å. Figs. 3 and 4 show the calculated electrostatic potentials around yeast aldolase, GAPDH, and actin.

FIGURE 3.

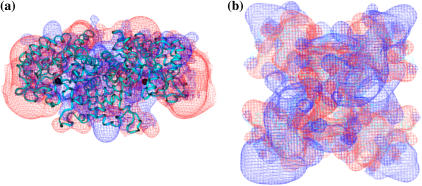
Electrostatic potential for (a) yeast aldolase (similar to that published for rabbit (29)) and (b) yeast GAPDH. The blue contours represent a positive electrostatic potential of +0.5 kcal/mol, and the red contours represent a negative field of −0.5 kcal/mol. Calculations were done at pH 7.0, ionic strength of 0.05 M, and temperature of 298.15 K.

FIGURE 4.

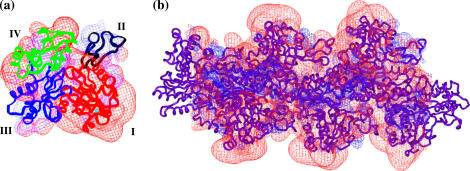
(a) Electrostatic potential for yeast G-actin with the subdomains colored and labeled. Subdomain I (red) included residues 1–32, 70–144, 338–375; subdomain II (black) included residues 32–69; subdomain III (green) included residues 145–180, 270–337; and subdomain IV (blue) included residues 181–269 (26). (b) Electrostatic potential for yeast F-actin hexamer; note, the red bulges in the electrostatic potential correspond to subdomain I on G-actin. The blue contours represent a positive electrostatic potential of +0.5 kcal/mol, and the red contours represent a negative field of −0.5 kcal/mol. Calculations were done at pH 7.0, ionic strength of 0.05 M, and temperature of 298.15 K.

BD simulations

The BD algorithm for the MacroDox package is detailed in Northrup et al. (62) and is a form of the Ermak-McCammon BD algorithm (63,64). For the simulations with F-actin, the BD algorithm was modified to mimic the periodic property of the actin filament as described in Ouporov et al. (29). To achieve this, the center of mass (COM) of the enzyme was initially placed at random orientations a fixed distance from the actin helical axis. As the simulation proceeded, each time the enzyme COM moved to +55.0 Å along the z axis, the whole enzyme was shifted and rotated by −27.5 Å and 166.14°, respectively. In the same way, when the enzyme COM was −55.0 Å along the z axis, the enzyme was subjected to a translation and rotation of +27.5 Å and −166.14°, respectively. These transformations correspond to the F-actin helical parameters, and as such, the enzyme movement was limited to a cylinder (−55.0 Å < z < +55.0 Å) simulating an infinitely long actin helix. This modification allowed for the possibility to model enzyme binding to internal subunits of the actin filament versus end units with different exposures. The diffusion coefficients were estimated by the Stokes-Einstein relation (Eq. 11).

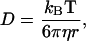(11)

where k_b is the Boltzmann constant, T is the temperature, η is the viscosity, and r is the radius of the protein being approximated as a sphere. The diffusion coefficients for the aldolases were 3.8 × 10⁻³ and 6.3 × 10⁻³ Ų/ps for rabbit and yeast, respectively; the diffusion coefficients for rabbit and yeast GAPDHs were 5.1 × 10⁻³ and 4.8 × 10⁻³ Ų/ps, respectively. A variable time step criterion was used so that at shorter protein-protein distances the time step was smaller. The lower limit of the time step was set to 25 ps.

Enzyme-G-actin

To simulate the interaction between yeast aldolase or GAPDH with yeast G-actin, 10,000 BD simulations of 10,000 trajectories took ∼72 CPU hours on an SGI-Octane workstation. Each trajectory began with the COM of yeast G-actin placed on the surface of sphere of radius 135 Å from COM of aldolase or GAPDH and was terminated when the G-actin COM reached a surface of 300 Å away. The initial angular position and orientation of G-actin were chosen randomly, and both G-actin and enzyme were allowed to rotate and move during the simulation. For each successful trajectory where the interaction energy between the two proteins was less than −8 kT, the structure of the most stable complex was saved. The reaction criterion of energy less than −8 kT was chosen based on the minimum interaction energy previously observed for interactions between rabbit enzymes and G-actin (29,30). This ensured that for these interactions only more favorable complexes were saved for further analysis. The saved complexes were subjected to a statistical (triplet) analysis that generated a list of contacts between charged amino acid residues in the proteins as well as the average electrostatic energy of all complexes analyzed. Only contact distances in the range 2 Å < d < 6 Å were considered since this range is reasonable for the formation of salt bridges. This analysis was complemented by manually stepping through and visually examining the complexes to find energetically stable complexes with favorable salt bridges (attractive) and contact distances. One hundred of the most energetically stable complexes saved were further analyzed to determine the frequent amino acid residues in interprotein contacts and determine the binding modes.

Enzyme-F-actin

To complement the results from enzyme G-actin interactions and to determine binding modes, 1000 BD trajectories simulated the binding of yeast aldolase or GAPDH to yeast F-actin. These simulations took ∼35 CPU hours on a SGI Fuel workstation. In this case, the F-actin was held fixed as the target molecule and each trajectory started with the COM of aldolase or GAPDH 130 Å away from the F-actin helical axis and terminated on a surface of 300 Å away. For each successful trajectory, the most intimate complex spatially and the most energetically favorable complex were saved; thus, two complexes were saved for each trajectory as opposed to the single complex saved for the G-actin simulations. This modification was done to provide more data per trajectory to save CPU time for simulations with large helical molecules. Further analysis of the most stable and intimate complexes saved revealed the most frequent amino acid residues occurring in interprotein contacts.

To follow the energetics of enzyme/F-actin (including mutants), 10 single long trajectories of 1.5 × 10⁷ BD steps were averaged. During each trajectory, if the distance between the COM of the enzyme and the F-actin helix reached 200 Å, the enzyme was relocated to a position 150 Å from the helix axis while maintaining the same orientation. Thus, the enzyme was forced to spend more time in a region close to the F-actin helix (R < 150 Å), rather than moving outside of this region where electrostatic interaction with actin was negligible. The reaction coordinate, R_c, was defined as the distance between the COM of the enzyme and the F-actin helix axis. A distribution ρ(R_c) of enzyme COM residence times in cylindrical concentric bins of 1 Å thickness located at R_c distances from F-actin helix axis was tallied and converted to a potential of mean force A(R_c) in the radial dimension by the statistical mechanical formula (63)

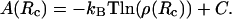(12)

The constant C was chosen to define the point at which the electrostatic potential surrounding F-actin was clearly zero A(R_c = 125 Å). The potential of mean force constitutes the effective radial free energy of enzyme-actin association, including Boltzmann statistical averaging over all orientational degrees of freedom. Each simulation took ∼2.5 CPU hours on an SGI Octane workstation. To evaluate and compare the enzyme-F-actin interactions from different species, simulations were done to follow the interactions of enzymes with F-actin from the same source (e.g., yeast GAPDH-yeast F-actin) as well as interactions of enzymes with F-actin from different sources (e.g., skeletal muscle aldolase-yeast F-actin).

RESULTS

Cosedimentation

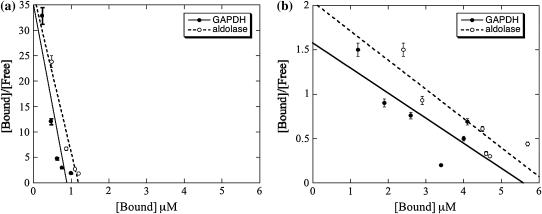
The experimental dissociation constants (K_D) of aldolase and GAPDH for muscle and yeast F-actin were determined using cosedimentation experiments. At low enzyme concentrations (1–2 μM) and a 25-fold excess of actin, most of the rabbit GAPDH and aldolase were bound to the muscle actin, thus revealing high affinity. The Scatchard plot analysis (see Materials and Methods) showed that both muscle aldolase and GAPDH displayed biphasic binding to muscle F-actin, indicating the presence of high (small value of K_D) and low-affinity binding sites (large value of K_D) (Fig. 5). The dissociation constants of muscle aldolase and GAPDH for high-affinity sites on muscle actin were near 0.7 μM (Table 2). The K_Ds of muscle enzymes for low-affinity sites were in the order of 10 μM.

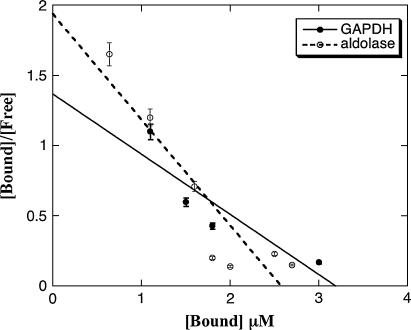
FIGURE 5.

Scatchard plots for muscle aldolase and GAPDH binding to skeletal muscle F-actin. [Free] is the concentration of free enzyme; [Bound] is the concentration of actin bound enzyme. Enzyme concentrations are in μM; actin concentration was 25 μM. Both aldolase and GAPDH show biphasic binding, indicating the presence of (a) high and (b) low-affinity sites for the rabbit muscle enzymes. The total enzyme concentration for the high-affinity site (a) is <1.0–1.5 μM, whereas the total enzyme concentration for the low-affinity site (b) is >1.5 μM.

TABLE 2.

Dissociation constants (K_D) for the binding of aldolase and GAPDH to actin in rabbit muscle and yeast

Actin source	Binding enzyme	Affinity	KD (μM)	n	“True” KD (μM)
Muscle	Muscle aldolase	High	0.67 ± 0.18	21	0.03 ± 0.08
		Low	12.3 ± 0.76	4	3.05 ± 0.19
Muscle	Muscle GAPDH	High	0.7 ± 0.2	28	0.03 ± 0.01
		Low	15.8 ± 0.9	5	3.50 ± 0.20
Yeast	Yeast aldolase	High	N/A	N/A	N/A
		Intermediate	12.9 ± 0.9	10	1.29 ± 0.09
Yeast	Yeast GAPDH	High	N/A	N/A	N/A
		Intermediate	8.4 ± 0.6	10	0.84 ± 0.06
Muscle	Yeast aldolase	High	N/A	N/A	N/A
		Low	23.4 ± 1.8	6	3.90 ± 0.30
Muscle	Yeast GAPDH	High	N/A	N/A	N/A
		Low	16.0 ± 3.5	5	3.20 ± 0.70
Yeast	Muscle aldolase	High	N/A	N/A	N/A
		Intermediate	9.2 ± 2.6	13	0.72 ± 0.20
Yeast	Muscle GAPDH	High	N/A	N/A	N/A
		Intermediate	15 ± 5	17	0.9 ± 0.3

The number of actin monomers bound per enzyme molecule is n. The K_D is obtained directly from the Scatchard plot as explained in Materials and Methods. The “true” K_D is the experiment K_D per actin subunit; i.e., K_D/n. The results represent the mean ± SE of the mean for four experiments for muscle and three experiments for yeast actin.

Differentiation of these binding sites is further stressed when the number of actin units bound to a single enzyme molecule, n (obtained from the same plot, see Materials and Methods), is considered (Table 2). Since one turn of the actin polymer involves 13–14 subunits, one can see that the low-affinity sites involve binding to one-third of a turn (only 4–5 subunits) whereas high-affinity sites bind to two turns (21–28 subunits), respectively; this could also be due to significant cross-linking occurring during this high-affinity binding (see the next section). When the dissociation constants are recalculated per molecule of actin rather than the actin subunit, the “true” dissociation constants, 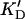(actin molecule) = K_D (subunit)/n, are two orders of magnitude apart for high- and low-affinity sites (Table 2).

By contrast, biphasic Scatchard plots were not observed for either yeast aldolase or yeast GAPDH (Fig. 6) and their K_D values for muscle actin were similar to those of low-affinity sites of muscle enzymes (Table 2). Therefore, high-affinity binding is characteristic only for the pairing of muscle actin and muscle enzymes. Besides these, the values of remaining binding constants presented in Table 2 can be divided into two groups: 1), the lowest affinity sites characteristic only for the muscle actin and either of enzymes and binding only 4–6 actin units, and 2), intermediate affinity sites characteristic for binding of either enzyme to the yeast actin (binding 10–17 actin units).

FIGURE 6.

Scatchard plots for yeast aldolase and GAPDH binding to skeletal muscle actin. [Free] is the concentration of free enzyme; [Bound] is the concentration of bound enzyme to actin filaments. Enzyme concentrations are in μM; actin concentration was 25 μM. No biphasic binding is observed.

Viscosity

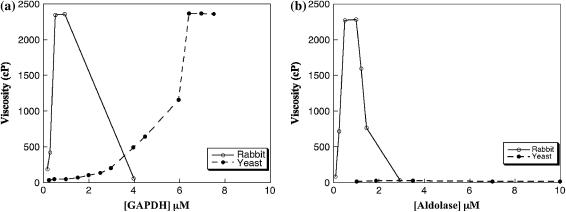
Additional experimental evidence for enhanced muscle enzyme binding to actin was obtained by using falling ball viscometry (Fig. 7). At higher concentrations of enzymes the viscosity decreased as observed earlier by Wang et al. (39). The increase of viscosity upon the increase of the enzyme/actin ratio observed in the intermediate enzyme concentration range is of greater significance to our study because it is apparently due to enzyme cross-linking, with the actin filaments forming a network with higher viscosity. The increase of viscosity, i.e., cross-linking, caused by rabbit muscle enzymes (both GAPDH and aldolase) increases within a narrow enzyme concentration range of 0.1−0.5 μM (Fig. 7). This is similar to the results for skeletal aldolase reported by Wang et al. (39). This concentration range is the same as that of cosedimentation forming high-affinity aggregates (Fig. 5 a) and corroborates with the values of the corresponding experimental binding constants, K_D (Table 2). Therefore, muscle enzyme-actin binding results in significant filament cross-linking, and high-affinity sites are involved.

FIGURE 7.

Effect of rabbit muscle and yeast glycolytic enzymes on modification of viscosity of rabbit muscle actin solutions. A constant concentration of 25 μM rabbit muscle F-actin was incubated with increasing amounts of rabbit muscle or yeast GAPDH (a) and aldolase (b) as described in the Materials and Methods. An increase in viscosity is caused by the enzymes' cross-linking the actin filaments, forming a network that slows or prevents movement of the steel ball. The falling ball method allows measurement to 2500 centipoises after which the ball did not move through the cross-linked filaments.

Yeast enzymes were less effective for cross-linking than muscle enzymes. The curve showing an increase of viscosity upon increasing the enzyme/actin ratio was rather broad for yeast GAPDH, indicating poor specificity. In addition, the enzyme concentration required to reach half maximum viscosity, 6 μM, was about an order of magnitude greater than the cross-linking concentration of muscle GAPDH (Fig. 7 a). This was also similar to the concentration range of cosedimentation experiments for the yeast proteins (Fig. 6) as well as those for muscle proteins in the low-affinity range (Fig. 5 b). Yeast aldolase did not cause cross-linking at concentrations up to 18 μM (Fig. 7 b).

BD snapshots of possible binding modes

Enzyme-G-actin

A total of 6000 BD trajectories produced 561 yeast GAPDH/yeast G-actin complexes, with average electrostatic interaction energy of −5.2 kcal/mol. Specific amino acid residues identified as critical in these interactions included Lys's 88, 257, 330, and Arg² for GAPDH, and Asp², Glu⁴, Asp²⁵, Glu¹⁰⁰, Glu³⁶³, and Asp³⁶⁴ for actin. The distribution of complexes showed that for most of the complexes, the G-actin locates at the four corners of the GAPDH tetramer (Fig. 8), which were initially shown by the electrostatic potential field calculations to be highly positively charged (Fig. 3 b). The densities of GAPDH around the highly negatively charged subdomains I and IV, however, were still clearly higher than the density around the more positive subdomains II and III.

FIGURE 8.

BD distribution of the COMs of actin around yeast enzymes. Each dot represents the COM of actin in an encounter snapshot with either yeast GAPDH (left) or yeast aldolase (right). For GAPDH, the COMs are concentrated around the corners where the electrostatic potential is predominantly positive; for aldolase, the encounters are randomly distributed and no large positive electrostatic potential patches are found because it is predominantly negative.

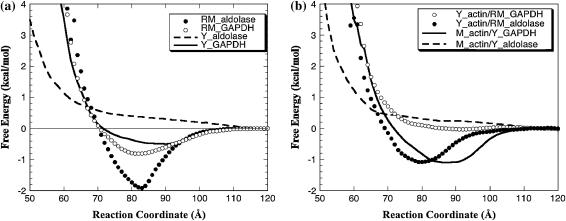
For the simulations of interactions between yeast aldolase and yeast G-actin, 10,000 trajectories produced 935 complexes. The distribution of complexes, however, did not exhibit any specificity in the location of either one of the proteins around the other; the apparently random distribution of actin COM around yeast aldolase compared to the results for GAPDH is shown in Fig. 8. This nonspecific distribution indicates that the complexes formed were a result of random collisions between the two proteins rather than significant electrostatic interaction. The average electrostatic energy of all complexes resulting from these interactions was ∼−1.3 kcal/mol, and the free energy profile for the interaction with F-actin (Fig. 9) did not show any minimum, thus supporting the lack of potential for yeast aldolase binding to the corresponding actin.

FIGURE 9.

Radial free energy profiles of various enzymes binding F-actin. (a) Each curve shows the binding of a given enzyme to F-actin from the same organism. The reaction coordinate is defined as the distance between the COM of the enzyme and the F-actin helix axis. (b) Each curve shows the binding of given enzyme to F-actin from a different organism.

The main difference between the interactions of yeast GAPDH with yeast G-actin and those of rabbit GAPDH with rabbit G-actin was that the latter pair had a much greater affinity for each other and formed many more complexes. For aldolase, however, the yeast form did not show any real affinity for G-actin, in contrast to the strong interactions earlier shown for rabbit aldolase/rabbit G-actin (29,30).

Enzyme-F-actin

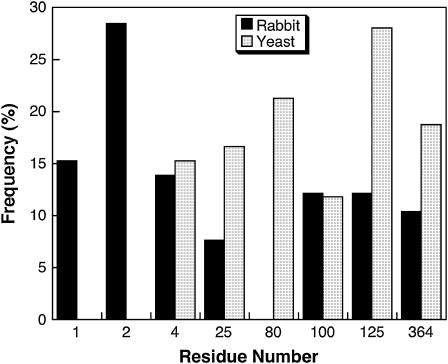
For yeast GAPDH, 1,000 BD trajectories generated 1,869 complexes. The average electrostatic interaction energy was −18.4 kcal/mol, and the majority of complexes showed a binding mode in which two subunits of GAPDH were interacting with two adjacent subunits of the F-actin hexamer. The most frequent amino acid residues involved in these interactions were similar to those noted in the GAPDH-G-actin interactions. The frequencies of occurrence of the critical amino acid residues identified for yeast and rabbit muscle F-actin are compared in Fig. 10. These results indicate that the N-terminal residues of muscle F-actin enhance its interaction with enzymes. For yeast aldolase, 1000 BD trajectories generated fewer complexes (1345) with a much weaker average interaction energy (–3.3 kcal/mol).

FIGURE 10.

Critical F-actin residues for yeast and muscle F-actin. The numbers in the x axis indicate the amino acid residue number in the actin sequence. These residues are all aspartates or glutamates and are located in subdomain I of actin.

BD simulations of energetics

The radial binding free energies of wild-type proteins (Table 1) and the free energy profiles (Fig. 9) demonstrate the orientationally averaged interactions between the proteins. The deeper the well, the more quickly a pair of proteins become oriented to create a complex; the shallower the well, the smaller the chance of finding a specific binding mode and the longer it would take to form a complex. Whereas the free energy profile for yeast aldolase interacting with any form of F-actin shows no well, those for yeast GAPDH, rabbit aldolase, and GAPDH exhibit minima in a range of 81–83 Å (Fig. 9 a). The curves show that the strongest interactions are obtained between rabbit muscle aldolase and rabbit F-actin, and the value of the calculated radial free energy is the most negative (Table 1). The strength of this interaction is further demonstrated by the specific electrostatic interaction energy calculated for the complex with the most salt bridges. The binding of rabbit enzymes to yeast F-actin (Fig. 9 b) is much weaker than when the rabbit enzymes bind muscle F-actin; this is also supported by less favorable specific interaction energies (Table 1). On the other hand, whereas yeast aldolase showed no radial free energy well with yeast or muscle F-actin, yeast GAPDH produced wells with muscle F-actin and, to a lesser degree, with yeast F-actin. This suggests the importance of the N-terminus of F-actin in its interactions with the enzymes. Previous BD studies involving mutations of the N-terminus of rabbit F-actin showed weaker interaction of resulting mutants with enzymes comparable to the interactions with yeast F-actin (30). This observation, although reaffirming the electrostatic nature of such interactions, also complements the multiple trajectory simulations results by emphasizing the importance of the mutated amino acid residues.

DISCUSSION

The interaction of microfilaments with proteins in the cytomatrix (i.e., glycolytic enzymes) in higher eukaryotic cells is supported by our results, which demonstrate affinities in the submicromolar to micromolar range. Furthermore, our results indicate that actin-enzyme interactions do occur in yeast, although with much decreased affinities (Fig. 6 and Table 2). The biphasic binding of muscle enzymes to muscle actin filaments, evident from the cosedimentation experiments and Scatchard analysis, is an indication of the presence of high- and low-affinity binding sites (Fig. 5). The micromolar range enzyme concentration at which a sharp increase in viscosity is observed with muscle enzyme and muscle actin (Fig. 7) means that the cross-linking of actin filaments by these enzymes involves the high-affinity binding sites. Yeast proteins, on the other hand, show neither biphasic binding nor any sharp increase in viscosity at 1–2 μM concentration (Fig. 7). In fact, whereas it required ∼10 times more yeast GAPDH to induce a sharp increase in viscosity (Fig. 7 a), yeast aldolase did not show any potential for actin filament cross-linking within a reasonable concentration range (Fig. 7 b). These observations, although indicating that interactions in yeast are of lower affinity, also show that yeast GAPDH is a better actin-binding protein and cross-linker than yeast aldolase. The binding of enzymes to yeast actin may be qualified as being of intermediate affinity (between the high and low affinities observed for rabbit muscle F-actin). This intermediate affinity site in yeast actin corresponds to the low-affinity site in rabbit muscle actin; however, it is more accessible in yeast actin because of its more open nature (53). Hence, even with the same residues involved, stronger interactions are obtained with yeast actin than with rabbit muscle actin, leading to somewhat intermediate affinity-type binding.

BD studies confirm the low affinity in binding of yeast enzymes to yeast actin and suggest that yeast aldolase does not bind yeast F-actin specifically (Fig. 9). Comparison of muscle and yeast actin reveals that the N-terminus plays an important role in the binding of aldolase and GAPDH. If the N-terminus were not critical, then both forms of actin would have the same affinity for the enzymes. On the contrary, both experiment and BD simulations reveal that the lower affinity of yeast actin for enzymes is probably due to the fact that yeast actin has two fewer charged amino acid residues at the N-terminus. The experiments show that muscle actin has a much higher affinity for both yeast and muscle GAPDH than does yeast actin (Table 2). BD simulations support this observation. Of the yeast enzymes, yeast GAPDH binds better, and it shows stronger binding with muscle actin compared to the yeast actin (Fig. 9 b). BD simulations using actin mutants showed a measurable increase in electrostatic interaction energy when one or more of the first four N-terminal actin residues were replaced with alanine (65). When two of the four residues in muscle actin were replaced, the resulting mutant had the same affinity for enzymes as the unmutated yeast actin. In the reverse mutation, where the two uncharged residues of the first four N-terminal residues of yeast F-actin were replaced by charged residues (aspartates), the binding affinity observed with rabbit muscle F-actin and muscle enzymes was reproduced (65). For both muscle and yeast actin, mutating any of the four residues caused a weakening of the actin-enzyme interactions, hence supporting the importance of these residues in the interactions (65). Complete neutralization of the N-terminus, however, does not completely eliminate binding (65). This suggests that although the N-terminus is important, there may be another enzyme-binding site on actin. This site comprises a number of negatively charged amino acid residues including the pairs D²⁴/D²⁵, D⁸⁰/D⁸¹, E⁹⁹/E¹⁰⁰, and E³⁶³/E³⁶⁴ as revealed by the BD simulations (Fig. 10). These amino acid residues, all found on subdomain I of actin (residues 1–32, 70–144, 338–375) (26), may constitute the low-affinity binding site that is very prominent in the yeast actin interactions and only becomes critical in muscle if the N-terminus charges are neutralized. Experimental studies in which these residues were mutated showed weaker binding with enzymes, with much larger K_D values (36). Hence BD simulations are capable of identifying a single binding affinity, especially since only one molecule of enzyme and one F-actin molecule are used during simulations. For muscle actin where the N-terminus is intact, BD results would correspond to the high-affinity binding. For yeast actin where the N-terminus has lost some of its activity, the low-affinity site is what BD results portray.

Yeast aldolase is only 48% identical in sequence to the muscle form; its functional form is a dimer as opposed to a tetramer for muscle aldolase, and yeast aldolase uses an entirely different reaction mechanism. Muscle and yeast GAPDH, on the other hand, have a 73% sequence similarity and are both tetramers that use the same reaction mechanism. This difference in quaternary structure may be the reason for the lack of actin-cross-linking ability shown by yeast aldolase. The theoretical analysis of the rabbit muscle aldolase/F-actin complexes revealed the dominant binding mode between these proteins—one of the aldolase's positively charged grooves (between subunits A and D or B and C) bound to subdomain I of an actin subunit in F-actin (29). Only a single aldolase molecule binding to one actin filament was simulated, and such a system would correspond to a binding experiment at low enzyme concentration. It is suggested here, therefore, that at low concentration, rabbit muscle aldolase uses both of its positive grooves to bind neighboring actin filaments and produce cross-linking. Both muscle and yeast GAPDHs, which are also tetramers, show a somewhat different mode of binding to actin (65). In this case, the reactive sites on the enzymes do not form a groove as in muscle aldolase, but remain spatially separated on each subunit. Hence the main enzyme/actin binding mode in muscle involves two subunits of GAPDH binding to two adjacent subunits of actin filament (31,65). The binding of one pair of subunits from the enzyme still leaves another pair that can bind another actin filament to produce cross-linking. Yeast aldolase, a dimer, would not be expected to cross-link actin filaments because it does not have the required quaternary structure and that is what was observed. Thus, the theoretical model agrees with the results from viscosity measurements and strongly suggests that the tetrameric structures of both aldolase and GAPDH may be a crucial factor that allows cross-linking of actin filaments. The observation that the full quaternary structure is needed for cross-linking also sheds light on the classic question “why are glycolytic enzymes so large”? In 1984, Paul Srere hypothesized that one reason enzymes are so big is to allow the outside surfaces of the proteins help to locate the enzyme in the cell (67). For aldolase or GAPDH, the large surface area of the tetramer provides the interactions possible to locate them on F-actin.

CONCLUSIONS

We have shown that there is a potential for actin-enzyme interactions in yeast cells. Our results show that in muscle, GAPDH is as good an actin-binding protein and cross-linker as aldolase, but it is much better than aldolase in yeast. We have attributed the lower-affinity interactions in yeast to the lack of a highly negatively charged N-terminus. Cross-linking of actin filaments by enzymes has been judged to be dependent on quaternary structure, with tetrameric structures being more favorable cross-linkers. In a system such as the glycolytic pathway, where enzyme-actin interactions have been suggested to play an important role in compartmentation and substrate channeling, the weak binding of yeast aldolase to yeast actin may suggest an alternative binding scheme. It is possible that yeast aldolase could possibly be “piggy-backing” to GAPDH, thus suggesting that GAPDH is a key organizing enzyme in yeast around which the cytoskeleton is organized. This hypothesis and the possibility of substrate channeling between aldolase and GAPDH in yeast will be further investigated.

Overall, however, the lower form of actin is a poorer binder of glycolytic enzymes than muscle actin. Given that interactions involving the mammalian nonmuscle actin have never been studied, and considering that processes such as axonal transport are speculated to have this binding as a component, it is obvious now that actins are not identical in binding of enzymes. Therefore, the difficult proposition of purifying nonmuscle actin for the purpose of determining interactions may be attempted. A better route, however, will be to use computational modeling because in this study, the interactions were compared to hands-on experiments, and the modeling showed results that correlate with the lab results. Thus, projecting with computational modeling of brain actin interactions with enzymes will be an obvious future study.