Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2005 Dec 2;90(4):1411–1418. doi: 10.1529/biophysj.105.069344

Sacrificial Bonds and Hidden Length: Unraveling Molecular Mesostructures in Tough Materials

Georg E Fantner *, Emin Oroudjev *, Georg Schitter *, Laura S Golde *, Philipp Thurner *, Marquesa M Finch *, Patricia Turner *, Thomas Gutsmann †, Daniel E Morse ‡, Helen Hansma *, Paul K Hansma *
PMCID: PMC1367291  PMID: 16326907

Abstract

Sacrificial bonds and hidden length in structural molecules and composites have been found to greatly increase the fracture toughness of biomaterials by providing a reversible, molecular-scale energy-dissipation mechanism. This mechanism relies on the energy, of order 100 eV, needed to reduce entropy and increase enthalpy as molecular segments are stretched after being released by the breaking of weak bonds, called sacrificial bonds. This energy is relatively large compared to the energy needed to break the polymer backbone, of order a few eV. In many biological cases, the breaking of sacrificial bonds has been found to be reversible, thereby additionally providing a “self-healing” property to the material. Due to the nanoscopic nature of this mechanism, single molecule force spectroscopy using an atomic force microscope has been a useful tool to investigate this mechanism. Especially when investigating natural molecular constructs, force versus distance curves quickly become very complicated. In this work we propose various types of sacrificial bonds, their combination, and how they appear in single molecule force spectroscopy measurements. We find that by close analysis of the force spectroscopy curves, additional information can be obtained about the molecules and their bonds to the native constructs.

INTRODUCTION

Many natural materials gain their strength from combinations of organic and inorganic components (1–5). In some of these materials, as well as in some pure organic materials, it has been shown that their molecules possess a reversible toughening mechanism which increases the energy needed to break the material (6–8). This mechanism often involves sacrificial bonds and hidden length. Sacrificial bonds are defined as bonds that break before the main structural link (often the molecular backbone) is broken (7). These bonds are frequently weaker than the covalent bonds of molecular backbones. The hidden length is defined as the part of the molecule that was constrained from stretching by the sacrificial bond. Several proposed sacrificial bond types with examples of polymers in which they may play a role are listed in Table 1.

TABLE 1.

Bond types that could function as sacrificial bonds

Candidate for sacrificial bond Example material References
Ionic Surlyn (32)
Hydrogen bond Titin (9,10,13,33)
Hydrophobic interactions Bacteriorhodopsin (34,35)
Van der Waals Gecko feet (36)
Organo-metalic Bonds Mussel byssal thread (37,38)
Open in a new tab

Interest in mechanically stretching single molecules has grown rapidly since the initial reports of unfolding titin (9,10), in part because of a series of elegant reports showing how far the technique could be pushed to obtain new information (11–14). Recently, atomic force microscopy (AFM) molecular pulling experiments have been used to investigate molecules in native constructs to understand their assembly mechanisms and their roles in native materials (15,16). In natural materials, many molecules are often involved in the formation of a network. In networks of cross-linked molecules, large amounts of length can be hidden from an applied load by a variety of cross-links, including both sacrificial bonds and entire cross-linking molecules. When investigating such systems with AFM single molecule spectroscopy, the force spectra soon become quite complicated. Here we present some characteristic features of more complicated force spectra and show how additional information can be extracted from them.

MATERIALS AND METHODS

We simulated the force spectra (also called pulling curves) using routines written in MATLAB 6 (MathWorks, Natick, MA) . The molecules were assumed to behave as worm-like chains (WLC) (17–19) for which the stretching force is described by

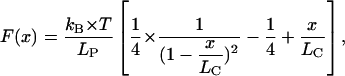graphic file with name M1.gif

where LP is the persistence length of the molecule, LC the contour length of the molecule, kB the Boltzmann constant, T the absolute temperature, and x the pulling distance. Breakage of sacrificial bonds was simulated by changes in the contour length of the molecules when the bond rupture force was reached. For rupture of a whole molecule, the contribution of that molecule was set to zero by setting the contour length to infinity. For sacrificial bonds that were initially shielded against applied forces by other sacrificial bonds (Fig. 2, case 2 and 3), the applied force was set to zero until the shielding sacrificial bond broke.

FIGURE 2.

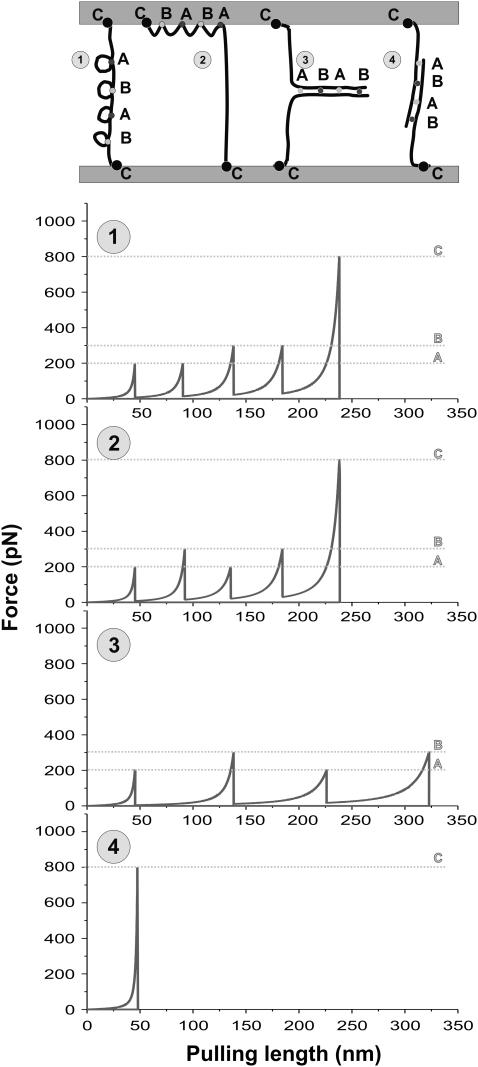
FIGURE 2

Open in a new tab

Various sacrificial bonds on single strand connections. (1) The molecule binds to itself with sacrificial bonds; the hidden length is the distance between the two binding sites on the molecule. When a force is applied and molecules are stretched, the sacrificial bonds will break according to their relative bond strengths (20). (2) The molecule binds to the surface with sacrificial bonds. The hidden length equals the distance between two neighboring sites on the molecule that bind to the surface. When a force is applied and the molecules are stretched, the sacrificial bonds break in the sequence that they are in on the molecule. (3) One molecule binds to a second molecule with complementary binding site sequence. The hidden length equals the distance between neighboring sacrificial bonds on one molecule plus the distance between the corresponding binding sites on the second molecule (in the figure this length is twice the distance between A and B). When a force is applied and the molecules are stretched, the bonds break in the sequence that they are in on the molecules (17,27,29). (4) One molecule bonds to a second molecule with a reversed complementary binding site sequence. The sacrificial bonds are loaded in parallel; therefore they will all break once a force is reached larger than the combined binding force. In this case, no hidden length is set free.

Simulations to determine the slopes before the ruptures for the cases of parallel molecules and a single molecule containing multiple, similar domains were done using MATLAB/SIMULINK. For each molecule the pulling distance dependent force was simulated using Eq. 1. For a better comparison to real pulling data, a white noise signal that is typical for such experiments was added to the simulated pulling force (noise power = 3e − 27, sampling time = 1 ms). To make the comparison between the force spectra more clear, the data have been filtered by a low-pass filter before taking the derivative.

Sample preparation and instrumentation

We chose two natural systems, an aggrecan and hyaluronic acid complex, and gluten, as representatives of natural systems in which sacrificial bonds and hidden length contribute to mechanical properties.

Aggrecan and hyaluronic acid

Complexes of aggrecan and hyaluronic acid substrates (20) were prepared using a concentration of 25 μg/ml aggrecan (SIGMA A-1960, St. Louis, MO) and 2.5 μg/ml hyaluronic acid (SIGMA H-1876), incubated for 24 h at room temperature. A total of 3 μl of the solution was placed on a freshly cleaved mica disk and dried for 30 min. The disk was washed with 1 ml high performance liquid chromatography grade water and dried for 30 min. AFM micrographs were taken in air at room temperature using a Nanoscope III atomic force microscope (Digital Instruments, Santa Barbara, CA) in tapping mode. Micrographs were taken to ensure adequate substrate coverage (data not shown).

Aggrecan pulling experiments were performed using a Multimode PicoForce (Digital Instruments) using soft SiN cantilevers (BioLever; Olympus, Tokyo Japan) with a typical spring constant of 27 pN/nm and a resonance frequency of 37 kHz. Pulling was performed in an aqueous environment containing Ca Buffer (40 mM CaCl, 110 mM NaCl, 10 mM HEPES at pH 7.01).

Gluten

Crude wheat gluten (G-5004, SIGMA) was used as a source of the total gluten protein. To produce a gluten film, wheat gluten was mixed with 50% isopropanol in ratio 1:10 and the resulting suspension was applied onto a glass slide for pulling on a total gluten network. We used a Molecular Force Spectroscopy apparatus (Molecular Force Probe (MFP-1D); Asylum Research, Santa Barbara, CA) to assess viscoelastic properties of the gluten protein network at the mesostructural level. All pulls were made at 300–500 nm/s pulling speed under MilliQ water. We used soft SiN cantilevers MLCT-AUHW from Veeco (Santa Barbara, CA) with a 50 pN/nm spring constant and a 15 kHz air resonant frequency.

RESULTS AND DISCUSSION

Sacrificial bonds and hidden length

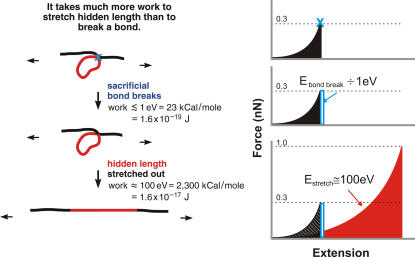
Sacrificial bonds and hidden length were discovered, with single molecule force spectroscopy, to function as a mechanistic origin for the toughness of natural fibers, composites, and adhesives (7). Part of the length of a polymer adhesive molecule, for example, can be hidden from external forces that are working to stretch the molecule, by isolating it with a sacrificial bond (see Fig. 1 A). To stretch the molecule, a force has to be applied against entropic, and in some cases, enthalpic elasticity (21). The entropic elasticity is always there, but sometimes there is also an enthalpic contribution to the elasticity from deforming molecular structures, for example, in chair-boat transitions of the glucopyranose ring (18). Initially, when the sacrificial bond is intact, only the entropy of the black part of the polymer contributes to the entropic spring. As the polymer is extended, the force on the polymer increases until the bond fracture force of the sacrificial bond is reached (typically 300 nN), and this bond breaks. The energy to break this bond is ≤1 eV (blue area in Fig. 1). From then on, the hidden length (the red part of the polymer) is released and the entropy of this part of the polymer also contributes to the entropic spring. This results in a drop in the force between the two ends of the polymer (see force-extension curves in Fig. 1). Further stretching of the polymer requires work against the entropy of the entire length of the molecule. This work is large (red area in Fig. 1 B) compared to the work to break even a strong bond. This mechanism could be reversible; when the force is relaxed, entropy collapses the polymer, and sacrificial bonds could reform. This is a self-healing mechanism for dissipating the energy exerted on the molecule. Energy is exerted on molecules in biomaterials, for example, by impacts on the macroscopic scale. The release of hidden length is determined by the force on the molecules, and the time for which it is applied, since the sacrificial bonds break at a higher rate as the force on the molecule increases. Sometimes, as a shorthand expression, we refer to the “rupture force” for a particular type of bond, which we define as the force at which almost all bonds of a particular type would be broken in the characteristic time of a particular macroscopic event.

FIGURE 1.

FIGURE 1

Open in a new tab

Schematic drawing of the basic principle of the sacrificial bond-hidden length mechanism. Before a sacrificial bond is broken, only the black length of the molecule contributes to entropic spring and therefore to the force with which the molecule resists the stretching. The red length of the molecule is hidden from the applied force by the sacrificial bond. When the bond breaking force is reached, only a small amount of energy is needed to break the sacrificial bond. After that, the whole length (black plus red) contributes to the entropy of the molecule. In total, the energy that has to be put in to break the molecule is increased by the shaded area under the first peak. Additionally, the initial slope of the force curve is steeper, which indicates that the molecule is initially stiffer.

If there are multiple bonds with hidden length present in a molecule, multiple peaks will appear in the force-extension curves. The amount of energy that can be dissipated by the molecule before it fractures can therefore be increased by the existence of several sacrificial bond and hidden length domains.

Cases of sacrificial bond mechanisms

There are several possible cases of the sacrificial-bond and hidden-length mechanism. In the mechanism described in Fig. 1, the sacrificial bond is formed between two binding sites on the same molecule, resulting in the hidden length being coiled up in a loop. This type of sacrificial bond can be found, for example, in proteins such as titin (9,13) and spectrin (22). However, the sacrificial-bond and hidden-length mechanism could be implemented in other ways as well. Fig. 2 shows several possible cases of this scheme, where the bonds indicated by A, B, and C are bonds with 200, 300, and 800 nN breaking force, respectively. Case 1 in Fig. 2 is equivalent to the case discussed in Fig. 1. There are loops within the structure of the polymer where hidden length is shielded from the force. When the polymer is stretched, an equal amount of force is exerted on all the sacrificial bonds. The sacrificial bonds will break in the order of their lowest rupture force (the weakest link will rupture first), regardless of their spatial order on the molecule (20). In this case, successive force rupture peaks are always higher than the preceding peak (see the corresponding force-extension curve in Fig. 2). However, when the rupture forces are almost equal and the molecules are pulled quickly, thermal fluctuations can, in some cases, cause stronger sacrificial bonds to break before weaker ones. The hidden length that is set free per rupture is the distance between the involved binding sites on the molecule.

Case 2 in Fig. 2 shows a molecule bound with multiple sacrificial bonds to a surface. This case could be important for polymer-crystal composites (natural composites such as bone (23) and molluscan nacre (7) or artificial composites such as artificial nacre (24)). When the molecule is stretched, only one of the sacrificial bonds is exposed to the applied force. The sacrificial bonds will rupture in the order in which they are arranged on the molecule. A rupture peak can be followed either by a subsequent rupture peak of greater, lesser, or comparable magnitude. The hidden length that is released per rupture is the distance between the binding sites on the molecule. This case is similar to the results from detailed studies of the continuous desorbtion of polyelectrolytes from surfaces (25,26).

Cases 3 and 4 in Fig. 2 show molecules bound with sacrificial bonds to other molecules. In case 3, the bonds rupture in the order in which they are arranged on the molecule, which means that the successive rupture forces could be higher or lower than that causing the preceding rupture (27–29). The hidden length that is released per rupture is the distance between the binding sites on the first molecule plus the distance between the complementary binding sites on the other molecule. In case 4, all the sacrificial bonds are loaded in parallel. The bonds will all break at the same time. In this case, however, no hidden length is released. This case has been seen with DNA molecules (27–29).

Molecules in natural constructs

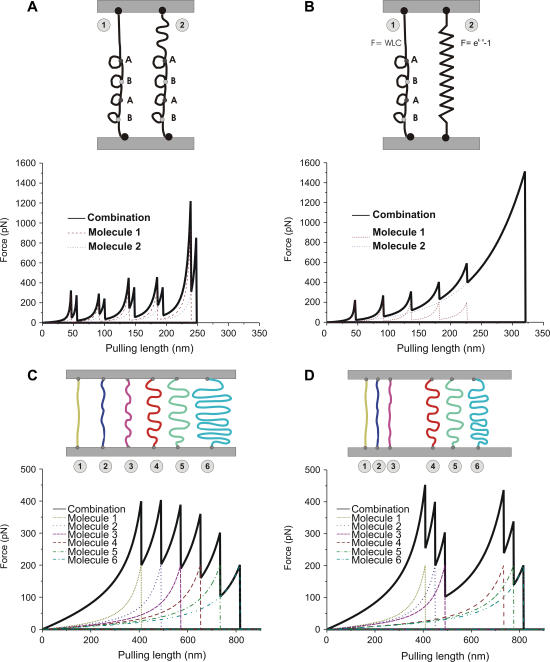
The sacrificial bond-hidden length mechanism has been found in several biological composites such as abalone nacre (7) and bone (21). To study these molecules in their natural state, molecular pulling experiments must be performed on the native molecules. Force versus distance curves of such experiments soon become very complex. These force curves can often not be explained by the simple sacrificial bond models of Fig. 2. In particular, during such experiments, one cannot always ensure that only one molecule is attached to the force probe. Fig. 3, A and B, shows examples of how two relatively simple parallel molecules stretched in parallel can result in complex force spectra. In Fig. 3 A the molecules are identical except for a difference in their initial length. The resulting pulling curve is a superposition of the individual pulling curves deluding four different sacrificial bonding forces. Fig. 3 B shows a molecule with sacrificial domains (case 1 in Fig. 2) in parallel with a molecule which acts as an exponential spring (16). In this case, the saw-tooth signature appears as a subtle pattern on the large force increase due to the exponential spring. An example of a force curve with this behavior is shown in Fig. 4 A obtained from pulling on gluten. Case 3B has some interesting implications: In force spectroscopy experiments with modular proteins like titin, an experimental force curve of type 3B would most probably classify as a single molecule event, with the rising rupture forces erroneously attributed to the stochastic n-effect—clearly leading to a considerable error in rupture force analysis.

FIGURE 3.

FIGURE 3

Open in a new tab

Various pulling curves for multistrand connections. (A) Two molecules with the same pattern of sacrificial bonds but different free contour length of molecules. The molecules get loaded in parallel and the force is distributed between the two strands. Since molecule 1 is shorter than molecule 2, the sacrificial bonds on molecule 1 will be loaded to the bond-breaking force first. After the hidden length from the weakest sacrificial bond on molecule 1 is released, the second molecule has the shorter free contour length. Therefore the next bond that breaks is the weakest sacrificial bond on molecule 2. The total registered force curve is a superposition of these two curves. (B) Two molecules in parallel where one molecule has domains with sacrificial bonds and hidden length and the other molecule has no sacrificial bonds but acts as an exponential spring. The sacrificial bonds on molecule 1 will break in the order of their bond strengths. In the force curve, they will appear as small spikes on a larger slope. (C) Multiple molecules with different lengths bound between the surfaces with equal bond strengths. The length increase between neighboring molecules is constant. The molecules are loaded in parallel; the pulling force is distributed over all molecules. If the distributed force on one molecule exceeds the binding force or the breaking force of that molecule, that connection will break. Each molecule breaks at the same distributed force, but this force occurs at different pulling lengths. The pulling curve shows a steep increase and a successive drop of the following peaks where each peak is followed by a lower peak. (D) Same as panel C but with molecules where the length is not equally spaced. Depending on the length distribution of the molecules, a peak can be followed by either a lower peak or a higher peak.

FIGURE 4.

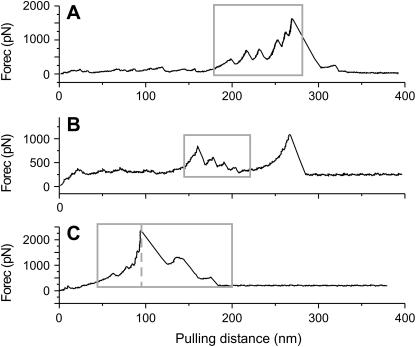
FIGURE 4

Open in a new tab

Pulling curves of gluten networks. (A) Pull with force ruptures on the increasing flank. (B) Pull with stepwise decreasing force ruptures. (C) Pull with force rupture peaks on the increasing as well as the decreasing flank.

Despite the complexity of pulling curves from natural constructs, some information about the arrangement of molecules and bonds can be extracted from them.

Stepwise decreasing bond rupture peaks

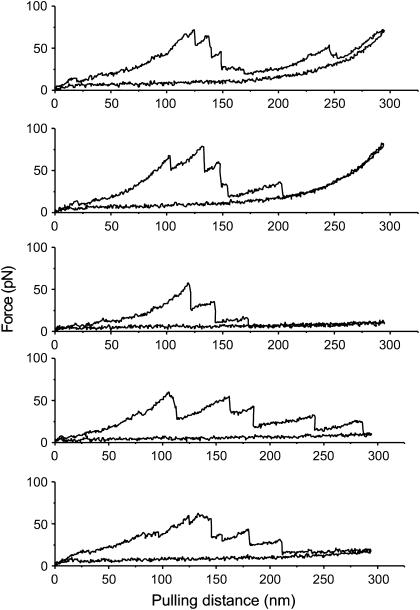
Of the simple sacrificial-bond and hidden-length cases from Fig. 2, only in types 2 and 3 might the rupture forces decrease in pulling curves (see the force curve in Fig. 3 C as an example of a decreasing force curve). For this, the binding forces of the individual sacrificial bonds must decrease progressively with their order in the molecule (for case 2 in Fig. 2: A < B < C). An alternative explanation for stepwise decreasing bond rupture peaks comes from multiple molecules in parallel (see Fig. 3 C). The pulling curve in Fig. 3 C is the result of a superposition of the force spectra of six identical WLC molecules with a constant increase in contour length. Fig. 4 B shows an example of such a stepwise decrease in rupture peaks within a larger pulling curve. Fig. 4 C shows an example where there are ruptures both on the increasing flank and the decreasing flank. Fig. 3 D shows the same arrangement of molecules as Fig. 3 C; however, with molecules of randomly distributed contour length a more arbitrary pulling pattern is observed. These results show that it cannot be unambiguously determined whether a pulling curve results from the behavior of one complex molecule or of several molecules in parallel; however, repeated stepwise decreases in bond rupture force point to the involvement of multiple molecules in parallel. Such stepwise decreasing forces of rupture occur especially often when pulling on molecules with multiple side chains. Fig. 5 shows examples of such pulls on an Aggrecan-Hyaluronic acid complex.

FIGURE 5.

FIGURE 5

Open in a new tab

Pulling curves of Aggrecan-Hyaluronic acid complex. Many of the pulls have a stepwise decrease in force ruptures either at the end of the pull or in between other force peaks. The high occurrence of these decreasing force ruptures could be a result of the branched nature of the molecular complex.

First derivative of force spectra

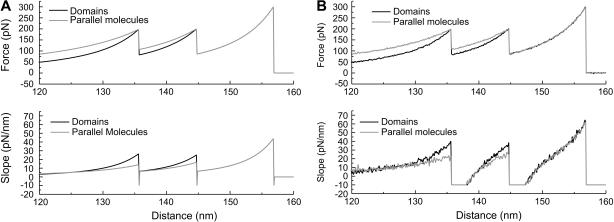
Another way to determine whether a pulling curve originates from a single molecule with multiple condensed domains or from multiple molecules in parallel is to take the first derivative of the force spectrum. If the persistence length of the molecule is known, the slope of the force curve before and after a rupture can be used to determine if one or multiple molecules are involved (see Fig. 6). Fig. 6 A shows calculated force spectra for i) one molecule with two condensed domains held by internal sacrificial bonds (LC = 170 nm, two hidden lengths of 10 nm each, bond-breaking force = 200 pN for the first two bonds, and 300 pN for the molecule backbone); and ii) three molecules in parallel with the same persistence length. The contour length and the binding force were chosen so that the rupture peaks for both situations occur at the same pulling distance and rupture force (LC1 = 158 nm, LC2 = 166 nm, LC3 = 170 nm, bond-breaking force = 200 pN for 1 and 2, and 300 pN for 3).

FIGURE 6.

FIGURE 6

Open in a new tab

Differentiation between force curves of single molecules with domains and of several molecules in parallel by analyzing the slope of the force curve before rupture. (A) Generated force curves of i), a single molecule with two domains, and ii), three parallel molecules. The contour length and the rupture forces were chosen so that the ruptures occurred at the same pulling length and the same force. The force curve of the single molecules with domains has a steeper slope before the rupture as can be seen when taking the derivative of the force curve (lower plot). (B) Same experiment but with typical noise. The difference in the slopes of the force curves can still be seen in the derivatives of the force curve (lower plot).

The force spectrum for the single molecule with the two condensed domains exhibits a steeper incline just before the rupture than the force spectrum of the three molecules in parallel. This can be seen more clearly when the first derivative of the pulling spectra is taken (lower curve of Fig. 6 A). This difference in slope can be used as a criterion for objective and automated determination of whether a pulling curve originates from a single molecule with multiple condensed domains or from several molecules in parallel. Fig. 6 B shows the same experiment but with typical measurement noise for pulling experiments with low noise cantilevers (30,31). Although the derivatives of these measurements are very sensitive to noise, the difference in the derivatives of the single molecule case and the multiple molecule case can still be clearly resolved. However, the energy dissipation is achieved in this simulation in the case of one molecule with condensed domains by a 170 nm long molecule, whereas with three parallel molecules it requires 493 nm of material. This shows that with a little more material, the energy dissipating capabilities of a molecule can be increased dramatically by incorporating hidden length within condensed domains.

Effects of sacrificial bonds and hidden length on material properties

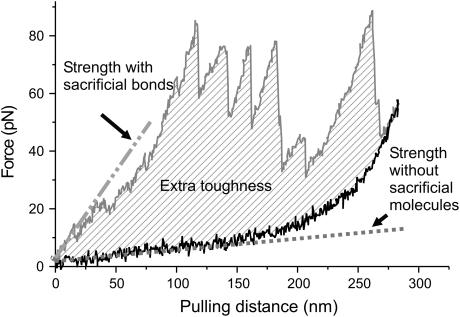
Sacrificial bonds and hidden length have been suggested to improve the fracture-resisting properties of several composite materials (6–8,16). The two main improvements of such mechanical properties are increased initial stiffness of the material and increased fracture toughness (see Fig. 7). A measure of the stiffness of the material is the initial slope on a force versus distance curve. In a material with sacrificial molecules (upper curve in Fig. 7), the slope is significantly steeper (dash-dotted line) than the slope (dotted line) of a material without sacrificial bonds (lower curve in Fig. 7; this curve equals the retraction curve). The increased gain in toughness is represented by the increased energy that is dissipated when deforming the material with sacrificial molecules (shaded area in Fig. 7), compared to the case in which no sacrificial bonds are present. These characteristics are true for each of the pulling curves discussed in this work. For the effectiveness of the sacrificial bond-hidden length mechanism, it is therefore not imperative to have condensed domains within a single polymer; rather, it is necessary that some of the molecular length is at least partially hidden from the applied force by sacrificial bonds. This can be realized with molecules that have built-in hidden length (as in titin and other molecules with functionally similar domains) or with multiple parallel molecules of different lengths. In many natural materials, a network of molecules is involved in the sacrificial bond-hidden length mechanism with a possible combination of sacrificial bonds as well as whole sacrificial molecules.

FIGURE 7.

FIGURE 7

Open in a new tab

Sacrificial molecules increase the stiffness and the toughness of a material. The initial slope of the pulling curve is a measure for the stiffness of a material. In the case with sacrificial molecules (upper curve) this slope is steeper (dash-dotted line) than the slope (dotted line) in the case without sacrificial molecules (lower curve). The extra energy that is dissipated through the sacrificial molecules (shaded area in the curve) is a measure for the increase in toughness of the material.

CONCLUSIONS

We have discussed some of the possible implementations of the sacrificial bond-hidden length mechanism and shown how they manifest themselves in molecular force spectroscopy pulls. Especially in more complex materials, it can be difficult to unambiguously explain the shape of a pulling curve. However, with some knowledge of the material's molecules and identification of common patterns in the pulling curves, one can distinguish fairly well between the case of pulling on a single molecule with multiple condensed domains and the case of pulling on several molecules in parallel (or one molecule with parallel branches). In particular, stepwise decreasing force ruptures in the pulling curve point to multiple parallel molecules. In addition, determining the slope of the pulling curve before and after rupture gives an indication of whether single or multiple molecules are involved, and this could be used as a basis for an automated interpretation of pulling curves.

Overall, the increased stiffness and toughness of materials resulting from the sacrificial bond and hidden length mechanism is not uniquely dependent on molecules with condensed domains within the molecule but rather on the presence of molecular length that is at least partially shielded from the applied force by sacrificial bonds.

Acknowledgments

This work is supported by the National Science Foundation through the UCSB Materials Research Laboratory under award No. DMR00-80034, by the National Institutes of Health under award No. GM65354, by National Aeronautics and Space Administration University Research Engineering and Technology Institutes on Bio-inspired Materials under award No. NCC-1-02037, National Science Foundation/MCB under award No. 0236093, by a research agreement with Veeco No. SB030071, by the Austrian Science Foundation through a DOC fellowship, Fonds zur Förderung der Wissenschaftlichen Forschung project No. J2395-N02, Swiss National Fund postdoctoral fellowship PBEZ2-105116, University of Califonia Santa Barbara Research Internships in Science and Engineering, and University of California Leadership Excellence through Advanced Degrees.

References

  • 1.Fernandez, M. S., K. Passalacqua, J. I. Arias, and J. L. Arias. 2004. Partial biomimetic reconstitution of avian eggshell formation. J. Struct. Biol. 148:1–10. [DOI] [PubMed] [Google Scholar]
  • 2.Katti, D. R., K. S. Katti, J. M. Sopp, and M. Sarikaya. 2001. 3D finite element modeling of mechanical response in nacre-based hybrid nanocomposites. Comput. Theor. Polym. Sci. 11:397–404. [Google Scholar]
  • 3.Okumura, K., and P. G. de Gennes. 2001. Why is nacre strong? Elastic theory and fracture mechanics for biocomposites with stratified structures. Eur. Phys. J. E. 4:121–127. [Google Scholar]
  • 4.Belcher, A. M., D. Margolese, P. K. Hansma, D. E. Morse, and G. D. Stucky. 1996. Protein-inorganic assembly to form biocomposite materials. Abstr. Pap. Am. Chem. Soc. 212:177 (Abstr.). [Google Scholar]
  • 5.Fratzl, P., I. Burgert, and H. S. Gupta. 2004. On the role of interface polymers for the mechanics of natural polymeric composites. Phys. Chem. Chem. Phys. 6:5575–5579. [Google Scholar]
  • 6.Thompson, J. B., J. H. Kindt, B. Drake, H. G. Hansma, D. E. Morse, and P. K. Hansma. 2001. Bone indentation recovery time correlates with bond reforming time. Nature. 414:773–776. [DOI] [PubMed] [Google Scholar]
  • 7.Smith, B. L., T. E. Schaffer, M. Viani, J. B. Thompson, N. A. Frederick, J. Kindt, A. Belcher, G. D. Stucky, D. E. Morse, and P. K. Hansma. 1999. Molecular mechanistic origin of the toughness of natural adhesives, fibres and composites. Nature. 399:761–763. [Google Scholar]
  • 8.Oroudjev, E., J. Soares, S. Arcdiacono, J. B. Thompson, S. A. Fossey, and H. G. Hansma. 2002. Segmented nanofibers of spider dragline silk: atomic force microscopy and single-molecule force spectroscopy. Proc. Natl. Acad. Sci. USA. 99:6460–6465. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Rief, M., M. Gautel, F. Oesterhelt, J. M. Fernandez, and H. E. Gaub. 1997. Reversible unfolding of individual titin immunoglobulin domains by AFM. Science. 276:1109–1112. [DOI] [PubMed] [Google Scholar]
  • 10.Rief, M., M. Gautel, A. Schemmel, and H. E. Gaub. 1998. The mechanical stability of immunoglobulin and fibronectin III domains in the muscle protein titin measured by atomic force microscopy. Biophys. J. 75:3008–3014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Carrion-Vazquez, M., A. F. Oberhauser, S. B. Fowler, P. E. Marszalek, S. E. Broedel, J. Clarke, and J. M. Fernandez. 1999. Mechanical and chemical unfolding of a single protein: a comparison. Proc. Natl. Acad. Sci. USA. 96:3694–3699. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Fisher, T. E., A. F. Oberhauser, M. Carrion-Vazquez, P. E. Marszalek, and J. M. Fernandez. 1999. The study of protein mechanics with the atomic force microscope. Trends Biochem. Sci. 24:379–384. [DOI] [PubMed] [Google Scholar]
  • 13.Oberhauser, A. F., P. E. Marszalek, M. Carrion-Vazquez, and J. M. Fernandez. 1999. Single protein misfolding events captured by atomic force microscopy. Nat. Struct. Biol. 6:1025–1028. [DOI] [PubMed] [Google Scholar]
  • 14.Fisher, T. E., P. E. Marszalek, and J. M. Fernandez. 2000. Stretching single molecules into novel conformations using the atomic force microscope. Nat. Struct. Biol. 7:719–724. [DOI] [PubMed] [Google Scholar]
  • 15.Gutsmann, T., G. E. Fantner, J. H. Kindt, M. Venturoni, S. Danielsen, and P. K. Hansma. 2004. Force spectroscopy of collagen fibers to investigate their mechanical properties and structural organization. Biophys. J. 86:3186–3193. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Becker, N., E. Oroudjev, S. Mutz, J. P. Cleveland, P. K. Hansma, C. Y. Hayashi, D. E. Makarov, and H. G. Hansma. 2003. Molecular nanosprings in spider capture-silk threads. Nat. Mater. 2:278–283. [DOI] [PubMed] [Google Scholar]
  • 17.Bustamante, C., J. F. Marko, E. D. Siggia, and S. Smith. 1994. Entropic elasticity of lambda-phage DNA. Science. 265:1599–1600. [DOI] [PubMed] [Google Scholar]
  • 18.Marszalek, P. E., A. F. Oberhauser, Y. P. Pang, and J. M. Fernandez. 1998. Polysaccharide elasticity governed by chair-boat transitions of the glucopyranose ring. Nature. 396:661–664. [DOI] [PubMed] [Google Scholar]
  • 19.Bouchiat, C., M. D. Wang, J. F. Allemand, T. Strick, S. M. Block, and V. Croquette. 1999. Estimating the persistence length of a worm-like chain molecule from force-extension measurements. Biophys. J. 76:409–413. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Li, H. B., A. F. Oberhauser, S. B. Fowler, J. Clarke, and J. M. Fernandez. 2000. Atomic force microscopy reveals the mechanical design of a modular protein. Proc. Natl. Acad. Sci. USA. 97:6527–6531. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Thompson, J. B., H. G. Hansma, P. K. Hansma, and K. W. Plaxco. 2002. The backbone conformational entropy of protein folding: experimental measures from atomic force microscopy. J. Mol. Biol. 322:645–652. [DOI] [PubMed] [Google Scholar]
  • 22.Rief, M., J. Pascual, M. Saraste, and H. E. Gaub. 1999. Single molecule force spectroscopy of spectrin repeats: low unfolding forces in helix bundles. J. Mol. Biol. 286:553–561. [DOI] [PubMed] [Google Scholar]
  • 23.Fantner, G. E., H. Birkedal, J. H. Kindt, T. Hassenkam, J. C. Weaver, J. A. Cutroni, B. L. Bosma, L. Bawazer, M. M. Finch, G. A. G. Cidade, D. E. Morse, G. D. Stucky, and P. K. Hansma. 2004. Influence of the degradation of the organic matrix on the microscopic fracture behavior of trabecular bone. Bone. 35:1013–1022. [DOI] [PubMed] [Google Scholar]
  • 24.Tang, Z. Y., N. A. Kotov, S. Magonov, and B. Ozturk. 2003. Nanostructured artificial nacre. Nat. Mater. 2:413–418. [DOI] [PubMed] [Google Scholar]
  • 25.Seitz, M., C. Friedsam, W. Jostl, T. Hugel, and H. E. Gaub. 2003. Probing solid surfaces with single polymers. ChemPhysChem. 4:986–990. [DOI] [PubMed] [Google Scholar]
  • 26.Friedsam, C., M. Seitz, and H. E. Gaub. 2004. Investigation of polyelectrolyte desorption by single molecule force spectroscopy. J. Phys. Condens. Matter. 16:S2369–S2382. [Google Scholar]
  • 27.Krautbauer, R., M. Rief, and H. E. Gaub. 2003. Unzipping DNA oligomers. Nano Lett. 3:493–496. [Google Scholar]
  • 28.Bockelmann, U., P. Thomen, B. Essevaz-Roulet, V. Viasnoff, and F. Heslot. 2002. Unzipping DNA with optical tweezers: high sequence sensitivity and force flips. Biophys. J. 82:1537–1553. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Lubensky, D. K., and D. R. Nelson. 2000. Pulling pinned polymers and unzipping DNA. Phys. Rev. Lett. 85:1572–1575. [DOI] [PubMed] [Google Scholar]
  • 30.Viani, M. B., T. E. Schaffer, A. Chand, M. Rief, H. E. Gaub, and P. K. Hansma. 1999. Small cantilevers for force spectroscopy of single molecules. J. Appl. Phys. 86:2258–2262. [Google Scholar]
  • 31.Schaffer, T. E., and P. K. Hansma. 1998. Characterization and optimization of the detection sensitivity of an atomic force microscope for small cantilevers. J. Appl. Phys. 84:4661–4666. [Google Scholar]
  • 32.Suh, K. S., S. J. Hwang, and C. R. Lee. 1997. Charge behavior in polyethylene-ionomer blends. Ieee Transactions on Dielectrics and Electrical Insulation. 4:58–63. [Google Scholar]
  • 33.Lantz, M. A., S. P. Jarvis, H. Tokumoto, T. Martynski, T. Kusumi, C. Nakamura, and J. Miyake. 1999. Stretching the alpha-helix: a direct measure of the hydrogen-bond energy of a single-peptide molecule. Chem. Phys. Lett. 315:61–68. [Google Scholar]
  • 34.Janovjak, H., J. Struckmeier, M. Hubain, A. Kedrov, M. Kessler, and D. J. Muller. 2004. Probing the energy landscape of the membrane protein bacteriorhodopsin. Structure. 12:871–879. [DOI] [PubMed] [Google Scholar]
  • 35.Muller, D. J., M. Kessler, F. Oesterhelt, C. Moller, D. Oesterhelt, and H. Gaub. 2002. Stability of bacteriorhodopsin alpha-helices and loops analyzed by single-molecule force spectroscopy. Biophys. J. 83:3578–3588. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Gao, H. J., and H. M. Yao. 2004. Shape insensitive optimal adhesion of nanoscale fibrillar structures. Proc. Natl. Acad. Sci. USA. 101:7851–7856. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 37.Lucas, J. M., E. Vaccaro, and J. H. Waite. 2002. A molecular, morphometric and mechanical comparison of the structural elements of byssus from Mytilus edulis and Mytilus galloprovincialis. J. Exp. Biol. 205:1807–1817. [DOI] [PubMed] [Google Scholar]
  • 38.Waite, J. H., H. C. Lichtenegger, G. D. Stucky, and P. Hansma. 2004. Exploring molecular and mechanical gradients in structural bioscaffolds. Biochemistry. 43:7653–7662. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES