Abstract
Blood coagulation in vivo is a spatially nonuniform, multistage process: coagulation factors from plasma bind to tissue factor (TF)-expressing cells, become activated, dissociate, and diffuse into plasma to form enzymatic complexes on the membranes of activated platelets. We studied spatial regulation of coagulation using two approaches: 1), an in vitro experimental model of clot formation in a thin layer of plasma activated by a monolayer of TF-expressing cells; and 2), a computer simulation model. Clotting in factor VIII- and factor XI-deficient plasmas was initiated normally, but further clot elongation was impaired in factor VIII- and, at later stages, in factor XI-deficient plasma. The data indicated that clot elongation was regulated by factor Xa formation by intrinsic tenase, whereas factor IXa was formed by extrinsic tenase on activating cells and diffused into plasma, thus sustaining clot growth. Far from the activating cells, additional factor IXa was produced by factor XIa. Exogenously added TF had no effect on the clot growth rate, suggesting that plasma TF does not contribute significantly to the clot propagation process in a reaction-diffusion system without flow. Addition of thrombomodulin at 3–100 nM caused dose-dependent termination of clot elongation with a final clot size of 2–0.2 mm. These results identify roles of specific coagulation pathways at different stages of spatial clot formation (initiation, elongation, and termination) and provide a possible basis for their therapeutic targeting.
INTRODUCTION
The function of blood coagulation is to prevent blood loss by forming a fibrin clot localized at the site of vascular injury (for a review of coagulation, see Butenas and Mann (1)). Spatial heterogeneity is an essential property of this system. The coagulation process is initiated by extravascular tissue factor (TF2)-expressing cells at the site of damage. Its propagation requires assembly of enzymatic complexes on the membranes of activated platelets, and it is tightly regulated by the inhibitors thrombomodulin and heparin expressed by endothelial cells of the undamaged regions of vessel wall. Molecules of activated coagulation factors dissociate from activating cells, overpass some distance by diffusion from the site of vascular damage to platelet membranes, and bind platelets to form enzymatic complexes. These complexes in their turn produce active factors, which diffuse further, resulting in a self-sustained process of enzyme generation and clot growth. At some stage, this process should be stopped to localize the fibrin clot and avoid thrombosis.
The most widely used concept of coagulation is the cascade model (2), picturing coagulation as a complex sequence of enzymatic reactions. However, a number of recent studies point out that, although it is correct for in vitro homogenous experiments, this model seems not to account for some important aspects of in vivo hemostatic and thrombotic processes (3,4). Indeed, different reactions of the coagulation cascade occur at different locations: in plasma or on extravascular cells, platelets, or endothelium. An adequate model of hemostasis/thrombosis should correctly describe the role of diffusion, which connects these “compartments”. The importance of spatial heterogeneity and diffusion in the control of blood coagulation is illustrated by studies of the diffusion barrier for active factor transfer from TF-expressing cells to platelets (5), of spatial propagation of coagulation from the activating cells (6,7), and of hindered diffusion of factor (f) Xa in platelet-rich thrombin (8).
Previously, we proposed an experimental in vitro model utilizing time-lapse videomicroscopy to directly monitor spatial clot formation in a thin layer of nonstirred plasma (9). Using plasma from patients with a coagulation disorder, hemophilia, we demonstrated that initiation of clot formation in hemophilic plasma occurs normally, whereas elongation of the clot is dramatically impaired (6). These results suggest that two pathways of coagulation cascade, intrinsic and extrinsic fX-activating complexes (tenases), are physically separated in space, and intrinsic tenase functions to produce fXa far from the activator, where extrinsic tenase is absent.
The objective of this study was to systematically analyze roles of extrinsic and intrinsic tenases in fX activation, and roles of extrinsic tenase and fXIa in fIX activation during clot formation in a reaction-diffusion system. Experimental and computer simulation approaches were combined to compare spatial clot formation in fVIII- and fXI-deficient plasmas. We were able to demonstrate that, despite the complexity of coagulation cascade, for each individual stage of clot propagation there is a single pathway of blood coagulation that regulates it. Initiation of coagulation is regulated by extrinsic tenase only and the clot propagation is controlled by fXa generation via intrinsic tenase, whereas fIXa is primarily formed by extrinsic tenase. At late stages of clot progression far from the activator, additional fIXa is produced by fXIa. The mechanism of clot localization upon thrombomodulin addition was studied. These results provide a link between the biochemical scheme of the cascade and the actual roles played by individual pathways at different stages of the fibrin clot formation.
MATERIALS AND METHODS
Experimental methods
Materials
Human recombinant TF (INNOVIN) was purchased from Baxter (Deerfield, IL). Functional TF concentration was determined by ACTICHROME TF chromogenic activity kit (American Diagnostica, Stamford, CT). FXIIa inhibitor from corn seeds (CTI) was purchased from Enzyme Research Laboratories (South Bend, IN). Rabbit lung thrombomodulin was from Haematologic Technologies (Essex Junction, VT). Frozen pooled fVIII- and fXI-deficient and control normal plasmas were from George King Biomedicals (Overland Park, KS). Sodium citrate and lactic acid were from Sigma (St Louis, MO).
Blood collection and plasma preparation
Blood from healthy donors and severe (fVIII < 1% of the normal level) hemophilia A patients was collected into 3.8% sodium citrate (pH 5.5) at a 9:1 v/v ratio and processed as described (10). Briefly, blood was centrifuged at 1500 g for 25 min. Supernatant was centrifuged at 10,000 g for 5 min to obtain platelet-free plasma. Its pH value was stabilized at 7.2–7.4 by lactic acid treatment (11). Fresh-frozen fVIII- and fXI-deficient and normal plasmas were processed as described (7). There was no significant difference between clot formation in plasma obtained from hemophilia A donors and commercially available fVIII-deficient plasma.
Cell culture
A human fetal lung fibroblast line was from the Research Institute of Virology (Russian Academy of Medical Sciences, Moscow, Russia). Cells were grown on polyethylene terephthalate (PET) film slips (Joint Institute for Nuclear Research, Dubna, Russia) placed on the bottom of 12-well plates (Corning, Acton, MA), as described earlier (10). Human macrophages were obtained as a result of the differentiation of monocytes (12) isolated from mononuclear leukocyte preparations obtained by apheresis procedure performed by the Research Blood Staff at the Holland Laboratory, American Red Cross, under a protocol approved by the Institutional Review Board. Primary culture of human aortic endothelial cells was purchased from Cambrex (Walkersville, MD) and was used at passages 4 through 10. Cells were grown on PET film slips as described earlier (7).
Spatial clot growth
Spatial fibrin clot growth was studied using a light-scattering video microscopy system described previously (6). A microchamber was assembled in a suspension cell culture nontreated 35-mm polystyrene petri dish (Corning) around a 1-mm-thick glass slide (FisherBrand, Fisher Scientific, Pittsburgh, PA) fixed to its bottom. The glass slide edge, which formed a vertical wall of the chamber, was wrapped around with a cell-coated PET slip. Plasma was recalcified by addition of 1 M CaCl2 at 2% v/v and rapidly transferred into the assembled chamber. The light-scattering data were monitored by digital microscopy; an image was captured every 30 s. All experiments were performed at 37°C.
Image processing
For each experiment, parameters of clot growth were determined on the basis of video image of the growing clot, as described previously (10). Briefly, a perpendicular to the cell monolayer surface was drawn and plots of light scattering versus distance from the activator (clot profiles) were calculated (see, e.g., Fig. 1 A). For each profile, the clot size was determined as a coordinate where the light-scattering intensity was half-maximal. Clot growth rate was determined as a mean slope of the plot of the clot size versus time in the range of 10–30 min after the beginning of the experiment.
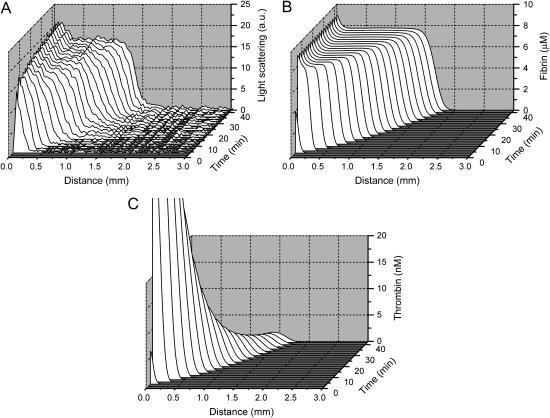
FIGURE 1.
Normal fibrin clot formation. (A) Time course of evolution of light-scattering profiles of the clot obtained from the complete series of light scattering images. Clots were formed on the surface of a fibroblast monolayer in the presence of 0.2 mg/ml CTI as described in Materials and Methods. (B) Computer simulation of clot formation: fibrin profiles, corresponding to the experimental light-scattering profiles in A. Simulations were performed using the model (Eqs. S1–S50) with parameters listed in Tables S1–S3 (see Supplementary Material). Fibroblast monolayer density in the model was 1000 cells/mm2. (C) Computer simulation of spatial clot formation: thrombin profiles. Simulations were performed as in B. A movie for this figure is available (see Supplementary Material).
Modeling methods
Concepts of the model
The mathematical model of this study was designed to describe spatial dynamics of clot formation in nonstirred recalcified plasma activated by a monolayer of TF-expressing cells at physiological temperature and ionic composition (37°C, pH 7.2–7.4, 2 mM Ca2+, 150 mM NaCl). Model equations (Eqs. S1–S50), initial concentrations (Table S1), rate constants (Table S2), and diffusion coefficients (Table S3) are supplied in the Supplementary Material. No model parameters were adjusted, and only the values reported in the literature were used. A typical model equation for a reagent in plasma is shown below for fVIIIa:
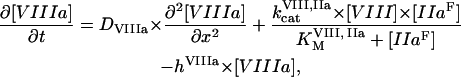 |
(1) |
where [VIIIa] ([VIII]) is the fVIIIa (fVIII) concentration, 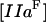 is the free thrombin (not in complex with its substrates) concentration,
is the free thrombin (not in complex with its substrates) concentration, 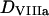 is the fVIIIa diffusion coefficient,
is the fVIIIa diffusion coefficient, 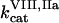 and
and 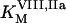 are catalytic and Michaelis constants of fVIII activation, and
are catalytic and Michaelis constants of fVIII activation, and 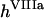 is the first-order constant of fVIIIa activity loss. For reagents located on the membranes of TF-expressing cells (TF, VIIa-TF, and VII-TF), we used surface densities instead of volume concentrations and ordinary differential equations. An example for TF is given below:
is the first-order constant of fVIIIa activity loss. For reagents located on the membranes of TF-expressing cells (TF, VIIa-TF, and VII-TF), we used surface densities instead of volume concentrations and ordinary differential equations. An example for TF is given below:
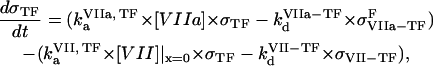 |
(2) |
where 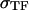 (
(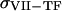 ) is the TF (VIIa-TF) surface density,
) is the TF (VIIa-TF) surface density, 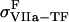 is the free VIIa-TF density,
is the free VIIa-TF density, 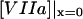 (
(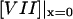 ) is the concentration of fVIIa (fVII) near the activator,
) is the concentration of fVIIa (fVII) near the activator, 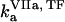 (
(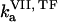 ) and
) and 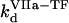 (
(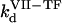 ) are association and dissociation constants, respectively, of the VIIa-TF (VII-TF) complex. Thus, the mathematical model is biphasic: it contains reagents on the activating surfaces and in plasma. To link these phases, boundary conditions are used. An example of boundary condition is given below for fVIIa:
) are association and dissociation constants, respectively, of the VIIa-TF (VII-TF) complex. Thus, the mathematical model is biphasic: it contains reagents on the activating surfaces and in plasma. To link these phases, boundary conditions are used. An example of boundary condition is given below for fVIIa:
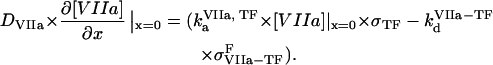 |
(3) |
A mathematical model of almost 30 differential equations containing >100 parameters from the literature required a special approach in the development. For many rate constants of coagulation reactions, values reported by different groups differ by orders of magnitude. If these values were chosen randomly, the behavior of such a model would be unlikely to agree with experimental results. On the other hand, voluntary adjustment of parameters to describe several selected experiments does not guarantee correctness of the obtained model either. Therefore, to create an adequate model, we initially developed and validated models of individual reactions of the coagulation cascade, in particular for the TF pathway inhibitor (TFPI) pathway (13) and for intrinsic tenase (14). Subsequently, we simulated larger subsystems using, for validation, experimental data of Ovanesov et al. (6,7,10) Diamond and Anand (15), Matveyev and Domogatsky (16), Hairer et al. (17), Lawson et al. (18), Gailani and Broze (19), Butenas et al. (20), and Giesen et al. (21). The range of kinetic parameters in these simulations was strictly limited to the values reported in experimental studies; no optimization of these values was done. Comparing increasingly more complex systems with experiments, the final version of the model for clotting in plasma was developed.
Assumptions about procoagulant membranes
We assumed that procoagulant surface for the assembly of coagulation enzymatic complexes is primarily provided by activated platelets. Of platelet-secreted substances, secretion of fV(a) only was included in the model. Platelet-secreted fV(a) is a partially proteolyzed form of fV with ∼30–50% of the activity of fully activated fVa (22); we assumed it to be an equimolar mixture of fVa and fV. Except for thrombin, platelet activators were omitted, as collagen was absent in the simulated experiments, and other physiological agonists do not cause significant alpha-granule secretion and procoagulant surface exposure in the absence of cell-cell contacts (23). On the basis of recent studies (24,25), we assumed that only a small fraction (δ = 4%) of thrombin-activated platelets can specifically bind coagulation factors and support membrane-dependent procoagulant reactions. Dependence of δ on thrombin concentration (24) was ignored in the model. The numbers of binding sites per platelet and the effective constants of platelet-dependent reactions (previously determined assuming all platelets to be identical) were corrected by the factor of δ or 1/δ, as indicated in Table S2. Platelet activation, secretion, surface exposure, and binding of factors were assumed to be rapid (14). Activated platelets shed microparticles, which bind coagulation proteins with parameters similar to those of platelets. In the model, we did not distinguish platelets and platelet-derived microparticles and used a common Na variable with dimensionality of nM, which described all membranes available for the binding of coagulation factors. Ni, the initial effective procoagulant activity of membranes in plasma represented by circulating microparticles, lipoproteins, etc., was estimated by comparing experiments and simulations of clot formation in ultracentrifuged (7) plasma titrated with platelets (data not shown).
Assumptions about diffusion
Diffusion coefficients of coagulation factors within fibrin clot were assumed to be the same as in liquid plasma due to the high clot porosity (for a detailed theoretical analysis see Oliver et al. (26)); this was confirmed experimentally by Scott and Coleman (27). Coagulation factors can bind to platelets, or fibrin, or other factors, and their diffusion is then slowed down. For the majority of factors, the portion of bound factor is small, and a diffusion operator was applied to the total protein concentration [F]. However, for fXa, thrombin, and fXIa this assumption can be incorrect, as their binding to platelets, substrates, or fibrin could be significant. For these factors, diffusion of free factor [FF] only was considered.
Other model assumptions
A number of reactions in the model were described by phenomenological equations, in particular, thrombin activation of fXI, TF-independent fVIIa activation of fX and fIX (modeled as pseudo-second-order reactions with rate constants proportional to the activated platelets concentration), and TFPI pathway (13). Fibrinogen cleavage was described by a Michaelis-Menten reaction with product inhibition (28). The equation for prothrombinase was obtained by analogy with a previously reported equation for intrinsic tenase (14) assuming that fXa binds to platelet-bound fVa (29) and platelet-bound prothrombin is activated by the Xa-Va complex in a two-dimensional reaction:
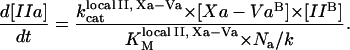 |
(4) |
For the activated protein C (APC)-independent action of phosphatidylserine (PS), we used a mechanism suggested earlier (30) and assumed that PS binds fVa in competition with fXa, and makes it accessible for APC. Intrinsic tenase inactivation by PS was described using a hypothesis that membrane-bound fVIIIa is directly and reversibly inhibited by PS (31). We included in the model activation of fV, fVIII, and fVII by thrombin only, ignoring their activation by fXa and other factors, because contribution of these slow membrane-dependent reactions appears not to be significant under the conditions of this study (21). Artificial contact activation from laboratory test tubes was simulated by fIXa inflow (32). The assumption of Michaelis-Menten kinetics is valid only for one-substrate reactions when enzyme concentration is much less than that of substrate. For reactions of coagulation, this condition does not always hold. Thus, for activation of a substrate Si by an enzyme E, which catalyzes the conversion of n substrates competing for the same active site, and concentration of which can be both below and in excess of that of the substrates, we used the equation:
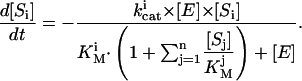 |
(5) |
This equation was obtained from the steady-state equations for transitory complexes. The derivation results in an equation identical to Eq. 3, with free substrate concentrations in the denominator, which can be substituted with total concentrations if any of the following conditions holds for each ith substrate:
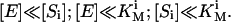 |
(6) |
We assumed that the activating surface is an infinitely thin layer of TF. This assumption is valid as long as a high-density monolayer of TF-bearing cells is used. Further, one-dimensional an assumption was used for the model, because the microchamber is completely covered with activator along the height dimension, and its width exceeds severalfold the observed clot lengths. The value of contact activation by the walls of the experimental chamber was estimated on the basis of the difference between clot growth rate in the absence and in the presence of CTI, and on the basis of activated partial thromboplastin time elongation upon addition of 0.2 mg/ml CTI to plasma (data not shown).
Computation
To integrate numerically the set of partial differential equations, we used the embedded Runge-Kutta-Fehlberg method of the 2nd (3rd) order (33), which was adapted for partial differential equations (3). The program was developed in Watcom C/C++ 10.0. Calculations were carried out on the 0–3 mm interval.
RESULTS
The reaction-diffusion model of spatial clot formation
Experimental and modeling methods used in this study are illustrated in Fig. 1. Light-scattering profiles obtained from the series of images of clotting in normal plasma on fibroblast monolayer are shown in Fig. 1 A in a three-dimensional plot. Fig. 1, B and C, shows theoretical fibrin and thrombin profiles, respectively, obtained using the mathematical model. Light-scattering intensity is linearly proportional to fibrin concentration in the clot (7), and thus fibrin concentration obtained by simulations can be compared with experimentally observed light-scattering intensity. Upon activation, thrombin concentration in the model near the activator was rapidly increased, and then decreased slowly. Thrombin profiles initially had diffusion-like form; subsequently, the front edge of the thrombin profile was transformed into a pulse, which started moving into the bulk of plasma. To characterize clot formation quantitatively, we used initiation time tin (time of half-maximal fibrinogen cleavage near the activator) and clot growth rate vclot (the slope of the clot size versus time plot).
Using the mathematical model, we studied correlation of tin and vclot with parameters usually used to characterize thrombin generation. Concentrations of coagulation factors and values of kinetic constants were varied into 10% or 200% of their normal values and changes in clotting parameters were determined (not shown). The correlation analysis revealed (Table 1) that the rate of clot elongation vclot correlated significantly and positively with maximal thrombin IIamax, thrombin potential PIIa, maximal rate of thrombin generation vmax (R = 0.68–0.83), and did not correlate with clot time tclot (time of the half-maximal fibrinogen cleavage), lag time tlag (time to achieve 10 nM of thrombin), thrombin maximum time tmax (R = –0.32 to –0.51). On the contrary, initiation time tin did not correlate with IIamax, PIIa, vmax (R = –0.07 to –0.16) and correlated positively with tclot, tlag, and tmax (R = 0.74–0.78). There was no correlation between parameters depicting initiation (tin) and growth (vclot) of the clot (R = –0.17).
TABLE 1.
Correlation matrix for parameters of spatial clot formation and thrombin generation
| tin | vclot | |
|---|---|---|
| tclot | 0.85 | −0.22 |
| tlag | 0.83 | −0.32 |
| tmax | 0.82 | −0.47 |
| vmax | −0.18 | 0.84 |
| PIIa | −0.11 | 0.57 |
| IIamax | −0.18 | 0.78 |
| tin | −0.17 |
Clot formation was simulated as described in the legend to Fig. 1; fibroblast density was 1000 cells/mm2. During each simulation, one of the following concentrations/constants was set to either 10% or 200% of its normal value:  , [VIIa], [VII], [IX], [X], [II], [Fg], [VIII], [V], [PC], [PS], [XI], [AT-III], [α2M], [TFPI],
, [VIIa], [VII], [IX], [X], [II], [Fg], [VIII], [V], [PC], [PS], [XI], [AT-III], [α2M], [TFPI],  ,
, 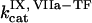 ,
, 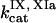 ,
, 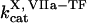 ,
, 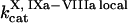 ,
, 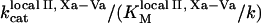 ,
, 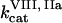 ,
, 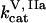 ,
, 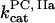 ,
, 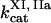 ,
, 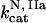 . The same simulations for thrombin generation initiated by 25 pM TF were performed using a homogenous version of the mathematical model, where reaction-diffusion partial differential equations were substituted with ordinary ones. Pearson correlation coefficients were then calculated for the obtained data sets.
. The same simulations for thrombin generation initiated by 25 pM TF were performed using a homogenous version of the mathematical model, where reaction-diffusion partial differential equations were substituted with ordinary ones. Pearson correlation coefficients were then calculated for the obtained data sets.
Contribution of intrinsic and extrinsic tenases to spatial clot formation
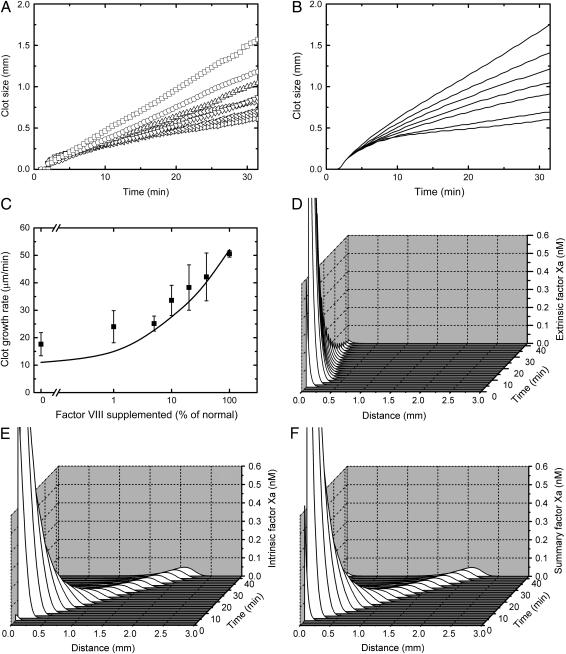
To examine relative contributions of the intrinsic and extrinsic tenase complexes to clot formation, studies of clot growth in fVIII-deficient plasma were undertaken. The clot size versus time plots in Fig. 2, A (experimental) and B (theoretical), show dose-dependent increase of the clot growth rate upon supplementation of hemophilia A plasma with normal plasma. The curves demonstrate that initiation of coagulation was not affected by fVIII supplementation, whereas clotting propagation is regulated by the presence/concentration of intrinsic tenase.
FIGURE 2.
Contribution of intrinsic and extrinsic tenases to spatial clot formation. Clots were formed on the surface of a fibroblast monolayer, as described in Materials and Methods. (A and B) Clot size versus time plots of clot formation in the plasma of a hemophilia A donor supplemented with normal plasma, from (A) a representative experiment (out of a total of four) and (B) the respective simulation. Normal plasma was at 0, 1%, 5%, 10%, 20%, 40%, and 100% v/v (bottom to top). (C) The rate of spatial clot growth in hemophilia A plasma versus concentration of added normal plasma, with experiments represented by symbols and simulations by the solid line. Mean values ± SD are shown, n = 4. (D–F) Simulated profiles of fXa during clot formation in normal plasma produced by (D) extrinsic tenase, (E) intrinsic tenase, and (F) both. A movie for this figure is available (see Supplementary Material).
As a visual representation of this conclusion, Fig. 2, D–F, shows concentration profiles of fXa produced by either extrinsic tenase (VIIa-TF), intrinsic tenase (IXa-TF), or the total fXa, which were obtained using a computer simulation model. Although extrinsic tenase-produced fXa was located near the activator and rapidly decayed (Fig. 2 D), the intrinsic tenase complex in plasma controlled the fXa formation and the clotting propagation from the activator (Fig. 2 E), accounting for all spatial effects (compare Fig. 2, E and F). Whereas at 4 min after initiation, the ratio of intrinsic/extrinsic total fXa (integrals from the fXa concentration over distance) was 0.44, at 20 min it was 2.83 and rapidly increased. Thus, during the propagation phase, fXa formation by intrinsic tenase is rate-limiting.
Contribution of fXI activation by thrombin far from the TF-expressing surface
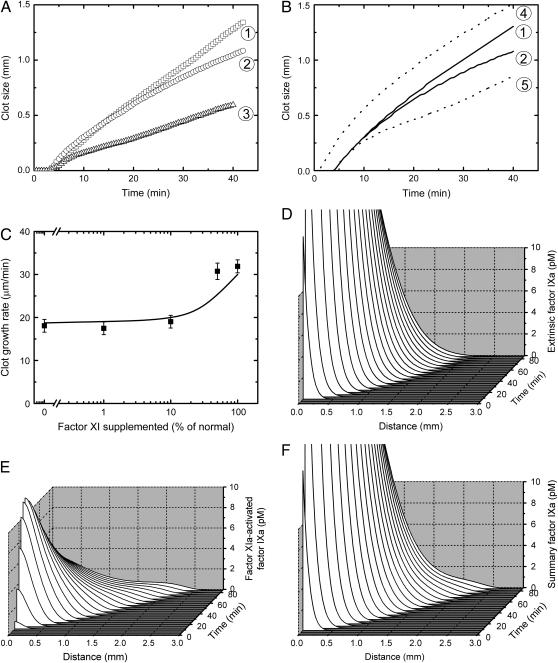
The limiting component of intrinsic tenase (15), fIXa, can be produced via two pathways, which generate either extrinsic tenase or fXIa. The latter factor can also be generated by thrombin in a feedback reaction (34). To determine the roles and contributions of these pathways, we studied clot formation in fXI-deficient plasma. To make the possible fXIa contribution more distinctive, macrophages, known to carry less TF than fibroblasts (7), were used as activating cells. Experimental (Fig. 3 A) and theoretical (Fig. 3 B) clot size versus time plots show that clot formation in fXI-deficient plasma (2) was impaired in comparison with control (1), although the pattern was distinctive from that of fVIII-deficient plasma (3). Differences in normal and fXI-deficient plasmas were seen only at ∼25 min after the beginning of the experiment, at ∼0.7 mm from the activator (∼7 min and ∼0.3 mm, respectively, for fVIII deficiency). However, at these later stages, formation of the clot was slowed down to an extent similar to that in fVIII deficiency, as can be seen in Fig. 3 C, where the rate of clot elongation during the 30- to 40-min interval is shown as a function of fXI concentration. To summarize, in contrast to the generation of fXa, fIXa formation by extrinsic tenase appears to control clot propagation, with the exception of the fXIa contribution at later stages.
FIGURE 3.
Contribution of fXI activation by thrombin far from the TF-expressing surface. Clots were formed on the surface of a confluent macrophage monolayer as described in Materials and Methods. Simulations were performed as described for Fig. 1, except that activation was by fibroblast monolayer with a density of 250 cells/mm2. (A and B) Clot size versus time plots of clot formation in normal (1), fXI-deficient (2), and fVIII-deficient (3) plasmas, from (A) a representative experiment (out of four total), and (B) the respective simulation. Dotted lines in B show computer simulations of clot growth in normal plasma, where diffusion coefficients of fXa (4) or fIXa (5) were decreased 100-fold. (C) The rate of spatial clot growth far from the activator (determined on the 30- to 40-min interval) in fXI-deficient plasma versus concentration of supplemented normal pooled plasma, with experiments represented by symbols and simulations by the solid line. Mean values ± SD are shown, n = 2–4. (D–F) Simulated profiles of fIXa during clot formation in normal plasma produced by (D) extrinsic tenase, (E) fXIa, and (F) both.
Computer simulations in Fig. 3, D and E, illustrate the contribution of extrinsic tenase and fXIa, respectively, into fIX activation in normal plasma. During the beginning of the propagation period, fIXa, in contrast to fXa, is mainly produced by extrinsic tenase (compare Fig. 3, D and F) and delivered to plasma by diffusion. Only far from the activator, fIXa generated by fXIa becomes significant (Fig. 3 E). This difference between fIXa and fXa seems to be caused by the low rate of fIXa inhibition in plasma, which allows its prolonged diffusion. To test this, the fIXa diffusion coefficient in the model was decreased 100-fold, resulting in an impairment of the clot formation (Fig. 3 B, 5) and confirming this suggestion. On the other hand, a 100-fold decrease of fXa diffusion coefficient had no effect on clot growth rate in the propagation phase, whereas initiation of coagulation was even significantly accelerated (Fig. 3 B, 4). Analysis of the fXa concentration profiles (not shown) suggested that this acceleration was due to the accumulation of fXa near the activating surface because of slowed diffusion. A 100-fold decrease of the diffusion coefficients of zymogens fIX and fX had almost no effect on clot formation (data not shown).
Inhibition of clot growth by thrombomodulin
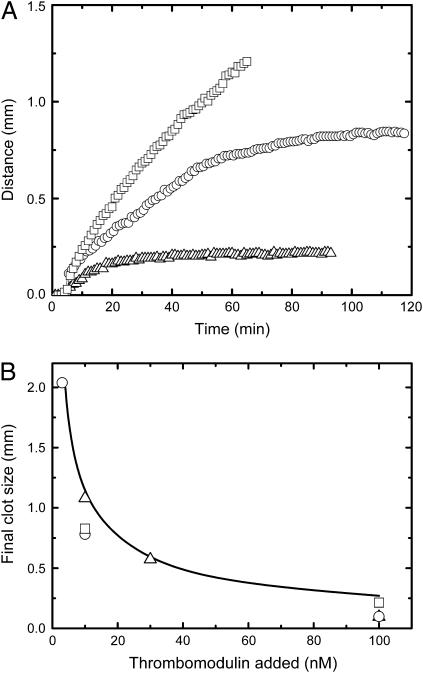
The above results suggest a mechanism of the diffusion-mediated control of blood coagulation. However, under any of the studied conditions, termination of clot propagation was never observed in our experimental model within the reasonable time-span of the experiment (1–2 h). Moreover, in some experiments on hemophilia A plasma, clot growth was monitored for >5 h, and the propagation of the clot still did not stop despite the small clot growth rate (data not shown). If we assume the spatial clot growth model to represent hemostatic or even thrombotic clot formation, this result provides some trouble in interpretation since the coagulation process in vivo is expected to be finite and localized. One of the most important components of hemostasis, which is absent in the in vitro system of this study, is the fact that the damaged vessel wall is surrounded by undisturbed endothelium that is known to have several surface anticoagulants. To introduce a possible effect of intact endothelium into our system, rabbit lung thrombomodulin was premixed with plasma at concentrations from 3 to 100 nM. This resulted in a complete, yet dose-dependent, termination of the clot growth (Fig. 4 A), yielding a final clot size of 0.2–1 mm (Fig. 4 B). The solid line in Fig. 4 B shows model simulations, which agree well with the experiments. These results provide experimental evidence of the localizing effect of thrombomodulin in the spatial clotting process.
FIGURE 4.
Clot growth termination and regulation of final clot size by thrombomodulin. Experiments and simulations were performed as described for Fig. 1. (A) Experimental clot size versus time plot for clot formation in normal plasma upon addition of thrombomodulin at 0 (▪), 10 (▴), and 100 (▵) nM. (B) Final clot size is shown as a function of the concentration of thrombomodulin added, for experiments (symbols , □, ○ and ▵ indicate three different donors) and simulations (solid line). A movie for this figure is available (see Supplementary Material).
Study of possible role of blood-borne TF in clot formation
Effect of exogenously added TF
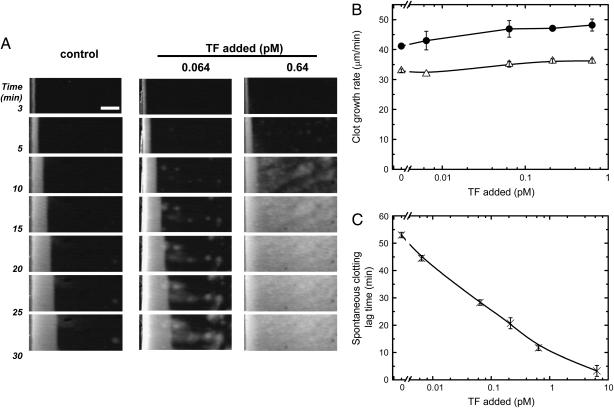
In recent years there was a considerable debate about the possible role of circulating TF activity (known as blood-borne TF) in clot initiation and growth (35,36). To evaluate the possible contribution of blood-borne TF to clot formation in the spatial model, we added relipidated recombinant TF to plasma at subpicomolar concentrations. Fig. 5 A shows typical images of clot formation in the presence of TF. The rate of clot growth was not significantly affected by TF (Fig. 5 B). However, in the presence of TF, plasma began to clot throughout the reaction volume independently of the activating cell monolayer. The time of the plasma clotting was a dose-dependent function of TF (Fig. 5 B). Computer simulations of clot growth experiments gave similar results: TF in the reaction volume had almost no effect on clot growth (data not shown). Together with our previous report that incubation of plasma with anti-TF antibodies did not inhibit spatial clot growth (7), these data indicate that plasma-associated TF does not contribute to clot formation in the absence of flow, yet it may contribute to activation of coagulation.
FIGURE 5.
Effect of exogenously added TF on clot formation. CTI-inhibited normal pooled plasma was supplemented with relipidated recombinant TF and placed in contact with monolayers of lung fibroblasts or endothelial cells. (A) Light-scattering time-lapse images of clot formation initiated by fibroblast monolayers. Addition of TF induced “spontaneous” (independent of fibroblasts) clot formation in all areas of the microchamber. Scale bar, 1 mm. (B) Effect of TF concentration on clot growth rate. Clot formation was activated by either fibroblasts (•) or endothelial cells (▵). (C) Effect of TF on spontaneous clotting lag time. To calculate spontaneous clotting lag time, an area 3 × 3 mm2 located at least 3 mm away from the surface of TF-bearing cells was selected on the first frame, and the mean light-scattering intensity within this square area was plotted versus time. The lag time of spontaneous clot formation was defined as the time interval required for the mean light scattering to reach half-maximal value. Mean values ± SD are shown, n = 2.
DISCUSSION
The roles of the extrinsic and intrinsic tenase complexes, fXI, and the protein C pathway in blood coagulation were studied in a reaction-diffusion experimental model of spatial clot formation, complemented by analysis utilizing a mathematical model. The data demonstrate the following:
Intrinsic and extrinsic tenases play different roles at different stages of clot formation. fXa generated by extrinsic tenase functions only near TF-expressing cells and is rapidly inhibited nearby, whereas clotting far from the activator requires fX activation by intrinsic tenase.
Functions of fIXa and fXa in the propagation of coagulation are also different. In contrast to fXa, fIXa produced by extrinsic tenase can diffuse from the activator, allowing intrinsic tenase assembly and clot expansion.
At long distances from the TF-expressing cells, additional fIXa is produced by fXIa, generated by thrombin in a feedback reaction.
Thrombomodulin is able to terminate clot expansion and to localize clotting in a dose-dependent manner.
These results were obtained experimentally, and a computer simulation model was used primarily for their independent confirmation and better insight into the mechanisms allowing separate monitoring of factor activation by different pathways, change of diffusion coefficients, etc.
The results of this study were obtained in an in vitro model system designed to analyze the significance of diffusion and spatial heterogeneity in coagulation. Like other in vitro models such as the thrombin generation assay (37), our system does not correspond specifically to either physiological or pathological coagulation, in contrast to more specialized in vivo, ex vivo, or in vitro models of thrombus formation (38–40). Thus, the conclusions about the roles of diffusion and of specific reactions at different stages of clot formation obtained in this model are general and should be applicable for both hemostasis and thrombosis.
A positive correlation (Table 1) between parameters of spatial clot formation in the reaction-diffusion model and parameters of homogenous thrombin generation demonstrated using the computer model indicates a functional similarity and provides a possible link between these two models. Indeed, in the thrombin generation assay, complete plasma clotting is rapidly catalyzed by initial traces of thrombin, before the detectable burst of thrombin generation occurs; still, it is the degree of generated thrombin that correlates with bleeding and thrombotic tendencies (37). Thus, physiological interpretation of the thrombin generation assay may seem unclear: why do we need all this thrombin when the clot is already formed? In a spatial reaction-diffusion model, this “superfluous thrombin” paradox could be solved, as active factors could diffuse to nearby locations where clotting has not yet occurred (37). It should be noted that correlation of spatial clot formation and thrombin generation parameters does not mean complete equivalency of these methods. For example, many aspects of clot formation in a reaction-diffusion system, such as termination of clot expansion, cannot be analyzed in a thrombin generation assay.
Previously, we showed that the propagation stage of spatial clot formation in hemophilia A and B plasmas is impaired, suggesting that spatial clot enlargement is controlled by fXa production by intrinsic tenase (6). Another group used thrombin generation activated by TF-bearing monocytes in a reconstituted system of coagulation proteins and platelets to demonstrate that fIXa and fXa are required for the “priming” of coagulation and for thrombin generation, respectively (5). They hypothesized that extrinsic tenase-produced fXa initiates coagulation, but is confined to TF-expressing cells because of its inhibition in plasma, whereas slowly inhibited fIXa can bind platelets to form intrinsic tenase. However, without spatial heterogeneity this concept might not be fully applicable, because fXa inhibition might not be rapid enough to prevent it from reaching nearby platelets, and stirring in this system allows enhanced fXa distribution to platelets. In this study, a system without stirring was used. Clot formation near the activator (∼0.2 mm) was regulated by extrinsic tenase (no difference between control and fVIII deficiency), whereas fXa formation farther away required intrinsic tenase (impairment in fVIII deficiency). However, this intrinsic tenase was formed by extrinsic tenase-produced fIXa but not by fXIa (no impairment in fXI deficiency). Only at distances of >∼0.8 mm from the activator did fXIa contribute to clot formation. The distance of effective diffusion of an enzyme is proportional to  , where D is the diffusion coefficient, and h is the first-order inhibition constant. Diffusion coefficients of fIXa and fXa are similar, whereas their inhibition rates by plasma inhibitors are ∼1 min−1 and ∼0.03–0.1 min−1, respectively. Thus, their distances of effective diffusion should differ three to sixfold, in agreement with our results. Furthermore, decreasing fIXa diffusion coefficient 100-fold resulted in clot formation impairment approaching that in factor VIII-deficient plasma. On the other hand, a 100-fold decrease of fXa diffusion coefficient did not decrease the clot growth rate, and initiation phase was even shortened. This also indicates that fXa diffusion is not important for the propagation of coagulation, whereas fIXa diffusion is rate-limiting. A recent study (8) demonstrated that effective diffusion of fXa in fibrin clot is slow, being dramatically (by three orders of magnitude) slowed down in platelet-fibrin clot, most probably due to the efficient binding of fXa to platelets. Our results demonstrating that clot propagation in a spatial model is mediated by fIXa diffusion and other mechanisms rather than by fXa diffusion are in line with that report. That study (8) also suggested that diffusion of zymogens fIX and fX in fibrin clot is also slowed down. Computer simulations in our study with 100-fold decrease of the diffusion coefficients of fIX and fX showed no effect of the slowed diffusion of clot formation. This seems to be at least partially due to very slow consumption of these zymogens during coagulation (15), so that they are always present in the reaction volume and their diffusion flux is small and nonessential.
, where D is the diffusion coefficient, and h is the first-order inhibition constant. Diffusion coefficients of fIXa and fXa are similar, whereas their inhibition rates by plasma inhibitors are ∼1 min−1 and ∼0.03–0.1 min−1, respectively. Thus, their distances of effective diffusion should differ three to sixfold, in agreement with our results. Furthermore, decreasing fIXa diffusion coefficient 100-fold resulted in clot formation impairment approaching that in factor VIII-deficient plasma. On the other hand, a 100-fold decrease of fXa diffusion coefficient did not decrease the clot growth rate, and initiation phase was even shortened. This also indicates that fXa diffusion is not important for the propagation of coagulation, whereas fIXa diffusion is rate-limiting. A recent study (8) demonstrated that effective diffusion of fXa in fibrin clot is slow, being dramatically (by three orders of magnitude) slowed down in platelet-fibrin clot, most probably due to the efficient binding of fXa to platelets. Our results demonstrating that clot propagation in a spatial model is mediated by fIXa diffusion and other mechanisms rather than by fXa diffusion are in line with that report. That study (8) also suggested that diffusion of zymogens fIX and fX in fibrin clot is also slowed down. Computer simulations in our study with 100-fold decrease of the diffusion coefficients of fIX and fX showed no effect of the slowed diffusion of clot formation. This seems to be at least partially due to very slow consumption of these zymogens during coagulation (15), so that they are always present in the reaction volume and their diffusion flux is small and nonessential.
The role of fXI in coagulation has been a subject of debate for a long time (41). It activates fIX and its deficiency is associated with a tendency to bleed. fXI can be activated by fXIIa, a contact pathway factor, but fXII deficiency is not associated with a bleeding tendency and the contact pathway is assumed not to function in physiological hemostasis. Some studies have shown that fXI is slowly activated by thrombin in the absence of cofactors, and that this reaction is accelerated 2000-fold in the presence of dextran sulfate (34). Other works demonstrated that in plasma this reaction is ineffective, which was ascribed to inhibition by fibrinogen (42). One study suggested that fXI activation by thrombin results in additional thrombin preventing the clot from fibrinolysis (43). Later, this reaction was shown to be stimulated by activated platelets (41,44), and fXIa was shown to increase thrombin generation, especially at low TF and in the presence of platelets (45,46). However, it seems unclear whether a small effect on thrombin generation is able to explain the significance of fXI illustrated by bleeding associated with its deficiency, hemophilia C. Our previous theoretical analysis suggested that fXI activation by thrombin may be important for the spatial propagation of coagulation (3). In our study, clot formation in fXI-deficient plasma was impaired far from the activator, confirming this hypothesis. These results provide a possible explanation of the significance of fXI: although its activation by thrombin is slow, this reaction and additional fIXa formed by fXIa become important during the formation of large clots, in the regions remote from TF-expressing cells. It should be noted that these results were obtained under conditions in which the contribution of extrinsic tenase is maximal (confluent monolayers of fibroblasts and macrophages) and intrinsic tenase assembly and fXI activation by thrombin are minimal (platelet-free plasma). Under in vivo conditions, the contribution of intrinsic tenase and fXIa-mediated feedback to clot propagation could be even more significant. On the other hand, self-sustained autocatalytic propagation of clotting seems not to be desirable in vivo, and fXI activation by thrombin may be potentially dangerous (40). In such cases, specific therapeutic inhibition of fXI can slow down thrombus propagation without affecting the initiation of hemostasis (Fig. 3, A and B).
The inhibitory effect of thrombomodulin, a cofactor of thrombin stimulating APC generation, has been studied in thrombin generation assays (47). For a long time it was hypothesized to participate in localization of the coagulation process (48). A recent study in a murine model of FeCl3-induced carotid artery thrombosis (39) has actually shown that, indeed, in mice with a functional thrombomodulin defect, complete occlusion of the artery occurred in 80% cases (27% in control), and mean time of occlusion was twofold less than that in control. In our study, we analyzed the effect of thrombomodulin in a reaction-diffusion spatial system. To our knowledge, this work was the first to directly demonstrate that thrombomodulin is able to localize clot expansion in a dose-dependent manner. Although thrombomodulin at 30–100 nM affected both the initiation and propagation phases, clot formation at 3–10 nM of thrombomodulin stopped at a distance of 1–2 mm from the activator without significant effects on the initiation phase. In addition to demonstrating a possible role of thrombomodulin in physiological hemostasis, this result indicates that thrombomodulin can be therapeutically used to suppress thrombus propagation with minor adverse effects on the initiation of hemostasis. Such an approach seems to be beneficial compared with therapy using such anticoagulants as heparin, which inhibits all stages of clot formation and may lead to hemorrhage.
Several recent studies identified the presence of TF protein and TF activity in blood and plasma (36,49). It was found to accumulate in ex vivo thrombi (38) and it was proposed that this blood-borne TF is essential for thrombus growth, because diffusion of coagulation factors in fibrin, and especially in platelet-fibrin clots, is slow (8). However, other studies challenged this concept (35,50). We assessed the possible role of blood-borne TF in clot growth by adding relipidated recombinant TF to normal plasma. TF had no effect on clot growth from the activating cell monolayer, but stimulated clotting of the whole volume in a dose-dependent manner (Fig. 5). The same result was obtained in the computer model. Taken together, these data indicate that TF activity in plasma is unlikely to contribute to spatial clot formation in the reaction-diffusion system to any significant extent. Thus, transition from the homogeneous model of coagulation to the spatial clot growth model appears not to increase the role of blood-borne TF: diffusion of fIXa and fXI activation by thrombin are effective enough to make clot enlargement rapid and independent of TF possibly present in plasma. However, this result may become invalid in the reaction-diffusion-convection models of thrombus formation because of the accumulation of blood-borne TF in growing thrombus due to the presence of blood flow and hindered diffusion of coagulation factors in platelet-rich thrombi.
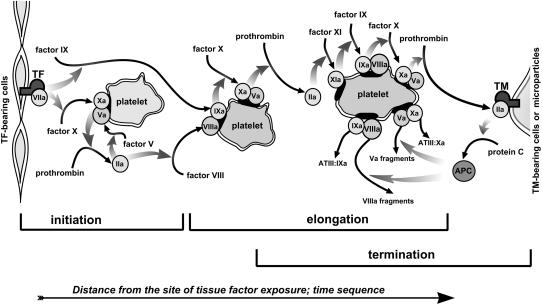
The conclusions of this study can be summarized in a spatial reaction-diffusion concept of the coagulation regulation presented in Fig. 6. Clot formation in this model is divided into three stages: initiation, spatial propagation (or expansion), and termination. Each of the consecutive stages is controlled by a specific pathway: 1), fXa production by extrinsic tenase; 2), fIXa diffusion and fXa generation by intrinsic tenase, followed at later stages by fIX activation in the fXI-mediated feedback; and 3), thrombomodulin-dependent protein C pathway. The novelty of this mechanism is the introduction of the conception of spatial heterogeneity into the basic scheme of the coagulation cascade, and the attempt to determine the roles of the specific pathways of the cascade at different temporal and spatial stages of clotting. In particular, this model may be useful in specific therapeutic targeting of different stages of hemostatic and thrombotic processes.
FIGURE 6.
Schematic representation of the reaction-diffusion model of coagulation. Blood coagulation is activated by TF-expressing cells (on the left) and propagates into the bulk of plasma. Coagulation near the activator (initiation) is determined by fXa production by extrinsic tenase located on TF-expressing cells. fXa is rapidly inhibited and does not diffuse at long distances. Far from the activator (propagation) it is formed by intrinsic tenase. The limiting component of intrinsic tenase, fIXa, is still produced by extrinsic tenase, because it is inhibited slowly and can diffuse efficiently. During further clot elongation, additional fIXa production by the fXIa-mediated long-range feedback becomes essential. Finally, clot formation is terminated because of the action of thrombomodulin: in a potent negative feedback, the thrombin-thrombomodulin complex produces APC, which stops thrombin formation by cleaving fVa and fVIIIa.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Supplementary Material
Acknowledgments
We thank Drs. E. S. Lobanova and A. A. Tokarev for stimulating discussions and helpful criticism. We thank Drs. O.P. Plyushch, K. G. Kopylov, and E. G. Lopatina for help with blood collection. We are grateful to Dr. V. I. Sarbash for his great contribution to the experimental setup development. This study was supported in part by grants 03-04-48338 and 05-01-22001 from the Russian Foundation for Basic Research, and by grants HL66101 and HL72929 from the National Institutes of Health.
Mikhail A. Panteleev and Mikhail V. Ovanesov contributed equally to this work.
Mikhail V. Ovanesov's and Aleksei M. Shibeko's present address is Division of Neurobiology, Department of Psychiatry, The Johns Hopkins University, Baltimore, MD 21218.
References
- 1.Butenas, S., and K. G. Mann. 2002. Blood coagulation. Biochemistry (Mosc.). 67:3–12. [DOI] [PubMed] [Google Scholar]
- 2.Davie, E. W., and O. D. Ratnoff. 1964. Waterfall sequence for intrinsic blood clotting. Science. 145:1310–1312. [DOI] [PubMed] [Google Scholar]
- 3.Zarnitsina, V. I., A. V. Pokhilko, and F. I. Ataullakhanov. 1996. A mathematical model for the spatio-temporal dynamics of intrinsic pathway of blood coagulation. II. Results. Thromb. Res. 84:333–344. [DOI] [PubMed] [Google Scholar]
- 4.Hoffman, M., and D. M. Monroe. 2001. A cell-based model of hemostasis. Thromb. Haemost. 85:958–965. [PubMed] [Google Scholar]
- 5.Hoffman, M., D. M. Monroe, J. A. Oliver, and H. R. Roberts. 1995. Factors IXa and Xa play distinct roles in tissue factor-dependent initiation of coagulation. Blood. 86:1794–1801. [PubMed] [Google Scholar]
- 6.Ovanesov, M. V., J. V. Krasotkina, L. I. Ul‘yanova, K. V. Abushinova, O. P. Plyushch, S. P. Domogatskii, A. I. Vorob’ev, and F. I. Ataullakhanov. 2002. Hemophilia A and B are associated with abnormal spatial dynamics of clot growth. Biochim. Biophys. Acta. 1572:45–57. [DOI] [PubMed] [Google Scholar]
- 7.Ovanesov, M. V., N. M. Ananyeva, M. A. Panteleev, F. I. Ataullakhanov, and E. L. Saenko. 2005. Initiation and propagation of coagulation from tissue factor bearing cell monolayers to plasma: initiator cells do not regulate spatial growth rate. J. Thromb. Haemost. 3:321–331. [DOI] [PubMed] [Google Scholar]
- 8.Hathcock, J. J., and Y. Nemerson. 2004. Platelet deposition inhibits tissue factor activity: in vitro clots are impermeable to factor Xa. Blood. 104:123–127. [DOI] [PubMed] [Google Scholar]
- 9.Ataullakhanov, F. I., R. I. Volkova, G. T. Guriia, and V. I. Sarbash. 1995. Spatial aspects of blood coagulation dynamics. III. Growth of clots in vitro. Biofizika. 40:1320–1328. [PubMed] [Google Scholar]
- 10.Ovanesov, M. V., E. G. Lopatina, E. L. Saenko, N. M. Ananyeva, L. I. Ul'yanova, O. P. Plyushch, A. A. Butilin, and F. I. Ataullakhanov. 2003. Effect of factor VIII on tissue factor-initiated spatial clot growth. Thromb. Haemost. 89:235–242. [PubMed] [Google Scholar]
- 11.Sinauridze, E. I., R. I. Volkova, Y. V. Krasotkina, V. I. Sarbash, and F. I. Ataullakhanov. 1998. Dynamics of clot growth induced by thrombin diffusing into nonstirred citrate human plasma. Biochim. Biophys. Acta. 1425:607–616. [DOI] [PubMed] [Google Scholar]
- 12.Ananyeva, N. M., D. V. Kouiavskaia, M. Shima, and E. L. Saenko. 2002. Intrinsic pathway of blood coagulation contributes to thrombogenicity of atherosclerotic plaque. Blood. 99:4475–4485. [DOI] [PubMed] [Google Scholar]
- 13.Panteleev, M. A., V. I. Zarnitsina, and F. I. Ataullakhanov. 2002. Tissue factor pathway inhibitor: a possible mechanism of action. Eur. J. Biochem. 269:2016–2031. [DOI] [PubMed] [Google Scholar]
- 14.Panteleev, M. A., E. L. Saenko, N. M. Ananyeva, and F. I. Ataullakhanov. 2004. Kinetics of factor X activation by the membrane-bound complex of factor IXa and factor VIIIa. Biochem. J. 381:779–794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lawson, J. H., M. Kalafatis, S. Stram, and K. G. Mann. 1994. A model for the tissue factor pathway to thrombin. I. An empirical study. J. Biol. Chem. 269:23357–23366. [PubMed] [Google Scholar]
- 16.van't Veer, C., and K. G. Mann. 1997. Regulation of tissue factor initiated thrombin generation by the stoichiometric inhibitors tissue factor pathway inhibitor, antithrombin-III, and heparin cofactor-II. J. Biol. Chem. 272:4367–4377. [DOI] [PubMed] [Google Scholar]
- 17.van't Veer, C., N. J. Golden, M. Kalafatis, and K. G. Mann. 1997. Inhibitory mechanism of the protein C pathway on tissue factor-induced thrombin generation. Synergistic effect in combination with tissue factor pathway inhibitor. J. Biol. Chem. 272:7983–7994. [DOI] [PubMed] [Google Scholar]
- 18.Butenas, S., K. M. Cawthern, C. van't Veer, M. E. DiLorenzo, J. B. Lock, and K. G. Mann. 2001. Antiplatelet agents in tissue factor-induced blood coagulation. Blood. 97:2314–2322. [DOI] [PubMed] [Google Scholar]
- 19.Butenas, S., R. F. Branda, C. van't Veer, K. M. Cawthern, and K. G. Mann. 2001. Platelets and phospholipids in tissue factor-initiated thrombin generation. Thromb. Haemost. 86:660–667. [PubMed] [Google Scholar]
- 20.Cawthern, K. M., C. van't Veer, J. B. Lock, M. E. DiLorenzo, R. F. Branda, and K. G. Mann. 1998. Blood coagulation in hemophilia A and hemophilia C. Blood. 91:4581–4592. [PubMed] [Google Scholar]
- 21.Butenas, S., C. van't Veer, and K. G. Mann. 1997. Evaluation of the initiation phase of blood coagulation using ultrasensitive assays for serine proteases. J. Biol. Chem. 272:21527–21533. [DOI] [PubMed] [Google Scholar]
- 22.Monkovic, D. D., and P. B. Tracy. 1990. Functional characterization of human platelet-released factor V and its activation by factor Xa and thrombin. J. Biol. Chem. 265:17132–17140. [PubMed] [Google Scholar]
- 23.Sims, P. J., T. Wiedmer, C. T. Esmon, H. J. Weiss, and S. J. Shattil. 1989. Assembly of the platelet prothrombinase complex is linked to vesiculation of the platelet plasma membrane. Studies in Scott syndrome: an isolated defect in platelet procoagulant activity. J. Biol. Chem. 264:17049–17057. [PubMed] [Google Scholar]
- 24.Panteleev, M. A., N. M. Ananyeva, N. J. Greco, F. I. Ataullakhanov, and E. L. Saenko. 2005. Two subpopulations of thrombin-activated platelets differ in their binding of the components of the intrinsic factor X-activating complex. J. Thromb. Haemost. 3:2545–2553. [DOI] [PubMed] [Google Scholar]
- 25.London, F. S., M. Marcinkiewicz, and P. N. Walsh. 2004. A subpopulation of platelets responds to thrombin- or SFLLRN-stimulation with binding sites for factor IXa. J. Biol. Chem. 279:19854–19859. [DOI] [PubMed] [Google Scholar]
- 26.Diamond, S. L., and S. Anand. 1993. Inner clot diffusion and permeation during fibrinolysis. Biophys. J. 65:2622–2643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Matveyev, M. Y., and S. P. Domogatsky. 1992. Penetration of macromolecules into contracted blood clot. Biophys. J. 63:862–863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mihalyi, E. 1988. Clotting of bovine fibrinogen. Kinetic analysis of the release of fibrinopeptides by thrombin and of the calcium uptake upon clotting at high fibrinogen concentrations. Biochemistry. 27:976–982. [DOI] [PubMed] [Google Scholar]
- 29.Tracy, P. B., M. E. Nesheim, and K. G. Mann. 1992. Platelet factor Xa receptor. Methods Enzymol. 215:329–360. [DOI] [PubMed] [Google Scholar]
- 30.Heeb, M. J., R. M. Mesters, G. Tans, J. Rosing, and J. H. Griffin. 1993. Binding of protein S to factor Va associated with inhibition of prothrombinase that is independent of activated protein C. J. Biol. Chem. 268:2872–2877. [PubMed] [Google Scholar]
- 31.Koppelman, S. J., T. M. Hackeng, J. J. Sixma, and B. N. Bouma. 1995. Inhibition of the intrinsic factor X activating complex by protein S: evidence for a specific binding of protein S to factor VIII. Blood. 86:1062–1071. [PubMed] [Google Scholar]
- 32.Kondratovich, A. Y., A. V. Pokhilko, and F. I. Ataullakhanov. 2002. Spatiotemporal dynamics of contact activation factors of blood coagulation. Biochim. Biophys. Acta. 1569:86–104. [DOI] [PubMed] [Google Scholar]
- 33.Hairer, E., S. P. Norsett, and G. Wanner. 1993. Solving Ordinary Differential Equations 1: Nonstiff Problems. Springer Verlag, Berlin.
- 34.Gailani, D., and G. J. Broze. 1991. Factor XI activation in a revised model of blood coagulation. Science. 253:909–912. [DOI] [PubMed] [Google Scholar]
- 35.Butenas, S., B. A. Bouchard, K. E. Brummel-Ziedins, B. Parhami-Seren, and K. G. Mann. 2005. Tissue factor activity in whole blood. Blood. 105:2764–2770. [DOI] [PubMed] [Google Scholar]
- 36.Giesen, P. L., U. Rauch, B. Bohrmann, D. Kling, M. Roque, J. T. Fallon, J. J. Badimon, J. Himber, M. A. Riederer, and Y. Nemerson. 1999. Blood-borne tissue factor: another view of thrombosis. Proc. Natl. Acad. Sci. USA. 96:2311–2315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hemker, H. C., and S. Beguin. 2000. Phenotyping the clotting system. Thromb. Haemost. 84:747–751. [PubMed] [Google Scholar]
- 38.Balasubramanian, V., E. Grabowski, A. Bini, and Y. Nemerson. 2002. Platelets, circulating tissue factor, and fibrin colocalize in ex vivo thrombi: real-time fluorescence images of thrombus formation and propagation under defined flow conditions. Blood. 100:2787–2792. [DOI] [PubMed] [Google Scholar]
- 39.Dorffler-Melly, J., M. de Kruif, L. A. Schwarte, R. F. Franco, S. Florquin, C. A. Spek, C. Ince, P. H. Reitsma, and H. ten Cate. 2003. Functional thrombomodulin deficiency causes enhanced thrombus growth in a murine model of carotid artery thrombosis. Basic Res. Cardiol. 98:347–352. [DOI] [PubMed] [Google Scholar]
- 40.Gruber, A., and S. R. Hanson. 2003. Factor XI-dependence of surface- and tissue factor-initiated thrombus propagation in primates. Blood. 102:953–955. [DOI] [PubMed] [Google Scholar]
- 41.Oliver, J. A., D. M. Monroe, H. R. Roberts, and M. Hoffman. 1999. Thrombin activates factor XI on activated platelets in the absence of factor XII. Arterioscler. Thromb. Vasc. Biol. 19:170–177. [DOI] [PubMed] [Google Scholar]
- 42.Scott, C. F., and R. W. Colman. 1992. Fibrinogen blocks the autoactivation and thrombin-mediated activation of factor XI on dextran sulfate. Proc. Natl. Acad. Sci. USA. 89:11189–11193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.von dem Borne, P. A., J. C. Meijers, and B. N. Bouma. 1995. Feedback activation of factor XI by thrombin in plasma results in additional formation of thrombin that protects fibrin clots from fibrinolysis. Blood. 86:3035–3042. [PubMed] [Google Scholar]
- 44.Baglia, F. A., and P. N. Walsh. 2000. Thrombin-mediated feedback activation of factor XI on the activated platelet surface is preferred over contact activation by factor XIIa or factor XIa. J. Biol. Chem. 275:20514–20519. [DOI] [PubMed] [Google Scholar]
- 45.Keularts, I. M., A. Zivelin, U. Seligsohn, H. C. Hemker, and S. Beguin. 2001. The role of factor XI in thrombin generation induced by low concentrations of tissue factor. Thromb. Haemost. 85:1060–1065. [PubMed] [Google Scholar]
- 46.Wielders, S. J., S. Beguin, H. C. Hemker, and T. Lindhout. 2004. Factor XI-dependent reciprocal thrombin generation consolidates blood coagulation when tissue factor is not available. Arterioscler. Thromb. Vasc. Biol. 24:1138–1142. [DOI] [PubMed] [Google Scholar]
- 47.van't Veer, C., N. J. Golden, M. Kalafatis, and K. G. Mann. 1997. Inhibitory mechanism of the protein C pathway on tissue factor-induced thrombin generation. Synergistic effect in combination with tissue factor pathway inhibitor. J. Biol. Chem. 272:7983–7994. [DOI] [PubMed] [Google Scholar]
- 48.Walker, F. J., and P. J. Fay. 1992. Regulation of blood coagulation by the protein C system. FASEB J. 6:2561–2567. [DOI] [PubMed] [Google Scholar]
- 49.Bogdanov, V. Y., V. Balasubramanian, J. Hathcock, O. Vele, M. Lieb, and Y. Nemerson. 2003. Alternatively spliced human tissue factor: a circulating, soluble, thrombogenic protein. Nat. Med. 9:458–462. [DOI] [PubMed] [Google Scholar]
- 50.Day, S. M., J. L. Reeve, B. Pedersen, D. M. Farris, D. D. Myers, M. Im, T. W. Wakefield, N. Mackman, and W. P. Fay. 2005. Macrovascular thrombosis is driven by tissue factor derived primarily from the blood vessel wall. Blood. 105:192–198. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.