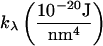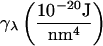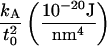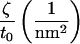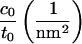A Consistent Model for Thermal Fluctuations and Protein-Induced Deformations in Lipid Bilayers

Abstract

We present an elastic Hamiltonian for membrane energetics that captures bilayer undulation and peristaltic deformations over all wavelengths, including the short wavelength protrusion regime. The model implies continuous functional forms for thermal undulation and peristaltic amplitudes as a function of wavelength and predicts previously overlooked relationships between these curves. Undulation and peristaltic spectra display excellent agreement with data from both atomistic and coarse-grained models over all simulated length scales. Additionally, the model accurately predicts the bilayer's response to a cylindrical protein inclusion as observed in coarse-grained simulation. This elastic response provides an explanation for gramicidin ion channel lifetime versus membrane thickness data that requires no fit constants. The physical parameters inherent to this picture may be expressed in terms of familiar material properties associated with lipid monolayers. Inclusion of a finite monolayer spontaneous curvature is essential to obtain fully consistent agreement between theory and the full range of available simulation/experimental data.

INTRODUCTION

At and near physiological temperatures, lipid bilayers exhibit significant thermal fluctuations in microscopic structure, composition, and shape as dictated by equilibrium statistical mechanics (1,2). Membranes are not static, flat homogeneous structures—not only because of metabolic activity and biological structures at the plasma membrane surface (cytoskeleton, caveolae, lipid rafts, coated pits, etc.), but also because of these purely physical considerations. Although living cells are certainly not equilibrium structures, it is important to fully understand the thermal behavior of model membrane systems as a preliminary step toward unraveling biologically relevant phenomena at membrane surfaces.

Thermal fluctuations in lipid bilayers have been implicated in a variety of biophysical phenomena, including (but not limited to) steric repulsions between proximal bilayers (3,4), shape fluctuations of the red blood cell (5), cellular motility (6), and entropically driven interactions between integral membrane proteins (7,8). Traditionally, our theoretical understanding of such phenomena has rested upon simplified analytical theories, in the spirit of work by Helfrich (9) and others (3,10,11). Since these theories describe the bilayer by one or more continuous fields in space without any atomic/molecular level resolution, we will refer to them as elastic pictures. Physical properties needed in the formulation of such theories (elastic moduli, interfacial tensions, etc.) are typically guessed or inferred (often indirectly) from experiment. More recently, molecular dynamics simulation has evolved as a potential means to connect theoretical models with specific lipid bilayers by providing physical parameters directly from computer experiments.

In principle, it should be possible to extract the parameters inherent to elastic models directly from atomistic simulations. In such a scheme, differences in behavior due to lipid composition would be fully predicted by detailed simulations of chemically distinct bilayers over relatively small length scales. In practice, the correspondence between elastic models and molecular simulations has yet to be fully developed. Although the extraction of bilayer bending moduli and surface tensions through analysis of thermal membrane height fluctuations (undulations) is well established (12–19), the corresponding interpretation of bilayer thickness (peristaltic) fluctuations is less common (13–15). (See Fig. 1 for an explanation of height versus thickness fluctuations.) Perhaps one reason for this is that current protocols for fitting peristaltic data involve separately analyzing simulations over multiple wavelength regimes, without clear rules for how to effect such a separation. Furthermore, one expects that the elastic properties involved in both peristaltic and height fluctuations derive from the same source, yet present theories do not fully account for the interrelations between these two types of deformation. Finally, it should be noted that there is some discrepancy in how various groups treat data stemming from the short wavelength protrusion regime (Fig. 1 A). Although numerous theoretical studies have considered long-wavelength undulation modes, long-wavelength peristaltic modes, and protrusion modes in separate contexts (3,9–11,13), to date no single unifying theory has been advanced that can account for all of these behaviors. So, although the physical basis for these behaviors is fairly well established, it is unclear how to best interpret data quantitatively, since it is not fully clear how all of these fluctuation modes are coupled and it is not known how thermal undulation and peristaltic amplitudes are expected to relate to one another.

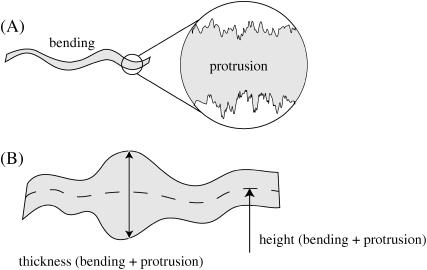
FIGURE 1.

(A) Fluctuation modes of lipid bilayers (3,11). Over long lengthscales, fluctuations are dominated by mesoscopic deformations involving the concerted motion of many lipids. At wavelengths of several nanometers and longer, molecular-level details are unimportant, with fluctuations dominated by these long-wavelength or bending modes. Molecular-level roughness is, of course, unavoidable at sufficiently short wavelengths. The bilayer motions associated with molecular level fluctuations are traditionally denoted “protrusions”. The two leaflets need not move in phase, which can result in a nonuniform thickness of the bilayer in both the protrusion and bending regimes. (B) Definition of height and thickness fluctuations. Shape fluctuations of the bilayer are conveniently decomposed into height and thickness contributions. In this work, we adopt the convention that the membrane is fluctuating around an average flat configuration with normal in the z direction. We denote the midplane between monolayer leaflets as a function of x,y coordinates as the height field of the membrane (denoted h, see Eq. 5). The distance between monolayer leaflets as a function of x,y position is referred to as the “thickness field of the membrane” (denoted 2t + 2t₀, the fluctuating variable t is defined as the thickness of a monolayer measured relative to the average tensionless thickness to conform with convention; see Eq. 6). In practice, the position of the individual monolayers is dictated by specific atomic groups associated with the interface between polar and hydrophobic groups along the lipid chain. We shall use the terms “height fluctuation” and “undulation” interchangeably to describe deviations of the height field away from the flat reference state. Likewise, we shall refer to “thickness fluctuations” and “peristaltic modes” interchangeably. In contrast to some authors, we allow these terms to refer to fluctuations over all wavelengths—i.e., bending and protrusions both contribute to undulations and peristaltic modes.

In addition to describing thermal fluctuations, the elastic properties of lipid bilayers should influence how an otherwise homogeneous membrane will respond to the insertion of an integral membrane protein with hydrophobic mismatch (see Fig. 5). Indeed, much theoretical work has gone into developing just such a picture (20–32), partly motivated by the interplay between bilayer properties and the functioning of integral membrane proteins (33,34). It stands to reason that the physical properties necessary to predict the bilayer deformation profile surrounding a protein inclusion are the same properties necessary to understand thermal fluctuations (assuming that both phenomena involve comparable energetics). However, some of the elastic theories best suited to explaining deformation profiles (31) contain a larger set of physical parameters than theories currently employed to explain homogeneous bilayer fluctuations. And, although coarse-grained simulations of proteins within bilayer environments sufficiently vast to test elastic theories have recently become feasible (35–37), simulation results have yet to be quantitatively analyzed in this context. It is still uncertain as to whether or not elastic theories can successfully predict bilayer response to an embedded protein. Similarly, it is unclear that a single elastic theory can be applied to both thermal fluctuations and deformations due to embedded proteins.

FIGURE 5.

Inclusion-induced deformation. A symmetric transmembrane protein with hydrophobic residues around its periphery and a thickness exceeding that of the surrounding membrane will tend to distort the bilayer as shown (not to scale). A protein thinner than the surrounding membrane is expected to induce the opposite effect. The nonmonotonic healing of the membrane thickness back to equilibrium separation as one moves away from the inclusion is predicted theoretically by our model (which nearly reduces to the theory of Aranda-Espinoza et al. (31) in the context of inclusion-induced deformations), and observed in our simulations and similar coarse-grained simulations (36,37).

This article presents an elastic model for bilayer energetics that captures bilayer undulation and peristaltic deformations over all wavelengths. In particular, the contributions of microscopic protrusions are handled on equal footing with the more traditional long-wavelength bending contributions to bilayer shape. The model is equally well suited to the study of thermal fluctuations in homogeneous bilayers and membrane response to embedded protein inclusions.

Other applications are certainly possible as well. Although many of the underlying components of our theory have been discussed in specific contexts previously, the unified formulation we present is new and appealing in its ability to consistently subsume a variety of different physical phenomena. This picture naturally resolves several open questions and inconsistencies, while serving as a convenient means to analyze simulated and experimental data. The picture we advance is fully consistent with an array of such data. Specifically, we call attention to the following aspects of this work:

1. We derive an expression for thermal peristaltic fluctuations from an underlying elastic model. The corresponding expressions for thermal undulations are derived from the same model and correspond to the expected (11) Helfrich behavior at long wavelengths and protrusion behavior over molecular wavelengths. Since both thickness and height fluctuations are derived from the same starting point, we find explicit correspondence between physical parameters quantifying both types of fluctuation. In particular, we predict identical bending moduli and protrusion-associated constants for both phenomena.

2. The possibility of nonvanishing monolayer spontaneous curvature is central to our model. Under certain parameter regimes, this leads to nonmonotonic behavior for thermal peristaltic fluctuation amplitudes as a function of wavelength (undulation modes are not affected). Such behavior has been observed in fully atomic simulations of dipalmitoylphosphatidylcholine (DPPC) (13) and sphingomyelin (SM) (15) bilayers, but has previously been attributed to poor sampling. Our treatment provides an appealing alternative explanation.

3. We have used our theory to fit existing fully atomic MD simulation fluctuation data from the literature for three different lipid bilayers (DPPC (13), glycerolmonoolein (GMO) (14), and SM (15)) and a coarse-grained (CG) bilayer model developed in our group (16). There are a total of five fit parameters involved in this process, with clearly defined physical meanings. Previous fitting schemes have all involved at least this many constants, yet did not account for the important contribution of finite monolayer spontaneous curvature. The obtained numerical values for these constants are physically reasonable and the quality of our fits to the data sets are universally very good (see Fig. 4).

4. We critically analyze the results of a coarse-grained simulation of a cylindrical protein embedded within an otherwise homogeneous bilayer. The proposed elastic picture quantitatively predicts the bilayer's response to protein-induced deformation, using elastic constants obtained (within error bars) via analysis of thermal fluctuations in the homogeneous bilayer. In other words, the elastic picture we advance finds fully consistent agreement between two very different simulations.

5. Using elastic properties derived from thermal fluctuation data of GMO, we predict the effect of bilayer thickness on gramicidin-A ion-channel lifetimes for monoglyceride-based bilayers. Our procedure involves no fit parameters and our model predicts relative lifetimes in good agreement with experiment.

6. Applied to protein-induced deformations, our model nearly reduces to the picture advanced by Aranda-Espinoza et al. (31). In contrast to that picture, we include the possibility of microscopic protrusions and solve for the thermal average of the deformation profile (numerically) as opposed to identifying the elastic minimum (analytically). These differences are expected to produce negligible effects for three of the four bilayers analyzed in this study and are explicitly shown to produce negligible effect for our CG simulation model. In this sense, we have provided the first direct validation of Aranda-Espinoza's theory for predicting membrane shape around symmetric inclusions with hydrophobic mismatch. In the case of GMO, protrusion-bending coupling is relatively strong and we predict that protrusions will affect the deformation profile, leading to quantitative disagreement with Aranda-Espinoza et al. (31). In the absence of appropriate simulation data on GMO, this prediction remains unverified.

7. Applied to thermal membrane fluctuations, our model predicts continuous functional forms for both undulation and peristaltic amplitudes over all wavelengths. This resolves the practical shortcomings of previously introduced piecewise fitting techniques and, as noted above, explains certain interrelations between these data sets.

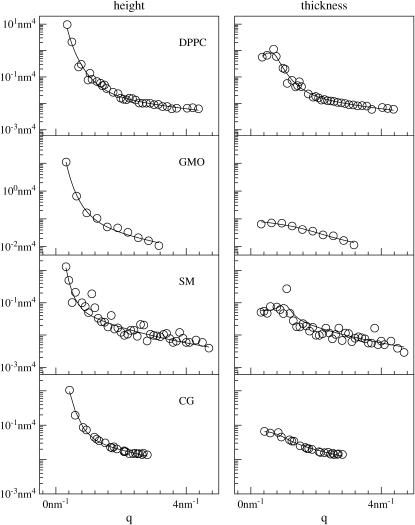
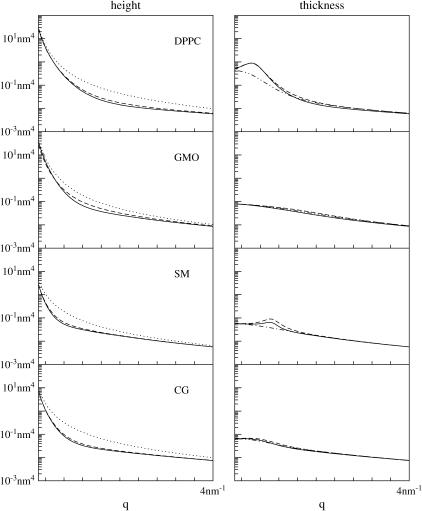
FIGURE 4.

Height (〈|h_q|²〉) and thickness (〈|t_q|²〉) fluctuations for DPPC (13), GMO (14), SM (15), and a coarse-grained model (CG). Simulation data are displayed as circles. The lines represent best fits of the data to the expressions in Eq. 32. Fit parameters are in Table 1.

This article is organized as follows: A General Model presents the general theory. Fluctuation spectra of homogeneous membranes apply this theory to height and thickness fluctuations, derive the expected spectra, and fit the four data sets. Protein-induced deformation profiles applies the general theory to inclusion deformations, presents simulation data for the CG model, and compares material constants derived by fitting to the deformation profile to those extracted from thermal fluctuations of the homogeneous membrane. Prediction of gramicidin-A channel lifetimes presents predictions for gramicidin channel lifetime as a function of the thickness of the surrounding bilayer, and compares to experimental data. Finally, we conclude with a brief discussion.

A GENERAL MODEL

We derive here our model for bilayer deformations. Because we seek to explain both height and thickness deformations (Fig. 1), our considerations begin with a bilayer composed of two opposing coupled monolayers. The two leaflets do not necessarily bend in unison, which leads to both height and thickness fluctuations/deformations. Our starting point is the general theory for surfactant monolayers presented in Safran (1), but we retain fluctuations in area per lipid. We assume a constant volume condition for hydrocarbon tails and additionally assume that lipids across from one another in opposing leaflets share the same local area/lipid. This leads to a theory for membrane elasticity in which thickness and height deformations are uncoupled. The thickness deformations obey energetics consistent with the picture developed in Aranda-Espinoza et al. (31), whereas height fluctuations are consistent with standard Helfrich energetics. We extend this approach to include microscopic protrusions as in the theory of Lipowsky and Grotehans (11), but the formulation discussed here is more general since it includes the contribution of peristaltic bending modes.

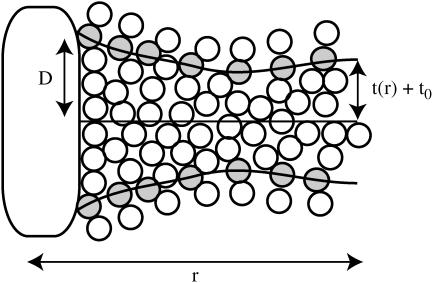
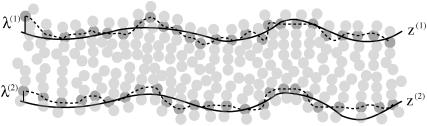
Each monolayer can exhibit bending deformations described by fields z^{(1, 2)} (denoted as such because we always assume the x,y plane as the reference configuration for bilayer midplane), and is also subject to microscopic noise, or protrusions, described by fields λ^{(1, 2)}. By convention, we always take the top leaflet to be monolayer (1). Consequently the bilayer is described by four separate (but coupled) fields: z⁽¹⁾(x,y), z⁽²⁾(x,y), λ⁽¹⁾(x,y), and λ⁽²⁾(x,y) (Fig. 2). From this point on and for notational simplicity, we assume the x,y dependence without explicitly writing it. It is convenient to define

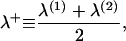(1)

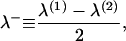(2)

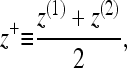(3)

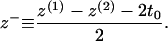(4)

Then, as commonly measured in simulations, the height h of the bilayer midplane and deviations in the bilayer thickness 2t are described by

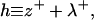(5)

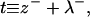(6)

respectively. From a theoretical perspective, we imagine these fields to reflect precisely defined interfaces between lipid hydrocarbon tails and surrounding water (Fig. 2). From a practical perspective, these fields are extracted from simulation by triangulating a surface using atoms along the lipid chain to represent the position of such an interface (see Fluctuation Spectra of Homogeneous Membranes for further elaboration). Note that our thickness field t refers to fluctuations of half the bilayer thickness and that these fluctuations are measured relative to t₀, the half-bilayer thickness for a flat sheet in its minimal energy configuration at vanishing tension. This seemingly odd definition has been adopted to facilitate later connection with thickness fluctuation spectra, as previously reported in the literature.

FIGURE 2.

Defining the elastic model for bilayer deformations. Microscopic fluctuations λ^{(1, 2)}(x,y) roughen the molecularly smooth interface z^{(1, 2)}(x,y) between each leaflet and water. The values of λ^{(1, 2)} are defined relative to z^{(1, 2)}, respectively. Note that it is the sum z^{(1, 2)} + λ^{(1, 2)} that defines the interface between polar and hydrophobic groups for each leaflet, as discussed in Fig. 1. The fields z^{(1, 2)} should be regarded as mesoscopic fields reflecting an implicit local averaging over molecular fluctuations in the sense of Landau order parameters. At short wavelengths there are too few molecules to provide a smooth coarse-grained average, and we include the effect of these molecular fluctuations via the fields λ^{(1, 2)}. This is essentially the picture adopted in Lipowsky and Grotehans (11).

In what follows, we derive the bilayer free energy per unit area f_z(x,y) due to mesoscopic bending contributions (z fields), and the free energy per unit area f_λ(x,y) due to microscopic protrusions (λ fields) and z,λ coupling. Free energies per molecule are denoted with a tilde notation 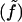to avoid possible confusion with energies per area.

Bending contribution

To treat bending energetics, we temporarily neglect the fields λ and treat the bilayer as the two opposing elastic sheets z⁽¹⁾ and z⁽²⁾. As in Safran (1), we Taylor-expand the free energies per molecule 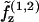to quadratic order in mean curvature H and molecular area deviation (Σ − Σ₀),

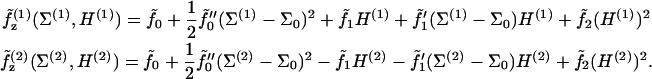(7)

The two monolayers share identical material properties; however, the bottom leaflet (2) is inverted relative to the orientation of the top (1), which accounts for the sign differences in terms with first-order curvature contributions. The value 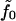is the molecular free energy for a flat monolayer evaluated at the area per molecule Σ₀ that minimizes the free energy under conditions of vanishing applied tension. The primes represent derivatives with respect to Σ evaluated at Σ₀. Subscripts simply reflect the power of H that the constants precede. Note that Σ⁽¹⁾ and Σ⁽²⁾ are the areas per molecule as measured perpendicular to the local monolayer normal—i.e.,

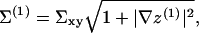(8)

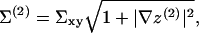(9)

where Σ_xy is area per molecule projected onto the reference x,y plane. As discussed below, we assume this area to be locally identical for the two leaflets.

We bind the two monolayers by requiring conservation of volume for hydrophobic lipid tails and assuming that lipids directly beneath one another (i.e., same x,y coordinates) in the bilayer configuration share the same projected area/molecule (and hence the same thickness by virtue of volume conservation). Stated mathematically, we assume an equation of state for lipids relating local monolayer thickness to local molecular area to be

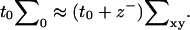(10)

Note that we have made no distinction in thickness or molecular area between the two leaflets, since we assume these quantities to be locally identical for the two monolayers. We comment that Eq. 10 represents only approximate conservation of volume since we do not include the effect of protrusions in this expression and we have neglected contributions due to surface slope and curvature. Furthermore, fixing identical local thickness between opposing monolayers represents a seemingly harsh constraint. The scheme we adopt has the advantage of mathematical simplicity, both in formulation and final results. These assumptions naturally lead to a decoupling between peristaltic and undulation modes with identical bending moduli characterizing these two types of deformation. Similar treatments invoking different assumptions at this stage predict different bending moduli and/or coupling between height and thickness fluctuations (unpublished work); such effects do not seem to be supported by simulation or experiment. In any event, the ultimate justification of these simplifications is the correspondence we find between simulation data and the predictions of our theoretical model. The following sections will demonstrate the correspondence to be very good.

Implementation of Eq. 10 on the expressions in Eq. 7 is handled conveniently in the Monge gauge. The bilayer free energy per area projected onto the x,y plane, f_z, is calculated by noting, for the total bending energy of the bilayer,

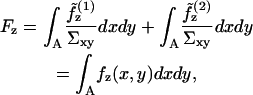(11)

where A is the area of the surfaces projected onto the x,y plane. Implementing the Monge representation for small curvatures ((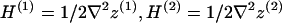)) in our monolayer free energy expressions, and truncating all expansions to second-order in deformation fields, we arrive at

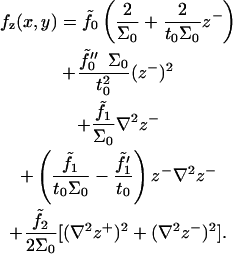(12)

It is clear from this expression that undulations and peristaltic excitations are decoupled. We identify one of the constants appearing in the above expression, by comparing the undulation term (the one involving z⁺) with the usual Helfrich formula (1,9). The term associated with 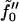involves compression of the bilayer, since z⁻ and (Σ − Σ₀) are connected through volume conservation, which allows us to identify this constant with the usual bilayer compression modulus. The term in braces on the first line integrates to the total number of lipids in the bilayer, and so we identify 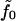with the lipid chemical potential. Under conditions of vanishing tension, this quantity vanishes. The remaining constants are clearly related to the spontaneous curvature of the component monolayers, as can be seen by examining Eq. 7 (1,31). Explicitly, we deduce

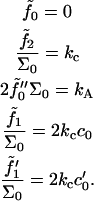(13)

For future convenience, the values k_A and k_c are defined here as the compressibility modulus and bending modulus for the bilayer. The analogous quantities associated with the monolayers are obtained by dividing the bilayer values in half. The spontaneous curvature c₀ and area derivative of the spontaneous curvature c′₀ ≡ ∂c₀/∂Σ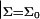 are the values associated with the individual monolayers. As is evident from Eq. 12, the derived behavior of the bilayer for two identical opposing leaflets yields vanishing bilayer spontaneous curvature regardless of the monolayer values. Spontaneous curvature of the monolayers manifests itself only through peristaltic deformations and fluctuations. Our convention for sign of c₀ insures that positive values encourage a monolayer to form micelles, and that negative values favor reverse micelles.

Adopting the notation specified above, Eq. 12 becomes

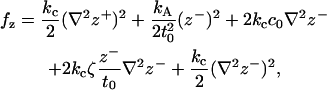(14)

where we have defined

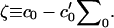(15)

The pieces of Eq. 14 are easily interpreted. The first term consists of the usual Helfrich bending component associated with a tensionless fluid surface with vanishing spontaneous curvature. It is this portion of the energetics that is usually considered in long wavelength studies of membranes, where peristaltic fluctuations are assumed to be unimportant. The remaining terms describe contributions to the energetics due to out-of-phase motion (peristaltic deformations) of the two monolayers. The second term corresponds to the energetic cost of area stretching/compression that accompanies a thickness fluctuation. The remaining terms reflect bending energetics due to the peristaltic modes analogous to the undulation expression. Note, however, the terms resembling (thickness-dependent) nonvanishing spontaneous curvature contributions for peristaltic deformations. Spontaneous curvature terms vanish in bilayer undulations (formed from identical monolayers), since the contributions from opposing leaflets exactly cancel. The opposite is true for peristaltic fluctuations—the two monolayers' energetics reinforce one another, and we expect to see a contribution to the peristaltic modes reflecting this fact (unless the monolayers themselves have a vanishing spontaneous curvature and vanishing area derivative of c₀).

Protrusion contribution

Thus far, we have neglected the microscopic protrusion fields λ^(1,2). We expect the interface between monolayers and water to be subject to microscopic noise, not represented in the coarse-grained bending energetics discussed in the previous section. At the oil-water interface, this noise has the potential to affect membrane energetics by altering the water structuring proximal to the membrane. Although more refined approaches are possible (11), we adopt an elastic description of this noise similar to that proposed by Lipowsky and Grotehans (11). The free energy per unit area is composed of a surface area term, reflecting the interfacial tension between hydrocarbon tails and water, plus a binding term to keep the fluctuations localized to the coarse-grained average fields z^(1,2),

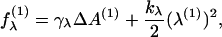(16)

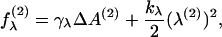(17)

where the additional surface area introduced by the fields λ is, to quadratic order,

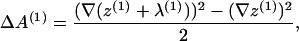(18)

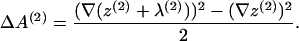(19)

We subtract off the areas of the bare sheets' z^(1,2) contribution because the interfacial free-energy-associated molecularly smooth shape changes are incorporated within the free energy f_z. In other words, if the membrane is microscopically smooth, this means λ = 0 everywhere, and f_λ should vanish.

The interfaces are assumed not to affect one another beyond those contributions seen in f_z, so the total contribution of protrusion energetics is the sum from both interfaces: f_λ = f_λ⁽¹⁾ + f_λ⁽²⁾. In terms of our symmetric/antisymmetric variables (Eqs. 1 and 2), the protrusion contribution to the free energy is

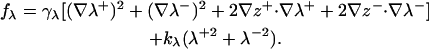(20)

The main difference between Eq. 20 and the expression of Lipowsky and Grotehans is the presence of the ∇z⁻ · ∇λ⁻ term. Lipowsky and Grotehans treated the bilayer as two microscopic fields grafted to one central elastic sheet, so z⁻ (the distance between elastic sheets) was necessarily zero everywhere. An additional minor difference is that in our model, λ⁺ and λ⁻ are naturally bound by the same constant (k_λ), whereas Lipowsky and Grotehans allow for two different constants. Given the present formulation, the use of a single k_λ constant is physically required. In some sense, the idea of two different protrusion constants comes about in our picture naturally through the incorporation of peristaltic bending modes (z⁻). The relation between peristaltic modes and undulations at short wavelengths is predicted in our model, based on the bending elastic constants previously discussed and two constants associated with protrusions.

The total free energy density for the membrane is f = (f_z + f_λ), yielding the entire free energy for the bilayer in a given configuration as

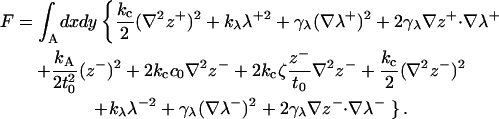(21)

We emphasize again that A reflects the area of the lipid bilayer projected to the x,y plane. If the bilayer encompasses regions devoid of lipids (as when a protein is embedded), the integral reflects that portion of space occupied by the lipids. Terms in the first line (+ terms) affect height fluctuations, whereas terms in the second and third lines (− terms) affect thickness fluctuations and the two portions are entirely decoupled. This expression is one of the main results of this article. All other calculations follow from this expression for bilayer energetics. We can immediately apply this Hamiltonian to both thermal fluctuation spectra for bilayers (next section) and the deformation profiles induced by membrane proteins (see Protein-Induced Deformation Profiles). For the most part, individual terms appearing within Eq. 21 (or slight variations) have appeared in one or more previous theoretical treatments of bilayer and/or monolayer energetics. We believe this to be the first time all relevant physical effects have been encompassed within a single framework to describe both undulation and peristaltic excitations over all wavelengths, including the protrusion regime. This formulation has significant practical and theoretical advantages, to be elaborated upon in the following sections.

FLUCTUATION SPECTRA OF HOMOGENEOUS MEMBRANES

The fluctuation spectra characterize the thermal height fluctuations 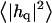and thickness fluctuations 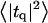of the bilayer as a function of wavevector q. Measurement of the height fluctuations via simulation has become a standard (12–19) method to calculate the effective bending rigidity and surface tension of homogeneous fluid membranes. Fewer studies (13–15) on thickness fluctuations have been conducted, perhaps because there are few direct experimental counterparts. The present model predicts continuous functional forms for both 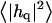and and 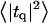represents an immediate application of our Hamiltonian. The following subsections derive the exact predicted forms for the two spectra and go on to suggest a physically motivated simplification that makes the expressions more compact and simpler to interpret. We demonstrate the close agreement between the full and approximate forms for reasonable physical constants in Appendix A. Using the approximate forms (exact forms yield identical results to within error bars), we fit four sets of simulation data from different lipid bilayer simulations. The calculated fits display excellent agreement with simulation results and predict physically reasonable elastic constants.

Theory

To derive the fluctuation spectrum for a homogeneous membrane, we consider the Hamiltonian in Eq. 21 for a membrane in a square periodic box of area A = L². We use the conventions for the Fourier-transform pair of

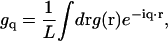(22)

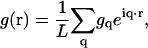(23)

for an arbitrary function g and q = 2π(n, m)/L for the integers n, m = 0, ±1, …N, where N is dictated by a short wavelength cutoff. In Fourier space, the Hamiltonian equation (Eq. 21) becomes

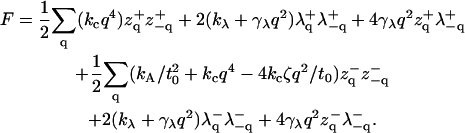(24)

Note that since

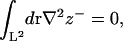(25)

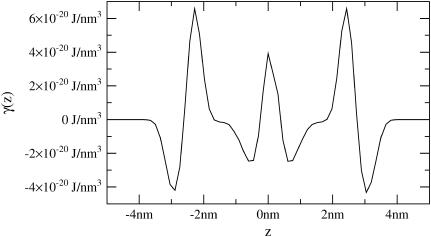
under periodic boundary conditions, one term from the general expression does not appear in Eq. 24. The remaining expression implies that one cannot measure c₀ and c₀′ independently using the fluctuation spectra, but only the linear combination contained within ζ. To measure c₀ independently, we use the membrane stress profile (Fig. 3).

FIGURE 3.

Stress profile for homogeneous coarse-grained bilayer with 128 lipids at constant vanishing tension. The monolayer spontaneous curvature is related to γ(z) through Eq. 33.

F contains terms for coupling protrusion and bending modes. Although certainly solvable, the resulting averages are somewhat complicated:

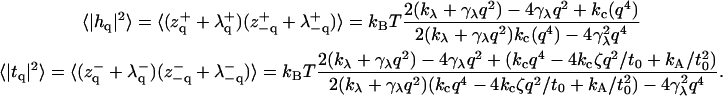(26)

It is well established (12–19) that for long wavelengths (small q), the height fluctuations of a nearly flat bilayer at zero tension follow

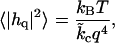(27)

where 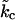is the effective bending rigidity, essentially defined by Eq. 27. Expanding Eq. 26 around small q,

(28)

we recover the form of Eq. 27, but with a renormalized bending rigidity,

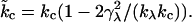(29)

This relationship demonstrates that, as first derived by Lipowsky and Grotehans (11), protrusions lower the effective bending rigidity relative to the bare value. Note that 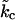remains positive only if 2γ_λ²/(k_λk_c) < 1, which sets obvious limitations on the relative magnitudes of the elastic constants as discussed by Lipowsky and Grotehans (11). The collection of constants 2γ_λ²/(k_λk_c) represents a measure of the coupling strength between protrusions and bending modes. If this coupling were to become very strong, our entire physical picture would be suspect. We expect (and find in Comparison to Simulation Data, below) this number to be quite small for actual lipid systems.

Decoupled protrusion/bending approximation

An obvious way to interpret fluctuation spectra would be to fit data to the full forms of Eq. 26. This is possible and we include such curves in Appendix A. The algebraically complex nature of these expressions makes interpretation difficult, however—and it would be desirable to have simpler approximate expressions. Previous analyses of simulated height fluctuation spectra have involved functions that display the same small q and large q behavior as in Eq. 26, such as (13–15)

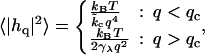(30)

where q_c is typically on the order of the membrane thickness, or (12)

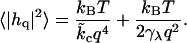(31)

The limiting forms suggested above are easily predicted from Eq. 26 in the two extreme regimes of q → ∞ and q → 0. Given actual lipid systems, however, these expressions do not faithfully reproduce the results of full calculations. In Appendix A, we compare Eqs. 31 and 26 for several parameter sets, and demonstrate that Eq. 31 is not a dependable approximation for wavelengths on the order of the membrane thickness.

We suggest alternate approximate forms for the spectra based on the assumption of decoupling between protrusion and bending modes. When all terms containing 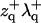and 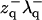are set to zero in Eq. 24, the spectra become

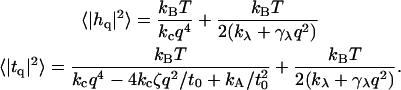(32)

The suitability of these expressions for describing numerous bilayer systems is demonstrated in Comparison to Simulation Data, below, and their numeric equivalence to the expressions in Eq. 26 for a range of constants is demonstrated in Appendix A. We note that these expressions could have been written down immediately by realizing that h and t both represent the sum of protrusion and bending fields (Eqs. 5 and 6). If these fields are independent of one another (i.e., no coupling), the variance of these sums is the sum of the variances associated with protrusion fluctuations and bending fluctuations. The two terms in both of the expressions in Eq. 32 reflect individual contributions from bending and protrusions. The most novel of all these terms is the bending contribution of the thickness spectra. To our knowledge, the incorporation of spontaneous curvature effects has not been pursued previously. Although the approximations in Eq. 32 do an excellent job for the lipid systems considered in this work, it is possible that other bilayers will exhibit stronger coupling between protrusion and bending modes. In such a case, it would be necessary to employ the full-forms (Eq. 26). In this work we use the expressions in Eq. 32 to fit simulation spectra and always find (see caption of Table 1) that the measure of coupling strength discussed above, 2γ_λ²/(k_λk_c), is 0.3 or smaller. This provides us with a consistency check on the use of this approximation.

TABLE 1.

Material properties of DPPC (13), GMO (14), SM (15), and CG bilayers, as measured by various methods

System	Method			kc(10−20 J)
DPPC	Present	14 (8.9−21)	1.5 (1.0−1.9)	4.3 (3.4−5.8)	1.1 (0.83−1.3)	0.18 (0.13−0.20)
	Original (13)		2.5	4	0.4†/8.2*
GMO	Present	2.9 (2.1−3.7)	1.3 (1.0−1.6)	3.8 (3.4−4.6)	41 (25−72)	0.73 (0.12−1.4)
	Original (14)		0.85	4	6†/27*
SM	Present	4.5 (2.9−8.3)	2.1 (1.7−2.5)	41 (25−110)	53 (17−170)	0.53 (0.23−0.63)
	Original (15)		4.0	41	6.5†/83*
CG	Spectra	6.3 (4.9−7.7)	1.3 (1.0−1.4)	14 (11−18)	12 (9.4−15)	0.085 (0−0.16)
	Area fluct.				3.1
	Stress profile						0.017
	Inclusion:No tilt				10.4 (3.3−16)	0.21 (0.10−0.25)	0.020 (0.0067−0.025)
	Inclusion:Tilt				8.2 (4.7−17)	0.23 (0.16−0.37)	0.020 (0.010−0.058)

Present or Spectra means that the undulation and peristaltic spectra were fit to the expressions in Eq. 32. Numbers in parentheses are the 95% confidence intervals. Original refers to the values reported in previously published work. Except where otherwise noted, these values were extracted from the fluctuation spectra. All data for the CG model is newly presented in this article, and so there is no Present/Original designation for that data. To calculate 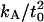from the area fluctuations, we used the following values of t₀: DPPC (13), 1.8 nm; GMO (14), 1.5 nm; SM (15), 2.5 nm; and CG, 2.4 nm. The coupling parameter 2γ²/k_λk_c is, for DPPC, 0.08; for GMO, 0.3; for SM, 0.06; and for CG, 0.04.

^*k_A derived from area fluctuations.

^†k_A derived from thickness fluctuations as interpreted in the original study.

Although the expressions in Eq. 32 appear similar to previously published expressions, we emphasize several key differences:

• They are continuous, rather than piecewise, expressions. This eases data fitting considerably, by avoiding a priori designation of individual data points to specific regimes. Although continuous expressions have been put forward (12) for the case of height fluctuations, no corresponding expressions have previously been discussed in the context of peristaltic fluctuations.

• The protrusion regimes of both spectra contain the constant term k_λ. In the limiting case of q → ∞ this constant is negligible, but, as shown in Appendix A, most large q-data for actual systems does not correspond to this limit.

• The monolayer spontaneous curvature contributes an effective negative surface tension to the thickness fluctuations (we find ζ > 0 for all simulated data sets). This term, which was neglected in previous analyses, can result in a nonmonotonic thickness fluctuation spectrum.

• Due to our assumption of volume conservation, the compressibility modulus k_A appears in the thickness fluctuations (as opposed to a separate leaflet binding constant k_e (13–15)). In Comparison to Simulation Data, we discuss the validity of calling this constant k_A.

• We predict the height and thickness spectra to be characterized by the same bending rigidity. Furthermore, this bending rigidity corresponds to twice the bending rigidity of each leaflet. In analyzing their simulations, the authors of Lindahl and Edholm (13), Marink and Mark (14), and Chiu et al. (15) allowed thickness and undulation bending rigidities to differ from one another.

• The protrusion regimes of both the height and thickness fluctuations are identical. Although both Lindahl and Edholm (13) and Marrink and Mark (14) noted such equivalence in their data, they did not mandate it in their fitting procedure. In fact, according to the expressions in Eq. 32, the height spectrum should, in principle, contain no information beyond that already contained in the corresponding thickness spectrum. In practice, it is easier to extract k_c from the height spectrum than the thickness spectrum, so it is worthwhile to analyze both data sets simultaneously.

In summary, we have presented a theory with the same overall number of fit constants (five) as that presented in Lindahl and Edholm (13), but which includes the protrusion restoring force, the monolayer spontaneous curvature, and the area dependence of this spontaneous curvature.

COMPARISON TO SIMULATION DATA

Four sets of simulation data collected at vanishing tension were analyzed using the analytical model just described. The three data sets taken from atomic simulations (DPPC(13), GMO(14), and SM(15)) have appeared elsewhere. The coarse-grained data was taken using a model presented in Brannigan et al. (16) and readers are referred there for a full description of the model. The model parameters remain unchanged from that study, with the exception of the temperature. The simulations discussed in this article were all run at k_BT = 0.85ε, while simulations in Brannigan et al. (16) were run at k_BT = 0.9ε, where ε represents the energy scale ε = 2.75 kJ/mol. Systems at the lower temperature equilibrate more quickly. They also have a much lower monomer fraction (fraction of molecules that are not in the membrane), which simplifies analysis. Studies of phase behavior (not presented here) put the melting temperature of the five bead bilayer at ∼k_BT = 0.7ε, so we are still well within the fluid region. Also, although Brannigan et al. (16) discussed a range of values for the molecular bending rigidity c_bend, all simulations in this article use c_bend = 7ε.

The height and thickness fluctuation spectra for DPPC, GMO, and SM are reproduced in Fig. 4, along with the corresponding data from our coarse-grained (CG) model. In the case of the atomistic studies, data presented in these figures necessarily reflect the conventions used in the original simulations. For DPPC, the position of the water-hydrophobic tail interfaces (z⁽¹⁾ + λ⁽¹⁾ and z⁽²⁾ + λ⁽²⁾ in our notation) were defined by the position of the carbon connecting the tails to the headgroup (13). A similar definition was used for SM (specifically, the location of the C13 atom (15)). In GMO, the interfaces were defined by the surfaces separating water from hydrophobic components of the bilayer core, irrespective of which carbon atom(s) along the chain happened to lie nearest the water (personal communication, S.-J. Marrink, 2005). In the CG model the interface was defined by the position of the second bead along the chain (the so-called interface bead (16)). In DPPC, GMO, and CG, the thickness is defined as one-half the distance between corresponding interface groups in opposing leaflets, whereas in SM the monolayer thickness was measured directly (the distance between leaflets and correlations between leaflets were neglected). It is worth emphasizing at this point that only the data collected for the CG model, GMO, and DPPC correspond well to the analytical model we have presented; SM data is somewhat different, due to the individualized treatment of monolayers.

For each system, we have two data sets (height and thickness spectra). We fit these data sets simultaneously to the expressions in Eq. 32 using the five elastic constants (k_c, k_A, ζ, k_λ, and γ_λ) as fit parameters. Our fitting algorithm is described in Appendix B and our fitting script is available on the Internet (38). Best-fit elastic constants are displayed in Table 1, along with the 95% confidence intervals for each fit parameter. The method for obtaining these confidence intervals is also described in Appendix B.

All four data sets are well described by the analytical model (expressions in Eq. 32), and, as demonstrated in Appendix A, the resulting numbers are consistent with the approximation that protrusion and bending modes are uncoupled. Furthermore, when we fit these data sets to the full form for the spectra (expressions in Eq. 26), we obtain curves that are essentially identical to those resulting from the approximate fits, and the fit parameters all agree within confidence intervals. As also shown in Appendix A, the effective negative tension induced by finite positive ζ can play a significant role in determining these spectra. In fact, this negative tension provides a possible explanation for the nonmonotonic behavior (previously (13) attributed to poor sampling) seen in two of the atomistic spectra.

The bending rigidities for undulations remain essentially unchanged from the original analyses, but we report different values for the remaining constants. Reported values for the interfacial tension γ_λ originally ranged from 8.5 mN/m² for GMO (14) to 40 mN/m² for SM (15). Since this number is expected to primarily represent the tension associated with the oil-water interface (with some renormalization due to lipid shape (11)), such variation is surprising. Upon reanalysis, we report γ_λ ranging from 13 mN/m for GMO to 23 mN/m for SM, which is a more reasonable range. Upon correcting for molecular shape as advocated by Lipowsky and Grotehans (11), we obtain a range of 11–18 mN/m. Theoretical predictions suggest that γ_λ should fall between 20 and 50 mN/m (39).

The compressibility modulus k_A is usually measured by area dependence of the surface tension (12) or fluctuations in the area per molecule (40). The latter method was used to measure k_A in the three studies already published (DPPC, GMO, SM) and, consequently, we have also used it to measure k_A in the coarse-grained model. Table 1 compares k_A as measured by the area fluctuations, to k_A as measured by the thickness spectrum, for all four systems studied. There is clear order-of-magnitude correspondence, and the discrepancies do not appear systematic: for DPPC and SM the area fluctuations suggest a greater k_A, whereas for GMO and CG, the thickness spectrum suggest a greater k_A. (We assume it is a coincidence that DPPC and SM are the double-chained lipids, although GMO and CG are single-chained.) Aside from finite size-effects and noted problems in converging k_A (40), other possible sources of the discrepancy are that:

1. The volume per lipid is not strictly conserved in real systems. In this case, our analytical model is still valid, but it is not appropriate to identify the constant we have been referring to as k_A with the true area compressibility modulus.

2. Our assumption that protrusions do not enter into the volume conservation condition may be incorrect. If the membrane can pull volume from λ as well as z, one expects our measurement of k_A via the thickness fluctuations to be too high. Protrusions allow for another degree of freedom to facilitate lipid compressibility. Since we do not see a systematic trend of thickness determined k_A being too large, this possibility cannot account for all observed discrepancies.

3. Definition of the bilayer thickness is subject to a certain amount of ambiguity as evidenced by the various procedures employed in calculating this field by the original workers. For instance, in GMO, the thickness spectrum reflects a more general definition of the interfacial surface than was introduced in the other simulations. Although the interfaces defined for GMO probably correspond more precisely with the true interfacial surfaces than the other simulations, this definition actually contrasts somewhat with our theoretical treatment of area/lipid, conservation of hydrophobic volume, and related issues. It is possible that the procedure used for collection of GMO data tends to underemphasize thickness fluctuations, relative to the other studies. Such an effect would lead to an anomalously high value for k_A. Similarly, in the SM data, each leaflet has been Fourier-transformed and squared separately; consequently, this data neglects correlations between the leaflets. If thickness fluctuations are anticorrelated across the two leaflets, then this data would result in a measurement for k_A that is too low. (These variations in collection methods of the original MD data could also potentially affect the values obtained for other elastic constants. Since k_A is the constant most directly responsible for thickness deformations, it is reasonable that we see the largest discrepancies here.)

As previously stated, we cannot directly extract c₀ or c₀′ from the thickness fluctuations; we can only measure ζ, which depends on both. Since fluctuation analysis does provide the value of monolayer bending rigidity, k_c/2, we may infer c₀ from analysis of the stress profile (1),

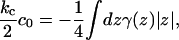(33)

where γ(z) is the surface tension density at height z and the integration is over the whole bilayer, centered at z = 0. The stress profile (Fig. 3) was measured for the CG model, as documented elsewhere (16,41,42). To avoid the smoothing effect of undulations (16), we measured the stress profile in a small system (128 molecules). Using this method (and k_c obtained from the spectra), we estimate c₀ = 0.041 nm⁻¹. Using the fluctuation spectra values ζ/t₀ = 0.1 nm⁻², t₀ = 2.4 nm, and Σ₀ = 0.59 nm², we can further estimate c₀′ = −0.34 nm⁻³. This information will be useful in comparing to the information obtained from the protein-induced deformation data of the following section.

PROTEIN-INDUCED DEFORMATION PROFILES

Theory

Consider the bilayer model discussed in Fluctuation Spectra of Homogeneous Membranes, above, but with a rigid cylindrical inclusion of radius R and thickness 2D embedded in its center. More precisely, 2D represents the thickness adopted by the membrane right at the edge of the protein. This value is presumably set by the presence of hydrophobic and interface favoring residues around the protein's exposed surface. We seek to predict the deformation profile 〈t(r)〉, where r is the distance to the inclusion center (Fig. 5). Since height and thickness deformations are uncoupled, we need only consider the second and third lines of Eq. 21:

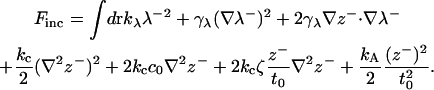(34)

Instead of integrating over the whole sheet, as in the previous section, our domain of integration is a square of side length L with a circle of radius R cut out of the center to accommodate the protein. Assuming that the inclusion cannot tilt, the membrane surface is subject to the boundary condition at r = R of

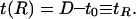(35)

It should be recalled that t₀ is the equilibrium monolayer thickness, whereas t is defined as the deviation in monolayer thickness away from this value.

We imagine λ^(1,2) to represent microscopic noise or roughness at the lipid interface. With this interpretation, it is reasonable to assume that our thickness condition above translates to λ⁻(R) = 0 and z⁻(R) = D − t₀, in terms of our field variables. Because protrusion and bending deformations are coupled, this condition is not equivalent to setting λ⁻(r) = 0 for all r, even for purposes of computing the thermally averaged deformation. As described below, however, the inclusion deformation profile for our CG bilayer is consistent with either constraint λ⁻(R) = 0 or λ⁻(r) = 0 everywhere since protrusions and bending modes are very weakly coupled in this system. If λ(r) is set to 0 for all r, Eq. 34 is equivalent to the free energy minimized analytically by Aranda-Espinoza et al. (31) to predict the zero temperature membrane deformation profile for a two-dimensional array of inclusions.

We solve for the average deformation profile predicted by Eq. 34 using Metropolis Monte Carlo simulation on a discretized periodic square lattice. Each lattice site has an associated value of z⁻ and λ⁻. A trial move consists of randomly choosing a lattice site, which field to perturb, and the perturbation size. The lattice has either 40 × 40 sites with a spacing of 0.75 nm (CG parameters) or 60 × 60 sites with a spacing of 0.25 nm (GMO parameters). These choices for the number of sites and spacing were verified to be sufficiently large and small, respectively, that further refinement and system expansion did not alter our results. Lattice sites within a radius R from the lattice center were discarded, since the membrane does not exist inside the inclusion radius. The only conditions directly imposed during the Monte Carlo were periodic boundary conditions and λ⁻ = 0 and z⁻ = t_R at the inclusion-lipid boundary. This means that membrane slope and curvature at the inclusion/lipid boundary are unrestricted and protrusions are allowed to occur everywhere except at the sites immediately adjacent to the inclusion.

We ran the lattice simulation for two sets of elastic parameters: those resulting from the CG simulations and those resulting from the GMO simulations (Table 1). These correspond to a system in which λ⁻ and z⁻ are very weakly coupled and a system in which λ⁻ and z⁻ are more strongly coupled, respectively. For the spontaneous curvature, which cannot be obtained from the fluctuation spectrum, we either used a value obtained from the stress profile (CG) or assumed that c₀ = 0 (GMO). In both cases we set R = 2.25 nm and t_R/t₀ = 0.094, which coincide with the radius and the height, respectively, of the nontilting inclusion used to induce a deformation in the CG membrane (described in Molecular Simulation, below).

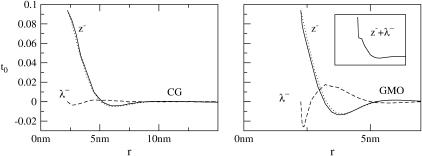
The numerical results for CG are shown in Fig. 6 A. Although λ⁻ does not vanish for all r, neither does it ever constitute an appreciable amount of the deformation. Both z⁻(r) and t(r) = z⁻(r) + λ⁻(r) very nearly obey the analytical expression derived in Aranda-Espinoza et al. (31). Analytical treatments based on Hamiltonians similar to Eq. 34 do not directly solve for the thermally averaged deformation profile (22,29–31,43–46). Instead, the minimum energy configuration is determined by taking the functional derivative of F_inc (in our example), with respect to z⁻(r), assuming λ⁻ = 0 everywhere and cylindrical symmetry of the solution around the inclusion (31). The resulting expressions for the minimum energy deformation profile are fourth-order differential equations, the order insured by the bending (k_c) terms in the Hamiltonian. In our Monte Carlo treatment, only two boundary conditions are necessary to run the simulation as discussed above and one of these relates to the protrusion modes that are neglected in analytical treatments. For the purposes of minimization, however, we need a total of four boundary conditions to solve the differential equation. In practice, two of these boundary conditions typically relate to the deformation profile at points distant from the inclusion (to keep the solutions bounded at infinity (22), or to enforce symmetry constraints within periodic boundary conditions (31)) with two boundary conditions to be specified at the edge of the inclusion. One obvious boundary condition simply sets t(R) = D as we have introduced above.

FIGURE 6.

Average deformation profiles of the fields z⁻ (solid) and λ⁻ (dashed) around a cylindrical inclusion, using Hamiltonian Eq. 34 and elastic parameters derived from CG (left) or GMO (right), and calculated by Monte Carlo on a square lattice. The dotted line is the minimum energy profile calculated analytically, employing natural boundary conditions (λ neglected) (31). In both cases the deformation in z⁻ is well described by the analytical solution. For CG, λ⁻ makes a negligible contribution to the overall thickness t = λ⁻ + z⁻, so we expect that the overall thickness deformation is also well described by the analytical solution. In GMO, λ⁻ exhibits a deformation of a more sizeable amplitude; because λ⁻ and z⁻ are anticorrelated, the overall thickness t (see inset) is detectably more smooth than z⁻ alone.

The specific form assumed for the remaining boundary condition has become a subject of some debate. Three main approaches have been taken: fixed slope boundary condition (22,27,47), relaxed slope boundary condition (23,27,45), and the so-called natural boundary condition (29–31). Those proponents of the fixed-slope boundary condition argue that the slope of the membrane at the inclusion boundary is a property of the inclusion/lipid system that cannot be determined by elastic models, but instead must be extracted from experiments. The relaxed slope boundary condition, on the other hand, requires that the membrane slope assume that value which minimizes the elastic free energy. The natural boundary condition argues on mathematical grounds that it is the membrane curvature, rather than the slope, which should be used for the fourth boundary condition. This condition falls out as a necessary condition when one carries out the functional derivative in the absence of additional constraints. Since our Monte Carlo simulation does not fix any membrane derivatives at the inclusion/membrane boundary, it is tempting to assume that natural boundary conditions are the most appropriate to employ in a minimization scheme aiming to reproduce the MC results. Fig. 6 A would tend to support this conclusion. However, we stress that thermal averages and free energy minima do not necessarily correspond with one another. Thermal fluctuations are not playing a significant role for the particular elastic constants (and temperature) seen in our CG model and the minimum energy profile does a very good job of reproducing the Monte Carlo. The more important question of whether our MC scheme (and treatment of the protein/bilayer boundary) applies to reality is addressed in the following section. We will see that treating the boundary without any additional constraints does a very good job of reproducing our CG simulations.

The success of the theory of Aranda-Espinoza et al. (31) in describing the CG lattice simulation depends upon the weak coupling between λ⁻ and z⁻. We now turn to a system for which this coupling is not weak: GMO. In GMO, the coupling constant 2γ_λ²/k_ck_λ = 0.3, although less than unity, is not tiny. The deformation profiles calculated using the GMO elastic parameters are shown in Fig. 6 B. Unlike the CG case, λ⁻ does contribute a detectable amount to the overall deformation, smoothing out the oscillations in the observable t = z⁻ + λ⁻. Although the analytical solution describes z⁻ decently, it fails to quantitatively describe λ⁻ + z⁻ (Fig. 6 B, inset). Mathematically, this failure is due to the coupling between λ⁻ and z⁻, which is negligible in the CG case. Physically, the coupling between λ⁻ and z⁻ causes protrusions to partially compensate for the bending deformation induced by the inclusion. In summary, when dealing with a molecular simulation of an inclusion in GMO, we do not expect the thickness deformation profile to closely follow the theory of Aranda-Espinoza et al. (31). However, we do expect a close correspondence between the thickness deformation profile and the analytical theory in a molecular simulation of our CG molecules. Simulation results for the CG model are presented in the following section. Inclusion simulations employing GMO are presently unavailable.

MOLECULAR SIMULATION

Our simulation model for inclusions is similar in spirit to recent studies by Nielsen et al. (37) and Venturoli et al. (36). We model the bilayer with our CG model, and inclusions are represented by an assembly of rigidified CG lipids; if the bilayer lipids were similarly inflexible, there would be no hydrophobic mismatch (Fig. 7). However, because the lipids are flexible and the inclusion is rigid, there is a mismatch between the average equilibrium thickness of the homogeneous bilayer and the rigid inclusion. The same interaction potentials are used for all the beads, regardless of whether they are in lipid or inclusion molecules. Four concentric rings comprise the inclusion, and all interbead distances within the inclusion are held fixed (translation and rotation of the inclusion are discussed below).

FIGURE 7.

(Left) A single lipid from the coarse-grained model presented in Brannigan et al. (16). Head beads are black, interface beads are gray, and tail beads are white. (Center) Eighty lipid molecules (400 beads) in four concentric rings form a rigid cylindrical inclusion. Although the molecules used in the lipids and the inclusions have the same number of beads, there is still a mismatch in preferred thickness because the lipids are flexible. (Right) Cross-section of the inclusion in the center of the membrane.

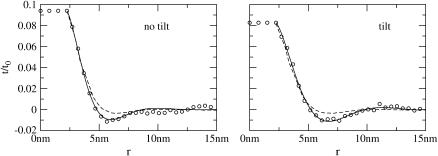
For the inclusion studies, four copies of an equilibrated bilayer with N = 836, as used in thermal fluctuations, were used to form a larger square bilayer, which was then equilibrated. Some lipids were then removed to make room for the inclusion, for a final total of 3214 lipid molecules and one inclusion (incorporating 80 lipids). Two different simulations were run. In one simulation, the inclusion was not allowed to tilt its major axis away from the z direction (translation of the protein was allowed), which directly corresponds to the case considered in our elastic theory. In the other simulation, the inclusion was allowed to translate and tilt (average root-mean-squared tilt angle of 7° over the course of the MC). Both simulations were run at the same temperature employed in the fluctuation simulations of the previous section. In the tilt-enabled simulation, the average thickness at the protein edge was measured to be (t_R/t₀ = 0.082) compared to (t_R/t₀ = 0.094) with tilt disabled.

The resulting deformation profiles are shown in Fig. 8, for both the tilting and nontilting inclusions. The deformation profiles are clearly nonmonotonic. This is consistent with continuum pictures in which large curvatures are unfavorable (22–31), and similar results were observed in recent solvated coarse-grained simulations by Venturoli et al. (36) and Nielsen et al. (37). Quantitative agreement with the theory proposed in Protein-Induced Deformation Profiles, Theory, above, using the best-fit parameters measured from the homogeneous membrane, is fair; although the theory captures the initial decay, the simulated well is deeper than theory predicts. To assess the source of this discrepancy we extracted the relevant physical parameters (k_A, ζ, and c₀) by fitting the simulated profiles directly to the analytical theory of Aranda-Espinoza et al. (31). The resulting fits are very good for both the tilting and nontilting cases, and the fit parameters are also shown in Table 1. Upon comparing the values extracted from the spectrum/stress profile and from the inclusions, we observe excellent agreement for k_A and c₀, and the measurements for ζ agree within the 95% confidence intervals. The fits from the deformation profile and the spectra show varying degrees of sensitivity to the parameters. For instance, the curve for the peristaltic spectra is not particularly sensitive to the value of ζ: using the value resulting from the deformation profile, rather than the spectrum best-fit value, leads to a very small change in the residuals. However, the deformation profile is particularly sensitive to the value of ζ, and using the value resulting from the spectrum, rather than the profile best-fit value, leads to a detectably worse fit. All three parameters extracted from the inclusion deformation profile are less for the tilting inclusion than the nontilting inclusion, but the two profiles are qualitatively similar. For the purpose of comparison with the theory presented in this article, the nontilting case is most relevant. In reality, however, proteins are free to tilt within the bilayer. Our results suggest that such tilting can be incorporated through a renormalization of the deformation parameters.

FIGURE 8.

(Circles) Thickness deformation profile for membrane with 3214 CG lipids and an embedded inclusion centered at r = 0. (Dashed lines) Prediction of Lattice Monte Carlo with parameters derived from homogeneous membrane thermal spectra data (Table 1, rows 7 and 9). (Solid lines) Prediction of lattice Monte Carlo using parameters obtained by fitting to the analytical solution outlined in Aranda-Espinoza et al. (31), with fit parameters in Table 1 (rows 10 and 11). Note that the parameters used for the solid-line calculations, although different from the best-fit values extracted from thermal spectra, all fall within the 95% confidence intervals associated with the best-fit values. Deformation profiles are extremely sensitive to the value of ζ, which accounts for most of the discrepancy between dashed and solid lines. (The best-fit analytical solutions are indistinguishable from the solid lines.)

Prediction of gramicidin A channel lifetimes

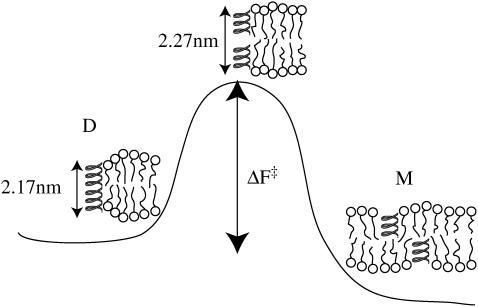
When embedded in a lipid bilayer, the dimeric gramicidin ion channel exists in equilibrium with its monomeric components (48). It is expected that the dimer configuration (state D) has thickness 2.17 nm (44), and must stretch by ∼0.1 nm (22) at the transition state before breaking into two monomers (state M, see Fig. 9). The equilibrium thickness of the surrounding bilayer cannot match that of both the stretched and unstretched dimer configurations (usually it matches neither), and therefore hydrophobic mismatch is expected to play a role in determining the dissociation rate constant k_d. This hypothesis is supported by the clear dependence (44,48,49) of gramicidin channel lifetime on the thickness of the surrounding bilayer.

FIGURE 9.

Dissociation of the gramicidin-A ion-conducting channel requires stretching the two components to break the connecting hydrogen bonds. The stretched configuration is expected to be the transition state in the dissociation process. Adapted from Goulian et al. (47).

Numerous analytical theories (22,43–46) on inclusion-induced membrane deformations have been tested against gramicidin-A channel lifetime data (44,49). This data has been used to support various claims regarding the slope of the membrane at the inclusion,(22,27,46,50) and the importance of spontaneous curvature (32,46) or surface tension (22,23,45) in the analysis. Reviewing the multiple approaches to fitting or predicting experimental gramicidin data is beyond the scope of this article. However, we do note that the theory of Aranda-Espinoza et al. (31) has not previously been compared against gramicidin lifetime data. In this section we compare both the Aranda-Espinoza et al. (31) theory and our own MC predictions against the gramicidin lifetime data, and find them to be both quite successful.

We take advantage of the fact that the lifetimes were measured for gramicidin in various monoglyceride bilayers, including GMO, as analyzed in Fluctuation Spectra of Homogeneous Membranes, above. The previously discussed simulation data on GMO provides us with estimates for elastic parameters, including those related to the spontaneous curvature, that have not been measured by experiment. As discussed in the previous section, however, the coupling between the macroscopic and microscopic fields in GMO suggests that our theory (solved by the lattice simulation) and the theory of Aranda-Espinoza et al. (31) should give at least slightly different results.

To begin, we calculate the free energy of a bilayer surrounding an unstretched gramicidin channel in the dimer configuration by using Eq. 34 and setting

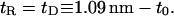(36)

For the stretched configuration, we do the same, but set

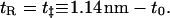(37)

The stretched configuration represents the transition state for dimer dissociation, and so the dissociation rate is expected to obey (Arrhenius equation (51))

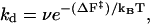(38)

where ν is the frequency factor and ΔF^‡ is the difference in free energy between the stretched and unstretched states. Separating out the bilayer contribution to ΔF^‡, we have

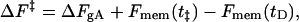(39)

where ΔF_gA is the free energy to stretch the channel associated with protein-specific changes (i.e., the free energy required to break hydrogen bonds, etc.), F_mem(t_‡) is the elastic energy of the membrane when the channel is stretched, and F_mem(t_D) is the corresponding energy of the membrane when the channel is unstretched. Since we expect that neither ν nor ΔF_gA depend on t₀, we relate the dissociation constants for two bilayers of thickness 2t₀ and 2t′₀ by

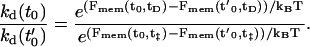(40)

Therefore, we can designate a reference rate constant k_d0 = k_d (t₀ = 1.09 nm), use the lattice simulation (or an analytical model) to calculate k_d(t₀)/k_d0 for a number of values of t₀, and compare with experimental data.

Up to this point, our analysis has mirrored that of Huang (22) and others (43–46). The difference in our approach lies in the calculation of F_mem, primarily in the inclusion of c₀ and c₀′ and the use of natural boundary conditions, as already discussed. We also use elastic parameters derived from the GMO simulations previously introduced, which contrasts with prior studies. The experiments (44,49) were conducted on various monoglyceride bilayers in aqueous solution including various organic co-solvents (squalene, decane, hexadecane, etc.). Ideally, a full set of elastic constants would be available for each bilayer-solvent system, making application of Eq. 40 an entirely straightforward exercise. Unfortunately, such data is unavailable. As indicated in Protein-Induced Deformation Profiles, above, bilayer elastic parameters could potentially be obtained by simulation of the full set of experimentally tested monoglycerides; unfortunately simulation data is presently available only for GMO (14) in pure water. Our extraction of most of the necessary parameters from GMO simulation data is detailed in Fluctuation Spectra of Homogeneous Membranes, above, and we apply these constants to all the studied bilayers. Using this simulation data for the elastic parameters is clearly not ideal: the simulations were conducted in pure water and only investigated one species of monoglyceride. The bending rigidity (and most likely other elastic constants) should certainly depend on the membrane thickness (see, for instance, (52)) but the present approach uses the same elastic constants for a range of bilayer thicknesses. Furthermore, we cannot extract from the available GMO data the spontaneous curvature of the monolayer, a necessary component in Eq. 34. For simplicity we simply set c₀ = 0 in the absence of any information to the contrary. Luckily, our predictions are most sensitive to the compressibility modulus k_A, and k_A is probably not particularly sensitive to chain length (52).

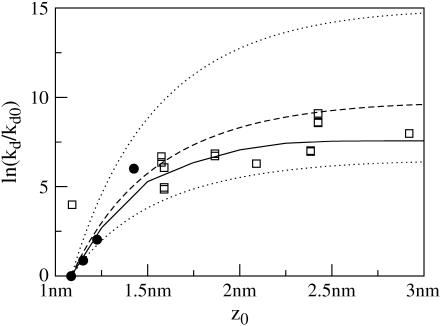
The predictions (Fig. 10) for our own theory were generated by calculating the average deformation profile using the procedure described in the previous section, and then calculating the corresponding value of F_mem = F_inc using Eq. 34. In these calculations, the lattice was 60 × 60 with a spacing of 0.25 nm, and R = 1 nm to correspond with the gramicidin channel radius. We used the constants measured from the atomic simulation of GMO and assumed c₀ = 0. As shown in Fig. 10, this method yields a successful prediction of the general trend of the data. We do not expect these predictions to be perfect for the reasons outlined above; however, it is satisfying to see that our model does reproduce the experimental trends and that it does so without incorporation of any fit parameters.

FIGURE 10.

Dependence of gramicidin-A dissociation rate on thickness of surrounding bilayer. Solid circles represent data on various monoglycerides in water with squalene, presented in Elliott et al. (44), and previously analyzed by Huang (22). Open squares correspond to the data presented in Kolb and Bamberg (49) on various monoglycerides in water and decane, hexadecane, or no additional hydrocarbon. The solid line is the MC prediction based on the full Hamiltonian (Eq. 34) and the dashed line is the prediction using the analytical theory of Aranda-Espinoza et al. (31). Both calculations used the following parameters: k_c = 3.8 × 10⁻²⁰ J, k_A = 92 × 10⁻²⁰ J nm⁻², ζ = 1.1 nm⁻¹, c₀ = 0, k_BT = 4.1 × 10⁻²¹ J, and R = 1.0 nm. Dotted lines are also predictions from the theory of Aranda-Espinoza et al. (31), but with k_A = 56 × 10⁻²⁰ J/nm² and k_A = 160 × 10⁻²⁰J/nm² for the lower and upper lines, respectively. (These k_A values are the lower and upper 95% confidence interval on k_A.) We emphasize that the lines are predictions using only the physical constants extracted from thermal spectra data collected for GMO. There is no fitting involved in this plot.

Analytically, the predictions (Fig. 10) can also be estimated by minimizing Eq. 34 (neglecting the protrusion terms, so this corresponds to the analysis of Aranda-Espinoza et al. (31)). For comparison, we have shown three curves generated analytically; each uses a different value of k_A. The dashed line in Fig. 10 uses the value for k_A measured from the thermal fluctuation spectrum, whereas the upper dotted line corresponds to the upper 95% confidence interval on k_A and the lower dotted line corresponds to the lower 95% confidence interval on k_A. Nearly all the data points fall within the prediction range delineated by the confidence intervals. So although the numerical solution to our theory does a slightly better job of predicting the data, the relative success is highly sensitive to k_A.

To our knowledge, no other single theory has been tested against all the experimental data shown in Fig. 10. Although we believe our favorable results in the absence of fitting constants calls into question the conclusiveness of other studies, we emphasize that other elastic models have successfully fit gramicidin lifetime data. Indeed, these previous studies motivated us to consider such data in the context of our own model. For instance, an alternate theory (22) uses the slope at the inclusion-membrane boundary as a fit parameter, and finds the slope to be near to vanishing. We predict the same data using natural boundary conditions. The deformation profiles resulting from our analysis suggests the slope at protein contact is relatively steep and depends on the size of the mismatch. Since both theories can be used to describe the data, more (and different) experimental data is clearly needed. Ideally, one would be able to measure the slope at the inclusion/bilayer boundary, and then easily distinguish between various theories. Although this is not currently possible using experiment, it is possible using simulations, and we have described such a test earlier in this article (see Protein-Induced Deformation Profiles). This test, while admittedly not on a GMO/gramicidin bilayer, supports the use of natural boundary conditions even when the inclusion is perfectly cylindrical. We feel this is an important point, since some statements in the literature (32) suggest that a cylindrical inclusion necessarily dictates vanishing slope at the protein/bilayer interface and consequently that monolayer spontaneous curvature is unimportant in predicting deformation profiles around a cylinder. Our simulation results contradict this. The simulations are well described by an elastic theory that includes spontaneous curvature with natural boundary conditions used at the protein/lipid interface; the resulting slope at the interface is nonzero.

DISCUSSION

The study of homogeneous lipid bilayers is motivated partly by the hope that these model systems can provide insights into real biomembranes. Although such correspondences are often vaguely discussed or tacitly assumed, only rarely are homogeneous bilayer properties carefully compared with related inhomogeneous counterparts. Although theoretical work is available spanning both homogeneous and inhomogeneous systems, the relation between physical constants, models, and approximations across different systems is often hard to justify and difficult to verify via experiment or direct simulation. In this article, we have verified that, at least for coarse-grained models, the elastic constants inferred by fluctuation analysis on homogeneous bilayers are the same constants that dictate the response of a bilayer to an inserted protein inclusion. The general elastic model explaining both of these phenomena draws from a number of existing theories, but represents the first successful synthesis to capture both homogeneous and inhomogeneous behavior consistently. The fact that the same theoretical model is able to explain fluctuation data for fully atomic bilayer systems in addition to our CG model raises the hope that this is a fully consistent elastic picture that could be applied to fully atomic systems once such data becomes available.

We stress that the correspondence between both types of behavior as discussed above is not obvious. It has been argued (50) that the bilayer's response to an inserted protein is heavily influenced by specific microscopic details of the bilayer-inclusion boundary, making it impossible to predict deformation profiles solely on the basis of lipid behavior in homogeneous environments. It has also been suggested (27,50) that even if elastic models are able to predict both thermal fluctuations and deformation response that the elastic constants involved might vary from situation to situation. For example, it has been suggested that the membrane's response to an inclusion, which typically ranges <5–10 nm, is determined by microscopic elastic constants. These microscopic elastic constants are presumed to be distinct from the traditional elastic constants used in Helfrich theory (and typically inferred in experiment by fluctuation analysis). This work indicates that both behaviors can be consistently described by one model employing identical elastic parameters and provides an important step toward the ultimate justification of elastic approaches in membrane biophysics across a range of length scales. (It is worth noting that, because simulated membranes are small compared to experimentally accessible length scales, elastic constants measured by simulation should correspond to bare values requiring renormalization (53,54) for direct comparison with experiment. This type of indirect correspondence between theory and experiment is straightforward to correct for and fundamentally different from the microscopic versus traditional debate discussed above.)

Our mathematical incorporation of protrusions is most consistent with a picture where protrusion modes are simply a manifestation of nonspecific microscopic fluctuations not accounted for in traditional bending pictures. We do not take the view that protrusions represent a specific type of membrane deformation, distinct from the nature of bending deformations. We view protrusions as an unavoidable consequence of noise present at the atomic level. Incorporation of protrusions as harmonically constrained fluctuations at the lipid/water interface amounts to smearing the bending results with a Gaussian profile. This picture seems to work well in describing both short wavelength thermal spectra and inclusion-induced deformations.

The presence of microscopic protrusions may affect measurements of the area compressibility modulus, k_A, as indicated by the discrepancy between k_A measured via the thickness fluctuation spectrum and k_A measured via area fluctuations. When measured via the thickness fluctuation spectrum, k_A represents a restoring force for deformations due entirely to bending, but when measured via area fluctuations, k_A restores any deformation that results in an area change. In the CG model, for instance, on average a given thickness deformation is due approximately half to monolayer bending and half to microscopic protrusions. If the membrane area were to strictly conserve volume, including contributions from protrusion-based roughness, then the measurement of k_A via area fluctuations will be lower than that via the thickness spectrum. However, the bare k_A (measured by the thickness fluctuation spectrum) seems to be the one that determines the membrane response to an inclusion. Our use of the name k_A in describing the harmonic potential energy associated with bending-induced thickness fluctuations should not be taken overly seriously. There are obvious discrepancies in the CG data between spectra and area-fluctuation values; however, k_A is such a difficult quantity to predict quantitatively in fully atomic MD that we believe our values are probably as reliable as the area fluctuation data available from the fully atomic studies considered in this work. For this reason, to keep our set of physical variables to a minimum and to conform with previous analysis (31), we have retained this somewhat misleading notation.

Overall, our results underscore the importance of the thickness fluctuations as a source of information about the elastic constants of a particular membrane. For instance, since the membrane bending rigidity manifests itself in thickness fluctuations as well as the height fluctuations, ignoring the thickness fluctuations means ignoring valuable data on the value of that constant. We were also able to extract the renormalized spontaneous curvature ζ from the thickness fluctuations, which proved essential to quantitatively understanding the membrane's response to an inclusion. Furthermore, proteins that are sensitive to the thickness of the surrounding bilayer are presumably not immune to fluctuations in the bilayer thickness. Gramicidin channels in the dimer configuration can exhibit rapid closing-opening events, before the final dissociation of the channel (55–57). It would be interesting to see if the frequency of such events is correlated to the amplitude of bilayer thickness fluctuations. In this article, however, we have not addressed membrane fluctuations around the inclusion (which may itself fluctuate among multiple conformations).

We find that the monolayer spontaneous curvature plays a significant role in determining both thickness fluctuations and inclusion-induced deformations. For DPPC and SM, spontaneous curvature effects are consistent with the nonmonotonic behavior of the thickness fluctuations. In these systems, the leaflets prefer to bend toward the oil, inducing an effective negative surface tension for thickness fluctuations that implies an hourglass or bulged configuration is actually favorable over some wavelengths. Such a configuration is clearly visible in Fig. 3 of Lindahl and Edholm (13). Many physiological membranes incorporate nonbilayer forming lipids, so the spontaneous curvature of each leaflet may be a property closely regulated by the cell. Although many studies regarding these lipids have focused on their role in membrane fusion (58,59), according to the present model they also affect thickness fluctuations and bilayer response to an embedded protein.

Finally, this article also highlights the promise and limitations of generic simulation models. It is heartening to notice that the material properties of our CG model, despite its simplified chain molecules and lack of explicit solvent, are reasonable numbers that lie within the range designated by DPPC, GMO, and SM. It is especially encouraging that the tension governing protrusion modes, γ_λ, which is closely related to the interfacial tension between oil and water (11), is the same for the solvent-free CG model as for GMO. This provides further evidence that CG models not containing explicit solvent are capable of reproducing the lipid-solvent interfacial tension inherent to a real bilayer. Additionally, the nonmonotonic behavior observed in the deformation profile is consistent with that observed in solvated (but also coarse-grained) models. At the same time, the wide range of measured elastic constants across the lipid systems studied here suggests that one must use caution when generalizing results extracted from a single system, whether it is coarse-grained or atomistic.

APPENDIX A: APPROXIMATIONS TO EQ. 26

The full expressions for the spectra (Eq. 26) are complicated functions of q. In Fluctuation Spectra of Homogeneous Membranes, above, we outlined the Goetz et al. (12) approximation for undulations, which is expected to work for small q and large q; and our own approximation, which is expected to work best when bending modes and protrusion modes are uncoupled (small 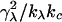). In this Appendix we make quantitative comparisons of these approximations. On the left side of Fig. 11, expected height spectra resulting from the full expression (Eq. 26), the Goetz et al. (12) approximation (Eq. 31) and our own approximation (Eq. 32) are compared for the four sets of constants displayed in Table 1. As should be expected, the quality of our approximation increases as decreases, or as the undulation and protrusion modes become less coupled. In contrast, the quality of the Goetz et al. (12) approximation increases as 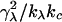increases, or as the undulation and protrusion modes become more coupled. The difference between our approximation and the full form is within typical data error bars for all four cases considered in this work. The Goetz et al. (12) approximation performs significantly worse (outside error bars) than the decoupling approximation for all four data sets.

FIGURE 11.

(Left, height) Plot of Eq. 26 (solid), Eq. 32 (dashed), and Eq. 31 (dotted) using the four sets of constants displayed in Table 1. The data sets have the following values for the coupling parameter 2γ_λ²/k_λk_c: DPPC, 0.08; GMO, 0.3; SM, 0.06; and CG, 0.04. The dashed approximation gets worse as the coupling parameter increases, whereas the dotted approximation gets slightly better. (Right, thickness) Plot of Eq. 6 (solid) and Eq. 33 (dashed), using the four sets of constants displayed in Table 1, whereas the dashed-dotted line is Eq. 33, with ζ set to 0.

Goetz et al. (12) did not measure thickness fluctuations, but if we attempt a similar approach as they applied to height fluctuations (i.e., take the small q limit and the large q limit and add them together) one obtains a nonsensical result with the small q regime dominated by interfacial tension rather than predicting a rollover to a constant value. Although there is no established continuous approximation to compare to for thickness spectra, we have compared our own approximation (Eq. 33) to the full form for thickness fluctuations (Eq. 6). It has a similar level of success for thickness fluctuations as it did for height fluctuations.

A further possible method for simplifying the expression for thickness fluctuations is to neglect the spontaneous curvature and its area derivative (i.e., set ζ to 0). Then the bending portion of the spectrum is equivalent to that used originally by Lindahl and Edholm (13). The dotted lines on the right-hand side of Fig. 11 represent this approximation: Eq. 33 with k_c, k_λ, γ_λ, k_A from Table 1 and ζ = 0. As demonstrated by the figure, neglecting spontaneous curvature effects can be a dangerous approximation that results in significantly different expected forms for the spectra for some parameter sets studied.

APPENDIX B: CURVE-FITTING AND ERROR ANALYSIs

Our curve-fitting algorithm minimizes the sum of the residuals, χ², with respect to k_c, γ_λ, k_λ, 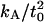, and ζ/t₀, where

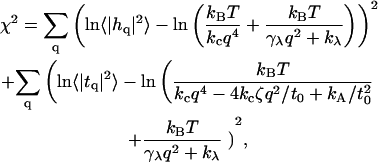(41)

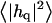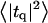and and represent actual data points. Minimization was accomplished using the MatLab (The MathWorks, Natick, MA) fitting procedure nlinfit, which employs a hybrid Gauss-Newton and Levenberg-Marquardt minimization algorithm. Equation 41 obviously corresponds to fitting the data to our approximate form (Eq. 32); an analogous expression was used when fitting to the full form (Eq. 26). Note that our residual function assesses quality of fit for the logarithms of 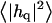and 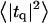. This choice insures that our best fit lines strive to reproduce the data sets as viewed on a semilog plot (i.e., the standard plotting method employed in Fig. 4).

Because the data is not perfectly converged, removing one data point alters the resulting fit parameters. Whether the new fit parameters are more or less accurate (i.e., close to their true values) depends on the accuracy of the removed data point. To determine the sensitivity of our fit parameters to individual data points (and hence our confidence in the extracted fit parameters) we used the Bootstrap Method (60). This method requires minimal knowledge of the errors associated with each data point, because it uses the distribution of the data points themselves to estimate error. Ninety-five percent confidence intervals reported in the text reflect the range of values extracted by application of the bootstrap algorithm.

The resulting fit parameters can be influenced by the fitting algorithm. For instance, instead of using a log transform, we could have weighted the data appropriately. Or, instead of fitting 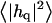and 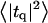simultaneously, we could have fit 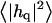first to obtain k_c, γ_λ, and k_λ and then fit 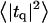to find ζ and k_A. We experimented with various different fitting procedures and found that, although best-fit values were predicted differently from algorithm to algorithm, the associated 95% confidence intervals (calculated as reported above) almost always bracket the range of fits obtained from different schemes. The present fitting procedure was ultimately adopted for its simplicity in use and explanation. Interested parties may obtain the MatLab compatible .m file that we used to determine the fits reported in this article (38).