Bistability in Apoptosis: Roles of Bax, Bcl-2, and Mitochondrial Permeability Transition Pores

Abstract

We propose a mathematical model for mitochondria-dependent apoptosis, in which kinetic cooperativity in formation of the apoptosome is a key element ensuring bistability. We examine the role of Bax and Bcl-2 synthesis and degradation rates, as well as the number of mitochondrial permeability transition pores (MPTPs), on the cell response to apoptotic stimuli. Our analysis suggests that cooperative apoptosome formation is a mechanism for inducing bistability, much more robust than that induced by other mechanisms, such as inhibition of caspase-3 by the inhibitor of apoptosis (IAP). Simulations predict a pathological state in which cells will exhibit a monostable cell survival if Bax degradation rate is above a threshold value, or if Bax expression rate is below a threshold value. Otherwise, cell death or survival occur depending on initial caspase-3 levels. We show that high expression rates of Bcl-2 can counteract the effects of Bax. Our simulations also demonstrate a monostable (pathological) apoptotic response if the number of MPTPs exceeds a threshold value. This study supports our contention, based on mathematical modeling, that cooperativity in apoptosome formation is critically important for determining the healthy responses to apoptotic stimuli, and helps define the roles of Bax, Bcl-2, and MPTP vis-à-vis apoptosome formation.

INTRODUCTION

The biochemical mechanism of apoptosis, or programmed cell death (PCD), is an area of extensive study because of the importance of maintaining the homeostatic balance in response to pro- or antiapoptotic stimuli (1). The balance between cell proliferation and apoptosis is indeed crucial for the healthy functioning of organisms. Dysregulation of apoptosis is implicated in many degenerative and autoimmune diseases, including cancer, acquired immune deficiency syndrome, neurodegenerative disorders, and viral and bacterial infections (2).

Apoptosis may be triggered by extracellular death signals, deprivation of survival signals, and genetic or toxicological damage (3). A common observation in response to these stimuli is the activation of caspases, a group of cysteine proteases that serve as main effectors of PCD. There are two major pathways of caspase activation: i), ligand-dependent or receptor-induced activation (extrinsic pathway), through death receptors such as Fas (CD95) or the members of tumor necrosis factor receptor (TNF-R) superfamily, and ii), mitochondria-dependent activation (intrinsic pathway), via cytochrome c (cyt c) release from mitochondria induced by stress, irradiation, or inflammation (4,5).

Binding of death ligands such as Fas ligand (FasL), TNF, or tumor necrosis-related apoptosis-inducing ligand (TRAIL) usually induces the oligomerization of the associated TNF-Rs, followed by recruitment of adaptor proteins—Fas-associated death domain proteins (FADD)—to the cytoplasmic portions of the receptors (6). The resulting death inducing signaling complex (DISC) recruits multiple procaspases-8 molecules that mutually cleave and activate one another through induced proximity. In Type I cells, activation of caspase-8 in large quantities leads to the activation of other caspases, including the executioner caspase-3 that ultimately leads to apoptosis. In Type II cells, the amount of caspase-8 generated at the DISC is small, and the activation cascade does not propagate directly but is instead amplified via the mitochondria (Fig. 1). This process is initiated by the cleavage of Bid by caspase-8, followed by the translocation of the truncated Bid (tBid) to the mitochondria, which induces the release of proapoptotic molecules such as cyt c and Smac/DIABLO to the cytoplasm (7). Cyt c release closely depends on the opening of mitochondrial permeability transition pores (MPTPs).

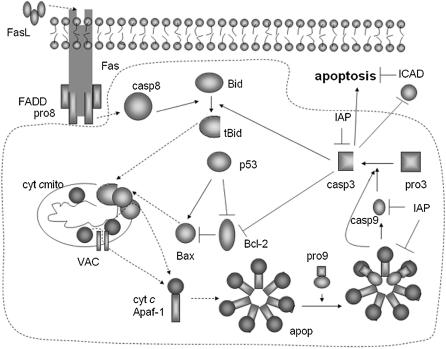
FIGURE 1.

Mitochondria-dependent apoptotic pathways. The dotted region indicates the interactions included in this model. Solid arrows denote chemical reactions or upregulation; those terminated by a bar denote inhibition or downregulation; and dashed arrows describe subcellular translocation. The following abbreviations are used: pro8, procaspase-8; casp8, caspase-8; pro9, procaspase-9; casp9, caspase-9; pro3, procaspase-3; casp3, caspase-3; ICAD, inhibitor of caspase activated DNase; cyt c, cytochrome c; apop, apoptosome; VAC, the complex formed by voltage dependent anion channel (VDAC), adenine nucleotide translocase (ANT), and cyclophilin D (CyP-D) at the mitochondrial permeability transition pore.

The mitochondrial apoptotic pathway is largely mediated through Bcl-2 family proteins, which include both proapoptotic members such as Bax, Bak, and BNIP3 that promote mitochondrial permeability, and antiapoptotic members such as Bcl-2 and Bcl-xL that inhibit their effects, or inhibit the mitochondrial release of cyt c (8). Another important component is the tumor suppressor protein p53, which simultaneously suppresses Bcl-2 and activates Bax. Cyt c leakage supports the formation of an apoptosome complex by binding to apoptotic protease activating factor-1 (Apaf-1), which activates the caspase-9 molecules (upon cleavage of the bound zymogen procaspases-9), which in turn activate caspase-3 (9). Caspase-3 cleaves the inhibitor of caspase activated DNase (ICAD), leading to DNA degradation or fragmentation (10), whereas the inhibitor of apoptosis (IAP) inhibits both caspase-3 and caspase-9 activities.

A recent study by Nair and co-workers (11) invites attention to the occurrence of a bifurcation into two states, favoring either cell death or cell survival, upon examination of a population of cells undergoing oxidative stress. Essentially, each cell is observed to activate either homeostatic or apoptotic signals early after H₂O₂ exposure; eventually, the stimuli that activate proapoptotic signals cause a given cell to succumb to PCD in accord with an all-or-none activation of the caspase cascade (12). The remaining cells, which undergo activation of the extracellular regulated kinase (ERK) signaling pathway at an early stage of oxidative stress, exhibit cytoprotective responses. The observed bistable behavior, or the choice of individual cells between these two competing and mutually exclusive responses is suggested to be a stochastic process (11), the origin and mechanism of which is still to be elucidated. A recent study by Bentele et al. (13), on the other hand, points to the occurrence of a transition from cell survival to cell death provided that the stimuli exceed some threshold values. In this case, the cells exhibit essentially a transition between two monostable regimes, rather than two states possibly coexisting under certain combination of stimuli as observed by Nair et al. (11).

In view of these different viewpoints, and knowing that bistability is a functional feature in many cellular networks (14–18), it is important to clarify if and how a mathematical model of apoptosis can explain the occurrence of a bistable response. Of particular interest is also to assess the conditions necessary for a transition from bistable to monostable behavior.

An insightful first study has been performed by Eissing et al. (19) for receptor-induced apoptosis of Type I cells. Bistability is shown therein to result from the interference of inhibitors of apoptosis (IAP and BAR). Our model demonstrates the possible occurrence of bistability in mitochondria-dependent pathways under certain conditions (see below), as well as a transition from bistable to monostable behavior, either apoptotic or cytoprotective, beyond threshold concentrations of particular components. Bistability is imparted by kinetic cooperativity in formation of a heptameric complex by Apaf-1 and cyt c molecules (apoptosome), after the release of cyt c from the mitochondria. The term kinetic cooperativity refers to an effective reaction order larger than unity in the formation of the heptameric complex from monomers. Cooperativity (20) is assumed in the formation of the apoptosome complex, a feature that has not been included in previous mathematical models (13,19,21,22). The initial apoptosis model proposed by Fussenegger et al. (21) includes both receptor-induced and mitochondria-dependent pathways and it is not bistable. The model proposed by Bentele et al. (13) is not bistable and suggests a transition from cell survival to cell death provided that the stimuli exceed some threshold values. The model proposed by Stucki and Simon (23) focuses on regulation of caspase-3 activation and degradation only.

In this study, we examine the response of the cell to changes in the accessible levels of two members of the Bcl-2 family, Bax and Bcl-2, as well as the numbers of MPTPs. Our analysis indicates that monostable cell survival is induced if the expression (or degradation) rate of Bax is lower (or higher) than a particular threshold, in qualitative agreement with other studies (24). We also show that high numbers of MPTPs may have a role in pathological cell death (25). Parameter space searches using both reduced and detailed mitochondria-dependent apoptosis models suggest that cooperativity in apoptosome formation is a plausible mechanism to ensure bistability in response to apoptotic stimuli. The loss of bistability manifested by monostable cell survival or cell death implicates Bax, Bcl-2, and MPTP in pathologies like cancer and neurodegenerative disorders.

MODEL AND METHODS

Kinetic model for mitochondria-dependent apoptotic pathways

A schematic description of the mitochondria-dependent (intrinsic) apoptotic pathways included in our model is given in Fig. 1. The involved reactions/interactions are summarized below, along with the corresponding rate constants (k_i) and fluxes (J_i). Explicit expressions for the differential rate equations and values of the parameters are presented in the respective Tables 1 and 2.

TABLE 1.

The set of ordinary differential equations (ODEs) and parameters adopted in the model

d[Apaf-1]/dt = −J1 + JApaf-1
d[cyt c·Apaf-1]/dt = J1 − 7J1b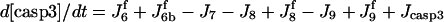
d[apop]/dt = J1b − J2 + J4b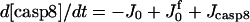
d[apop·pro9]/dt = J2 − J3	d[Bid]/dt = −Jo − J8 + JBid
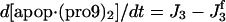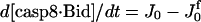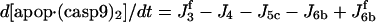	d[Bcl-2]/dt = −J9 − J13 + JBcl2
d[apop·casp9]/dt = J4 + J4b − J5b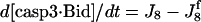
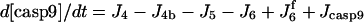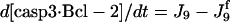d[pro9]/dt = −J2 − J3 + Jpro9	d[Bax]/dt = −J12a − J12b − J13 + JBax
d[IAP]/dt = −J5 − J5b − J5c − J7 + JIAP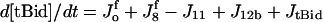
d[casp9·IAP]/dt = J5	d[tBid·Bax]/dt = J12a − J12b + JtBidBax
d[apop·casp9·IAP]/dt = J5b	d[cyt cmito]/dt = −J14 + Jcytmit
d[apop·(casp9)2·IAP]/dt = J5c	d[Bax2]/dt = J12b + JBax2
d[casp3·IAP]/dt = J7	d[tBidmito]/dt = J11 − J12a + JtBidmit
d[pro3]/dt = −J6 − J6b + Jpro3	d[cyt c]/dt = J14 − J1 + Jcytc
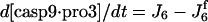with
Reaction rates (or fluxes)	Production-degradation rates
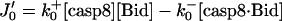	JApaf-1 = ΩApaf-1 − μ[Apaf-1]
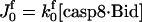	JIAP = ΩIAP − μ[IAP]
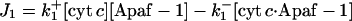	Jpro3 = Ωpro3 − μ[pro3]
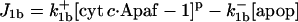	Jpro9 = Ωpro9 − μ[pro9]
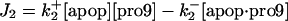	JBid = ΩBid − μ[Bid]
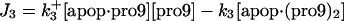	JBcl2 = ΩBcl2 − μBcl2[Bcl-2]
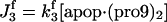	JBax = ΩBax − μBax[Bax]
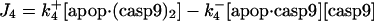	Jcytmit = Ωcytmit − μ[cyt cmito]
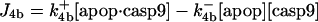	Jcasp9 = −μ[casp9]
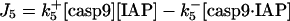	Jcasp3 = −μ[casp3]
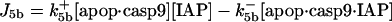	JtBid = −μ[tBid]
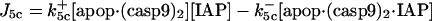	JtBidBax = −μ[tBid·Bax]
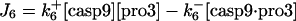	JBax2 = −μ[Bax2]
	JtBidmit = −μ[tBidmito]
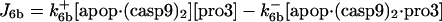	Jcytc = −μ[cyt c]
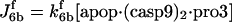	Jcasp8 = −μ[casp8]
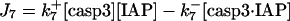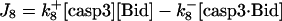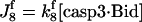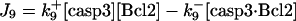J11 = k11[tBid]
J12a = k12a[tBidmito][Bax]
J12b = k12b[tBid·Bax][Bax]
J13 = k13[Bcl2][Bax]
J14 = k14[Bax2][cyt cmito]

TABLE 2.

The model parameters*

Rate constants		Other parameters
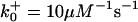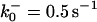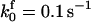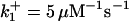		p = 4
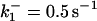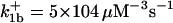		[p53thresh] = 0.004 μM
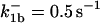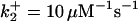		μ = 0.006 s−1
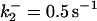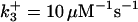		ΩApaf-1 = 3 × 10−4μM/s
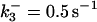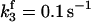		ΩIAP = 3 × 10−5μM/s
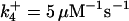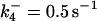		Ωpro3 = 3 × 10−4μM/s
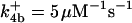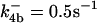		Ωpro9 = 3 × 10−4μM/s
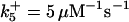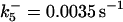		ΩBid = 3 × 10−5μM/s
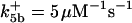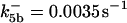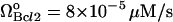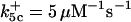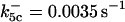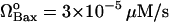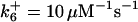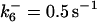		Ωcytmit = 3 × 10−4μM/s
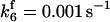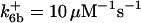		[p53] = 0.0066 μM
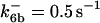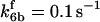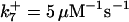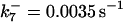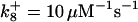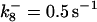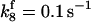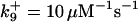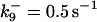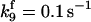k11 = 10 s−1	k12a = 10 μM−1s−1
k12b = 10 μM−1s−1	k13 = 10 μM−1s−1
k14 = 10 μM−1s−1

*All rate constants, except for 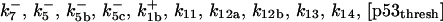, are set up to within one order of magnitude difference with respect to those used by Asthagiri and Lauffenburger (43) in their simulations of mitogen-activated protein kinase pathways. The ratio of 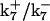ensures an equilibrium constant of 0.7 nM (56), as well as those used for defining 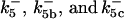. The values of 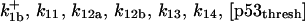are suitably set to achieve fluxes comparable to other compounds' fluxes; 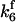is assigned a value smaller than 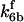because of experimental observations by Riedl et al. (30). The degradation constant of all species is assigned as 0.006 s⁻¹ unless specified otherwise in the text. This value is within the range of parameters used for degradation rate constants adopted by Chen et al. (42) The rates of synthesis are within the range of values used by Chen et al. (42).

Cleavage of Bid by caspase-8

The cleavage of Bid to truncated Bid (tBid) by caspase-8 (casp8) (26) is described by the following reactions, rate constants, and fluxes

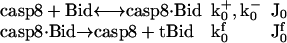(1)

Apoptosome complex formation

The apoptosome complex (apop) is a multimeric assembly composed of seven Apaf-1 and seven cyt c molecules (27,28). To include in our model the cooperative nature of apoptosome formation, we adopt the reactions

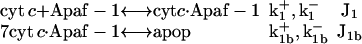(2)

with the forward reaction rate of 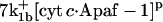for the second reaction. A reaction order (p) higher than unity for the apoptosome complex entails a kinetic cooperativity conducive to bistability, as will be illustrated in the results from calculations.

Initiator caspase-9 activation

This involves five reactions; the binding of the procaspase-9 (pro9) to the apoptosome complex, succeeded by the binding of a second pro9 to form the complex apop·(pro9)₂ and the cleavage of the bound procaspases to yield the holoenzyme apop·(casp9)₂, the dissociation of which finally leads to caspases-9 (21,29), i.e.,

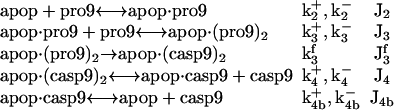(3)

Activation of caspase-3 by caspase-9

This is described by two reactions, the complexation of caspase-9 with the pro3, and the succeeding cleavage of pro3 to yield the active (executioner) caspase-3 (casp3) molecule (21), i.e.,

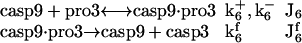(4)

Another mechanism of activation of caspase-3

This is the complexation of holoenzyme apop·(casp9)₂ with the zymogen pro3, succeeded by the cleavage of pro3 to yield casp3 (29,30), i.e.,

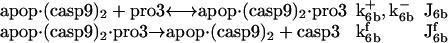(5)

Inhibition of caspase-9 and -3 by IAPs

IAP inhibits both casp9 (31) and casp3 molecules by the following reactions (21)

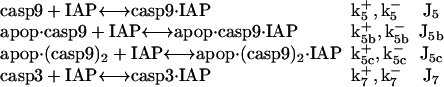(6)

Cleavage of Bid by caspase-3

In addition to caspase-8 that initiates the cleavage of Bid, caspase-3 produced downstream also truncates Bid to tBid in Type II cells (26,32). The corresponding reactions are

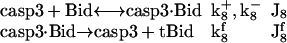(7)

The activation of Bid by casp3 completes the first of two positive feedback loops present in our model. The second is ensured by the cleavage of the inhibitory protein Bcl-2 by casp3 (see “Inhibition of Bax by Bcl-2, and cleavage (inactivation) of Bcl-2 by casp3” below). Upon cleavage, Bcl-2 can no longer inhibit the channel-opening activity of Bax (8). Therefore, casp3 indirectly enhances the formation of channels for proapoptotic cyt c release.

Cyt c release from mitochondria to cytoplasm

In the model proposed by Fussenegger and co-workers (21), cyt c is released when the concentration of casp3 relative to that of Bcl-2 exceeds a threshold value. Here, we adopt a different mechanism based on experimental observations (33–36), summarized by the following sequence of events

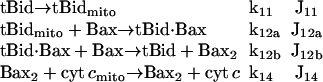(8)

Accordingly, tBid translocates to the mitochondria (k₁₁), and forms a complex with Bax (k_12a) to initiate Bax oligomerization and channel (Bax₂) formation (k_12b). Cyt c is then released through the channel (k₁₄).

Inhibition of Bax by Bcl-2, and cleavage (inactivation) of Bcl-2 by casp3

The cleavage of antiapoptotic Bcl-2 by casp3 (37), which otherwise would inhibit Bax, is described by

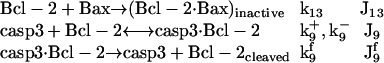(9)

p53 Regulation of Bax and Bcl-2 synthesis

p53 upregulates the synthesis of Bax and downregulates that of Bcl-2 (38,39). Joers et al. (40) observed that although p53 levels increase in all cells subject to DNA damage, only in some cells is the transcriptional activity of p53 switched on, whereas in the remainder it is switched off. To account for this switch-like response of p53 to DNA damage, the following expressions are used for the rates of formation of Bax and Bcl-2.

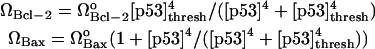(10)

The above two expressions closely approximate the qualitative switch-like activity of p53. The adoption of continuous functions as opposed to discrete threshold values permits us to perform a bifurcation analysis using the AUTO package.

Synthesis and degradation reactions

In addition to the above sets of reactions, the model includes the synthesis and degradation of a number of components. The proteins being synthesized (and corresponding synthesis rates) are Apaf-1 (Ω_Apaf-1), IAP (Ω_IAP), pro3 (Ω_pro3), pro9 (Ω_pro9), Bid (Ω_Bid), Bcl-2 (Ω_Bcl2), Bax (Ω_Bax), and cyt c_mito (Ω_cytmit). Recent studies show that many molecules involved in apoptotic pathways are regulated by the ubiquitin-proteasome pathway (41). A first-order degradation kinetics with a uniform rate constant of μ is adopted here for casp8, casp9, casp3, pro9, pro3, Apaf-1, IAP, Bcl-2, Bid, tBid, tBid_mito, Bax, Bax₂, tBid·Bax, cyt c, and cyt c_mito. The initial concentrations of all compounds are zero, except for pro3 and pro9, Apaf-1, Bid, Bax, Bcl-2, IAP, and cyt c_mito that are all taken as 0.004 μM because the concentrations of proteins are usually in the nanomolar range (42), unless otherwise stated or varied. Initial concentrations of casp8 and casp3 are indicated for each simulation.

METHODS

The above model contains 31 components, including the different forms of the same molecule (e.g., Bid and tBid) and the same protein in different subcellular environments (e.g., cyt c in the cytosol and in the mitochondria). All interactions (chemical or physical) are treated as chemical reactions, and their time evolution is described by classical chemical reaction kinetics.

We do not have conservation of the enzyme and thus do not use Michaelis-Menten (MM) simplification for our reactions. We use standard mass action models from which MM kinetics is derived when the total enzyme concentration is constant. In all of our reactants, we maintain a small source as well as degradation for the enzyme, such that the total enzyme concentration is not conserved until steady-state conditions are reached. This provides robustness to the model, which a simple conservation model lacks. In absence of the source and degradation, our model reduces to MM kinetics under the pseudosteady-state hypothesis. The equations for [E] and [ES] satisfy

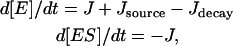so that in the presence of the source and decay of the enzyme, there is no longer conservation of the total enzyme and the MM assumption is violated.

The associated set of rate equations and parameters are listed in the respective Tables 1 and 2. Most parameters have been assigned values within an order of magnitude of those used in previous studies (42,43). These parameters, corresponding to MAP kinase pathways, were adopted in view of the lack of experimental data on the rate parameters of the above-listed reactions, and experimental data have been incorporated when available (see Table 2 footnote). With these choices of parameters, it will be shown that the model exhibits resistance to caspase-3 activation when p53 level is low and and bistability to apoptotic stimuli when p53 level is high in agreement with experiments (44). In view of the lack of precise quantitative information on most parameters, these results should be viewed as qualitative, rather than quantitative. The coefficient p was chosen to be 4. Smaller values were also observed to lead to bistability, although the associated threshold concentrations of caspase-3 were unrealistically low. The simulations and bifurcation analysis have been performed using the software XPPAUT (http://www.math.pitt.edu/∼bard/xpp/xpp.html) developed by our group at the University of Pittsburgh, Department of Mathematics (45).

RESULTS AND DISCUSSION

First, we present the results for a few reduced models to provide insights into the basic mechanisms that potentially elicit a bistable response to apoptotic stimuli. We then proceed to the analysis of a more detailed mathematical model containing the above listed 31 components and their interactions (Table 1).

Comparison of the robustness of possible mechanisms of bistability using reduced models

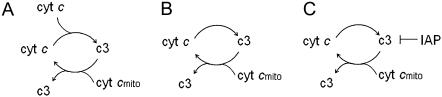
Reduced model A: bistability induced by cooperative formation of a component (Fig. 2 A)

We adopt first a reduced model composed of three components, cyt c, cyt c_mito and casp3 which possesses two basic features of the detailed model: i), a step involving cooperative interaction of multiple molecules, and ii), a positive feedback loop, expressed by the reaction scheme

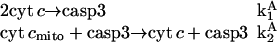(11)

where 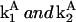are corresponding rate constants. Here two molecules of cyt c interact cooperatively to lead to caspase-3 activation; and the positive feedback loop is ensured by the product from the second reaction (cyt c) serving as reactant in the first. The associated rate equations are

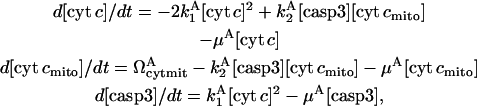(12)

where 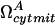is the rate of formation of cyt c_mito; μ^A is the degradation rate constant for cyt c, casp3, and cyt c_mito. The superscript denotes the reduced model A.

To test the robustness of the model, we repeated our simulations by assigning the parameters 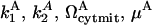values of 0.1, 1, and 10 leading to a total of 3⁴ = 81 combinations, of which 26 exhibited a bistable behavior in response to apoptotic stimuli. The initial concentration of casp3 serves here as the apoptotic stimulus.

Reduced model B with positive feedback loop by no cooperativity in any component formation (Fig. 2 B)

The following interactions define this model

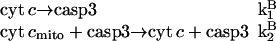(13)

With the corresponding rate equations

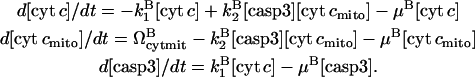(14)

We repeated our calculations for the same set of 81 choices of parameters. None of the simulations led to a bistable response, indicating that the kinetic scheme in Fig. 2 B, is not likely to lead to bistability.

FIGURE 2.

Reduced models of apoptosis (A) in the presence of cooperative interactions and positive feedback loop; (B) in the presence of positive feedback but absence of cooperative interactions; and (C) with inhibition of caspase-3 by IAP, in the absence of cooperativity.

Reduced model C: inhibition by IAP (Fig. 2 C)

In this model, cyt c release induces casp3 activation without cooperativity. Two more reactions are included to account for the inhibition of apoptosis by IAP. This reduced model has mechanisms comparable to those described by Eissing and co-workers (19). It essentially contains a feedback loop and takes into consideration the inhibition of casp3 by IAP via formation of a complex casp3.IAP by the following reaction scheme

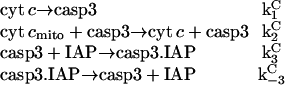(15)

The associated rate equations are

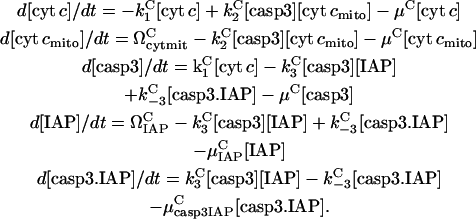(16)

The parameters 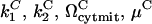were again assigned values of 0.1, 1, 10, and 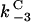is taken as 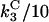, giving rise to 3⁴ = 81 simulations. To account for the two new interactions, we assigned to the new parameters (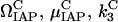) one at a time, the same discrete values, whereas holding the other two equal to 1, which leads to a total of 81 × 9 combinations. Only three out of all these combinations exhibited a bistable response, whereas in all other cases, a monostable cell survival or apoptosis has been observed.

Reduced model D: inhibition by IAP with cooperativity similar to the model by Stucki and Simon (23)

In this reduced model, we explored if some other type of cooperativity could be effective for ensuring bistability. We assumed the degradation of caspase-3 by IAP to be modulated allosterically as proposed by Stucki and Simon (23). The same interactions and rate equations as those used in the reduced model C are adopted here, except for the inclusion of an additional term for caspase-3 degradation in which we use the expression and coefficients (including the Hill coefficient 4) proposed by Stucki and Simon (23). The differential rate equation for the time evolution of caspase-3 becomes

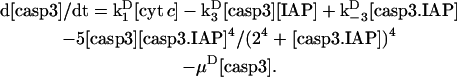(17)

The same set of simulations as those described above for the reduced model C were repeated to end up with the same number (3) of combinations leading to bistability. However, we noted that the steady-state concentration of caspase-3 was lower for this reduced model.

The above analysis demonstrates that a pathway that involves a positive feedback loop with cooperative interactions (reduced model A) is more likely to elicit a bistable response, among the different cases investigated. Also, it is seen that kinetic cooperativity is not the only possible mechanism for inducing bistability, and does not always imply cooperativity. We now proceed to the illustration of the validity of the same mechanism in our detailed model that contains both features, described in detail in the Model and Methods section.

Cooperativity in apoptosome formation ensures bistability in detailed model

Any stimulus that produces caspase-8 may initiate mitochondria-dependent apoptotic interactions (Fig. 1). Caspase-8 truncates Bid to tBid, which results in the activation of caspase-3 by a cascade of reactions after the translocation of tBid to mitochondria. The activation of caspase-3 gives rise to two positive feedback loops (Eqs. 7 and 9) that amplify the response to the initial triggering effect of caspase-8. Our model does not include the pathways upstream of caspase-8 activation. We assume that a transient proapoptotic stimulation results in production of caspase-8 in proportion to the exposure of the cell to death signal ligands. Here the coefficient p involved in the formation of apoptosome (Eq. 2) is taken as p = 4. Although p might be as large as seven for a fully cooperative formation of a heptameric structure, a value of four was observed to be sufficient to ensure bistability, whereas lower p-values would necessitate unrealistic (picomolar) concentrations of caspase-3 to elicit a bistable response.

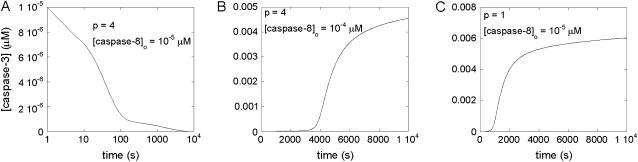
Fig. 3, A and B, illustrate two opposite behaviors observed in response to small changes in proapoptotic stimuli (represented here by the initial caspase-8 concentration) provided that the apoptotic pathways involve a cooperative step. When the original caspase-8 level is relatively low, [casp8]₀ = 10⁻⁵ μM, for example, cell survival is observed as a monostable response (Fig. 3 A) using the differential rate equations and parameters listed in the respective Tables 1 and 2. Cell survival is manifested therein by a decrease in the concentration of executioner caspase-3 to negligibly small values. On the other hand, the opposite behavior, i.e., monostable PCD, is induced (Fig. 3 B) if the proapoptotic stimulus exceeds a threshold level (see below). In Fig. 3 B the concentration of casp3 is shown to increase by two orders of magnitude, to 4.5 × 10⁻³ μM, from the same initial concentration (10⁻⁵ μM) as in Fig. 3 A. The only difference in panel B as compared to panel A is the increase (10⁻⁴ μM) in the initial concentration of the proapoptotic stimulus ([casp8]₀).

FIGURE 3.

Time evolution of caspase-3 in response to minor changes in initial caspase-8 concentration [casp8]₀. (A) Cell survival when [casp8]₀ is small (10⁻⁵ μM), indicated by the decrease in the caspase-3 concentration (initially 10⁻⁵ μM) to zero at steady state; (B) apoptosis, implied by the increase in caspase-3 concentration to a high value (4.5 × 10⁻³ μM) at steady state despite the same initial value of caspase-3 as in panel A, when [casp8]₀ is higher (10⁻⁴ μM); (C) monostable apoptosis, in the absence of cooperativity (p = 1) using the same initial concentrations of caspase-3 and caspase-8 as in panel A. Here caspase-3 concentration reaches a high value (6 × 10⁻³ μM) at long times indicative of apoptotic response. Note that the ordinate scales are different in the panels.

We note that the model is not restricted to apoptosis caused by extracellular stimuli exclusively. The PCD in panel B was verified to also occur with a zero initial caspase-8 concentration and nonzero initial caspase-3 concentration (e.g., [casp3]₀ = 5 × 10⁻⁴ μM, which eventually leads to [casp3] = 4.8 × 10⁻³ μM; data not shown). Therefore, apoptosis may be equally driven by intrinsic proapoptotic stimuli that induce caspase-3 activation. In our analysis, caspase-3 steady-state concentrations of the order of nanomolars were accepted to lead to apoptosis, whereas cell survival would refer to vanishingly small concentrations.

Finally, in the absence of cooperativity (p = 1), the same initial conditions for caspase-8 and caspase-3 that led to cell survival in Fig. 3 A, are now observed to induce apoptosis, as implied by the high concentrations (6 × 10⁻³ μM) caspase-3 reaches at steady state (Fig. 3 C). This is an example of pathological cell death rather than a normal response to small apoptotic stimuli (cell survival/protection). The system does not exhibit a bistable behavior in response to variations in [casp8]₀. Instead, apoptosis is the only stable state, despite the low original concentration of caspase-8.

Taken together, these results suggest that the cooperativity in apoptosome formation, might be a mechanism in cells to ensure healthy functioning of cells to apoptotic stimuli, instead of invariably leading to apoptosis in response to minimal stimulation.

Biological significance of the bistable model: roles of Bax, Bcl-2, and MPTP in pathological PCD

Bax degradation and expression rates can determine the transition between bistable and monostable responses

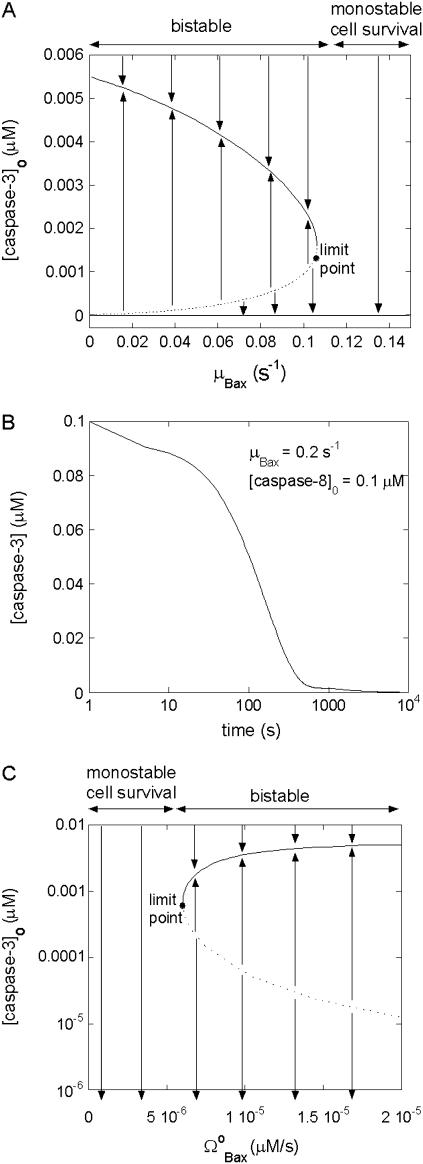
Apoptosis can be controlled by the degradation rate of proapoptotic proteins such as Bax (46). We examined if our mathematical model confirms this behavior. Fig. 4 A depicts the bifurcation diagram as a function of the degradation rate (μ_Bax) of Bax and the initial concentration of caspase-3. The limit point for saddle-node bifurcation is found as μ_Bax = 0.11 s⁻¹ using the parameters listed in Table 2. Below this limit point, there exist three steady states, two of which are stable and one unstable. Therefore, the system is bistable in this regime. Conversely, above the limit point, there is only one stable state, i.e., the system is monostable. The arrows in Fig. 4 A, indicate the direction of evolution of casp3 levels, starting from any region of the diagram (i.e., any combination of the two parameters). The solid curve represents the stable apoptosis loci achieved with casp3 concentrations above the dotted curve, and the lower solid line represents the stable cell survival state, characterized by zero casp3 concentration. The dashed curve represents the loci of unstable steady state leading to either cell death or cell survival, upon slight perturbation. It also defines the threshold concentration of apoptotic stimuli (casp3) to trigger apoptosis as a function of the degradation rate of Bax. In the monostable regime, even very high initial casp3 concentrations decay to zero. Therefore, when the rate of degradation of Bax is higher than the limit point, apoptosis cannot occur, regardless of caspase levels.

FIGURE 4.

Effect of degradation rate of Bax (μ_Bax) on cell behavior. (A) Bifurcation diagram for μ_Bax. Limit point for saddle-node bifurcation is μ_Bax = 0.11 s⁻¹. Below this limit point, there are three steady states, two of which are stable and one unstable; above the limit point, there is only one stable state, cell survival. The arrows indicate the equilibrium concentrations reached when starting from any point in the diagram; (B) the high initial concentration of caspase-3 (0.1 μM) decreases to zero when μ_Bax is in the monostable cell survival region (0.2 s⁻¹) despite the high [casp8]₀ value; (C) bifurcation diagram for 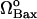. Limit point for saddle-node bifurcation is 6.03 × 10⁻⁶ μM/s. The stable cell survival line ([casp3]_o = 0) is not shown because the y axis is logarithmic.

Fig. 4 B illustrates the time evolution toward monostable cell survival. With μ_Bax = 0.2 s⁻¹ (higher than the limit point), the concentration of casp3 decays from [casp3]₀ = 0.1 μM to zero, even when [casp8]₀ is also high (0.1 μM). Notably, our results are in accord with those of Li and Dou, who demonstrated that elevated Bax degradation is a survival mechanism in human cancer cells (46).

Fig. 4 C is the bifurcation diagram for rate of formation of Bax. The limit point for the saddle-node bifurcation is 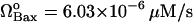. Above this point, a bistable behavior is predicted in response to proapoptotic stimuli. For 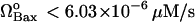, on the other hand, the response is monostable cell survival, even in the presence of high apoptotic stimuli. This result is consistent with observations of decreased Bax expression in human breast cancers (47).

This model thus predicts that cells will exhibit a monostable cell survival response to apoptotic stimuli if the degradation rate of Bax is above some threshold value or if the expression rate of Bax is below some threshold value (shown in the respective panels A and C of Fig. 4) In this monostable regime, the caspase-3 concentration always diminishes to zero because there is not a sufficiently high concentration of Bax to open up channels on mitochondrial membrane for releasing cyt c. The net result is that the activation rate of caspase-3 becomes lower than its degradation rate, eventually leading to vanishingly low concentrations of caspase-3. In the bistable regime, on the other hand, a dichotomous response favoring either cell survival (vanishingly small casp3 concentration) or programmed cell death (casp3 above nanomolar concentration) is elicited, depending on the original casp3 concentrations. Overall, the model predicts that there exists a critical point at which the amount of Bax leads to monostable cell survival that might be associated with the onset of cancer in living cells.

Bcl-2 counteracts the effect of Bax

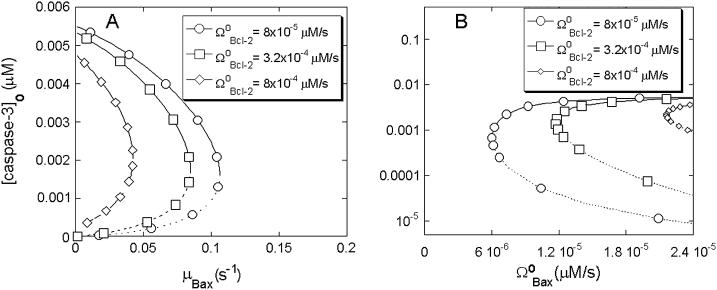
Bcl-2 is the classical, antiapoptotic member of the Bcl-2 family. Danial and Korsmeyer state in their recent review (48) that the ratio of Bcl-2/Bax constitutes a rheostat that sets the threshold of susceptibility to apoptosis for the mitochondria-dependent pathway. Accordingly, we tested if our mathematical model would demonstrate a counteracting role of Bcl-2 vis-à-vis the effects of Bax. We illustrate the effect of Bcl-2 on the proapoptotic effects of Bax in Fig. 5 A. The series of curves in this figure represent the bifurcation diagrams as a function of the degradation rate of Bax for different expression rates of Bcl-2. Fig. 5 B displays the results as a function of the synthesis rate of Bax. Therefore, Fig. 5, A and B, are the counterparts of the respective Fig. 4, A and C, obtained for different rates of formation of Bcl-2.

FIGURE 5.

Effects of Bcl-2 expression rate on cell behavior in response to changes in Bax levels. (A) Effect on the bifurcation diagram for μ_Bax; (B) effect on the bifurcation diagram for .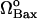

The increase in the rate of formation of Bcl-2, 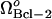, is observed to have several effects (Fig. 5 A). First, the limit point for the saddle-node bifurcation decreased to lower Bax degradation rates. When 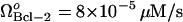, the limit point was μ_Bax = 0.11 s⁻¹ (Fig. 4 A). This result is included in Fig. 5 A for comparative purposes. The limit point decreased to μ_Bax = 0.085 s⁻¹ for 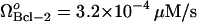, and to μ_Bax = 0.042 s⁻¹ for 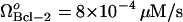. Hence, the bistable cell survival region, which may possibly give rise to apoptosis becomes narrower, whereas the monostable cell survival region becomes broader, when Bcl-2 is overexpressed. This result is consistent with the observation that Bcl-2 is overexpressed in many types of tumors that exhibit low rates of apoptosis (49). Second, the threshold concentration of casp3 for undergoing apoptosis with a given Bax degradation rate μ_Bax, tends to increase with increase in Bcl-2 expression rate, as indicated by the vertical shifting of the dashed portions of the curves in Fig. 5 A. This result implies that larger or more potent proapoptotic stimuli are needed for PCD when Bcl-2 expression levels are relatively high. Third, the apoptotic concentration of casp3 for given degradation rates of Bax (i.e., the solid portions of the bifurcation curves) are lowered with increasing Bcl-2 expression rates.

In Fig. 5 B, we observe the equilibrium caspase-3 concentrations as a function of Bax expression rate, 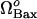, again for various rates of formation of Bcl-2, 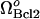. First, the limit point for the saddle-node bifurcation shifts to higher 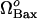values with increasing 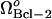. The limit point of 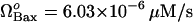(also shown in Fig. 4 C) is shifted to 1.17 × 10⁻⁵ μM/s, and then to 2.16 × 10⁻⁵ μM/s as 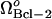increases from 8 × 10⁻⁵ μM/s to 3.2 × 10⁻⁴ μM/s, and then to 8 × 10⁻⁴ μM/s. Hence, the bistable region becomes narrower and the monostable cell survival region, broader, when Bcl-2 expression levels increase. Second, the threshold [casp3]₀ for entering apoptosis shift to higher values in the bistable regions. Third, the steady-state concentrations of casp3 in the case of apoptosis slightly shift to lower values, similarly to their counterparts in Fig. 5 A.

These results suggest that the proapoptotic effect of a low rate of Bax degradation or high rate of Bax expression can be counteracted by high rate of Bcl-2 expression, and is in keeping with the known interaction of these proteins (48). High Bcl-2 oncogene expression can sensitize the cells to cancer. Conversely, downregulation of Bcl-2 can sensitize melanoma cells to apoptosis (50,51). In a broader sense, the relative production and degradation rates of Bax and Bcl-2 determine whether the cell will survive or undergo apoptosis (48), consistent with our analysis.

Effect of MPTP on the detailed mitochondria-dependent apoptosis model

The mechanisms of cyt c release from mitochondria are highly diverse and controversial (52,53). In this model, we assume that cyt c release is closely dependent on the formation/activation of MPTPs (25,54) irrespective of Bax channel formation on mitochondria. The nonspecific MPTP involved in cyt c release is proposed to be a complex formed by the proteins VDAC-ANT-CyP-D (54). We denote this nonspecific pore by (VAC) here. The release of cyt c from the nonspecific pore, cyt c_mito + VAC → cyt c, with rate constant of 1μm⁻¹s⁻¹ is included in the model to account for this dependence.

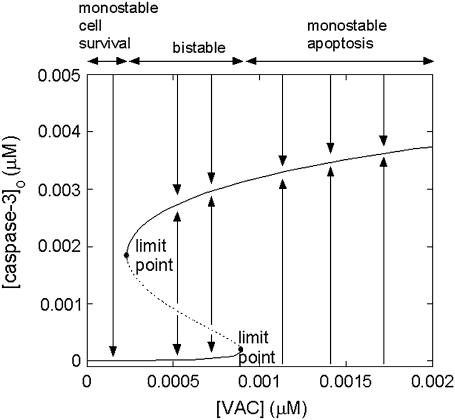
The bifurcation diagram in Fig. 6 illustrates the effect of VAC level on the steady-state concentration of caspase-3. In these calculations, the p53 concentration was assigned a relatively low value (0.0022 μM) so that the response to apoptotic stimulus (here [casp3]₀) would be monostable cell survival in the absence of VAC. At low levels of VAC (<2.3 × 10⁻⁴ μM), the system exhibits a monostable cell survival. At intermediate VAC levels (2.3 × 10⁻⁴ μM < [VAC] < 9.0 × 10⁻⁴ μM), a bistable behavior is observed, in accord with the healthy functioning of cells. At VAC levels above the limit point of 9.0 × 10⁻⁴ μM, apoptosis is induced, which may be pathological in some cases (25).

FIGURE 6.

Bifurcation diagram as a function of the concentration of mitochondrial permeability pore complex [VAC]. The limit points for saddle-node bifurcation are at [VAC] =2.3 × 10⁻⁴ μM and 9.0 × 10⁻⁴ μM.

Robustness of cooperative apoptosome formation as a mechanism that imparts bistability

Inhibition of caspases (19) was proposed previously as a mechanism that can lead to bistability. Our study of the robustness of different possible mechanisms using different reduced models (Fig. 2) indicated that the reduced model A, containing a positive feedback loop and a cooperative interaction, had a much higher propensity to exhibit a bistable behavior than the other three models. We conducted a similar computation for the detailed model proposed for mitochondria-dependent apoptosis. We mainly compared the robustness of two different mechanisms in inducing bistability: inhibition of caspase-3 by IAP and cooperative formation of apoptosome. To this aim, we organized the parameters into 13 groups and varied them within an order of magnitude, which led to 2¹³ = 8192 parameter sets. In the absence of cooperativity (i.e., when the coefficient p was set equal to unity), none of the 8192 simulations led to a bistable response to apoptotic stimuli despite the IAP inhibition of caspase-3. In the presence of cooperativity, or when p was assigned the respective values of 2 and 3, we observed that 320 and 736 of the runs resulted in a bistable response, supporting the importance of cooperative apoptosome formation for inducing bistability over a wide range of parameters.

Comparison with experiments

Inhibition of Bax degradation induces apoptosis in Bcl-2 overexpressing cells

Li and Dou (46) studied the effect of a proteasome inhibitor, N-carbobenzoxy-L-leucyl-norvalinal (LLnV), on Bcl-2 overexpressing Jurkat T cells that are protected from apoptosis. LLnV was shown to induce caspase-mediated apoptosis after cyt c release. It was also shown that LLnV inhibited Bax degradation in a cell-free assay. These findings are consistent with a role for the ubiquitin-proteasome pathway in regulating key players in the apoptotic cascade (41).

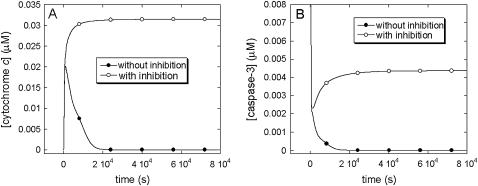
To test this conjecture, we carried out the following simulations. First, we examined the response of Bcl-2-overexpressing cells to apoptotic stimuli in the absence of a proteasome inhibitor. We assigned the values of μ_Bax = 0.1 s⁻¹ and 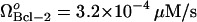, which result in monostable cell survival as the Bax degradation rate is higher than the limit point (0.085 s⁻¹) (See Fig. 5 A). The curve with the solid circles in Fig. 7, A and B, displays the time evolution of cyt c and caspase-3, respectively, under these conditions. Both curves show the depression of apoptotic molecules to negligibly low concentrations, suggesting the occurrence of monostable cell survival under these conditions. Second, we simulated the time evolution of the same Bcl-2-overexpressing cells in the presence of proteasome inhibitor, by linearly decreasing μ_Bax to 0.04 s⁻¹ in 1200 s, and maintaining this rate constant thereafter. The initial concentrations for both casp8 and pro3 were assigned to be 0.1 μM. This simulation resulted in an increase in cyt c release and an increase in casp3 level (curves with open circles in panels A and B of Fig. 7). The qualitative agreement between simulations and experiments suggests that the onset of cancer may be associated with a Bax degradation rate higher than a certain threshold value (the limit point in the bifurcation diagram shown in Fig. 5 A).

FIGURE 7.

Time evolution of (A) cyt c; (B) caspase-3 levels with (open circles) and without (solid circles) inhibition of Bax degradation. Inhibition of Bax degradation induces an accumulation in cyt c and caspase-3 levels.

Simulating the effect of silymarin on apoptosis

In a recent study by Katiyar et al. (44), it was shown that silymarin, a plant flavonoid that is known to inhibit skin carcinogenesis in mice, induced caspase-3 activation in JB6 C141 cells (preneoplastic epidermal keratinocytes). The concentration of silymarin is shown therein to be correlated with p53 concentrations, suggesting that silymarin acts via increasing the p53 levels.

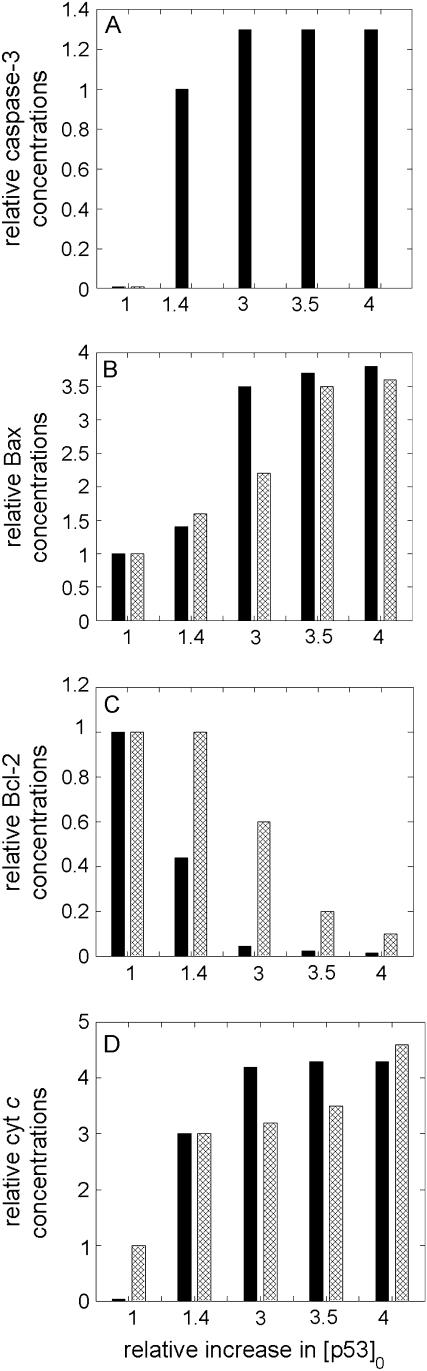
To explore if our model could explain/interpret the experimental data collected by Katiyar et al., we performed a mathematical analysis of the effect of changes in p53. We varied p53 concentration from a low value (0.0022 μM) characteristic of monostable cell survival, to higher values in accord with the relative increases reported in Fig. 3 of Katiyar et al. (44). The selected [p53]₀ values and resulting caspase-3 concentrations are shown in panel A of Fig. 8. The accompanying changes in the relative levels of Bax, Bcl-2, and cyt c are displayed in the respective panels B–D of the same figure. The comparison of the computational results (solid bars) with those from experiments (44), shown by the crisscrossed bars, shows that there is a good qualitative agreement between the two sets, except for Bcl-2 concentrations at relatively high p53 levels, which seem to deplete faster in computations than in experiments. This discrepancy may be due to the adoption of Eq. 10 for describing the time evolution of Bcl-2 (and Bax) expression levels as a function of p53 concentration. The threshold p53 concentration for inducing transcriptional activity refers to a relative increase in [p53]₀ of approximately two (abscissa in Fig. 8), and the computed abrupt decrease in Bcl-2 may be attributed to this change in regime. Additionally, experiments show the average behavior of an ensemble of cells (with a distribution of p53 concentrations), which would be expected to lead to a smoother change in [Bcl-2] compared to that predicted by computations.

FIGURE 8.

Comparison of the experimental and theoretical changes in caspase-3, Bax, Bcl-2, cyt c, in response to the relative changes in p53 (that are induced by changes in the flavanoid silymarin concentrations). Panel A displays the caspase-3 levels corresponding to each selected [p53] computed by present simulations. Panels B–D display the results from computations (solid bars) and those from experiments (criss-crossed bars).

CONCLUSION

In this study, the cooperative formation of heptameric apoptosome complex is proposed to be an important mechanism for the bistable behavior (survival or apoptosis) of cells in response to apoptotic stimuli of extracellular or intracellular origin. We examined the effects of Bax, Bcl-2, and MPTP levels on the time evolution of mitochondria-dependent apoptotic events, and show that there are subtle changes from monostable to bistable response, which may also be counteracted, depending on the relative concentrations of these components. We concentrated on two positive feedback loops in particular, which are suggested to play an important role in ensuring bistability (14–16,18,55). The former is initiated by the cleavage/inhibition of Bcl-2, and the latter by the truncation of Bid to tBid, both by the executioner caspase-3.

Several conclusions with possible biomedical implications are inferred from this analysis:

• There are critical values for the synthesis or degradation of Bax beyond which cells would exhibit a monostable cell survival. This result is in accord with observations suggesting that human prostate cancer cells might use Bax degradation as a survival mechanism (46). Our results are also consistent with the observed decreases in Bax expression levels in primary human breast tumors (47).

• Bcl-2 can counteract the proapoptotic effect of Bax to result in monostable cell survival, in line with the overexpression of Bcl-2 in many types of tumors (49) and the known role of Bcl-2 in countering the effects of Bax (48).

• The extent of MPTP may result in a diversity of responses, ranging from monostable cell survival, to bistable behavior, or monostable apoptosis. As shown in Fig. 6, an increase in [VAC] converts monostable cell survival response into a bistable response. The figure also shows that high [VAC] can lead to pathological cell death, in accord with the role of MPTPs in pathological cell death suggested by Green and Kroemer (25).

• The inhibition of Bax degradation can induce apoptosis. This result is in agreement with the observation of Li and Dou (46).

• Our model predictions are in quantitative agreement with the experimental data reported by Katiyar et al. (44) where p53 was induced by silymarin to induce casp3. The concentrations of cyt c and Bax are shown in both analyses to increase with the increases in p53 levels, whereas that of Bcl-2 would decrease.

Taken together, our results suggest that there might be a transition from bistable to monostable behavior in response to proapoptotic stimuli. The changes in synthesis and degradation rates of Bax and Bcl-2 and in the number of MPTPs may have a role in leading to aberrant phenotypes such as cancer and neurodegenerative disorders (2).

Previous mathematical models proposed for apoptosis (13,19,21–23) differ from this study in: i), the choice of apoptotic pathways, ii), their mathematical methods and parameters, and iii), the network properties focused on. With regard to apoptotic pathways, the model by Fussenegger et al. (21) and Bentele et al. (13) included both receptor-dependent (extrinsic) and receptor-independent (mitochondria-dependent) pathways. Eissing et al. (19) focused on receptor-dependent pathways observed in Type-I cells, Stucki and Simon (23) concentrated on pathways that regulate casp3, and Siehs et al. (22) focused on the interactions of Bcl-2 family members and consequent cyt c release. In terms of method of approach, Siehs et al. (22) simulated the time evolution of Bcl-2 family molecules using discrete time and space variables in a lattice molecular automaton. A systematical approach has been performed by Bentele et al. (13), not only to determine the parameters from experiments, but also to unravel the most important interactions by a rigorous sensitivity analysis. Fussenegger et al. (21) pioneered the mathematical modeling of apoptosis. However, this model would invariably progress toward apoptosis, containing no antiapoptotic mechanisms for cells. More recent models (13,19,22,23) including this study, point to the requirement of a homeostatic balance between the two responses, manifested by a bistable behavior or a switch from one response to another under well-defined conditions.

We examined mitochondria-dependent pathways here, which are connected to receptor-dependent pathways through cleavage of Bid by caspase-8, only. Our work differs from that of others in that caspase inhibition is not necessarily the only mechanism that leads to bistability. Instead, cooperativity in apoptosome formation is demonstrated to play an important role. This model is the first bistable model for mitochondria-dependent apoptosis, and suggests plausible roles for Bax, Bcl-2, and MPTP in pathologies such as cancer and diseases characterized by excessive apoptosis, which will need to be further established by experiments.