Can Conformational Change Be Described by Only a Few Normal Modes?

Abstract

We suggest a simple method to assess how many normal modes are needed to map a conformational change. By projecting the conformational change onto a subspace of the normal-mode vectors and using root mean square deviation as a test of accuracy, we find that the first 20 modes only contribute 50% or less of the total conformational change in four test cases (myosin, calmodulin, NtrC, and hemoglobin). In some allosteric systems, like the molecular switch NtrC, the conformational change is localized to a limited number of residues. We find that many more modes are necessary to accurately map this collective displacement. In addition, the normal-mode “spectra” can provide useful information about the details of the conformational change, especially when comparing structures with different bound ligands, in this case, calmodulin. Indeed, this approach presents normal-mode analysis as a useful basis in which to capture the mechanism of conformational change, and shows that the number of normal modes needed to capture the essential collective motions of atoms should be chosen according to the required accuracy.

INTRODUCTION

Although there are standard methods to experimentally probe conformational change (x-ray crystallography, NMR, cryoelectron microscopy (cryo-EM), fluorescence resonance energy transfer, etc.) (1–4), it is theoretically difficult to explain and predict this phenomenon. Conformational change usually occurs in timescales currently inaccessible to molecular dynamics (MD) simulations available today (∼1 ms) (5,6), and therefore other computational methods have to be applied, which may be limited to simpler or coarse-grained representations of the protein structure.

Normal-mode analysis (NMA) has proven successful in representing domain and hinge-bending motions in proteins (7–9). Indeed, it has been shown that for several systems, the lowest frequency modes contribute the most to a conformational change (10–13). NMA expresses the dynamics of a protein in terms of coordinates that involve the collective displacement of a large number of atoms.

The beauty of NMA lies in its theoretical simplicity, the speed of calculation, and the need for few parameters, relying mostly in the geometry and mass distribution of the system. NMA handles the effects of solvent implicitly, and when the elastic network model is used (13–24), it does not involve energy minimization. In addition, nonatomistic NMA methods (25) have shown the application of NMA in studying conformational change even when the resolution of the experimental data is poor, by calculating the normal modes of cryo-EM density maps.

NMA is based on a harmonic approximation of a perturbation around an equilibrium position. In theory, when considering the conformational change of a protein between two states A ↔ B, the atomic displacements are large and the condition of single energy minimum is not met: the system is out of the range of the quasiharmonic regime. Nonetheless, in many systems, such as lysozyme, crambin, and ribonuclease (7), citrate synthase (26), hemoglobin (22), and many others (11), the lowest-frequency modes still compare well with the experimentally observed conformational change upon ligand binding.

On the other hand, there are numerous cases where the NMA approach might fail. These could include large conformational changes where the protein assumes a new secondary structure upon ligand binding, or when the protein becomes disordered when losing the ligand. However, the various successful applications of NMA give reason to believe that normal modes are not merely a mathematical construction, but in fact do capture physical properties that are inherent to the connectivity and mass distribution of the system.

Furthermore, the complex motions and fluctuations of proteins may be decoupled into a linear combination of orthogonal basis vectors, each representing an independent concerted harmonic motion with a characteristic frequency. Although other complete coordinate systems could also serve to represent conformational change, normal modes can discriminate between large-scale (low-frequency) and local (high-frequency) motions. This is useful in many ways, such as restricting the degrees of freedom of our system to just those that are critical to determine a conformational change.

So far, NMA has primarily been employed to qualitatively characterize a conformational change: given two atomic structures and a set of collective atomic displacements, it is found that one or a few of these modes describe the observed direction of structural change. In fact, a comparative study of many systems by Tama et al. (11) indicates that a great deal of information about the conformational change is often found in a single low-frequency mode of the open form of a protein that exhibits open/closed conformations, therefore reducing the number of modes relevant to understand the conformational change. The relative importance of normal modes in a conformational change is assessed in different works by estimators such as “involvement coefficients” and “overlap coefficients” (11,12,24,26).

However, in general, these results do not quantify the contribution of each normal mode to the transformation between two protein conformations, as measured by typical measures of conformational change, such as the root mean square deviation (RMSD). Since the NMA methods do produce an orthogonal set of vectors, it is natural to use the normal-mode vectors as a coordinate basis set for understanding conformational change. However, due to the approximations often used to generate normal modes, such as simple, single force constant spring networks, the absolute values of the mode frequencies should likely not be considered quantitatively. Thus, in our work, we employ a different philosophy: we consider the normal-mode vectors as just a coordinate basis on which to map conformational change, whereas the frequencies associated with each mode are simply a way of indexing the basis vectors.

The primary goal of this study is to assess to what extent one can map one crystal structure onto another using normal modes, i.e., how many normal modes are sufficient to represent this transformation and whether these results can be generalized or are intrinsic to a particular system. These findings are especially relevant to model conformational change based on a coarse-grain model of a protein as well as to fit low-resolution maps where there is no available atomic-detailed information describing the structural change.

We employ an analytical method to determine the contribution of each mode to the conformational change. Given a reference conformation A and target B, we seek to obtain a good mapping of target B by taking A and a linear combination of its normal modes (Methods, Results). Using this method, we quantitatively show that the lower-frequency modes typically bring the reference conformation only 50% closer to the target conformation based on their RMSD, whereas the rest of the modes make a significant contribution (Methods, Results). We also calculate the average per-residue RMSD to assess to what extent the normal modes capture the collective displacements between the reference and the target, without affecting the residues that are not significantly displaced from the original conformation.

For normal-mode calculations involving conformational change, previous studies typically have cropped the original structures in such a way that the reference and target x-ray structures have the same number of atoms. It is a general belief that the normal-mode approach is robust enough to ignore these deletions. However, when studying conformational change, it is the difference and not the similarities between structures that becomes the focus of our attention. By deleting the differences (missing atoms in one conformation), we lose information that could contribute to the conformational change.

Here we apply a different methodology: the restricted-vector approach. This scheme allows us not only to retain the information that makes the structures different, but also to predict the positions of those atoms that have been omitted in the crystal structure of the target conformation (Methods, Results). Technically, in the restricted-vector approach, we calculate normal modes using the full set of atoms present in the Protein Data Bank (PDB) file of the reference structure. However, we restrict the RMSD comparison to the atoms present in both the reference and target structures. We then find the best amplitudes for the normal modes, which will map the reference conformation onto the target conformation, based on this reduced set of coordinates. In the end, we express the results in terms of the complete set of atoms of the reference structure.

For a test set, we use proteins that have been widely studied, both theoretically and experimentally: myosin motor domain, NtrC, calmodulin, and hemoglobin. These proteins have different sizes and conformational change is induced by different mechanisms: ATP hydrolysis and product release, phosphorylation, ligand binding, and oxygen binding, respectively. Previous normal-mode analyses of myosin (24,27), emphasize the importance of the lower-frequency modes to describe the motion of the converter region. Similar conclusions apply for calmodulin's central hinge (28). We observe that the number of relevant normal modes in all these systems depends on the accuracy we wish to obtain in the transformation between two protein conformations.

MATERIALS AND METHODS

Normal-mode theory

Normal-mode theory involves a harmonic approximation of the potential energy around a global minimum. Under this approximation, the forces in such systems become linear in the atomic coordinates, and a generalized force matrix can be written (14). The diagonalization of this matrix provides both the generalized coordinates (“normal modes”) in which the system is decoupled and the frequencies involved in the oscillation around the minimum. Complex fluctuations of the protein can be therefore expressed in terms of harmonic components, and every atomic displacement vector r_i(t) is a linear superposition of 3N normal modes α, each weighted by its eigenvector coordinate ξ_i^α for the atom mass m_i, an amplitude C^α, phase φ^α and frequency ω^α:

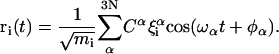(1)

The eigenvector coordinates form a transformation matrix Q, which transforms Cartesian coordinates into normal-mode coordinates.

However, obtaining the relevant spring constants could be quite a challenge. Instead, Tirion (14) suggested replacing the complex interatomic potential by a pairwise Hookean spring potential between atoms a and b:

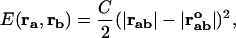(2)

where 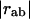is the distance between atoms a and b and 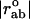is their distance in the equilibrium conformation. The constant C is phenomenological and can be assumed to be the same for all pairs inside a cut-off distance K_cut. In our calculations, we use K_cut = 8 Å, as suggested in previous studies (11,15).

We use the code developed by Sanejouand and co-workers (13–15,29). We apply the RTB (rotational-translational block) approximation, (13,30) implemented in the code, which treats selected groups of residues as rigid entities. The number of blocks determines the number of degrees of freedom in the system. In our calculations, we define that 1 residue = 1 block. Therefore, there are M = 6R − 6 eigenvectors (normal modes), where R is the number of protein residues, and the first six eigenvectors are subtracted because they correspond to the rotations and translations of the entire system as a rigid body. In addition to the published code, we implemented here the restricted-vector method as described in the following section.

Restricted-vector normal modes

In the alignment and RMSD calculation of two crystal structures A and B, a pairwise mapping between corresponding atoms is technically necessary. However, in general, the crystal structures do not have the same number of atoms. Indeed, if the conformational change involves a ligand, this will not be included in the alignment. When a ligand is the cause of the conformational change, its presence could have a major contribution to the perturbations around the minimum and affect the normal-mode vectors. To retain as much information as possible from the crystal structure, we perform the normal-mode calculation on the intact structure taken as the reference, using its full PDB coordinates (31).

Given two crystal structures, we chose reference and target structures A and B, (N_A, N_B number of atoms, respectively). We calculate the normal modes on structure A, in its complete form (all N_A protein and ligand atoms, no solvent ions or water). We compare PDB coordinates and select the number N_AB of atoms present in both (A∩B) the reference and the target structures. The alignment and RMSD calculation are restricted to this common set of N_AB atoms. Amplitudes C^α for each mode α will be found as explained in the next section. The final output is given in terms of the 3N_AB variables x, y, and z; and is a linear superposition of the reference structure A and its normal modes α, each weighted by its amplitude C^α.

Obtaining the normal-mode amplitudes

Given two conformational states A and B, of a protein with N atoms, if we consider B a small perturbation from the equilibrium position A, and if at time t = 0 every atom in position r_i is found in conformation B with velocity v_i = 0, then to a first-order approximation of state B:

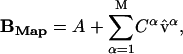(3)

where B and A are 3N-dimensional vectors with the atomic coordinates of all N atoms in conformations B and A. The normal mode 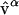corresponds to each of the 3N normalized eigenvectors of the force matrix (Hessian) and represents a collective displacement of atoms expressed in the Cartesian coordinates.

Because of the symmetric characteristic of the Hessian, there is a linear transformation Q that preserves distances, such that:

(4)

Q is the transformation that has the eigenvectors calculated on state A arranged in columns. The weight ξ_i^α is the displacement of each Cartesian degree of freedom i in normal mode β. The eigenvectors 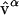are orthonormal such that 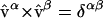, hence

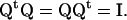(5)

The transformation Q maps any Cartesian set of coordinates X onto the normal-mode coordinates (amplitudes) C:

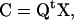(6)

where 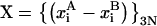is defined as a displacement vector from the reference structure A.

In particular, given conformation B, we can obtain the normal-mode amplitudes of B:

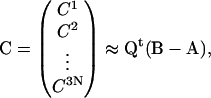(7)

and express B in terms of the normal modes of A and the amplitudes C^β:

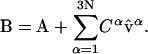(8)

In our work, because we use the RTB method (1 block = 1 residue), the number M of normal modes depends on the number of residues R as

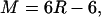(9)

for which the previous equations still hold and the eigenvector matrix Q is rectangular (3N × M). The eigenvectors of A, constructed using the RTB method, do not form a complete base; the intraresidue displacements are not represented.

We define B_Map as the mapped structure of B:

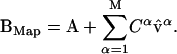(10)

If the structural change B-A is small, then 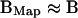, and therefore B_Map is a good approximation of the target structure B.

RMSD using normal-mode coordinate basis

Given the equilibrium conformational state A and a small perturbation B, of a protein of N atoms, the RMSD distance between these two conformations is

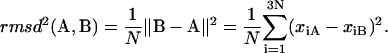(11)

Under the transformation Q, the normal-mode matrix calculated on conformation A is

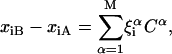(12)

where 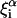is each of the coefficients of Q, α indexes the normal-mode coordinates, and i stands for the atomic coordinates. C^α is the amplitude of each normal mode.

Substituting Eq. 12 in Eq. 11 for the RMSD:

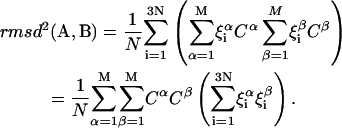(13)

Because the orthonormality relation between eigenvectors 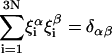holds,

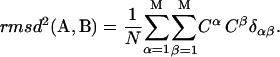(14)

We obtain a simple equation for the RMSD distance between two structures, based only on the amplitudes C^α of the M normal modes:

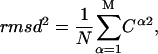(15)

where the sum in α includes all available normal-modes. In vector form:

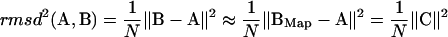(16)

As shown below (Results), these amplitudes C^α are not necessarily smaller for the higher-frequency modes; even high-frequency modes can have a major contribution to B_Map.

Proteins used in case studies presented

In this work we used several test systems: myosin, calmodulin, NtrC, and Hemoglobin. In the case of myosin, we used two protein analogs: scallop myosin and Dictyostelium myosin II. As regards the scallop myosin, we observe the transition from the reference state ADP-BeFx (ATP-analog) (PDB code 1KK8), to the nucleotide free “near-rigor” state (PDB code 1KK7) (32,33). For the Dyctyostelium myosin II, the available structures are reduced to the heavy chain: we consider the Mg-ATP complex (PDB code 1FMW) as the reference structure and the Mg-ADP complex as the target structure (PDB code 1VOM) (34,35). All coordinate files available at the RCSB Protein Data Bank (31).

For calmodulin, the reference structure is the ligand-free calmodulin structure (PDB code 1CLL). We chose two target structures: calmodulin complexed with trifluoroperazine (TFP) (PDB code 1LIN (37)) and calmodulin complexed with KAR-2 (PDB code 1AX5, (38)). For the molecular-switch NtrC, we take the unphosphorylated NMR structure (PDB code 1DC7) of the receiver domain as reference, and the structure with Asp-54 phosphorylated (PDB code 1DC8) as the target. For hemoglobin, we consider deoxy (PDB code 1A3N) and carbonmonoxy (PDB code 1BBB) human hemoglobin (39), respectively.

RESULTS

Normal-mode spectra as a representation of conformational change

Given two crystal structures of a protein (reference and target) we want to express the target structure in terms of the reference structure and a series of weighted normal modes. Each normal mode has an amplitude (weight) that is obtained by projecting the conformational change along the directions of the different normal modes calculated on the reference structure (see the Methods section for details). The study of how each normal mode contributes to the conformational change is important not only methodologically but also because it provides insight about the functional components and subprocesses leading to conformational change. We can find, for example, whether a bound ligand activates collective or individual atomic displacements, or compare the conformations induced by two different ligands. Because the unbound protein is more likely to populate the low-frequency modes in equilibrium, the activation of high-frequency modes suggests that the bound ligand is populating a different protein conformational state, which would be otherwise infrequent.

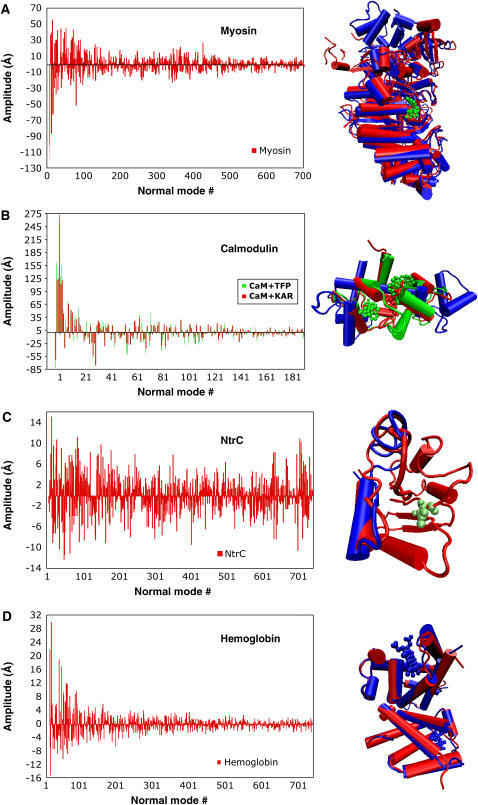
In Fig. 1, we show the amplitude of the normal modes for the structures studied (myosin, calmodulin, NtrC, hemoglobin). We call these graphs normal-mode spectra, since it is an analog to the Fourier transform of a complicated function into a basis set of orthogonal functions. Amplitudes can be positive or negative, but their absolute value yields the contribution of each mode to the conformational change. We stress that we use the normal-mode vectors simply as a coordinate basis in which to project the structural change. For our analysis, we only use the directions and amplitudes of these vectors; the frequencies associated with each normal mode simply serve as a way to rank the vectors in increasing order and separate those modes that entail more cooperative motions (low frequency).

FIGURE 1.

(Left) Normal-mode spectra for myosin, calmodulin, NtrC, and hemoglobin. (Right) Reference structure (blue) and target structure (red) for all cases. All the normal modes are calculated on the reference structure. Modes are indexed according to increasing frequency. (A) Myosin. The target structure (PDB code 1VOM), the reference structure (PDB code 1FMW), and the ATP ligand (green). (B) Calmodulin bound to KAR-2 (red) and TFP (green) (PDB codes: 1XA5 and 1LIN, respectively), ligand-free calmodulin (PDB code 1CLL). (C) NtrC molecular switch (reference PDB code 1DC7, target PDB code 1DC8), phosphorylated in residue Asp-54 (green). (All 3-D molecular visualization graphics in figures were done with visual molecular dynamics (41).)

It is interesting to notice the large differences in spectra between the systems presented here. In general, the lower-frequency modes bear the larger amplitudes, coinciding with previous works that suggest that the lower-frequency modes are the ones responsible for the conformational change (10–13) . However, we see that this is not always the case, and the first 20 normal modes do not necessarily have the largest amplitudes. In myosin (Fig. 1 A), the first normal modes are definitely relevant, but modes that rank between index 90–110 and 450–550 have larger amplitudes than some of the lower-frequency modes.

In calmodulin (Fig. 1 B), the first 20 normal modes have the larger amplitudes, but as we show below, they account for only 50% of the conformational change. In the case of calmodulin, the normal-mode spectra also provide comparative information about the displacements incurred by the protein when bound to two different ligands, TFP and KAR-2. We observe in Fig. 2 B that the spectra of the two different complexes follow a similar pattern of amplitude, and it agrees well with the fact that even if the ligands make different contacts with the residues in the cleft, both structures are very similar. In the case of the molecular switch NtrC, the conformational change is restricted to a small set of residues that are perturbed by the phosphorylation of Asp-54 (Fig. 1 C). As a result, the normal-mode basis proves extremely inefficient to probe this conformational change, which would be better expressed in terms of the rotation and translation of a few residues. However, we can still project this change into the normal-mode basis, and obtain a mapped structure, as we show in the next section, provided that we use a large number of normal-mode vectors (∼700 vectors).

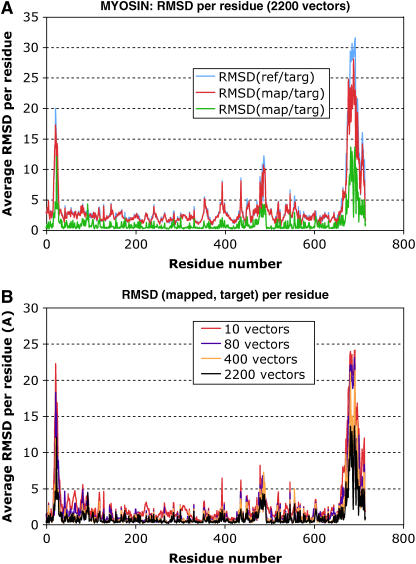
FIGURE 2.

(A) Average RMSD difference per residue between the target and both mapped and reference using all calculated normal modes (2214). (B) RMSD(mapped, target) shows that using 2214 vectors, the deviation is reduced considerably when compared to the deviation using 10, 80, and 400 eigenvectors.

These examples show that even if the first normal modes present larger weights, some higher-frequency modes are also important for mapping the reference into the target structure. The issue of how many modes must be included in the mapping of two structures should be addressed by taking into account the accuracy expected in this process. We define an accurate mapping as one that yields a structure similar to that of the target. As we show later in Results, we use the all-atom root mean-square-distance (RMSD) and the Cα-RMSD as our metric for accuracy between the target structure and the mapped structure (obtained by projection). Because the RMSD has a very simple expression in terms of the normal-mode basis (Eqs. 15 and 16), we can easily express how RMSD between the reference and target structures depends on the number of normal-mode vectors included in the mapping.

Mapping of structures: myosin and calmodulin as examples

Starting with the reference structure and the normal-mode spectra as presented in Fig. 1, we can obtain a fairly good approximation of the target structure B provided we use a large number of normal-mode vectors. We build the mapped structure B_Map by adding normal modes to the reference structure A, according to Eq. 10 (see Methods):

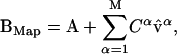where 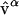is each of the M normal-mode vectors included in the projection, and C^α is the respective mode amplitude as shown in the normal-mode spectra (Fig. 1).

In Figs. 2–4, we show two examples: calmodulin and myosin. In the case of myosin (Figs. 2 and 3), we base our study on the crystal structures of the motor domain (Methods). ATP binds to myosin and it is thought that changes in the nucleotide, as it hydrolyzes from ATP to ADP and phosphate, are transmitted through the protein residues to change the interaction of myosin and actin. The converter domain in the myosin head is the one that undergoes the major conformational change when the phosphate group is released; and it is responsible for the power stroke that pushes myosin along the actin filament.

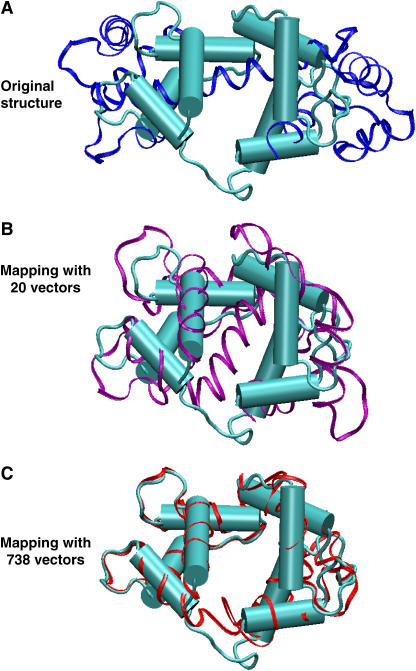
FIGURE 4.

Mapping of calmodulin using 744 normal-mode vectors, all-atom RTB normal modes. The reference structures (ligand-free) are in blue, and the target structures (CaM-TFP complex) in cyan. (A) Reference (blue ribbons) and target (cyan). The reference and the target structures differ with RMSD = 15.09 Å. (B) Reference with 20 added normal modes (purple ribbons) fit the target with RMSD = 2.26 Å. (C) Reference with 738 added normal modes (red ribbons) fit the target with RMSD = 2.26 Å.

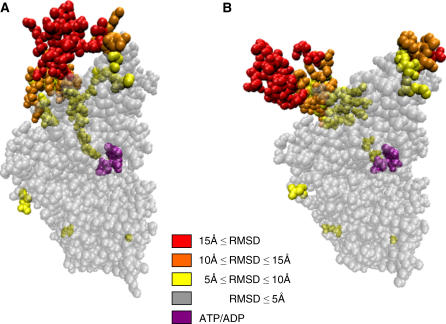
FIGURE 3.

Reference and target structure of myosin. Residues are colored according to the average RMSD(reference, target) per residue. ATP residue is in purple.

The ADP-myosin complex structure is thought to be close to the conformation of myosin before the power stroke (34). The ATP-myosin complex structure is thought to capture the prehydrolysis state, and we take this structure as the reference conformation (35). The all-atom RMSD(reference, target) = 5.4 Å. Because of the computational cost, we only computed the lower 2214 of the available M = 4434 normal-mode vectors. By adding 2214 weighted normal modes to the reference, we obtain a fairly good approximation of the target: RMSD(mapped, target) = 1.81 Å.

We can calculate the average per-residue RMSD between two aligned structures A and B by

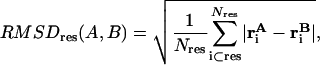(17)

where we average the distances between all atoms in a certain residue.

In Fig. 2 A, we plot the average per-residue RMSD(reference, target) and the RMSD(reference, mapped) for all residues in the myosin structure. Because the mapped structure should be close to the target structure, we expect the deviation from the reference to be localized in the same residues. We can see from this graph that both RMSD curves overlap, showing that this method captures the conformational change incurred by the protein. However, the fact that both target and mapped structure deviate in the same residues from the reference does not ensure that they will be similar. We need to test that the RMSD per residue between the mapped structure and the reference is not significant, especially in the converter region. Fig. 2 B plots the average RMSD per residue between mapped and target. These plots are made for a variable number of normal modes: 10, 80, 400, and 2200 (out of 2200 total computed normal-mode vectors). We show here that there is not much improvement in RMSD by adding from 10 to 80 vectors as regards the most variable residues, but adding 400 certainly makes a significant difference in the RMSD. Still, it can be noted that further high-frequency modes are needed to improve the fit for residues 660–716, which are the most variable ones in the converter region (Fig. 2 B).

In Fig. 3, A and B, we can compare and contrast the reference structure and the target structure, where the converter region has switched to an open conformation. In Fig. 3 B, residues in the mapped structure are colored according to the average RMSD (reference, target) per residue. It is interesting to point out that residues around the ATP/ADP do not undergo a big conformational change. The mechanisms that drive and amplify the perturbation from the ATP binding site to the converter region are still an interesting unsolved puzzle.

Fig. 4 shows the mapping of the ligand-free calmodulin structure into the TFP-bound structure. Fig. 4 A shows the “open form” of calmodulin as the reference structure, with RMSD(reference, target) = 15.09 Å. By adding the first 20 weighted normal modes to the reference structure, we achieve a closed structure: RMSD(mapped, target) = 7.47 Å; however, other modes are still needed to get the final position of helices and loops. As we are using the RTB approximation (Methods) by which each residue is taken as a rigid body, there are M = 738 normal-mode vectors (Table 1). Using all 738 normal modes, we obtain an all-atom RMSD(mapped, target) = 2.26 Å for the TFP-bound structure (Fig. 4 C). Similar results apply for the structure bound to KAR-2, where the RMSD(mapped, target) = 2.15 Å.

TABLE 1.

Name and details of proteins taken as case studies

Protein	A, NA (reference structure)	B, NB (target structure)	NA∩NB	Residues (= blocks)	RMSD (reference/target)	RMSD (map/target)	No. of vectors used
Myosin	1FMW, 5884	1VOM, 5775	5601	740	5.40	1.81	2214
Calmodulin	1CLL, 1130	1LIN (TFP), 1244 1AX5 (Kar), 1152	1104	144	15.09	1.97	858
			1071	864	13.80	1.96	858
NtrC	1DC7, 1911	1DC8, 1910	1910	123	2.53	1.17	738
Hemoglobin	1A3N, 2271	1BBB 2282	2271	288	2.02	1.08	894

Which and how many normal modes are needed depend on the desired accuracy

In this section, we analyze the importance of each normal-mode vector in the context of the total RMSD incurred in the conformational change. The RMSD is the distance between two structures in Cartesian space and thus serves as a common metric for comparing structures. Previous works have analyzed the decrease in the RMSD as a function of the included normal modes (10). Here, we compare this decrease for different case studies to address the question of how many modes are needed to describe conformational change.

As shown in Methods (Eq. 15), the all-atom RMSD has a very simple expression in terms of the amplitudes of the different modes,

where C^α are the amplitudes of the different normal modes. As we add the weighted contributions of the normal modes to the reference structure A, it becomes more similar to the target structure B, and the RMSD drops, as in Figs. 5 and 6. In Fig. 5, we present the all-atom RMSD between the reference and the target as a function of normal-mode vectors added to the reference. Each added vector is weighted by the mode amplitude obtained by projection, as shown before (see Normal-mode spectra as a representation of conformational change, and Fig. 1), and contributes to drive the reference structure further toward the target. Fig. 6 parallels the results of Fig. 5, but with the Cα-RMSD (instead of all-atom RMSD) between the reference and the target.

FIGURE 5.

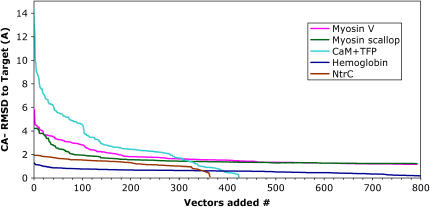
All-atom RMSD between the reference and the mapped structure, as a function of the number of normal-mode vectors included in the mapping. Vectors are weighted by the amplitudes obtained by projection, and are added in order of increasing frequency. Different systems are shown: myosin (pink), calmodulin bound to TFP (cyan), hemoglobin (blue), and NtrC (brown).

FIGURE 6.

C^α RMSD between the reference and the mapped structures, as a function of the number of the normal-mode vectors included in the mapping.

Figs. 5 and 6 address the question of how many modes are needed to achieve certain accuracy in the mapping. These results suggest that the answer depends on the system in particular, but in general, many modes (>10) should be considered. We observe from Fig. 6 (Cα-RMSD) that similar conclusions apply in the case where the side chains have been excluded from the model. In the case of calmodulin, for example, the first 20 normal modes have larger amplitudes, yet only allow an RMSD drop from RMSD(reference, target) from 15.09Å to 7.09Å (47% of the total conformational change as measured by RMSD). Including all the computed modes (738), the RMSD(mapped, target) = 2.26 Å becomes 15% of its original value. However, this is not the case for the other systems (myosin, hemoglobin, and especially NtrC) where other modes seem to contribute to the RMSD in a similar amount.

In principle, it would be necessary to include all 3N normal-mode vectors to be able to obtain an exact projection between reference and target. However, as we are using the RTB method (13), by which residues are kept as fixed entities, the basis set is reduced to M = 6R − 6 degrees of freedom, where R is the number of residues. Because intraresidue motions are constrained, the perfect projection cannot be attained.

In addition, there is another source of error that prevents the RMSD(mapped, target) from converging to zero. Namely, the normal modes are calculated using Cartesian coordinates. Cartesian coordinates fail when dealing with large torsional displacements. By construction, Cartesian normal modes work properly for infinitesimal torsions but, when weighted by large amplitudes, they stretch the residues in nonphysical ways (i.e., angles are pulled apart, the peptide bond plane is not preserved). The basis set of the RTB approximation lacks the intraresidue degrees of freedom needed to compensate for this distortion. Every algorithm that uses Cartesian normal modes will suffer from this effect to some extent.

In the case of large proteins, such as myosin, it is computationally very expensive to compute and diagonalize an all-atom Hessian. To avoid the RTB method and the stretching of residues, the protein can be coarse-grained into a system of effective residues, adopting, for example, a Cα-reduced model (Fig. 6), but if the aim is to obtain an atomic-detailed model of the structure, reintroducing the side chains into the model is not straightforward. Because the normal-mode transformation is orthonormal, it preserves distances. Accordingly, if instead of using the normal modes of A, we use another orthonormal linear transformation of the Cartesian space (e.g., the normal modes of B), we obtain similar results for the projection of the change B–A, provided we use the same number of normal-mode vectors M (Methods).

This analysis differs from other estimators such as overlap or involvement coefficient used in previous works (11,12,24,26) since it places the contribution of each normal mode in the context of the total RMSD distance between the reference and the target. It greatly facilitates answering how many modes are needed in terms of the desired accuracy.

DISCUSSION

Normal-mode spectra provide a new framework for studying conformational change, allowing the ranking of the different components of that change into collective (low-frequency) versus local (high-frequency) contributions. At the same time, analyzing the relative importance of the different normal modes can provide insight into the nature of the conformational change.

It has been observed in the modeling of experimental data that the amplitudes of conformational dynamics can be larger than the equilibrium thermal fluctuations if one considers the protein as a system of coupled harmonic oscillators (8). “Flexible-fitting” of cryo-EM structures (36), and refinement of x-ray structures in which the mode amplitudes are refined against the experimental data show that this is true for several systems. However, most of these refinements are carried out using <50 normal modes.

When bound to a structure, a ligand can stabilize a conformation that is generally unpopulated in the ligand-free state, or else can stretch the structure along the direction of certain normal modes that were irrelevant in the unbound state. Because of this, there is little reason to anticipate which modes will be active in the ligand-bound state (and fitting should include as many modes as computationally affordable). An extreme example of this point is the case of NtrC, where the phosphorylation of Asp-54 produces a localized displacement that does not correlate with any of the normal modes of the unbound state. To represent such conformational change, many (if not all) of the modes are needed, but if restricted by computational cost, then the selection has to be done based on relevance, not on frequency number. Our conclusions agree with a recent normal mode study on loop motions in the binding pocket of protein kinases. Cavasotto et al. (40) showed that using a relevance measure, few low-frequency modes (<∼10) are necessary to describe loop flexibility but, remarkably, these relevant modes are not the first modes in the spectra.

The normal-mode spectra are useful to select the most relevant degrees of freedom (those with larger amplitudes) and better understand the conformational change. In the case of calmodulin, its flexible structure is open in the ligand-free form. Upon binding, it closes upon the ligands like a clamp, adopting different conformations, resulting in a distinct protein function. In our work, we study the complexes of calmodulin with two noncompetitive drugs, TFP and KAR-2 (38). The spectral analysis allows the comparison between these ligand-bound structures. Even if the mode amplitudes that correspond to KAR-2 and TFP differ, it can be observed (Fig. 1 B) that they follow a certain pattern, especially regarding the sign (positive/negative) of the normal-mode vectors.

This kind of analysis correlates well with the experimental result (38) that similar tertiary structures form when KAR-2 or TFP bind to calmodulin, even though the two ligands interact (for the most part) with different residues in the ligand-binding site. Indeed, calmodulin binds KAR-2 as a “noncompetitive”, “nonantagonist” partner of TFP, and as suggested by the authors, KAR-2 does not prevent calmodulin from binding most of its physiological targets. By construction, the normal-mode analysis we use here does not discriminate between different atoms. Thus, our analysis is useful to study the tertiary structure and allosteric similarities between two complexes, independent of the underlying nature of the interacting contacts.

CONCLUSIONS

Because conformational change implies collective motions of atoms, NMA offers a natural set of coordinates in which to map conformational displacements. Thus, we can expect that a macromolecule fluctuates around the ligand-free equilibrium state (8), populating the conformation space along the low-frequency mode directions. Following the model of a protein as an elastic system in equilibrium, the square of the amplitude of each mode is proportional to the temperature and inversely proportional to the frequency of oscillation, and thus we expect the energy of the macromolecule to increase when stretched along one of its high-frequency modes. However, even if in the majority of cases ligand binding perturbs a system along its lower-frequency normal modes, this is not always the case. The ligand can stretch the protein in ways that involve higher-frequency modes provided that there is an energy gain in the process, and therefore the system can populate a new conformational state.

Here we obtain the amplitude of many normal modes (>700) for several widely studied allosteric systems and observe that some higher-frequency modes can indeed be activated by a ligand. As the RMSD (all-atom and Cα) has a simple expression in terms of the mode amplitudes, we have an easy way to estimate how many modes are needed to achieve a certain degree of accuracy between a target structure and the projection obtained by adding weighted normal modes to a reference structure.

In regard to applications, the normal-mode spectra of a protein allow the tertiary-structure comparison between proteins that bind to different ligands, independently of the residues involved in the contacts. The spectral analysis points out which are the important normal modes that are involved in the conformational change. Because of this, NMA could be a useful tool to generate starting structures for MD simulations. As in the case of calmodulin bound to KAR and TFP, it is reasonable to expect that new drugs would produce similar conformations. By sampling on the amplitudes of the most relevant modes, we could generate starting conformations that would never be attained by standard MD time steps. This type of analysis is also useful to reconstruct x-ray structures of different conformations where some residues are missing. Using the more complete structure as a reference, missing residues can be reconstructed in the target by adding normal-mode vectors to the reference with information drawn from comparison of the existing atoms.

The analysis we present here shows that the normal-mode basis can be useful to capture the relevant degrees of freedom of the system. However, it must be taken into account that these degrees of freedom might not necessarily be found among the lower-frequency modes, provided that there is a free-energy cost paid to activate higher-frequency modes. These conclusions are especially important at the times of coarse-graining large biomolecules, where computational time is the limiting factor and an important challenge for the future.