Evaluating Tilt Angles of Membrane-Associated Helices: Comparison of Computational and NMR Techniques

Abstract

A computational method to calculate the orientation of membrane-associated α-helices with respect to a lipid bilayer has been developed. It is based on a previously derived implicit membrane representation, which was parameterized using the structures of 46 α-helical membrane proteins. The method is validated by comparison with an independent data set of six transmembrane and nine antimicrobial peptides of known structure and orientation. The minimum energy orientations of the transmembrane helices were found to be in good agreement with tilt and rotation angles known from solid-state NMR experiments. Analysis of the free-energy landscape found two types of minima for transmembrane peptides: i), Surface-bound configurations with the helix long axis parallel to the membrane, and ii), inserted configurations with the helix spanning the membrane in a perpendicular orientation. In all cases the inserted configuration also contained the global energy minimum. Repeating the calculations with a set of solution NMR structures showed that the membrane model correctly distinguishes native transmembrane from nonnative conformers. All antimicrobial peptides investigated were found to orient parallel and bind to the membrane surface, in agreement with experimental data. In all cases insertion into the membrane entailed a significant free-energy penalty. An analysis of the contributions of the individual residue types confirmed that hydrophobic residues are the main driving force behind membrane protein insertion, whereas polar, charged, and aromatic residues were found to be important for the correct orientation of the helix inside the membrane.

INTRODUCTION

Due to the extremely high computational cost of molecular mechanics simulations using explicit lipid bilayer membranes (1–3), there has been an increasing interest in implicit membrane representations (4–8) to explore membrane protein insertion and orientation (9–11) or structure prediction and folding (8,12). But the relative paucity of structural data has impeded the development of knowledge-based potentials that have been successfully applied in globular protein structure prediction (13). Instead, a set of methods with increasing levels of sophistication has been developed to predict the topology of transmembrane (TM) α-helices in membrane protein sequences, reaching accuracies close to 100% (14–16). A recent study, however, demonstrated that the number of membrane protein structures is now sufficient to derive meaningful potentials of mean force (17). Adapting a method used for globular proteins (18,19), an implicit membrane representation was derived from the distributions of amino acids along the membrane normal. These distributions were calculated from all α-helical membrane protein structures at resolutions better than 4 Å available at the time (April 2004; an up-to-date summary of current structures is provided by S. H. White—http://blanco.biomol.uci.edu/).

Since the lipid bilayer environment provides the dominant driving forces for membrane protein folding and integration (20,21), it was assumed that the preference of different amino acids for clearly defined regions along the membrane normal is a direct result of the specific interactions of these amino acids with the membrane environment. Indeed it was found that the distributions could be used to calculate a potential of mean force along the membrane normal for each amino acid corresponding to an effective implicit membrane potential. The resulting overall potential as well as the individual residue potentials are in good agreement with experimental and computational data (22–24).

This work was motivated by the recent successes in using solid-state NMR methods in oriented lipid bilayers to determine the orientation (i.e., tilt and rotation angles) of TM helices in lipid bilayer membranes (25). So far seven systems have been studied: Gramicidin (26), the M2 channel segment of the δ-subunit of the nicotinic acetylcholine receptor (AchR) (27), the influenza A M2 channel (28), the α-factor receptor M6 helix (29), the membrane conformation of the FD coat protein (30), virus protein U (VPU) from HIV-1 (31), and a synthetic peptide derived from the NR1 subunit of the N-methyl-D-aspanate (NMDA)-glutamate receptor (27). These systems allow an assessment of the usefulness and accuracy of the implicit membrane representation to predict correct orientations of TM helices in their native environment. For each structure the minimum energy position and orientation as well as the insertion energy landscape in the membrane was calculated and compared with experimental data.

To further investigate whether the implicit membrane model can distinguish a native TM from a non-TM conformation, we repeated the calculations for a number of antimicrobial peptides. This class of antibiotics is generally believed to form amphipathic α-helices that oriented parallel to the membrane in a surface-bound fashion (32–35). The peptides work by disrupting the electrochemical gradients across the cell membranes for a broad spectrum of bacteria, and in some cases also fungi and red blood and some tumor cells. Solution NMR structures determined in dodecylphosphocholine micelles are currently available for magainin (36) and a number of cecropin-magainin hybrids (37). The model peptides ovispirin and novispirin (38) representing the 18 residue N-terminal segment of the powerful endogenous sheep antibiotic SMAP-29 were determined in trifluoroethanol.

In the last section we examine the individual contributions of each residue family (hydrophobic, polar, charged, and aromatic) to the overall free-energy landscape of a peptide, as well as exploring future improvements to the implicit membrane model.

METHODS

Potentials of mean force membrane model

The implicit membrane was parameterized using all 46 α-helical membrane protein structures currently available in the protein database with resolutions >4 Å and has been described in more detail in a previous publication (17). Where several structures of the same protein were available, the highest resolution structure was used. Any identical chains were removed and the proteins were structurally aligned with respect to the membrane center, which was placed at the origin 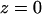. The proteins were aligned so that residues in the TM region facing the extracellular side are along the negative z axis and residues facing the cytoplasm are along the positive z axis.

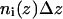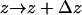The normal distance of the backbone carbon α−atom from the membrane center was measured for each residue. Subsequently, the distribution along the bilayer normal was derived by counting the number of amino acids of type in the interval , which was chosen to be 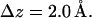The distributions were fitted using the trial function

(1)

giving smooth potential functions. Gaussians were chosen in good agreement with experimental evidence from lipid distortion (39,40), x-ray, and neutron diffraction experiments on fluid liquid-crystalline bilayers (41–43), partitioning experiments on a variety of tryptophan analogs (44,45) as well as hexane (46) in lipid bilayers and computer simulations of membrane proteins in explicit fluid lipid bilayers (22).

For each amino acid type i a potential of mean force 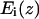was calculated as a function of the membrane normal (z axis) only. The potentials were derived by adapting a method used for globular proteins (18,19). The measured frequency of residues 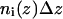was normalized giving

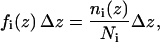(2)

where .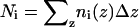

This normalized frequency distribution corresponds to a potential of mean force

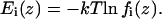(3)

Here k is the Boltzmann constant and T is the temperature of the native state of the protein. The potential of mean force of the overall residue distribution was chosen as the reference state

(4)

where the sum is over all amino acid types 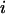. The resulting potentials of mean force are given by

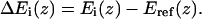(5)

For hydrophobic residues (Ala, Ile, Leu, Val, and Phe) the potentials of mean force exhibit a single broad potential energy well at the center of the membrane, whereas charged residues have a narrow peak at the membrane center and a slight depression at the cytoplasmic interface. Aromatic residues (His, Trp, and Tyr) have potentials with two wells, one at each membrane interface, and polar residue potentials (Asn and Gln) display a single broad peak centered in the membrane. Pro was found to occur predominantly in the interfacial loop regions. Nevertheless, unlike charged and polar residues, it is also represented throughout the membrane region. No potentials were calculated for residues Cys, Ser, and Thr—Cys because it occurs too infrequently to be statistically valid and Ser and Thr because the potential is essentially flat after subtraction of the reference state. The potentials are generally in good agreement with experimental free energies of solvation both for buried and interfacial locations (23).

Calculating the minimal energy conformation

The minimal energy conformation was calculated by exploring the entire translational and rotational space of the peptide in the membrane, represented by the above potentials. For each peptide the range of residues defining its helical part was selected (see Tables 1 and 2). This segment was then used to calculate the center of mass using the heavy backbone atoms (N, C, Cα, and O). The long axis of the helix was determined through diagonalization of the inertia tensor of the segment, again using only the heavy backbone atoms. The tilt angle was defined as the angle of the helix long axis with respect to the membrane normal, whereas the rotation angle was defined as the angle of rotation around the helix long axis.

TABLE 1.

Experimental data and computational results for the transmembrane helices

Transmembrane helices
		Experimental			Calculated
PDB	Name	Helix (Residues)	Tilt (°)	Tilt (°)	z (Å) (kcal/mol)	ΔE
1a11	Acetylcholine M2 (1cek)	2–24	11 (12)	20 ± 5	−0.5 ± 0.2	−4.7 ± 0.1
				158 ± 4	−2.5 ± 1.3	−4.7 ± 0.1
				92 ± 1	−10.0 ± 0.4	−3.3 ± 0.4
1mzt	FD coat protein	21–44	19 (26)	23	−4.0	−9.7
				164	3.0	−7.8
				88	−11.0	−5.8
1fdm	FD coat protein	28–46		27 ± 10	−4.7 ± 0.5	−7.2 ± 1.2
				152 ± 8	−1.0 ± 4.8	−5.6 ± 1.9
				87 ± 6	13.8 ± 0.9	−7.2 ± 1.0
1mp6	Influenza A M2	23–45	37 (38 ± 3)	41	1.0	−7.8
				137	−2.0	−7.2
				86	−8.0	−5.9
1pje	VPU	8–25	16 (13)	50 ± 1	0.0 ± 0.0	−10.2 ± 0.0
				130 ± 1	−1.6 ± 0.8	−9.8 ± 0.2
				92 ± 2	−6.9 ± 0.3	−7.8 ± 0.1
1pjd	α-Factor receptor M6	4–17	4 (13)	151 ± 1	1.0 ± 0.0	−5.2 ± 0.0
				26 ± 1	−2.0 ± 0.0	−4.8 ± 0.0
				76 ± 1	−8.0 ± 0.0	−4.1 ± 0.0
2nr1	NMDA receptor	6–26	–	40 ± 2	2.3 ± 1.6	−4.8 ± 0.0
				145 ± 7	0.8 ± 1.4	−4.6 ± 0.2
				91 ± 1	−9.8 ± 0.5	−4.8 ± 0.0

The table lists the residues defining the helical segment (Helix), the helix tilt angle (Tilt), the displacement of the center of mass of the helix with respect to the membrane center (z), as well as the insertion energies (ΔE) for TM, upside-down, and surface-bound configurations. Where several NMR structures were available, the calculations were repeated for all conformers. For these cases, the conformational average and standard deviations are given. The membrane center is located at z = 0, and −ve z-values correspond to shifts toward the extracellular side, whereas +ve z-values correspond to shifts toward the cytoplasm. The experimental tilt angles were calculated from the aligned solid-state NMR structures deposited in the Protein Data Bank (PDB) using the method described in the text (see “Calculating the minimal energy conformation”). The values in the bracket are the numbers given in the publications. The dissimilarities are a reflection of the different methods used to calculate tilt angles.

TABLE 2.

Results for the surface-adsorbed helices. For each peptide 20 solution, NMR structures were available

		Surface-adsorbed helices
PDB	Name	Helix (Residues)	Tilt (°)	z (Å)	ΔE (kcal/mol)
2mag	Magainin	4–21	87 ± 7	13.0 ± 0.0	−3.52 ± 0.07
1hu5	Ovispirin 1	4–16	94 ± 11	15.0 ± 0.0	−3.85 ± 0.06
1hu6	Novispirin G10	4–11	88 ± 6	16.0 ± 0.5	−3.40 ± 0.10
1hu7	Novispirin T2	7–17	87 ± 12	16.0 ± 0.0	−3.37 ± 0.13
1f0d	Magainin-cecropin hybrid	11–17	89 ± 7	17.6 ± 0.9	−3.63 ± 0.15
1f0e	Magainin-cecropin hybrid P2	10–17	91 ± 8	18.7 ± 0.7	−3.54 ± 0.21
1f0f	Magainin-cecropin hybrid P1	4–13	88 ± 4	19.3 ± 0.7	−3.43 ± 0.09
1f0g	Magainin-cecropin hybrid P3	NA	90 ± 10	17.4 ± 0.7	−3.55 ± 0.17
1f0h	Magainin-cecropin hybrid P4	13–19	86 ± 11	18.2 ± 0.8	−3.37 ± 0.19

Magainin and the magainin-cecropin hybrids were determined in dodecylphosphocholine micelles, whereas the ovispirin and novispirin structures were determined in trifluoroethanol. The values represent averages over all 20 models.

The helix was translated from −50 Å to +50 Å along the membrane normal (membrane center = 0 Å) in 0.5 Å steps. At each step the helix was rotated through all space to find the orientation of minimum energy by first tilting it with respect to the membrane normal and subsequent rotation around its long axis until all tilt and rotational states have been sampled with a step size of 1°.

For a 30 residue helix each full scan will take ∼15 min on a 3 GHz Xeon CPU. Where several models were present from the NMR experiments, the calculations were repeated for each structure.

NMR structures

The following TM helices were analyzed in this study (see Table 1). AchR M2 (1cek) (27), influenza A M2 (1mp6) (28), α-factor receptor M6 (1pjd) (29), FD coat protein (1mzt) (30), VPU (1pje) (31), and a synthetic peptide derived from the NR1 subunit of the NMDA-glutamate receptor (2nr1) (27). The tilt angle of the above proteins was obtained using solid-state NMR techniques with the exception of the NR1 subunit, which was nevertheless found to have a TM orientation.

For VPU (1pje) and α-factor receptor M6 (1pjd), not all residues present in the peptide were located by the NMR experiment. The missing residues are the polar and charged residues at the helix termini, which are important for the correct orientation of the helix in the membrane (see Contributions of individual residues, below). To be able to compare the current analysis with the experiment, the missing residues were added with optimized geometry in an α-helical secondary structure. Ten model structures were generated for each helix via molecular dynamics simulations with the backbone of the residues located in the NMR structure held in place by strong harmonic restraints. For 1pjd Ala-Gln was added at the N-terminus and Lys at the C-terminus. For 1pje five residues (Gln-Pro-Ile-Gln-Ile) were added to the N-terminus and five residues to the C-terminus (Ile-Ile-Glu-Gly-Arg). The remainder of the C-terminal chain (Gly-Gly-Lys-Lys-Lys-Lys) is a six-residue “solubility tag” that facilitates the isolation, purification, and sample preparation and was therefore not modeled.

In the case of the solid-state NMR structure of the AchR M2 (1cek), which also lacks the charged residues at the termini, the equivalent solution NMR structures (27) (1a11) were used, which have the complete sequence.

All nine antimicrobial peptide structures investigated in this study have been determined by solution NMR in micelles (see Table 2), namely, Magainin (36), 5 cecropin-magainin hybrids (1f0d, 1f0e, 1f0f, 1f0g, and 1f0h) (37), and the model peptides ovispirin (1hu5), novispirin G10 (1hu6), and T2 (1hu7) (38).

RESULTS AND DISCUSSION

Transmembrane helices

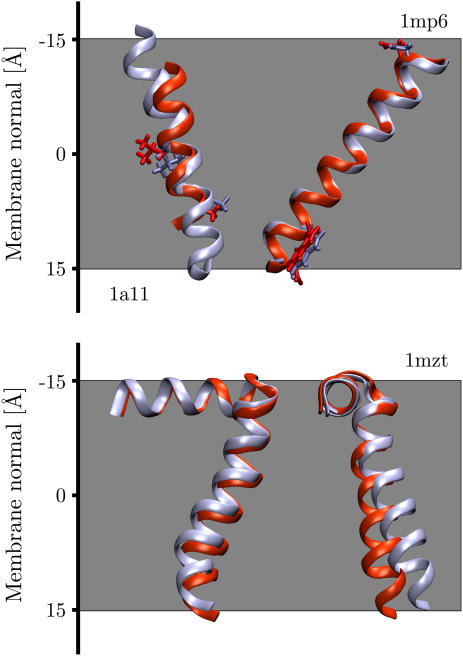
Figs. 1 and 2 show the global minimum energy orientation of the TM helices with respect to the membrane together with the corresponding orientations determined from solid-state NMR experiments. Values for the position along the membrane normal, tilt angle, and minimum insertion energy are listed in Table 1 together with experimental tilt angles. Since the position along the membrane normal (i.e., z axis) is not known from NMR studies, the figures show the helices with their centers of mass superimposed. All three peptides have the correct orientation with respect to the cytoplasmic side of the membrane (down), and in each case the minimum energy conformation corresponds to a TM orientation.

FIGURE 1.

Overlay of computational and solid-state NMR structures (in red) for acetylcholine M2 (1a11), influenza A M2 (1mp6), and FD coat protein (1mzt). Each helix lies flat in the plane of the page except 1mzt, where the tilt into the page is shown. The cytoplasmic side is down (+ve z axis). Residues Ser⁸, Gln¹³, and Asp²⁴, and Trp⁴¹ have been highlighted for acetylcholine and influenza A, respectively, showing that the helices have virtually identical rotation angles.

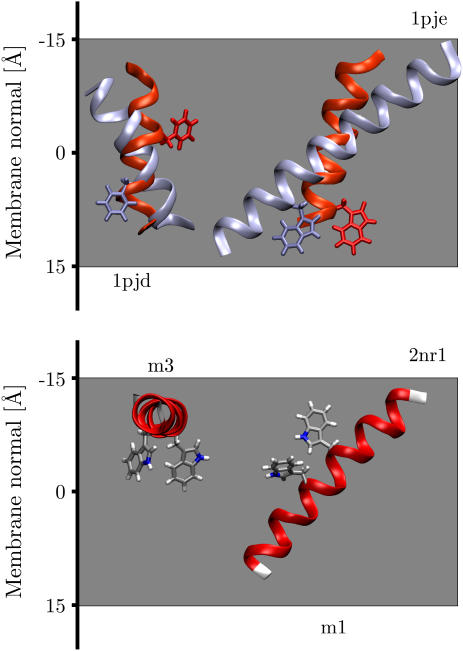
FIGURE 2.

Overlay of computational and solid-state NMR structures (in red) for α-factor receptor M6 (1pjd) and VPU (1pje). The 10-solution NMR structures of a synthetic peptide derived from the NR1 subunit of the NMDA receptor exhibited two minimum energy conformations (2nr1, models 1 and 3). Each helix lies flat in the plane of the graph except for model 3 of 2nr1, which lies perpendicular. The cytoplasmic side is down (+ve z axis).

Fig. 1 shows the predicted minimum energy orientation of AchR M2 (1a11, model 2) together with the solid-state NMR structure (1cek). Whereas the tilt angle differs slightly, the rotation angle is virtually identical. All 10 AchR M2 solution NMR structures (1a11, models 1–10) were analyzed. Models 1 and 2 were found to have the best overlap with the solid-state NMR structure, having tilt angles of 19° and 18°, respectively, only slightly higher than the 11° found by the experiment (27). The AchR M2 minimum energy conformations fall into two distinct categories. One with a TM configuration (mean tilt 20° ± 5°) and another orientation with a tilt of 158° ± 4°, corresponding to a 22° ± 4° angle with respect to the membrane normal but with the protein upside down in the membrane (see Table 1). This conformational dependence will be explored in more detail below (see Conformational sensitivity).

The orientation of influenza A M2 (1mp6) was found to be in excellent agreement with the NMR results, with tilt angle deviations of only 4° and almost identical rotation angles (see Fig. 1). Both the NMR and the calculated values are slightly larger than the 32° ± 6° tilt angle obtained from site-directed infrared dichroism spectra reconstituted in lipid vesicles (47). For the FD coat protein (1mzt), the minimum energy orientation shows a perfect overlap of the extracellular surface-bound helix and only a slight 4° tilt deviation of the TM helix compared to the NMR results (see Fig. 1).

Fig. 2 shows the global minimum energy conformation with respect to the membrane for α-factor receptor M6 (1pjd, model 1) and VPU (1pje, model 1) together with the corresponding orientations determined from solid-state NMR experiments. The minimum energy conformations clearly correspond to TM orientations; nevertheless there are significant differences in the tilt angles. Whereas the NMR data found a tilt angle of 16° for VPU, the implicit membrane found a tilt angle of ∼50°, both in turn are much larger than the 6.5° ± 1.7° found by infrared dichroism of synthetic VPU_1–31 (48). The discrepancy is almost certainly the result of modeling the five terminal residues on either side of the peptide in a conformation differing from the solid-state NMR experiment, which unfortunately could not resolve these residues. Nevertheless, the rotation angle is in good agreement with the NMR structure. For the α-factor receptor M6, the disagreement of the implicit membrane model with experimental data can be explained by the fact that the 1pjd peptide only represents the cytoplasmic half of the M6 TM helix. This also explains why it was found to be upside down with respect to the cytoplasmic side, since the implicit membrane model incorporates the known preference of charged amino acids for the intracellular side of a membrane (17,49). Repeating the calculations for α-helical models with a complete sequence of the presumed TM segment of the M6 TM helix (50) resulted in tilt angles of 10°–20° (data not shown), much closer to the values known for TM helices in general (21°–24°) (17,51,52).

Interestingly, the 10-solution NMR structures of the NR1-derived synthetic peptide revealed both TM (models 1, 2, 4, 5, 8, and 9) and parallel surface-bound orientations (models 3, 6, 7, and 10). Two models representative of each orientation (2nr1, models 1 and 3) are shown in Fig. 2. Each conformation has a well-defined tilt angle and position along the membrane normal, with only small deviations between the models (see Table 1). Both orientations have nearly identical insertion energies. In the intact NMDA receptor this region is probably not entirely α-helical but may form a P-loop similar to potassium channels (53). Solid-state NMR experiments point to an inserted TM orientation, but the exact tilt angle could not be determined (27).

In general the analysis of the TM helices showed three distinct minimum energy conformations: i), TM, ii), upside-down TM, and iii), conformations with the helix long axis parallel to the membrane in a surface-bound configuration. All TM helices were found to have an energy minimum close to the membrane center (see Table 1). The relative energy differences with respect to the aqueous domain range from −4.7 kcal/mol for AchR M2 to −10.2 kcal/mol for VPU. These values compare well with experimental estimates of the free energy of insertion for a single TM helix, which are in the range of 5–12 kcal/mol (54–57). It should be noted, however, that experimental difficulties make these values somewhat unreliable (58,59).

Recent spectroscopic and NMR measurements of the tilt angles of the M13 major coat protein, influenza A, and VPU peptides in lipid bilayers with different hydrocarbon tail lengths have shown that the helix tilt angle is in fact dependent on the hydrophobic thickness h of the host membrane (60–63). In all cases a decrease of the hydrophobic thickness resulted in an increased tilt angle as the helix tries to bury as many of the hydrophobic central residues as possible in the membrane core. For example, the tilt angle of the M13 major coat protein increased from 19° ± 4° in dieicosenoyl-phosphatidylcholine (h = 33.0 Å) to 23° ± 4° in dioleoyl-phosphatidylcholine (h = 29.5 Å), 26° ± 4° in dipalmitoleoyl-phosphatidylcholine (h = 26.0 Å), and 33° ± 4° in dimyristoleoyl-phosphatidylcholine (h = 22.5 Å) lipid bilayers, indicating that the change in tilt angle of the TM helix is a principal compensation mechanism for hydrophobic mismatch (60).

The hydrophobic thickness is difficult to estimate for the implicit membrane model, since the Gaussian residue potentials represent averages over proteins from different membrane environments with diverse lipid compositions. However, the reasonable agreement with the experimental tilt angles suggests that it lies in the 23–31 Å range of the lipids used in the solid-state NMR measurements.

Surface-bound helices

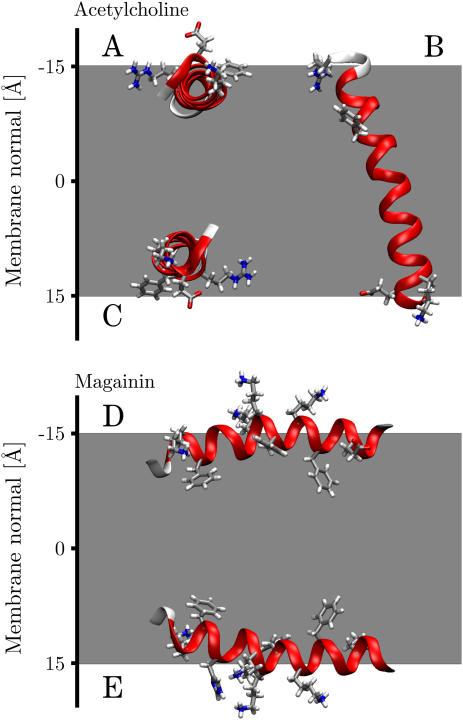
All antibiotic peptides analyzed in this study were found to orient parallel to the membrane in a surface-bound configuration, in excellent agreement with theoretical considerations (64,65), solid-state NMR experiments (33,35,36,66), spectroscopic methods, (67,68) as well as computer simulations (69). Panel A of Fig. 3 shows the minimum energy orientation for ovispirin (1hu5), novispirin (1hu6), and a cecropin-magainin hybrid (1f0d). Results for the remaining antibacterial peptides investigated (1hu7, 1f0e, 1f0f, 1f0g, 1f0h, and 2mag) exhibit exactly similar behavior and are summarized in Table 2. All peptides are oriented such that their hydrophobic residues face the membrane, whereas hydrophilic residues point toward the aqueous phase, again in excellent agreement with theory and experimental observations (33,35). The mean tilt angles of the peptides are in a narrow range of 90° ± 4°, identical to the ∼90° found for ovispirin by solid-state NMR (35).

FIGURE 3.

(A) Global minimum energy configurations of ovispirin (1hu5), novispirin (1hu6), and a magainin-cecropin hybrid (1f0d). (B) Global minimum conformations of FD coat protein from micelles (1fdm, models 12 and 17).

Table 2 also lists the distance of the minimum energy conformations from the center of the membrane. The distances can be seen to be in the range of 13–19 Å from the membrane center. Magainin was found to bind closest of the peptides studied with a distance of 13 Å. Experimental studies using colorimetric and time-resolved fluorescence techniques in biomimetic phospholipid/poly(diacetylene) vesicles found magainin to insert close to phospholipid glycerol backbone in bilayers incorporating negatively charged phospholipids (67). This corresponds to a membrane displacement of ∼15 Å, comparable to the 13 Å found in this study. Similar displacements were found for cecropin-melittin hybrids using paramagnetic resonance spectroscopy (70).

Insertion “pathways”

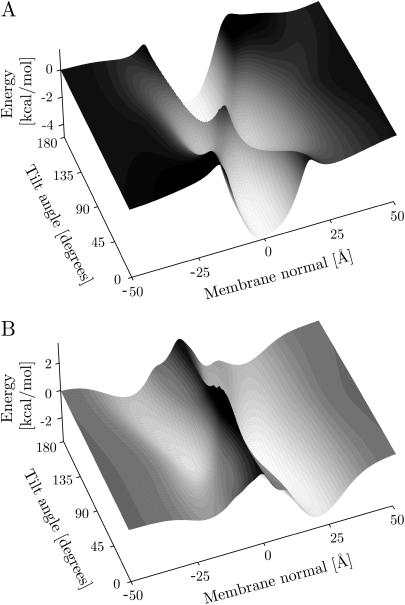
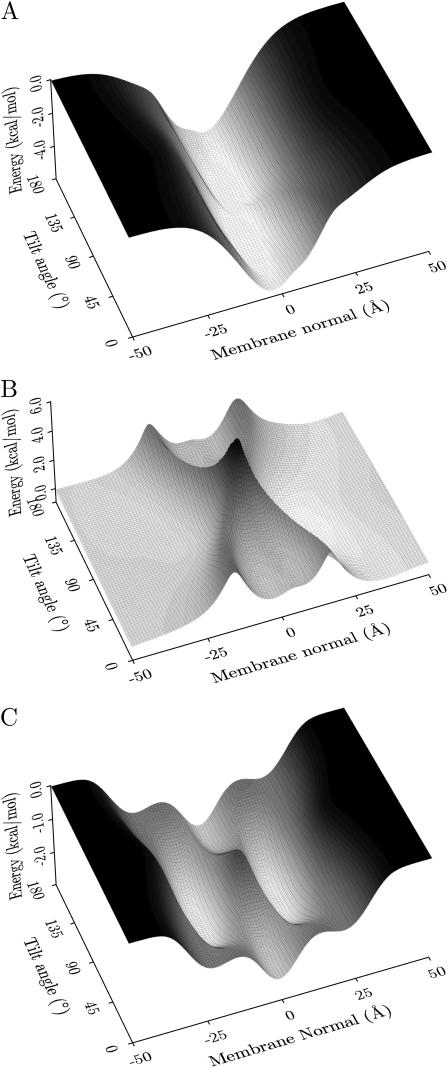
It is interesting to investigate the free-energy landscape of the proteins for other, local minimum energy orientations. To do this the membrane potential was plotted as a function of position and tilt angle, whereas the rotation angle was optimized (i.e., the rotation angle for each position and tilt angle is such that the energy is minimal). The resulting free-energy landscapes for AchR M2 (1a11, model 2) and magainin (2mag, model 1) are shown in Fig. 4. The potential zero was chosen at an infinite distance from the membrane. AchR can be seen to have four distinct minima, with the two deepest minima corresponding to TM configurations with the helices approximately parallel to the membrane normal. One is the global minimum oriented correctly with respect to the cytoplasmic side (−0.5 Å, 18°, −4.8 kcal/mol; minima for model 2, the other models have similar values; cf., Table 1), whereas the other one is upside down in the membrane (−1.0 Å, 162°, −4.8 kcal/mol). The other two minima correspond to helices bound to the interfacial membrane surface in a parallel orientation on the cytoplasmic (9.0 Å, 93°, −3.5 kcal/mol) and extracellular (−10.5 Å, 92°, −3.1 kcal/mol) sides, respectively (see Fig. 5). They are not as deep as the corresponding TM minima but are the preferred orientations of the helix near the membrane surfaces. Thus when inserting a helix into a membrane, the current calculations support a model where it binds to the membrane in a parallel orientation first and subsequently changes to a perpendicular TM configuration. This is in accordance with general theoretical considerations (3) as well the two-stage folding model for α-helical membrane proteins (21,71), which has recently been modified to include a third stage (21). There is strong experimental evidence for independent helix formation and insertion in the first stage. At the second stage, helices associate in the membrane-forming concave cavities and clefts that may facilitate the insertion of loops (e.g., the pore region in KcsA (72)), more hydrophilic polypeptide sequences (e.g., the TM2a helix in SecY (73)), or prosthetic groups (e.g., the retinal in bacteriorhodopsin (74)) in the third stage.

FIGURE 4.

Insertion energy profiles. The figure shows the free energy of the helix as a function of the helix tilt and center-of-mass position along the membrane normal for optimized rotation angle (around the long axis of the helix). Panel A shows the profile for the AchR helix M2 (1a11, model 2), and panel B shows the profile for magainin (2mag, model 5). The membrane potentials were chosen such that they are zero at an infinite distance from the membrane.

FIGURE 5.

Local minimum energy orientations of AchR M2 (1a11, model 2) and magainin (2mag, model 1). The upside-down orientation of AchR M2 is not shown but has a similar tilt angle and central position to panel B.

Repeating the analysis for all 10 AchR M2 solution NMR structures gave topologically identical free-energy landscapes to that shown in Fig. 4. Generally inserted TM configurations are the most stable, with the correctly orientated conformation having an insertion energy of −4.7 ± 0.1 kcal/mol at the center of the membrane (−0.5 ± 0.2 Å). The upside-down TM orientation has identical insertion energy but is displaced slightly to the extracellular side (see Table 1). Adsorption of the peptide onto the membrane surface is also favorable but to a lesser extent, with energy minima of −3.7 ± 0.4 kcal/mol for the cytoplasmic (8.6 ± 0.5 Å) and −3.3 ± 0.4 kcal/mol for the extracellular interface (−10.0 ± 0.4 Å). These results are in very good agreement with a recent theoretical study of the same structures (75,76), which found average energies of −4.7 ± 2.1 kcal/mol and −2.6 ± 2.4 kcal/mol for inserted and surface-bound configurations, respectively. The study used a theoretical continuum-solvent method developed by Ben-Tal (77) that has been successfully applied to estimate the insertion energies of TM peptides and proteins (78). To compare the results, the helix-coil transition free energy (ΔG_con = −2.4 kcal/mol) was subtracted, since the current data estimate the insertion energy of a folded helix.

Interestingly the free-energy landscapes of the other TM helices investigated in this study displayed topologically similar behavior, with four distinct energy minima at similar locations, suggesting that it might be considered a “fingerprint” of a TM helix.

For the antibiotic peptide magainin the free-energy landscape can be seen to differ substantially in topology. There are only two minima and the membrane is represented by a large barrier spanning the entire tilt range of the helix with an energy penalty for insertion into the membrane (the barrier height is 4–6 kcal/mol, with respect to the minima). Fig. 4 shows that the two energy minima correspond to surface-bound conformations at z = 13 Å and −14 Å, with tilt angles of 82° and 95°, respectively (ΔE = −3.6 and −2.7 kcal/mol).

The global minimum was located on the cytoplasmic side of the membrane. This is a consequence of the implicit membrane model. Membrane protein structures have on average a third more charged residues at their cytoplasmic side, resulting in a potential well. Therefore a highly charged peptide will prefer the cytoplasmic side. The free-energy landscapes for ovispirin and the two novispirins are topologically similar to magainin with only two minima, one for each surface-bound conformation. However, the cecropin-magainin hybrids displayed more complicated free-energy landscapes with several local minima at inserted configurations, albeit at much higher energies than the surface-bound global minima, which were virtually identical for all antimicrobial peptides investigated (see Table 2).

Conformational sensitivity

Comparing the minimum energy orientations of the solution FD coat protein NMR structures (1fdm) with the structure determined from oriented lipid bilayers (1mzt) can provide some insight into the sensitivity of the implicit membrane representation in distinguishing native TM from nonnative TM conformations. Analyses showed a broad spread of tilt angles ranging from 15° in an inserted TM orientation (z = −4 Å) to 94° where the TM helix orients in a surface-bound conformation (z = 15 Å). Only two narrowly defined positions were found, one at the membrane surface 13.8 ± 0.9 Å and the other near the membrane center −4.7 ± 0.5 Å (see Table 3). Panel B of Fig. 3 shows the energy minimum orientation of one member from each group (1fdm, models 12 and 17). In both cases the polar surface-bound helix has folded toward the TM helix. Whereas model 12 still inserts into the membrane in a near-native conformation, the polar surface-bound helix of model 17 is almost parallel to the TM helix, thus preventing it from inserting correctly due to the energy penalty associated with inserting a polar helix into the hydrophobic core of the lipid bilayer. This suggests that the implicit membrane is capable of correctly identifying a TM fold and that it can distinguish it from a structurally similar non-TM conformation.

TABLE 3.

Positions, tilt angles, and insertion energies for the minimum energy configurations of the 20 solution NMR structures of FD coat protein (1fdm)

FD coat protein solution NMR structures (1fdm)
Model	z (Å)	Tilt (°)	ΔE (kcal/mol)
1	−4	16	−8.24
5	−4	22	−8.71
8	−4	15	−7.83
9	−4	31	−9.10
13	−5	26	−7.00
14	−5	38	−6.32
15	−5	22	−6.47
16	−5	30	−6.07
17	−5	42	−5.51
18	−5	21	−7.76
19	−5	14	−7.62
20	−5	41	−5.73
Mean	−4.7 ± 0.5	27 ± 10	−7.20 ± 1.18
2	14	87	−7.44
3	13	83	−7.87
4	13	91	−7.76
6	13	80	−7.98
7	13	88	−7.57
10	14	93	−7.27
11	15	94	−5.19
12	15	80	−6.31
Mean	13.8 ± 0.9	87 ± 6	−7.17 ± 0.96

The structures were sorted into two groups according to their position along the membrane normal.

This conformational sensitivity might explain why the calculated orientations of structures that required modeling of missing residues (1pjd, 1pje) differed considerably from the solid-state NMR data, whereas structures that did not require modeling were generally found to be in good agreement with experimental results (1mzt, 1mp6).

Interestingly the structures which best resemble the solid-state NMR orientation in the membrane also have the lowest insertion energies (models 1, 5, 9), whereas surface-bound configurations are generally higher in energy. This finding is important since for a realistic implicit membrane potential it is essential that the correct TM conformation has the lowest free energy.

Contributions of individual residues

It is generally recognized that overall hydrophobicity is the main driving force for the integration of TM helices into the lipid bilayer (79). Indeed the vast majority of residues in TM helices are hydrophobic (52). Nevertheless, polar, charged, and aromatic residues are known to be important for anchoring the helix termini into the lipid headgroup environment at the membrane interfaces (44,80,81).

To investigate the relative roles of hydrophobic, polar-charged, and aromatic groups, their contributions to the total insertion potential was calculated. Fig. 6 shows the contributions of hydrophobic residues (panel A) and polar-charged residues (panel B) to the overall free-energy landscape of AchR M2 (1a11, model 2) shown in panel A of Fig. 4. Hydrophobic residues are the main contributors to the helix insertion potential. However, they favor no tilt angle in particular. On the other hand polar-charged residues show low energy penalties for helix orientations parallel to the membrane surface, especially on the cytoplasmic side, whereas TM orientations correspond to local minima separated by high barriers. Nevertheless the overall potential favors TM orientations since hydrophobic residues strongly prefer an inserted to a surface-bound configuration.

FIGURE 6.

Contributions to the overall insertion energy. Panel A shows the contribution of hydrophobic residues, and panel B shows the contribution of polar and charged residues for AchR M2 (1a11, model 2). The total insertion energy landscape is shown in panel A of Fig. 4. Panel C shows the contribution of aromatics at the termini of the artificial WALP peptide (see text).

Panel C of Fig. 6 shows the aromatic contribution to the insertion energy of the artificial WALP peptide (82). This peptide has two tryptophan residues, one at each helix terminus flanking a hydrophobic core made up of alternating alanine and leucine residues. The aromatic potential landscape exhibits four minima. Two represent parallel surface-bound configurations, whereas the other two are TM orientations. Again, the overall conformation of the helix is determined by combining the aromatic and hydrophobic potentials (similar to panel A), resulting in a TM orientation even thought the aromatic contribution favors a surface-bound orientation.

This suggests that although hydrophobic residues are essential for the overall insertion of the peptide, it is the polar, charged, and aromatic residues that are crucial for determining the correct orientation in the membrane. However, the Gaussian hydrophobic residue potentials have a tendency to try to orient a purely hydrophobic sequence parallel to the membrane at the center (cf., strong tilt angle of VPU). Nevertheless, the termini of naturally occurring TM segments are generally abundant in charged and polar residues, which prevent their burial in the hydrophobic core of a bilayer.

CONCLUSION

Helical membrane protein insertion is thought to occur by secondary structure formation at the surface and subsequent insertion of α-helical segments into the lipid bilayer (20,21). This model is consistent with this study, which found that all TM helices possess local insertion energy minima for configurations bound parallel to the membrane surface as well as for inserted orientations with low tilt angles. The inserted configurations were generally found to have lower minima than those bound to the membrane surface, as expected for a TM peptide.

Comparison of the calculated tilt and rotation angles with solid-state NMR structures in oriented lipid bilayers showed good agreement for AchR, FD-coat protein, and influenza A. For VPU the calculated tilt angle was much larger, possibly due to the modeling of the terminal residues, which were not located in the NMR experiments; nevertheless the rotation angle was found to be nearly identical. The α-factor receptor was the only system to show significant differences with experimental findings, which is most likely a reflection of the fact that the structure represents only the cytoplasmic half of a TM helix.

Calculating the minimum energy orientations of solution NMR structures of FD coat protein demonstrated the conformational sensitivity of the implicit membrane in distinguishing native TM from structurally closely related but nonnative TM conformers. It was found that the structures most closely resembling the native state also exhibited the lowest overall insertion energies, a necessary prerequisite for a realistic implicit membrane potential.

All antimicrobial peptides investigated were found to have minimum energy conformations for orientations parallel to the membrane in a surface-bound configuration, pointing their hydrophobic residues toward the membrane center while exposing their polar residues to the aqueous environment, in excellent agreement with experimental data. The free-energy landscapes showed that there is a penalty for peptide insertion into the membrane regardless of the tilt angle.

Analysis of the contributions of the individual residues toward the total insertion energy showed that hydrophobic residues are the main driving force for insertion of the peptide into the membrane, whereas polar, charged, and aromatic residues are crucial for determining the correct orientation.

In general the translational and rotational energy landscapes described here represent a detailed search of the orientation space of the peptides considered. The smoothness of the energy landscapes is remarkable, and the good overall agreement with theoretical, experimental, and simulation data is encouraging.