Flexural Rigidity of Individual Microtubules Measured by a Buckling Force with Optical Traps

Abstract

We used direct buckling force measurements with optical traps to determine the flexural rigidity of individual microtubules bound to polystyrene beads. To optimize the accuracy of the measurement, we used two optical traps and antibody-coated beads to manipulate each microtubule. We then applied a new analytical model assuming nonaxial buckling. Paclitaxel-stabilized microtubules were polymerized from purified tubulin, and the average microtubule rigidity was calculated as 2.0 × 10⁻²⁴ Nm² using this novel microtubule buckling system. This value was not dependent on microtubule length. We also measured the rigidity of paclitaxel-free microtubules, and obtained the value of 7.9 × 10⁻²⁴ Nm², which is nearly four times that measured for paclitaxel-stabilized microtubules.

INTRODUCTION

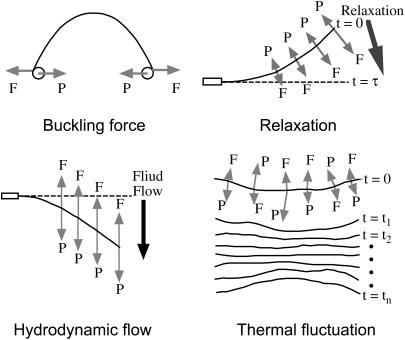
Microtubules are important components of cytoskeletal structures, which, in conjunction with actin and intermediate filaments, provide both the static and dynamic framework that maintains cell structure. Microtubules resist various internal/external forces to maintain cell shape and they support motor proteins to generate the force required for cell movement and changes in shape. Given the fundamental contribution of microtubules to cellular architecture, we were interested in quantifying microtubule deformation in response to an external force. Flexural rigidity is one of the parameters used to quantitate microtubule deformation. The mechanical principle is analogous to Hooke's law for a spring (1) and represents the deforming force required under the assumption that the microtubule is a homogenous thin rod. Microtubule rigidity was first estimated by statistical measurement of microtubule curvature in electron microscopic images (2). Since then, microtubule rigidity has been further estimated from dynamic video images using four methods: 1), buckling force measurement using optical traps and beads (3,4); 2), image analysis of the relaxation process following microtubule bending (5,6); 3), image analysis of microtubule bending via hydrodynamic flow (7,8); and 4), image analysis of thermal fluctuations of microtubule shapes in solution (7–13). These methods are illustrated in Fig. 1. Although these methods are based on the same mechanical principle, they differ with regard to the following (summarized in Table 1): whether the selected process is a static or dynamic process; whether the analysis involves classical mechanics, statistical mechanics or hydrodynamics; the type of force applied to manipulate the microtubule; the type of working force on the microtubule; the balance and direction of working forces and the microtubule internal spring force; and the number of force fulcrums. Consequently, results obtained using the above methods differ over a wide range of two orders of magnitude, and thus there is no reasonable consensus value for microtubule rigidity (Table 2). Although the reasons for the large, method-dependent discrepancies in the rigidity value are unclear at present, we made simple improvements to the buckling force method toward the goal of achieving a reliable estimate, as described below.

FIGURE 1.

Four types of methods for a single microtubule rigidity measurement. F is the microtubule internal spring force caused by deformation and P is the synthetic external force working on a microtubule.

TABLE 1.

Features of four different methods to evaluate microtubule rigidity

Methods	Process	Analysis	Working force on MT (P)	Force balance	Force direction	Number of force fulcrums	Manipulation force
Buckling force	Static	Classical mechanics	Compressive force	P = F (keep buckling)	P = F	Two points	Optical trap(s)
Hydrodynamic flow	Static	Hydrodynamics	Hydrodynamic drag force	P(s) = F(s) (keep bending)	P(s) = F(s)	Continuous	Fluid flow
Relaxation	Dynamic	Hydrodynamics	Hydrodynamic drag force	P(s,t) < F(s,t) (relaxation)	P(s,t) = F(s,t)	Continuous	Optical trap
Thermal fluctuation	Dynamic	Statistical mechanics	Thermal force + Hydrodynamic drag force	P(s,t) > F(s,t) (bending) P(s,t) = F(s,t) P(s,t) < F(s,t) (relaxation)	P(s,t) ≠ F(s,t) P(s,t) = F(s,t)	Continuous	Nothing

The value s is the distance along a microtubule, and t is the time.

TABLE 2.

Flexural rigidity of microtubules obtained with different experimental methods

Microtubules	Methods	Flexural rigidity (× 10−24 Nm2)	Temperature (°C)	References
Paclitaxel-free MT (Pure MT)	Buckling force	7.9	33	This work
	Buckling force	6.8		(4)
	Hydrodynamic flow	8.5	37	(7)
	Hydrodynamic flow	35.8	37	(8)
	Relaxation (RELAX)	3.7	22–25	(5)
	Relaxation (WIGGLE)	4.7	22–25	(5)
	Thermal fluctuation	26.0	37	(11)
	Thermal fluctuation	4.6	37	(7)
	Thermal fluctuation	26.5*	37	(8)
	Thermal fluctuation	18.5		(12)
	Thermal fluctuation	13.7–27.0*	23	(13)
Paclitaxel-stabilized MT	Buckling force	2.0	33	This work
	Buckling force	2.0–22	37	(3)
	Buckling force	2.4		(4)
	Relaxation (RELAX)	1.0	22–25	(5)
	Relaxation (WIGGLE)	1.9	22–25	(5)
	Thermal fluctuation	21.5	25	(9)
	Thermal fluctuation	32.0	37	(11)
	Thermal fluctuation	2.4	37	(7)

^*These values of EI were calculated from the measured values of persistence length, L_p (EI = k_BT L_p).

In a previous report, microtubule rigidity was measured using an optical trap and immobilized beads (3). The distinctive features of this method are that the analysis uses classical mechanics for the static process of microtubule buckling under an external force provided by an optical trap. Each microtubule was balanced at the force fulcrums and the technique measured the minimum force required to maintain microtubule buckling. This method is very specific with respect to its simple mechanical analysis in that there are only two working forces that do not change over time. The optical trap approach has also been used to measure microtubule bending in image analyses of the relaxation process (5,6), features of which clearly differ from buckling force measurements (Fig. 1 and Table 1). This type of study uses hydrodynamics to analyze the dynamic process of microtubule relaxation from the bent to the straight form. The relaxation process is caused by a balance between the internal spring force of a deformed microtubule and the viscous drag force of solution flow. The viscous drag force changes continuously both along the microtubule and with time, and the position of the microtubule is monitored over time. Thus, these two phenomena are very different, and the relaxation method is complicated by the inherent challenges of using hydrodynamics and time-dependent analysis. Of the above methods, buckling force measurement is the simplest method to measure microtubule rigidity because it employs the fewest number of assumed parameters. There are, however, experimental problems with buckling force measurements caused by the use of poly-L-lysine and a single optical trap for the microtubule; moreover, the data are dependent on microtubule length. One previous buckling measurement revealed that rigidity increases 10-fold depending on microtubule length, although the reason for this effect was not made clear (3).

In this study, we minimized the experimental difficulties (see Discussion) and improved the microtubule buckling force measurement system as follows. Anti-tubulin-coated beads, instead of poly-L-lysine-coated beads, were adopted as force fulcrums to bind the microtubule. These antibody-coated beads eliminated problems associated with nonspecific binding and incomplete immobilization, and affected specific and stable immobilization between the beads and microtubule. We also constructed two optical traps that applied a model for buckling the microtubule in which the constraint conditions at both force fulcrums were the same—free to rotate but not to move laterally. This system enabled the force fulcrums to be located on the same focal plane and provided for easier manipulation of microtubule buckling. During the experiments, we carefully confirmed the manipulation depth, the microtubule states, buckling shape, contrast of image, and so on. To further increase the accuracy of the analysis, we adopted a realistic analytical model, namely nonaxial buckling with consideration of the bead radius, which fit well with the experimental design and facilitated data processing. The above improvements yielded a novel system to measure single-microtubule buckling force using dual optical traps and beads. We used this method to measure rigidity in both paclitaxel-stabilized and paclitaxel-free microtubules, and we discuss the dependency of rigidity on microtubule length.

MATERIALS AND METHODS

Preparation of microtubules and antibody-coated beads

Microtubule proteins were prepared from bovine brain by cycling of temperature-dependent polymerization and depolymerization (14). Purified tubulin was obtained by phosphocellulose column chromatography of microtubule proteins (15). Protein concentration was determined by the Bio-Rad protein assay (Nippon Bio-Rad Laboratories, Higashi-Nippori, Japan) calibrated using bovine serum albumin as the standard.

Microtubules were polymerized from 3 mg/ml purified tubulin in BRB80 (80 mM PIPES, pH 6.9, 1 mM EGTA, and 1 mM MgCl₂) containing 1 mM GTP and 8% DMSO at 37°C for 30–60 min. In these experiments, we used both paclitaxel-stabilized and paclitaxel-free microtubules. Paclitaxel-stabilized microtubules were obtained by diluting polymerized microtubules 10,000-fold with BRB80 containing 10 μM paclitaxel (Molecular Probes, Eugene, OR), 1 mM GTP, and 10 mg/ml BSA. Paclitaxel-free microtubules were obtained by diluting polymerized microtubules 1000-fold with BRB80 containing 73.7% (v/v) deuterium oxide (D₂O) (Sigma-Aldrich, St. Louis, MO), 1 mM GTP, and 10% (v/v) glycerol. D₂O was added to suppress disassembly of microtubules (16), and its addition increased the density of the solution, thereby causing the antibody-coated beads (see below) to float. The viscous drag of the solution on the beads was increased by adding 10% glycerol to solve this problem, and, as a result, the floating beads were more evenly distributed in solution.

We prepared antibody-coated beads that were used to attach microtubules. Recombinant protein G (Zymed Laboratories, San Francisco, CA) was covalently coupled to carboxylated polystyrene beads (1.909-μm diameter; Polyscience, Niles, IL) using the carbodiimide kit for carboxylated microparticles (Polyscience). We tested two monoclonal antibodies against tubulin (TUB-1A2, T9028; and 6-11B-1, T6793; Sigma-Aldrich) with respect to their ability to adhere microtubules to beads. Each antibody was incubated with protein G-coupled beads at 37°C for 60 min. The antibody-coated beads were washed twice with PBS containing 0.05% (v/v) TWEEN 20 and dispersed in the same buffer. The binding of these antibodies to protein G-coupled beads was confirmed with Vectastain-phycoerythrin (Vector Laboratories, Burlingame, CA) under a fluorescence microscope.

The diluted microtubule suspensions were mixed with antibody-coated bead suspensions at a volume ratio of 20:1. Then, 20 μl of the mixture was perfused into a chamber consisting of a coverslip and glass slide separated by two pieces of laboratory film as spacers. The edges of the coverslip were sealed with vaseline/lanolin/beeswax (1:1:2, by weight). The specimen was set on the microscope stage, which was maintained at 33°C. The adhesion of antibody-coated beads to microtubules was examined under the microscope, and for this purpose, we found no difference between the two antibodies TUB-1A2 and 6-11B-1. In this study, we primarily used TUB-1A2-coated beads.

Optical setup for laser trapping and image processing

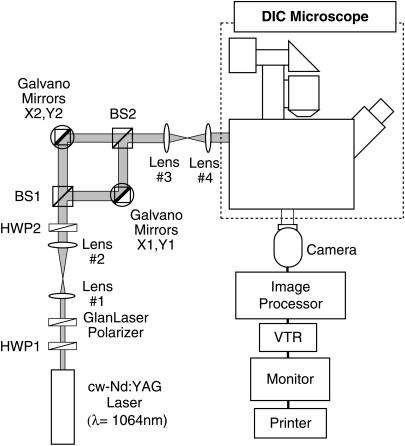
A schematic diagram of our optical system is shown in Fig. 2. Microtubules and beads were observed under a differential interference contrast (DIC) microscope (Diaphot TMD300, Nikon, Tokyo, Japan) equipped with a Plan Apochromat 100× oil-immersion objective lens (NA = 1.4), high transmission polarizer and analyzer, an oil-immersion condenser lens for high magnification objectives, a 100-W halogen lamp, DIC prisms, and 5× TV relay lens. Images were detected with a Newvicon camera (C2400-07, Hamamatsu Photonics, Hamamatsu, Japan), enhanced with an image processor (DVS-3000, Hamamatsu Photonics), and recorded with an S-VHS video cassette recorder (SVO-9650, Sony, Tokyo, Japan). Real-time and recorded images were printed with a video printer (UP-860, Sony). The light source for laser trapping was a linear polarized laser beam in the TEM₀₀ mode of the cw-Nd:YAG laser (SL902T, Spectron Laser Systems, Rugby, Warwickshire, UK) emitting at 1064 nm. The laser beam was divided into two beams using a polarizing beam splitter (BS1). To manipulate two laser spots independently for optical trapping in the microscopic field of view (∼33 μm × 21 μm), these laser beams were steered with two pairs of two galvano mirrors oriented orthogonally. These beams were merged with a polarizing beam splitter (BS2), and were introduced into the epifluorescence port of the microscope with the aid of collimating lenses. The ratio of the intensity of the two laser beams was controlled by rotating the half-wave plate (HWP2) and was fixed at 1:3 during experiments. The laser power was controlled with a variable attenuator consisting of a rotatable half-wave plate (HWP1) followed by a Glan-Laser polarizer. The laser power incident on the microscope was measured by a thermal detector (Model 835, Newport, San Diego, CA). The temperature of the microscope stage was maintained at 33 ± 1°C with a handmade air incubator.

FIGURE 2.

Schematic diagram of the video-enhanced DIC microscope with optical traps. The laser power was controlled by rotating the half-wave plate, HWP1, followed by a Glan-Laser polarizer. The ratio of the two beams was changed by rotating the half-wave plate, HWP2. Two laser beams were independently manipulated by changing the angles of the galvano mirrors X1, Y1 and X2, Y2.

The trapping forces of the two optical traps were calibrated by applying a viscous drag force to the bead at 5 μm of depth relative to the inner surface of the coverslip. The position of an optically trapped bead was manipulated sinusoidally in constant amplitude (∼7 μm) along one axis in the solution by driving a galvano mirror controlled by an external signal from the function generator (SG-4101, Iwatsu, Tokyo, Japan). The driving frequency was increased gradually, and the frequency at which a bead escaped from the trap was measured. Frequencies were measured at various laser powers. Each measurement was repeated several times at the same laser power. The viscosity of the solution under two different conditions (for paclitaxel-stabilized and paclitaxel-free microtubules) was obtained by averaging the values of three measurements with an Ubbelhöde viscometer at 33°C. The viscometer was calibrated using water and 10% (v/v) glycerol. The viscous drag coefficient was corrected by considering the drag on a bead near the coverslip surface (Faxen's law) and was used to calibrate the trapping force (17). The calibration results revealed a linear dependence of the trapping force on laser power: 0.12 pN/mW in the range of 0–7.8 mW (0–0.94 pN) for the solution containing paclitaxel-stabilized microtubules, and 0.092 pN/mW in the range of 0–11.8 mW (0–1.03 pN) for the solution containing paclitaxel-free microtubules.

The buckling force was measured as follows. A bead adhered to a microtubule was captured with one optical trap. The adhesion of a trapped bead to a microtubule was confirmed with relative flow by moving the stage. Subsequently, another bead, captured with another optical trap, was attached to the microtubule, yielding a dumbbell-shaped structure. We carefully confirmed that a single microtubule was attached to the two beads by causing it to straighten and buckle. If two or more microtubules adhered to the beads, the microtubules aggregated, and distorted, buckled microtubules were observed in the system; hence, that system was abandoned. The depth of the focal plane for both of the captured beads was set at 5 μm of depth relative to the inner surface of the coverslip. The distances between two captured beads having a straightened microtubule and those having a buckled microtubule were measured by temporarily changing the microscopic illuminator to the bright field. The microtubule was buckled by decreasing the distance between two captured beads to approximately one-half or one-third of the initial distance by manipulating one of the two optical traps. In such experiments, the weaker trapped bead was manipulated and the stronger trapped bead was fixed. After changing back to DIC illumination to observe the bead escaping from the trap, the trapping force was decreased gradually by decreasing the laser power by rotating the half-wave plate (HWP1) under computer control. When a captured bead escaped from the weaker trap, the laser power was measured and was used to evaluate the trapping force. In the case of paclitaxel-free microtubules, all steps had to be performed within 10 min because of the lability of these microtubules. In the case of paclitaxel-stabilized microtubules, all steps were performed within 30 min.

Evaluation of microtubule rigidity

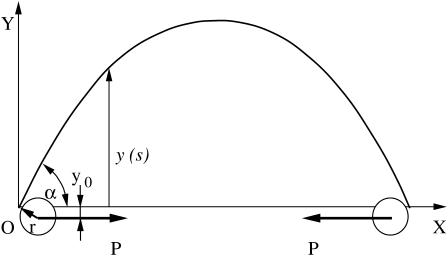
The ideal state under which the buckling of a single microtubule takes place is shown schematically in Fig. 3. Two polystyrene beads of radius r are attached to a single microtubule and then trapped and manipulated by two laser beams. In the ideal case, when no other forces act on the single microtubule, two compressive loads P are equal in size but opposite in direction to ensure mechanical equilibrium.

FIGURE 3.

Schematic representation of a buckled microtubule. The X axis is chosen to pass through two fulcrums that represent attachment points of beads to a microtubule. The origin, O, is located at one of the fulcrums. The two polystyrene beads of radius r illustrate the nonaxial buckling case.

By choosing the XY coordinate system shown in Fig. 3, we can write a differential equation describing single microtubule buckling as (18)

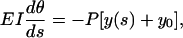(1)

where EI is the flexural rigidity of a single microtubule, E is Young's modulus, I is the geometrical moment of inertia of the cross section, s is the coordinate along the single microtubule, and θ(s) is the deflection angle at point s. If α is the deflection angle at one end, then y₀ = r cos α. By differentiating the above equation with respect to s, one obtains

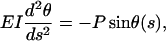(2)

an equation identical to the case of pure compressive buckling. The boundary conditions are, however, different. If L is the total length of the single microtubule having two ends, then

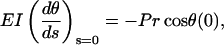(3)

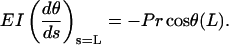(4)

This problem is nonlinear, both in the equations and in the boundary conditions; therefore, it can be solved only by numerical methods. To this end, the second-order differential equation (Eq. 2) with the boundary conditions (Eqs. 3 and 4) has been transformed into a first-order two-point boundary value problem:

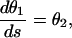(5)

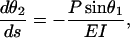(6)

with the boundary conditions

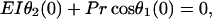(7)

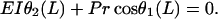(8)

The solution was computed using a finite-difference technique with deferred correction allied to a Newton iteration to solve the finite-difference equations (19). In the actual buckling experiments, the load and deformation are the measured quantities. For this reason, we developed a second program to obtain the flexural rigidity from these measured values. This program contained the following steps:

• Step 1. Flexural rigidity was estimated from the measured deflection length x (in μm) and force P (in pN). The problem of large deflections of a perfectly straight sample of flexural rigidity, EI, loaded by two perfectly axial forces, P, has a well-known solution, Eq. 1, given in terms of elliptic integrals. This solution was computed first and used as an initial approximation, a necessary step before starting the calculation.

• Step 2. The deflection was calculated by solving the differential equations, i.e., Eqs. 5 and 6, with the boundary conditions of Eqs. 7 and 8; the calculated deflection usually will be higher than the experimental value.

• Step 3. A small correction to the flexural rigidity was estimated, and Step 2 was repeated until the calculated deflection equaled the experimental value.

RESULTS

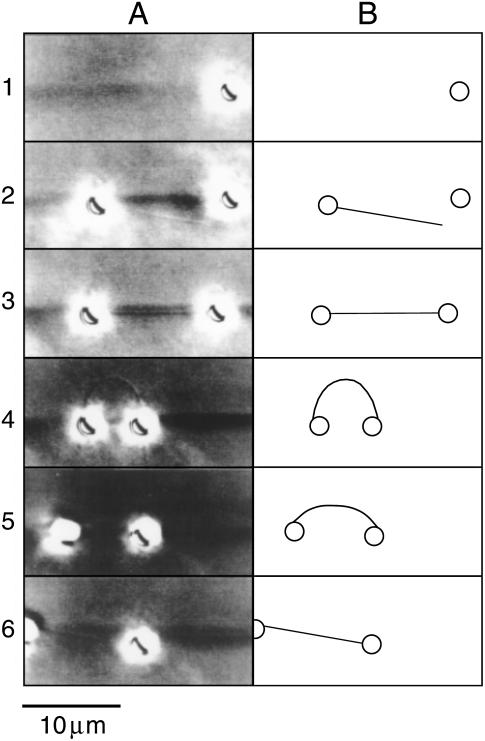
Our novel system using two optical traps and antibody-coated beads facilitated the measurement of the direct buckling force of a single microtubule, as fitted using the new analytical model we developed in this study. The typical sequence for the analysis of a single microtubule is shown in Fig. 4. Two antibody-coated beads were coupled with the microtubule and were captured with optical traps to yield a dumbbell shape (Fig. 4, Rows 1–3). The microtubule and beads readily bound each other, usually within several attempts of touching the bead to a microtubule. The binding between beads and a microtubule via the antibody was stable and was usually maintained for >30 min in the absence of experimental manipulation. When verifying the depth of micromanipulation, a bead or beads often attached to the surface of the coverslip despite the fact that 10 mg/ml BSA was included in the solution to suppress the binding between beads and the glass surface. When the microtubule was buckled by decreasing the distance between the two beads, the DIC image of the microtubule was often not observed because of bead rotation. Therefore, we confirmed the microtubule-bead structure using the relative flow of solution by moving the stage when the microtubule image was not observed. The buckled microtubule was never observed to break regardless of the magnitude of the deflection. The shape of the buckled microtubule fluctuated slightly as a result of thermal fluctuation when the DIC image was observed (Fig. 4, Row 4). The trapped beads also fluctuated just before escape from the optical trap. When the trapping force was just below the buckling force as the laser power decreased, the bead escaped the weaker optical trap and the buckled microtubule relaxed to the straight form (Fig. 4, Row 5). We were able to perform 1–5 measurements of each microtubule-bead complex before the beads either escaped the optical traps or the binding between the bead and microtubule was broken.

FIGURE 4.

A typical example of single-microtubule capturing, buckling, and release with micromanipulation of antibody-coated beads and optical traps. (A) Video-printed images of the procedure for a paclitaxel-stabilized microtubule. The single microtubule can be seen faintly (the dark shadow of bead images makes it difficult to observe the microtubule). DIC images were used to observe the single microtubule, and thus the beads appear larger than their actual size due to halation. The background darkness of each image is slightly altered because the light source fluctuated slightly and contrast was strongly enhanced. (B) The trace of the images in A. Circles and lines represent beads and microtubules, respectively. Row 1 shows the first bead being captured with the right (stronger) optical trap. Row 2 shows the second bead with a single microtubule being captured with the left (weaker) trap. The microtubule on the bead could be observed by relative flow upon moving the stage. Row 3 shows the dumbbell-shaped image resulting from a single microtubule and beads. Row 4 shows just the buckling state of the microtubule upon moving the right bead toward the left. The left bead also moved fractionally to the left due to the buckling force. An additional short microtubule, which was not relevant to the analysis, can be seen on the right bead. Row 5 shows the left bead escaping from the trap and the buckling microtubule relaxing back to its straight form. The microtubule cannot be observed. Row 6 shows the final state in which the right bead is held by the trap and the bent microtubule straightens by its own elasticity. The left bead is free from the optical trap but remained bound to the microtubule. The right bead moved slightly toward the left in response to the release from the buckling force.

To increase the accuracy of the analysis, we adopted a realistic nonaxial buckling model to process the data, in which the bead diameter was the same size as the microtubule length. We assumed that the microtubule was a homogenous, thin rod, which buckled with compressive force through the beads in Fig. 3. Using the buckling model with or without the arm, we present examples of the analysis in Table 3. The rigidities calculated using the new model having an arm that ranged from 0 to 38% for paclitaxel-stabilized microtubules and from ∼2 to 5% for paclitaxel-free microtubules; these values were higher than those calculated using the simple model without the arm, which depended on the deflection length and microtubule length. This nonaxial buckling model was effective for short deflection lengths and short or paclitaxel-free microtubules.

TABLE 3.

The comparison of microtubule rigidity, EI, calculated using the new nonaxial buckling model (the model with arm) and the simple buckling model (the model without arm)

Samples	Microtubule length (μm)	Buckling force (pN)	Deflection length (μm)	Rigidity, EI (with arm) (× 10−24 Nm2)	Rigidity, EI (without arm) (× 10−24 Nm2)
Paclitaxel-stabilized microtubules	8.4	0.36	3.7	1.9	1.8
	10.0	0.32	4.8	2.5	2.4
	15.7	0.11	7.6	2.0	2.0
	17.3	0.11	5.8	2.5	2.2
Paclitaxel-free microtubules	8.8	1.35	4.7	8.4	8.1
	12.2	0.58	7.0	7.1	6.7
	13.6	0.50	8.0	7.8	7.4
	16.0	0.43	8.3	8.5	8.3

These data were taken from microtubules that were measured once for buckling force.

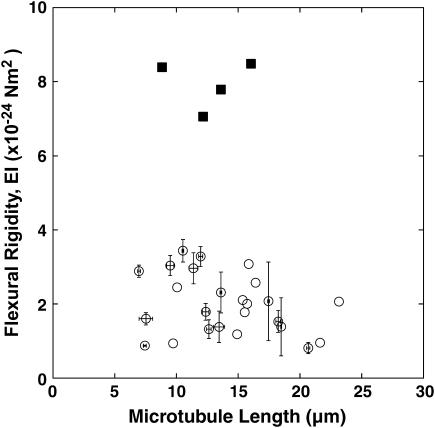
The plot of the rigidity of paclitaxel-stabilized microtubules versus microtubule length is shown in Fig. 5. The average rigidity of a single microtubule was 2.0 ± 0.8 × 10⁻²⁴ Nm² (mean ± SD), with a range of 0.82 to 3.4 × 10⁻²⁴ Nm². Each microtubule was buckled and analyzed 1–5 times, and we performed 48 trials of 25 microtubules in total. When single microtubules were subjected to the buckling processes more than two times, the maximum standard deviation of rigidity was 1.1 × 10⁻²⁴ Nm², which should correspond to the maximum deviation of this measurement. There was essentially no length dependency of the flexural rigidity. Indeed, the linear function fit was: EI (× 10⁻²⁴ Nm²) = −0.051L + 2.717 (L = Length; μm), with γ = 0.28. Both the small negative slope and small correlation coefficient argue that there is no length dependency of the flexural rigidity.

FIGURE 5.

The plot of flexural rigidity of a single microtubule against microtubule length. Paclitaxel-stabilized microtubules (open circles) were buckled 1–5 times and 48 measurements of 25 microtubules were performed in total. The average and standard deviations for individual microtubules measured repeatedly are shown as a marker and error bars, respectively. Note that there was no length dependency of the flexural rigidity. For paclitaxel-free microtubules (solid squares), only four measurements of four microtubules were done. The average rigidity of paclitaxel-free microtubules (7.9 × 10⁻²⁴ Nm²) was approximately four-times-higher than that of paclitaxel-stabilized microtubules (2.0 × 10⁻²⁴ Nm²).

The rigidity values for the paclitaxel-free microtubules are also shown in Fig. 5. Only a few reliable measurements were taken due to the difficulties encountered in binding the beads to the microtubule. Because there were large amounts of free tubulin subunits due to the high critical concentration of tubulin under these conditions, it is likely that the antibody binding sites were primarily occupied by free tubulin subunits. The rapid shortening of microtubules also made these measurements rather difficult, because the concentration of tubulin in this experiment was somewhat lower than the critical concentration. Thus, only four binding and buckling procedures could be completed. The mean value of rigidity was 7.9 × 10⁻²⁴ Nm² (SD = 0.7 × 10⁻²⁴ Nm²). Even though we could complete only four sequences, the average rigidity of paclitaxel-free microtubules was clearly higher than that of paclitaxel-stabilized microtubules (p < 0.001; t-test).

DISCUSSION

Evaluation of experimental errors

Here we have calculated the rigidity of an individual microtubule using a novel direct force measurement for buckling with a dual optical trap and antibody-coated beads. The distinctive features of this method are that the analysis uses classical mechanics to assess a static process and applies a simple external force via an optical trap. Even though we carefully controlled the boundary conditions of the measurements, experimental errors remained, as shown in Fig. 5. Possible error sources stem from replicate measurements of the same microtubule and from the lack of homogeneity of the bead pairs and microtubules. The former sources of error result from fluctuations in the trapping force, errors in measuring the microtubule length, and thermal fluctuations of beads and microtubules that correspond to deviations in repeated measurements of a single microtubule (Fig. 5). The latter errors are caused by deviations in the trapping force, deviation in the protofilament number in each microtubule, and torsion of the microtubules. These six sources of error are discussed below.

1. Fluctuation in the trapping force is caused by the instability of the laser power, which was <1% and therefore negligible.

2. The microtubule length measurement had an average error of 0.21 μm. This error, at a maximum, was 0.55 μm, corresponding to beads with a total tilt angle of 17° to the long axis of the microtubule. This is equivalent to ∼10% of the rigidity for a 7.5-μm-long microtubule. This error was caused by difficulty in judging the straightness of each microtubule.

3. Thermal fluctuations of the beads and microtubule also present a source of error during force measurements. The thermal force of the linear diffusion of the bead under free conditions was calculated as 27 pN, and the average mean-square-velocity and correlation time were calculated as (1.8 × 10⁻³ m/s)² and 0.25 μs, respectively. Although this thermal force of the beads was sufficiently large to affect the escaping force from the optical trap, it was difficult to estimate its value because Brownian motion is random and its correlation time is quite short. Using our rigidity value, the average bending thermal force of a 10-μm-long microtubule was estimated as 0.02 pN for a mean-square-distance of (0.2 μm)² for mode n = 1, and 0.056 pN for a mean-square-distance of (0.07 μm)² for mode n = 2. These estimated thermal forces were sufficiently large to disturb the ability to hold the beads just before escape from the optical trap(s) (refer to Table 3) and should affect the rigidity value by ∼50% and ∼15% for 15-μm- and 10-μm-long microtubules, respectively. The contribution of these errors to the rigidity should increase as microtubule length increases because the buckling force tends to decrease with increasing microtubule length.

4. The trapping force was also affected by deviations in bead diameter, which varied by ±5%, corresponding to ∼5% of the trapping force (17).

5. Differences in microtubule protofilament number should affect the estimation of flexural rigidity, because the second moment of inertia of the cross-section of a microtubule increases with protofilament number. The majority of microtubules in this study should have 14 protofilaments, and protofilament number is distributed into four classes: 13 (14%), 14 (72%), 15 (11%), and 16 (3%) protofilaments (20). Assuming the same Young's modulus for microtubules having 13–16 protofilaments, reducing the protofilament number from 14 to 13 is expected to decrease the flexural rigidity by ∼20% (≈1−[13:14]³; the rigidity depends on the third power of the protofilament number because the thickness of the microtubule wall is constant, as described in (9)), whereas increasing the protofilament number from 14 to 15 or 16 is expected to increase the rigidity by ∼23% (≈[15:14]³−1) or ∼49% (≈[16:14]³−1), respectively. Therefore, we expect that the measured flexural rigidity would vary by ±70% of the average rigidity.

6. In the ideal case, the two beads should bind the same side of the microtubule; however, we could not discount the possibility that two beads had a torsional angle in our binding procedure. If torsion on the microtubule caused by the two trapped beads contributed substantially to the rigidity, then the deviation of the rigidity should be dependent on microtubule length because the force of microtubule torsion decreases linearly with microtubule length at the same torsional angle. However, we did not measure a strong dependency on microtubule length with regard to the deviation of rigidity in Fig. 5, implying that the contribution of torsion to the flexural rigidity of a microtubule is not large.

The sum of the sources of error in items 1–3 above should be ∼0.3 × 10⁻²⁴ Nm² on average (range = 0.013–1.1 × 10⁻²⁴ Nm²), corresponding to errors for repeated measurements of a single microtubule. The deviation of rigidity for each pair of beads and a microtubule, caused by items 4–6 above, should be 0.8 × 10⁻²⁴ Nm² on average (range = 0.8–3.4 × 10⁻²⁴ Nm²), which is comparable to the average overall error of the trial data, 0.9 × 10⁻²⁴ Nm².

Length dependency of rigidity

Our measurement of flexural rigidity for paclitaxel-stabilized microtubules is consistent with previous data (3) for microtubules <10-μm long. This previous work showed a length dependency of microtubule rigidity, with ∼15-μm-long microtubules having 10-fold higher rigidity compared with ∼5-μm-long microtubules; however, we did not observe length dependency in this study. In the previous study, a single optical trap was used to manipulate a glass bead coated with poly-L-lysine adhered to a microtubule for buckling, and the other end of the microtubule was bound to a glass bead adhered to the inner surface of a coverslip. This analytical model involved clamping one end of the microtubule, while the other end was free to rotate and translate laterally (Fig. 6.4 D in (1)). These experimental conditions offer several possibilities for overestimating the buckling force caused by using poly-L-lysine and a single optical trap, as follows. First, using poly-L-lysine to adhere the microtubule to the bead constitutes nonspecific binding and incomplete immobilization. This suggests that the experimental buckling conditions deviated from the analytical model. If the clamped end changed to a rotational end, then both ends would have rotational freedom (Fig. 6.4 A in (1)), and the result of the analysis must be to overestimate fourfold compared with that of the supposed model at maximum. In the case of long microtubules (i.e., >15 μm), the constraint conditions should make it possible to change the end that is clamped while the other end remains free to rotate but not move laterally (Fig. 6.4 B in (1)) due to the direction of the compressive force. The overestimation would increase to ∼8.2-fold under this condition. Nonspecific adherence between contaminating free poly-L-lysine in solution, the microtubule, and the glass surface (except the clamped end) also increase the overestimation of rigidity due to the increased buckling force. Adherence using poly-L-lysine often causes microtubule bundling and aggregation due to the nonspecificity of the binding interaction. If two microtubules are bundled, rigidity increases by at least twofold. In preliminary trials, we observed examples of nonspecific binding and incomplete immobilization of microtubules by poly-L-lysine-coated beads and abnormalities in the buckling of microtubules having an asymmetric buckling shape, a hinged shape, or an inhomogeneous contrast along the microtubule.

An additional source of overestimation of rigidity is the depth of manipulation. In this study, we performed a force calibration, and all measurement procedures were performed at a distance of 5 μm relative to the glass surface, a distance that was strictly monitored during each measurement. In previous reports, however, the corresponding distance was not strictly controlled (3). By increasing the depth of the manipulation, optical traps have decreased the trapping force due to distortion of the focus. In the case of the objective lens in our experiments, the optical traps maintained the same force with focusing depths up to 6 μm, but the force quickly decreased up to a depth of ∼20 μm. If the manipulation depth is greater than the calibration depth, then the decreasing trapping force will increase the possibility of overestimation. All of these problems may cause the overestimation of the buckling force and rigidity and increase the inaccuracy of the measurements. If the above possibilities were to overlap, then the rigidity may be overestimated by 10-fold or more.

The effect of paclitaxel binding and Young's modulus

The rigidity of paclitaxel-free microtubules was 7.9 ± 0.7 × 10⁻²⁴ Nm², which is approximately fourfold higher than that measured for paclitaxel-stabilized microtubules. This value is essentially the same as that (6.8 ± 3.9 × 10⁻²⁴ Nm²) measured using another buckling method (4), and the ratio of +/− paclitaxel values was the same as that measured using a variation of their analysis of the relaxation process (5). Our data agree with previous results showing that paclitaxel imparts flexibility (4,5,7,10) and stability to microtubules. The effects of paclitaxel may reflect changes in fundamental interactions inside the microtubule, such as those within or between protofilaments, because paclitaxel also binds the interprotofilament region of microtubules (21). Microtubules produced using tubulin bound to a nonhydrolyzable GTP analog (GMPCPP) with a higher rigidity than those produced using GTP-bound tubulin (4,7,11). This difference may reflect changes in the interactions within tubulin dimers, and such interactions likely contribute to microtubule rigidity.

Young's modulus for a single microtubule was also estimated from the rigidity value. We assumed a microtubule was a homogenous hollow cylinder with outer and inner diameters of 25 nm and 14 nm, respectively. The Young's modulus was estimated as 1.2 × 10⁸ N/m² for paclitaxel-stabilized microtubules, and 4.6 × 10⁸ N/m² for paclitaxel-free microtubules. These values are very close to that of actin filaments, 3.1 × 10⁸ N/m², obtained by measuring resistance to bending via optical traps (22), assuming an actin filament is a thin rod of 5.6-nm diameter (23). These data suggest that cytoskeletal proteins have essentially the same modulus as the materials, and thus cytoskeletal proteins may change their polymer structure to adapt to various cellular environments. Recently, it was reported that the Young's modulus of a microtubule fixed with glutaraldehyde is at least two orders-of-magnitude higher (∼1 × 10⁸ N/m²) than shear elastic modulus (1.4 × 10⁶ N/m²) using an atomic force microscope (24). They proposed that such a large difference could be found only in highly anisotropic materials. Because it is likely that paclitaxel binding reduces microtubule rigidity by decreasing the strength of the interactions between protofilaments, as proposed in Dye et al. (10), intact microtubules may also have anisotropic mechanical properties similar to those described for glutaraldehyde-fixed microtubules.

Comparison with other methods

Our measurement of microtubule rigidity uses the most static method and is the most direct because it uses a method based on classical mechanics for the estimation of rigidity. As shown in Table 2, however, our values are not completely consistent with flexural rigidity values previously measured with various methods. The values vary depending on the method used for measurement. There are many clear differences among the four methods (Fig. 1 and Table 1), because the methods analyze different movements and microtubule responses. The flexural rigidities we measured (7.9 ± 0.7 × 10⁻²⁴ Nm² for paclitaxel-free microtubules and 2.0 ± 0.8 × 10⁻²⁴ Nm² for paclitaxel-stabilized microtubules) are in good agreement with previous values (6.8 ± 3.9 × 10⁻²⁴ Nm² for paclitaxel-free microtubules and 2.4 ± 1.1 × 10⁻²⁴ Nm² for paclitaxel-stabilized microtubules) obtained using a similar buckling force measurement method (4). This strongly suggests that the difference among measurement methods, especially whether the process is static or dynamic, is the reason for the inconsistent rigidity values previously described. Using the hydrodynamic flow method, which is also a static method, others have determined the microtubule rigidities as 8.5 × 10⁻²⁴ Nm² (7) and 35.8 × 10⁻²⁴ Nm² (8) for paclitaxel-free microtubules. The divergence of the two values demonstrates the difficulty of estimation by this method. Not only is this method quite difficult to perform, but the data are also difficult to analyze precisely; this is accompanied by the difficulty of precisely estimating the hydrodynamic drag force.

The relaxation method involves the measurement of the dynamic process of relaxation time of bent microtubules moving back to a straight form. This depends on a balance between the microtubule's own elastic force and that of hydrodynamic drag. The hydrodynamic drag force is not homogenous along a microtubule over time, and thus it is quite difficult to estimate the rigidity of a microtubule precisely. Using the relaxation method, values of 4.7 × 10⁻²⁴ Nm² [WIGGLE] and 3.7 × 10⁻²⁴ Nm² [RELAX] for paclitaxel-free microtubules, and 1.9 × 10⁻²⁴ Nm² [WIGGLE] and 1.0 × 10⁻²⁴ Nm² [RELAX] for paclitaxel-stabilized microtubules, have been calculated (5). These relaxation methods were recently modified (25), resulting in rigidity values ∼2.0 times greater for [WIGGLE] and ∼1.4 times greater for [RELAX] than previously measured, respectively. The modified values are more consistent with the values we obtained.

The rigidity of microtubules estimated by the thermal fluctuation method, the most dynamic method, tends to yield a value that is one order-of-magnitude higher than that obtained from the three methods described here (8,9,11–13). This tendency was also evident in the case of actin flexural rigidity measurements (9,22,26,27). Thermal fluctuation analysis is based on statistical analysis of the microtubule shape change in response to thermal force. Microtubule shape changes corresponding to bending and relaxation can be measured because the microtubule is exposed to both thermal and hydrodynamic drag forces continuously over time. This thermal fluctuation analysis is different from static buckling force measurement in two ways: 1), the loading rate; and 2), the direction of the working force on a microtubule, both of which are uncontrolled. The correlation time of thermal fluctuation averaged ∼1 s for mode n = 1 and ∼0.1 s for mode n = 2, corresponding to microtubule external and internal forces at ∼1 Hz for n = 1 and ∼10 Hz for n = 2. The average loading rate for a ∼50-μm-long microtubule by thermal fluctuation analysis was calculated as ∼±0.006 pN/s for the first mode and ±0.14 pN/s for the second mode using data from Howard (1). In our static measurement, the loading rate was 0 pN/s, because we maintained a constant force to buckle the microtubule. Only the thermal fluctuation analysis includes the bending movement caused by the uncontrolled thermal force; the other methods do not assess any bending process (Table 1). Because the same results were obtained using critical load and deflection length analysis (3), the amplitude of deformation of a microtubule does not affect the rigidity measurement. For the direction of the working force for a microtubule, our measurement depended only on a pair of compressive forces, whereas the thermal force used in other studies was applied in random directions continuously along the microtubule. Local mechanical stress varies along the length of a microtubule; therefore, such variations suggest that microtubule rigidity is dependent on time-dependent local stress caused by bending and relaxation movements of the microtubule. A report extending the use of the thermal fluctuation method that analyzed the data with better hydrodynamic curvature of the bending shape of the microtubule found an internal friction effect of the microtubule (13). The authors presented data demonstrating that internal friction within a filament can make its relaxation movement slow at the higher mode. The phenomenon of internal friction was first observed in the thermal bending movement of chromosomes (28), and may also occur in microtubule thermal bending movement. It has been proposed that the axial slippage (shear displacement) between two adjacent protofilaments (10), which is caused by internal friction, should then affect the rigidity of the microtubule. This internal friction is a time-dependent quantity that is affected by loading rate and the curvature of the bending microtubule (working state of the external force) (28). Therefore, this biofilament including internal friction should show viscoelastic properties like the combination of dashpot (viscous) and spring elements. The same phenomenon may also occur in the microtubule during thermal fluctuation movement.

All of the methods, including ours, assume that the microtubule is a homogenous and isotropic slender elastic rod. However, in fact, it is clear from the observation of electron microscopic images (29) that microtubules have an anisotropic structure of sparsely connected protofilaments, so this assumption is far from true. Recently, simulation results using the finite element method, which incorporates the contribution of interactions within each dimer to estimate microtubule rigidity, were reported (30). Therefore, when measuring and analyzing microtubule rigidity, we should regard the microtubule as a more realistic, precise structure that considers the intrinsic properties of tubulin dimers and the interactions between neighboring dimers. In fact, the effects of paclitaxel (4,5,7,10) and a nonhydrolyzable GTP analog (4,7,11) suggest that intrinsic properties of or interactions between dimers affect microtubule rigidity. The inconsistent values obtained with different methods suggest that the simple model is limited—a reasonable conclusion given that the relevant phenomena, responses, and microtubule structure are not simple in actuality. Now may be the time to begin regarding the microtubule as a complex structure assembled from protofilaments or dimers instead of as a homogenous isotropic slender elastic rod when conducting experiments to measure and analyze microtubule rigidity.