Intracellular Transport Dynamics of Endosomes Containing DNA Polyplexes along the Microtubule Network

Abstract

We have explored the transport of DNA polyplexes enclosed in endosomes within the cellular environment by multiple particle tracking (MPT). The polyplex-loaded endosomes demonstrate enhanced diffusion at short timescales (t < 7 s) with their mean-square displacement (MSD) 〈Δx(t)²〉 scaling as t^1.25. For longer time intervals they exhibit subdiffusive transport and have an MSD scaling as t^0.7. This crossover from an enhanced diffusion to a subdiffusive regime can be explained by considering the action of motor proteins that actively transport these endosomes along the cellular microtubule network and the thermal bending modes of the microtubule network itself.

Intracellular transport of organelles and endosomes is crucial for diverse processes such as neuronal signaling, protein secretion, and cell cycle regulation. Cargo is shuttled along the microtubule and actin polymeric transport networks by molecular motors bound to the surface of the organelles. These motors include the myosin family for travel along actin, and the kinesin and dynein families for travel along the microtubule network. Many recent in vitro experiments have examined the mechanical and biophysical properties of these networks (1). However, their role and organization is only beginning to be explored intracellularly. This work focuses on microtubule-mediated transport of endosomes containing DNA polyplexes from the cell surface toward the nucleus and the incipient biophysical processes and timescales required for such transport.

Microtubules and the kinesin and dynein motor protein families are primarily responsible for trafficking of cargo and vesicles. These motors function by converting chemical energy derived from ATP hydrolysis into mechanical work and both classes can be simultaneously present on vesicles and cargo, as shown by bidirectional organelle transport. Bidirectional switching during transport leads to questions of how transport is orchestrated among the opposed motors on the organelle surface (2,3). Recent studies suggest that the motors may be regulated by dynactin or other proteins (4). This enables them to engage cooperatively, allowing for processive motion for hundreds of nanometers in a single direction. However, intracellular organelle motion can also appear disorganized, with the organelle seeming to wander randomly in the cytoplasm. Indeed, both behaviors have been detected for polyplexes internalized into endosomes analyzed by image correlation spectroscopy (ICS) (5).

Previous studies of intracellular transport along microtubules employed large micron-sized beads that were engulfed by endocytosis (6,7). Because most cellular endosomes are much smaller than this (8), we examined microtubule-mediated transport of fluorescently labeled endosomes. In our studies, the endosomes were filled with labeled nonviral DNA-containing polyplexes ranging from 100 to 200 nm in diameter; they are transported by the microtubule network in a retrograde fashion, from the cell membrane toward the nucleus. Such polyplexes are often utilized for gene transfection and delivery. It is therefore critical to examine the cytoskeletal mechanics of endosome transport, including microtubule motor activities, to better understand the dynamics of this delivery pathway.

For this study, we labeled the endosomes with Cy5-labeled β-cyclodextrin (β-CD)/DNA polyplexes as previously described (5). The polyplexes were introduced into the media of growing HeLa cells for 2 h. Measurements were made on a Zeiss (Jena, Germany) 510 confocal microscope equipped with an oil-immersion 100×/1.4 NA objective. Images were taken at 2 Hz for 2–3 min continuously.

Our previous work using endosomes labeled with 200 nm β-CD polyplexes has shown that the aggregate trajectories of such polyplexes appear random although the individual polyplexes exhibit a diverse range of behaviors (5). We thus wanted to further characterize the range of individual endosome motions in terms of the underlying microtubule and motor behaviors. Here, we used multiple particle tracking (MPT) (9) to accomplish this by simultaneously obtaining information on a large number of individual polyplex-loaded endosomes as they traveled from the cell membrane toward the nucleus. We performed MPT on the acquired data frames using a correlation-based approach to identify particles and a local search algorithm to assemble individual trajectories from the acquired frames. The coordinate data from the trajectories were then used to compute the two-dimensional mean-square displacements (MSD) as a function of time. The MSD plot for each trajectory was obtained by using all independent time segments for a given time interval. For short times there are many such intervals, which gives a more accurate estimation. At longer times, there are fewer intervals leading to more uncertainty in parameter estimation.

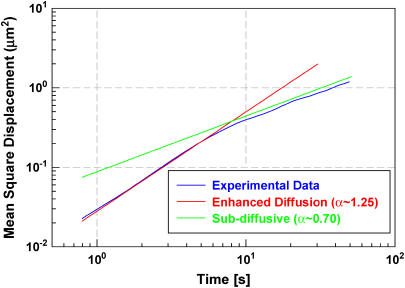
The trajectories for 35 particles in 20 different cells were averaged to generate the final MSD plot (〈Δx(t)²〉 vs. t) in Fig. 1, which shows two distinct regimes. At short timescales (t < 7 s) the polyplex-containing endosomes demonstrate enhanced diffusion with a scaling exponent α = 1.25 ± 0.04 so that 〈Δx(t)²〉 ∼ t^1.25. At longer timescales (t > 10 s), the endosomes exhibit subdiffusive behavior with α = 0.7 ± 0.07. The uncertainty in individual trajectories is larger in this regime because fewer independent time intervals are available to compute the MSD values.

FIGURE 1 .

Plot of mean-square displacement of polyplex-loaded endosomes as a function of time lag. Crossover from enhanced diffusive motion (α > 1) to subdiffusive motion (α < 1) occurs at ∼7 s.

The transition from enhanced diffusive (1 < α < 2) to subdiffusive (α < 1) transport can be explained using the framework described by Caspi et al. that utilizes a generalized Einstein relationship with time-dependent friction, which is a result of the non-Newtonian environment in the cell (6,7). This model considers the microtubules as a weakly entangled network and the movement of particles in this medium is affected by the equilibrium modes of the filaments. The motion of particles results in deformations of the microtubule network and in the process activates various bending modes of the filaments. Because the damping rate of each bending mode of the filaments is wavelength dependent, the effective drag experienced by the particle also becomes time dependent. Nonmotor-driven passive particles in such a medium have been shown to perform subdiffusive motion with t^3/4 scaling, which in turn implies a time-dependent friction μ(t) ∼ t^1/4 (7). Consequently, particles subjected to an external driving force (i.e., microtubule motors) can be shown to exhibit enhanced diffusive motion with t^3/2 scaling for times that are small compared to the correlation time of the force, and subdiffusive motion with t^1/2 scaling for longer timescales.

The correlation time of the driving force provides a crossover timescale and is a function of the interaction mechanism of the molecular motors with the endosome. For short time intervals, kinesin and dynein are highly correlated and can apply continuous force for hundreds of steps (generally up to 10 s), leading to the observed enhanced diffusion behavior (2,3). However, at longer times, the motors' driving force is uncorrelated because many individual motors act on the endosome at different instances during its trajectory, leading to subdiffusive motion. The crossover phenomenon between these two regimes of motion assumes an intimate contact between the particle and the surrounding microtubules, which is true for particles that are large compared to the tubule mesh size. The random motion of such large particles is then dominated by the driving force exerted by multiple motors acting on them simultaneously. Particles that are small compared to the mesh size can move without the action of motors in a restricted region and their random motion is caused by a combination of thermal excitations and driving due to motor proteins. This results in a lower exponent at short times, which would be expected to decrease as the size of the particle decreases.

In our experiments, the endosome size is between 100 and 200 nm and we observe an exponent of 1.25 in the enhanced diffusion regime, which is less than that observed for micron-sized beads. The small polyplex-containing endosomes are not completely trapped by the microtubule mesh and can wiggle laterally due to thermal motions (5,7). This small thermal contribution should reduce the exponent from the theoretically expected value of 1.5. At long times, in the subdiffusive regime, decreasing the particle size would be expected to increase the exponent (from α = 0.5) because the contribution due to the thermal excitation increases. We also observed this trend and obtained an average exponent of 0.7 as compared to the theoretically predicted value of 0.5.

To determine the role of interactions of the filamentous actin network with these endosomes, cells were treated latrunculin A to depolymerize actin, which should increase the mesh size and therefore the thermal contribution to α. We find that α = 1.02 ± 0.13 for short times and α = 0.74 ± 0.09 for long times, as predicted. Finally, to verify that these dynamics are primarily due to microtubule transport, cells were treated with nocodazole to depolymerize the microtubules. Long-range endosome motions were not observed and enhanced diffusion was eliminated, with α = 0.74 ± 0.07, solely reflecting the subdiffusive thermal contribution to endosomal motion.

In this work, we have studied the intracellular transport of endosomes with relation to the microtubule network and its associated motors. The observed crossover behavior from enhanced diffusive to subdiffusive transport is consistent with a time-dependent friction model for transport through semiflexible polymeric networks. Furthermore, the small size of the polyplexes (and other biologically significant organelles) relative to the microtubule mesh allows for a thermal contribution to motion resulting in a modified exponent in both regimes. These results of polyplex dynamics are important for better understanding the endocytic pathway and transport mechanisms for similar sized objects within the intracellular milieu.