Abstract
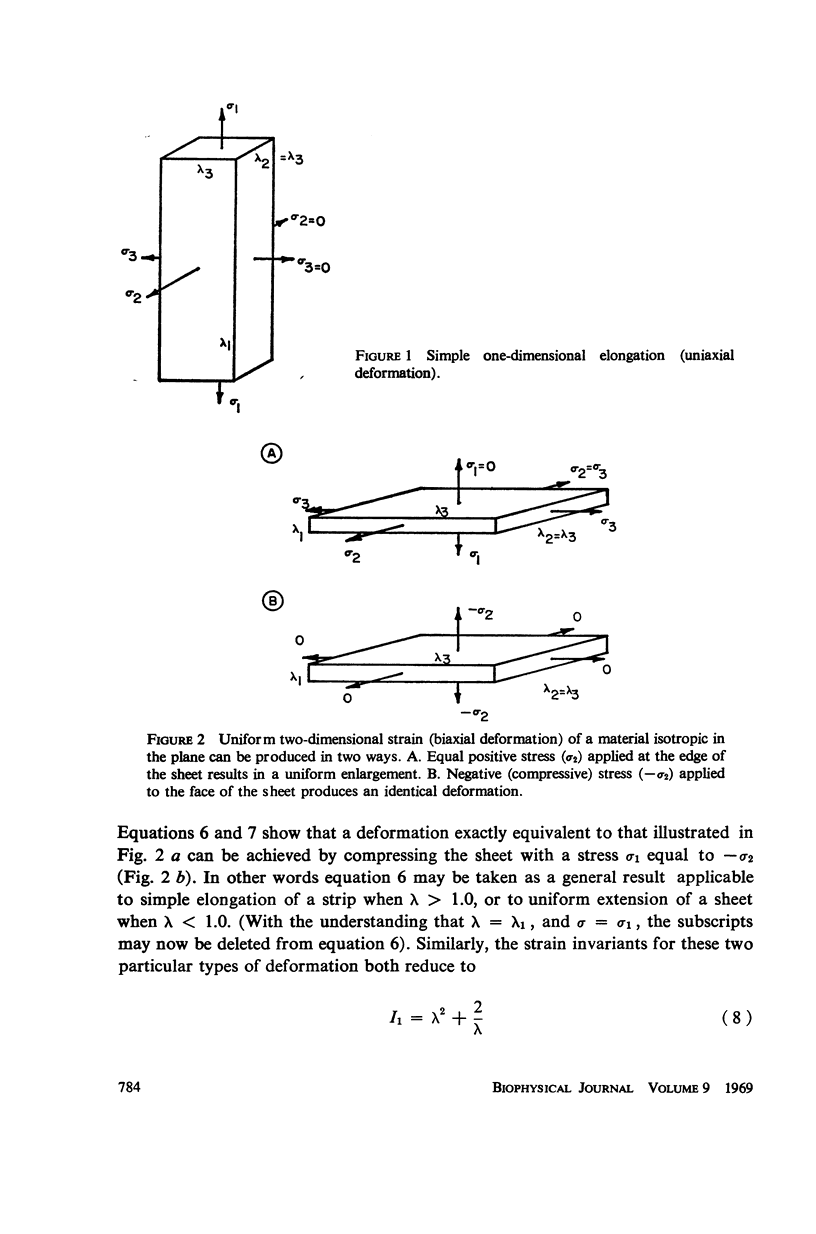
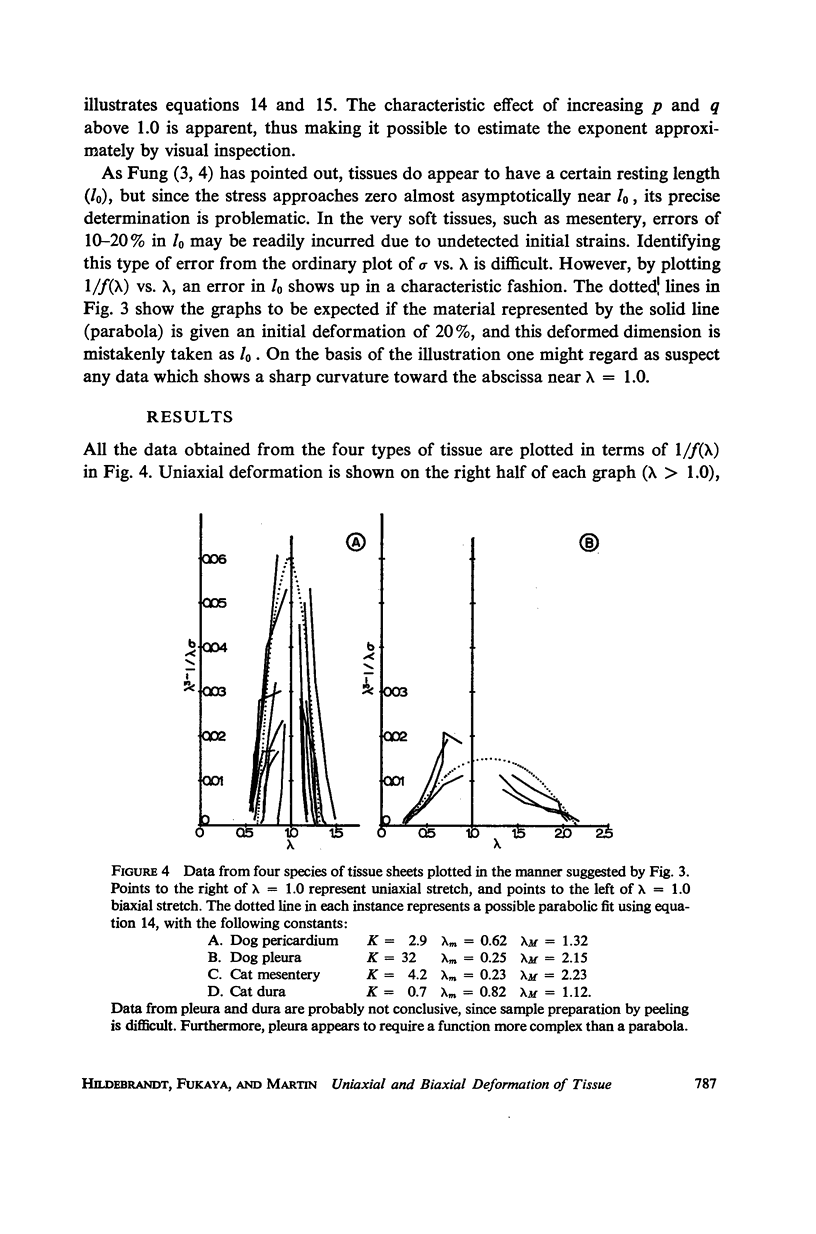
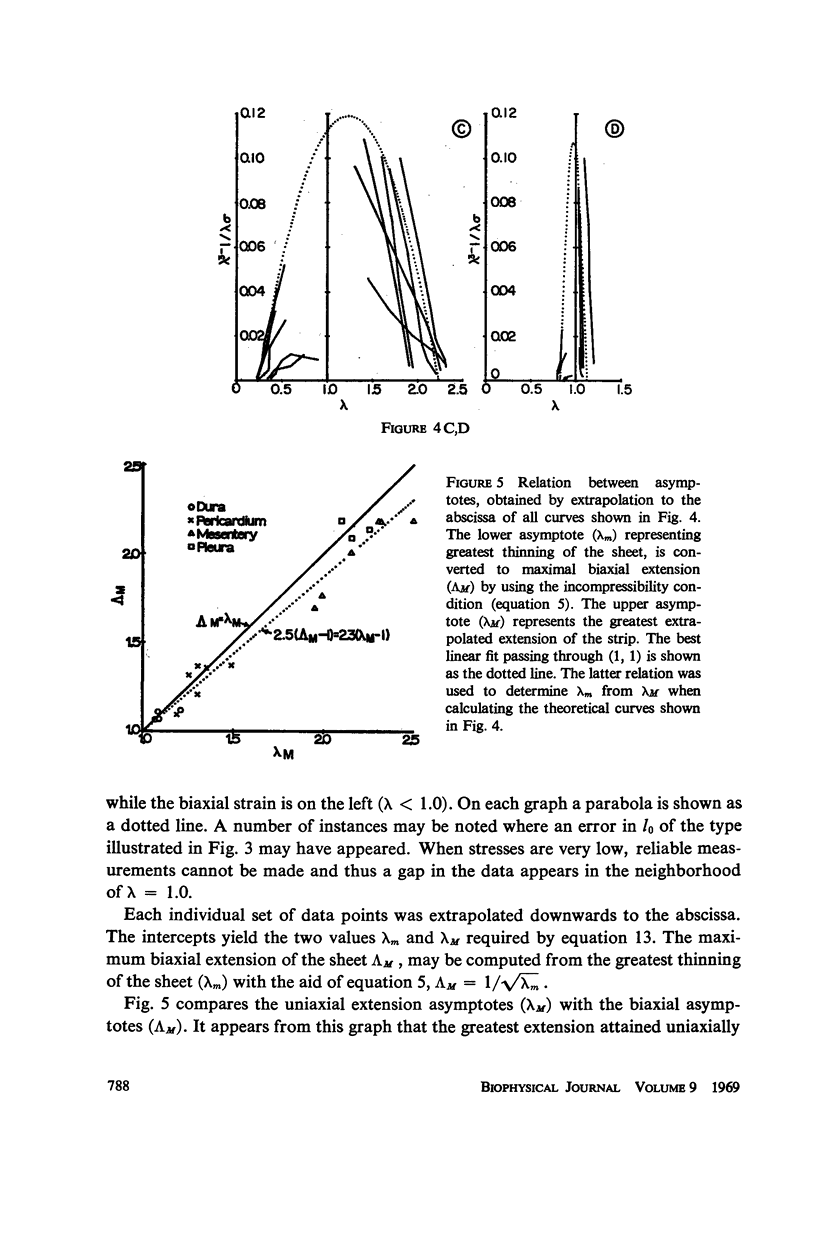
A method is developed for analyzing in a unified manner both uniaxial and uniform biaxial strain data obtained from nearly isotropic tissues. The formulation is a direct application of nonlinear elasticity theory pertaining to large deformations. The general relation between Eulerian stress (σ) and extension ratio (λ) in soft isotropic elastic bodies undergoing uniform deformation takes the simple form: σ = ((λ3 - 1)/λ) f(λ), where f(λ) must be determined for each material. The extension ratio may be either greater than 1.0 (uniaxial elongation), or lie between zero and 1.0 (uniform biaxial extension). Simple analytical functions for f(λ) are most readily found for each tissue by plotting all data as (λ3 - 1)/λσ vs. λ. Of those tissues investigated in this way (dog pericardium and pleura, and cat mesentery and dura), all but pleura could be adequately described by a parabola: 1/f(λ) = 1/k{[(λM - λ)(λ - λm)]/[λM - λm}. In these instances, three material constants per tissue (K, λM, λm) served to predict approximately the stresses attained during both small and large deformations, in strips and sheets alike. It was further found that the uniaxial strain asymptote (λM) was linearly related to the biaxial strain asymptote (ΛM), thus effectively reducing the number of constants by one.
Full text
PDF







Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Carew T. E., Vaishnav R. N., Patel D. J. Compressibility of the arterial wall. Circ Res. 1968 Jul;23(1):61–68. doi: 10.1161/01.res.23.1.61. [DOI] [PubMed] [Google Scholar]
- Fukaya H., Martin C. J., Young A. C., Katsura S. Mechanial properties of alveolar walls. J Appl Physiol. 1968 Dec;25(6):689–695. doi: 10.1152/jappl.1968.25.6.689. [DOI] [PubMed] [Google Scholar]
- Fung Y. C. Elasticity of soft tissues in simple elongation. Am J Physiol. 1967 Dec;213(6):1532–1544. doi: 10.1152/ajplegacy.1967.213.6.1532. [DOI] [PubMed] [Google Scholar]


