Alcohol Use from Ages 9–16: A Cohort-Sequential Latent Growth Model *

Abstract

This study examined alcohol use from pre-adolescence to mid-adolescence and determined the influence of hypothesized covariates on changes in alcohol use rates during this developmental period. The sample comprised 405 randomly recruited youth from three age cohorts (9, 11, and 13 years), assessed annually for 4 years. Youth were 48.4% female, 50.4% African-American, and 49.6% White. A cohort-sequential latent growth model was employed which modeled alcohol use (use vs. non-use) from ages 9–16 years, accounting for demographic variables of gender, race, parent marital status, and family economic status. Covariates of alcohol use included parent alcohol use, family alcohol problems, family cohesion, parent supervision, peer deviance, peer alcohol use, and peer encouragement of alcohol use. Results showed that proportions of alcohol users increased steadily from ages 9–16 years. Significant covariates were found on the intercept and slope. Being female and higher levels of parent alcohol use were associated with higher initial rates of alcohol use whereas greater friends’ encouragement of alcohol use was related to lower initial rates of alcohol use (intercept). Alternatively, more peer deviance and friends’ encouragement of alcohol use was related to an increase in alcohol use rates from ages 9–16 years (slope), as was being White and from a single-parent family.

1. Introduction

The proportion of youth who use alcohol increases during adolescence (Bahr et al., 1995) but a number of children start using alcohol before they reach their teens (Fournet et al., 1990). Although the majority of youth who initiate alcohol do not become problem drinkers, early initiation of alcohol use is one of the strongest predictors of subsequent alcohol abuse and alcohol-related problems, including drinking and driving, school or work absenteeism, and injuries (Brook et al., 1996; DeWitt et al., 2000; Gruber et al., 1996; Peterson et al., 1995). Use during adolescence also directly increases risk for other adverse outcomes, including accidents, homicides and sexually transmitted diseases (Gillmore et al., 1991; Peterson et al., 1995), and may interfere with the development of social, coping, and related skills needed for effective social functioning in late adolescence and early adulthood (Brook et al., 1996; Wechsler et al., 2002).

To accurately assess changes in alcohol consumption and to determine the predictors of various developmental trajectories in youth alcohol use, it is important to conduct longitudinal studies in which the same respondents are followed over time (Barnes et al., 2000). Developmental studies have emphasized the importance of examining growth models of representative samples of youth and including sociodemographic factors such as age, gender, and race (Schulenberg et al., 1996). However, although researchers (e.g., Duncan et al., 1997; Gruber et al., 1996) have established that early adolescent alcohol use is related to later problems, only limited research has focused on alcohol use and predictors of use among pre- and early adolescents. Because general population base rates of alcohol use are typically low in pre- and early adolescence, it is difficult to model alcohol trajectories among younger ages using continuous variables. Fortunately, statistical applications now exist which allow researchers to test growth models using categorical variables (e.g., Muthén and Muthén, 2004), creating new opportunities to examine development in alcohol use among younger age groups.

Using a cohort-sequential design following three cohorts over 4 years, the current study examined change and development in alcohol users from ages 9–16. Developmental trajectories of a dichotomous alcohol outcome (alcohol use vs. non-use) were tested while accounting for demographic covariates of gender, race, parent marital status, and family economic status. The role of family and peer influences on alcohol use development also was tested by the inclusion of several social contextual covariates in the model.

1.1 Influences on Early Youth Alcohol Use

Family members have reciprocal influences on one another that likely affect their alcohol and other substance use, directly and indirectly (Conger, 1997). Social learning theories, well-supported in the substance use literature, state that youth alcohol use behavior is acquired primarily from role models such as parents and peers (Andrews et al., 1997; Petraitis et al., 1995). Parental alcohol use and family alcohol problems consistently have been shown to positively associate with adolescent use of alcohol (Dielman et al., 1993; Green et al., 1991; Hops et al., 1996). In fact, it has been shown that most youth are with parents or other family members when they first use alcohol and, especially among early initiators, they tend to be at home (Porter-Serviss et al., 1994; Strycker et al., 2003).

Besides influencing youth alcohol use directly, family substance use likely also exerts an indirect effect through its impact on family relations and parenting practices (Patterson et al., 1992; Reid and Patterson, 1991). For example, a large body of theoretical and empirical work points to the importance of family climate and parenting practices on the development of a variety of adolescent problem behaviors, including alcohol use (e.g., Barnes, 1990; Barnes and Farrell, 1992). According to Patterson et al.’s (1992) model of the risk factors for problem behavior, low family involvement and poor parenting practices place children at high risk of engaging in problem behaviors. Similarly, in family socialization theory, a key dimension is parental control (also referred to as discipline, punishment, supervision, and monitoring) (Barnes and Olson, 1985; Guilamo-Ramos et al., 2004). Research suggests that poor parental monitoring and discipline are associated with higher adolescent alcohol use (Ary et al., 1993; Dishion and Loeber, 1985). Newcomb et al. (1986) reported that poor relationships with parents predict substance use, and family cohesion has been found to play a protective role in suppressing levels of alcohol consumption among youth (Duncan et al., 1994).

Although family influences and parenting practices account for a considerable amount of variance in the prediction of youth alcohol use, it has long been recognized that the family represents only one of several inter-related social contexts that affect the development of alcohol use, other substance use, and problem behaviors among youth (Conger, 1997). The literature on peer influences on adolescent alcohol use suggests that the influence of peers is at least equal to, if not greater than, that of parents and other family members (e.g., Kandel, 1985). Association with deviant, alcohol- and drug-using peers, and peer encouragement to use alcohol, have been shown to influence adolescent alcohol use (Duncan and Duncan, 1996; Duncan et al., 1994; Hawkins et al., 1992).

As children age, they spend more time with friends compared to family, increasing the potential for negative peer influences (Coombs et al., 1991; Quine and Stephenson, 1990). There is evidence that peer influence on youth becomes greater with age and is particularly influential in the early stages of substance use (Coombs et al., 1991; Kandel, 1985; Quine and Stephenson, 1990).

The purpose of the current study was to examine growth in alcohol use among youth from ages 9–16 years and to determine the influence of hypothesized covariates on change in alcohol use during this developmental period. A cohort-sequential latent growth model (LGM) was employed which modeled alcohol use (use vs. non-use) over time while accounting for demographic variables of gender, race, parent marital status, and family economic status. Contextual covariates included parent alcohol use, family alcohol problems, family cohesion, parent supervision, peer deviance, peer alcohol use, and peer encouragement of alcohol use. Based on prior research, it was hypothesized that: (1) It would be possible to use a cohort-sequential analysis to combine the three age cohorts to reflect a developmental trajectory of alcohol use from ages 9–16 years; (2) The developmental trajectory would be linear; (3) White youth, boys, and youth from single-parent families would have higher levels of alcohol use; (4) Higher levels of parent alcohol use and family alcohol problems would be positively related to increases in alcohol use whereas family cohesion and parent supervision would be negatively related to alcohol increases; and (5) Peer deviance, peer use and encouragement of alcohol use would be positively related to alcohol use.

2. Method

2.1 Participants

Data were collected across 4 years (1999–2003) from residents of a large metropolitan area in the Northwest. The sample comprised 405 youth and their families. Youth were 48.4% female, 50.4% African American, and 49.6% White. Families were randomly recruited via telephone using a computer-assisted telephone interviewing system. A total of 72,412 cold calls were made over 12.5 months, of which 45.5% resulted in contact, 1.3% were eligible, and 75% of those eligible agreed to participate. Quotas were established to ensure a final target youth sample with age (9-, 11-, and 13-year-old cohorts), gender (male and female), ethnicity (African American and White), and neighborhood groups equally represented. More detailed recruitment information is presented elsewhere (Duncan et al., 2002).

The three age cohorts (N = 139 9-year-olds; N = 138 11-year-olds; N = 128 13-year-olds) were selected as part of the study design so that a long-term longitudinal study could be approximated by combining, in a cohort-sequential model, the temporally overlapping short-term longitudinal studies of the different cohorts. Thus, with only 4 years of data collection, the 9-, 11-, and 13-year-old cohorts were linked to form a common developmental trajectory spanning ages 9–16.

In addition to the target child, all family members aged 9 years or older were invited to participate. Telephone calls were used for recruitment and scheduling only. All assessments took place in the participants’ homes. Family members completed annual surveys in their homes under the supervision and guidance of a research assistant. In the first year, families were paid $100 for completing the assessment with a $20 bonus if all eligible family members participated. Each participating child also was paid $5. Family payments were increased by $10 in each subsequent assessment year. Attrition from T1 to T4 was 7.4%.

2.2 Measures

Adolescent alcohol use

Adolescent current alcohol use was measured in each year of the study (T1–T4). Youth were asked, separately for beer, wine/wine coolers, and hard liquor, “How often do you drink [beer/wine/liquor] now?” Responses ranged from 1=don’t use at all to 8=use 2–3 times per day or more. The maximum frequency of use among the three alcohol types was retained, and, because of its highly skewed nature, was then recoded to form a dichotomous current alcohol use construct with 0=non-use and 1=use.

Parent/Guardian alcohol use

Parent/guardian alcohol use was defined as use of beer, wine, and hard liquor, averaged for two-parent households. Responses ranged from 1=never used to 9=use 2–3 times per day or more.

Family alcohol problems

To assess family alcohol problems, parents/guardians were asked, “Have any members of your family ever had a serious problem with drinking?” The question was posed for each of the following: brothers or sisters, mother or father, grandparents, children, and partner. Responses were dichotomous, either 0=no problems or 1=problems. Maximum values were used in two-parent households. To create the construct of family alcohol problems, indicators of problems for the five family members listed above were summed

Family cohesion

Family cohesion was measured using the 10-item FACES scale (Olson et al., 1985). Items included, “Family members ask for each other’s help,” “Family members feel very close to each other,” and “Family togetherness is important.” Respondents were asked to describe how often these occur in the family on a Likert scale ranging from 1=hardly ever to 5=almost always. For the present analyses, parent/guardian scores (averaged in two-parent households) were averaged with youth scores for the family construct. Reliability, assessed using coefficient alpha, was α = .87.

Parent supervision

Five items assessed parental supervision of youth in the family (Capaldi and Patterson, 1989; Reid, 1990). Parents/guardians responded to items such as “I know or have met most of this child’s neighborhood friends” and “I have met or spoken to the parents of this child’s friends,” while youth responded to similar items, such as “At least one of my parents or guardians knows or has met most of my neighborhood friends.” Responses were on a Likert scale ranging from 1=almost always false to 5=almost always true. Parent/guardian scores were averaged in two-parent households. Reliability for this scale was α = .72.

Peer alcohol use

Youth were asked “How often in the past year did your friends drink alcohol?” Responses ranged from 1=don’t use at all to 8=use 2–3 times per day or more.

Peer encouragement of alcohol use

Peer encouragement of alcohol use was assessed via a single self-report item, “Do your friends generally encourage or discourage your use of alcohol? Responses were on a 5-point scale ranging from 1=strongly discourage to 5=strongly encourage.

Alcohol use norms among school peers

Youth were asked “How many of the kids at your school do you think drink alcohol?” Responses were on a 5-point scale ranging from 1=very few to 5=almost all.

Peer deviance

Both parents and youth responded to 8 identical questions related to the target’s friends’ deviance. These items were based on prior measures (Elliott et al., 1989) and included questions such as: “In the past year, how often did your friends . . . Damage public or private property that did not belong to them just for fun? . . . Steal or try to steal things worth $50 or less?” Responses were on a 5-point scale ranging from 1=not at all to 5=very often. Each item was first dichotomized to reflect that the friends either did not (0) or did (1) engage in the behavior. The items were then summed to create a score from 0–8 reflecting friends’ deviance. Separate summary scores were created for parent and youth reports and both were used in the analyses. Reliability for both parent and youth reports of friends’ deviance was α = .82.

Marital status

Parent/guardian reports of their current marital status were dichotomized as 0=single/not living in a committed relationship or 1=married/living in a committed relationship.

Income

Parents and guardians were asked to report “the total income last year in your household (before taxes).” Response categories on the questionnaire ranged from 1=under $5,000 to 11=$90,000 or more.

Demographic variables

Youth gender was coded 1=male and 2=female. Youth ethnicity was coded 0=African-American and 1=White.

Table 1 presents the means (and standard deviations) or frequencies at baseline for the variables used in the conditional model.

Table 1.

Descriptive Statistics for all Variables at Baseline (Time 1)

	Mean (SD) or %
% Two-Parent Households	56.8%
Parent-Reported Income
% Under $5,000	6.2%
% $5,000 to $9,999	8.9%
% $10,000 to $19,999	12.6%
% $20,000 to $29,999	13.1%
% $30,000 to $39,999	12.4%
% $40,000 to $49,999	13.4%
% $50,000 to $59,999	10.1%
% $60,000 to $69,999	7.7%
% $70,000 to $79,999	4.0%
% $80,000 to $89,999	2.5%
% $90,000 +	9.2%
% Female Youth	48.4%
% African-American Youth	50.4%
% Overall Youth who have used Alcohol	17.8%
Parents’ Alcohol Use (Scale: 1–9)	3.94 (2.10)
Family Alcohol Problems (Scale: 0–5)	1.39 (1.27)
Family Cohesion (Scale: 1–5)	3.77 (0.47)
Parent Supervision (Scale: 1–5)	4.57 (0.57)
Peer Alcohol Use (Scale: 1–8)	1.36 (1.03)
Peer Deviance – Parent Report (Scale: 0–8)	1.29 (1.46)
Peer Deviance – Target Report (Scale: 0–8)	1.88 (1.95)
Peer Encouragement of Alcohol Use (Scale: 1–5)	3.69 (1.14)
Alcohol use norms among school peers (Scale: 1–5)	1.46 (.77)

2.3 Analytical Model

Researchers have begun exploring new ways of constructing more complex and dynamic models that are better suited for assessing change than traditional methods (e.g., Collins and Sayer, 2001). One such strategy is the latent variable growth modeling (LGM) approach used in this study. LGM offers a flexible and efficient means of modeling longitudinal behavioral outcome variables, such as alcohol use, and of handling non-normal distributions.

Although applications of LGM typically have modeled normally distributed continuous outcome variables, the present study models alcohol use as a binary variable which distinguishes between any positive level of alcohol use (coded 1) from non-use (coded 0). Use vs. non-use, therefore, was regressed on the growth factors using a probit model within a random effects growth modeling framework. Detailed specifications for the modeling of ordered categorical dependent variables are described in Muthén (2001). Analyses for this study were conducted using Mplus software (Muthén and Muthén, 2004).

Cohort-sequential LGM

Although desirable, true longitudinal designs present some practical problems. Given time constraints, concerns about attrition, and the cost of multiple assessments, researchers have long sought ways to maintain the advantages and minimize the disadvantages of the longitudinal design (Duncan et al., 1999). In 1953, Bell introduced the idea of “convergence.” This method calls for limited repeated measurements of independent age cohorts, resulting in temporally overlapping measurements of the various groups. This technique, which has gained recent popularity as the “cohort-sequential” (Nesselroade and Baltes, 1979) or accelerated design, provides a way to link adjacent segments of limited longitudinal data from different age cohorts to determine the existence of a common developmental trend, or growth curve. In this way, the researcher approximates a long-term longitudinal study by simultaneously conducting and connecting several short-term longitudinal studies of different age cohorts.

Based on the various sets of staggered age-group curves arising from the accelerated design of the study, a cohort-sequential LGM was specified and is depicted in Figure 1. Because of the overlap between ages, it was possible to test the hypothesis that a common developmental trajectory from ages 9–16 existed for alcohol use. This particular method of analysis has been used extensively by McArdle and colleagues (McArdle and Anderson, 1990; McArdle and Hamagami, 1992). Each age cohort contributes a different section of the overall curve. Because each cohort represents a different pattern of “missingness” in the context of the overall developmental curve, it is possible to build the complete curve using information from all cohorts simultaneously. The same developmental model is assumed in each cohort, allowing for tests of convergence across separate groups and the feasibility of specifying a common growth trajectory across the 8 years represented by the design. Prior experience with adolescent samples suggested that a cohort-sequential model was viable and that a linear growth function would accurately describe the growth trajectories for this set of curves (e.g., Duncan et al., 1996, 1999).

Figure 1.

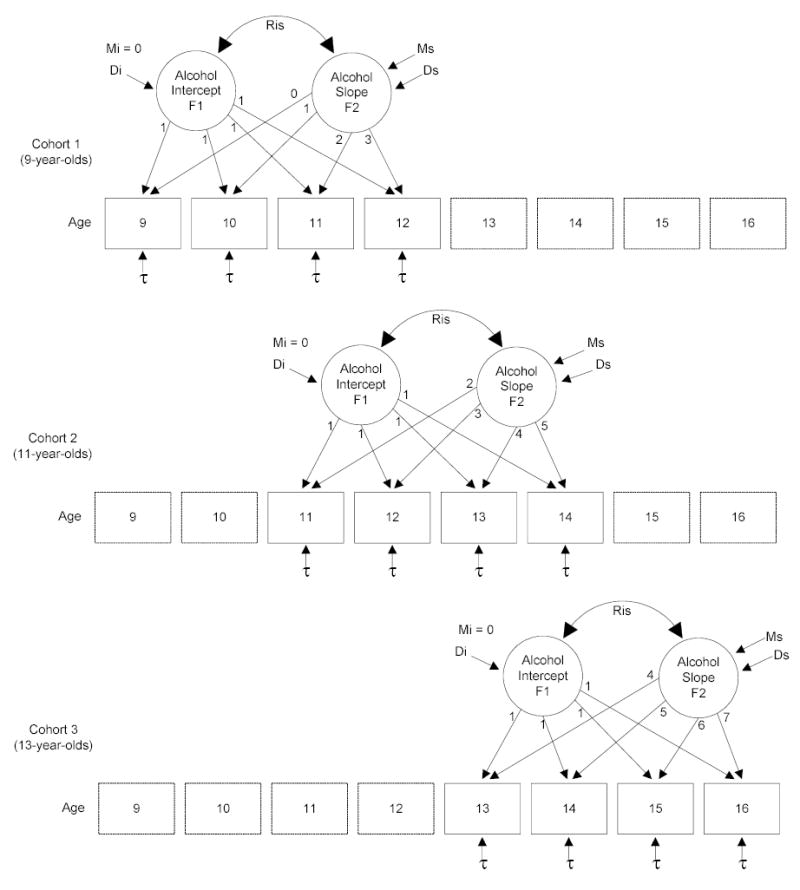
Representation of the cohort-sequential LGM for change in adolescent alcohol use from ages 9 to 16 years. Cohort 1 represents the 9-year-old cohort with data for ages 9, 10, 11, and 12 years across years 1 to 4, respectively. Cohort 2 represents the 11-year-old cohort with data for ages 11, 12, 13, and 14 years. Cohort 3 represents the 13-year-old cohort with data for ages 13, 14, 15, and 16 years. Boxes with dotted lines represent the “missing” data by design for each cohort. F1 represents Factor 1, the intercept, and F2 represents Factor 2, the slope. The mean of the slope, M_s, and variances of the intercept, D_i, and slope, D_s, as well as the correlation, R_is, between the intercept and slope, are estimated. The mean of the intercept, M_i, is fixed at 0. Thresholds for each observed variable are estimated and constrained to be equal across time and cohort. A linear growth trajectory is specified by fixing the factor loadings on the slope from 0–7 across ages 9–16 years.

In Figure 1, Cohort 1 represents the 9-year-old cohort with data for ages 9, 10, 11, and 12 years at Time 1 (T1), Time 2 (T2), Time 3 (T3) and Time 4 (T4), respectively. Cohort 2 represents the 11-year-old cohort with data for ages 11, 12, 13, and 14 years. Cohort 3 represents the 13-year-old cohort with data for ages 13, 14, 15, and 16 years. F1 represents Factor 1, the intercept, and F2 represents Factor 2, the slope. The basis terms (factor loadings) of the intercept are fixed at 1. The basis terms of the slope are fixed (0–7) to represent a linear growth trend from ages 9–16 years. The mean of the intercept, M_i, is constrained to zero. The slope mean, M_s, and variances of the intercept, D_i, and slope, D_s, are estimated, as well as the correlation, R_is, between the intercept and slope.

For the categorical y variables, τ‘s (threshold parameters), rather than e’s (measurement errors), which are typically modeled for continuous normally distributed outcome variables, are specified to represent category intervals. In the case of a dichotomous outcome, one threshold is specified for alcohol use at each time point (T1 to T4). Across-time measurement invariance is imposed by specifying τ₁ = τ₂ = τ₃ = τ₄. Although the model involves categorical dependent variables, the latent variables (growth parameters F1 and F2) are continuous in nature, as they are in the case of continuous normally distributed repeated measures variables.¹

The cohort-sequential models were estimated within a multiple-sample (multiple-group) context. Cross-group (cohort) equality constraints were specified for all free parameters in the model, including the latent slope means, latent variances for the intercept and slope, the latent covariances between the intercept and slope, and threshold parameters of the observed variables. The mean intercept was already fixed at 0 for each cohort, and the linear trend also is fixed using basis terms from 0 to 7. Because the same developmental model is assumed in each group, tests are possible regarding convergence across separate cohorts and the feasibility of specifying a common “true longitudinal” growth trajectory over the 8 years represented by the design.

A two-step procedure was used for testing the LGM: (1) identifying the unconditional functional form and significance of the growth parameters, and (2) examining the impact of theoretically relevant covariates on growth in alcohol use estimated from the converged curves. Models were estimated using a robust weighted least squares estimator, and model fit was assessed using the chi-square goodness of fit test, Comparative Fit Index (CFI; Bentler, 1990), and Root Mean Square Error of Approximation (RMSEA; Brown and Cudeck, 1993).

Mplus handles missing data on the dependent, y, variables through use of the Expectation Maximization (EM) algorithm. Thus, for the unconditional models, all 405 cases were used.² For the conditional analyses, missing data on the covariates were handled listwise, causing the exclusion of five cases from those analyses.

3. Results

Table 2 presents the alcohol use proportions for the three cohorts analyzed in the accelerated LGM.

Table 2.

Summary of Categorical Data Proportions (% of Alcohol Users) by Age Cohort Over Time (9–16 years)

	Age
	9	10	11	12	13	14	15	16
% Current Alcohol Users
Cohort 1	12.9	9.8	8.5	10.9
Cohort 2			13.0	15.0	23.1	27.0
Cohort 3					28.1	28.0	38.2	44.2

3.1 Testing the Linear Growth Model

Fitting a linear accelerated latent growth model to the data for alcohol use produced an acceptable chi-square test statistic, χ²(11, N = 405) = 16.153, p = .135, and fit indices, CFI = .994, and RMSEA = .059. Generally, a value of .90 or greater on the CFI (Bentler, 1990) and .05 or lower on the RMSEA (Browne and Cudeck, 1993) represent an acceptable model fit. These fit statistics indicate that the accelerated or cohort-sequential latent growth model provides an adequate fit to the data. In addition to the adequate fit of the model, an examination of the model’s modification indices suggested that, although there were a few differences in parameter estimates across cohorts, these were trivial differences that would not result in a substantial improvement in model fit. Such results justify the use of a cohort-sequential model to approximate a true longitudinal curve in these data and suggest that the three cohorts were sampled from the same true longitudinal population.

The linear model resulted in a significant mean slope, M_s = .105, t = 2.757, p < .01, suggesting that the cohort-sequential model showed a steady increase in the prevalence of alcohol use from ages 9–16 years. The M_s value of .105 can be interpreted as the increase in use per unit of time (i.e., .105 X 3 [T4-T1 = 3 units of time] = .315), which corresponds to the actual increase in proportion of users from ages 9–16 years (i.e., .442 [proportion of users at T4 for cohort 3] – .129 [proportion of users at T1 for cohort 1] = .313 [see Table 2]). The variances for the intercept and slope were D_i = 1.050, t = 5.610, p < .001 and D_s = .104, t = 2.483, p < .05, respectively, indicating substantial variation across individuals in initial alcohol use and in the developmental trajectory for alcohol use. The results of the model fit, modification indices, and significant slope mean and variance support the proposed hypotheses regarding the use of the cohort-sequential model and the linear developmental trajectory of alcohol use. Tests revealed no significant quadratic trend in the slope. The latent variances also were estimated. Figure 2 shows the trajectory of alcohol use for each cohort over time and the estimated linear trajectory from the cohort sequential model of alcohol use from age 9–16 years.³

Figure 2.

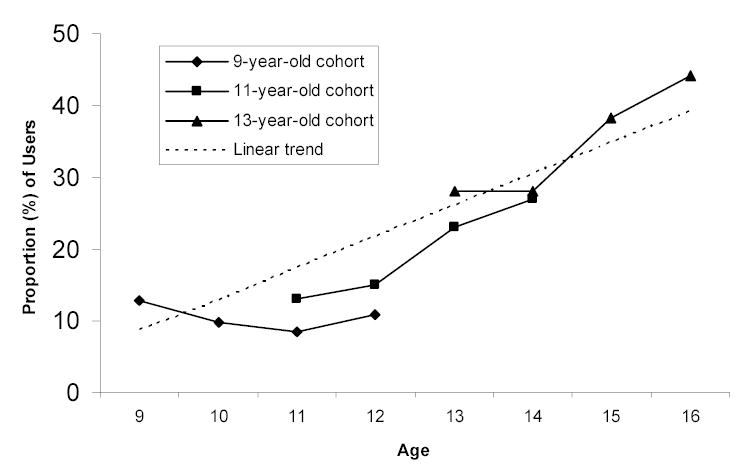
Proportion of alcohol users by cohort (9, 11, and 13 years), joined together to form a trajectory of alcohol use from ages 9–16 years.

3.2 Testing the Conditional Linear Model

Having modeled a common linear trajectory from the three cohorts, a conditional model was tested. The conditional model included covariates hypothesized to have a significant impact on the growth parameters representing individual differences in alcohol use patterns over time. Demographic covariates included gender, race (White or African American), parent/guardian marital status, and family income. Parent/guardian alcohol use, family alcohol problems, family cohesion, parent supervision, peer deviance, peer alcohol use, alcohol use norms among school peers, and peer encouragement of alcohol use all were assessed at the first time point. Effects of covariates were tested on the intercept and slope. Of particular interest was the impact of these covariates on alcohol use trajectories (i.e., change in the proportion of alcohol users over time). Backwards elimination of independent variables was used in the LGM analyses (at a significance level of p < .05) to derive the most parsimonious model among the pool of predictors. Backwards deletion is advantageous because it reduces problems associated with multicollinearity and avoids the elimination of potentially important predictors. In conditional analyses, multicollinearity among a set of covariates may lead to distortions in the estimation of the regression coefficients and seriously threaten their interpretation as indices of effects. When correlated variables are simultaneously used, the regression coefficient may inaccurately reflect the contribution of each variable and the researcher may mistakenly conclude that none of the predictors has a statistically significant effect on the dependent variable (Pedhazur, 1997). With the backwards elimination method, all independent variables are initially included in the model and each variable is treated as if it were entered last in the equation. Variables that do not significantly add to the equation are deleted. The final model yielded a chi-square statistic of χ² (36, N = 400) = 53.392, p = .031, and fit indices of CFI = .967 and RMSEA = .060. Parameter estimates for this model revealed three covariates that were significantly related to initial status of alcohol use (intercept) and four covariates that were significantly related (p < .05 or greater) to change in alcohol use from ages 9–16 years. Standardized betas for the 6 significant covariates are shown in Figure 3.

Figure 3.

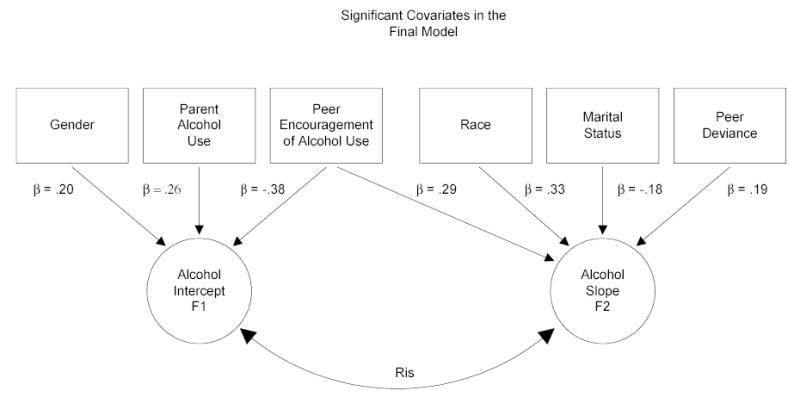
Depiction of the effects (standardized betas) of the significant covariates on the LGM alcohol intercept and slope. All effects are significant at p < .05 or greater.

Being female and higher levels of parent alcohol use were associated with higher initial levels of alcohol use whereas greater friends’ encouragement of alcohol use was related to lower levels of initial alcohol use (intercept). Alternatively, more peer deviance (target report) and encouragement of alcohol use was related to an increase in alcohol use from ages 9–16 years (Slope), as was being White and from a single-parent family.

4. Discussion

Latent growth curve methodology for analyzing longitudinal youth alcohol use data was used in the present study to test hypotheses concerning growth in alcohol use from pre- through early adolescence, and covariates influencing the developmental trajectories. Using a cohort-sequential design, longitudinal curves spanning an 8-year period from 9–16 years were successfully estimated using only 4 years of data. This study adds support to other research (e.g., Duncan et al., 1996, McArdle and Hamagami, 1992; Raudenbush and Chan, 1992) demonstrating that the accelerated design procedure is an efficient method for examining longitudinal data. In addition, although applications of LGM typically model normally distributed continuous outcome variables, this is a difficult practice with early youth data because of the generally low base rates in this population. Thus, the present study used an alternative approach and modeled alcohol use as a binary variable distinguishing alcohol use (coded 1) from non-use (coded 0).

Results indicated an upward linear trend in the proportion of youth alcohol users between the ages of 9 and 16, consistent with developmental studies of alcohol use during adolescence (e.g., Bahr et al., 1995; Duncan et al., 1994). Three significant findings emerged regarding the intercept or initial status of alcohol use. This study found that girls initially had higher prevalence of alcohol use than boys. Prior studies generally have shown that boys have higher levels of alcohol use than girls (e.g., Duncan et al., 1994; Windle, 1994), although there is evidence of a diminishing difference in these trends over time (Johnston et al., 1995). In contrast to most prior studies, the current study focuses on prevalence or rates of alcohol use (users vs. non-users) rather than level of alcohol use; thus, the results do not necessarily contradict prior findings measuring different aspects of alcohol use. Future research examining gender differences in alcohol use/non-use and levels of use is encouraged to take a multiple-sample approach wherein boys and girls can be compared as separate groups.

Similar to other studies (e.g., Dielman et al., 1993; Green et al., 1991; Hops et al., 1996), parent alcohol use was positively related to youth alcohol use. This finding supports social learning theories stating that youth alcohol use behavior is often acquired from role models such as parents (Andrews et al., 1997; Petraitis et al., 1995). This is further supported by the fact that studies have shown that most youth are with parents or family members when they first use alcohol (Porter-Serviss et al., 1994; Strycker et al., 2003). Educating parents not to involve their children in their use of alcohol may provide a means by which to reduce risk of adolescent alcohol use (Peterson et al., 1995).

Peer encouragement of alcohol use also was significantly, but negatively, related to youth alcohol use at baseline. Thus, greater friends’ encouragement of alcohol use was related to a lower prevalence of alcohol use at the first time point. Although this finding may appear counterintuitive, the effect must be evaluated in the context of the effect of peer encouragement on the slope of alcohol use. Because the effect of peer encouragement on the slope is positive (see following section for further details), the negative relation with the intercept reflects a lagged effect such that peer encouragement precedes initiation and subsequent increases in the prevalence of alcohol use over time.

Four covariates significantly influenced the slope of alcohol use. From ages 9–16, White youth had a greater rate of increase in alcohol use compared to African American youth. These findings are consistent with many studies showing that early initiation of alcohol is more prevalent among White than among African American youth (e.g., Catalano et al., 1993; Johnston et al., 1987; Rachel et al., 1980). In addition, Barnes et al. (2000) found that African American adolescents had lower intercepts and slopes than their White counterparts. Thus, current adolescent rates of alcohol use appear to be lower for African Americans than for White youth.

Also, in accordance with findings from other studies, youth from single-parent families had greater rates of increase in alcohol use from ages 9–16 compared to youth from two-parent families. Parent marital status has consistently been found to predict adolescent substance use, with youth from single-parent families having more alcohol use than youth from two-parent families, a finding that appears to be consistent across White and African American families (Duncan et al., 1998; Parker et al., 1995).

Several researchers have argued that during pre-adolescence and adolescence children spend increasing amounts of time with friends compared to family, thus the peer context has considerable potential for influencing the development of alcohol use during adolescence (Coombs et al., 1991; Kandel, 1985; Quine and Stephenson, 1990). The findings of this study support this view. While family influences were not found to be significantly related to increases in the rate of alcohol use from ages 9–16, peer influences did have a significant effect on increased rates of alcohol use during this developmental period. Specifically, higher levels of peer deviance and peer encouragement of alcohol use were related to greater increases in the rate of alcohol use between the ages of 9 and 16. These peer factors and others have been found in prior studies to be related to youth alcohol use (e.g., Barnes et al., 1995; Duncan and Duncan, 1996; Duncan et al., 1994; Hawkins et al., 1992). Since peer social reinforcement is an influential force in an adolescent’s life, it makes sense that youth will be more likely to engage in deviant behaviors such as alcohol use when their peers engage in or encourage such behaviors (Dishion et al., 2003; Guilamo-Ramos et al., 2004). Future studies are needed to further examine the effects of peer and family influences on early adolescent alcohol use, particularly on changes or growth in alcohol use during pre-adolescence and early adolescence.

This study has strengths and limitations. Relatively few studies have examined the development of adolescent alcohol use, especially among pre-adolescents and early adolescents. While it is often preferable to examine growth trajectories using continuous variables, in this study, due to the age of the sample and associated low base rates in alcohol use, it was necessary to determine trajectories based on a dichotomous variable: use vs. non-use. The fact that changes in the prevalence of alcohol use/non-use could be modeled successfully among such young ages is a strength of the study. Although the model presented here suggests an additive model, the covariates may exert their effects in a more interactive manner. Despite fairly high participation rates, the study is still limited by its agreement rate bias (75%) and study design selection bias of only 9-, 11-, and 13-year-old White and African American youth. The study also was limited in terms of the number of covariates used. The current study included demographic, family, and peer factors; however, there may be other personal and social contextual factors (e.g., psychiatric problems, school or neighborhood environment) that also need to be considered when attempting to gain insight into the process of alcohol use development during youth (Conger, 1997; Gottfredson and Koper, 1996).

This investigation has a number of strengths. These include the randomly recruited sample, use of youth- and parent-report data, 4 years of longitudinal data, and use of a cohort-sequential LGM to determine growth in alcohol use rates among youth ages 9–16. The randomly recruited sample has relatively equal numbers of similar age male and female African American and White youth. Families reflect the economic status of the county and state from which they were recruited. The cohort-sequential design allowed assessment of an 8-year developmental span using only 4 years of data, and the use of categorical variables within the LGM framework made it possible to examine changes in rates of alcohol use during pre-adolescence as well as early and mid-adolescence, and to include predictors of use measured as early as 9 years of age. A particular strength of this study is its focus on pre-adolescent and early adolescent youth, a period which is somewhat neglected but important in the initiation and subsequent development of alcohol use. Fournet et al. (1990) showed that a large proportion of alcohol use had its onset before children reached their adolescent years; thus, it is critical to measure and assess use and predictors of use prior to adolescence. In addition, Kosterman et al. (2000) suggest that the pre-teen years may be particularly appropriate for alcohol prevention and intervention work.

Recent reports indicate that alcohol use is increasing among youth in the United States (Jensen, 1997; MacNeil et al., 1999), presenting a challenge to researchers to study patterns of use, as well as risk and protective factors of youth alcohol use, at different stages of development, over time, across genders, and across ethnicities (Duncan et al., 2003). Future research is encouraged to continue to study early predictors of youth alcohol use, along with trajectories of use among pre-teens, adolescents, and beyond, and, where possible, to incorporate multiple-sample analyses to determine trajectories by age, gender, and ethnicity. Longitudinal studies such as these have the ability to increase our understanding of the nature and causes of adolescent and young adult alcohol misuse and to lay the groundwork for designing effective alcohol prevention and intervention strategies.

Appendix 1 Mplus program specifications for the unconditional cohort-sequential model

TITLE:

LGM COHORT-SEQUENTIAL MULTISAMPLE ANALYSIS

Y1=T1ALC Y2=T2ALC Y3=T3ALC Y4=T4ALC COHORT

COHORT(1=G1[AGE 9] 2=G2 [AGE 11] 3=G3 [AGE 13]);

DATA:

FILE IS ALCATA.DAT;

VARIABLE:

NAMES ARE Y1-Y4 COHORT;

USEVAR = Y1-Y4;

GROUPING IS COHORT(1=G1 2=G2 3=G3);

CATEGORICAL ARE Y1-Y4;

MISSING ARE ALL (-999.00);

ANALYSIS: TYPE = MGROUP MISSING H1;

ITERATIONS = 100;

MODEL:

INT BY Y1-Y4@1;

SLP BY Y1@0 Y2@1 Y3@2 y4@3;

INT*(I);

SLP*(S);

INT WITH SLP*(IS);

[INT@0];

[SLP*](MS);

MODEL G1: ! MODEL FOR COHORT 1

INT BY Y1-Y4@1;

SLP BY Y1@0 Y2@1 Y3@2 y4@3;

INT*(I);

SLP*(S);

INT WITH SLP*(IS);

[INT@0];

[SLP*](MS);

[Y1$1-Y4$1@1];

MODEL G2: ! MODEL FOR COHORT 2

INT BY Y1-Y4@1;

SLP BY Y1@2 Y2@3 Y3@4 y4@5;

INT*(I);

SLP*(S);

INT WITH SLP*(IS);

[INT@0];

[SLP*](MS);

[Y1$1-Y4$1*.50](T);

MODEL G3: ! MODEL FOR COHORT 3

INT BY Y1-Y4@1;

SLP BY Y1@4 Y2@5 Y3@6 y4@7;

INT*(I);

SLP*(S);

INT WITH SLP*(IS);

[INT@0];

[SLP*](MS);

[Y1$1-Y4$1*.50](T);

OUTPUT: TECH1 STANDARDIZED;

Note: The model statement (e.g., model G1:) for the C-S LGM consists of the following commands

BY Short for measured by -- defines latent variables.

Example: INT by Y1-Y4

WITH Short for correlated with -- defines correlational relationships.

Example: INT WITH INT

list of variables; Refers to variances;

Example: INT

[list of variables]; Refers to means or regression intercepts

Example: [INT SLP]

[$1] Refers to threshold parameters for ordered categorical dependant variables

Example: [Y1$1]

* Freely estimated parameter and specific starting value

Example: INT* [Y1$1-Y4$1*.50]

@ Fixed parameter at a specific value

Example: [INT@0]

( ) Refers to cross-group parameter constraints

Example: [SLP*](MS) - constrains the slope mean to be equal across groups (cohorts)