Changes in DNA bending and flexing due to tethered cations detected by fluorescence resonance energy transfer

Abstract

Local DNA deformation arises from an interplay among sequence-related base stacking, intrastrand phosphate repulsion, and counterion and water distribution, which is further complicated by the approach and binding of a protein. The role of electrostatics in this complex chemistry was investigated using tethered cationic groups that mimic proximate side chains. A DNA duplex was modified with one or two centrally located deoxyuracils substituted at the 5-position with either a flexible 3-aminopropyl group or a rigid 3-aminopropyn-1-yl group. End-to-end helical distances and duplex flexibility were obtained from measurements of the time-resolved Förster resonance energy transfer between 5′- and 3′-linked dye pairs. A novel analysis utilized the first and second moments of the G(t) function, which encompasses only the energy transfer process. Duplex flexibility is altered by the presence of even a single positive charge. In contrast, the mean 5′–3′ distance is significantly altered by the introduction of two adjacently tethered cations into the double helix but not by a single cation: two adjacent aminopropyl groups decrease the 5′–3′ distance while neighboring aminopropynyl groups lengthen the helix.

INTRODUCTION

DNA structure plays a critical role in biological processes. A clear example is the formation of nucleosomes by the wrapping of DNA around histone octamers. The wound helix in these nucleoprotein complexes is locally and transiently remodeled to facilitate interactions with transcription proteins, which in turn reconfigure the DNA concurrently with binding. Indeed, appropriate DNA deformation appears to be the essential function of many transcription activating and regulatory proteins. The TATA binding-protein induces sequence-dependent bending of ∼30–102° in ‘TATA’ boxes (1–13), with the degree of bending hypothesized to determine the probability for binding of subsequent factors (12). The Escherichia coli lactose repressor dramatically loops DNA in order to correctly orient critical sequences with their targets (14). The literature is now replete with additional and diverse examples of protein-induced DNA structural changes (12,15–24).

DNA deformation arises from a complex interplay among sequence-related base stacking, intrastrand phosphate repulsion, and counterion and water distribution (5,15,21,22,25–33). The approach and binding of a protein to the double helix further complicates this picture, resulting potentially in formation of hydrogen bonds and van der Waal's contacts, coulombic attraction between cationic side chains and DNA phosphates, release of condensed counterions, and dehydration. This altered environment elicits a structural response from the DNA, although the relative contribution of each of these factors and indeed their interactions remain unclear.

In an effort to better understand the electrostatic effects introduced by protein binding, Strauss and Maher (34) substituted methylphosphonates for DNA backbone phosphates, asymmetrically neutralizing charge in various phasings along the minor groove. This experimental design followed the phantom protein model of Manning et al. (26) and was intended to isolate the electrostatic component of protein binding to DNA. Electrophoretic analysis was consistent with significant DNA bending towards the minor groove, but subsequent experiments suggested structural changes attributable to the methylphosphonates themselves. An alternate approach in which ${\text{NH}}_4^{+}$ cations were covalently tetherered by aminoalkyl chains to selected nucleotides likewise resulted in aberrant gel mobility which was interpreted as DNA bending up to 8° (35,36). Associated electrostatic footprinting studies and molecular modeling both showed the side chain on the floor of the major groove extending in the 3′ direction from the modified nucleotide (37,38). This orientation was subsequently found to be consistent with NMR data for a duplex incorporating the same 3-aminopropyl substitution at the 5-position of a deoxyuracil (39). Analysis of the NMR data based on the constrained side chain location, from molecular modeling, yielded a bent DNA structure, although unconstrained calculations gave an unbent helix which also satisfied the experimental NOE data (39).

The importance of understanding electrostatic effects on DNA helices and the ambiguity in the interpretation of the electrophoretic mobility and NMR results led to the present study. We pursue the question: how does introduced localized charge affect the bending and flexibility of duplex DNA? We have selectively modified one strand of a 14 bp DNA oligomer using centrally located deoxyuricils substituted at the 5-position with either a flexible 3-aminopropyl group or a rigid 3-aminopropyn-1-yl group. This site-specific introduction of one or two adjacent cationic charges simulates the effects of proximate basic side chains from bound proteins. Previous work has demonstrated the stability of these altered duplexes with maintenance of normal Watson–Crick base pairing (37,39–41). We have used time-resolved Förster resonance energy transfer (FRET) to obtain the mean 5′–3′ distances for these modified duplexes for comparison with the corresponding distance for the unmodified duplex. Changes in these distances can be determined to very high precision using FRET fluorometry and have been shown to relate directly to differences in the extent of helical bending (7,8,10–13,18,42–44). Additionally, we have determined the distributions of these distances, which reflect the extent of duplex flexibility. The results, obtained using a novel and robust method of analysis, provide direct evidence for changes in DNA structure in response to the altered electrostatic environment introduced by the tethered cations. Notably, while introduction of a single cation alters helical flexibility, two adjacently tethered cations are required for FRET detected changes in the 5′–3′ distance.

MATERIALS AND METHODS

Materials

The five 14 bp DNA duplexes studied herein were composed of a common, dye-labeled top strand hybridized to an unmodified 5′-GCCCTATTATAGCG-3′ (DNA_TT) or aminoalkly-modified complementary strand. The latter included either one (DNA_8ap) or two (DNA_7,8ap) aminopropyl groups substituted at the 5-position of deoxyuricil, or one (DNA_8apn) or two (DNA_7,8apn) analogous aminopropynyl substitutions (Table 1). These modified bottom strands were synthesized as described previously (41). Briefly, the 5-(3-aminoalkyl-modified)-2′-deoxyuridine was prepared by coupling 5-iodo-2′-deoxyuridine with either 1-aminopropyl or 1-aminoprop-2-yne (protected as the N-phthalimide) in the presence of [(PPh)₃]₄Pd(0)₄ (45). The deoxynucleoside was then converted into the 5′-O-dimethoxytrityl-3′-O-phosphoramidite using standard procedures (46) and the structure was confirmed by ¹H NMR and mass spectrometry (41). The phosphoramidites were then incorporated into oligomers on an ABI (Foster City, CA) synthesizer, purified by reverse phase high-performance liquid chromatography (HPLC), and shown to be homogeneous by PAGE. Modified oligonucleotides were characterized by sequential hydrolysis and HPLC analysis. The top strands were either single-labeled on the 3′ end with fluorescein (DNA*F) or double-labeled with both 3′ fluorescein and 5′ TAMRA (T*DNA*F), with both dyes tethered by a six-carbon chain. Fluorescein and TAMRA serve as a donor–acceptor pair, respectively, for FRET. Both dye-labeled strands were synthesized by Sigma-Aldrich Genosys, Inc. (The Woodlands, TX) and highly purified using HPLC/PAGE and PAGE, respectively. Duplexes were formed with ≥2× complement and sufficient incubation times to ensure full top-strand saturation. Measurements were collected in phosphate (10 mM phosphate, pH 7.4, with 0.05 mM EDTA and 100 mM NaCl) buffer at 30 ± 0.05°C.

Table 1.

The parent (DNA_TT), one and two aminopropyl (DNA_8ap and DNA_7,8ap), and one and two aminopropynyl (DNA_8apn and DNA_7,8apn) bottom strands used herein

All five duplexes had a common dye-labeled top strand: TAMRA-5′-CGCTATAATAGGGC-3′-fluorescein.

Preliminary steady-state anisotropy measurements

Previous steady-state and time-resolved anisotropy measurements provided direct evidence for significant rotational mobility of the linked dyes for the unmodified duplex and strong support for dye mobility of the modified duplexes (12,13,47–49). This conclusion was validated by obtaining steady-state anisotropy measurements following the method of Giblin (50), a modification of the Wampler and DeSa (51) method in which the modulator precedes the sample. An Alphascan fluorimeter (Photon Technology, Inc.) was used with an INNOVA 70-4 Coherent Ar⁺ laser (Santa Clara, CA), with a photoelastic modulator (PEM-80; HINDS International, Inc., Portland, OR) positioned between the light source and the sample compartment oriented with its principal axis 45° to the optical plane consisting of the light source, sample and detector. The modulator acts as an oscillating variable retarder with a maximum retardance of 1.22π radians (51). The steady-state emission intensity is measured with the modulator alternately off and on. Because the 50 kHz modulation frequency is much faster than the response of the circuitry following the photomultiplier, the measured emission intensity obtained with the PEM ‘on’ is a dc average of the modulated intensity. These values are related to the sample anisotropy according to the following expression:

$$r=\left[\frac{4-4\gamma }{\gamma (2-3H)+(2.20828+3H+0.62712H)}\right],$$ 1

where H = (1 − G)/(1 + G), G is the grating factor (52), and γ is the ratio of the fluorescence intensity with the PEM on to that with the PEM off.

For the unmodified and each of the four modified complements, anisotropy data were collected at the peak emission wavelength using 4 nM DNA*F duplex and analyzed as described (53). Five sets of paired PEM ‘off’ and PEM ‘on’ data were obtained for each duplex with stirring after each set to eliminate the effects of fluorescein photobleaching. The steady-state anisotropy value, r, was calculated using Equation 1 for each paired set. The reported anisotropy values are the averages for each case.

Determination of end-to-end distance distributions for unmodified and modified duplexes from time-resolved fluorescence decays

Detailed discussions of FRET and its applications to the study herein have been published (8,12,13,43,44,52,54–58). Briefly, fluorophores are flexibly tethered to both the 5′ and 3′ ends of DNA duplexes. The resonance interaction between these two fluorophores results in the direct transfer of excited state energy from the donor to the acceptor fluorophore. Because the rate of transfer varies with the inverse sixth power of the distance between the two fluorophores, the emission of the fluorophores is exquisitely sensitive to changes in the interdye distance. The six-carbon linker arms to which the fluorophores are attached are flexible in solution so that the distance between the 5′- and 3′-dye varies over some probability distribution P(R). The fluorescence decay of the donor in the presence of the acceptor is described by the following equation:

$$I_{\text{da}}\left(t\right)=I_d^0{\displaystyle \underset{0}{\overset{\infty }{\int }}}\hat{P}\left(R\right)\sum {\alpha }_{\text{d}i}\text{ exp}[-(\frac{1}{{\tau }_{\text{d}i}}+\frac{t}{{\tau }_{D^{*}}}{\left(\frac{R_0}{R}\right)}^6)]\text{d}R,$$ 2

where I_da(t) is the observed emission from the donor in the presence of an acceptor, 1/τ_D* (R₀/R)⁶ is the rate constant for decay due to transfer, R₀ is the Förster distance at which the efficiency of transfer is 0.5, and τ_D* is the donor lifetime uniquely associated with a particular value of R₀. The value of τ_D* (4.1 ns) remains constant for constant donor emission and acceptor absorption spectra. $\hat{P}\left(R\right)$ is the normalized probability density function.

Semi cone angles determined previously from time-resolved anisotropy decays of both fluorescein and TAMRA for the T*DNA_TT*F duplex reflect a high degree of rotational freedom for both dyes (12,59), validating the assumption that the value of κ² = 2/3 is reasonable (42–44). The close correspondence of the fluorophore environments in that study and the present study, with identical dyes and linkers and with sequences identical for ≥6 bp at both the 5′ and 3′ ends, strongly implied that this value of κ² was appropriate for determination of the value of R₀ herein. Even so, steady-state anisotropy data were collected as described above to further strengthen this assumption. We have shown previously that the decays from myriad duplexes have been very well described with P(R) modeled as a shifted Gaussian distribution (7,10–13,18,57), described by the following expression:

$$\hat{P}\left(R\right)=A\text{ exp}\left[\frac{-{\left(R-\overline{R}\right)}^2}{2{\sigma }^2}\right],$$ 3

where A is a normalization constant and the two fitted parameters are then the mean 5′-dye to 3′-dye distance, $\overline{R}$, and the width of the distribution, σ. This expression was thus used in Equation 2 to obtain the probability distance distributions.

Fluorescence decays were obtained for duplexes formed using 30 nM single-labeled and 60 nM double-labeled duplexes with excess complement in a total sample volume of ∼1 ml. These time-resolved emission measurements were made using a LaserStrobe spectrofluorometer (Photon Technology International, Inc., Lawrenceville, NJ) as detailed previously (12,13,18,59). Briefly, detection began just prior to fluorescence emission and ended ∼30 or 25 ns later for the donor-only and donor–acceptor labeled duplexes, respectively. For each decay, three independent curves were collected and automatically averaged to create one representative decay curve. The fluorescence decay of the donor was extracted from the total emission, which includes the instrument response function, using an iterative reconvolution procedure incorporated into the nonlinear regression analysis. Six such representative decay curves were defined as one set and three such sets were obtained for both the single- and double-labeled duplexes for each of the five cases. The normalized average curve representing each set was analyzed using nonlinear regression analysis to bi- and tri-exponential decay models of the form Y_i = Σα_iexp(−t/τ_i). The relative quality of these fits was assessed according to the values of χ² and the Durbin–Watson parameter (60–62). The model selection criterion in Scientist (Micromath, St Louis, MO), which is based on information theory (63,64), showed that without exception the biexponential model was optimal, yielding for each case three independent parameters: α₁, τ₁ and τ₂, since Σα_i = 1.

These average α and τ values describing the multiphasic fluorescence decay of each labeled duplex were then used to obtain the parameters characterizing the distance distribution, $\overline{R}$, the most probable 5′-dye to 3′-dye distance, and σ, the width of the distribution of the 5′–3′ distances. This analysis utilized a method of moments for the function G(t), which reflects only the pure transfer process (43). G(t) gives the average value for the transfer process at each time, t, where the average is over the interdye distances described by the distribution function $\hat{P}\left(R\right),$ as in the following expression:

$$G\left(t\right)={\displaystyle \underset{0}{\overset{\infty }{\int }}}\hat{P}\left(R\right)\text{ exp}[-\left(\frac{t}{{\tau }_{D^{*}}}{\left(\frac{R_0}{R}\right)}^6\right)]\text{d}R.$$ 4

Briefly, I_da(t) is the product of the donor decay [I_d(t)] and the emission from a hypothetical donor that can decay only by energy transfer, G(t) (18). Because (i) G(t) comprises a distribution of lifetimes for the excited state for transfer, (ii) a distribution is uniquely described by its moments, and (iii) two moments are sufficient to extract two parameters, $\overline{R}$ and σ could be extracted from the first two moments of G(t).

Dividing the measured I_da(t) decay by the measured I_d(t) decay yielded G(t). The corresponding zero and first moments, denoted μ⁰ and μ¹, are the respective areas under G(t) and t*G(t) from time zero to infinity (43). μ⁰ is the average lifetime for pure transfer and has dimensions of time (t) whereas μ¹ has dimensions of t². These two moments were obtained both by numerical integrations of G(t) and t*G(t) to ≥99.8% of each curve and by analyzing G(t) using sums of exponentials. In the latter case, μ⁰ = Σα_iτ_i and μ¹ = Σα_iτ_i². The two moments were then related to the desired parameters first using the ratio (μ¹)^1/2/μ⁰, denoted ‘P’, a dimensionless value shown previously to be a function of only $\sigma /\overline{R}$ (43). For each experimentally determined value of P, the corresponding value of $\sigma /\overline{R}$ was determined using a Newton–Raphson analysis.

The second relationship between the moments and the desired parameters is given by the following expression:

$$\overline{R}=R_0{\left(\frac{{\mu }^0}{S_0{\text{τ}}_D^{*}}\right)}^{1/6},$$ 5

where S₀ is a polynomial in $\sigma /\overline{R}$ (43). μ⁰ is the primary determinant of $\overline{R}$ and for σ = 0, S₀ becomes 1 and $\overline{R}$ is then a function only of μ⁰. For all nonzero σ values, the exact value of $\overline{R}$ can be obtained from μ⁰ and $\sigma /\overline{R}$ according to Equation 5. The value of $\overline{R}$ was thus obtained using Equation 5 and the corresponding value of σ was obtained from the known parameter ratio. This analysis was used to generate nine values of $\overline{R}$ and σ from the nine independent combinations of donor-only and donor–acceptor α and τ values determined for each of the five duplexes. Each set of nine values was averaged to obtain the reported parameter values and error estimates and a t-test analysis was used to identify statistically significant differences among these values.

RESULTS

We have conducted previously a rigorous determination of the rotational mobility of the unmodified T*DNA_TT*F duplex dyes using time-resolved anisotropy decay measurements (12). Those data demonstrated large semi cone angles for both the fluorescein and TAMRA, consistent with high degrees of dye mobility. Because the four modified duplexes are identical to the unmodified duplex in the dyes, linkers and 6 bp from both the 5′ and 3′ ends, similar rotational freedom for the modified duplex dyes seemed highly probable. This assumption was confirmed by the steady-state fluorescein anisotropy values of 0.061 ± 0.001 for all five duplexes. These values are consistent with those measured previously for oligomer-tethered fluorescein by our laboratory and others (49,65–70).

The end-to-end distance and relative flexibility of each duplex was obtained from measurements of time-resolved fluorescence emission decay in conjunction with FRET. This experimental methodology affords a rigorous and sensitive measure of changes in the mean distance, $\overline{R}$, between the donor and acceptor fluorophores and has been shown to be highly precise, reliably differentiating 0.1 Å differences in $\overline{R}$ values (10,12,13,18,44). In addition, differences among the widths of the corresponding distance distributions, σ, can be clearly distinguished (10,12,13,18,44).

The distance distribution, P(R), is determined by comparing the decays from the donor dye in the absence (single-labeled duplex, Figure 1) and presence (double-labeled duplex, Figure 1) of an acceptor dye. A total of 79 decays of the former and 71 decays of the latter were collected overall for the five duplexes. Without exception, these decays were very well described by biexponential decay (Figure 1, inset) with no improvement in the parameter errors or statistics found for a tri-exponential decay model. The overall average value of χ² was 0.90 ± 0.01. The average Durbin–Watson parameter value, 1.93 ± 0.03, significantly exceeded the lower limit of 1.75, reflecting an absence of correlated residuals. The average α and τ values describing the decay of each of the five duplexes were then analyzed using the method of moments described in Materials and Methods to obtain the P(R) parameters.

Figure 1.

A typical set of normalized raw (solid line) double- and (broken line) single-labeled time-resolved fluorescein decays, for the DNA_7,8ap duplex. (Inset) The same two curves deconvoluted to remove the instrument response function and fit to biexponential decay models.

The $\overline{R}$ values for the DNA_TT, DNA_8ap and DNA_8apn oligomers of 53.5 ± 0.2, 53.6 ± 0.2 and 53.2 ± 0.1 Å, respectively, are statistically indistinguishable (Table 2). Introduction of two adjacent cations on flexible tethers, however, effects a statistically significant decrease in the mean interdye distance to 52.2 ± 0.2 Å (P ≤ 0.05). Conversely, the presence of two neighboring cations on rigid tethers significantly lengthens the oligomer, to 54.2 ± 0.1 Å (P ≤ 0.05). The implications of an apparent requirement for two cations to effect a change in the duplex length are discussed in the next section.

Table 2.

Optimal values for the mean end-to-end the distance, $\overline{R}$, and the associated width of the distribution, σ, describing the 5′–3′ distance distribution, P(R), for the unmodified and four modified oligomers

Sequence	$\overline{R}$(Å)a	σ (Å)
T*DNATT *F Unmodified	53.5 ± 0.2b	5.4 ± 0.1
T*DNA8ap*F	53.6 ± 0.2	5.8 ± 0.1
T*DNA7,8ap*F	52.2 ± 0.2	5.8 ± 0.1
T*DNA8apn*F	53.2 ± 0.1	5.8 ± 0.1
T*DNA7,8apn*F	54.2 ± 0.1	5.1 ± 0.1

^aEach of the five pairs of $\overline{R}$ and σ values shown in the table derives from ∼10⁶ laser shots.

^bThe five $\overline{R}$ error estimates were rounded up from 0.18 (DNA_TT), 0.15 (DNA_8ap), 0.16 (DNA_7,8ap), 0.05 (DNA_8apn) and 0.08 (DNA_7,8apn).

In contrast to $\overline{R}$, the width of the distance distribution, σ, changes with introduction of even a single positive charge (Table 2). The σ value for the unmodified duplex of 5.4 ± 0.1 Å increases significantly to 5.8 ± 0.1 Å for both single cation modifications and for two cations on the propyl tethers (P ≤ 0.05). These changes imply increased duplex flexibility in response to the introduced charge. Interestingly, the distribution narrows significantly to 5.1 ± 0.1 Å with the two propynyl groups (P ≤ 0.05), consistent with increased helical rigidity.

DISCUSSION

A succession of related studies in several laboratories laid the foundation for this investigation. UV melting, circular dichroism and electrostatic footprinting studies on similarly modified oligomers have demonstrated that duplex stability is minimally affected by the introduction into the helix of one or two aminoalkly groups (37,40,41). That a single 3-aminopropyl group is positioned in the major groove, oriented in the 3′ direction from the modified base, with maintenance of normal Watson–Crick base pairing and no salt bridge formation has been shown by molecular modeling (37,38) and demonstrated experimentally using electrostatic footprinting studies (37,38,71,72) and NMR using the self-complementary Dickerson–Drew dodecamer backbone (39). Recent crystallographic data of the same dodecamer show that only one of four aminopropyl groups lies near the major groove floor toward the 3′ direction with the other three pointing out into solution (73). Phasing analysis of aminoalkyl-modified duplexes yielded aberrant gel mobility consistent with altered helical structure which was interpreted as helical bending (36,74). The subsequent NMR data were analyzed with and without a constraint requiring the amino group to be specifically positioned based on results of molecular modeling (39). The restrained structure exhibited a localized bend of ∼30°, although both the constrained and unconstrained datasets satisfied the experimental NOE data. In contrast to the flexible aminopropyl moiety, rigid 5-(3-aminopropyn-1-yl)-2′-deoxyuridines (DNA_8apn and DNA_7,8apn) incorporated in a helix can form significant electrostatic interactions (35,36,75). However, neither electrophoretic mobility analysis (74) nor NMR data (75) show evidence for helical bending in duplexes incorporating this rigid side chain.

Our long-term interest in DNA distortion and demonstrated success in reliably quantifying DNA structural changes (13,17,18) led to a collaborative FRET-based study of the helical response to the introduction of these tethered cations. Our previous work includes a Class II transcriptional activator, GCN4, characterized by a basic region leucine zipper (bZIP) DNA-binding motif. Class II proteins engage the helix in the major groove, making contact through electrostatic interactions between cationic amino acids and the DNA sugar-phosphate backbone (17,18) and bending the helix toward the protein. The extent to which inter-phosphate repulsion mediates DNA bending was probed using a series of GCN4 homodimers having from two to six charge mutations in the side chains that reside very close to the DNA helix. A strong correlation was observed between the extent and direction of helical bending (from ∼9 to 21°), on one hand, and the number and sign of the charge mutations, on the other, consistent with helical distortion in response to asymmetric changes in local charge density (18,76–78). The present findings support and extend these results and those of the aforementioned studies and are summarized as follows: (i) the mean end-to-end distance of duplex DNA is significantly altered by the introduction of two adjacently tethered cations into the double helix but not by a single cation and (ii) duplex flexibility is altered by the presence of even a single positive charge. These changes in the helical structure are attributed to selective perturbation of the electrostatic potential of the helix around the cation(s).

Precision in distances to 0.1 Å using time-resolved FRET has been definitively demonstrated in a series of publications reporting various protein-induced DNA bending (10–13,17,18) with the sources of such precision detailed therein. Such precision is comparable with that of steady-state emission measurements obtained with appropriate filtering and dual beam detection, in that a change in $\overline{R}$ of ∼0.2 Å corresponds to a ∼1% change in steady-state intensity for $\overline{R}\approx R_0$. Notably, the statistical differences reported herein are all valid for P ≤ 0.01 excepting that for the $\overline{R}$ value of DNA_8ap relative to that of DNA_7,8apn. The difference in the $\overline{R}$ values between the parent duplex and DNA_7,8ap and DNA_7,8apn hold for P ≤ 0.001.

The method of moments analysis described in Materials and Methods was utilized for the first time with these data. We have previously used variance minimization with a Simplex nonlinear regression analysis to obtain the P(R) parameters (7,10–13,18,43,57). In numerous simulations and in side-by-side comparisons of the two methods using the same real datasets, the new procedure has shown itself to be more reliable and robust. It is insensitive to outlying points and free from converging to false local minima, the latter being an acknowledged problem with explicit or implicit gradient search techniques such as Simplex. In practice, the method of moments is much more rapid for obtaining distance parameters, particularly when G(t) is fitted by sums of exponentials.

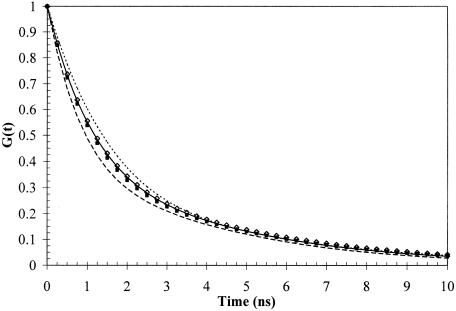
The relative areas under the G(t) curves correlate directly with $\overline{R}$ for a set of distributions having similar σ values. Inspection of these curves thus gives an accurate graphic representation of the relative interdye distances (Figure 2). Because the distribution for DNA_7,8apn has the smallest σ value, the difference between this $\overline{R}$ value and those for the other oligomers is actually larger than suggested by the figure. Differences in $\overline{R}$ can arise from changes in either inherent bending or flexibility. The $\overline{R}$ values for DNA_8ap and DNA_8apn are indistinguishable from that for the DNA_TT and their σ values are identical to that for DNA_7,8ap. The significant decrease in $\overline{R}$ observed for DNA_7,8ap must therefore derive primarily from helical bending in the presence of the neighboring diffusible cations and concomitant asymmetric charge neutralization.

Figure 2.

G(t) curves for (solid line) the unmodified DNA_TT, (diamond) DNA_8ap, (dashed line) DNA_7,8ap, (closed square) DNA_8apn and (dotted line) DNA_7,8apn duplexes. G(t) was in all cases found to be biexponential and, since G(0) = 1, each curve is described by three independent parameters. The relative areas under the curves closely approximate the relative $\overline{R}$ values.

A different picture emerges for DNA_7,8apn. Because changes in the value of σ reflect changes in helical flexibility, the decrease in σ resulting from introduction of two adjacent rigidly tethered cations connotes rigidification of the helix. This finding is consistent with evidence from thermal melting experiments and molecular modeling that aminopropynyl modified bases increase duplex rigidity (74) and is perhaps not surprising since these side chains can engage in electrostatic interactions with phosphates (35,36,75). This loss of helical flexibility is the source of the corresponding increase in the DNA_7,8apn $\overline{R}$ value, particularly in the absence of evidence for an inherent bend in the unmodified duplex.

A model-dependent helical bend angle can be determined from the difference in the donor fluorescein time decays in the absence and presence of the acceptor dye. The simplest single central bending model (12) yields a bend angle for DNA_7,8ap of 25 ± 3° relative to its parent DNA_TT. Ongoing work in our laboratory involves measuring $\overline{R}$ and σ for a related series of oligomers having n base pairs for n = 11–29 and with fluorescein-rhodamine dyes as in the present work. A plot of $\overline{R}$ versus n yields nearly a straight line with only slight periodicity reflecting the DNA helicity (L.J. Parkhurst, unpublished data). This result provides convincing evidence that, for these tethered fluorophores, the average dye position is nearly axial, engendering confidence that these measured interdye distances accurately reflect axial distortions. Even so, the possibility that other changes in the helical geometry may be occurring upon incorporation of these base analogs cannot be excluded.

Surprisingly, the $\overline{R}$ values for the two singly modified duplexes are indistinguishable from that of the parent duplex, while the $\overline{R}$'s for the doubly modified duplexes are clearly distinguishable from both. Two possible interpretations present themselves: based on the parameter errors, it is conceivable that the interdye distance decreases initially with the introduction of a single aminopropyl group and then to the final observed value with both groups present, so that the effects of adjacent modifications are simply additive. However, assuming that both one and two aminopropyls decrease $\overline{R}$ and considering the uncertainties, the maximum possible contribution from the 8ap modification is small compared with the minimum contribution from the 7,8ap modification. The precision of the mean values reported in Table 2, supported by the power of ensemble averaging and our past successes in identifying small parameter differences, lead us to favor the alternate interpretation that bending is the structural manifestation of cooperative behavior between the cations. The mobility of the single tethered cation would lead to low occupancy on the groove floor, resulting in intermittent phosphate neutralization and localized anisotropic helical flexing that falls short of a true bend. Such induced asymmetric distortion would produce the anomalous mobility shifts observed for oligomers bearing a single aminopropyl group (40). Fractional occupancy of the groove floor by the first cation would facilitate occupancy of a second, neighboring cation with enhanced local stability of both amino groups and subsequent helical collapse due to asymmetrical neutralization of the backbone. Increased entropy deriving from release of the mobile counterions associated with the backbone would contribute to the cooperativity (29,37,79,80).

The aminopropynyl substituents yielded helical lengthening and stiffening observed with introduction of two neighboring groups but not with one. Even taking into account the parameter errors, introduction of a single rigidly tethered cation results in no increase in the length of the original duplex. Therefore, a simple additive model cannot accommodate these data and we again conclude that the data reflect a cooperative interaction between the rigidly tethered cations. The limited mobility of this cation around the ω-carbon–nitrogen bond together with the normal helical dynamics may be sufficient to depress groove occupancy with only one side chain while incorporation of a second aminopropynyl decreases the amplitude of the helical dynamics sufficiently to stabilize both side chains in the major groove. Maher and co-workers (74) found stabilization of duplexes by propynyl chains alone and suggested enhancement of base stacking in propyne-modified pyrimidines. Such an effect may contribute to the observed helical rigidification.

The time-resolved FRET measurements reflect static distributions on time scales significantly greater than the average excitation transfer time of 2 ns, as well as a complex mixing of bending dynamics on shorter time scales. Molecular dynamics simulations to 2 ns of DNA bending and dye motion currently in progress in our laboratory are not yet at a sufficiently advanced stage to clarify details of all of the interrelations between $\overline{R}$ and σ. Even so, the introduction of a single tethered cation in the major groove increases helical flexibility. This increased flexing may facilitate the cooperative positioning of adjacent side chains for both the aminopropyls and aminopropynyls. The data point clearly to such a cooperative interaction. It is only with stable positioning of neighboring side chains that essentially full occupancy of the critical site is achieved, with different structural outcomes depending on the tether characteristics.

Seeking to understand the energetic factors that regulate DNA distortion has motivated a host of theoretical and experimental investigations. The complex task of illuminating the relative contributions to and mechanisms for helical deformation is further compounded when effects may be cooperative rather than simply additive. The series of collaborative studies including the present work provide complementary new insights for the role of altered electrostatic potential in helical restructuring. Our FRET-derived data provide the first direct spectroscopic evidence that positively charged side chains within the helix alter the conformation and flexibility of DNA. The convergence to a common perspective from several independent laboratories employing diverse methodologies lends strong support for significant DNA structural distortions in response to asymmetric changes in local charge density.