Abstract
The speed at which RNA molecules decompose is a critical determinant of many biological processes, including those directly involved in the storage and expression of genetic information. One mechanism for RNA cleavage involves internal phosphoester transfer, wherein the 2′-oxygen atom carries out an SN2-like nucleophilic attack on the adjacent phosphorus center (transesterification). In this article, we discuss fundamental principles of RNA transesterification and define a conceptual framework that can be used to assess the catalytic power of enzymes that cleave RNA. We deduce that certain ribozymes and deoxyribozymes, like their protein enzyme counterparts, can bring about enormous rate enhancements.
Keywords: Ribozyme, deoxyribozyme, RNA transesterification, RNA cleavage, enzymatic mechanism, catalysis
INTRODUCTION
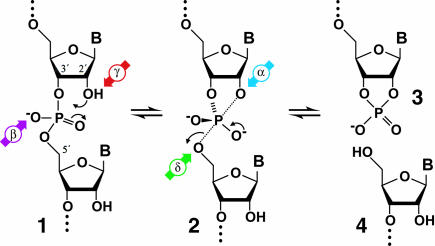
Understanding the detailed mechanisms of catalysis used by enzymes that cleave RNA via internal phosphoester transfer has been a major research focus since RNA strand scission was described in the early 1950s (Bacher and Kauzmann 1952; Brown and Todd 1952, Brown and Todd 1953; Lipkin et al. 1954; Brown et al. 1956). This reaction proceeds when the 2′-oxygen atom adjacent to a given internucleotide linkage executes a nucleophilic attack on the phosphorus center (Fig. 1 ▶). The 5′- and 3′-cleavage products created by this reaction carry 2′,3′-cyclic phosphate and 5′-hydroxyl termini, respectively. Under reaction conditions similar to those found inside human cells, the spontaneous cleavage of RNA typically occurs with a rate constant of ~10−7 min−1 (Li and Breaker 1999), which reflects a half-life of >1 year. In comparison, pancreatic ribonuclease A (RNase A) accelerates this phosphoester transfer reaction by >12 orders of magnitude (Adams et al. 1992; Raines 1998), resulting in a half-life for an RNA linkage that is measured in microseconds. RNase A is thought to achieve this impressive rate acceleration by using four catalytic strategies (Fig. 1 ▶): correct in-line substrate positioning, neutralization of negative charge at a nonbridging oxygen, activation of the 2′-hydroxyl nucleophile, and enhancement of the 5′-oxygen as a leaving group.
FIGURE 1.
Mechanism for RNA cleavage by internal phosphoester transfer involving the 2′-hydroxyl group. The RNA linkage (1) passes through a pentacoordinate species (2) that degrades into fragments that carry either a 2′,3′-cyclic phosphate terminus (3) or a 5′-hydroxyl terminus (4). The four catalytic strategies that can influence the reaction are identified as follows: α, in-line nucleophilic attack (blue); β, neutralization of negative charge on a nonbridging phosphate oxygen (purple); γ, deprotonation of the 2′-hydroxyl group (red); and δ, neutralization of negative charge on the 5′-oxygen atom (green).
For many years, researchers have worked to create artificial nucleases by coupling the enormous rate enhancements exhibited by enzymes like RNase A with the sequence-specific targeting ability that is required for the selective destruction of specific mRNAs. To this end, numerous chemical compounds that mimic ribonuclease function have been created (for reviews, see Kirby 1996; Trawick et al. 1998), and some have been made to show selectivity for the sequences they cleave. However, these agents typically do not promote RNA cleavage with the same rate constant that can be achieved by most protein enzymes. Presumably, these ribonuclease mimics take advantage of only a subset of the catalytic strategies that are used by enzymes like RNase A, or otherwise do not exploit these catalytic strategies fully.
Nucleic acid enzymes also can catalyze RNA cleavage by the same internal phosphoester transfer mechanism. Four of the eight ribozymes that are known to exist in nature (Butcher 2001) promote site-specific RNA cleavage by this mechanism. This collection of “self-cleaving” ribozymes includes the hammerhead (Stage-Zimmermann and Uhlenbeck 1998; Scott 1999), hairpin (Walter and Burke 1998; Fedor 2000), HDV (Taylor 1997; Wadkins and Been 2002), and Neurospora VS RNAs (Lafontaine et al. 2001; Sood and Collins 2002). Unfortunately, most engineered versions of these ribozymes, like ribonuclease mimics, exhibit rate constants for RNA cleavage that fall far short of that achieved by RNase A. These findings are consistent with the view held by some enzymologists that ribozymes might be incapable of generating the same rate enhancements as those achieved by protein enzymes.
We have been exploring the details of ribozyme catalytic mechanisms in order to assess whether nucleic acid enzymes could ever match the catalytic power and sophistication of protein enzymes. Recent findings indicate that certain ribozymes and deoxyribozymes might use a combination of catalytic strategies that place an upper limit on speed (Breaker et al. 2003). Meanwhile, other catalytic RNAs and DNAs seem to use combinations of the four possible catalytic strategies that would permit high-speed RNA transesterification. In this report, we provide an overview of the reaction of RNA transesterification and the catalytic strategies that are exploited by RNA-cleaving agents. We use the kinetic behavior of ribozymes and deoxyribozymes to draw general conclusions about biological catalysis of this reaction. From this framework, we conclude that it is possible to create nucleic acid enzymes that exhibit catalytic rate enhancements that match those of their protein counterparts.
RNA and DNA enzymes as model catalysts
Ribozymes and deoxyribozymes are well suited to serve as model enzymes for studying the factors that are responsible for biological catalysis. Novel ribozymes and deoxyribozymes can be created by in vitro evolution (Breaker 1997; Wilson and Szostak 1999), and nucleic acid enzymes with diverse structural and functional characteristics typically emerge from such efforts (Williams et al. 1995; Santoro and Joyce 1997; Tang and Breaker 1997, Tang and Breaker 2000). As a result, we have access to many distinct RNA-cleaving ribozymes and deoxyribozymes, of which at least some are expected to be simple in structure and function. In contrast, natural protein enzymes that cleave RNA have relatively complex structures and undoubtedly use multiple catalytic strategies that are not easy to separate experimentally from one another. Furthermore, methods for the preparation, manipulation, and kinetic characterization of nucleic acid enzymes are well established, and thus permit direct comparisons to be made among numerous examples.
These factors have enabled us to examine the kinetic characteristics of 14 distinct structural classes of ribozymes and deoxyribozymes that catalyze RNA cleavage (Breaker et al. 2003). The results of this study revealed that half of the nucleic acid enzymes examined cannot exceed a rate constant of ~2 min−1. Interestingly, this “speed limit” corresponds to a theoretical maximum value that can be attained if the enzymes fully exploit only two of the four possible catalytic strategies that could be used to accelerate internal phosphoester transfer (Fig. 1 ▶; Breaker et al. 2003; see below).
RNA transesterification as a reaction of interest
RNA molecules are integral participants in all the fundamental processes carried out by modern living systems. Although its propensity for spontaneous cleavage by internal phosphoester transfer is considered to be its greatest liability, RNA is nevertheless capable of carrying genetic information in the form of messenger RNAs and of performing chemical reactions such as ribosome-mediated peptidyl transfer. Despite this reputation of chemical instability, enzymes that cleave RNA must increase this instability by a million-fold or more in order for enzymatic RNA cleavage to occur on a time scale that is of relevance to biology (Li and Breaker 1999; Breaker et al. 2003).
A detailed understanding of the chemical processes that accelerate internal RNA transesterification would therefore provide a scientific basis for understanding the inherent instability of RNA, as well as offer insight into how enzymes promote RNA processing reactions. Unfortunately, RNA transesterification is not a simple chemical reaction. Both the stability of phosphate esters and their chemical pliability have been suggested as foremost reasons why a phosphate ester has emerged as the backbone of choice for the molecules responsible for genetic information storage and transfer (Westheimer 1987). Thus, it follows that in order for RNAs to be processed as required by certain biological undertakings, the chemistry of RNA transesterification must offer multiple and powerful catalytic strategies for enzymatic exploitation. Given the fundamental importance of internal phosphoester transfer, and given the availability of a diverse collection of ribozymes and deoxyribozymes that catalyze RNA cleavage, we see this reaction as an ideal system for further examination. The basic principles that we advance in this report, however, should be applicable to the study of other enzymes that catalyze different reactions.
Nonenzymatic phosphoester transfer to an RNA 2′ oxygen: Identifying the four catalytic strategies
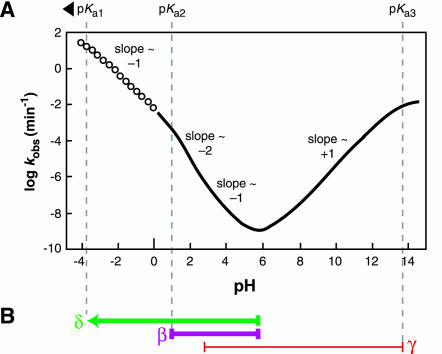
The backbone of RNA (Fig. 1 ▶, structure 1) is cleaved when a phosphoester bond is transferred to an adjacent 2′ oxygen (2) to form a strained 2′,3′-cyclic phosphate compound (3) and release a second product with a 5′-hydroxyl group (4). This proceeds via an associative (SN2-like) mechanism in contrast to the dissociative (SN1-like) mechanism of cleavage of phosphoanhydrides, phosphomonoesters, and phosphoramidates (Benkovic and Schray 1973; Guthrie 1977; Westheimer 1987; Thatcher and Kluger 1989; Admiraal and Herschlag 1995; Oivanen et al. 1995; Almer and Strömberg 1996). RNA transesterification occurs spontaneously in the absence of any added catalyst with a first-order rate constant that varies with changing pH (Järvinen 1991; Li and Breaker 1999). By combining data acquired at high temperature with data taken at high pH for the cleavage of a natural RNA linkage, a characteristic profile for the logarithm of the rate constant of nonenzymatic RNA cleavage versus pH emerges (Fig. 2A ▶). This profile shows that RNA transesterification is accelerated many orders of magnitude at extreme pH conditions by specific acid (hydronium ion) catalysis or specific base (hydroxide ion) catalysis. The maximum values for rate constant (k) are ~0.01 min−1 at either pH 0 or pH 14. We assume for this study that the reaction pathway does not vary with pH. Therefore, the pH profile for spontaneous RNA degradation should provide clues to the chemical nature of the RNA transesterification reaction and define upper limits for rate enhancement by different catalytic mechanisms.
FIGURE 2.
Dependence of RNA transesterification on specific acid and specific base catalysis. (A) Plot of the logarithm of the rate constant (predicted, see Materials and Methods) for cleavage versus pH at room temperature. Solid line indicates the region of the curve for which measured data exists for comparison value (Järvinen et al. 1991; Li and Breaker 1999). Open points indicate the region of the curve that is extrapolated based on the assumption that the pKa of the bridging 5′ oxygen is less than zero (~−3.5) and that no other rate-determining protonations occur below pH 0. The overall shape and slope of the curve match the previously reported data collected at 90°C (Järvinen et al. 1991). (B) Interpretation of the slope transitions of the curve depicted in A. The pH range over which the rate constant is dependent on protonations (β and δ) are shown with thick purple and green lines, respectively. The pH range in which the rate constant is affected by a deprotonation (γ) is shown with a thin red line. Measurements at 90°C show that the region between approximately pH 3 and 5 appears to have a slope of −1, which we interpret as reflecting two rate-determining protonations and one rate-determining deprotonation (see text).
The reaction progression detailed in Figure 1 ▶ shows the predominant ionization state of each group as it is presumed to be at neutral pH. At pH 7, the 2′ oxygen nucleophile exists primarily as a protonated (hydroxyl) species (Fig. 1 ▶, 1). The nonbridging phosphate oxygen (NBPO) atoms share a resonant negative charge and double bond to phosphorus that results in a dianionic state of the pentacoordinated species (2) formed upon nucleophilic attack. The 5′ oxygen (Fig. 1 ▶) will depart as a negatively charged alkoxide ion at neutral pH and become protonated after cleavage has occurred. The low background rate of spontaneous RNA cleavage at neutral pH reflects the poor nucleophilicity of a 2′-hydroxyl and the high negative charge developed during the reaction at the NBPO atoms and the 5′-oxyanion leaving group. That is, there are multiple rate-determining proton transfer events that can be exploited for catalysis. This conclusion is supported by the observed pH-dependent character of spontaneous RNA cleavage (Fig. 2 ▶), as detailed in the next sections.
Spontaneous RNA cleavage is also affected by the position of the nucleophile, electrophile center, and leaving group relative to one another. In an “in-line” configuration, the nucleophilic 2′ oxygen and the departing 5′ oxygen are in-line with the phosphorous center and thus occupy the two apical positions in a trigonal bipyramidal geometry prior to backbone cleavage. Pseudorotation is a rearrangement that allows the nucleophile to attack and the leaving group to depart at an angle to one another (Westheimer 1968). The products of RNA transesterification produced by protein enzymes such as RNase A and by ribozymes such as the hammerhead indicate that the in-line configuration most likely is used in the active site and that no pseudorotation occurs (Linn et al. 1993; Wedekind and McKay 1998; Fersht 1999). Because the flexibility of an unconstrained RNA linkage is such that the appropriate in-line arrangement will occur only on occasion (Soukup and Breaker 1999), a fourth chemical effect that an enzyme could exploit for rate enhancement is the promotion of proper substrate orientation for in-line attack (Fig. 1 ▶, 2).
Together, the chemical barriers to the spontaneous breakdown of RNA by transesterification are as highlighted on Figure 1 ▶: the lack of constraint of the atoms in proper geometry for formation of the pentacoordinate species (α catalysis, blue), the high negative charge of the dianion species (β catalysis, purple), poor nucleophilicity of the 2′-hydroxyl (γ catalysis, red), and poor departure of the 5′-oxyanion leaving group (δ catalysis, green). The absolute limits of rate enhancement that can be achieved by the reduction of each of these barriers are discussed.
Dissecting the speed limits of RNA cleavage by phosphoester transfer
It should be possible to establish the maximum, chemically allowed rate enhancement for β, γ, and δ catalysis by assigning identities to the rate-determining proton transfer events that are critical to the nonenzymatic cleavage of RNA and by determining the pH range over which a particular strategy productively impacts spontaneous RNA cleavage (Fig. 2 ▶). These proposed pH ranges and the corresponding proton transfer assignments are derived from known pKa values for relevant groups. The maximum, chemically allowed rate enhancement then sets the speed limit for each catalytic strategy.
Speed limit for total deprotonation of the 2′-hydroxyl group: γ catalysis
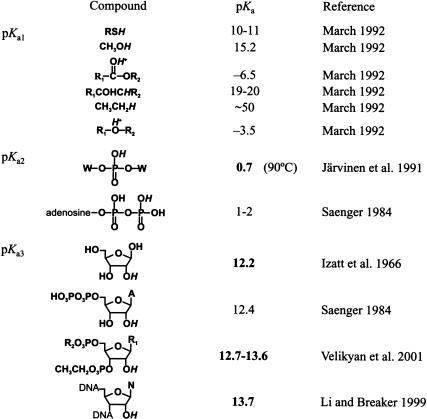
Figure 2A ▶ summarizes how the first-order rate constant of spontaneous RNA cleavage by transesterification is expected to vary with pH at ~23°C when no buffer-dependent catalysis is observed. The simplest explanation for the slope of one above neutral pH is that for every 10-fold increase in specific base (hydroxide ion), there is a corresponding 10-fold increase in RNA degradation due to a single rate-determining deprotonation event in the RNA linkage. The rate constant reaches a plateau as the pKa of this deprotonation event is approached and exceeded because the group becomes fully deprotonated, and thus no further rate enhancement can be gained. The only rate-determining deprotonation with a pKa > 13 that is likely to dominate alkaline RNA cleavage is at the 2′-hydroxyl group. The pKa for the transition on Figure 2A ▶ (pKa3) is 13.7. This value has been determined experimentally for cleavage of a single ribonucleotide imbedded in a short DNA oligonucleotide under conditions relevant to a cell (23°C, 250 mM K+; Li and Breaker 1999). A value of 13.7 is consistent with other measured pKa values (Velikyan et al. 2001) that indicate that the actual pKa of a 2′-hydroxyl in an oligonucleotide (Table 1 ▶, pKa3) is not as low as previously estimated (Izatt et al. 1966; Saenger 1984).
TABLE 1.
pKa values for functional groups related to those of an RNA phosphodiester
The three rate-determining pKa values for spontaneous RNA degradation due to specific acid and base catalysis are as follows: pKa1 defines protonation at the 5′-oxygen; pKa2 is for the first NBPO; and pKa3 relates to protonation of the 2′-oxygen from the oxyanion to a hydroxyl. The pKa values are listed for the functional groups depicted in italics. Values in bold type were determined experimentally, whereas the remainder are estimates. W indicates adenosine or uridine.
The slope of 1 from pH ~5.5–13.5 indicates that there is at least 108-fold in rate enhancement to be gained by specific base catalysis. In other words, the nucleophilic power of a 2′-oxyanion over a 2′-hydroxyl group in RNA is at least 108. An enzyme could realize this level of rate enhancement at pH 5.5 by forming an active site that exploits general base catalysis to deprotonate the 2′-hydroxyl group completely. It should be noted that under conditions of physiological pH, ~102-fold rate enhancement has already been provided by specific base in bulk solvent, and an enzyme could do no better than to make up the remaining 106. However, specific base catalyzed, RNA triester cleavage is observed even at acidic pH conditions (Kosonen and Lönnberg 1995). As a result, the 2′-oxyanion has been proposed to a better nucleophile than a hydroxyl by a factor of up to 1010 (Oivanen et al. 1998). This parallels the observation that cyclic and acyclic phosphorous compounds are 1010-fold more susceptible to nucleophilic attack by hydroxide than by water (Almer and Strömberg 1996). Therefore, the slope of one depicted in Figure 2A ▶ under basic pH is established by a rate-determining deprotonation of the 2′-hydroxyl group (Li and Breaker 1999). Furthermore, it is likely that the 2′-oxyanion is the dominant nucleophile for transesterification down to pH ~ 3 (Fig. 2B ▶).
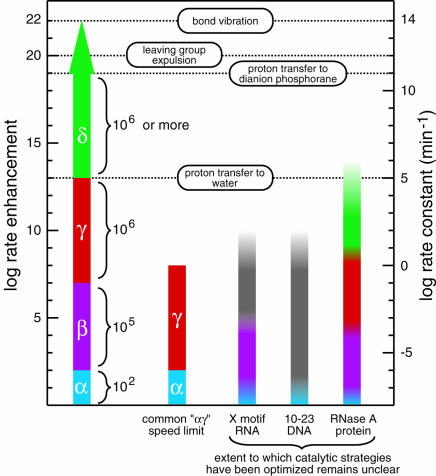
Thus, the maximum rate enhancement for an enzyme that uses deprotonation of the 2′-hydroxyl group to the exclusion of all other catalytic strategies (a “γ enzyme”) is at least 1010. This can be achieved only if the enzyme remained fully active at pH 3. For a γ enzyme that is fully active only at neutral pH, a maximum rate enhancement of ~106 would be possible (Fig. 3 ▶).
FIGURE 3.
Magnitudes of rate enhancement for the four catalytic strategies. The individual and cumulative rate enhancements derived from enzymes perfecting each catalytic strategy are shown (left scale) from a baseline rate constant value of 10−8 min−1 (right scale) for the rate constant of RNA cleavage at neutral pH and 23°C without divalent metals (Li and Breaker 1999). The rate enhancement for perfect utilization of a combined αγ strategy, a commonly encountered speed limit of engineered ribozymes and deoxyribozymes (Breaker et al. 2003), is depicted next to the putative catalytic strategies used by several nucleic acid and protein enzymes. Open-top columns denote the fact that the highest rate constants measured for these enzymes do not reflect the rate constant of the chemical step. The X-motif RNA and 10–23 DNA columns are colored to reflect possible explanations for their rate enhancement, but structures and catalytic mechanism have not been definitively solved for either enzyme. The graded coloring is used to note the fact that it is not evident that the enzymes use the various catalytic strategies to their fullest extent. First-order rate constants of bond vibration and proton transfer from imidazolium ion to water were taken from Fersht (1999). Those of proton transfer to, and leaving group expulsion from, the dianion phosphorane intervening species of phosphoester transfer were taken from Perreault and Anslyn (1997).
Speed limit for total protonation of a NBPO: β catalysis
Specific acid catalysis of RNA transesterification must involve at least two rate-determining protonations, representing β and δ catalysis. This conclusion is based on the fact that the pH profile displays an apparent slope of ~−2 between pH 1 and pH 2 (Oivanen et al. 1998). Additionally, if γ catalysis by specific base continues into the acidic pH range, the slope of ~−1 in the pH range between 2 and 5 can only be explained in the simplest case by two rate-determining protonations and 1 rate-determining deprotonation, all of which act simultaneously to influence the overall rate constant of RNA degradation (Fig. 2B ▶).
Protonation of one NBPO (β catalysis) is expected as the solution becomes acidic. The pKa of an NBPO is 0.7 at 90°C (Järvinen et al. 1991) and probably between 1 and 2 at room temperature (Saenger 1984). At 90°C, the minimum rate constant of RNA transesterification (the onset of catalysis of presumably both the β and δ effects) occurs at pH ~5, whereas the rate-determining pKa of a protonated NBPO is slightly less than one (Järvinen et al. 1991). This sets a maximum rate enhancement for β catalysis at ~104 at 90°C. As the temperature is lowered to 23°C, pKa values will increase in a manner specific to each type of functional group, and so this range may change by perhaps an order of magnitude (Table 1 ▶; pKa2). The rate enhancement observed in acyclic phosphotriesters over diesters (Westheimer 1968; Kosonen and Lönnberg 1995), which is similar to direct metal coordination to a NBPO in a phosphodiester (simulating the effect of protonating a NBPO; Bruice et al. 1996), can be as much as 105. Therefore, at 23°C, the rate enhancement for β catalysis is likely not to exceed 105 (Fig. 3 ▶). This indicates that an internucleotide linkage with one protonated NBPO is ~105-fold more susceptible to nucleophilic attack by the 2′-oxygen atom compared with an internucleotide linkage that carries two unprotonated NBPO atoms.
Speed limit for total protonation of the 5′-oxygen: δ catalysis
The existence of just the β and γ catalytic strategies is insufficient to explain the pH profile of nonenzymatic RNA transesterification. A second rate-determining protonation event must be occurring to explain the slope of −2 and to explain a slope of −1 in the slightly acidic range in which β and γ catalysis are proposed to overlap. Protonation of both NBPO atoms would suffice as the two protonation events required to explain the slope of the pH profile in the acidic range. Accordingly, the slope of −2 has been explained previously (Oivanen et al. 1998) to be due to rate-determining protonations at both of the nonbridging oxygens, and it has been suggested that such protonation would significantly increase the rate of attack of the 2′-nucleophile (Gerlt 1993). The two schemes describing protonations at either one NBPO plus the leaving group or at both nonbridging oxygens are kinetically indistinguishable (Fig. 4 ▶, upper and lower pathways). However, it has also been observed that the 2′- and 3′-oxygen atoms are 105-fold better able to depart as oxyanions than the oxyanion of a primary alcohol of a phosphotriester (Kosonen and Lönnberg 1995). This indicates that the 5′-oxygen atom cannot depart easily without prior protonation.
FIGURE 4.
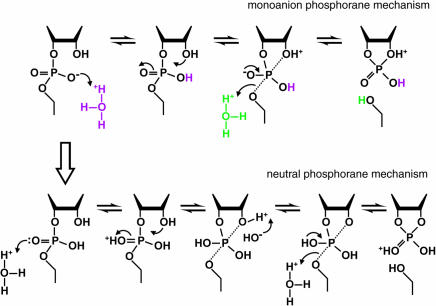
Mechanism of RNA cleavage at low pH. In the range of pH 1 to 2, the rate constant for RNA cleavage is dependent on two protonations. These may represent specific acid β (purple) and δ (green) catalysis (upper pathway; monoanion phosphorane mechanism) or specific acid β catalysis with another protonation at the second NBPO (lower pathway; neutral phosphorane mechanism). Only the chemical structure of the RNA linkage that is directly involved in the transformation is depicted. The apical bonds to the pentacoordinated phosphorous in the trigonal, bipyramidal structure are indicated with dotted lines. Deprotonation of the 2′-oxygen nucleophile would be required in the lower pathway to prevent it from departing more readily than the 5′-oxygen atom. The upper and lower pathways will be kinetically indistinguishable if deprotonation of the 2′ oxygen in the neutral phosphorane is more rapid than cleavage of the P-O5′ bond, and protonation also occurs at the 5′ oxygen.
Consistent with this suggestion is the proposal that the departure of the leaving group can be rate-determining under defined conditions (Shiiba and Komiyama 1992; Zhou et al. 1996) and that a 5′ thioate is a better leaving group by a factor of ~105 (Kuimelis and McLaughlin 1995; Thomson et al. 1996), which is also the extent of increase in basicity from R-O− to R-S− (March 1992). Invoking a protonation at the departing 5′-oxygen as the candidate for the second required protonation also provides a rationale to explain the simultaneous appearance of specific acid β and δ catalysis as the pH dips below 5.5. Protonation of the NBPO (β catalysis) changes the chemistry of transesterification in a subtle but fundamental way. It converts the pentacoordinated, trigonal bipyramidal species from a dianion, 2, to a monoanion (Fig. 5 ▶, 5). The dianion phosphorane has been calculated to be too unstable to exist long enough to be considered an intermediate, to pseudorotate, or to allow diffusion controlled processes including proton transfer (Lim and Karplus 1990; Perreault and Anslyn 1997). Experimental support of this calculation includes the observation that isomerization of the 3′,5′ and 2′,5′ links, which requires pseudorotation to place the departing 3′-O at an apical position (Fig. 4 ▶; Westheimer 1968), has never been detected in alkaline solution (Perrault and Anslyn 1997). Likewise, the products of decomposition of RNA analogs indicate that a monoanion or neutral species is required for pseudorotation (Almer and Strömberg 1996). Furthermore, pseudorotation of a dianion would place an electron-donating group unfavorably in an apical position (Zhou and Taira 1998).
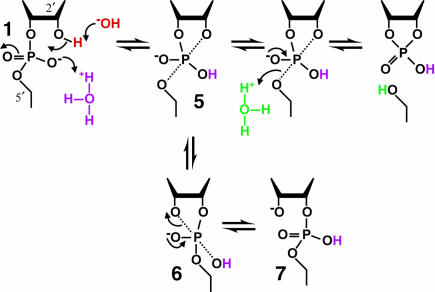
FIGURE 5.
Mechanism of RNA cleavage under mildly acidic conditions. In the range of approximately pH 3 to 5, specific acid and base produce β (purple), γ (red), and δ (green) catalysis. β Catalysis by specific acid changes the nature of the reaction pathway by allowing 5 to exist as an intermediate long enough to allow pseudorotation to 6. This in turn allows departure of the 3′ oxygen to form a 2′,5′-phosphodiester linkage, 7. Other notations as in the legend of Figure 4 ▶.
This means that proton transfer events subsequent to formation of the pentacoordinate species are possible only if the phosphorane is a monoanion. Therefore, the protonation of the 5′-oxygen would have to occur either prior to the formation of the pentacoordinated dianion, or only when the phosphorane is in the protonated monoanion form. However, it can be predicted that protonation of the 5′-oxygen could be as much as 1030 times less likely prior to formation of the phosphorane as after this event. Because the pKa of the protonated 5′-oxygen has not been determined in either case, this conclusion was derived from a comparison to carbon chemistry (Table 1 ▶, pKa1). The change of pKa value of the 5′-oxygen as the phosphodiester linkage approaches a pentacoordinated geometry reflects the influence of a double-bonded phosphoryl oxygen on an adjacent group compared with the two single-bonded oxygens of the phosphorane. In carbon chemistry, the pKa value of a proton of a methylene group decreases by ~30 units when positioned adjacent to a carbonyl group due to the electron withdrawing character of this group, making the methylene proton 1030 times more acidic (Table 1 ▶). Compare the pKa of a methylene proton in a ketone, pKa ~19 to 20 for RCOCH2R, to a saturated hydrocarbon, pKa of ~50, for C2H6 (March 1992). Because it can be concluded that pKa1 is <0 from the pH profile (Fig. 2A ▶), protonation of the 5′-oxygen prior to the formation of the phosphorane would indicate that the protonated leaving group is as much as 1035-fold better able to depart (effective range pH, −30 to 5.5) than the oxyanion. It seems unrealistic that any catalyst, specific acid or enzymatic, could impact such an extraordinarily unfavorable event.
If our assumptions are correct, then protonation of the leaving group most likely does not occur until the linkage has attained significant pentacoordinated character. Because the dianion is not stable enough to allow for proton transfer, rate enhancement from protonation of the 5′ leaving group (δ) can only occur in conjunction with protonation at a NBPO (β). This is one plausible explanation for the proposed chemical interdependence of two rate-determining protonations in RNA transesterification (Fig. 2 ▶). The magnitude of δ catalysis then will be a minimum of 105 or 106 at 23°C (Fig. 3 ▶) given that δ catalysis is observed from slightly below pH 0 to approximately pH 5 at 90°C. The maximum rate enhancement using δ catalysis could be much higher depending on the pKa of the 5′-oxygen atom in the phosphorane (pKa1). Again, considering carbon chemistry, the pKa of the protonated 5′-oxygen might be expected to increase dramatically as the phosphorane is formed, perhaps to the neighborhood of that for a protonated ether (~−3.5). If no other chemical effects become significant at this low pH, the pH profile should change from a slope of −1 to a slope of zero when the pH reaches pKa1, which cannot be experimentally obtained. However, we expect that the rate enhancement could be as much as 109, assuming that pKa1 is near −3.5.
Speed limit established by proper geometric alignment for in-line nucleophilic attack: α catalysis
The rate enhancement for α catalysis is dictated by the extent to which the 2′-oxygen, phosphorous, and 5′-oxygen atoms are oriented for direct in-line attack and also by the distance between the 2′-oxygen nucleophile and the phosphorous center. The value of the potential rate enhancement derived from constraining a free RNA linkage to an in-line configuration has been determined to be at least 10- to 20-fold by observing the cleavage rates of individual phosphodiester bonds in structured RNAs (Soukup and Breaker 1999; and references therein). This is most likely a modest underestimate of the maximum rate enhancement for α catalysis, as the geometries of most linkages used to determine this rate enhancement range are less than optimal. However, we speculate that the maximum rate enhancement for α catalysis is probably no greater than 102 (Fig. 3 ▶). For example, extrapolation of the data described previously (Soukup and Breaker 1999) implies that only a modest increase in the rate enhancement generated by perfect in-line positioning is likely. Furthermore, the fitness for in-line nucleophilic attack is largely dictated by rotation around two bonds in RNA. From a highly simplified perspective, we assume that a structurally unrestricted linkage would permit each of the two bonds to sample an orientation that is permissive of in-line attack ~10% of the time (assuming that a 36° rotational window around a given bond permits reactivity). Therefore, the linkage as a whole would be in a configuration that would permit productive nucleophilic attack ~1% of the time. Although this is a crude estimate of the uncatalyzed reactivity of a typical RNA linkage, it seems unlikely that maximal α catalysis can significantly exceed 100-fold.
The speed limit hypothesis of enzymatic catalysis
The rate enhancement that can be generated by maximally using all four catalytic strategies (α, β, γ, and δ) is more than sufficient to account for the speed of RNA-cleaving enzymes. At neutral pH, the total rate enhancement that is theoretically available for enzymes to exploit is at least 1019 (Fig. 3 ▶; 102 × 105 × 106 × 106 for α through δ, respectively), and may be orders of magnitude higher depending on the value of pKa1. A key assumption of this rate-enhancement accounting approach is that each chemical effect is independent of every other effect. In other words, the maximum possible catalytic rate enhancement derived from a particular strategy is fixed whether or not any other strategy is engaged. With the exception of the proposal that δ mediated by protonation requires β to occur, we suggest that the magnitude of the rate enhancements are not dependent on one other. This hypothesis is supported by the fact that the changing slope observed throughout the pH profile (Fig. 2A ▶) can be explained by one, two, or three catalytic strategies, each contributing separately to catalysis. As a result, the combination of catalytic strategies has a multiplicative effect on the rate of the reaction. The ability to attribute all changes on the pH profile to particular chemical events also supports the validity of assuming in this analysis that the reaction pathway does not change with pH. The formidable power of RNA-cleaving enzymes therefore can be wholly explained as the ability to bring combinations of catalytic strategies (or in some instances, all four strategies discussed herein) to bear on the substrate simultaneously.
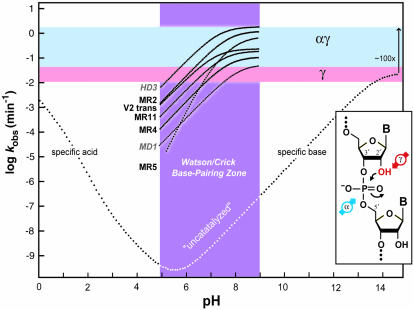
Analysis of crystal structures of RNase A indicates the enzymatic use of all four strategies, although the exact amount of rate enhancement contributed by any one strategy is still vigorously debated (Richards and Wyckoff 1971; Carlson 1976; Breslow 1991; Perreault and Anslyn 1997; Raines 1998). The rate-determining step of the reaction mediated by RNase A under multiple turnover conditions is substrate desolvation and not the rate of chemistry (Thompson et al. 1995). So the resulting rate enhancement of 1013-fold at pH 6 does not indicate whether the enzyme has maximally exploited any of the four chemical effects. In contrast, the seven engineered ribozymes and deoxyribozymes that meet a common speed limit are proposed to have perfected the implementation of α and γ catalysis, but not make use of either β or δ catalysis (Breaker et al. 2003). Briefly, when tested under each respective set of optimum reaction conditions, these αγ ribozymes and deoxyribozymes each approach a rate constant for RNA cleavage that is limited by the chemistry of the reaction. Typically, each enzyme has a pH profile for activity between the range of 5 and 9 that increases log-linearly with a slope of one until approaching a maximum pseudo first-order rate constant for RNA cleavage of ~2 min−1, indicating 108-fold rate enhancement (Fig. 6 ▶). The pH profiles are consistent with a base-catalyzed reaction mechanism wherein the pKa of the 2′-hydroxyl has been shifted down by the enzyme to between pH 7 and 9 (γ catalysis; pink zone; Fig. 6 ▶). The maximum rate constant of ~2 min−1 corresponds to the expected rate constant for complete deprotonation at the 2′ position combined with ideal alignment of the 2′-oxygen, phosphorous, and 5′-oxygen (α + γ catalysis; blue zone). What is striking is that so many enzymes share both this profile and maximum rate constant. Although other suboptimal combinations of catalytic strategies could achieve the same maximum rate constant, it seems unlikely that all seven enzymes manage this task while also producing a general base type of pH profile.
FIGURE 6.
Engineered ribozymes that appear to maximize two catalytic strategies. The composite plot depicts the kinetic behavior of seven RNA-cleaving ribozymes (black text) and deoxyribozymes (gray, italics text) compared with the profile expected for the spontaneous cleavage of RNA (see Fig. 2A ▶). The pH range from 5 to 9 (purple) is expected to permit Watson/Crick pairing without pH-induced disruption. The range for the maximum rate constants for γ catalysis (pink), and for the combination of α and γ catalysis (light blue) are indicated. The pH profiles for the enzymes were derived from (Breaker et al. 2003). The distinct slope of the MR5 ribozyme could be explained by a combination of αγ catalysis and the need for a second deprotonation event to satisfy a structural requirement. (Inset) The α and γ catalytic strategies that, when used in combination, can explain the maximum rate constants and the kinetic profiles of the enzymes depicted.
With four effects to manipulate, an enzyme has 16 different combinations of catalytic strategies that could be used to catalyze RNA cleavage (Table 2 ▶). Note that one combination of catalytic strategies is the state of no catalysis at all, and this total will be further reduced to 11 combinations if protonation (or metalation) of the leaving group can only occur in conjunction with protonation (or metalation) of a NBPO. This treatment of catalysis as a combinatorial problem is valid only if each effect is independent, outside of the δβ exception, and if it can explain all possible rate limiting steps inherent to the chemistry of the reaction itself. To test whether or not this speed limit hypothesis can explain the rate-limiting steps of RNA transesterification, two pathways must be considered: that of the unstable dianion phosphorane intervening species, and that of the monoanion phosphorane intermediate.
TABLE 2.
Considering the presence or absence of four independent catalytic strategies results in 16 possible combinations for enzymatic mechanism. The first entry is the state of no catalysis and is the background rate constant from which the remaining speed limits are calculated (23°C, 250 mM K+). Speed limits are the predicted rate constants for perfect use of the indicated catalytic combination. The highlighted speed limit is the common αγ speed limit. Asterisks (*) denote those speed limits for δ catalysis without β catalysis that are predicted not to be chemically permitted. Exceptions to this prediction might be permitted if an enzyme can metalate the 5′ oxygen without regard for the protonation or metalation state of the NBPO.
The reaction pathway of the dianion phosphorane species has no intermediates and has a single high-energy transition state. Once the dianion species is formed, the rate of leaving group expulsion is faster than diffusion controlled processes (Perreault and Anslyn 1997). Thus, catalysis can only promote the formation of the dianion phosphorane and not its decomposition. It is clear that through both α and γ catalysis, the rate of formation of the dianion will be enhanced. By definition, β catalysis is not occurring because both NBPOs are unprotonated. Furthermore, because the leaving group is expelled faster than it can receive a proton, δ catalysis cannot be occurring either. Thus, consideration of the reaction pathway of the dianion phosphorane does not change any conclusions of the speed limit hypothesis.
On the other hand, the monoanion phosphorane could occupy an energetic well between two transition states corresponding to the energy(s) of forming the intermediate and of decomposing into products. If one of these two states is significantly higher energy than the other, a rate-limiting barrier will occur (Jencks 1987). Again by definition, β catalysis is occurring in the monoanion because one of the NBPOs is protonated. The validity of the speed limit hypothesis then rests on whether the same catalytic rate enhancements can be derived from each of the remaining chemical effects, regardless of this change in the chemistry of the reaction.
Under slightly acidic conditions, the pH profile of the degradation of RNA and its triester most likely reflects the continued contribution of γ catalysis due to hydroxide ion with a log-linear relationship down to pH ~3 (Fig. 2B ▶). This indicates that although this simulated β catalysis is fully active due to charge neutralization in the triester, no change can be observed in the ability of specific base to catalyze formation of the monoanion intermediate. Thus, γ catalysis is independent of the presence or absence of β catalysis. Either activation of the nucleophile impacts the rate-limiting step or neither of the energetic barriers is high enough to become a rate-limiting step.
Similarly, α catalysis is likely independent of β catalysis based on the following results. An enzyme that correctly positioned atoms for in-line attack (α), and that catalyzed transesterification, would be required to continue to keep these atoms in position for the duration of the reaction. Otherwise, pseudorotation of the monoanion intermediate would be allowed. Because departure of the 3′-oxygen atom is more favorable than departure of the 5′-oxygen atom under conditions of αβγ catalysis (e.g., analogous to the specific acid catalyzed reaction at pH 3 to 4; Kosonen and Lönnberg 1995), isomerization rather than transesterification would result. Therefore, α catalysis must reduce both energetic barriers by promoting both formation and decomposition of the intermediate to the desired products.
With δ catalysis, it should be noted that β catalysis by specific acid never occurs without specific acid δ catalysis as well (Fig. 2B ▶). Similarly, β and γ catalysis never occur together without δ. However, RNA analogs complexed with metal ions to simulate β catalysis show enhanced rates of cleavage at pH 6, at which the specific acid contribution to δ catalysis is predicted to be very low (Bruice et al. 1996). It is possible that this experiment demonstrates that catalysis due to neutralizing the negative charge on a NBPO does not require neutralization of the 5′-oxyanion leaving group as well in order to enhance the rate of the reaction. As for γ catalysis then, either β catalysis impacts the rate-limiting step or neither of the energetic barriers is high enough to become a rate-limiting step. Although δ catalysis might require β catalysis in order to occur (see Table 2 ▶ for possible exceptions), the two strategies are not cooperative and they affect the rate of cleavage independently.
Predictions and scope of the speed limit hypothesis
The question of how fast a ribozyme or deoxyribozyme can catalyze RNA phosphoester transfer has implications for basic research and for commercial applications of nucleic acid enzymes. The rate constant of 2 min−1 is the theoretical maximum for αγ enzymes regardless of whether the polymeric composition of the enzyme is RNA, DNA, protein, or any other form. One of the main conclusions of the speed limit hypothesis is that individual catalytic strategies have specific limitations, and that higher speed enzymes must make use of multiple catalytic strategies to exceed the maximum allowable rate constants permitted by individual strategies. Thus, the αγ enzymes described (Breaker et al. 2003) might never exceed a rate constant of ~2 min−1 under typical physiological conditions without making use of additional catalytic strategies. Because certain ribozymes and deoxyribozymes do exceed the αγ speed barrier, nucleic acid enzymes inherently must be able to use a set of catalytic strategies that, in principle, could permit them to be as fast as proteins. Interestingly, a ribozyme that uses only three catalytic strategies in combination (α, β, δ) could attain the same speed as RNase A if the ribozyme were to use these strategies to their full potential (Fig. 3 ▶). In addition, we expect that the creation and characterization of engineered ribozymes and deoxyribozymes can be made more efficient by understanding the chemical nature of catalysis of RNA transesterification.
Several other influences on catalysis that have not been considered in this discussion could also contribute to the catalytic function of RNA-cleaving enzymes. For example, the structured environment of an enzyme active site could also directly modify the strength of bonds through induction of strain. However, the contacts that would create bond strain would be the same contacts that would promote α through δ catalysis, and so bond strain is not likely to be independent of the catalytic strategies described herein. Ignoring bond strain does not seem to have complicated the application of the speed limit hypothesis to the example of the common αγ combination, as we have observed no indication that the αγ enzymes benefit from bond strain (Breaker et al. 2003). It seems reasonable then to conclude that the most common structural effect that the active site of an enzyme can use is α catalysis, although bond strain in combination with other catalytic strategies might be applied less frequently. Furthermore, as enzymatic catalysis becomes increasingly more efficient through perfection of given strategies or through addition of more strategies, the demands on substrate positioning increase. In other words, the formation of multiple contacts between active site groups and the substrate promote multiple catalytic strategies, but also constrain the RNA linkage. If this constrained geometry is not in-line, then the reaction most likely cannot proceed. Therefore, the more efficient an enzyme is, the more likely it is to have perfected α catalysis. That makes catalytic combinations lacking α catalysis less common, and thus, the number of the most frequently encountered combinations of catalytic strategies drops to just six (Table 2 ▶). Specifically, proposed examples exist of the αγ combination (Breaker et al. 2003), α alone (Soukup and Breaker 1999), and the αβγδ combination used by RNase A (although probably suboptimally). The remaining combinations that are most likely to occur then would be αβ, αβγ, and αβδ unless αδ and αγδ are possible via metalation.
The speed limit hypothesis of enzymatic catalysis is based on the premise that enzymes can do no more than bring chemistry to its physically determined maximum rate. The scope of the hypothesis does not address the energetic exchanges that enzymes use to bring about rate enhancement. Enzymes may bring about changes in the entropy of activation or the enthalpy of activation and may do so by exploiting intrinsic binding energy or transition state stabilization (Jencks 1987; Trawick et al. 1998; Fersht 1999; Bruice and Benkovic 2000). However, the molecular events that lead to enzymatic catalysis will have their impact realized ultimately by a change in catalysis of each strategy. For example, α catalysis must have entropic effects, whereas the same molecular contacts that allow enzymatic enhancement of β, γ, and δ catalysis must have contributions to the stability of the transition state in order to impact the rate of the reaction. Overall, the effect of energetic interchanges will be expressed as an ability by the enzyme to bring about α, β, γ, and δ catalysis.
Existing evidence indicates that RNA and DNA both have the structural complexity to form active sites that seemingly perfect both α and γ catalysis for RNA cleavage (Breaker et al. 2003). In addition, ribozymes that exhibit modified rates in the presence of Rp or Sp sulfur containing substrates, such as the X-motif and the hammerhead, demonstrate that nucleic acid enzymes can make use of β catalysis (Scott and Uhlenbeck 1999; Derrick et al. 2000; Breaker et al. 2003). The rate enhancement of the X-motif ribozyme (Breaker et al. 2003; Lazarev et al. 2003) is too great to be explained by either β catalysis alone or by a combination of α and β catalysis. Interestingly, the second-order dependence of the X-motif on magnesium is consistent with a double-metal-ion mechanism (Steitz and Steitz 1993) wherein the ribozyme uses two metals to achieve simultaneously β and δ catalysis. Regardless, a combination of any three of the catalytic strategies described herein, when optimized, should yield an enzyme that can achieve a rate enhancement that compares favorably with RNase A. Furthermore, through the use of their own functional groups and metal ions, structured RNA and DNA molecules have the ability to surmount unfavorable functional pKa values in local microenvironments by shifting pKa values by at least 106 pH units (Cai and Tinoco 1996; Legault and Pardi 1997; Nakano et al. 2000; Lupták et al. 2001; Breaker et al. 2003). This ability should make nucleic acid enzymes entirely capable of exploiting β, γ, and δ catalytic strategies to their maximum extent.
Conclusions
Numerous protein enzymes and ribozymes catalyze RNA cleavage by a phosphoester transfer reaction wherein the 2′-oxygen of the target linkage attacks the adjoining phosphorus center. This mechanism of RNA degradation also is the dominant route by which RNA spontaneously degrades under a wide range of conditions. Although this reaction is of fundamental importance in enzymology, the precise strategies used by natural and engineered ribozymes performing this reaction remain a subject of much debate. We have summarized the catalytic strategies that could be used to accelerate RNA phosphoester transfer, and then used these points to create a conceptual framework for understanding the function of RNA-cleaving enzymes. Recent studies on the kinetic characteristics of engineered ribozymes and deoxyribozymes provide data that are consistent with this conceptual framework and thus support the hypothesis that certain classes of ribozymes could exhibit the same catalytic power as protein enzymes. A proposal that the self-cleaving ribozyme from hepatitis δ virus could also attain a rate enhancement as high as RNase A if optimal general base catalysis were used has been made previously (Nakano et al. 2000). Furthermore, the conceptual basis of the speed limit theory described herein could be applied to other reactions to establish the limitations of other enzyme classes.
It is likely that nucleic acid enzymes are capable of achieving rate enhancement by influencing any of the four catalytic strategies described herein that accelerate RNA transesterification, either individually or in combination. The potential rate enhancement to be gained by catalyzing all effects at once far outstrips physical limitations on chemistry such as the time to transfer a proton or break the bond to the leaving group. Therefore, even suboptimal application of all four effects at once will result in rate enhancements that are equivalent to RNase A. Because there appear to be no theoretical barriers that would preclude nucleic acid enzymes from attaining the extraordinary rate enhancements that are created by protein enzymes, we suspect that such high-powered ribozymes might have once existed in biology, and that such enzymes could be created by enzyme engineers in the future.
MATERIALS AND METHODS
Construction of Figure 2A ▶
The plot of the logarithm of predicted rate constants for RNA cleavage by phosphoester transfer versus the pH of an enzyme was derived as follows: The measured 2′-hydroxyl pKa (pKa3) of 13.7 and the maximum rate constant for cleavage at room temperature at high pH (kmaxγ) of 0.02 min−1 (Li and Breaker 1999) were used to predict a minimum rate constant (kmin) of 2 × 10−13 min−1 for cleavage in the absence of any catalysis. This is a theoretical value only, because some catalysis will occur at any pH, and is used only for the purposes of projecting rate enhancement. This value was calculated by presuming that the nucleophilicity of a 2′-oxyanion is 1011 greater than that of a 2′ hydroxyl and thus kmin = 0.02 ÷ 1011. The approximate increase in nucleophilicity had previously been estimated to be at least 1010 (Oivanen et al. 1998) based on a slightly lower pKa value (Järvinen et al. 1991).
The measured maximum rate constant for cleavage at low pH is presumed to reflect the contribution of two protonation events. The independent maximum rate constants for either β or δ catalysis were estimated as follows. Using the rate enhancements determined in the text and kmin, kmaxβ was approximated by multiplying 2 × 10−13 by 5 × 104, and similarly, kmaxδ = kmin × 109. This is based on the assumption that the value pKa1 for the bridging 5′-oxygen atom is ~−3.5. The value of pKa2 for the first NBPO is assumed to be 1. Each pair of pKa and kmax values was used to calculate the predicted observed rate constant versus pH due to specific acid/base catalysis of each of these protonations individually by using the Henderson-Hasselbalch relationship and the assumption that kobs = kmax × ratio of molecules in the catalyzed protonation state to molecules in the uncatalyzed state. For specific base catalysis (γ), this is expressed as
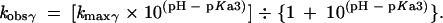 |
For specific acid catalysis at the NBPO (β), the equation is
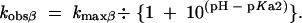 |
The equation for specific acid catalysis of δ follows the same form, using kmaxδ and pKa1.
The fold rate enhancement (enh) was calculated for each effect in order to predict the overall rate constant for cleavage. The kmin term was included to account for the point at which observed the rate constant becomes for RNA cleavage becomes independent of the β, γ, and δ effects. This shown for γ catalysis:
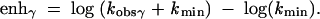 |
The overall log of predicted observed rate constant for RNA cleavage by phosphoester transfer versus pH is then given by
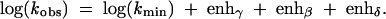 |
Acknowledgments
We thank members of the Breaker laboratory for helpful discussions and Fritz Eckstein for insightful comments on the manuscript. This work was supported by NIH grant GM57500 for deoxyribozyme research and by NIH grant GM559343 for ribozyme research. RNA science in the Breaker laboratory also is supported through a fellowship to R.R.B. from the David and Lucile Packard Foundation.
Article and publication are at http://www.rnajournal.org/cgi/doi/10.1261/rna.5680603.
REFERENCES
- Adams, R.L.P., Knowler, J.T., and Leader, D.P. 1992. Degradation and modification of nucleic acids. In The biochemistry of the nucleic acids, 11th ed., pp. 97–133. Chapman & Hall, New York.
- Admiraal, S.J. and Herschlag, D. 1995. Mapping the transition state for ATP hydrolysis: Implications for enzymatic catalysis. Chem. Biol. 2: 729–739. [DOI] [PubMed] [Google Scholar]
- Almer, H. and Strömberg, R. 1996. Base catalysis and leaving group dependence in intramolecular alcoholysis of uridine 3′-(aryl phosphorothioate)s. J. Am. Chem. Soc. 118: 7921–7928. [Google Scholar]
- Bacher, J.E. and Kauzmann, W. 1952. The kinetics of hydrolysis of ribonucleic acid. J. Am. Chem. Soc. 74: 3779–3786. [Google Scholar]
- Benkovic, S.J. and Schray, K.J. 1970. Chemical basis of biological phosphoryl transfer. In The enzymes, 3rd ed., Vol. VIII (ed. P.D. Boyer), pp. 201–238, Academic Press, New York.
- Breaker, R.R. 1997. In vitro selection of catalytic polynucleotides. Chem. Rev. 97: 371–390. [DOI] [PubMed] [Google Scholar]
- Breaker, R.R., Emilsson, G.M., Lazarev, D., Nakamura, S., Puskarz, I.J., Roth, A. and Sudarsan, N. A common speed limit for RNA-cleaving ribozymes and deoxyribozymes. RNA (this issue). [DOI] [PMC free article] [PubMed]
- Breslow, R. 1991. How do imidazole groups catalyze the cleavage of RNA in enzyme models and in enzymes? Evidence from “negative catalysis.” Acc. Chem. Res. 24: 317–324. [Google Scholar]
- Brown, D.M. and Todd, A.R. 1952. Nucleotides. Part X. Some observations on the structure and chemical behaviour of the nucleic acids. J. Chem. Soc. 52–58.
- ———. 1953. The action of ribonuclease on simple esters of the monoribonucleotides. J. Chem. Soc. 2040–2049.
- Brown, D.M., Magrath, D.I., Neilson, A.H., and Todd, A.R. 1956. Hydrolysis of esters of monoribonucleotides. Nature 177: 1124–1125. [Google Scholar]
- Bruice, T.C. and Benkovic, S.J. 2000. Chemical basis for enzyme catalysis. Biochemistry 39: 6267–6274. [DOI] [PubMed] [Google Scholar]
- Bruice, T.C., Tsubouchi, A., Dempcy, R.O., and Olson, L.P. 1996. One- and two-metal ion catalysis of the hydrolysis of adenosine 3′-alkyl phosphate esters. Models for one- and two-metal ion catalysis of RNA hydrolysis. J. Am. Chem. Soc. 118: 9867–9875. [Google Scholar]
- Butcher, S.E. 2001. Structure and function of the small ribozymes. Curr. Opin. Struct. Biol. 11: 315–320. [DOI] [PubMed] [Google Scholar]
- Cai, Z. and Tinoco Jr., I. 1996. Solution structure of loop A from the hairpin ribozyme from tobacco ringspot virus satellite. Biochemistry 35: 6026–6036. [DOI] [PubMed] [Google Scholar]
- Carlson, W.D. 1976. “X-ray diffraction studies of bovine pancreatic ribonuclease-S and E. coli alkaline phosphatase.” Ph.D. thesis, Yale University, New Haven, CT.
- Derrick, W.B., Greef, C.H., Caruthers, M.H., and Uhlenbeck, O.C. 2000. Hammerhead cleavage of the phosphorodithioate linkage. Biochemistry 39: 4947–4954. [DOI] [PubMed] [Google Scholar]
- Fedor, M.J. 2000. Structure and function of the hairpin ribozyme. J. Mol. Biol. 297: 269–291. [DOI] [PubMed] [Google Scholar]
- Fersht, A. 1999. Structure and mechanism in protein science: A guide to enzyme catalysis and protein folding. W.H. Freeman, New York.
- Gerlt, J.A. 1993. Mechanistic principles of enzyme-catalyzed cleavage of phosphodiester bonds. In Nucleases, 2nd ed. (eds. S.M. Linn et al.), pp. 1–34. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY.
- Guthrie, J.P. 1977. Hydration and dehydration of phosphoric acid derivatives: Free energies of formation of the pentacoordinate intermediates for phosphate ester hydrolysis and of monomeric metaphosphate. J. Am. Chem. Soc. 99: 3991–4001. [Google Scholar]
- Izatt, R.M., Rytting, J.H., Hansen, L.D., and Christensen, J.J. 1966. Thermodynamics of proton dissociation in dilute aqueous solution, V. An entropy titration study of adenosine, pentoses, hexoses, and related compounds. J. Am. Chem. Soc. 88: 2641–2645. [DOI] [PubMed] [Google Scholar]
- Järvinen, P., Oivanen, M., and Lönnberg, H. 1991. Interconversion and phosphoester hydrolysis of 2′,5′- and 3′,5′-dinucleoside monophosphates: Kinetics and mechanisms. J. Org. Chem. 56: 5396–5401. [Google Scholar]
- Jencks, W.P. 1987. Catalysis in chemistry and enzymology. Dover Publications, New York, NY.
- Kirby, A.J. 1996. Enzyme mechanisms, models, and mimics. Angew. Chem. Int. Ed. Engl. 35: 707–724. [Google Scholar]
- Kosonen, M. and Lönnberg, H. 1995. General and specific acid/base catalysis of the hydrolysis and interconversion of ribonucleoside 2′- and 3′-phosphotriesters: kinetics and mechanisms of the reactions of 5′-O-pivaloyluridine 2′- and 3′-dimethylphosphates. J. Chem. Soc. Perkin Trans. 2: 1203–1209. [Google Scholar]
- Kuimelis, R.G. and McLaughlin, L.W. 1995. Cleavage properties of an oligonucleotide containing a bridged internucleotide 5′-phosphorothioate RNA linkage. Nucleic Acids Res. 23: 4753–4760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lafontaine, D.A., Norman, D.G., and Lilley, D.M.J. 2001. Structure, folding and activity of the VS ribozyme: Importance of the 2–3–6 helical junction. EMBO J. 20: 1415–1424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazarev, D., Puskarz, I., and Breaker, R.R. 2003. Substrate specificity and reaction kinetics of an X-motif ribozyme. RNA 9: 688–697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Legault, P. and Pardi, A. 1997. Unusual dynamics and pKa shift at the active site of a lead-dependent ribozyme. J. Am. Chem. Soc. 119: 6621–6628. [Google Scholar]
- Li, Y. and Breaker, R.R. 1999. Kinetics of RNA degradation by specific base catalysis of transesterification involving the 2′-hydroxyl group. J. Am. Chem. Soc. 121: 5364–5372. [Google Scholar]
- Lim C., and Karplus, M. 1990. Nonexistence of dianionic pentacovalent intermediates in an ab initio study of the base-catalyzed hydrolysis of ethylene phosphate. J. Am. Chem. Soc. 112: 5872–5873. [Google Scholar]
- Linn, S.M., Lloyd, R.S., and Roberts, R.J. 1993. Nucleases, 2nd ed. Cold Spring Harbor, Cold Spring Harbor Laboratory, NY.
- Lipkin, D., Talbert, P.T., and Cohn, M. 1954. The mechanism of the alkaline hydrolysis of ribonucleic acids. J. Am. Chem. Soc. 76: 2871–2872. [Google Scholar]
- Lupták, A., Ferré-D’Amaré, A.R., Zhou, K., Zilm, K.W., and Doudna, J.A. 2001. Direct pKa measurement of the active-site cytosine in a genomic hepatitis δ virus ribozyme. J. Am. Chem. Soc. 123: 8447–8452. [DOI] [PubMed] [Google Scholar]
- March, J. 1992. Acids and bases. In Advanced organic chemistry, 4th ed., pp. 248–272. John Wiley & Sons, New York.
- Nakano, S.-I., Chadalavada, D.M., and Bevilacqua, P.C. 2000. General acid-base catalysis in the mechanism of a hepatitis δ virus ribozyme. Science 287: 1493–1497. [DOI] [PubMed] [Google Scholar]
- Oivanen, M., Ora, M., Almer, H., Strömberg, R., and Lönnberg, H. 1995. Hydrolytic reactions of the diastereomeric phosphoromonothioate analogs of uridylyl(3′,5′)uridine: Kinetics and mechanisms for desulfurization, phosphoester hydrolysis, and transesterification to the 2′,5′-isomers. J. Org. Chem. 60: 5620–5627. [Google Scholar]
- Oivanen, M., Kuusela, S., and Lönnberg, H. 1998. Kinetics and mechanisms for the cleavage and isomerization of the phosphodiester bonds of RNA by bronsted acids and bases. Chem. Rev. 98: 961–990. [DOI] [PubMed] [Google Scholar]
- Perreault, D.M. and Anslyn, E. 1997. Unifying the current data on the mechanism of cleavage-transesterification of RNA. Angew. Chem. Int. Ed. Engl. 36: 432–450. [Google Scholar]
- Raines, R.T. 1998. Ribonuclease A. Chem. Rev. 98: 1045–1066. [DOI] [PubMed] [Google Scholar]
- Richards, R.M. and Wyckoff, H.M. 1971. Bovine pancreatic ribonuclease. In The enzymes, vol. 4 (ed. P. Boyer), pp. 647–806. Academic Press, New York.
- Saenger, W. 1984. Physical properties of nucleotides: Charge densities, pK values, spectra, and tautomerism. In Principles of nucleic acid structure, pp. 105–115. Springer-Verlag, New York.
- Santoro, S.W. and Joyce, G.F. 1997. A general purpose RNA-cleaving DNA enzyme. Proc. Natl. Acad. Sci. 94: 4262–4266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott, E.C. and Uhlenbeck, O.C. 1999. A re-investigation of the thio effect at the hammerhead cleavage site. Nucleic Acids Res. 27: 479–484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scott, W.G. 1999. Biophysical and biochemical investigations of RNA catalysis in the hammerhead ribozyme. Q. Rev. Biophys. 32: 241–284. [DOI] [PubMed] [Google Scholar]
- Shiiba, T. and Komiyama, M. 1992. Phenyl ester of adenosine 3′-phosphate as a novel probe for the rate-limiting step in RNA hydrolysis. Tetrahedron Lett. 33: 5571–5574. [PubMed] [Google Scholar]
- Sood, V.D. and Collins, R.A. 2002. Identification of the catalytic subdomain of the VS ribozyme and evidence for remarkable sequence tolerance in the active site loop. J. Mol. Biol. 320: 443–454. [DOI] [PubMed] [Google Scholar]
- Soukup, G.A. and Breaker, R.R. 1999. Relationship between internucleotide linkage geometry and the stability of RNA. RNA 5: 1308–1325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stage-Zimmermann, T.K. and Uhlenbeck, O.C. 1998. Hammerhead ribozyme kinetics. RNA 4: 875–889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steitz, T.A. and Steitz, J.A. 1993. A general two-metal-ion mechanism for catalytic RNA. Proc. Natl. Acad. Sci. 90: 6498–6502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang, J. and Breaker, R.R. 1997. Examination of the catalytic fitness of the hammerhead ribozyme by in vitro selection. RNA 3: 914–925. [PMC free article] [PubMed] [Google Scholar]
- ———. 2000. Structural diversity of self-cleaving ribozymes. Proc. Natl. Acad. Sci. 97: 5784–5789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor, J.M. 1997. Organization and expression of the hepatitis δ virus genome. Semin. Virol. 8: 59–64. [Google Scholar]
- Thatcher, G.R.J. and Kluger, R. 1989. Mechanism and catalysis of nucleophilic substitution in phosphate esters. Adv. Phys. Org. Chem. 25: 99–265. [Google Scholar]
- Thompson, J.E., Kutateladze, T.G., Schuster, M.C., Venegas, F.D., Messmore, J.M., and Raines, R.T. 1995. Limits to catalysis by ribonuclease A. Bioorg. Chem. 23: 471–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomson, J.B., Patel, B.K., Jimenez, V., Eckart, K., and Eckstein, F. 1996. Synthesis and properties of diuridine phosphate analogues containing thio and amino modifications. J. Org. Chem. 61: 6273–6281. [DOI] [PubMed] [Google Scholar]
- Trawick, B.N., Daniher, A.T., and Bashkin, J.K. 1998. Inorganic mimics of ribonucleases and ribozymes: From random cleavage to sequence-specific chemistry to catalytic antisense drugs. Chem. Rev. 98: 939–960. [DOI] [PubMed] [Google Scholar]
- Velikyan, I., Acharya, S., Trifonova, A., Földesi, A., and Chattopadhyaya, J. 2001. The pKa’s of 2′-hydroxyl group in nucleosides and nucleotides. J. Am. Chem. Soc. 123: 2893–2894. [DOI] [PubMed] [Google Scholar]
- Wadkins T.S., and Been, M.D. 2002. Ribozyme activity in the genomic and antigenomic RNA strands of hepatitis δ virus. Cell Mol. Life Sci. 59: 112–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walter, N.G. and Burke, J.M. 1998. The hairpin ribozyme: Structure, assembly and catalysis. Curr. Opin. Chem. Biol. 2: 24–30. [DOI] [PubMed] [Google Scholar]
- Wedekind, J.E. and McKay, D.B. 1998. Crystallographic structures of the hammerhead ribozyme: relationship to ribozyme folding and catalysis. Annu. Rev. Biophys. Biomol. Struct. 27: 475–502. [DOI] [PubMed] [Google Scholar]
- Westheimer, F.H. 1968. Pseudo-rotation in the hydrolysis of phosphate esters. Acc. Chem. Res. 1: 70–78. [Google Scholar]
- ———. 1987. Why nature chose phosphates. Science 235 1173–1178. [DOI] [PubMed] [Google Scholar]
- Williams, P.P., Ciafré, S., and Tocchini-Valentini, G.P. 1995. Selection of novel Mg2+-dependent self-cleaving ribozymes. EMBO J. 14: 4551–4557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson, D.S. and Szostak, J. W. 1999. In vitro selection of functional nucleic acids. Annu. Rev. Biochem. 68: 611–647. [DOI] [PubMed] [Google Scholar]
- Zhou, D.-M. and Taira, K. 1998. The hydrolysis of RNA: From theoretical calculations to the hammerhead ribozyme-mediated cleavage of RNA. Chem. Rev. 98: 991–1026. [DOI] [PubMed] [Google Scholar]
- Zhou, D.-M., Usman, N., Wincott, F.E., Matulic-Adamic, J., Orita, M., Zhang, L.-H., Komiyama, M., Kumar, P.K.R., and Taira, K. 1996. Evidence for the rate-limiting departure of the 5′-oxygen in nonenzymatic and hammerhead ribozyme-catalyzed reactions. J. Am. Chem. Soc. 118: 5862–5866. [Google Scholar]