Dynamics of the IRE RNA hairpin loop probed by 2-aminopurine fluorescence and stochastic dynamics simulations

Abstract

The iron responsive element (IRE) RNA hairpin loop contains six phylogenetically conserved nucleotides, which constitute part of the sequence-specific binding site of the IRE-binding protein. The NMR structure of the loop has been solved, showing that 3 of the 6 nt are poorly constrained. Here, two purine nucleotides in the IRE loop are individually replaced with the fluorescent purine analog 2-aminopurine (2AP). Steady-state and time-resolved fluorescence methods are used to describe the structure and dynamics of 2AP in the IRE loop. The data indicate that 2AP at the position of the adenosine in the loop moves between stacked and unstacked positions, whereas 2AP at the adjacent guanosine is predominantly solvent exposed. Stochastic dynamics simulations are used to provide a physical description of how those nucleotides might move.

INTRODUCTION

The IRE-binding protein (IRE-BP) recognizes the IRE RNA loop sequence, 5′CAGUGN, where N is C, U, or A, in addition to a conserved bulge in the IRE hairpin stem (Barton et al. 1990; Leibold et al. 1990; Bettany et al. 1992; Jaffrey et al. 1993; Kikinis et al. 1995). The mechanism of RNA:protein interaction is not known, but will depend, in part, on how the bases of the IRE loop are displayed in solution. For example, a highly structured loop could be recognized by its static conformation; alternatively, the protein would disrupt the loop structure to make sequence-specific contacts with the bases. In the case of the IRE loop, NMR data show that its structure is poorly defined in solution (Laing and Hall 1996; Addess et al. 1997; McCallum and Pardi 2003), which could facilitate recognition of individual nucleotide bases by the IRE-BP. A flexible IRE loop could eliminate an energetically unfavorable requirement for disruption of a stable structure.

The metazoan IRE-BP (or iron regulatory factor, IRF) is a phylogenetically conserved bifunctional protein: When it contains a [4Fe-4S] cluster, it functions as a cytosolic aconitase; in the absence of the metals, it binds the IRE RNA (Hirling et al. 1994). Its size (90 kD) has precluded NMR studies, and there is no crystal structure of the protein with or without RNA. It is presumed to be structurally homologous to the mitochondrial aconitase (mAcn), which does not bind RNA (Robbins and Stout 1989). The binding site for RNA was modeled in the cleft of the two domains (Basilion et al. 1994; Hirling et al. 1994; Kaldy et al. 1999). The first structure of a bifunctional aconitase is that of the Escherichia coli aconitase B (Williams et al. 2002) and it is similar in three dimensions to the mAcn structure. Unfortunately, there are no biophysical data describing this RNA: protein interaction, so the importance of RNA loop flexibility to binding is inferential, based on the properties of the isolated RNA loop measured in solution.

The IRE loop sequence, C6A7G8U9G10C11, sits on an AU loop closing base pair, which is conserved in the ferritin mRNA (Casey et al. 1988; structure shown in Fig. 1 ▶; numbering refers to the hairpin construct used in these experiments). NMR structures of the IRE hairpin loop showed a base pair formed between Cytidine 6 and Guanosine 10, which accounts for the higher than predicted melting temperature of the IRE hairpin (Laing and Hall 1996; Addess et al. 1997). As a consequence of this base pair interaction, Cytidine 11 is extruded from the loop; NMR data (NOEs) were consistent with an anti glycosidic bond angle. Similarly, the Uridine 9 base was not located within the loop structure, and structures generated from the NMR data placed it in solution at the turn of the loop. On the 5′ side of the loop, Adenosine 7 was stacked over Cytosine 6, but the Guanosine 8 base did not appear to be proximal to any element of the loop.

FIGURE 1.

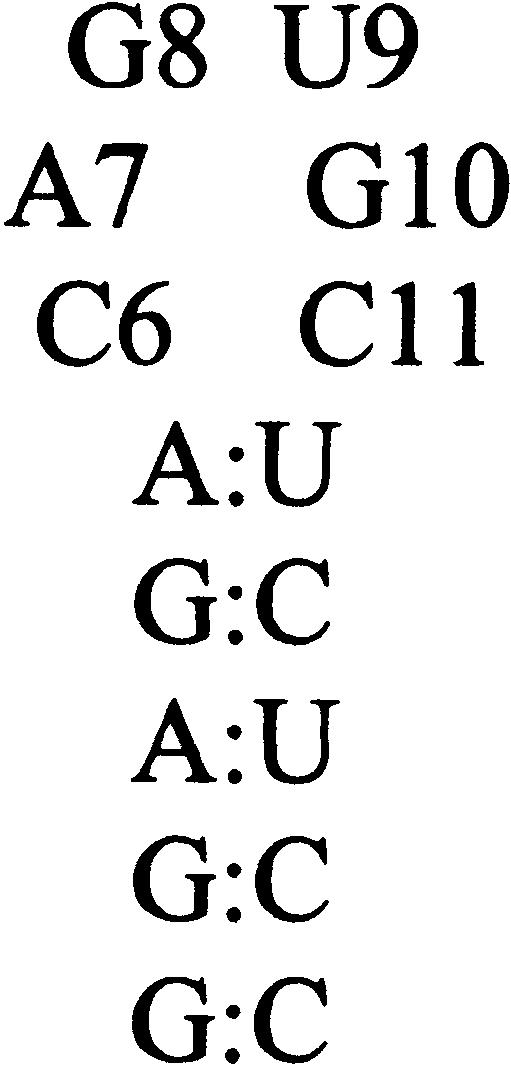
Sequence and structure of the human IRE RNA hairpin used in these experiments.

The lack of NMR constraints to describe the loop structure led to a picture of the IRE in which several bases in the loop were mobile. To measure the dynamic motions of the bases, a ¹³C NMR relaxation study was carried out on the IRE hairpin (Hall and Tang 1998), where, for technical reasons, only the purine bases were studied. Results showed that at 20°C, where the NMR structure was solved, all purines in the loop appeared to experience the same amplitude of dynamic motion. The implication is that although the G8 base could not be located within a structured loop, it did not appear to be more flexible than the G10 base in its C6:G10 base pair. However, at 37°C, ¹³C NMR data showed a significant increase in the motions experienced by all three purine bases in the loop, indicating that the entire loop had become more mobile on the picosecond–nanosecond timescale.

Now, to further probe the structure and dynamics of the IRE hairpin loop, we have replaced either A7 or G8 with the fluorescent base 2-aminopurine (2AP). Neither of these purines in the IRE loop forms hydrogen bonds with other loop moieties, so introduction of 2AP should not perturb the IRE structure. By measuring the temperature dependence of the steady-state fluorescence of these substituted IRE RNAs, the structural environment of the A7 and G8 positions can be compared. Temperature dependence of the time-resolved fluorescence emission decay and fluorescence anisotropy decay of 2AP in these RNAs allows a comparison of the properties of 2AP in the different loop environments and a measure of the local correlation time of the 2AP base. The results from the fluorescence experiments are compared to previous NMR data that describe motions of the bases and to models of the base dynamics from simulations.

RESULTS

Characterization of the 2AP-IRE RNAs

To determine the effect of 2AP substitution on the structure and stability of the IRE hairpins, the two RNA molecules (IRE P7 and P8) were examined by NMR and thermal denaturation experiments. Imino proton spectra and proton TOCSY spectra of the pyrimidines and ribose regions of IRE P7 and P8 were identical to spectra of wild-type IRE RNA, indicating that the loop structure was not perturbed (data not shown). Thermal denaturation experiments were analyzed to determine the melting temperature of the RNAs: in 10 mM sodium cacodylate (pH 7), the T_M of wild-type, P7, and P8 IRE RNAs was 60.7°C–60.9°C ± 0.4°C. Complete thermodynamic parameters of the IREs with 2AP in sodium cacodylate buffer are given in Table 1 ▶. In the presence of 1 M NaCl, the RNA formed a dimer, making thermodynamic data difficult to interpret; in 25 mM NaCl, 10 mM sodium cacodylate (pH 7), the solution conditions of the NMR experiments, the melting temperatures of the three RNAs were the same within error (data not shown). We conclude that IRE P7 and IRE P8 behave like the wild-type IRE, such that fluorescence properties of the substituted 2AP will accurately describe the behavior of the normal molecule.

TABLE 1.

Thermodynamics of IRE P7 and P8

RNA sequence	ΔH° [kcal/mole]	ΔS° [cal/mole-K]	TM [°C]	ΔG° (55) [kcal/mole]	ΔG° (37) [kcal/mole]
-ACP7GUGCU-	57.9 ± 0.6	170 ± 30	60.9 ± 0.4	1.0 ± 0.1	4.1 ± 0.8
-ACAP8UGCU-	58.2 ± 0.5	170 ± 30	60.7 ± 0.4	1.0 ± 0.1	4.1 ± 0.8

Results from global analysis of three or more UV/Vis melts (15°C–95°C) measured at 260 nm with a heating rate of 1°C/min. Buffer: 10 mM sodium cacodylate, 0.5 mM EDTA (pH 7). IRE RNA sequence is GGAGACAGUGCUCUCC. The melting temperature (T_M) of the wild-type RNA is 60.8°C ± 0.4°C in this buffer.

Steady-state fluorescence of the IREs

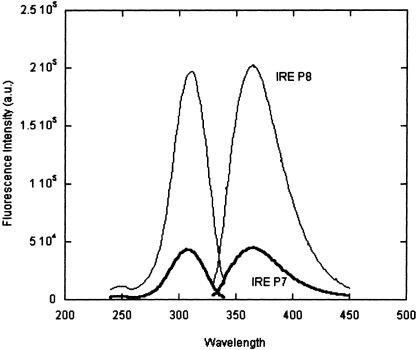
The fluorescence emission and excitation spectra of the IRE RNAs are compared in Figure 2 ▶. Free 2AP has an excitation maximum at 307 nm and an emission maximum at 370 nm; the emission wavelength can change if the environment of the 2AP is desolvating (Rachofsky et al. 2001a). In the IRE RNAs, the spectral properties of 2AP match those of the free nucleotide, indicating that their positions in the IRE loop are solvent accessible. At 20°C, 2AP fluorescence intensity of IRE P7 is 24% of that of 2AP in IRE P8; the fluorescence intensity compared to free 2AP (4 μM) at 20°C, is 60% for P8, but only 14% for P7. Addition of 2 mM MgCl₂ did not alter the emission or excitation spectra of either RNA (data not shown).

FIGURE 2.

Fluorescence excitation and emission spectra of IRE P7 and IRE P8. 4 μM RNAs, 30 mM NaCl, 10 mM potassium phosphate (pH 7.0), 20°C. The buffer baseline was subtracted from each spectrum (the Raman line is at 350 nm).

Temperature dependence of steady-state fluorescence

The difference in fluorescence intensity with position in the RNA loop can be explained by stacking of P7 on its neighboring C6:G10 base pair, leading to quenching of its fluorescence (Nordland et al. 1989; Guest et al. 1991). By comparison, P8 stacking appears minimal. The structure of the IRE, solved at 20°C, is consistent with this interpretation. However, NMR experiments showed that the structure of the IRE loop is disrupted at 37°C, and the bases become more flexible (Hall and Tang 1998). 2AP fluorescence emission in the two IREs was examined as a function of temperature to further probe the loop structure.

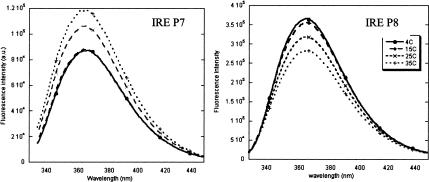
As shown in Figure 3 ▶, left panel, 2AP fluorescence intensity at position P7 increases with temperature from 4°C–35°C. These data are consistent with a structural model in which the stacking of P7 is disrupted at higher temperatures; quenching of its fluorescence due to formation of an electronic “supermolecule” state (Jean and Hall 2001) is progressively diminished as the 2AP spends less of its time stacked. In contrast, 2AP fluorescence emission at P8 has its highest intensity at 4°C, and becomes progressively less with increasing temperature (Fig. 3 ▶, right panel). This behavior is analogous to that of free 2AP, which undergoes quenching of its fluorescence due to collisions with solvent; higher temperatures increase the efficiency of collisional quenching.

FIGURE 3.

Temperature dependence of the fluorescence emission of IRE P7 (left) and IRE P8 (right) under the conditions of 4 μM RNAs, 30 mM NaCl, 10 mM potassium phosphate, pH 7.0. Temperatures of both RNAs follow the legend on IRE P8.

Time-resolved fluorescence decay

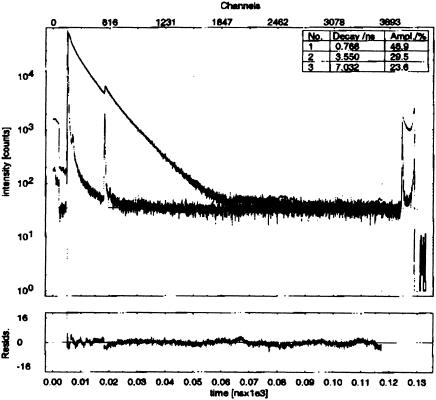
The isotropic fluorescence emission decay components of the IRE RNAs were also determined as a function of temperature (Fig. 4 ▶; Table 2 ▶). Addition of MgCl₂ to 2 mM did not alter the data. The decay curves of both molecules can be fit by three or, for IRE P7, by three or four exponentials. The fourth lifetime is short, from 62–85 psec. Simulations of the data, using as input the four lifetimes, the instrument IRF, and the time resolution of the experiment (32 psec/channel), indicate that this short component cannot be accurately defined. The fits to four exponentials are reported here for completeness, because it is probable that there is a short lifetime in the IRE P7 decay that we cannot accurately determine (Table 2 ▶).

FIGURE 4.

Time-resolved isotropic fluorescence decay curve of IRE P8 at 20°C. The glitch at 13 nsec is due to incomplete filtering of the n + 1 pulse by the pulse picker.

TABLE 2.

Isotropic fluorescence emission lifetimes of IRE P7 and P8 RNAs

T (C)	τ1 (ns)	%	τ2 (ns)	%	τ3 (ns)	%	τ4 (ns)	%	≤τ>ampl	χr2
IRE P7
5	0.36 ± 0.05	61 ± 5	3.4 ± 0.3	26 ± 1	9.1 ± 0.4	13 ± 2			2.28	2.4
20	0.34 ± 0.08	52 ± 7	2.6 ± 0.3	37 ± 2	7.7 ± 0.4	13 ± 2			2.08	2.2
35	0.28 ± 0.10	46 ± 7	2.0 ± 0.2	42 ± 3	6.3 ± 0.3	13 ± 2			1.79	2.0
5	0.085 ± 0.038	57 ± 22	0.72 ± 0.15	21 ± 3	4 ± 0.4	13 ± 2	9.5 ± 0.5	7 ± 1	1.44	1.4
20	0.067 ± 0.043	56 ± 36	0.74 ± 0.19	20 ± 2	3.2 ± 0.4	18 ± 2	8.1 ± 0.4	7 ± 1	1.31	1.4
35	0.062 ± 0.053	51 ± 44	0.69 ± 0.21	21 ± 3	2.4 ± 0.3	22 ± 3	6.6 ± 0.4	7 ± 1	1.14	1.5
IRE P8
5	0.91 ± 0.13	44 ± 5	3.7 ± 0.7	30 ± 3	8.7 ± 0.4	26 ± 5			3.81	2.2
20	0.72 ± 0.14	45 ± 5	3.2 ± 0.7	29 ± 3	7.0 ± 0.5	26 ± 6			3.10	2.4
35	0.17 ± 0.09	37 ± 22	1.4 ± 0.5	33 ± 6	5.0 ± 0.2	30 ± 3			2.02	2.6

Fraction (f_i) is the relative amplitude of the decay component. ≤τ>_ampl is amplitude weighted lifetime, defined as ∑α_iτ_i/∑α_i = ∑_if_iτ_i. Data were processed with FluoFit software (PicoQuant) and are averages of two experiments. Reduced χ_r² values for three fits reflect the poor fits at the rise of the decay (short components) as well as the fit of the data at the n + 1 pulse point in the decay.

The proportions of the decay components vary for the two RNAs. For IRE P8, there is a 25%–30% contribution of an 8.7 ± 0.4-nsec component (5°C) that becomes 5.0 ± 0.2 nsec at 35°C. In IRE P7, at 5°C, there is a 13% contribution of a 9.1 ± 0.4-nsec decay time, which becomes 6.3 ± 0.3 nsec at 35°C (using three exponential fits to the decays). This long lifetime is close to that of free 2AP (10–11 nsec at 20°C), suggesting that 2AP at P7 and P8 spends a varying proportion of its time unstacked in the IRE structures.

The shortest isotropic decay component of IRE P7 is measured as 360 ± 50 psec at 5°C, and 280 ± 100 psec at 35°C. It seems likely that this lifetime is an average of several decay times that are not resolved in the experiment. Fitting the data with four lifetimes produces an 85-psec component and a 720-psec component (5°C), which becomes 62 psec and 690 psec at 35°C (Table 2 ▶). The width of the instrument response function (191 psec) and the time resolution (32.5 psec/channel) limit the short components that can be reliably extracted from the fit, and certainly those <100 psec will have large errors on their amplitudes and lifetimes. A short lifetime is anticipated in the P7 decay, because when P7 is stacked over C6:G10 (even though this stacking is not canonical A-form geometry), stacking of the aromatic bases is sufficient to form an electronic “supermolecule” where electronic states of the bases are mixed. This construct will lead to very rapid fluorescence decay (τ) through charge transfer to the neighboring base (Wan et al. 2000; Jean and Hall 2001). Fluorescence emission decay components as short as 9–20 psec (Larsen et al. 2001) and 30–70 psec (Guest et al. 1991) have been measured for 2AP in a stacked conformation. The short lifetime in the four-exponential fit is likely to result from stacking; this component is certainly present in the ~300-psec component fit to the data. Other lifetimes ranging from 200–400 psec (Nordland et al. 1989) are also assumed to be present, but not resolved.

The shortest decay lifetime of IRE P8 at 5° and 20°C is two times longer than that of IRE P7. This difference is significant, and indicates that the conformation of 2AP at this position is unlikely to include a large fraction of a stacked state, because that state would lead to more rapid decay times. Instead, other geometries accessible to P8 could lead to nonradiative charge transfer to surrounding bases. At 35°C, the shortest lifetime of P8 is comparable to that of P7, which might be ascribed more frequent interactions of P8 with other bases due to the increased flexibility of the IRE loop.

2AP in both IRE molecules exhibits a third decay component ranging from 2–3 nsec. Again, this lifetime should be viewed as an average of unresolved lifetimes that arise from different structural contexts of the 2AP in the RNA. Possible scenarios include exchange between a stacked and unstacked conformation occurring on the nanosecond timescale (dynamic motion), or the opposite situation, in which 2AP is held proximal to another base in a geometry that allows only weak electronic interactions to occur between the two. In the canonical A-form stacked structure, electronic overlaps can be extensive (strong interactions); a weak interaction would arise if two bases are at a longer distance from each other, or have a relative orientation that reduces their shared π electron density.

One puzzling feature of the IRE P7 isotropic fluorescence data is its apparent lack of correlation of the amplitude-weighted average lifetime with the steady-state fluorescence intensity: The lifetime (τ) is proportional to the steady-state intensity (I_SS = ∞I₀e^−t/τdt = I₀τ; Lakowicz 1999). For IRE P8, the trend of decreasing steady-state fluorescence intensity with increased temperature is reflected in the respective values of τ_ampl. However, for IRE P7, this correspondence is lost. Because the steady-state and time-resolved measurements are made on the same sample during the course of the day, and because the steady-state fluorescence intensity at a given temperature is measured at the beginning and the end of the series of experiments, this discrepancy cannot be attributed to degradation of the RNA sample. The most likely explanation of the data is that the uncertainty in the lifetime and amplitude of the shortest component make calculation of τ_ampl unreliable.

Time-resolved fluorescence anisotropy

The components extracted from an anisotropy decay curve are generally considered to correspond to the global tumbling of the molecule and to any local dynamic motion of the fluorophore (Fleming 1986; Guest et al. 1991; Rachofsky et al. 2001b). To characterize the dynamic motions of 2AP in the IREs, the fluorescence emission anisotropy decay was measured as a function of temperature.

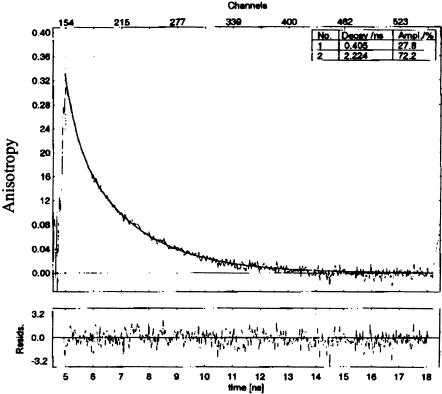
Anisotropy decay data from both molecules were fit by two components: a long component of 1–4 nsec and a shorter component ranging from 300–500 psec (Fig. 5 ▶; Table 3 ▶). The longest depolarization time is similar for the two RNAs, and so, by convention, might be attributed to the overall tumbling time of the molecule. There is a notable difference in the amplitudes of this long depolarization time for the two RNAs. In IRE P8, it comprises from 72%–87% of the total amplitude of the decay, whereas in IRE P7, it accounts for about 25% of the decay amplitude.

FIGURE 5.

Time-resolved anisotropy decay of IRE P8 at 20°C.

TABLE 3.

Fluorescence anisotropy decays of IRE P7 and P8 RNAs

Temp (C)	τr1 (ns)	r01	τr2 (ns)	r02	r(0)	χr2
IRE P7
5	0.53 ± 0.04	0.22 ± 0.01	3.2 ± 0.2	0.09 ± 0.005	0.31	1.3
20	0.40 ± 0.02	0.22 ± 0.01	1.9 ± 0.2	0.09 ± 0.004	0.31	1.25
35	0.36 ± 0.03	0.22 ± 0.01	1.4 ± 0.3	0.07 ± 0.007	0.29	1.26
IRE P8
5	0.35 ± 0.12	0.037 ± 0.005	3.5 ± 0.08	0.26 ± 0.01	0.29	1.14
20	0.41 ± 0.06	0.093 ± 0.006	2.2 ± 0.09	0.24 ± 0.01	0.33	1.05
35	0.31 ± 0.05	0.071 ± 0.003	1.3 ± 0.06	0.21 ± 0.01	0.28	1.61

τ_r1 are anisotropy times obtained from exponential fits of the anisotropy decay curves. r₀₁ are the fractional anisotropies of the components. Anisotropy decay times were fit using the equation r(t) = [r₀₁e^−t/τ1 + r₀₂e^−t/τ2]; r₀₁ = r(0)A₁, and so forth, where r(0) is the intrinsic anisotropy of the fluorophore and A_i is the anisotropy fraction of the ith component (r(0) = r₀₁ + r₀₂). Data were analyzed using FluoFit (PicoQuant).

The shorter depolarization decay is often attributed to local motion of the fluorophore on a timescale shorter than the global molecular tumbling time. Both RNAs show comparable short depolarization times, but again the difference between the two molecules lies in the relative proportion of these components. If this depolarization is attributed to motion of the 2AP base, then it would appear that it has more flexibility in the IRE P7 molecule. However, another mechanism that could give rise to fluorescence depolarization is the fluctuations of the transition dipole as 2AP moves relative to a proximal base. Stacked bases give rise to mixing of ground or excited electronic states of the fluorophore, and the resulting charge transfer character tilts the transition dipole moment out of the plane of the 2AP base. Motions of the two bases relative to each other will also move the transition dipole moment within the supermolecule assembly, leading to rapid depolarization. This mechanism would dominate in the IRE P7 molecule. Again, however, a caveat with these fits of the data is that the two times extracted from the curves are likely to consist of a weighted sum of motions on several timescales, which cannot be resolved in these experiments.

Table 3 ▶ gives the anisotropy decay times (τ_i) and their corresponding fractional anisotropies (r_0i). The sum of the amplitudes equals the apparent r₀ anisotropy value, which here varies from 0.29 to 0.33; the theoretical maximum value of r₀ for free 2AP is 0.4. Larsen et al. (2001) attribute similar r₀ values observed in 2AP-DNA experiments to solvent relaxation, but based on electronic structure calculations (Jean and Hall 2001,Jean and Hall 2002), interactions with other bases could lead to very rapid depolarization that lower the apparent initial value.

Stochastic dynamics simulations

Fluorescence data suggest that there is considerable motion of the A7 and G8 loop nucleotides. The spectroscopic data do not give a physical description of the motions, however, and to obtain some insight into what types of motions are allowed in the IRE loop, several stochastic dynamics simulations were run. Three 13-nsec simulations are analyzed here to provide visualization of the loop conformations as a function of time. The rapid timescales of base motion suggested by fluorescence measurements should be represented here, because in a 13-nsec simulation, motions that occur on timescales of ≤1 nsec will be efficiently sampled. The timescales of motions and the allowed motions of the IRE might be exaggerated in these stochastic dynamic simulations, given the choice of viscosity (frictional coefficient γ = 5 psec⁻¹) and the absence of explicit solvent (Zagrovic and Pande 2003). These data could be viewed as the upper limit of possible motions in the RNA.

Three different starting structures for the simulations were selected, consistent with NMR data. They are referred to as the Unstacked (Uns) structure, in which the G8 base is not stacked on the A7 base; the Stacked structure, where G8 is stacked on A7; and the Syn structure, in which the G8 base adopts the syn orientation. These initial starting structures are also consistent with the time-resolved fluorescence anisotropy data that suggest that G8 and A7 adopt both stacked and unstacked positions in the loop.

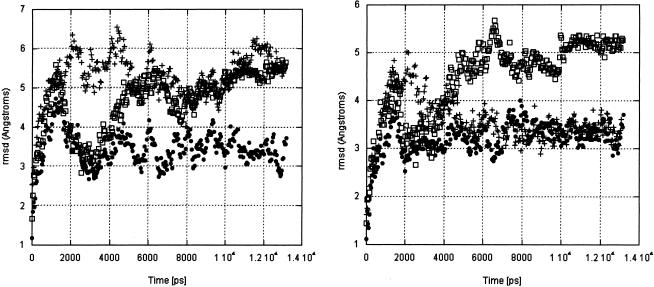
During the course of the simulations, the IRE structures move away from their starting conformations (Fig. 6 ▶, left panel; Table 4 ▶). In the Uns and Syn simulations, the structures converge to an average structure (although not to a common structure; see Table 4 ▶); the Stacked simulation is anomalous, for it has not converged. A significant portion of the root mean square deviation (rmsd) change with time comes from the stem (Fig. 6 ▶, right panel), and is due to fraying of the first base pair. (NMR data show that the first 3 bp of the stem fray in solution.) The behavior of the stem will not be discussed further, because our focus is on the loop. The behavior of the Stacked simulation makes it a less reliable representation of allowed structural variations, so we will discuss the other simulations in more detail.

FIGURE 6.

Rmsd (Å) of UNS (solid circles), Sta (open squares), and Syn (+) simulations, calculated from their starting structures. (Left) The entire IRE. (Right) Nucleotides G4–C13.

TABLE 4.

Rmsd summary for three 13-ns GB/SA simulations

Uns starting		Syn starting		Sta starting
Alla	G4-C13b	Alla	G4-C13b	Alla	G4-C13b
3.43 Å	3.20 Å	5.31 Å	3.56 Å	4.64 Å	4.44 Å

Uns averagec	Syn averagec	Uns/Syn averaged	Sta averagec
Self G4-C13	self G4-C13	cross G4-C13	self G4-C13
aRmsd (root mean square deviation) from the starting NMR structure for all residues.
bRmsd from the starting NMR structure for the loop residues and two uppermost stem base pairs.
cRmsd about the average simulation structure for the residues G4 to C13.
dRmsd of snapshots of the uns simulation about the syn simulation average structure.
2.62 Å	2.79 Å	3.71 Å	3.97 Å

Two structural parameters are the most convenient to describe dynamic motions of the nucleotides: the glycosidic angle, χ, between the base and ribose that moves from anti to syn, and the pseudorotation angle (P) of the ribose, which can vary over a range of configurations, but here we summarize as C2′-endo or C3′-endo pucker. Data are represented in plots of angle versus time; the angles are signed (for example, 0 to +180/−180 to 0) rather than 0 to 360, so that C3′-endo puckers have pseudorotation angles from 0°–36°, and C2′-endo puckers have P = 145–190° (meaning that it will appear as a negative 180 angle in some plots). Glycosidic angles vary from syn at ~50° to anti at −150° (with high anti at −80°). The average values of χ and P from the three simulations are summarized in Table 5 ▶.

TABLE 5.

Chi and pseudorotation dihedral angles for the residues of three stochastic dynamics simulations of the IRE: average plus standard deviation

	Uns χa	Sta χb	Syn χc	Uns Pa	Sta Pb	Syn Pc
G1	−171 ± 11	36 ± 99	150 ± 80	14 ± 16	16 ± 21	11 ± 32
A2	−158 ± 9	−143 ± 86	−157 ± 21	18 ± 11	23 ± 22	12 ± 15
A3	−153 ± 11	−171 ± 17	−160 ± 53	20 ± 13	5 ± 17	13 ± 36
G4	−158 ± 12	−168 ± 13	−165 ± 12	19 ± 13	8 ± 18	23 ± 15
A5	−149 ± 12	−162 ± 10	−159 ± 12	21 ± 12	12 ± 13	14 ± 12
C6	−132 ± 20	−155 ± 11	−160 ± 13	28 ± 17	27 ± 13	17 ± 14
A7	−126 ± 21	60 ± 78	173 ± 15	10 ± 17	27 ± 22	13 ± 24
G8	54 ± 49	−167 ± 22	34 ± 19	58 ± 58	140 ± 30	166 ± 13
U9	−115 ± 39	37 ± 41	−131 ± 18	163 ± 21	51 ± 23	118 ± 56
G10	−78 ± 20	−25 ± 63	−141 ± 16	−49 ± 72	153 ± 43	39 ± 34
C11	−124 ± 24	−133 ± 105	−138 ± 21	144 ± 23	54 ± 41	151 ± 16
U12	−160 ± 10	−161 ± 12	−156 ± 11	20 ± 15	20 ± 18	46 ± 16
C13	−149 ± 12	−146 ± 15	−155 ± 16	21 ± 11	25 ± 13	25 ± 15
U14	−148 ± 18	−145 ± 13	−145 ± 18	29 ± 41	27 ± 12	27 ± 16
U15	−109 ± 25	−145 ± 14	−118 ± 82	143 ± 52	25 ± 15	156 ± 28
C16	−114 ± 26	−128 ± 18	−141 ± 22	96 ± 49	59 ± 55	119 ± 37

^aA 13.20-ns (unstacked) GB/SA simulation.

^bA 13.16-ns (stacked) GB/SA simulation.

^cA 13.08-ns (syn) GB/SA simulation.

U9 and C11

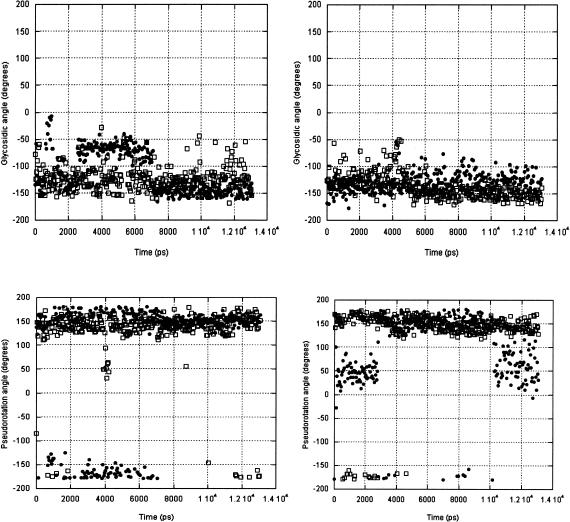
Of the nucleotides in the loop, the motions of pyrimidines U9 and C11 are of interest because NMR structural data could not constrain these bases by NOEs. The Uns and Syn simulations show that their average χ structure is anti, and their ribose puckers hover about C2′-endo (Fig. 7 ▶), although the U9 ribose does repucker in the Syn simulation. The U9 nucleotide facilitates the turn of the loop, whereas the C11 base is extruded from the loop structure by the base pair formed by C6:G10. Their positions in the IRE loop do appear to provide some constraints to their allowed conformations, although the standard deviations from the average angular value indicate that these nucleotide structures are not as constrained as those in the stem.

FIGURE 7.

U9 (solid circles) and C11 (open squares) glycosidic angles and pseudorotations calculated in 50-psec shapshots from the Uns (left) and Syn (right) simulations.

C6:G10

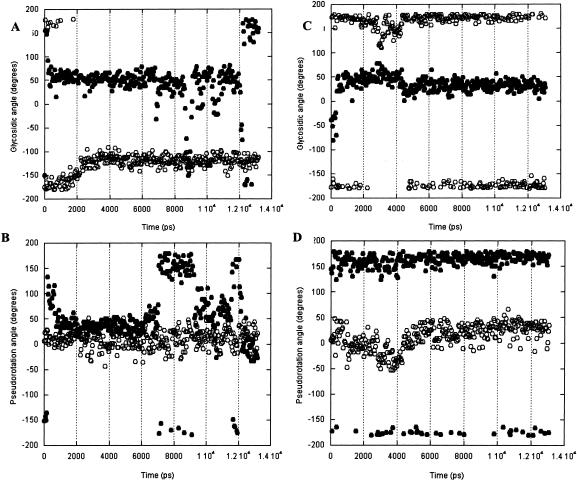
This base pair is responsible for the stability of the IRE hairpin, because it forms the central core upon which other bases are arranged. The C6:G10 pairing is stable in the Uns simulation, as shown by the intramolecular hydrogen bond statistics of the C₆:O₂•••H-N₂:G₁₀ (imino), C₆:N₃•••H-N₁:G₁₀ (amino) and C₆:N₄-H•••O₆:G₁₀ (Table 6 ▶). The two former hydrogen bond pairs have a frequency of 0.97–0.92, and the third an average frequency of 0.74. These frequencies are comparable to those of the most stable base pair in the IRE stem. In the Syn simulation, these frequencies drop to 0.71/0.7/0.0, respectively, indicating that the base-pair geometry is not equivalent, nor as stable. By comparison, the first base pair in the stem (G₁:C₁₆) frays in all simulations, and its hydrogen bond occupancy ranges from 0.170–0.595. During the Syn simulation, the C6 and G10 glycosidic angles remain anti, whereas the sugar puckers remain C3′-endo following an initial (750 psec) residence of the G10 ribose in the C2′-endo conformation. The Uns simulation shows more dynamic behavior of the G10 ribose: Even as the C6 ribose remains C3′-endo, the G10 ribose samples various puckers with time steps as short as 50 psec (snapshots were saved every 50 psec). While the G10 ribose is repuckering, its glycosidic angle moves only from anti to high anti (Fig. 8 ▶). There is no correlation between ribose repuckering and base motions for this nucleotide.

TABLE 6.

Intramolecular hydrogen bond geometry

Hydrogen bond	〈Freq.〉	〈RDA〉 (Å)	〈δRDA2〉1/2 (Å)	〈θDHA〉 (deg.)	〈δθDHA2〉1/2 (deg.)
G1:N2−H•••O2:C16	0.193a	4.117	0.845	127.628	18.274
	0.170b	6.040	2.141	99.904	37.593
	0.595c	5.888	4.294	122.945	45.607
G1:N1−H•••N3:C16	0.178	4.401	0.781	137.727	15.349
	0.258	4.499	1.111	112.019	37.948
	0.567	5.928	4.062	125.122	51.086
G1:O6•••H−N4:C16	0.160	4.986	0.953	121.843	19.361
	0.355	4.155	1.108	132.694	23.518
	0.396	6.384	4.358	115.917	46.053
A2N1•••H−N3:U15	0.819	3.206	0.372	147.340	20.071
	0.294	8.817	5.735	114.946	32.735
	0.604	4.856	2.899	125.767	46.137
A2:N6−H•••O4:U15	0.538	3.384	0.391	134.411	17.066
	0.261	8.178	5.449	101.255	45.332
	0.274	5.447	2.582	130.715	40.542
A3N1•••H−N3:U14	0.918	3.165	0.672	157.015	14.928
	0.539	3.859	0.956	140.074	26.603
	0.409	6.369	3.821	119.801	36.709
A3:N6−H•••O4:U14	0.722	3.471	1.025	158.151	15.271
	0.779	3.171	0.507	152.267	19.696
	0.348	7.092	4.174	130.983	38.438
G4:N2−H•••O2:C13	0.903	3.079	0.537	158.728	15.630
	0.900	3.042	0.401	157.923	16.452
	0.948	3.041	0.446	162.073	13.488
G4:N1−H•••N3:C13	0.897	3.167	0.491	159.362	14.877
	0.824	3.165	0.417	155.623	17.987
	0.939	3.147	0.394	162.626	12.258
G4O6•••H−N4:C13	0.828	3.221	0.531	154.482	21.594
	0.733	3.444	0.825	152.194	19.534
	0.866	3.192	0.448	157.497	18.570
A5N1•••H−N3:U12	0.973	3.065	0.187	161.816	10.282
	0.924	3.132	0.311	159.219	13.381
	0.820	3.286	0.630	155.458	15.331
A5:N6−H•••O4:U12	0.894	3.147	0.354	160.977	10.492
	0.652	3.325	0.629	144.369	23.951
	0.378	3.965	1.170	146.079	19.003
C6:O2•••H−N2:G10	0.973	2.922	0.182	156.135	13.778
	0.970	2.944	0.212	155.882	13.696
	0.713	3.193	0.519	150.226	22.583
C6:N3•••H−N1:G10	0.918	3.108	0.295	159.565	10.985
	0.945	3.054	0.200	160.517	11.472
	0.698	3.457	0.716	155.829	14.693
C6N4−H•••O6:G10	0.743	3.304	0.559	143.987	22.637
	0.845	3.147	0.329	153.694	19.836
	0.000	6.916	1.276	125.601	18.493

^aA 13.20-ns (unstacked) GB/SA simulation.

^bA 13.16-ns (stacked) GB/SA simulation.

^cA 13.08-ns (syn) GB/SA simulation. Normalized hydrogen bond frequencies (i.e., donor-acceptor distance less than 3.5 Å and donor-hydrogen-acceptor angle greater than 120°).

FIGURE 8.

C6 (solid circles) and G10 (open squares) glycosidic angles and pseudorotations calculated in 50-psec snapshots from the Uns (left) and Syn (right) simulations.

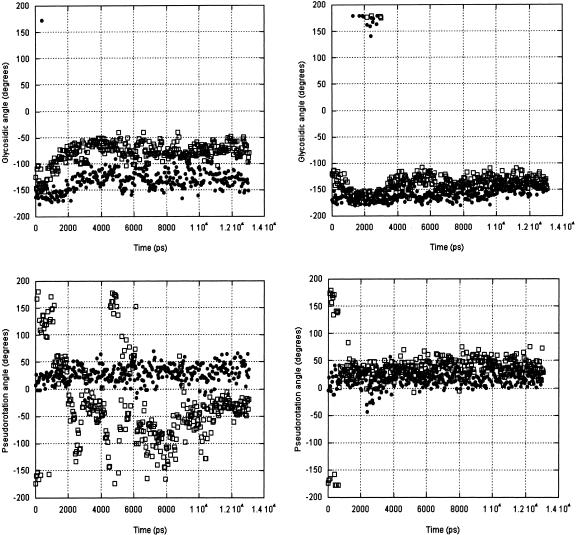
A7 and G8

These nucleotides were replaced by 2-aminopurine for fluorescence experiments, so it was of particular interest to see what conformations could be accessed by these 2 nt in the simulations. The details of their motions are shown in Figure 9 ▶.

FIGURE 9.

A7 (open circles) and G8 (solid circles) glycosidic angles and pseudorotations calculated in 50-psec snapshots from the Uns (A, B) and Syn (C, D) simulations.

It is immediately apparent that A7 and G8 base and ribose conformations can be considered independently on this timescale; these adjacent nucleotides do not experience correlated motions, and neither do the sugar and base of a given nucleotide move in concert. Nucleotide A7 has the more stable conformation of the 2 nt. The ribose of A7 maintains a constant C3′-endo pucker, and in the Uns and Syn simulations, the nucleotide retains the anti or high anti glycosidic angle.

In the Uns simulation, the G8 ribose repuckers, moving in <500 psec from its starting C2′-endo pucker to C3′-endo, where it resides for 6 nsec before switching back to C2′-endo for 2 nsec, then rapidly moving from one to the other pucker. At the same time, the glycosidic angle remains syn, making several short (100–500 psec) excursions to anti. In the Syn simulation, the G8 ribose remains in the C2′-endo pucker, while the glycosidic angle remains syn.

DISCUSSION

This combination of fluorescence and simulation data gives a more complete description of the dynamics of the IRE loop structure. Two parameters to be extracted from the fluorescence experiments are an estimate of the number of conformations adopted by the nucleotides in the loop and the timescales of their motions. This information is compared to the physical description of the base orientation in the loop and the time associated with the conformational changes they undergo, as observed in the simulations. The conclusion is that motions are complicated, for there appears to be independent motion of most bases, and riboses repucker within the shortest time step of the simulations.

What is particularly striking is the different behavior of the A7 and G8 bases as reported by the fluorescence data. These bases are nearest neighbors in the loop, yet they undergo completely different motions and inhabit different electronic environments. As a consequence, 2AP in each position exhibits a unique and complex spectroscopic signature, illustrating the utility of this fluorophore as a probe of RNA structure and dynamics in noncanonical elements.

2AP in IRE position A7

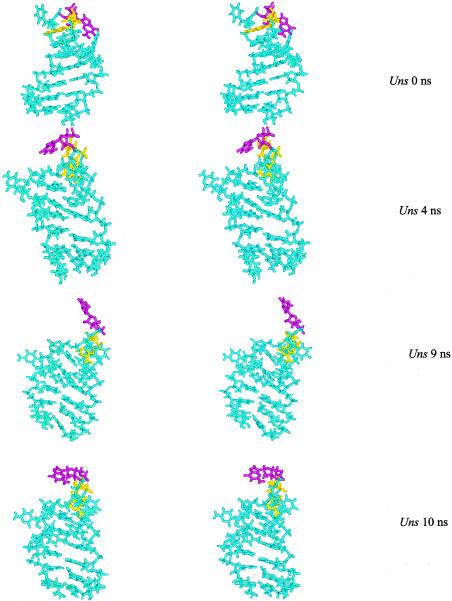
NMR data show that this base is stacked over the 5′C6 base. Although A7 appears to spend a majority of its time in a stacked conformation (although not a canonical A-form structure), the fluorescence data and the simulations show that it can move away from this position (Fig. 10 ▶).

FIGURE 10.

Stereo snapshots of the IRE structure, highlighting A7 (yellow) and G8 (magenta) from the Uns simulation at t = 0, t = 4 nsec, t = 9 nsec, and t = 10 nsec. Figure constructed in MolMol.

Steady-state fluorescence emission intensity of 2AP at P7 is significantly quenched, and the fluorescence emission decay lifetimes of IRE P7 include one short component that accounts for about 50% of the isotropic decay; these properties are consistent with a stacked conformation. The reported value of this short isotropic decay component (60–80 psec and/or 300–400 psec) is a composite of several lifetimes. The short isotropic decay lifetimes undoubtedly arise from formation of the supermolecule state when 2AP is stacked with C6. 2AP is predicted to undergo excited electronic state mixing with pyrimidines stacked on its 5′ side, leading to formation of a lower-lying “dark” charge-transfer state (Jean and Hall 2001). Nonradiative decay from the normal 2AP excited state to this dark state will result in the observation of a short lifetime.

The presence of long isotropic decay lifetimes indicates that 2AP in IRE P7 also spends a fraction of its time in a conformation where stacking is minimal. Of the two longer isotropic decay lifetimes of 2AP at A7, one is comparable to free 2AP; this 9.1-nsec decay time represents only 13% of the total amplitude and so the unstacked state of P7 is not its dominant configuration. There is another isotropic decay component at about 3 nsec. Together, these longer components comprise about 50% of the isotropic decay amplitude.

Simulation data illustrate that A7 remains within the loop structure, even though its orientation with respect to other nucleotides varies with time. It is likely that P7 moves in and out of a stacked conformation: If these motions are rapid but infrequent, then the fluorescence lifetime could be longer than in a purely stacked conformation but shorter than that of free 2AP.

Most (70%) of the anisotropy decay of P7 is rapid (390 psec). The usual physical explanation for such depolarization is small amplitude, rapid motions of the base that occur on a timescale faster than the overall global tumbling time of the molecule. As the simulations show, there is only a small variation in the average glycosidic angle of A7 in the loop (−126° ± 21° in the Uns simulation, and 173° ± 15° in the Syn simulation), which is comparable to base motion in duplex regions. These rapid motions could account in part for the rapid depolarization observed, as noted by Larsen et al. (2001) in their calculations of the changes in the geometry of the excitation and emission dipoles on the timescale of the depolarization experiments. However, we propose that excited electronic state mixing of the stacked bases could also lead to rapid depolarization of emitted fluorescence. The 2AP transition dipole moment reorients in the supermolecule (Jean and Hall 2001), tilting out of the plane of the base. Small local motions of 2AP within the supermolecule assembly could exaggerate changes in the direction of the transition dipole moment, leading to more rapid depolarization of fluorescence.

The long anisotropy decay component (1.7 nsec at 20°C) contributes about 30% of the amplitude of the decay curve. This anisotropy decay would conventionally be interpreted as the overall correlation time of the IRE. Here, where the IRE loop has considerable flexibility, other motions of the entire loop structure, such as loop bending, twisting, and global reorganization, could also contribute to this longer correlation time. Another problem with the interpretation of this value as the overall correlation time of the RNA is that the fluorescence data do not agree with the correlation time of the IRE RNA calculated from NMR relaxation experiments, which give an overall correlation time (global tumbling time, τ_c) of the IRE at 20°C of 3.45 nsec (Hall and Tang 1998; those NMR relaxation data simply could not be fit with a value of τ_c of 1.7 nsec). Given the time resolution of the anisotropy decay experiments, and the subsequent calculation of the difference between the parallel and perpendicular polarization curves, if two anisotropy times were present that differed by a factor of two (for example, 1.7 and 3.4 nsec), it is unlikely that they could be extracted from the data (Lakowicz 1999). We therefore interpret the long anisotropy time as a weighted sum of several dynamic motions, one of which is the global tumbling time of the molecule.

2AP in IRE position G8

This base and ribose have the greatest conformational flexibility of all the loop nucleotides. The G8 glycosidic angle varies from 54° ± 49° in the Uns simulation, moving between anti/syn on timescales from picoseconds to nanoseconds. In the Syn simulation, its excursions are smaller, as it hovers around syn. The G8 ribose fluctuates between C3′-endo and C2′-endo configurations in the Uns simulation; it remains in C2′-endo for the Syn simulation. NMR structural data show that the G8 ribose is best described as a mixture of these two conformations, as it appears to rapidly interconvert. Those NMR data are consistent with the data from the Uns simulation; snapshots are shown in Figure 10 ▶.

All fluorescence data for IRE P8 indicate that 2AP at this position is predominantly unstacked, but there are several conformations of the base, as it exhibits three isotropic fluorescence decay components. One of those decay components has a 7-nsec lifetime, similar to that of free 2AP. The moderate quenching of P8 steady-state fluorescence emission intensity also indicates that this base spends some of its time free of interactions with other bases. In its unstacked state, P8 could be rigidly held within the loop structure, and/or be free to rotate about its glycosidic bond. These behaviors would lead to different fluorescence properties that could allow the discrimination of these dynamics.

P8 could be able to reorient freely within the context of the IRE loop, moving about its glycosidic bond or in response to changes in the torsions of the phosphate backbone. Such rapid and unconstrained motions would mimic free 2AP in solution, which has a 10–11-nsec isotropic decay. Indeed, P8 exhibits 25% amplitude of a 7-nsec lifetime at 20°C. Free 2AP has a very rapid depolarization time (30–70 psec; Nordland et al. 1989), because it is a small molecule that tumbles freely in solution. The most rapid depolarization component of P8 is 300–400 psec, which comprises from 13% (5°C) to 25% (35°C) of the total anisotropy amplitude. Even assuming that this depolarization time contains very rapid components that cannot be resolved, these data suggest that P8 is in fact not freely rotating in the IRE loop.

If P8 is rigidly held or undergoes restricted dynamic motion when it is unstacked, then its isotropic and anisotropic lifetimes will depend on its environment. For example, if P8 were to spend some time stacked with another base, then its isotropic emission would have a short τ_i component, as would its anisotropy decay (due to mixing of the electronic states of the proximal bases). If P8 were rigidly held in the IRE loop, separated from interactions with other bases, then its fluorescence depolarization would have a long component due to the overall tumbling time of the RNA molecule. Indeed, the dominant contribution to P8 fluorescence depolarization does come from a 1.3 to 3.5-nsec component (from 75%–90% of the anisotropy decay), which undoubtedly represents a weighted sum of several decay times. We therefore describe the dynamics of this base as undergoing motions on the nanosecond timescale, with few opportunities for interactions with other bases.

Simulations show that when G8 is unstacked, it exhibits a range of motions that the coarse statistics reported here from the simulations do not adequately represent. An examination of the IRE structures pulled from the Uns simulation shows that, although the glycosidic bond is primarily syn, the amplitudes of the base excursions about the loop structure are large (Fig. 10 ▶). The specific snapshots shown are chosen to report on conformational transitions during the simulation: t = 0 is the starting conformation, where G8 has an anti glycosidic angle, and a C3′-endo ribose pucker; at t = 4 nsec, the G8 base has changed to the syn orientation, and its ribose is now C2′-endo; at t = 9 nsec, the sugar is again C3′-endo and χ is in transition between syn/anti; at 10 nsec, both base and ribose are in transition between their two major conformations. What is clear from the snapshots is that not only is there motion of the G8 nucleotide, but there are large-scale deformations of the entire IRE loop.

The IRE loop structure and dynamics

Simulation data indicate that motions of the A7 and G8 nucleotides occur in the background of an RNA loop that is itself undergoing global conformational changes. In solution, these global loop motions could occur on timescales from nanoseconds to milliseconds, and be coupled to the motions of each base or independent of them.

Previous NMR ¹³C relaxation data (Hall and Tang 1998) also probed the motions of the bases and riboses in the IRE. Those data are best discussed in terms of the order parameter, S², which describes the spatial distribution of rapid (picosecond to nanosecond) internal motions of the specific ¹³C-¹H vector (using the Lipari and Szabo [1982] model free formalism). Completely unrestricted motion of the vector would have S² = 0, whereas a vector held rigid in the molecular frame would have S² = 1. Because the base ¹³C-¹H vectors used in the NMR experiments are fixed by sp² geometry in the plane of the aromatic purine base, the motion reported is that of the base itself. Values of S² for each purine base in the RNA were calculated from the data as a function of temperature. The results showed that at 20°C, where the structure was solved, purine bases in the stem and the loop had order parameter of about 0.78. At 37°C, there was a significant difference in the value of the order parameters for those bases in the stem (0.8) and those in the loop (0.6). Those data were interpreted to indicate that the loop structure had become more flexible at the higher temperature (which is far below the melting temperature of 65°C). Subsequent experiments to probe ribose dynamics (using ¹³C_1′-¹H_1′ spin pairs) showed that at 20°C, the order parameter of the G8 ribose was very low (S² = 0.6), whereas others in the stem and loop were near 0.8 (data not shown). A striking feature of the NMR relaxation results is the independence of ribose repuckering and rotation about χ: At 20°C, the G8 ¹³C₈ nucleus has an order parameter of 0.8, but its ¹³C_1′ has S² = 0.6 (data not shown). At 37°C, the order parameters of C6, A7, G8, G10, and C11 riboses were lower than those of the flanking base-paired A5 and C13, suggestive of a global loop flexibility (there were no NMR data on uridine nucleotides).

To quantitatively model the base motions about the glycosidic bond, their standard deviation of rotation about χ was calculated using the Gaussian axial fluctuation model (Bruschweiler and Wright 1994), which is a variant of the wobbling in a cone model. As expected, a larger angle was explored by those bases with a smaller order parameter (Hall and Tang 1998). However, the fluorescence data and simulations reported here illustrate the fallacy of this simple application, for it is apparent that not only is the base moving in the molecular frame, but the IRE loop itself is adopting new conformations. As Figure 10 ▶ illustrates, base motions cannot be described as wobbling in a cone.

We can propose one possible description of the motion of the G8 nucleotide in the IRE. Fluorescence data indicate that the base is most often exposed to solution and unstacked. NMR data suggest that its ribose is rapidly interconverting between conformations on the picosecond to nanosecond timescale. Snapshots from the Uns simulation are consistent with this picture. However, fluorescence anisotropy data show that the base is not undergoing rapid reorientation in the context of the RNA. Together, these data are consistent with a picture in which the G8 base is stiffly held away from other bases whereas the A7 base is stacked with an adjacent base; motions occur in torsion angles of the phosphate backbone throughout the loop.

The timescale of the motions of the IRE loop is not completely described. These experiments and analyses describe rapid (picosecond to nanosecond) motions of individual nucleotides that are assumed to undergo uncorrelated motions. That assumption is an approximation, and it can be addressed by an examination of the simulations (Prompers and Bruschweiler 2001). In addition, it is possible that motions on the microsecond to millisecond timescale are also present in the IRE loop, either as local motions or as correlated motions that involve the entire loop structure. The presence of slower motions is also important to characterize, for they could retard protein binding if a protein:RNA collision occurs at a time when the RNA structure is not optimized for recognition. Alternatively, slow global conformational changes could facilitate protein binding if multiple states present suitable target sites to the protein.

MATERIALS AND METHODS

All RNAs were purchased from Dharmacon. They were HPLC purified, desalted on a 50-mL G25 column, and lyophilized. For NMR and fluorescence measurements, the solutions contained 30 mM NaCl, 10 mM potassium phosphate (pH 7). NMR data were acquired on a 500-MHz Varian spectrometer with a Nalorac triple resonance microprobe, using 1 mM RNAs. For observation of imino protons, solutions contained 90% H₂O/10%D₂O. Proton TOCSY experiments were done in 100% D₂O. Melting experiments were carried out in a Gilford 260 spectrometer equipped with a Peltier heating block; heating proceeded at a rate of 1°C/min. RNA concentrations varied from 10⁻⁴ to 10⁻⁶ M in 10 mM sodium cacodylate (pH 7), 0.5 mM EDTA. All hairpin melts were reversible. The spectrophotometer was interfaced to a PC for data collection; data were processed with Conlin (Williams and Hall 2000).

Steady-state fluorescence data were collected with a PTI fluorometer, using a temperature-calibrated water bath for heating and cooling. Excitation and emission spectral slit widths were 2 nm. Data were processed using PTI software. Time-resolved fluorescence data were acquired with a home-built time-correlated single photon counting (TCSPC) instrument (www.biochem.wustl.edu/~stump/TCSPC_05-2003.htm). The 75.7 MHz repetition rate of the Ti-Sapphire laser was reduced 10× with a NEOS pulse picker. The 900-nm-wavelength Ti-Sapphire laser output was tripled to 300 nm with an UOplaz tripler. With 300 nm incident light, the instrument response function of the photomultiplier tube was typically 190 psec FWHM. Isotropic emission decay curves were accumulated to ~65,000 (2¹⁶) counts in the peak channel. Fluorescence decay data were processed with FluoFit (PicoQuant). Isotropic decay data were fit with from two to four exponentials; the best fit was judged by the shape of the support planes and the reduced χ² values; precedence was given to the support plane analysis for judging goodness of fit. It was usually the case that using four exponentials produced a smaller reduced χ², but invariably, the added lifetime was short (22–70 psec); support planes for the amplitude and numerical value of this component were often unbounded. Given that the resolution of the experimental data is 32.5 psec/channel, even if such a short component were present, it would not be accurately determined by the experiment, considering also that the instrument response function had a 190-psec width.

Anisotropy decays for the parallel and perpendicular components were collected for a time determined by the count rate of the I_||(t) sample orientation. Anisotropy decay curves were calculated using the equation r(t) = [VV(t) − G*VH(t)]/[VV(t) + 2 G*VH(t)], and were fit by exponential models. The G factor was determined by tail matching of the VV and VH curves using FluoFit (PicoQuant) software; for our instrument, G = 0.997–1.004.

Simulations

The stacked and unstacked starting structures are representative RNA hairpins from the corresponding NMR families (Laing and Hall 1996). A representative NMR structure from the work of Pardi and colleagues containing the A[CAGUGC]U motif (Addess et al. 1997) served as the starting point for the Syn stochastic dynamics simulation. The stem was shortened in SYBYL (SYBYL 1995) and its sequence changed to match that used in structures determined by Laing and Hall (1996). Fifteen sodium counterions were placed using MacroModel V5.5, the structures minimized for 1500 steps, and simulations carried out using the Batchmin V5.5 molecular modeling protein (Mohamadi et al. 1990; Guarnieri and Still 1994). The Uns, Sta, and Syn simulations were run for 13.20, 13.16, and 13.08 nsec, respectively. Counterions were restrained to a spherical volume (radius approximately 25 Å) about the RNA hairpins using flat-bottom restraint wells. The equilibrium positions were 12 Å from the center of mass of the molecules, the half-width of the flat bottom well was 13 Å, and the force constant was 100 kJ/Ų. All simulations were carried out at a nominal temperature of 295 K, with a 1-fsec time step, 0.1-psec time constant (frictional coefficient γ of 5 psec⁻¹) and SHAKE (Ryckaert et al. 1997) applied to all bonds involving hydrogen atoms (X-H). Nonbonded cutoff distances were set at 1000 (infinite cutoffs) and the entire pair list was used in the evaluation of nonbonded interactions at every time step. The AMBER94 forcefield (Cornell et al. 1995) was used in all calculations with the GB/SA continuum model (Still et al. 1990). All bonded and nonbonded terms are identical to the original Cornell et al. force field. For the GB/SA model, solvent polarization and surface area derivatives were updated every 10 and 50 time steps, respectively. Analytical approximations for the Born radius and surface area implemented in Batchmin allow calculation of all relevant first and second derivatives for the solvent polarization and surface area contributions (Qui et al. 1997). The average and instantaneous temperature, kinetic energy, and potential energy were monitored over the course of the simulation and molecular snapshots were saved every 50 psec. All further simulation properties were derived from analyses of these snapshots. Pairwise mass weighted rmsd of structures were calculated using the SUPERPOSE routine in TINKER (Dudek and Ponder 1995). The rmsd value from the NMR structure was calculated by averaging the mass-weighted rmsd of each snapshot from the initial NMR structure. The self-rmsd was calculated in a similar fashion except that in place of the NMR structure, the average structure of the given simulation was used as reference. Cross rmsd refers to the mass-weighted rmsd between snapshots of one simulation and the unminimized average structures from a different simulation. Cross rmsd comparisons for the GB/SA simulation of the unstacked and syn structures are computed for RNA heavy atoms (hydrogens and counterions not included) and are reported for residues G₄ through C₁₃ only (G₄A₅[C₆A₇G₈U₉G₁₀C₁₁]U₁₂C₁₃). Simulations were run on a 12 processor R10000 SGI at the Center for Computational Biology at Washington University.