BayesFold: Rational 2° folds that combine thermodynamic, covariation, and chemical data for aligned RNA sequences

Abstract

BayesFold is a Web application that folds an alignment of closely related sequences and evaluates hypotheses about their shared structure. It uses Bayes’s Theorem to combine information from several sources, including chemical mapping (if available), thermodynamic folding, and observed sequence variations. Its method provides a rational basis for integrating results, even when these methods conflict. On a gapped alignment of 86 tRNA^Phe sequences each 77 bases long, BayesFold takes 31 sec to perform the calculations; the best structure contained 95% of the base pairs in the true structure, and the true structure was ranked second. Notably, similar results come from random samples of only 10 sequences from the alignment (running time 3 sec), suggesting that remarkably few sequences are required for good results. In contrast, folding single sequences with BayesFold produced structures 9.6 bp different, or with the Vienna package, 13.4 bp different, from the true structure . Similar results were obtained for other families of tRNAs. We especially recommend BayesFold for alignments of 3–50 closely related sequences, such as the sequence families frequently found in SELEX. In addition to providing a convenient way to explore the effects of each of the criteria on the plausibility of different structures, BayesFold also makes it easy to produce publication-quality secondary-structure graphics. The Web interface, available at http://bayes.colorado.edu/fold/, includes the flexibility to thread any of the sequences (or the consensus sequence) through any of the structures, including the one judged most probable.

INTRODUCTION

Finding the common structure for an RNA sequence alignment has been difficult, especially when combining statistical predictions from several methods. Methods that fold individual sequences often disagree for similar sequences even when the true structure (although unknown) must be the same. Methods that use the alignment itself often require inconveniently large numbers of sequences. Here we present a way to integrate information from chemical mapping, thermodynamic folding, and sequence variations to find the best overall structure for aligned sequences. Our program, BayesFold, provides a user-friendly environment for exploring candidate structures, and uses Bayes’s Theorem to calculate the relative plausibility of each structure when different types of information are taken into account. BayesFold thus addresses a common complaint about existing RNA packages (whether they deal with a single sequence or with an alignment), which is that the results are often difficult to compare or interpret. BayesFold also provides publication-quality figures without extensive redrawing in a graphics program.

Several existing programs combine multiple types of data to estimate the best secondary structure for a sequence alignment. For example, AliFold (Hofacker et al. 2002) allows users to select weightings for contributions from thermodynamics and from mutual information (based on sequence variations in an alignment). The Maximum Weighted Matching technique (Tabaska et al. 1998) also implemented in Circles (unpublished, but available at http://taxonomy.zoology.gla.ac.uk/rod/circles/) in principle allows any type of data to be incorporated. However, these techniques require users to make arbitrary choices about the weight given to different sources of information. Another approach is to use thermodynamic folding directly on two sequences at once, as in DynAlign (Mathews and Turner 2002), but this approach is very slow and does not take all the information from the alignment into account. FoldAlign (Gorodkin et al. 2001) uses a combination of thermodynamic and covariation data to find short regions of similarity in unaligned sequences, but its generality makes it very slow for longer alignments of sequences that are globally identical. Additionally, FoldAlign only finds one stem–loop structure, thus finding multiple stem–loops in the tRNA cloverleaf structure, for example, is not possible. FoldAlign also requires users to enter parameters such as the maximum motif length, which are often not known in advance. Thus, FoldAlign is not suitable for finding the global structure of closely related sequence families. Packages such as ConStruct (Luck et al. 1999) and pfold (Knudsen and Hein 2003) allow the user to fold an alignment of sequences, but consider only one kind of information (thermodynamics and covariation, respectively) and cannot incorporate constraints from chemical mapping.

BayesFold allows users to assess a list of suboptimal folds rapidly, using Bayes’s Theorem to combine results from multiple sources of data. This method provides an objective way of combining the different folding methods, and does not force the user to make choices, sometimes arbitrarily, about the relative importance of different parameters. Bayes’s Theorem provides a unique, optimal method of updating beliefs in the light of new data:

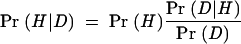(1)

In other words, the posterior probability of a hypothesis H given some new data D, Pr(H|D), is equal to the prior probability of the hypothesis before the new data were observed, multiplied by the conditional probability of observing the data if the hypothesis were true, divided by the unconditional probability (summarizing over all scenarios and their respective probabilities) of observing the data when the hypothesis is unknown or chosen at random. In keeping with common sense, a hypothesis becomes more likely when an outcome that it predicts to be frequent is actually observed, especially when the alternative hypotheses predict that the outcome is rare. When the evidence is overwhelming, even hypotheses that were originally considered extremely unlikely can become plausible.

For example, after decades of research in which every enzyme activity turned out to be catalyzed by a specific protein, it was once natural to assume that all biological catalysts were proteins. However, in the cases of the Tetrahymena Group I intron and RNase P, Cech and Altman obtained results (such as activity from in vitro transcripts) that were highly implausible if proteins were the catalysts, but made perfect sense if RNA was the catalyst (Guerrier-Takada and Altman 1984; Zaug and Cech 1986). Catalytic activity associated with a transcript newly synthesized from purified components, with no contact with Tetrahymena or its proteins, is an example of data D that has a very low probability given one hypothesis (that proteins catalyze the reaction), but a very high probability given an alternative hypothesis (that RNA catalyzes the reaction). In other words, Pr(D|H_protein) is much less than Pr(D|H_RNA), so that Pr(H_RNA) is greater than Pr(H_protein) after observing the data. The observation also raises the probability that other reactions are also catalyzed by RNA, thus changing the prior assumptions for new experiments. Bayes’s Theorem formalizes this type of reasoning and makes it quantitative.

When considering several hypotheses, Bayes’s Theorem provides the probability that, given the evidence, each of the hypotheses is the true hypothesis. In practice, Pr(D), the probability of the data, is usually unknown. However, if an exhaustive list of possible hypotheses H is known in advance, then Pr(D) can be calculated by a technique called marginalization. This technique takes into account the probability of observing D under each particular hypothesis H_i, weighted by the probability of H_i, as follows:

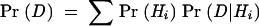(2)

Bayes’s Theorem can be used with multiple types of data D_j by calculating posterior probabilities Pr(H|D_j) for the first type of data, using these posteriors as priors for the next type of data, and so on until the last kind of data is reached. This method assumes that the different types of data are not correlated with each other.

Applying Bayes’s Theorem to secondary-structure prediction, we would ideally want to find the probability of all possible structures (where each structure is defined as a list of base pairs). Unfortunately, the number of structures increases exponentially with the length of the sequence. We reduce the complexity of the task by considering only a list of structures that is known beforehand to be near the optimum.

Thus, we find the plausibility of each of a list of possible structures that a sequence (or set of sequences) might fold into. The researcher typically seeks to choose among a finite number N of hypotheses about the structure H_i, given an alignment containing a number n of aligned sequences S_k (we use this notation throughout the paper and use “structure” interchangeably with “structural hypothesis”). Each structure consists of a list of positions of bases that must be paired: all other bases are unpaired. The structures must be ranked according to their posterior probabilities (the probability that each is the true structure) once all the data are taken into account. Treating the structures as hypotheses in this manner captures the common situation in which the researcher has folded each of a set of closely related sequences individually, perhaps returning a few structures of similar energy for each. When the structures conflict, it is hard to predict objectively which structure is most plausible for all the sequences. Worse yet, the true structure (as revealed by chemical or physical techniques) is often not the least-energy structure for any sequence. Because there is little basis for choosing among structures at this early point, we assign equal prior probabilities Pr(H_i) to each of the N structures H_i, giving 1/N for each structure.

For a predefined list of structures obtained by any method (automatic or manual), BayesFold then assigns each structure a posterior probability by successively taking into account each of the types of data. For this version, we generate the structures H_i by suboptimally folding each sequence using RNAsubopt (Wuchty et al. 1999) as implemented in version 1.4 of the Vienna RNA folding package (Hofacker et al. 1994) using the Mathews-Turner energy parameters (Mathews et al. 1999). The Vienna package gives results almost identical to the better-known mfold (Zuker and Stiegler 1981), and is more freely distributed. We use an energy window of 2 kcal/mole and take a maximum of 10 suboptimal structures for each sequence to reduce computing time, although these parameters are adjustable. BayesFold’s assumption is that all the sequences fold to give an identical active structure; it therefore works best on relatively short sequences that are at least 90% identical (such as the 75–200-nt “sequence families” routinely isolated by SELEX). However, it may also be useful for folding sequences from closely related organisms. The current version of BayesFold does not allow pseudoknots, but we believe it will be possible to address this issue in future versions.

In the following discussion, we assume that all of the sequences fold into precisely the same structure (i.e., the positions of the paired and unpaired bases are identical in every sequence). If the sequences do not fold into a common structure, the posterior probabilities are unreliable. However, the results often indicate which sequences cannot share the best overall fold, making it easy to refold without these outliers. Although only hypotheses about the whole structure can be tested now, we plan to add the ability to assess local structures (e.g., “active sites”) later. In the present version of BayesFold, better results can be obtained by entering a few sequences that definitely fold into the same overall structure rather than entering many sequences that might actually have different structures.

If we assume conditional independence, so that the different types of data are statistically uncorrelated, we need only determine Pr(D_j|H_i) for each individual type of data (rather than the joint probability distribution for all data simultaneously). Conditional independence is a useful approximation even when some of the variables are in fact correlated, because it tends to exaggerate the relative support for the best solutions rather than changing the rank order. Given Pr(D_j|H_i) for each type of data, we can use marginalization to find Pr(D_j) and apply Bayes’s Theorem to each type of data in turn (the results do not depend on the order in which the types of data are considered):

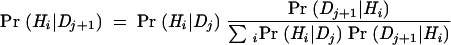(3)

Here, Pr(H_i|D₀) = 1/N, because we are starting with a uniform prior probability distribution that weights each of the N structures equally. More details on the above mathematics can be found in standard references on Bayesian statistics (Jaynes 2003).

METHODS

We consider three major types of data in BayesFold 1.0, and sometimes several kinds of experiment within each type:

• Thermodynamics: What is the energy of each of the sequences folded into each of the structures?

• Covariation: How likely would we be to see the pattern of changes across the alignment if each of the structures were true?

• Chemical mapping: How likely would we be to see the observed pattern of reactive and unreactive nucleotides when a sequence is mapped with each chemical if each of the structures were true?

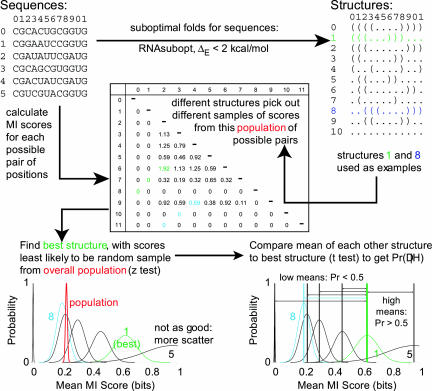
We now explain how to estimate Pr(D_j|H_i), the probability of the data given each of the hypotheses, for measurements derived from each of these criteria. First, we give an overview of the calculations BayesFold performs. Then, we show in detail how to apply the method to calculate Pr(D_j|H_i) for data that applies to single positions in a sequence alignment, using chemical mapping as an example. Finally, we extend the method to data that can be calculated for pairs of positions in an alignment, such as thermodynamic pairing probabilities and mutual information (Fig. 1).

FIGURE 1.

BayesFold’s method for assigning conditional probabilities, using Mutual Information (MI) as an example. First, calculate scores for each position in the alignment (for per-position data such as chemical mappings) or for each possible pair of positions (for per-pair data, such as mutual information). Second, find the population mean and variance of these scores. Third, identify the scores that correspond to the unpaired bases (for per-position data) or the paired bases (for per-pair data) that each of the structures chooses. Fourth, use a z-test to find the sample of scores that is most significantly better than the population mean. Finally, compare this “best” sample of scores with the sample chosen by each of the other structures using a two-sample t-test to find the probability that, if the “best” sample of scores came from the true structure, the other samples of scores would be at least as high as actually observed. This gives the conditional probability Pr(H_i|D_j) for each of the structures H_i using the current type of data D_j. The conditional probabilities for each type of data can then be combined using Bayes’s Theorem.

Overview of calculations

We need to calculate the probability that we would see the observed data if each of the structures were the true structure. Here the “data” are typically not the sequences themselves, but a set of scores for each position or for each pair of positions calculated from the sequence alignment. For example, the data might be the relative intensity of nuclease S1 cleavage at each position in one of the sequences. We expect that the true structure’s unpaired positions have a high mean S1 cleavage and that its paired positions have a low mean S1 cleavage: the reverse result would be most unexpected. The structures thus differ in how frequently they predict that we would see the observed pattern of cleavage, or, in other words, the probability of the data given the structure differs for different structures. This probability depends on the distribution of scores at the positions that each structure selects as paired or unpaired.

The general method of finding Pr(D_j|H_i) is as follows. First, we find H_max, the structure that has the best statistical support. We then get a corresponding Pr(D_j|H_i) for each structure H_i by assuming that some test statistic calculated for H_max is the true value, and asking how surprising it would be to find the observed value of the test statistic for each of the H_i based on the observed distribution of values in H_max. Using the best-supported difference in means rather than the largest difference limits the effects of sampling error, because Pr(D_j|H_max) is always 0.5 by definition (because if the true value were that calculated for H_max, chance predicts that we would find a higher value half of the time and a lower value the other half of the time if we chose another sample from precisely the same population). Consequently, even a measurement (such as a difference in means) based on a very small sample, and therefore subject to error, can confer apparent support of at most twice that for H_max, and such artifacts are unlikely to be consistent across independent types of data.

We calculate conditional probabilities for each structure for each of the following types of data:

Scores for each position

• Chemical mapping (if available: possibly several chemicals applied to several sequences at different concentrations).

Scores for each pair of positions

• Pair Probabilities (from folding individual sequences).

• Fraction Pairable (from the sequence alignment).

• Mutual Information (from the sequence alignment).

We provide an interface for combining any or all of these forms of information using Bayes’s Theorem for multiple updates, easily revealing which criteria influence the decision for particular structures the most and allowing users to disregard any particular type of data they suspect to be unreliable. BayesFold’s appeal is that it produces an optimal secondary structure using all the information automatically at hand for a group of aligned sequences. It also ranks the other structures rationally, providing a basis for further experimentation. BayesFold also calculates and displays several additional statistics that are useful for evaluating particular combinations of sequences and structures as shown in Table 1.

TABLE 1.

Statistics displayed for evaluating structures and sequences

Displayed on structure diagram
Name	Description
% occupied	Fraction of sequences that have a base at each position in the sequence alignment
Information	Shannon uncertainty (equation 5) at each position in the sequence alignment, subtracted from 2
No. mismatches	Number of mismatched pairs in current sequence and structure
Folding energy	Energy of current structure folded into current sequence
Best index	Identification of the best sequence for each structure, and of the best structure for each sequence, using each of the criteria for which likelihoods were calculated
Average	Average score across sequences and structures for each statistic calculated on combinations of sequences and structures

We have implemented a system to perform these calculations using a client/server model: the server, written in Python 2.3 and tested on Linux and MacOS X, performs all the calculations; the client, written in Javascript, runs in a Web browser and displays the results. The client can be accessed at http:// bayes.colorado.edu/fold/. It is also possible to run BayesFold from the command-line on the server. Currently, the Web client only supports Internet Explorer 6 on Windows with version 3 of the Adobe SVG plugin, but we plan to add support for the Mozilla and Safari/ Konqueror browsers in a later release. The client takes user input as an alignment of sequences (plain text or FASTA format), and optionally any chemical mapping data for one or more of the sequences. The client then transfers the input to the server using CGI, the common gateway interface. The server performs the calculations, and returns the results as a single XML document. This XML document is parsed in the Web browser, which by default shows the user the IUPAC consensus sequence threaded through the overall best structure. However, the interface makes it easy for the user to display any of the sequences threaded through any of the candidate structures. Additionally, the user can examine the table of sequences and the table of structures, examining the fit of each structure to each sequence using any combination of the evaluation criteria.

We particularly emphasize that the interface also produces publication-quality graphics, either printed directly from the browser or exported into an SVG-compliant graphics package. SVG is the W3C Consortium’s approved format for vector graphics on the Web, and support for this file format is likely to increase rapidly in the near future. As an XML language itself, SVG is easy to manipulate programatically.

Per-position data

Per-position data, such as a pattern of light and dark bands on a gel derived from chemical or nuclease mapping, indicates whether the base at a particular position is paired but says nothing about the identity of the partner. Any structure, by providing a list of base pairs, implicitly divides the bases into two groups: paired and unpaired. A structure whose unpaired (or, depending on the chemical or enzyme, paired) positions correspond to particularly dark bands is better supported by the mapping data. We focus on unpaired positions because they are rarer than paired positions.

Each position in the alignment can be assigned a score (corresponding to the intensity of the band at that position), and each structure selects groups of “paired” and “unpaired” scores from this single overall population of per-position scores.

In principle, we could calculate the probability of a particular matrix of intensities from the structure if we knew enough about the details of the response of chemical mapping to specific secondary-structure features. Unfortunately, such data are not readily available. Instead, we reduce the dimensionality of the problem by considering the difference in means between the “paired” and “unpaired” scores. Even if the underlying distribution of scores is not normally distributed, the t-test is relatively robust against violations of this assumption.

Consequently, we calculate the mean and variance of the overall population of scores. The best structure, then, is the structure whose unpaired positions have the most different mean score from the population mean for all possible pairs of positions (including those not actually asserted to be paired by any hypothesis). For example, an enzyme like S1 that cleaves unpaired bases has an average rate of cleavage over all the positions in the molecule: the best structure is the one whose unpaired positions have the highest cleavage, which can be compared with the average cleavage over all positions. The difference between the sample and population mean can be assessed using a standard z-test. Here, μ and x̄ are the population mean and standard deviation, x and s are the sample mean and standard deviation, and SEM, the standard error of the mean of a randomly chosen sample of size n, is 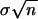. The most significant distance D_max is that for which (x̄ − μ)/SEM is maximized, thereby choosing the best structure H_max.

Having found the structure H_max with the best support, we need to find the conditional probability of each structure given the data. We expect that the population of scores at unpaired positions should differ from the overall population, in that the structure should choose scores that are particularly high (or particularly low, depending on the specificity of the chemical or enzyme) to be unpaired. To find the probability of the observed scores for each structure, we can use a standard two-sample t-test to compare the scores of the unpaired positions in the best structure and in the structure currently under consideration:

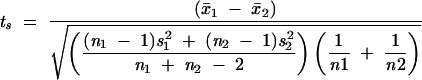(4)

Here, the two samples are the scores for unpaired bases in the best structure and the currently considered structure:x̄₁ and x̄₂ are the two sample means, n₁ and n₂ are the two sample sizes, and s₁ and s₂ are the two sample standard deviations (Sokal and Rohlf 1995).

The t-test gives the probability that we would see a mean as bad as that actually observed for each structure if the scores for its unpaired bases were drawn from the same population as the scores for the best structure’s unpaired bases (whether the bad scores are high or low depends on whether the chemical or enzyme affects paired or unpaired bases). This is equivalent to finding Pr(D_j|H_i) for each structure.

In the particular case of chemical mapping, the chemical typically cleaves the sequence at particular bases that are paired or unpaired, or modifies certain bases in a way that prevents primer extension. When the RNA is treated, reverse-transcribed, end-labeled (often by reverse transcription with an end-labeled primer), and run on a sequencing gel, the intensity of the bands at each position in the sequence indicates the extent to which that position was modified. Table 2 contains a list of specificities for some widely used modifying agents. Because the efficiency of modification or cleavage is often base-specific, we normalize the scores for each of the four bases individually (excluding bases that a particular chemical cannot modify).

TABLE 2.

Preferences of modifying agents for particular bases and structure

Probe	Specificity
S1 nuclease	Any unpaired base
RNase VI	Any paired or stacked base
DMS	N3-C, N1-A, N7-G (typically unpaired for A and C)
CMCT	N3-U, N1-G (typically unpaired)
kethoxal	N1-G, N2-G (typically unpaired/unstacked)
Pb2+	Backbone phosphate, any unpaired or flexible base

See Ehresmann et al. (1987) for review. N1, N3, and N7 indicate particular nitrogen atoms within the base.

For chemical mapping, this method allows far more flexibility than does fixing particular bases as paired or unpaired after examining the sequencing gel, because it allows uncertainty in the assignment of paired/unpaired states (in that we are looking at whether a sample of light or dark bands is chosen overall, rather than requiring each specific position to be paired or unpaired). This is important because the results of chemical mapping can be influenced by several factors other than the secondary structure (including “docking” between loops and helices, and inflexibility in unpaired regions at close-packed helix junctions).

Per-pair data

Several methods, notably mutual information, provide data about pairs of positions in an alignment rather than about individual positions. Our strategy here is similar to that with per-position data, except that instead of scores for the l positions in the alignment, there are scores for each of the l(l − 1)/2 possible combinations of two positions. To evaluate each hypothesis H_i, we need to determine whether the pairs that make up a particular structure have surprisingly high or low scores. Specifically, the question is whether the mean of the sample of all possible pairs that corresponds to the actual pairs in a structure differs from the expected mean of a set of the same number of pairs chosen at random.

As is the case for per-position data, we are reducing the dimensionality of the problem by comparing the means of groups of scores rather than trying to find the probability of a particular matrix given a structure directly. Again, the main issue is that the interpretation of the distribution of individual elements in the matrix is unclear, whereas the distribution of differences in the means of groups of elements corresponding to paired and unpaired positions is both convenient to calculate and straightforward to interpret.

Even if every position in a sequence were paired, there could only be l/2 pairs, therefore the number of actual pairs can only be a small fraction of the number of possible pairs. Again, we calculate the population mean and standard deviation for the set of all possible pairs, and choose the structure whose set of pair scores would be most surprising as a random sample from the set of possible scores as H_max, using the z-test. Each structure is then compared to H_max via a two-sample t-test, treating the scores from that structure and the scores from the best structure as the two samples. The result is the probability of getting a mean score as bad as that found in each structure if the true distribution were the population from which the scores in the best structure were sampled, which is Pr(D_j|H_i).

We calculate three kinds of per-pair data:

Pair probability

The RNAfold program in the Vienna package (Hofacker et al. 1994) can provide, for a single sequence, the probability that each base pairs with each other base in the ensemble of all possible structures (McCaskill 1990). By averaging these probabilities across the set of sequences, we get an idea of how frequently the positions pair across the alignment. The best-supported structure has pairs with a particularly high average probability.

Fraction pairable

For any two positions in the alignment, we can ask how often the bases in the two positions could participate in a base pair (giving a static estimate of pairing, contrasted with the dynamic estimate based on the sequence variations presented in the next section). Here we calculate, for each pair of positions, the fraction of sequences in which the two bases are the potential pairs (GC), (CG), (AU), (UA), (GU), or (UG) rather than some other combination. The best-supported structure chooses pairs of positions that have relatively few mismatches across the alignment, that is, a high probability of being paired.

Mutual information

If two positions are paired, it should be possible to predict the base in one position from the base in the other. The mutual information between two positions in an alignment (Gutell et al. 1992) is defined as the difference between the uncertainty about the two positions taken individually and the uncertainty about the two positions taken together.

In this case, uncertainty has a specific technical meaning from information theory: one bit of uncertainty is the same as the uncertainty about a fair coin toss (or any experiment that has two equiprobable outcomes). The information conveyed by a particular position p in a sequence alignment is the uncertainty H about which character c is present at that position p in any one of the sequences chosen at random:

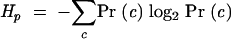(5)

As an example of mutual information, suppose position p in an alignment is observed to be only A or C, and position q is only G or U. If p and q are not paired with each other, then the state of p should be independent of the state of q: In other words, if q is G, p should have equal chances of being A or C, leading to a low mutual information score. In contrast, if p and q are paired, we might expect p to be A whenever q is U, and to be C whenever q is G, leading to a high mutual information score. Thus, the formula for the mutual information M_p,q between two positions p and q is:

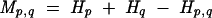(6)

Here, H_p,q is calculated as for H_p only with 16 possible characters instead of four, excluding gaps (Eddy and Durbin 1994). A high mutual information score thus indicates that there is greater uncertainty when examining two positions individually than when examining them together, as would be the case when two positions must pair (allowing only six possibilities instead of 16). The best-supported structure thus chooses pairs of positions with surprisingly high mutual information scores.

RESULTS

Here we present information about the speed and accuracy of BayesFold, along with an example of its use to analyze a real data set. For the tests, we use the well-known structure of tRNA^Phe for speed measurements, because there is a large alignment of related sequence and the true structure has been determined by crystallography to 1.93 Å (Shi and Moore 2000). tRNAs are also about the same size as the sequences typically recovered by SELEX. The negative effect of modified bases on thermodynamic folding for tRNAs is well known in the computational RNA community, and we expect that comparative methods such as those used by BayesFold will greatly improve accuracy when multiple sequences are considered.

For the example demonstrating how to use the BayesFold client, we examine a set of recently selected isoleucine aptamers (Lozupone et al. 2003).

Performance tests

We tested BayesFold’s performance on an alignment of the 86 known bacterial phenylalanine tRNAs, downloaded from the tRNA Database (Sprinzl et al. 1998) on August 11, 2003. We were primarily interested in the speed and accuracy of folding as the number of sequences increases.

Table 3 shows the effects on the speed and accuracy of using random samples of different sizes chosen from the full set of 86 tRNAs. The number of sequences chosen (first column) varies from 1 to 80, with “V” representing the results from the RNAsubopt program in the Vienna package using an energy window of 2 kcal/mole and with the -s option to sort structures by minimum free energy.

TABLE 3.

Speed and accuracy of BayesFold when used for tRNA^Phe sequences

Number of sequences	Time (CPU sec)	Accuracy/differences	True structure found?	Rank of true structure
V	0.03	13.38	0.56	5.29
1	0.81	9.64	0.48	2.29
2	1.06	3.84	0.8	2.13
3	1.3	1.1	0.94	2.21
4	1.55	0.82	0.98	2.2
5	1.8	0.94	0.98	2.08
6	2.05	0.96	0.98	2.06
7	2.29	0.84	1	1.92
8	2.51	0.84	1	2.06
9	2.86	1.32	1	2.24
10	3.07	0.86	1	2.06
20	6.43	0.96	1	1.96
30	9.8	0.88	1	1.84
40	13.35	1.06	1	1.84
50	17.01	0.84	1	1.94
60	20.75	0.72	1	1.7
70	24.42	0.82	1	1.82
80	28.4	0.96	1	1.84

Each row gives means for 50 independent samples of sequences, sampling with replacement. In the first column, V indicates the Vienna package’s RNAsubopt program run on a single sequence, showing the accuracy of thermodynamic folding alone. Numbers in the first column indicate the number of randomly chosen samples in each sample run through BayesFold. See text for full description.

The time taken (second column), in CPU seconds on a 1.7-GHz Pentium 4 processor, scales linearly with the number of sequences, ranging from 0.81 sec for a single sequence up to 31 sec for the full alignment of 86 sequences (not shown in the table). The accuracy (third column) is displayed in terms of the number of base pairs that differ between the “best” structure identified by BayesFold (or the Vienna package for the first row) and the true structure, measured by counting the number of pairs that must be broken and formed to change one structure into another. The accuracy is rather poor for single sequences (rows V and 1 for RNAsubopt and BayesFold, respectively: the “best” structure differs by 13.4 and 9.6 bp, respectively). However, BayesFold quickly converges on a structure that differs from the true structure by just one base pair on average with as few as three sequences in the alignment. Similarly, the fraction of the time the true structure was returned in the results at all (column 4) increases rapidly from about half the time in a single sequence to 98% of the time with four sequences. For RNAsubopt, the true structure is quite a long way down the list (fifth to sixth position on average), whereas with BayesFold the true structure starts off near the top of the list (at the second or third position) and slowly improves to between the first and second positions by the time about seven to 10 sequences are aligned.

In the full alignment of tRNAs, we found significant pairwise correlations between the conditional probabilities for different kinds of evidence: r = 0.68 between Mutual Information and Pair Probability; r = 0.38 between Mutual Information and Fraction Pairable; and r = 0.46 between Fraction Pairable and Pair Probability. Although highly significant (P < 10⁻⁴ in all cases; n = 100 structures), these correlations are too low to predict one kind of evidence for a structure from another. Thus the assumption of conditional independence does not hold rigorously. However, because none of the correlations are negative, the rank order of overall probabilities will not be affected (although the differences between the probabilities assigned to particularly good or bad structures will be somewhat exaggerated).

Table 4 shows the effects of including or excluding each of the particular kinds of evidence individually on the number of base pairs that are different between the best structure and the true structure (second column) and the rank of the true structure (third column). In particular, Mutual Information performed poorly, selecting a structure that was 7 bp different from the true structure. However, either including Pair Probability along with Mutual Information or combining Pair Probability with Fraction Pairable raised the true structure to second or third (in general, Mutual Information provided the least improvement in accuracy throughout our tests). This example shows that two of the three kinds of information are often sufficient, but that including more kinds of information allows the true structure to be found more reliably.

TABLE 4.

Contribution of each kind of information to the overall Best Result

PP	MI	FP	Difference	Rank
+	+	+	1	2
	+	+	7	3
+		+	1	2
+	+		1	2
+			1	2
	+		7	7
		+	1	3

(PP) Pair Probability, (MI) Mutual Information, (FP) Fraction Pairable. Results are shown for all three ways of leaving out one of these kinds of information, and for the three kinds of information individually.

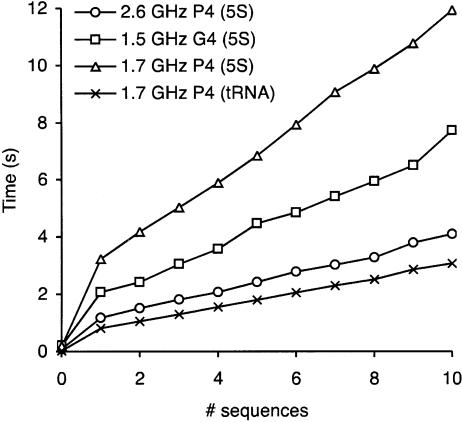
We also characterized the time taken on different processors and operating systems as shown in Figure 2. We tested the speed on the tRNA alignment and on an alignment of 5S bacterial sequences on two Dell machines with Pentium 4 processors running at 1.7 and 2.6 GHz under Mandrake Linux 9.2, and on an Apple PowerBook G4 with a 1.5-GHz processor under MacOS X 10.3. The time taken was roughly linear in the number of sequences. Longer sequences take disproportionately longer times to process.

FIGURE 2.

Performance of BayesFold on different processors. We tested BayesFold on bacterial 5S rRNA sequences, alignment length 120 nt, on 1.7 GHz and 2.6 GHz Pentium 4 machines (Dell) running Mandrake Linux 9.2 (triangles and circles, respectively), and on a 1.5-GHz PowerPC G4 machine (Apple) running MacOS X 10.3 (squares); we also tested tRNA^Phe sequences, alignment length 79 nt, on the 1.7 GHz P4 (crosses). The time taken (Y-axis) was approximately linear in the number of sequences (X-axis), and at least cubic in the length of the sequences (as expected from the dependence on the dynamic programming algorithm used by the Vienna package for the thermodynamic calculations). The point at zero sequences gives the figure for single-sequence folds with the Vienna package alone.

To test the robustness of BayesFold’s results, we tested two additional data sets. The first of these data sets was the manually aligned Sprinzl genomic tRNA database (Sprinzl et al. 1998), from which we extracted 5923 tRNA sequences (excluding sequences containing non-IUPAC symbols) falling into 61 families with at least 10 well-aligned sequences each (the 20 canonical amino acids in each of Eukaryota, Bacteria, and Archaea, plus bacteral tRNA^fMet). Each sequence is annotated with its secondary structure. These sequences were downloaded from http://www.unibayreuth.de/departments/biochemie/trna/. The second data set was the 5S Ribosomal RNA database (Szymanski et al. 2002), from which we extracted 463 bacterial sequences and 58 archaeal sequences (again, excluding sequences containing non-IUPAC symbols). These sequences were downloaded from http://biobases.ibch.poznan.pl/5SData/. All sequences were downloaded on May 5, 2004.

BayesFold performed well on most tRNA families when given as few as five sequences. On average, the minimum free energy structure of individual sequences as estimated by RNAfold differed from the annotated structure by 13.2 bp. The structure BayesFold picked as the most probable differed by 7.6 bp when given two sequences from a family, 5.2 when given five, and levels out with 4.0 at 40 sequences. With as few as five sequences from each family, BayesFold’s preferred structure was within 1 bp of the true structure 3% of the time, within 2 bp 23% of the time, and within 5 bp 55% of the time, and always within 20 bp. In contrast, RNAsubopt’s minimum free energy structure was within 5 bp of the true structure only 4.9% of the time, and was >20 bp different almost 20% of the time. These results are the mean of 50 trials for each number of sequences (1 to 10 in steps of one, and 15 to 50 in steps of five) for each sequence family.

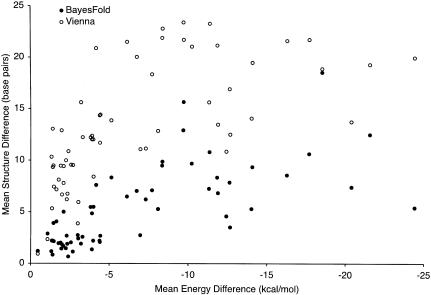
For the tRNA families, there was no significant correlation between the average base pair difference from the true structure and any of the following: mean similarity between pairs of sequences (ranging from 62% to 83% of positions identical, mean 74%), number of sequences in the family (14 to 476 sequences, mean 97), average energy of the minimum free energy structure for each sequence (−42.6 to −29.2 kcal/mole, mean 29.2), or fraction of the alignment consisting of gaps (3.1% to 22%, mean 8.8%). The two variables that had a large effect on the base pair difference were the mean energy of the annotated structure on each sequence (−32.9 to −1.2 kcal/mole, mean -22.5: correlated with the mean number of differences at 25 sequences, r² = 0.25, P = 3.5 × 10⁻⁵) and the mean difference between the energy of the minimum free energy structure and the annotated structure (0.45 to 24.4 kcal/mole, mean 6.8: correlated with the mean number of differences at 25 sequences, r² = 0.52, P = 4.3 × 10⁻¹¹). The effect of this latter relationship is shown for the Vienna package and for BayesFold (using samples of five sequences) in Figure 3.

FIGURE 3.

Correlation between accuracy and free energy difference. Differences between the predicted structure and the true structure (Y-axis) were significantly larger for both BayesFold (closed circles, five sequences) and for the Vienna package’s RNAfold program (open circles) when the difference in energy between the annotated structure and the minimum free energy structure (X-axis) was large. However, at all levels of energy difference, BayesFold’s predictions with five sequences were much closer to the true structure than were the Vienna package’s single-sequence predictions. Note that these predictions use only the sequence data; further improvements would be possible if chemical mapping data were included. Interestingly, RNAfold performs poorly even in cases in which the true structure is very close in energy to the minimum free energy structure. The results shown are for the mean of 50 samples of sequences from each of the 61 tRNA families.

To test whether the manual alignments we used from the Sprinzl database had an undue effect on the results, we tested the CLUSTALW alignment of the tRNA^Phe sequences after removing all gaps. This alignment was performed using the default parameters, and results were within sampling error of those presented above for the manually aligned sequences (data not shown).

The second test we performed examined BayesFold’s performance on 5S rRNA, which is substantially longer than tRNA (120 vs. 74 bases on average). Although annotated structures were provided by the 5S rRNA database, these structures fit many of the individual sequences poorly. In particular, stems of individual sequences often extended into regions annotated as unpaired in the database, and individual sequences contained various bulges, gaps, and broken base pairs. Consequently, BayesFold’s assumption that all the sequences fold into the same structure was unlikely to be correct, and the results illustrate the effects of imperfections in this assumption.

To reduce these effects, we started with the known crystal structures of 5S rRNA from Haloarcula marismortui (Ban et al. 2000), Thermus thermophilus (Yusupov et al. 2001), and Deinococcus radiodurans (Harms et al. 2001). Although our initial intention was to examine sequences at increasing distances from known crystal structures, none of these characterized sequences had many close relatives in the database. For example, only three other sequences in the database were at least 80% identical to the Thermus sequence, providing insufficient data for the tests. However, 96 sequences were between 75% and 80% identical, 237 were between 70% and 75%, 93 were between 65% and 70%, and 28 were between 60% and 65%.

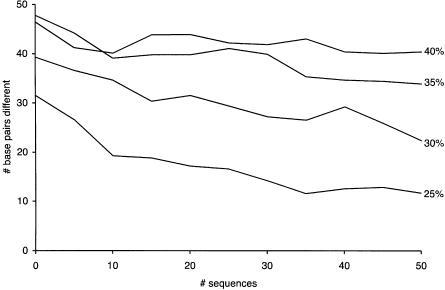
To our surprise, BayesFold still performed relatively well even on these highly divergent sequences. For the group of sequences that were at least 75% identical, BayesFold reduced the average error from 31.5 bp to 11.6 bp with samples of 35 sequences. With only 10 sequences, the error was still reduced substantially (to 26.6 bp) when compared with single-sequence folds. For more divergent sequences, more sequences were required to approach the true structure, although we observed substantial improvements in accuracy as more sequences were added for all but the most divergent set (Fig. 4). Results are the mean of 50 random samples. We show only the results for Thermus, but the results for the other two species are similar.

FIGURE 4.

BayesFold’s accuracy on 5S rRNA sequences. Effect of the number of sequences (X-axis) on accuracy (Y-axis, measured as the number of base pairs different between the inferred structure and the crystal structure of Thermus thermophilus 5S rRNA, counting only Watson-Crick and wobble pairs). Each point is the mean of 50 samples. The four series refer to random samples of 5S rRNAs that are at least x% identical in sequence to the T. thermophilus 5S sequence, where x is 25%, 30%, 35%, or 40%. The point at 0 sequences refers to individual sequence folding using the RNAfold program from the Vienna package.

Usage example

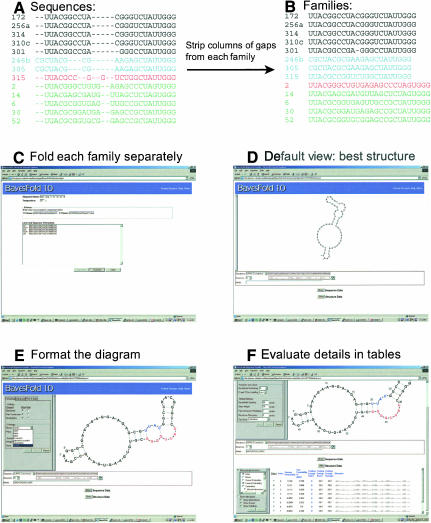
Finally, we demonstrate how to use the BayesFold interface and illustrate real output. For this task, we use an alignment of isoleucine aptamers (Fig. 5; Lozupone et al. 2003). This alignment was obtained with CLUSTALW (Thompson et al. 1994) after removing primers from each sequence. In this example, as is typical, the sequences fall into several families derived from distinct ancestral sequences in the starting pool. Because BayesFold assumes that all the sequences in the input have identical overall structures, and because the underlying Vienna package that generates the structural hypotheses deals poorly with gaps, we manually remove any columns of gaps from each individual family and choose a single family to fold (Fig. 5B).

FIGURE 5.

Using BayesFold to fold aligned sequences. (A) Identify sequence families with an alignment program such as CLUSTAL or Pileup, aligning without primers. (B) Remove columns of gaps from each family. (C) Paste the sequences into BayesFold, entering the primers in the appropriate fields. Chemical mapping data can be added as an additional step. (D) Default view after folding the sequences. The IUPAC consensus sequence is shown, folded into the overall best structure. (E) Format the sequence. Here, we show motifs highlighted on the sequence, but other coloring options for bases and pairs can be selected from the formatting palette menus. The sequence can be scaled, moved, and rotated within the browser. Alternative sequences and structures can be selected from the sequence and structure pull-down menus. (F) Display the alignments and data tables. Clicking the Sequences and Structures buttons displays the sequence and structure information, respectively. It is possible to view the sequences and/or structures, the current probability (taking into account just the types of data currently selected for display in the table), the conditional probabilities for each type of evidence, and the ranks, averages, and raw scores for additional kinds of information such as energy and mismatches (the number of mismatches and the energy when each sequence is folded into each structure).

The BayesFold input page (Fig. 5C) provides areas to paste in the primers and sequences, and allows the user to enter a folding temperature and a name for the alignment. Sequences can be entered in FASTA format (with separate label and sequence lines), or one per line with labels separated from the sequence by spaces and/or tabs. Clicking “Validate” checks that the sequences are in the right format. If the sequences are valid, the user can click “Continue.”

On the next two screens (not shown), the user can correct any mistakes in the labels and/or sequences and enter any chemical mapping data. Chemical mapping can be entered as a list of numbers on any arbitrary scale, with larger numbers indicating darker bands. BayesFold knows about the specificities of common chemicals and enzymes, and treats each base separately to account for differences in efficiency in modification or cleavage; it will ignore data for bases that the chemical is not supposed to modify. Chemical mapping data can be provided for multiple chemicals and sequences, even if the results for some chemicals and sequences conflict with each other. A wait page is displayed after the data are submitted to the server, which checks for results every 30 sec and indicates how long the process has taken.

When the calculations are finished, BayesFold shows the consensus sequence (using the IUPAC degenerate symbols) folded into the overall best structure (Fig. 5D). Any sequence can be displayed in any structure by selecting a different sequence or structure from the pull-down menus; the structures are ranked by overall probability, with the most probable structure at the top. Because the structure is drawn in SVG, the user can zoom in or out by right-clicking on the picture and selecting the appropriate option from the context menu. The picture can be moved around by holding down the Alt key and dragging. The structure can also be rotated by clicking and dragging anywhere in the drawing area. Bases and position labels will automatically snap upright when the rotation is complete.

The drawing can be formatted in many ways (Fig. 5E) by expanding the formatting palette at the left-hand side of the drawing area. BayesFold can color bases using criteria involved in calculating the best structure, such as mismatches and mutual information, as well as user-selected motifs. Here we see the two parts of the minimal Ile-binding motif highlighted on the structure. Additional options include the ability to add nucleotide numbering, change the font size or style, or show or hide the backbone, base labels, or pair connectors. The formatting is maintained when a new sequence is chosen, but must be reapplied for a new structure by clicking the refresh button next to the text representation of the current structure.

Finally, tables displaying detailed information for particular sequences and structures can be evaluated (Fig. 5F) by clicking “Show” for the sequence data or the structure data. By default, the structure table displays the name, rank, overall probability for each structure, and the Vienna-format structure (in dot-bracket notation, where each open parenthesis corresponds to the upstream base of a pair, and each closed parenthesis corresponds to the downstream partner in the last pair opened). The sequence table is similar, except that individual sequences do not have probabilities, thus this column is omitted. However, by expanding the info palettes at the left-hand side of the sequence and structure alignments, detailed information about any of the types of evidence is available. This includes the raw score, average, best index, and Pr(D|H) for each type of evidence; the best index is the sequence (structure) for which the current structure (sequence) has the best score. The table can be sorted by any column by clicking on the title (click again to sort in the other direction), making it very easy to see which structures a particular type of evidence best supports. Of particular interest are the folding energy, which shows the energy of each of the sequences folded into each of the structures, and the number of mismatches, which shows how many base pairs in each structure could not form correctly in each sequence.

The current probability is particularly important, because it shows the probability, given whatever data are currently visible, that each structure is the true structure. Large differences in probability (twofold or greater) suggest that one structure is much more probable than another, or, in other words, that the data provided distinguished the structures. Small differences (e.g., in the second or third decimal place) mean that the structures are about equally likely, or, in other words, that additional data are needed for a rational choice among the H_i. In general, very similar structures that differ by only 1 or 2 bp have similar probabilities, because there is little evidence to discriminate between them. In the table shown in Figure 5F, for instance, the displayed structures are almost identical, and their probabilities are correspondingly similar. In this case, the second structure (Fig. 5F) seems somewhat more reasonable than the best structure (Fig. 5E), even though its probability score is a little lower. However, if the second structure had instead been assigned a very low probability (e.g., 0.001), we should be far more skeptical about the possibility that it might be the true structure. Notably, in the performance section above, we show that BayesFold actually yields better accuracy on average than thermodynamic folding (Table 3), even though it often fails to form obvious pairs at the ends of stems (see Discussion).

DISCUSSION

We have demonstated that BayesFold performs well on short, functional RNA sequences such as tRNAs, and that the program itself makes it easy to analyze and output RNA secondary structures. Here we elaborate on some specific points about BayesFold’s performance, accuracy, and usability.

BayesFold assigns each structure a probability score. Because the different types of data are not entirely independent, the probabilities assigned to the best structures will be higher, and those assigned to the worst structures lower, than they should ideally be. However, these numbers can still be treated as probabilities: a structure with twice the score of another structure really should be twice as likely, and probabilities can be summed over a family of similar structures if desired. Conversely, when two structures have almost the same probability (common for structures that differ by a single base pair), there is little evidence to choose one over the other and they should be treated in further work as equally likely. These combining properties of the probabilities make BayesFold’s results much easier to interpret than arbitrary scores or weightings.

Although the different types of data provide conditional probabilities that are correlated with one another, they often select completely different structures when applied individually or in pairwise combination. The strategy of combining multiple forms of data with a sound probabilistic approach seems to produce especially reliable folds, with the true structure often appearing in the top three under a wide range of conditions.

BayesFold tends to choose structures with fewer, better-supported pairs rather than more, less-well-supported pairs. This tendency can lead to decisions that seem surprising, such as failure to close the last pair in a loop when the bases are compatible. The reason for this outcome is that BayesFold finds structures with the best average support for each base pair, rather than (for example) the best sum of folding energies across base pairs. We expect that adding other types of data (such as the compositions of paired and unpaired regions of RNAs with known structure) will resolve this issue. However, as Table 3 shows, BayesFold already does better on average than using a thermodynamic folding package to fold individual sequences.

The principal assumption that BayesFold makes is that all of the sequences in the alignment fold into the same overall structure. Owing to this assumption, folding a small alignment of definitively similar sequences is better than folding a larger alignment of less closely related sequences, especially if it is not certain that all sequences share the same global fold. Fortunately, BayesFold’s accuracy is good even on small alignments, making it suitable both for SELEX and for orthologous sequences from related species. For biological sequences, however, it should be noted that BayesFold ignores phylogenetic considerations, and thus uses somewhat less data than is potentially available. We plan to add support for phylogeny in a future version.

BayesFold runs almost instantly on alignments of few, short sequences (e.g., 3 sec on 10 tRNA sequences). Apparently, good information is obtained from even three or four sequences, and almost all of the power is obtained from the first 10 sequences. Thus, folding a large sequence alignment all at once is typically unnecessary. A better approach would be to choose small samples randomly from the large alignment and to check that the results agree. Analysis of sequences isolated from SELEX is improved greatly by folding those sequences that are obviously derived from a common ancestor and excluding unrelated sequences, because BayesFold will always return a list of structures even with random sequences. Because of the way the underlying Vienna package handles gaps and degenerate bases (essentially, as bases that never pair and do not contribute to stacking interactions), any columns composed only of gaps should be removed from the alignment before folding. Sequences with many degenerate bases or gaps should also be excluded. However, good results can typically be obtained with one to five gaps or degenerate bases per sequence if they are in different places in different sequences.

The tRNA results demonstrate that BayesFold robustly finds structures that are much closer to the true structure than single-sequence folding. In particular, the relationship between the minimum free energy difference and the accuracy of the fold presented in Figure 3 shows that BayesFold can use other forms of information to overcome and correct energy differences of several kilocalories per mole, which corresponds to several thousandfold in the predicted abundance at equilibrium. Manual examination of some of the sequences that had very high energies when folded into the annotated structure suggested that these structures are often incorrect (e.g., potential Watson-Crick pairs within stems were marked as unpaired bases), suggesting that BayesFold’s ability to find the true structure may be even better than these results suggest. Excluding families of sequences for which the energy of the annotated structure was anomalous (>-20 kcal/mole) reduced the difference between Bayes-Fold’s best structure and the true structure by ~1 bp for a given number of sequences.

Because BayesFold uses RNAsubopt to generate candidate structures, BayesFold’s performance is bounded by the performance of RNAsubopt (linear in the number of sequences, and cubic in the length of each sequence). In other words, longer sequences take disproportionate amounts of time to fold. For instance, it might take several days of CPU time to analyze an alignment of LSU rRNA sequences. This limits BayesFold’s utility for longer sequence alignments; however, these initial folding calculations could potentially be performed in parallel over a cluster, because the results are independent for each sequence. We are investigating clustering approaches that would allow us to fold even long mRNA sequences. On our own server, we limit BayesFold to alignments up to 150 nt to minimize CPU load for each alignment, but it is capable of folding much longer alignments if installed locally.

BayesFold’s ability to fold multiple sequences at once makes exploratory analysis much easier than in programs that return results for each structure individually. In particular, BayesFold allows visualization of sequence folded into any of the possible structures. In practice, we find that the mismatch and motif base colorings are surprisingly useful for exploring the various structures: the mismatches show at a glance if the sequence and structure are compatible (this is important for finding out whether a particular sequence does not really belong in the alignment), and the motifs make it easy to check whether the conserved sequences are typically treated in the same way in most of the plausible structures.

Compared with other programs that fold multiple sequences, BayesFold’s main advantages are that it can handle complex secondary structures (albeit excluding pseudo-knots), does not require the user to choose parameters such as arbitrary weightings or motif lengths at the beginning of the process, allows fine-grained control of the types of data that are included in the final result, and provides a convenient interface for exploring the results both graphically and numerically. Also, BayesFold runs quickly: whereas FoldAlign took >30 min to analyze a sample of 10 tRNA^Phe sequences using the default parameters and found only a single stem–loop, BayesFold processed the same alignment in <3 sec and chose a structure that differed from the true structure by only 1 bp.

Although BayesFold’s current performance is good, further improvements may be possible by avoiding the reduction of the problem space and of the dimensionality of the data that it currently performs. In particular, if the true structure is not in the list of candidate structures, BayesFold cannot find it. To address this issue, we are exploring techniques that would allow us to work in the full problem space of all possible secondary structures. Reducing the dimensionality of the data (by considering means of scores for groups of base pairs rather than considering the full matrix of scores) allows BayesFold to run rapidly, but at the same time may discard additional information contained in the data matrix. It is possible that using alternative dimensionality reduction methods, or using techniques such as MCMC (Markov Chain Monte Carlo) on the full data matrices, could improve accuracy at the expense of speed. Consideration of the full folding space and the full data matrices remains a challenging problem.

We are exploring several specific directions for improving BayesFold. Perhaps most importantly, we hope to use the same method to test hypotheses about local, rather than global, structures. This could potentially find combinations of sequence and structure motifs in unaligned sequences, possibly even including pseudoknots. We plan to extend the GUI to allow interactive manipulation of selected bases, loops, and helices, including coloring and rotation. Additionally, the GUI should provide a way of selecting local structures and/or a subset of the initial alignment for re-folding and further analysis. Finally, there is an increasingly large data set of known RNA secondary and 3D structures.

We plan to use this existing knowledge base to further refine the secondary-structure predictions.

Conclusions

BayesFold seems a significant advance over other tools for exploring RNA secondary structure, because it makes it convenient to view any sequence folded into any structure and provides a simple, probabilistic basis for assessing the plausibility of different structures. Additionally, BayesFold is free to install and use, convenient to try out over the Web, and produces publication-quality graphics. We hope that this combination of features will assist researchers in the field and accelerate the pace of discovery by reducing the effort currently associated with finding RNA secondary structures.