Abstract
We have developed a computational approach for the comparison and classification of RNA loop structures. Hairpin or interior loops identified in atomic resolution RNA structures were intercompared by conformational matching. The root-mean-square deviation (RMSD) values between all pairs of RNA fragments of interest, even if from different molecules, are calculated. Subsequently, cluster analysis is performed on the resulting matrix of RMSD distances using the unweighted pair group method with arithmetic mean (UPGMA). The cluster analysis objectively reveals groups of folds that resemble one another. To demonstrate the utility of the approach, a comprehensive analysis of all the terminal hairpin tetraloops that have been observed in 15 RNA structures that have been determined by X-ray crystallography was undertaken. The method found major clusters corresponding to the well-known GNRA and UNCG types. In addition, two tetraloops with the unusual primary sequence UMAC (M is A or C) were successfully assigned to the GNRA cluster. Larger loop structures were also examined and the clustering results confirmed the occurrence of variations of the GNRA and UNCG tetraloops in these loops and provided a systematic means for locating them. Nineteen examples of larger loops that closely resemble either the GNRA or UNCG tetraloop were found in the large ribosomal RNAs. When the clustering approach was extended to include all structures in the SCOR database, novel relationships were detected including one between the ANYA motif and a less common folding of the GAAA tetraloop sequence.
Keywords: tetraloops, RNA motif, RMSD, distance matrix, cluster analysis, UPGMA
INTRODUCTION
Large RNAs are constructed in part from a variety of recurrent motifs such as the U-turn (Quigley and Rich 1976), the E-loop (Varani et al. 1989; Wimberly et al. 1993), the GNRA tetraloop (Jucker and Pardi 1995), the A-minor motif (Nissen et al. 2001), the kink-turn (Klein et al. 2001), the SRP motif (Gundelfinger et al. 1984; Keenan et al. 2001), and the T-loop/lone pair triloop motif (Nagaswamy and Fox 2002; Lee et al. 2003). Some of these motifs were originally observed in three-dimensional structures and whenever possible subsequently defined in terms of primary sequence and secondary structure rules, which facilitate detection of additional examples without detailed examination of three-dimensional structures (Gutell et al. 1994, 2000; Brown et al. 1996). This is advantageous when molecular structures are not available. However, when structures are available, regions that correspond to a particular motif can be overlooked if they do not satisfy the standard rules.
A more general approach is to define motifs in terms of their three-dimensional structure. The SCOR database (Klosterman et al. 2002, 2004) has sought to do exactly this by a manual comparison of all known loop structures. Like any classification scheme, depending on what facets of a structure one considers to be of primary or secondary importance this approach produces alternative classifications. An automated analysis such as that described here can be used to rapidly examine very large numbers of structures according to objective rules to identify regions with similar structure. Detailed examination can then be used to understand the nature of the similarity and whether it can usefully be considered to represent a folding motif. In instances where the similarity correlates with an already recognized motif, the comparisons clarify how much variation exists between examples and whether the motif is really distinct.
As pointed out by Reijmers et al. (2001), there are at least four different representations that can be used to describe and compare RNA molecular structures. These include Cartesian coordinates, torsion angles (Hershkovitz et al. 2003), pseudotorsion angles (Duarte and Pyle 1998; Duarte et al. 2003), and representations based on lists of backbone atom distances (Reijmers et al. 2001). Another simplified vectorial representation of the nucleic acid bases via graph theoretic method was utilized by Harrison et al. (2003) to search for the substructural patterns in nucleic acid structural coordinate databases. Reijmers et al. argue that the Cartesian coordinate representation is the gold standard, since all other representations can be derived from it. Indeed, conformational comparisons with three-dimensional Cartesian coordinates have been widely and successfully applied to both proteins (Irving et al. 2001; Oldfield 2002; Qian and Goldstein 2002; Yang 2002; Jewett et al. 2003) and RNAs (Gendron et al. 2001; Reijmers et al. 2001; Yang et al. 2003).
Gendron et al. (2001) previously defined a “distance metric” between two nucleotide conformations in terms of the root-mean-square distance (RMSD) between the backbone heavy atoms of the two nucleotides after an optimal superimposition of their local referentials in three-dimensional space. This allowed them to develop automated tools to annotate local structural details such as sugar pucker, base orientation, presence of base stacking and base pairing. Their approach does not directly detect the presence of larger scale similarities that might represent motifs. Reijmers et al. (2001) has advocated the use of clustering techniques to find hidden relationships in RNA data sets. Using RNA trinucleotides as a model system they focused their studies on the effect of the type of structural representation used on the results of a cluster analysis. It was concluded that distance based representations were best when examining global features such as those of interest here. Their distance representation was obtained by the summation of all the distances between six backbone atoms (i.e., P, O5, C5, C4, C3, and O3) of the RNA nucleotides after alignment of two structures by means of Procrustes analysis (Gower 1975; ten Berge 1977).
The objective of the work described here is to ultimately extend these ideas to the detection and classification of the larger scale features of an RNA that are generally referred to as motifs. To this end, we have developed software tools that allow rapid comparisons of regions of atomic resolution RNA structures by RMSD values. In our simple and straightforward method, the three-dimensional coordinates of 15 atoms per RNA residue (including all of the backbone and sugar atoms) are utilized to calculate the RMSD distance between two RNA fragments of the same length after they are superimposed with Kabsch’s (1976, 1978) method. Even if the RNA fragments have different nucleotide sequences, their conformations can be compared by the methodology described here as long as they have the same nucleotide lengths. For instance, all known examples of RNA segments that might belong to a particular motif are interchangeably used as initial probes to find all the other candidate examples with RMSD resemblance. Then the recalculated RMSD values of pairwise comparisons among all the candidate motifs with fixed length are tabulated and analyzed by cluster analysis using the unweighted pair group method with arithmetic mean (UPGMA).
This approach allows the exhaustive identification of sequence segments that resemble one another in their three-dimensional structure in the RNA structure database. It can also locate (or verify) previously undetected sequences that resemble those associated with a previously defined motif. To illustrate the approach, we present herein a comprehensive analysis of the terminal hairpin tetraloops found in 15 RNA molecules whose structure was determined by X-ray crystallography. In doing this, we also consider the closing base pair due to its important role in loop definition. In addition, the inclusion of the closing pair facilitates comparison by providing a solid match to begin the comparison. This analysis reveals two major clusters of similar structure corresponding to the well-known GNRA and UNCG tetraloop motifs. If additional characteristic tetra-loop structures exist, they are not sufficiently represented in the set of structures used to be detected. Finally, larger loops were examined to determine the extent to which the GNRA or the UNCG tetraloop motifs were incorporated into those structures.
RESULTS
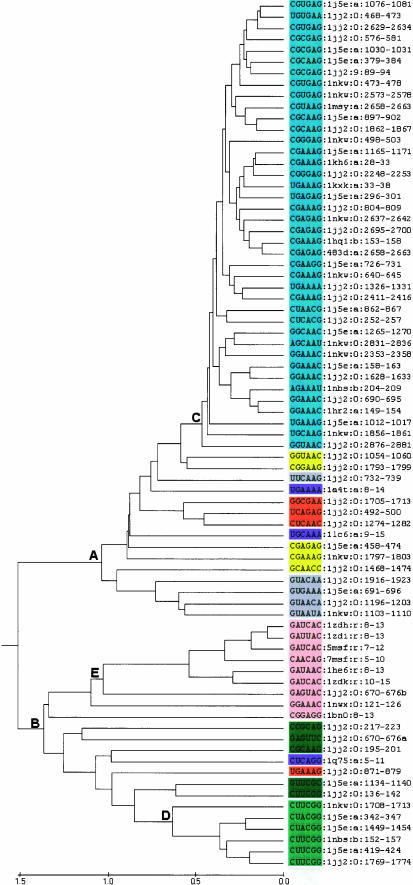
A computational approach that can rapidly and quantitatively classify local RNA folds in known RNA structures was developed. Depending on the nature of the shared structural similarity seen in the resulting clusters, the results may, if the cluster has not been previously recognized, lead to the definition of new structural motifs. In principle, the methodology can also find novel or overlooked examples of known motifs, e.g., such as the UMAC loop, which has a typical GNRA fold (Leontis and Westhof 2002; Klosterman et al. 2004; Tamura et al. 2004). To validate the approach and demonstrate its utility, we examined all the terminal hairpin loops of each size class in 15 RNA X-ray structures, which includes the high resolution (1.41 Å) tetraloop mutant from Escherichia coli 23S rRNA (Protein Data Bank [PDB] code 1MSY). All loops of size 5–13 found in these molecules were initially included in the analysis. The results for 68 four base terminal hairpin loops are represented as a dendrogram (Fig. 1), and these loops will be discussed in detail herein. The results for additional loops of length 5–13 are provided as Supplementary Material (http://prion.bchs.uh.edu/~jhuang/tetraloop.html).
FIGURE 1.
UPGMA cluster analysis of the tetraloops (four base loop plus closing pair) found in 15 RNA molecules whose structure has been determined by X-ray crystallography. Individual loops are designated as described in the Materials and Methods. Three key branch points in the tree, which are discussed in the text, are labeled as A, B, and C. The distance scale at the bottom of the tree is in angstroms.
Analysis of tetraloops in X-ray structures
In Figure 1, each tetraloop is denoted by its primary sequence (including closing pair) followed by the PDB ID of the structure in which they appear, chain ID, and the position numbers in the sequence of the underlying molecule. Thus, loop 1076–1081 of 16S rRNA is represented as CGUGAG:1j5e:a:1076–1081. The dendrogram in Figure 1 has a large well-defined cluster of 40 hairpin loops emanating from branch point A, i.e., from loop 1j5e:a:1076–1081 at the top to loop 1jj2:0:2876–2881. Within this cluster, pairs of loops as similar as 0.253 Å RMSD (i.e., 1hq1:b:153–158 vs. 483d:a:2658–2663 with a branch point distance value, b, on the tree of 0.1265 Å) are observed. With the exception of two loops to be discussed in detail below, all of the loops in this cluster have the canonical GNRA loop sequence. Five additional loops, 1nkw:9.88–93 to 1nkw:0:1235–1240, would fall within the GNRA cluster, if the defining branch point is moved back to point B in Figure 1. A second well-defined cluster, 1nkw:0:1708–1713 to 1jj2:0:1769–1774, is found at branch point C in Figure 1. This cluster contains all the tetraloops of the UNCG type. The remaining loops, including five with the GNRA primary sequence, are in straggler clusters. There are occasional pairs with different loop sequences that closely resemble one another, but there are at present not enough examples in the 15 X-ray structure data set to propose a novel loop fold.
Effect of data quality on results
Many RNA structures are solved at modest resolution with the result that there may be substantial levels of coordinate noise. To determine whether the inherent noise in the data affects the clusters obtained, we weighted the importance given to various structures in accordance with either the B-factor or the atomic mass of the atoms included as described in the Materials and Methods section. The B-factor was used to put the atom’s thermal fluctuation into the weighting and atomic mass was used to put each atom’s signal response to X-ray into weighting.
The resulting B-factor weighted dendrogram (Supplementary Material, http://prion.bchs.uh.edu/~jhuang/tetraloop.html) was effectively identical to the original tree with only four minor changes within the GNRA major cluster. In particular, the precise locations of 1jj2:0:576–581, 1j5e:a:1030–1031, 1j5e:a:1165–1171, and 1j5e:a:1012–1017 were changed with essentially no effect on the various subclusters within the GNRA group. The atomic-mass weighted tree (Supplementary Material, http://prion.bchs.uh.edu/~jhuang/tetraloop.html) likewise had only four minor variations in the GNRA cluster, two of which were the same as seen in the B-factor weighted tree. Except for these minor differences, all other loops are clustered exactly the same way as in the original tree. In summary, all the differences between the un-weighted and weighted trees are within subclusters of the major GNRA cluster defined by A in Figure 1. Although concerns regarding variable atom flexibility as measured by the B-factor or the unnormalized coordinate resolutions among the analyzed structures can be compensated for during the calculations, it is clear there is no compelling need to do so.
Analysis of tetraloop families listed in the SCOR database using cluster analysis
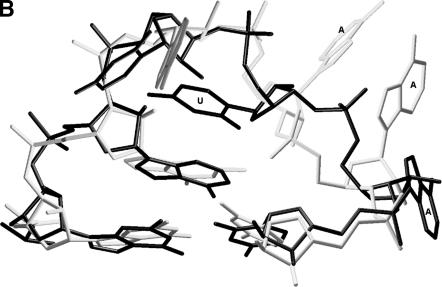
In view of the favorable results obtained with the X-ray structures, the approach was subsequently extended to include all the tetraloops (NMR and crystal structures) listed in the SCOR database (Klosterman et al. 2002; Tamura et al. 2004). The analysis again found clusters corresponding to all the major tetraloop families, including the GNRA, UNCG, and CUUG tetraloops. In the many instances where redundant structures exist due to studies of ligand binding, etc., the multiple versions all were placed in the same sub-cluster with b values below 0.75 Å. In addition to the major clusters, a modest cluster, with a b value of 1.5 Å, containing multiple loops was found. This new cluster is represented by point A in Figure 2A. It includes the RNYA tetraloops often observed in phage coat protein binding RNAs (Witherell et al. 1991; Convery et al. 1998) and several loops with the generalized sequence GRAD (D is A or G or U). In this extended cluster, there is a subcluster at point B that includes the two known examples of the ANYA tetraloops (Convery et al. 1998; Klosterman et al. 2004) represented by point C and a rare GAAA structure represented by point D (e.g., 1nwx:0:122–125 or 1nkw:0:122–125). Upon close examination of their folding, it is evident that these two sets of structure have a very similar backbone fold. The major difference is the orientation of the third loop base, which is stacked in the ANYA loop and destacked in the GAAA loop, where it is pointing in the minor groove (Fig. 2B). In light of the similarity between this rare GAAA structure and the ANYA tetraloop, it should likely be recognized as a variant of the ANYA tetraloop. To determine the reasonableness of this notion, a sequence alignment of 930 23S rRNA sequences from the CRW Web site (Cannone et al. 2002) where the GAAA tetraloop occurs was examined. Although the primary sequence is generally conserved, it does occasionally exchange with ANYW tetraloops and AAU triloops in the sequence space, which is consistent with the clustering of these two loops seen here.
FIGURE 2.
(A) Dendrogram showing the similarity between GAAA and ANHA loops (H is A or C or U). Multiple examples of the same loop determined under slightly different experimental conditions (i.e., redundant loops) are included in this particular figure to illustrate how the methodology handles them. (B) Superimposition of a GAAA loop versus an AUUA loop. Black color for AUUA:1zdi:r:9–12 and gray color for GAAA:1nwx:0:122–125; closing base pairs are also shown.
The effect of the number of atoms used to represent the base
To examine the reliability of the three-atom representation of the base, all the RRRR tetraloops in SCOR were analyzed with two approaches (Supplementary Material, http://prion.bchs.uh.edu/~jhuang/tetraloop.html). The initial calculation used three atoms in the base ring (see Materials and Methods) and a subsequent analysis utilized all the atoms in the base ring (except the side atoms connected to the ring) for the RMSD measurement. An all-atom calculation on the ring is possible for the RRRR tetraloops because both purines have the same total number of atoms on the base ring. Comparison of these two sets of calculations showed that little deviation occurred when the RMSD calculations were based on only three atoms. The major cluster relationships in these two analyses are very similar although some minor distinct differences were seen (Supplementary Material, http://prion.bchs.uh.edu/~jhuang/tetraloop.html). Other secondary clusterings were also conducted with similar results. For example, once the large cluster of GNRA tetraloops (emanating from branch point A in Fig. 1) is established, its largely shared GNRA sequence allows inclusion of most of the purine base atoms in the calculation. The results of this and several other secondary clusterings are provided as Supplementary Material, http://prion.bchs.uh.edu/~jhuang/tetraloop.html.
Tetraloop-like folds in larger hairpin loops
It has previously been observed that pentaloops in several nonribosomal RNAs closely resemble tetraloops of the GNRA or UNCG type (Legault et al. 1998; Huppler et al. 2002; Leontis and Westhof 2002; Theimer et al. 2003). In addition, at least one example has been recognized in Haloarcula marismortui 23S rRNA (Leontis and Westhof 2002). We therefore sought to examine larger loop structures in some detail. Initially, the approach described herein was used to intercompare all the terminal hairpin loops in the 15 RNAs included in the primary data set in each length class. Clusters of loops with similar three-dimensional folding were again found in the UPGMA trees generated from the RMSD distance matrix (Supplementary Material, http://prion.bchs.uh.edu/~jhuang/tetraloop.html).
This initial analysis was followed up by a specific effort to identify larger loops in the 15 RNA structures that bear significant resemblance to the GNRA or UNCG loops. Hairpin loops of varying lengths were examined by ignoring properly selected residues in order to create equal length segments (see Materials and Methods). Figure 3 shows the results of a cluster analysis that included the typical GNRA and UNCG tetraloops, the larger tetraloop-like loops observed in the 15 structures included in this study, and the three previously identified examples of larger loops that resemble them. Including the previously identified 1jj2:0:492–500 loop (Leontis and Westhof 2002), 19 additional large loops were found in the ribosomal RNA structures that closely resemble the GNRA or UNCG canonical tetraloops.
FIGURE 3.
UPGMA dendrogram showing clustered tetraloops and tetraloop-like longer hairpin loops. Individual loops are designated as described in the Materials and Methods. The distance scale at the bottom of the tree is in angstroms. GNRA tetraloops are highlighted in blue and the GNRA-like pentaloops are highlighted in yellow. UNCG tetraloops are highlighted in light green and the UNCG-like pentaloops are highlighted in dark green. Pentaloops occurring in nonribosomal RNAs that were previously identified as resembling either GNRA or UNCG tetraloops (Legault et al. 1998; Huppler et al. 2002; Theimer et al. 2003) are highlighted in purple. Hexaloops that closely resemble the GNRA tetraloop are highlighted in gray. Four tetraloop-like heptaloops are highlighted in orange. Pink-shaded loops resemble the ANYA tetraloop. To keep the total length for all the hairpin loops the same, the bulged out base in the 7-nt pentaloops, the closing pair of the 8-nt hexaloops, and both the bulged base and closing pair of the 9-nt heptaloops are ignored. All hairpin loops fall within a branch point value of 1.4 Å.
Figure 3 illustrates the relationship between these 19 loops and the various tetraloops. The cluster defined by A contains the canonical GNRA loops in subcluster C and the larger loops that most resemble them. Typical GNRA tetraloops are highlighted in blue. The cluster defined by B contains the canonical UNCG type hairpin loops in sub-cluster D and similar larger loops. Also present in cluster B is an ANYA-like subcluster shaded in pink. The portion of this subcluster defined by E includes the canonical ANYA tetraloops. Interestingly, the canonical ANYA cluster also contains an AUAA tetraloop (1he6:r:8–13) and hence the third position in this tetraloop category might more appropriately be referred to as H (A/C/U). The larger loops are distributed in the two primary clusters A and B in Figure 3 as follows. Within cluster A, five GNRA-like pentaloops are highlighted in yellow and five GNRA-like hexaloops are highlighted in gray. Within cluster B, five UNCG-like pentaloops are highlighted in dark green. The three previously recognized pentaloops occurring in nonribosomal RNAs are highlighted in purple to distinguish them from the new rRNA examples. These three pentaloops cluster very well with the rRNA examples in the respective category of the cluster analysis. In addition, there are four heptaloops, highlighted in orange, that resemble the tetraloops. Only one of these (1jj2:0:871–879) is in the UNCG category. These results clearly demonstrate that the addition of extra bases to a tetraloop resulting in a larger loop sequence can result in minimal distortion in the overall folding.
DISCUSSION
The immediate lesson of the dendrograms of Figure 1 is that there are clear clusters corresponding to the usual GNRA and the UNCG tetraloop motifs. However, as is often the case with cluster analysis, it is frequently subjective as to where to define the boundary of a cluster. Thus, in the case of the GNRA tetraloop motif (Fig. 1), two reasonable alternatives exist. Should the GNRA cluster be restricted to encompassing the loops included at point A or should the definition be relaxed to include the larger number obtained if the cluster boundary is at point B. One should not make this distinction from the cluster analysis alone. Rather, the decision should be made in the context of what makes sense in terms of defining the GNRA tetraloop motif and is consistent with the structure of the clusters. The original tetraloop examined (Jucker and Pardi 1995) had specific stabilizing interactions: a GA pair between the first and the last loop base (i.e., between 0 and +3 base as described by Gutell et al. 2000), a hydrogen bond between the imino hydrogen of G1 (base 0) and phosphate oxygen of R3 (base +2), a hydrogen bond between 2′-OH of G1 and N7 of R3 and the 3′ stacking of loop bases excepting G1. Additionally, the overall backbone fold is that of a U-turn and bases n + 2 and n + 3 are frequently seen to be part of three-way interactions via their shallow groove edge mediating tetraloop-receptor interactions. Table 1 examines the extent to which the various GNRA loops included in the GNRA cluster defined by point A satisfy these criteria. Whereas essentially all have the overall U-turn backbone fold, many lack one, the other, or even both of the two characteristic hydrogen bonds. Moreover, examples that satisfy both hydrogen-bonding properties are intermingled with those that do not. If the boundary of the GNRA cluster (Fig. 1) is extended to point B, five additional GNRA-like loops are included (1nkw:9:88–93 to 1nkw:0:1235–1240). This further expands the variability seen. The choice of point B as the cluster boundary allows us to be more inclusive, whereas if A is chosen we are left with a group of five loop structures that must then be regarded as “GNRA-like”. Point A in fact is consistent with a much more stringent definition of the GNRA motif and is in our view probably the preferable choice. This is especially the case when one considers that four of the five questionable loops are from the ribosomal RNAs, parts of whose structures are determined at relatively low resolution. Thus, the failure of these loops to fall within the main cluster may reflect difficulty in structure refinement rather than novel loop geometries.
TABLE 1.
Characteristics of the motifs in GNRA cluster A, UNCG cluster C, and other GNRA tetraloops as seen in Figure 1
| Position | Tetraloopa | 1-hbb | 2-hbc | nd | n + 1 | n + 2 | n + 3 | U-turn | |
| Molecule cluster A | |||||||||
| 16S-TT | 1165–1171 | cGAAAg | N-3.73 | Y-3.08 | GA | none | bb | Triple-SE | Y |
| HCV-IRES | 28–33 | cGAAAg | N-4.66 | Y-2.60 | none | none | none | none | Y |
| 23S-HM | 2248–2253 | cGGGAg | N-4.05 | Y-3.22 | none | none | none | none | Y |
| gll-intron | 33–38 | uGAAAa | N-3.68 | Y-2.60 | none | none | none | none | Y |
| 16S-TT | 296–301 | uGAGAg | N-3.68 | Y-2.57 | GA | trans WC/WC | trans WC/HG | cis SE/WC | Y |
| 23S-HM | 804–809 | cGAAAg | N-4.19 | Y-2.68 | GA | none | none | none | Y |
| 23S-DR | 2637–2642 | cGAGAg | N-4.99 | Y-2.61 | GA | none | none | none | Y |
| 23S-HM | 2695–2700 | cGAGAg | N-4.53 | Y-2.71 | GA | none | none | none | Y |
| 4.5S | 153–159 | cGAAAg | N-4.81 | Y-2.81 | GA | none | none | none | Y |
| SRL | 2658–2663 | cGAAAg | N-3.98 | Y-2.76 | GA | none | none | none | Y |
| 23S-DR | 498–503 | cGGGAg | N-4.92 | Y-3.15 | none | bb | bb | bb | Y |
| 16S-TT | 897–902 | cGCAAg | N-4.0 | Y-2.67 | bb | cis WC/SE | Triple-SE | bb | Y |
| 23S-HM | 1862–1867 | cGCAAg | N-4.10 | Y-2.75 | none | bb | Triple-SE | Triple-SE | Y |
| 23S-DR | 2573–2578 | cGUGAg | N-3.68 | Y-3.15 | none | bb | Triple-SE | Triple-SE | Y |
| 23S-DR | 473–478 | cGUGAg | N-3.60 | Y-2.92 | none | stacking | Triple-SE | Triple-SE | Y |
| 16S-TT | 379–384 | cGCGAg | N-3.67 | Y-2.98 | bb | bb | bb | bb | Y |
| 5S-HM | 89–94 | cGCGAg | N-3.73 | Y-2.77 | none | bb | prot-residue | pro-residue | Y |
| 16S-TT | 1030–1031 | cGCGAg | N-4.10 | Y-2.69 | none | none | none | none | Y |
| 23S-HM | 576–581 | cGCGAg | Y-3.09 | Y-2.91 | none | bb | Triple-SE | Triple-SE | Y |
| 23S-HM | 2629–2634 | cGUGAg | Y-2.88 | Y-2.85 | pro-residue | bb | Triple-SE | Triple-SE | Y |
| 16S-TT | 1076–1081 | cGUAAg | Y-2.8 | Y-2.79 | pro-residue | bb | Triple-SE | Triple-SE | Y |
| 23S-HM | 468–473 | uGUGAa | Y-2.79 | Y-2.86 | none | bb | Triple-SE | Triple-SE | Y |
| 16S-TT | 726–731 | cGAAGg | Y-2.77 | N-4.54 | GA | bb | Triple-SE | bb | Y |
| 23S-DR | 640–645 | cGAAAg | Y-2.50 | Y-2.66 | GA | cis WC/SE | bb | bb | Y |
| 23S-HM | 1326–1331 | cGAAAg | Y-2.54 | Y-2.79 | GA | bb | Triple-SE | Triple-SE | Y |
| 23S-HM | 2411–2416 | cGAAAg | Y-2.78 | Y-2.65 | GA | pro | prot-residue | pro-residue | Y |
| 16S-TT | 862–867 | cUAACg | N-5.28 | Y-2.88 | UC | bb | AU-WC | GC-WC | Y |
| 23S-HM | 252–257 | cUCACg | N-5.32 | Y-2.88 | UC | none | none | none | Y |
| 16S-TT | 1265–1270 | gGCAAc | Y-2.81 | Y-2.71 | GA | bb | Triple-SE | Triple-SE | Y |
| 23S-DR | 2831–2836 | aGCAAu | N-4.26 | N-3.87 | GA | bb | Triple-SE | Triple-SE | Y |
| 23S-DR | 2353–2358 | gGCAAc | N-3.78 | Y-3.38 | GA | none | none | none | Y |
| 16S-TT | 158–163 | gGAAAc | N-4.27 | Y-2.54 | GA | trans WC/SE | bb | bb | Y |
| 23S-HM | 1628–1633 | gGAAAc | N-4.18 | Y-2.84 | GA | bb | Triple-SE | Triple-SE | Y |
| RNase-P | 204–209 | aGAAAu | N-4.40 | Y-2.96 | GA | bb | Triple-SE | Triple-SE | Y |
| 23S-HM | 690–695 | gGAAAc | N-3.78 | Y-2.75 | GA | trans SE/SE | none | none | Y |
| gl-intron | 149–154 | gGAAAc | N-4.36 | Y-2.89 | GA | trans SE/SE | trans SE/SE | Triple-SE | Y |
| 16S-TT | 1012–1017 | uGAAAg | N-4.12 | Y-2.79 | GA | bb | Triple-SE | Triple-SE | Y |
| 23S-DR | 1856–1861 | uGCAAg | N-5.74 | N-4.01 | GA | none | none | none | Y |
| 23S-HM | 2876–2881 | gGUAAc | N-4.24 | Y-2.70 | GA | none | none | none | Y |
| Extension of cluster A | |||||||||
| 5S-DR | 88–93 | cGCAGg | N-3.85 | N-3.61 | GG | none | none | none | Y |
| Hammerhead | |||||||||
| Ribozyme | 104–114 | cGAAAg | N-4.05 | Y-2.67 | GA | trans WC/WC | Triple-SE | Triple-SE | Y |
| 23S-DR | 1376–1381 | cGAACg | Y-3.54 | N-7.47 | none | bb | bb | bb | Y |
| 16S-TT | 1515–1520 | cGGAAg | Y-2.86 | N-5.19 | none | Triple-SE | Triple-SE | Triple-SE | Y |
| 23S-DR | 1235–1240 | cGGAAg | Y-3.08 | N-5.57 | GA | bb | bb | Triple-SE | Y |
| Cluster C | |||||||||
| 23S-DR | 1708–1713 | cUUCGg | NA | NA | UG-bi | none | none | none | no |
| 16S-TT | 342–347 | cUACGg | NA | NA | UG-be | none | none | none | no |
| 16S-TT | 1449–1454 | cUACGg | NA | Na | UG-bi | none | none | none | no |
| Rnase-P | 152–157 | cUUCGg | NA | NA | UG-bi | none | none | none | no |
| 16S-TT | 419–424 | cUUCGg | NA | NA | UG-bi | none | none | none | no |
| 23S-HM | 1769–1774 | cUUCGg | NA | NA | UG-bi | AU-WC | none | pro | no |
| Others | |||||||||
| 23S-DR | 133–138 | cGUAAg | N-6.60 | N-7.41 | none | none | none | none | no |
| 23S-DR | 622–627 | cGAAAg | N-9.67 | N-5.16 | none | none | none | none | no |
| 23S-DR | 146–151 | cGCAAg | N-6.67 | N-6.00 | none | none | none | none | no |
| 23S-HM | 2737–2742 | cGAGAg | NA | NA | GC-WC | AU-WC | none | none | no |
| 23S-DR | 121–126 | gGAAAc | N-6.53 | N-10.40 | none | none | none | none | no |
aTetraloop sequence in capital and closing pairs in small letters.
bHydrogen bond between imino proton of G or U at n and phosphate oxygen of n + 2 in Ångstrom units.
cHydrogen bond between 2′-OH of n and N7 of R at n + 2 in Ångstrom units.
dUnless otherwise mentioned, this is a trans SE/HG pair.
etrans SE/WC bifurcated pair.
(Y) yes; (N) no; (WC) Watson–Crick; (SE) Sugar edge; (Triple-SE) triple base interaction involving the sugar edge of the loop base; (bb) backbone interaction; (pro-residue) interaction with protein residues; (bi) bifurcated pair.
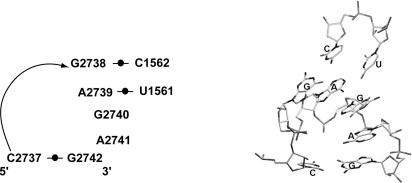
The results dramatically point out that the presence of the GNRA canonical loop sequence is definitely not sufficient to guarantee the presence of the GNRA motif. There are in fact five loops (Table 1) that have the canonical GNRA sequence but do not even form the U-turn, which is shared by all members of even the extended GNRA cluster. For example, loop 1nkw:0:121–126 has a very unusual fold and it is in fact interacting with Adenine 55 and a nearby helical stem containing the nucleotide Cytosine 114. Hairpin loop 1jj2:0:2737–2742 of HM-23S rRNA has the GNRA consensus sequence but instead of the usual structure, all 4 nt stack on the 3′ side of the loop, which is very unusual for an RNA hairpin loop. Examination of the long-range tertiary interactions in 23S rRNA reveals that this loop interacts with residues 1561 and 1562 on the 5′ half of the 23S rRNA via specific Watson–Crick hydrogen bonds (Fig. 4). Its unique fold contributes to the specific interaction between the 3′ and the 5′ halves of HM 23S rRNA. In this case, one might argue that during initial folding the loop forms a GNRA motif and subsequent interaction with the 1561–1562 nucleotides causes a rearrangement of the loop structure to give the unusual geometry seen in the crystal structure. However, the lack of sequence conservation (Gutell et al. 2000) associated with this loop argues otherwise. It appears to be a genuine example of a GNRA sequence that simply does not form the usual motif.
FIGURE 4.
Three-dimensional structure of loop 2737–2742 and residues 1561–1562 in Haloarcula marismortui-23S rRNA. RNA labeling is based on the scheme proposed by Leontis and Westhof (2001). Additional bases from the 5′ half of the 23S rRNA that form Watson–Crick pairs with bases in the loop are also shown.
The cluster analysis approach described here does not depend on any a priori knowledge of the existence of any tetraloop motifs. Clusters are found objectively, and if motifs are defined in a manner that is consistent with structural similarity, there will be a correspondence. Thus, the clusters corresponding to the GNRA and UNCG motifs were found. If other characteristic tetraloop folds existed they would have been revealed as additional clusters, if sufficient examples were present in the data set. If such additional clusters were found, it would require careful analysis of the structures in the cluster to determine whether they should be regarded as representing a new motif or just a group of structures with some similarity of fold.
This potential utility of cluster analysis based methods to reveal a previously overlooked type is illustrated by the unambiguous inclusion of two loops with the canonical loop sequence UMAC in the GNRA cluster. The similarity of these loops to the GNRA types is certainly not a novel finding, as this has been pointed out previously (Leontis and Westhof 2002) and they are already included in the GNRA class in the SCOR database (Klosterman et al. 2004; Tamura et al. 2004). The point to be noted here is that the cluster analysis approach found a relationship that was not immediately recognized during the initial structural investigations and might have been overlooked for an extended period of time.
When the cluster analysis was extended to include all of the tetraloop structures in the SCOR database a previously unreported similarity between a rare GAAA tetraloop (1nkw:0:122–125) and the ANYA tetraloop was observed. The SCOR classification is based on visual inspection of the structures and utilizes readily observable features such as the number of bases in the main stack to classify tetraloops. Alternative classifications are produced in SCOR when such multiple observable features can be equally used as primary, secondary, or tertiary keys in the classification. The cluster analysis approach described here utilizes backbone atoms and three atom points in the base to construct the tree and therefore gives more weight to overall similarity of the backbone fold than the SCOR database currently does, which is why the GAAA/ANYA similarity was detected.
More weight can be given to base orientation if one incorporates additional base atoms in the analysis. This is straightforward to do following the initial clustering in those cases where the primary sequence of the loops in a cluster of interest is partly constrained. For example, the large cluster of GNRA tetraloops (emanating from branch point A in Figure 1) can be subjected to a second clustering, which provides more weight to base orientation because three of the bases (i.e., G, R, and A) can now be essentially fully represented by including most of the purine base atoms. In the present study, such second clustering of the GNRA tetraloop types and the RRRR tetraloops did not change the results in a material way. Nonetheless, a more accurate analysis is obtained by taking into account all the atoms on the RNA base rings whenever possible.
The cluster analysis approach allowed the systematic examination of larger hairpin loops to determine the extent to which they resembled the canonical tetraloop structures. It was found that for many larger loops, when extra bases were selectively ignored a significant structural superposition with one of the standard tetraloops became possible. Nineteen such loops, most of which are new, were found in the ribosomal RNAs (Fig. 3). This included 10 pentaloops, five hexaloops, and four heptaloops. In the case of the pentaloops, one of the bases is essentially an insertion that is bulged out without affecting the structure. When structural similarity with a tetraloop motif is seen, low RMS deviations (~2.0 Å) with either the GNRA or UNCG tetraloops are obtained. However, these pentaloops (with appropriate bases ignored) never fell fully into one of the main clusters. This presumably reflects the fact that the inserted base(s) does cause some disruption of the structure. Consistent with the presence of tetraloop motifs in many of the ribosomal RNA pentaloops, many of these loops exchange with tetraloops in the ribosomal RNA sequence space as represented by comparison of sequenced ribosomal RNAs. This analysis illustrated that by simply treating extra bases as possible bulges the clustering approach could be extended for use in comparison of loops of differing size.
Finally, the reader should appreciate that the results of a cluster analysis such as that presented may have use in practical applications. At its simplest, the current cluster analysis approach can flag tetraloop structures that may require further refinement. A straightforward direct comparison to a well-resolved standard structure might seem like a simpler approach. However, there will inevitably be some deviation, and experience is needed to know when there should be concern about quality of the refinement. Cluster analysis inherently provides the “experience”. Through its use of multiple examples, one obtains an immediate quantitative indication of how unusual the structure is or isn’t. Beyond the possible assessment of refinement quality, it is also necessary to properly annotate the presence of motifs in future structure determinations. Even in the simple case of loop structures, this may be more subtle than it seems, and the cluster analysis approach by its inherently exhaustive approach can reveal unexpected relationships. This was well illustrated in the results presented here (Fig. 3), where it is found that two different annotations are possible for the 1jj2:0;670–676 pentaloop, depending upon which one of the loop residues is ignored. Accordingly, this loop resembles either the ANYA tetraloops (1jj2:0:670–676b) or the UNCG tetraloops (1jj2:0:670–676a).
CONCLUSION
A quantitative approach has been developed for comparing RNA loops in which all sequence segments of a specific length are superimposed in a pairwise fashion. The resulting RMSD distance matrix is subjected to cluster analysis to reveal groups of sequence segments with similar folds. As shown herein, cluster analyses of RMSD distance matrices derived from exhaustive binary comparisons of fixed length RNA fragments can confirm and categorize well-characterized RNA motifs as well as providing a possible means to discover previously unrecognized three-dimensional folding motifs.
When applied to tetraloops found in the primary molecules that have been characterized by X-ray crystallography, the methodology successfully identified clusters of structures corresponding to the well-known GNRA and UNCG tetraloop motifs. Loops with the unusual primary sequence UMAC that were previously shown to have the standard GNRA fold were readily incorporated into the GNRA cluster by the algorithms, thereby illustrating the robustness of the approach. Extension of the analysis to larger loops confirmed the presence of GNRA- and UNCG-like folding motifs in many of these loops and provided a systematic way of identifying them. Finally, when the analysis was extended to include all the structures currently in the SCOR database, previously unidentified structural similarities were seen, including one between a GAAA tetraloop with an unusual fold and the ANYA tetraloop found in phage coat protein binding RNAs. This demonstrates that the cluster analysis approach can uncover unexpected similarities in even small data sets. Such relationships may be modest, as is likely the case for the GAAA/ANYA similarity, or substantial, perhaps leading to the recognition of a novel motif.
In the future, significant refinements in the core algorithms may be possible. For example, appropriate inclusion of more atoms in the analysis in a more general way would be a desirable improvement. This would require development of a universal representation that allows comparison of different nucleotide bases. In the context of the current algorithm design, it will be highly desirable to further relax the requirement that intercomparisons be restricted to RNA fragments of a fixed length. As demonstrated for the larger loops examined here, this might be accomplished by incorporating operations that are often utilized in sequence-based comparisons (e.g., insertions, deletions, and gaps) into the algorithms. A further complication is presented by RNA motifs that are formed by residues that reside on two or more discrete RNA segments such as the well-defined complex E-loop motifs. Analysis of such features may be possible by dividing putative examples into discrete RNA segments, performing pairwise RMSD calculations on the equivalent discrete segments, followed by averaging the individual segment RMSDs to get the overall RMSD for each example being considered. Several of these refinements are currently being pursued.
MATERIALS AND METHODS
In the beginning stages of the work presented here, the three-dimensional coordinates of an individual motif were initially used to probe atomic resolution structures of the large ribosomal RNAs (rRNAs) and other RNA molecules of interest for the presence of similar structural features. The probe molecule was moved along the RNA molecule and RMSD values were calculated for each superimposition between the small probe and every area of the target RNA. From the calculated RMSD values, we could determine how similar the shapes were between the probe and each area of the RNA. All the similar fragments were then pooled and recalculated pairwise to obtain the RMSD values between each two of them. This approach was subsequently generalized. To implement the strategy, we used TCL (Tool Command Language; http://www.tcl.tk/) codes to perform calculations under the VMD program (Humphrey et al. 1996) using a Linux platform (http://www.linux.org). PERL (http://www.perl.org) codes were used for sorting, statistical, extracting, and formatting purposes on the output data derived from VMD/TCL calculations. The TCL and PERL codes used may be obtained by request or at http://prion.bchs.uh.edu/~jhuang/tetraloop.html. The implementation of the UPGMA algorithm found in MEGA2 (Kumar et al. 2001) was used to perform cluster analyses on the PERL-formatted distance matrices derived from the RMSD values. The Swiss-PDB viewer (Kaplan and Littlejohn 2001) was used to observe and analyze the structures of RNA fragments as needed. VMD (Humphrey et al. 1996) and Raster3D (Merritt and Bacon 1997) were utilized together to obtain the rendered images.
RNA structures used for comparisons
Fifteen molecules whose structures have been determined by X-ray crystallography were used in the initial phase of the studies described here. These were Thermus thermophilus 16S rRNA (PDB 1J5E), the 5S and 23S rRNA from H. marismortui (PDB 1JJ2), the 5S and 23S rRNA from Deinococcus radiodurans (PDB 1NKW), the yeast Phe-tRNA (PDB 1EHZ), the mutant P4-P6 domain of Tetrahymena thermophila group I intron (PDB 1HR2), domains 5 and 6 of the yeast AI5G group II intron (PDB 1KXK), the specificity domain of ribonuclease P (PDB 1NBS), domain IV of E. coli 4.5S RNA (PDB 1HQ1), the J III ABC four-way junction RNA of HCV IRES (PDB 1KH6), the sarcin/ricin domain (SRL) from E. coli 23S rRNA (PDB 483D), the RNA of a hammerhead ribozyme (PDB 1HMH), U6 RNA (PDB 1LC6), telomerase mutant RNA (PDB 1Q75), P22 BoxB RNA (PDB 1A4T), and a high resolution (1.41 Å) tetraloop mutant of Sarcin/Ricin domain from E. coli 23S rRNA (PDB 1MSY).
Specific loops from different structures are denoted by the primary sequence followed by the PDB file name in which it occurs, chain number, and the residue number. Thus GAAU:1nkw:0:653–656 corresponds to a GAAU tetraloop in DR 23S rRNA structure. There are some fragments with nonconventional numbering in the PDB files and they are listed below.
6-nt fragments with special numberings
1J5E:190B-190G: 190B, 190C, 190D, 190E, 190F, and 190G; 1J5E:1030–1031: 1030, 1030A, 1030B, 1030C, 1030D, and 1031; 1J5E:1165–1171: 1165, 1166, 1167, 1168, 1169, and 1171; and 1HMH:104–114: 104, 21L, 22L, 23L, 24L, and 114.
Loops of interest in these 15 molecules were identified as follows. Initially, all the hairpin loops in the molecules were located by examination of secondary structures and three-dimensional structures. These identifications were confirmed by RMSD calculations using similar loops as probes to trace each molecule to make sure (after sorting the comparison pairs) that all loops were actually found. Looplike segments (with low RMSD values to known loops), which were not found visually, were included in the sample pool for hairpin loops. This procedure prevented us from overlooking loops of interest, which exist in the three-dimensional coordinates but are not readily seen in secondary structures. Such loop-searching procedures can in the future be fully automated with an RMSD cutoff value. The list of loops in the 15 molecules identified in this way was verified to be in agreement with the loops associated with these structures in the SCOR database (Klosterman et al. 2004). All the loops in the 15 molecules of primary interest were categorized according to the length of the loop ranging from 5 nt to 13 nt. For the purpose of the results presented here, all the loops with 6 nt (closing pair plus four base loop) were then recalculated and clustered according to pairwise RMSD distances. Subsequent to the initial studies, a number of follow-up calculations were conducted in which all tetraloop structures in the SCOR database (Klosterman et al. 2002, 2004) were included. These included loops associated with RNA structure studies conducted by NMR and loops in X-ray studies that are largely redundant with the primary studies included initially. This set includes, e.g., structures with various ligands bound. The coordinates for these loops were extracted from the corresponding PDB files, which were initially downloaded from the Protein Data Bank (http://www.rcsb.org/pdb/).
Superimpositions and RMSD calculations with VMD
Once an RNA length is selected for comparison, all the sequence segments of the same length (6-nt segments with 4-nt loops in the primary examples presented here) in the selected RNA structures are intercompared. Each pair is best fitted and superimposed (Kabsch 1976, 1978) via a transformation matrix calculated by the VMD program (Humphrey et al. 1996), and the RMSD value between each two segments is then calculated according to the following formula:
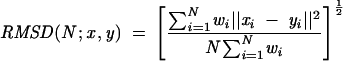 |
where, given N atom positions for structure x and the corresponding N atoms from structure y with a weighting factor w(i), the RMSD is defined. Details are provided in the VMD manual at http://www.ks.uiuc.edu/Research/vmd/.
In the initial studies, 15 atoms per RNA residue were used in the best-fitting and superimposition. RMSD calculations were performed with three alternative weighting options, none, B-factor, or “atomic mass”, as implemented in the VMD software (Humphrey et al. 1996). These were applied to the included atoms. This included all the backbone and sugar atoms, as well as three base atoms in each RNA residue. The base atoms used were N9, C8, C4 on purines and N1, C2, C6 on pyrimidines. When a purine was best fitted to a pyrimidine (or vice versa), N9 was superimposed to N1, C8 to C2 (due to their equivalent positions on the bases, i.e., both of their neighbor atoms are nitrogens), and C4 to C6. The choice of three atoms on the RNA nucleotide bases approximates the orientations and positions of the base plane in three-dimensional space. In follow-up studies in which the loop sequence was constrained by conserved residue(s), as many additional base atoms as possible were used. After the RMSD distance matrices were filled, the data were converted to MEGA2 (Kumar et al. 2001) format with PERL.
Cluster analyses
A standard statistical approach known as unweighted pair-group method with arithmetic mean (UPGMA) as implemented in the MEGA2 software package (Kumar et al. 2001) was used to cluster the RMSD distance matrices of the pairwise loop comparisons. Unlike clustering methods used in evolutionary analysis, UPGMA does not attempt to adjust for changes in rate along branches, which would be irrelevant in the present context. The UPGMA method is based on the following equation:
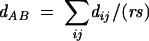 |
where r and s are the numbers of loops in clusters A and B, respectively, and dij is the RMSD distance between loop i in cluster A and loop j in cluster B; dAB is the RMSD distance between cluster A and cluster B. The b-point is defined as half the distance dAB between two clusters A and B. To objectively intercompare tetraloops with larger loops in the current algorithms, it is necessary to keep the total length of the segments being compared the same. Thus, in the case of the 7-nt pentaloops, one base is selected as a “bulge base” and excluded from the comparison. For the 8-nt hexaloops the closing pair is ignored, and for the 9-nt heptaloops a hypothetical bulged base and closing pair were excluded to keep the total length the same.
Additional data files
Additional data files (http://prion.bchs.uh.edu/~jhuang/tetraloop.html) are available at the Fox Lab Web site. The following materials can be found there: (1) Perl and TCL scripts used in the initial cluster analysis studies of hairpin loops of various lengths in the 15 RNA X-ray structures, (2) cluster analysis results for all hairpin tetraloops derived from the SCOR database, and (3) the analyses of SCOR nonredundant data from all the hairpin tetraloops and GNRA tetraloops with extra labeling according to the “SCOR_2_0_1.xml” file obtained from the SCOR Web site.
Acknowledgments
This work was supported in part by grants from the Robert A. Welch Foundation (E-1451) and the National Aeronautics and Space Administration (NAGS5-12366) to G.E.F. H.C.H. thanks Dianhui Zhu for the help in learning PERL in the early stage of this work.
Article and publication are at http://www.rnajournal.org/cgi/doi/10.1261/rna.7104605.
REFERENCES
- Brown, J.W., Nolan, J.M., Haas, E.S., Rubio, M.A., Major, F., and Pace, N.R. 1996. Comparative analysis of ribonuclease P RNA using gene sequences from natural microbial populations reveals tertiary structural elements. Proc. Natl. Acad. Sci. 93: 3001–3006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cannone, J.J., Subramanian, S., Schnare, M.N., Collett, J.R., D’Souza, L.M., Du, Y., Feng, B., Lin, N., Madabusi, L.V., Muller, K.M., et al. 2002. The comparative RNA Web (CRW) site: An online database of comparative sequence and structure information for ribosomal, intron, and other RNAs. BMC Bioinformatics 3: 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Convery, M.A., Rowsell, S., Stonehouse, N.J., Ellington, A.D., Hirao, I., Murray, J.B., Peabody, D.S., Phillips, S.E., and Stockley, P.G. 1998. Crystal structure of an RNA aptamer-protein complex at 2.8 A resolution. Nat. Struct. Biol. 5: 133–139. [DOI] [PubMed] [Google Scholar]
- Duarte, C.M. and Pyle, A.M. 1998. Stepping through an RNA structure: A novel approach to conformational analysis. J. Mol. Biol. 284: 1465–1478. [DOI] [PubMed] [Google Scholar]
- Duarte, C.M., Wadley, L.M., and Pyle, A.M. 2003. RNA structure comparison, motif search and discovery using a reduced representation of RNA conformational space. Nucleic Acids Res. 31: 4755–4761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gendron, P., Lemieux, S., and Major, F. 2001. Quantitative analysis of nucleic acid three-dimensional structures. J. Mol. Biol. 308: 919–936. [DOI] [PubMed] [Google Scholar]
- Gower, J.C. 1975. Generalised Procrustes analysis. Psychometrika 40: 33–50. [Google Scholar]
- Gundelfinger, E.D., Di Carlo, M., Zopf, D., and Melli, M. 1984. Structure and evolution of the 7SL RNA component of the signal recognition particle. EMBO J. 3: 2325–2332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutell, R.R., Larsen, N., and Woese, C.R. 1994. Lessons from an evolving rRNA: 16S and 23S rRNA structures from a comparative perspective. Microbiol. Rev. 58: 10–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutell, R.R., Cannone, J.J., Konings, D., and Gautheret, D. 2000. Predicting U-turns in ribosomal RNA with comparative sequence analysis. J. Mol. Biol. 300: 791–803. [DOI] [PubMed] [Google Scholar]
- Harrison, A.M., South, D.R., Willett, P., and Artymiuk, P.J. 2003. Representation, searching and discovery of patterns of bases in complex RNA structures. J. Comput. Aided Mol. Des. 17: 537–549. [DOI] [PubMed] [Google Scholar]
- Hershkovitz, E., Tannenbaum, E., Howerton, S.B., Sheth, A., Tannenbaum, A., and Williams, L.D. 2003. Automated identification of RNA conformational motifs: Theory and application to the HM LSU 23S rRNA. Nucleic Acids Res. 31: 6249–6257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humphrey, W., Dalke, A., and Schulten, K. 1996. VMD: Visual molecular dynamics. J. Mol. Graph. 14: 33–38, 27–28. [DOI] [PubMed] [Google Scholar]
- Huppler, A., Nikstad, L.J., Allmann, A.M., Brow, D.A., and Butcher, S.E. 2002. Metal binding and base ionization in the U6 RNA intramolecular stem-loop structure. Nat. Struct. Biol. 9: 431–435. [DOI] [PubMed] [Google Scholar]
- Irving, J.A., Whisstock, J.C., and Lesk, A.M. 2001. Protein structural alignments and functional genomics. Proteins 42: 378–382. [DOI] [PubMed] [Google Scholar]
- Jewett, A.I., Huang, C.C., and Ferrin, T.E. 2003. MINRMS: An efficient algorithm for determining protein structure similarity using root-mean-squared-distance. Bioinformatics 19: 625–634. [DOI] [PubMed] [Google Scholar]
- Jucker, F.M. and Pardi, A. 1995. GNRA tetraloops make a U-turn. RNA 1: 219–222. [PMC free article] [PubMed] [Google Scholar]
- Kabsch, W. 1976. A solution for the best rotation to relate two sets of vectors. Acta Crystallogr. A 32: 922–923. [Google Scholar]
- ———. 1978. A discussion of the solution for the best rotation to relate two sets of vectors. Acta Crystallogr. A 34: 827–828. [Google Scholar]
- Kaplan, W. and Littlejohn, T.G. 2001. Swiss-PDB Viewer (Deep View). Brief Bioinform. 2: 195–197. [DOI] [PubMed] [Google Scholar]
- Keenan, R.J., Freymann, D.M., Stroud, R.M., and Walter, P. 2001. The signal recognition particle. Annu. Rev. Biochem. 70: 755–775. [DOI] [PubMed] [Google Scholar]
- Klein, D.J., Schmeing, T.M., Moore, P.B., and Steitz, T.A. 2001. The kink-turn: A new RNA secondary structure motif. EMBO J. 20: 4214–4221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klosterman, P.S., Tamura, M., Holbrook, S.R., and Brenner, S.E. 2002. SCOR: A Structural Classification of RNA database. Nucleic Acids Res. 30: 392–394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klosterman, P.S., Hendrix, D.K., Tamura, M., Holbrook, S.R., and Brenner, S.E. 2004. Three-dimensional motifs from the SCOR, structural classification of RNA database: Extruded strands, base triples, tetraloops and U-turns. Nucleic Acids Res. 32: 2342–2352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar, S., Tamura, K., Jakobsen, I.B., and Nei, M. 2001. MEGA2: Molecular evolutionary genetics analysis software. Bioinformatics 17: 1244–1245. [DOI] [PubMed] [Google Scholar]
- Lee, J.C., Cannone, J.J., and Gutell, R.R. 2003. The lonepair triloop: A new motif in RNA structure. J. Mol. Biol. 325: 65–83. [DOI] [PubMed] [Google Scholar]
- Legault, P., Li, J., Mogridge, J., Kay, L.E., and Greenblatt, J. 1998. NMR structure of the bacteriophage λ N peptide/boxB RNA complex: Recognition of a GNRA fold by an arginine-rich motif. Cell 93: 289–299. [DOI] [PubMed] [Google Scholar]
- Leontis, N.B. and Westhof, E. 2002. The annotation of RNA motifs. Comp. Funct. Genom. 3: 518–524 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merritt, E.A. and Bacon, D.J. 1997. Raster3D: Photorealistic molecular graphics. Methods Enzymol. 277: 505–524. [DOI] [PubMed] [Google Scholar]
- Nagaswamy, U. and Fox, G.E. 2002. Frequent occurrence of the T-loop RNA folding motif in ribosomal RNAs. RNA 8: 1112–1119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nissen, P., Ippolito, J.A., Ban, N., Moore, P.B., and Steitz, T.A. 2001. RNA tertiary interactions in the large ribosomal subunit: The A-minor motif. Proc. Natl. Acad. Sci. 98: 4899–4903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oldfield, T.J. 2002. Data mining the protein data bank: Residue interactions. Proteins 49: 510–528. [DOI] [PubMed] [Google Scholar]
- Qian, B. and Goldstein, R.A. 2002. Optimization of a new score function for the generation of accurate alignments. Proteins 48: 605–610. [DOI] [PubMed] [Google Scholar]
- Quigley, G.J. and Rich, A. 1976. Structural domains of transfer RNA molecules. Science 194: 796–806. [DOI] [PubMed] [Google Scholar]
- Reijmers, T.H., Wehrens, R., and Buydens, L.M. 2001. The influence of different structure representations on the clustering of an RNA nucleotides data set. J. Chem. Inf. Comput. Sci. 41: 1388–1394. [DOI] [PubMed] [Google Scholar]
- Tamura, M., Hendrix, D.K., Klosterman, P.S., Schimmelman, N.R., Brenner, S.E., and Holbrook, S.R. 2004. SCOR: Structural Classification of RNA, version 2.0. Nucleic Acids Res. 32: D182–184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ten Berge, J.M.F. 1977. Orthogonal procrustes rotation for two or more matrixes. Psychometrika 42: 267–276. [Google Scholar]
- Theimer, C.A., Finger, L.D., and Feigon, J. 2003. YNMG tetraloop formation by a dyskeratosis congenita mutation in human telomerase RNA. RNA 9: 1446–1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varani, G., Wimberly, B., Tinoco Jr., I. 1989. Conformation and dynamics of an RNA internal loop. Biochemistry 28: 7760–7772. [DOI] [PubMed] [Google Scholar]
- Wimberly, B., Varani, G., and Tinoco Jr., I. 1993. The conformation of loop E of eukaryotic 5S ribosomal RNA. Biochemistry 32: 1078–1087. [DOI] [PubMed] [Google Scholar]
- Witherell, G.W., Gott, J.M., and Uhlenbeck, O.C. 1991. Specific interaction between RNA phage coat proteins and RNA. Prog. Nucleic Acid Res. Mol. Biol. 40: 185–220. [DOI] [PubMed] [Google Scholar]
- Yang, A.S. 2002. Structure-dependent sequence alignment for remotely related proteins. Bioinformatics 18: 1658–1665. [DOI] [PubMed] [Google Scholar]
- Yang, H., Jossinet, F., Leontis, N., Chen, L., Westbrook, J., Berman, H., and Westhof, E. 2003. Tools for the automatic identification and classification of RNA base pairs. Nucleic Acids Res. 31: 3450–3460. [DOI] [PMC free article] [PubMed] [Google Scholar]