In vitro RNA random pools are not structurally diverse: A computational analysis

Abstract

In vitro selection of functional RNAs from large random sequence pools has led to the identification of many ligand-binding and catalytic RNAs. However, the structural diversity in random pools is not well understood. Such an understanding is a prerequisite for designing sequence pools to increase the probability of finding complex functional RNA by in vitro selection techniques. Toward this goal, we have generated by computer five random pools of RNA sequences of length up to 100 nt to mimic experiments and characterized the distribution of associated secondary structural motifs using sets of possible RNA tree structures derived from graph theory techniques. Our results show that such random pools heavily favor simple topological structures: For example, linear stem–loop and low-branching motifs are favored rather than complex structures with high-order junctions, as confirmed by known aptamers. Moreover, we quantify the rise of structural complexity with sequence length and report the dominant class of tree motifs (characterized by vertex number) for each pool. These analyses show not only that random pools do not lead to a uniform distribution of possible RNA secondary topologies; they point to avenues for designing pools with specific simple and complex structures in equal abundance in the goal of broadening the range of functional RNAs discovered by in vitro selection. Specifically, the optimal RNA sequence pool length to identify a structure with x stems is 20x.

INTRODUCTION

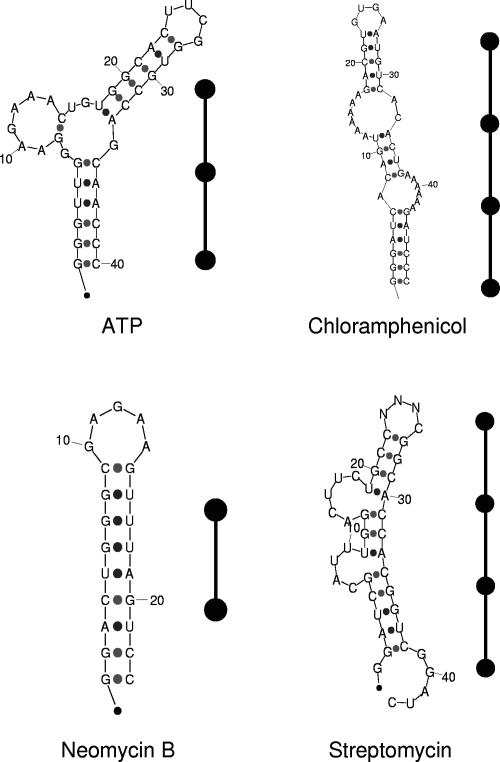
RNA in vitro selection technology has greatly advanced the field of RNA structure and function. Indeed, in vitro selection experiments have revealed novel functional RNAs from random sequence pools, including a wide range of RNA aptamers that bind to particular compounds, such as ATP, antibiotics or proteins, and catalytic RNAs (Wilson and Szostak 1999; Hodgson and Suga 2004); see the collection of several hundred aptamers in the Aptamer Database (http://aptamer.icmb.utexas.edu). However, an analysis of existing aptamers has shown that RNA sequences isolated from selection experiments tend to have simple topologies (Bae et al. 2002; Fukusho et al. 2002; Khoo et al. 2002; Komatsu et al. 2002; Ulrich et al. 2002; Zinnen et al. 2002; Meli et al. 2003; Laserson et al. 2004). That is, linear or slightly branched structures occur far more often than highly compact structures. For example, aptamers that bind to ATP, chloramphenicol, neomycin B, and streptomycin all have simple, linear stem–loop structures (Laserson et al. 2004; see Figure 1). Moreover, while in vitro selection is efficient when searching for an RNA sequence that binds to a specific ligand, it is often unsuccessful in discovering novel functional RNAs, such as ribozymes because of their rarity in random pools (Sabeti et al. 1997); self-ligating ribozymes are prominent examples of in vitro selected ribozymes (Schultes and Bartel 2000). Novel and improved ribozymes have also been found using in vitro experiments by exploiting structural modules of existing RNAs (Jaeger et al. 1999; Ohuchi et al. 2002, 2004; Yoshioka et al. 2004). The frequency of occurrence of a functional (or active) RNA in random pools also depends on how the functional properties are defined; for example, many sequence solutions are possible when the definition of an aptamer involves a range of dissociation constants, as done in recent selection experiments (Carothers et al. 2004). A theoretical understanding of such sequence/structural/functional yields from random pools is crucially needed because an understanding of motif distribution can help in the discovery of new RNA motifs by in vitro technology and this, in turn, can lead to new functional RNAs and applications.

FIGURE 1.

Four antibiotic-binding aptamer structures and their tree graphs.

In recent years, efforts have been made toward understanding pool complexity via statistical analysis of RNA secondary structures (Fontana et al. 1993), combinatorial analysis of the number of interacting segments in a random RNA sequence (Sabeti et al. 1997; Knight and Yarus 2003), information theory (Carothers et al. 2004), and design of partially structured pools to improve selection of high affinity aptamers (Davis and Szostak 2002). In particular, statistical analysis of RNA secondary structures in random pools via computational folding has determined the characteristic distributions of bases in stacks, loops, junctions, and free ends (Fontana et al. 1993). Later, Schuster and Stadler (2002) found that stable conformations in random pools tend to be linear or slightly compact structures. Combinatorial analysis of random sequences revealed that the probability of finding a structural motif, as specified by the number of interaction segments, increases with sequence length; structural complexity in this approach is determined by the number of elements forming stems. Interestingly, Szostak and collaborators have recently used an informational measure of RNAs (a combination of both sequence and base-pairing contents) to show the plausibility of a general relation between the complexity of RNA structures and their functional activity (Szostak 2003; Carothers et al. 2004). Furthermore, functional RNA molecules are thermodynamically different from the vast majority of random sequences (Higgs 1993, 1995; Schultes et al. 1997; Seffens and Digby 1999; Kitagawa et al. 2003), implying that functional molecules are not common. These studies have provided insights into the properties of random pools and highlighted the importance of quantifying structural complexity.

Here we use complete sets of RNA topologies from graph theory to quantify shape complexity in random pools. Understanding shape distribution is significant because functional RNA classes are correlated with their secondary folds; for example, 5S ribosomal RNA, tRNA, and hepatitis delta virus ribozyme have distinct topologies suited for their biological functions. Thus, quantifying the distribution of distinct RNA topologies in random pools helps interpret the range of functional RNAs that such pools can yield by in vitro selection technology.

Recently, we developed and applied graphical representation and enumeration of 2D RNA topologies to systematically catalog libraries of existing and hypothetical motifs (Gan et al. 2003); see our RNA-As-Graphs (RAG) Web resource (http://monod.biomath.nyu.edu/rna) for a complete catalog of tree and pseudoknot topologies, arranged by vertex number and motif complexity (Fera et al. 2004; Gan et al. 2004). These theoretically enumerated RNA structures covering RNA secondary-structure repertoire allow a comprehensive assessment of structural diversity in random pools with different sequence lengths. Briefly, an RNA graph is a formal construct composed of lines (edges) and linking nodes (vertices) representing an RNA secondary structure; for tree graphs, stems are represented as edges and loops/bulges/junctions as vertices. Here we use cataloged tree topologies, measures of graphs, and the Vienna RNA folding algorithm (Hofacker 2003) to characterize the distribution of RNA secondary structures in random pools. While our analysis is similar to that of Fontana et al. (1993) in that tree graphs are used to compile statistics of RNA structures, it differs from that work in two major ways: We employ exhaustive sets of enumerated graphs, and our tree graphs emphasize shape or topology, whereas those of Fontana et al. focus more on base-pair information. Our enumerated tree graphs provide a more pertinent analysis of structural diversity in RNA pools.

This analysis is applied here to five generated random RNA pools, containing sequences which are of length 25, 40, 60, 80, and 100 nt, respectively. We quantify the distribution of associated secondary-structural motifs using tree graphs and graph theory measures of size and complexity (particularly, tree diameter and second smallest Laplacian eigenvalue, which are defined in the Materials and Methods section). Our results show that such random RNA pools heavily favor (>90%) simple topological structures like linear stem–loop and low-branching motifs, as confirmed by many known aptamers (Bae et al. 2002; Fukusho et al. 2002; Khoo et al. 2002; Komatsu et al. 2002; Ulrich et al. 2002; Zinnen et al. 2002; Meli et al. 2003; Laserson et al. 2004). For example, the 25-nt and 40-nt pools are almost completely populated by hairpin and stem–bulge–stem–loop structures. This finding explains why complex structural motifs with high-order junctions are rare in selected aptamers and ribozymes. More generally, we show that random sequences do not lead to a uniform distribution of RNA secondary topologies regardless of pool size and sequence length. This is likely an outcome of the thermodynamics of RNA folds. Moreover, we find that structural complexity rises with sequence length and that each random pool is dominated by a specific tree structural class (characterized by vertex number, V) determined by sequence length. Interestingly, the most abundant tree structures in pools follow a simple rule: an L-nt pool has the most abundant structures with ~L/20 stems (L/20 stems correspond roughly to the number of tree graph vertices minus one). Thus, 40-, 60-, 80-, and 100-nt pools have abundant two-, three-, four-, and five-stem structures, respectively. The importance of increasing pool length to access complex structures (with rare activities) is also supported by combinatorial considerations, although only the number of paired elements is predicted and not the abundance of specific topologies (Sabeti et al. 1997; Knight and Yarus 2003).

Our analyses have implications for designing sequence pools possessing greater structural diversity than those found in random pools. Ideally, to access various functional RNAs, including structurally complex motifs, the pool should be engineered to contain a uniform distribution of simple and complex topologies specified by enumerated tree graphs. Already, designing structured RNA pools has been suggested, although not guided by graphical analysis of structural diversity (Davis and Szostak 2002). Another implication of our analysis is that the optimal sequence length for a target structure with known number of stems (S) should be ~20S. Since the number of possible topologies rises with the number of stems (according to graph theory), our simple rule can be used as a guide to access complex structures by optimally choosing sequence length. This could help increase efficiency of in vitro selection experiments by reducing requirements for sequence synthesis.

RESULTS

The technical concepts and methods used to derive the results are detailed under Materials and Methods, including graphical representation of RNA, the RNA tree library, Laplacian eigenvalue and tree diameter measures of RNA structures, conversion of RNA structures into tree graphs, and sources of error in computational methodology.

Pool generation and filtering

Here we describe how, equipped with sets of possible RNA tree structures (Fig. 2), we explore the distribution of different trees in the random RNA pools used for in vitro experiments. Using the Mersenne twister pseudorandom number generator (Matsumoto and Nishimura 1998), we generated five random RNA pools of different sequence lengths (25, 40, 60, 80, and 100 nt), each pool consisting of 10⁴ components. (Below, we discuss the significance of using pools of this relatively small size compared to the pool size used in wet experiments.)

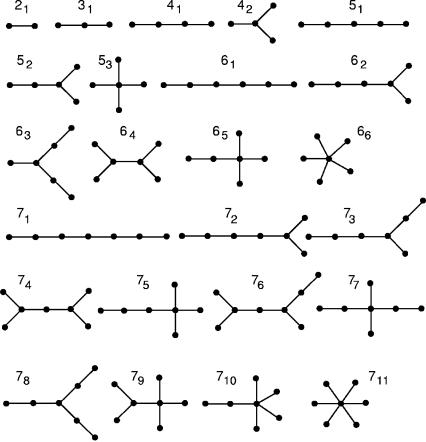
FIGURE 2.

Complete sets of tree graphs having two to seven vertices. Each graph is assigned an identification number (ID) for easy reference.

In each pool, all sequences were generated as input into RNAfilter, a program that converts the secondary structures predicted by Vienna RNAfold (Hofacker 2003) into their respective tree diagrams; the Vienna RNAfold program can fold sequences into tree structures but not pseudoknot topologies. Within each pool, we calculated separately the distribution of structures by vertex number, and the distribution of motifs (tree structures) for a given vertex subpool. For the 100-nt pool, we also computed the distribution of structures by compactness as measured using graph diameter and second smallest Laplacian eigenvalue.

The above statistics were calculated using all sequences in the pool. In addition, we analyzed the 100-nt pool by imposing a free-energy restriction, based on free-energy values determined by Vienna RNAfold (Hofacker 2003) to remove sequences with unstable folds from the pool that had a free-energy value less than the peak of the distribution (−23 kcal/mol). This filtering process allowed us to analyze 65%–78% of the sequences in the original pool. We also imposed two other free-energy constraints: One cutoff was set to be the average free energy (−27 kcal/mol) in the pool (leaving us somewhere between 42% and 49% of the sequences to analyze), and another cutoff (−31 kcal/mol) was randomly selected to be more stringent than the first two (leaving us somewhere between 13% and 30% of the sequences to analyze). We found that vertex number and motif distributions are not sensitive to the free-energy cutoffs. Below, all results are reported without cutoffs unless indicated otherwise for the 100-nt pool.

Distribution of structures by vertex number

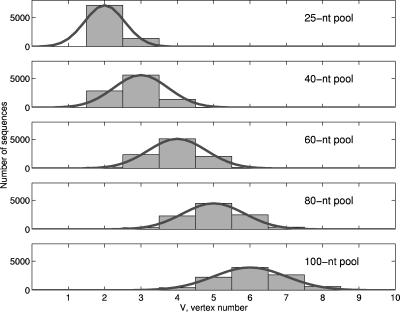
The vertex number V, an indication of the structural complexity, corresponds to the number of structural elements, including bulges, loops, and junctions (chain ends also count as a vertex), in an RNA secondary structure. The mathematically possible V-vertex tree structures are shown in Figure 2; the simplest structure is a hairpin containing a loop and chain ends (V= 2). Figure 3 shows the vertex number distributions for structures in all five random RNA pools. In the 25-nt pool, only V= 2, 3 structures contribute significantly. The hairpins (V=2) and stem–bulge–stem–loops (V= 3), respectively, account for 70% and 15% of structures in the pool; 15% of sequences in the pool are unstructured. As the pool sequence length increases, structures with higher vertex numbers also contribute, diminishing the contribution of the dominant vertex number structures. For example, in the 100-nt pool, V= 4–8 tree structures are abundant with the dominant six-vertex structures accounting for ~40%. An interesting feature of the plots in Figure 3 is that the peaks for 40-, 60-, 80-, and 100-nt pools are at three, four, five, and six vertex, respectively. We thus infer the relation

FIGURE 3.

Distribution of structures by vertex number (unfiltered data) and Gaussian fit: 25-nt pool (centered at two vertices), 40-nt pool (centered at three vertices), 60-nt pool (centered at four vertices), 80-nt pool (centered at five vertices), and 100-nt pool (centered at six vertices). See Figure 2 for elaboration of the structures for each vertex number.

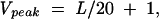(1)

where V_peak is the peak’s vertex number and L is the pool sequence length. This relation allows the prediction of the stem number (V−1) of the most abundant structures in L-nt random pools. Significantly, for GTP-binding aptamers, stem number is correlated with binding affinity (Carothers et al. 2004), indicating that our relation may be used to improve the yield of functional molecules.

The distributions of secondary structures by vertex number, except for the 25-nt and 40-nt pools, have normal probability plots. We thus fitted the plots for the five pools using the Gaussian function P(V) = α exp[−(V−V_peak)²/(2β²)], where V_peak and α are the location and height of the peak, and β is the distribution’s width, as shown in Figure 3. The width of the Gaussian function varies from pool to pool: β = 0.55, 0.75, 0.80, 0.85, and 1.00 for the 25-, 40-, 60-, 80-, and 100-nt pools, respectively. For the 25-nt and 40-nt cases, the Gaussian distribution in the range 0<V<2 is not physically meaningful since the simplest and smallest secondary fold is a hairpin (V = 2). Using relation 1, we obtain the distribution as a function of vertex number and pool sequence length:

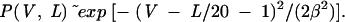(2)

This fitting function works well for all pools with length 60 and greater. (The 40-nt pool has an asymmetric distribution with twice as many two-vertex structures compared with four-vertex motifs.)

We also determined the effects of energetic filters and pool size on vertex-number distributions. Surprisingly, the vertex-number distribution is not sensitive to our three free-energy cutoffs. For example, the tree abundance for any V using no cutoff versus cutoffs of −23, −27, −31 kcal/mol has a variation of ~1% for the 100-nt pool analyzed. To ascertain that our observed distributions were not a result of our sample size (10⁴ RNA sequences), we also determined the vertex-number distribution of the 40-nt pool for pool sizes of 10³, 0.5 × 10⁵, and 10⁶ sequences. As shown in Table 1, the distribution of structural motifs by vertex number is not sensitive to the pool size. This result reflects the simplicity of tree graphs specifying only shape rather than more detailed information about the structural elements (e.g., sizes of stems, bulges, and loops). The distribution of the detailed aspects of structural elements (e.g., base numbers in stems, loops, and bulges) becomes relevant when similar motifs must be distinguished.

TABLE 1.

Effect of pool size on distribution of percent of sequences in 40-nt pools

V/pool size	103	104	0.5 × 105	106
2	29.67	28.94	28.88	29.58
3	57.32	56.46	56.63	56.87
4	12.71	14.30	14.21	13.32
5	0.30	0.30	0.27	0.22

Distribution of structures by tree topology and diameter

The distribution of structures by vertex number quantifies the abundance of various tree structure classes, as displayed in Figure 2. Information about the abundance of individual tree structures will yield more specific properties of random pools. For this purpose, we assign a motif identification (ID) number to each tree structure in Figure 2. This ID is indexed as n_m, where n is the motif’s vertex number (V), and m indicates the order in which the motif occurs within the V-vertex tree structures. For example, motif ID numbers 5₁ and 7₁₁ refer to specific five- and seven-vertex trees, respectively. We order motifs by increasing topological complexity or compactness, as measured by the second smallest Laplacian eigenvalue λ₂ (Gan et al. 2004); in addition, we use graph diameter d to analyze compactness of structures in random pools (see Materials and Methods).

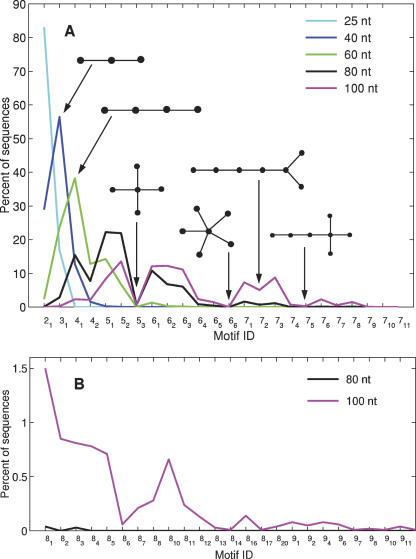
Figure 4 shows the abundance of 47 tree motifs with V < 10 in our five random pools. Two features emerge from this plot: (1) the diversity of motifs increases with sequence length, as expected; and (2) the distribution within each pool strongly favors elongated over compact structures (small m values for each n in the motif ID n_m). The first feature is clearly evident by comparing the 25-nt pool with the 80-nt or 100-nt pool. The 25-nt pool is dominated by two- and three-vertex structures, whereas the 100-nt pool contains significant percentages of five-, six-, and seven-vertex structures, including a few percentages of eight- and nine-vertex structures. The second feature is manifested by the multiple peaks in the motif distribution curves (Fig. 4). In the 80-nt pool, the motif distribution curve has peaks at motifs 4₁, 5₁, 5₂, 6₁, 7₁, and 8₁. These motifs correspond to unbranched or low-branching tree structures (Fig. 2). Also evident are the minima occurring at motifs 4₂, 5₃, and 6₄, which are branched structures. Motifs with high-order junctions (6₅, 6₆, 7₅, 7₆, etc.) are rare or absent in the 80-nt pool. The 100-nt pool has a similar trend as the 80-nt pool, with significant proportions of 5₁, 5₂, 6₁, 6₂, 6₃, 7₁, 7₂, and 7₃ motifs and negligible representation of complex motifs such as 5₃, 6₅, 6₆, 7₆, 7₇, 7₈, 7₉, 7₁₀, 7₁₁, 8₆, and 8₁₃. The distribution of structures by graph diameter in the 100-nt pool conveys a similar pattern (data not shown). The distributions for five-, six-, and seven-vertex structures are skewed toward elongated structures with larger diameters.

FIGURE 4.

Distribution of structural motifs for various pools. (A) Motif distribution of 2–7 vertex structures. (B) Motif distribution of eight and nine vertex structures. The tree motifs are indexed (ID) by vertex number and order within the group (e.g., 5₁, 5₂, 5₃ for the three five-vertex members—see Fig. 2). Note that any motif IDs not represented on the horizontal axis are omitted because none of the sequences in the pool folded to such a structure.

Distribution of structures by pool sequence length

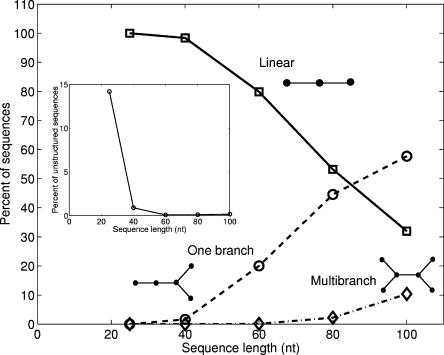
Figure 5 compares the percentages of three categories of tree structures as a function of pool length. We define the following tree structure categories in increasing complexity: unbranched, singly branched, and multibranched trees. This definition of motif complexity is more intuitive than the graph diameter and Laplacian eigenvalue measures. As shown in Figure 5, the 25-nt and 40-nt pools are completely populated by unbranched structures, represented by hairpins (two-vertex) and two-stem (three-vertex) structures. The frequency of such structures declines rapidly with pool sequence length, approaching ~30% for the 100-nt pool. In contrast, the singly branched and multibranched structures increase monotonically with sequence length. The proportion of singly branched trees equals or exceeds unbranched motifs when the sequence length is 80 nt or greater. However, the multibranched structures remain rare even in the 100-nt pool, where it accounts for only ~10% of such folds.

FIGURE 5.

Percent of sequences in each pool that fold to linear structures (represented by solid line), structures with one branch (dashed line), and structures with two or more branches (dash-dotted line). (Inset) Percent of structures in each sequence pool that could not be properly folded into a tree structure by the Vienna RNAfold; these unstructured sequences could not be converted into tree diagrams.

Abundance of structured RNAs

We consider a “structured RNA” as a secondary fold that can be converted into one of the tree graphs in Figure 2. This is a reasonable minimal requirement since most folds possess at least a stem–loop (V= 2). Folds by Vienna RNA-fold that do not possess any base pairs or form isolated, single base pairs cannot be converted into a tree graph (our rules state that a stem must have two or more complementary base pairs) (Gan et al. 2003). Figure 5 (inset) shows the percentage of unstructured RNAs as a function of pool length. The 25-nt and 40-nt pools have 14% and 1% unstructured RNAs, respectively, whereas larger pool lengths are completely dominated by structured RNAs. This result reflects the propensity of nucleic acid bases to form complementary base pairs. That is, the probability of forming stems from sequences with only four base types is high, as shown in other folding experiments and theoretical studies (Fontana et al. 1993; Schuster et al. 1994). Short sequences are less likely to be structured because of fewer possibilities of forming base pairs to stabilize their folds.

Generally, structured RNAs can be defined using the vertex number (V), or the number of stems formed (V−1); above, we used a minimal value V= 2 (i.e., one stem). The proportions of structured RNAs for other V cutoff values can be calculated from the data in Figure 3. If we use the V= 3 cutoff, we find that the 40-nt pool has only 70% structured RNAs compared to 99% for the V= 2 cutoff. By this criterion, the 60-, 80-, and 100-nt pools are still almost completely populated by structured RNAs. The 100-nt pool, in particular, consists of mostly five or more vertex structures.

Estimates of functional structures in the 100-nt random pool

Data from many in vitro selection experiments suggest that the probability of finding a functional sequence in a random pool is typically 10⁻¹⁰ (Wilson and Szostak 1999). This implies that there are ~10³ functional molecules in a pool of 10¹³ sequences. Results also imply that the probability of finding a functional molecule of length n is higher than 4⁻ⁿ because many variants of a molecule can perform the same function, as found for hammerhead ribozymes (Salehi-Ashtiani and Szostak 2001) and GTP-binding aptamers (Carothers et al. 2004). Such experimental estimates of the frequency of functional molecules can be combined with our data on motif distribution (Fig. 4) to calculate the expected number of sequences with functional properties for each tree structure. This yields the estimate that the number of functional sequences is 10³ times the abundance of a tree topology in the random pool.

Our simple estimate, based on the 100-nt pool with freeenergy cutoff of −23 kcal/mol, shows that most functional sequences belong to five-, six-, seven-, and eight-vertex structures; the expected numbers of functional sequences for these vertex numbers are 212, 397, 274, and 7, respectively. We find that functional sequences folding to two-, three-, four-, and nine-vertex structures are rare. Within each vertex subpool, dramatic differences in abundance are observed. For example, the three five-vertex tree motifs 5₁ (λ₂ = 0.3820), 5₂ (λ₂ = 0.5188), and 5₃ (λ₂ = 1.0000) are represented by 82, 124, and seven possible functional sequences, respectively. The 5₁ motif is unbranched, 5₂ has a three-stem junction, and 5₃ is a star-shaped tree with a four-stem junction. If structural complexity is measured by the degree of branching, then the occurrence of functional molecules drops sharply with complexity. The frequency distribution of functional sequences is similarly broad for the seven-vertex subpool. The most abundant motifs are 7₁ (λ₂ = 0.1981), 7₂ (λ₂ = 0.2254), and 7₃ (λ₂ = 0.2603) with 75, 49, and 92 possible functional sequences, respectively. In contrast, the motifs 7₅, 7₉, 7₁₀, and 7₁₁ are estimated to have less than one functional sequence. Consequently, functional molecules for these motifs will not likely be found in the 100-nt random pool. Similar estimates of the abundance of functional structures can be made for other pool lengths.

DISCUSSION

Our analysis of tree-motif distribution in random sequence pools using direct folding of RNA sequences in various pools quantifies the abundance of possible tree structures with or without known functional properties. Results show that simple secondary motifs (e.g., linear and low branching structures) commonly occur in 25–100-nt pools, whereas highly branched structures are rare. The rarity of complex structures in random pools is also suggested by several in vitro selection experiments and estimates based on statistical and combinatorial considerations (Sabeti et al. 1997; Wilson and Szostak 1999; Knight and Yarus 2003; Carothers et al. 2004). For example, GTP-binding aptamers having simple stem–loop (Class II) and stem–bulge–stem–loop (Class I) motifs are common, whereas those with extra bulges and/or stems are rare (Carothers et al. 2004). Significantly, the binding affinity of GTP aptamers rises with stem number, highlighting the importance of increasing the presence of complex structures in selection pools. Our results on structural distribution, either by vertex number (Fig. 3) or specific motif (Figs. 4, 5), might help experimentalists assess the chance of finding particular motifs or of finding a particular class of structures.

The results in Figures 3–5 clearly show that sequence length is a strong determinant of structural diversity in random pools. As sequence length increases, the motif distribution shifts toward higher vertex numbers or stems (Fig. 3), and the population of branched motifs increases while that of unbranched structures decreases. Sabeti et al. (1997) also reached the conclusion that complex structures and functions can be accessed by increasing sequence length; however, they used a combinatorial analysis of motifs without folding specific sequences, estimating free energies, or reference to specific topologies. Accessing complex structures by increasing sequence length indefinitely is not a desirable solution; according to our estimate of equation 1, a target structure with S stems (V = S + 1) can be obtained optimally from a pool length L=20S.

We illustrate this application of relation 1 for GTP-binding aptamers. GTP aptamers with varying binding affinities, characterized by dissociation constant K_d, range from 31 to 69 nt; see Table 2. Specifically, the three-stem Class V GTP aptamer with a high binding affinity (K_d = 17 nM) corresponds to the 4₁ motif in Figure 2. Our motif distribution patterns in Figure 4A and Table 2 suggest that the 60-nt pool has the highest abundance of 4₁ tree motifs (38%) and therefore is the optimal pool length for finding the Class V GTP aptamer. Indeed, the actual length (68 nt) of this aptamer is comparable with this optimal pool length (60 nt). As shown in Table 2, there is a rough agreement between predicted pool length and actual aptamer length for other GTP aptamers. Further, as we have shown elsewhere, the empirical formula 1 is a good approximation for natural functional RNAs (Gan et al. 2003).

TABLE 2.

Percent of tree motifs in computed random pools (columns 2–6) and properties of GTP-binding aptamers reported in Carothers et al. (2004) corresponding to different tree motifs

Motif ID	25 nt	40 nt	60 nt	80 nt	100 nt	Kda	Lb (nt)
21	83	29	2	—	—	250–900	30–56
31	17	56	24	3	—	30–8000	41–60
41	—	13	38	15	2	17	68
52	—	—	7	22	14	9	69

^aDissociation constant.

^bAptamer length.

Clearly, our RNA pool analysis emphasizes the need to generate biased, nonrandom sequence pools possessing greater structural complexity to access rare RNA folds (e.g., highly branched motifs). This effort is especially important for improving the in vitro selection technology since high-affinity aptamers and complex functional RNAs are rarely found in random pools, as shown by several recent experimental and theoretical studies (Sabeti et al. 1997; Davis and Szostak 2002; Knight and Yarus 2003; Carothers et al. 2004). One intriguing avenue is to design sequences yielding a uniform distribution of tree structures (Fig. 2) used to characterize the pools. This will ensure that simple and complex structures are sufficiently present in the pool. Indeed, it was shown that engineering even partially structured pools with a constant stem–loop segment in the GTP-binding element already yielded higher affinity aptamers than those found in totally random pools (Davis and Szostak 2002). However, a more general approach is required to generate structured pools (see Conclusion).

An alternative approach for enhancing the selection of complex functional RNAs is to use modules of existing RNAs to generate pools possessing variants of specific structures. The structural variants are obtained by introducing short random (variable) sequence regions in constant regions specifying the module of an existing RNA. Specifically, the P3–P7 domain of the group I ribozyme has been successfully exploited to enhance the ribozyme’s activity (Ohuchi et al. 2002, 2004), and the P4–P6 domain used to evolve a complex ligase ribozyme (Jaeger et al. 1999; Yoshioka et al. 2004). Intriguingly, RNA modules have also been used to construct complex assemblies with interesting functional and technological possibilities (Westhof et al. 1998; Jaeger et al. 2001; Ikawa et al. 2002; Chworos et al. 2004).

Nucleotide base composition is yet another factor influencing the structural distribution in random pools. As done in experimental studies, we have performed our analysis based on a uniform base distribution (25% A, C, G, and U). Several theoretical studies have shown that variation of base composition can alter the distribution of structures in random pools (Fontana et al. 1993; Schultes et al. 1997). To test the influence of nonuniform base composition, we also performed calculations for 40-nt and 100-nt pools with two different base compositions: (1) 20% A, U and 30% G, C, and (2) 30% A, U and 20% G, C. For the 40-nt pool, a higher percentage of C, G bases (case 1) increases the proportion of higher vertex structures, whereas a lower percentage of C, G bases (case 2) increases the proportion of lower vertex structures. For the 100-nt pool, the vertex-number distribution remains largely unchanged. It is likely that small RNA structures (~40 nt) are more significantly influenced by base composition variation than large RNA structures, a finding consistent with that by Schultes et al. (1997). Thus, our preliminary calculations suggest that the effects of base composition on structural distribution should be further investigated in future studies.

A limitation of the present analysis is that the Vienna RNA folding program cannot predict pseudoknot folds, yet these topologies have been identified in random pools (Wilson and Szostak 1999; Stuhlmann and Jaschke 2002). The abundance of pseudoknots is expected to increase with sequence length, as shown in our recent theoretical analysis of RNA structure space (Kim et al. 2004). Existing pseudoknot folding algorithms, for example, PKNOTS by Rivas and Eddy (1999), is not efficient for folding large sets of sequences as attempted here. Other numerical limitations are discussed at the end of the Materials and Methods section.

CONCLUSION

An analysis of five RNA pools reveals that the probability distribution of secondary structures in random sequence pools is not uniform respect to complete sets of tree topologies derived from graph theory (Harary 1969; Gan et al. 2003). While vertex number (stem number) has a normal distribution in some pools, each random sequence pool heavily favors structures of a particular vertex number according to the relation V_peak = L/20 + 1. This simple relation allows the design of optimal pool lengths for specific target structures with a known or desired number of stems. Furthermore, random pools are strongly biased to form RNAs with simple, linear and low-branching topologies. This trend is more pronounced in pools consisting of short sequences of RNA (25, 40, and 60 nt in length) than in pools consisting of longer RNA sequences (80 and 100 nt), in agreement with other analyses (Sabeti et al. 1997; Knight and Yarus 2003). Thus, while some motifs are commonly found in random RNA pools, other fold patterns occur rarely. This explains why functional RNAs possessing complex folds are largely absent in in vitro selection experiments using fully random pools (Carothers et al. 2004). Our quantitative characterization of structural diversity in random pools and its dependence on pool length predict nonuniform abundance of specific tree structures, suggesting design of sequence pools to improve the yield of target and underrepresented structures.

Such a characterization of random RNA pools immediately suggests methods that can enhance variation in an RNA pool and can increase the probability of finding a functional RNA. For example, the random sequence pool can be designed in a way that will maximize the likelihood of finding a specific set of motifs by pre-selecting starting topologies combined with biased pool synthesis; we are currently exploring this approach (H.H. Gan and T. Schlick, in prep.). These and other specific proposals for such a combination of experiment and theory into a targeted design approach may be the most productive way to identify rare functional RNAs and contribute to the discovery and synthesis of novel RNAs.

MATERIALS AND METHODS

Graphical representation of RNA secondary structures

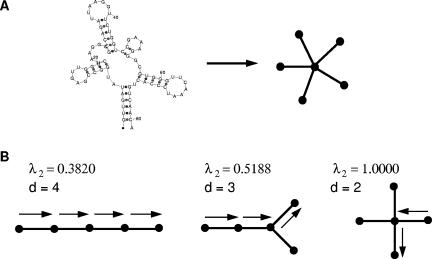
Several tree graphical representations of RNA structures have been used for analyzing structural similarity (Le et al. 1989; Shapiro and Zhang 1990) and for estimating RNA’s structural repertoire (Gan et al. 2003). Our tree representation emphasizes RNA shape rather than information at the base-pair level (Gan et al. 2003). Figure 6A shows an unlabeled star-shaped tree for the tRNA secondary structure.

FIGURE 6.

(A) The star-shaped six-vertex tree diagram represents a tRNA structure with five stems. (B) Diameter (d) and second smallest Laplacian eigenvalue for five-vertex tree graphs.

To represent a secondary structure as an unlabeled tree graph, four rules apply: (1) A bulge, hairpin loop, or internal loop is considered a vertex (•) when there is more than one unmatched nucleotide or noncomplementary base pair. (2) A junction (the location where three or more stems meet) is considered a vertex. (3) The 3′- and 5′-ends of a helical stem are considered a vertex. (4) An RNA stem, defined as having more than one consecutive complementary base pair, is represented as an edge (—); the complementary base pairs are AU, GC, and GU. Detailed descriptions of these rules can be found in our previous work (Gan et al. 2003) and at the RNA-As-Graphs Web resource (Fera et al. 2004; Gan et al. 2004).

Repertoire of RNA tree topologies

A fundamental advantage of RNA graphical representation is the enumeration of all possible RNA shapes, including existing and hypothetical topologies (Gan et al. 2003). Knowing the entire repertoire of RNA trees allows assessment of motif abundance in random pools. The complete repertoire of unlabeled trees for any V has been enumerated analytically by Harary and Prins using a counting polynomial (Harary and Prins 1959). For V from 1 to 12, the numbers of topologically distinct trees are 1, 1, 1, 2, 3, 6, 11, 23, 47, 106, 235, and 551, respectively. These sets of distinct graphs represent libraries of theoretically possible RNA topologies with different sequence lengths. As a rule, RNA length (L) is related to vertex number, L = 20(V−1). The explicit tree structures for V < 11 are displayed in Harary (1969); they are also cataloged and ranked by motif ID and Laplacian eigenvalues in our RAG Web resource (http://monod.biomath.nyu.edu/rna). Figure 2 shows complete sets of trees for V up to 7.

Spectral analysis of RNA graphs: Laplacian eigenvalues

The RNA topological properties can be quantitatively analyzed using spectral techniques in graph theory (Fiedler 1989; Gan et al. 2004). Such tools establish the relation between a graph (topology) and the eigenvalues corresponding to the matrix representation of the graph (the matrix specifies the degree of connectivity among the nodes). Specifically, we use the Laplacian (V by V) matrix defined as D−A, where A and D are the adjacency and degree matrices of the graph, respectively. The elements (a_ij) of the V × V symmetric matrix A specify the number of links or edges connecting i and j vertices; the elements (d_ij) of the square diagonal matrix D specify the valency or the degree of connectivity of vertex i. Although a graph’s connectivity pattern is specified by the full Laplacian spectrum (λ₁, λ₂, . . ., λ _V), the second smallest nonzero eigenvalue (λ₂) is a measure of the compactness of an RNA tree graph. For example, for a specific V, a branched tree has a larger λ₂ value compared with that for an unbranched structure.

We also assign a motif identification number (ID), derived from its ordering by λ₂, to each tree, as shown in Figure 2. The motif ID is indexed as n_m, where n is the motif’s vertex number (V) and m indicates the order in which the motif occurs within the V-vertex tree structures.

Diameter of RNA graphs

While λ₂ is a useful measure of the compactness of a tree graph, the number of different λ₂ values increases with the number of vertices. An alternative and intuitive choice for measuring graph compactness is to use graph diameter. The diameter (d) of a tree graph is the largest number of vertices that must be traversed in order to travel from one vertex to another (Chung 1989). Formally, the graph diameter is related to λ₂ by the following lower and upper bounds,

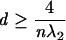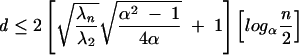where α is any real number >1, and the choice of n depends on α (Mohar 1991). These bounds show that d and λ₂ likely have an inverse relationship, although no equality relation has been found.

Figure 6B displays three five-vertex tree graphs and their diameters; the unbranched tree has the largest diameter (d=4, λ₂=0.3820), while the highly branched tree has the smallest diameter (d=2, λ₂=1.000). When the number of vertices is small (seven or less), the diameter and the second eigenvalue provide similar measures of compactness. That is, as the size of the diameter decreases, the size of λ₂ increases. Observe that while larger values of λ₂ represent the more compact structures, smaller values of the diameter represent the more compact structures. It is also important to note that in the case that a structure has eight or more vertices, the diameter of a graph and the second eigenvalue are no longer equivalent measures of compactness (data not shown).

Converting RNA structures to tree graphs

We use the Vienna RNAfold algorithm to determine the 2D RNA fold and its corresponding free energy (Hofacker 2003). The topology of the fold is determined using its tree graph and its (Laplacian) spectral properties as implemented in our RNAfilter program. RNAfilter uses the base-pairing information in the .ct file generated by the RNAfold program and tree graph rules to convert a secondary fold into a tree graph and then computes its spectral properties (e.g., Laplacian eigenvalues). Our automated computational procedure is efficiently executed by determining consecutively each fold and its corresponding tree graph, approximately represented as a complete spectrum of Laplacian eigenvalues.

Sources of error in computational methodologies

There are several possible sources of error that can potentially affect our distributions of structural motifs, including the algorithm for converting secondary structures into tree graphs (RNA filter program), pool size, pseudorandom number generator, and RNA folding programs:

1. In each pool, the RNAfilter program could not properly convert <0.5% of the sequences into tree diagrams (Fig. 2) because of unusual base-pairing configurations. Discarding such a small fraction of sequences does not affect our conclusions.

2. Our pool sizes are of order 10⁴ sequences compared to the ~10¹³ synthesized in typical in vitro selection experiments. However, our analyses in Table 1 of 10,000-member versus 1,000,000-member 40-nt pools do not suggest a marked difference for the ranges we consider. This is a consequence of our use of simplified (coarse-grained) tree graphs.

3. The pseudorandom number generator may cause some error, since no generator is truly random. However, the generator used here is a proven one that has passed a battery of tests for randomness and has a periodicity of 2¹⁹⁹³⁷−1, or ~10⁶⁰⁰² (Matsumoto and Nishimura 1998).

4. Finally, all programs that determine RNA secondary structure from sequence are imperfect. Folding algorithms cannot consider the effects of divalent ions and solvents on RNA folding.

Furthermore, the RNAfold algorithm cannot fold a sequence into a pseudoknot, even if this is the ideal structural conformation. This is a concern because functional RNA pseudoknots have been found in random pools (Stuhlmann and Jaschke 2002). Although pseudoknot-folding algorithms exist (Rivas and Eddy 1999), the folding of large sets of sequences as done here is not yet feasible. Thus, our results are subject to the limitations of current 2D structure prediction algorithms.