Size, constant sequences, and optimal selection

Abstract

Because the abundance of functional molecules in RNA sequence space has many unexplored aspects, we compared the outcome of 11 independent selections, performed using the same affinity selection protocol and contiguous randomized regions of 16, 22, 26, 50, 70, and 90 nucleotides. All affinity selections targeted the simplest isoleucine aptamer, an asymmetric internal loop. This loop should be abundant in all selections, so that it can be compared across all experiments. In some cases, two primer sets intended to favor selection of different structures have also been compared. The simplest isoleucine aptamer dominates all selections except with the shortest tract, 16 contiguous randomized nucleotides. Here the isoleucine aptamer cannot be accommodated and no other motif can be selected. Our results suggest an optimum length for selection; surprisingly, both the shortest and the longest randomized tracts make it more difficult to recover the motif. Estimated apparent initial abundances suggest that the simplest isoleucine motif was 20- to 40-fold more frequent in selection with 50- or 70-nucleotide randomized regions than with any other length. Considering primer sets, a pre-formed stable stem within fixed flanking sequences had a five-to 10-fold negative effect on apparent motif abundance at all lengths. Differing random tract lengths also determined the probable motif permutation and the most abundant helix lengths. These data support a significant but lesser role for primer sequences in the outcome of selections.

INTRODUCTION

The unexpected functional versatility of nucleic acids has substantial implications for the biological sciences, though such implications are easily underestimated because the versatility appears piecemeal in experiments from different laboratories. The abilities of nucleic acids are still being rapidly expanded by experimentation. For instance, nucleic acids bind reaction transition states, thus accelerating reactions (Breaker 2004); they bind unusual ligands such as amino acids, thus suggesting an origin for the genetic code (Yarus et al. 2005); and they participate in unanticipated processes such as photoreactivation (the deoxyribozyme, Chinnapen and Sen 2004) and guide metal deposition (Gugliotti et al. 2004). Recently, versatile binding capabilities have been recognized in the regulation of gene expression by riboswitches (for reviews, see Winkler and Breaker 2003; Mandal and Breaker 2004), and RNAs have also yielded many new biotechnological possibilities, such as aptameric sensors (Stojanovic and Kolpashchikov 2004) and large self-assembling nanostructures (Chworos et al. 2004).

RNA versatility is frequently perceived using selection–amplification or SELEX, in which nanomole quantities of initially randomized sequences yield descendants of a few individuals after repeated rounds of purification (Ellington and Szostak 1990; Robertson and Joyce 1990; Tuerk and Gold 1990). An important aspect of such procedures is the length of the randomized tract of nucleotides used, as this length has a role in determining the initial abundance and likely complexity of selected structures (Knight and Yarus 2003; Yarus and Knight 2004; R.D. Knight, H.R.M. De Sterck, S. Smith, A. Oshmyansky, and M. Yarus, in prep.). However, this experimental variable is both subtle and somewhat controversial. It is subtle because the effect of the randomized tract length is not intuitive and has usually been approached only by extensive calculation (Sabeti et al. 1997; Knight and Yarus 2003; Yarus and Knight 2004). It is controversial, with different laboratories using long and short randomized regions, following individual reasoning. On one hand, the class I RNA ligase was isolated initially from an RNA with 220 randomized nucleotides (nt) (Bartel and Szostak 1993). This catalytic core was later reduced to 93 nt (Ekland et al. 1995), though it is hard to be sure that this was a minimum, given the many possible ways to reconstruct an RNA by deletion. On the other hand, activities such as the isoleucine aptamer are sometimes obtained from shorter starting tracts, for example 22 nt in Lozupone et al. (2003).

These are not trivial distinctions from a biological point of view—only short RNAs were probably available to ribocytes with rudimentary biosynthetic capabilities (Yarus and Knight 2004). Thus, the functional capabilities of RNA pools of different lengths is a significant evolutionary question, particularly for the initiation of an RNA world.

The significance of randomized region length has been approached experimentally by Huang and coworkers (2000) and Coleman and Huang (2002), searching for RNA-mediated CoA-thioester synthesis using mixed 30-, 60-, 100- and 140-nt randomized regions in the same randomized pool. In this selection, only 30- and 60-nt sequences succeed. This is puzzling because successful motifs found in shorter molecules should also be present amongst the same number of longer randomized molecules. This outcome was apparently attributable to the replicative disadvantage of the longer randomized RNAs (Coleman and Huang 2002), which disappear from the mixed pool in the course of selection. This led these investigators to suggest that a 60-nt randomized tract might yield optimal selections. However, this was not clear because the outcome might be different in the absence of replicative disadvantage. Here we perform selections in which different RNA lengths do not compete for replication.

Calculation suggests that the number of randomized sequences of a specified length required to find a given sequence will decrease with the length of the randomized tract. The number of required molecules also decreases when the sequence is divided into separated conserved modules, and this effect has been calculated based on a corrected Poisson frequency of occurrence (Yarus and Knight 2004). A general algorithmic approach to this calculation that requires no sampling corrections was developed as an improvement for these calculations (Knight and Yarus 2003). Finally, large-scale computation on paralleled computational grids can be used to estimate the probability of finding the same conserved sequence modules accompanied by essential helices, and also the probability that these essential sequences, once found, will fold correctly to give an active site structure (R.D. Knight, H.R.M. De Sterck, S. Smith, A. Oshmyansky, and M. Yarus, in prep.). These latter calculations, which are the most recent, comprehensive, and likely the most accurate of all available, nevertheless agree with earlier approximations that selections ought to improve (motifs should become more frequent in starting pools) as the randomized region is lengthened. This is so even though the probability of correct folding declines with length. As random nucleotides are added around the rare motif, they are more likely to interfere with its folding. This calculated increase in misfolding is not large enough, however, to offset the intrinsic statistical advantage of longer randomized tracts.

This computational expectation is inconsistent with the suggestion of Coleman and Huang (2002) that there is an optimal length for selection. To clarify this matter experimentally, we selected the same activity from random regions that varied greatly in length. To make this possible, we targeted the isoleucine aptamer (Majerfeld and Yarus 1998), apparently the simplest structure that can meet a selection for isoleucine affinity (Lozupone et al. 2003). That consideration made it likely that this simplest internal loop would be recovered from all selections, so that the ease of isolating it could be compared at all randomized lengths. Publications showing the recurrence of a solution for a variety of targets (Hanczyc and Dorit 2000; Salehi-Ashtiani and Szostak 2001; Cruz et al. 2004; Nutiu and Li 2005) supported the idea that the recurrence of the simplest isoleucine motif is highly probable in our case. Our experiments show that the probability of this motif, judged by the apparent initial abundance, does not increase monotonically as randomized RNA tracts are lengthened (as calculation suggested). Instead, there appears to be an optimal randomized tract length for selection of the UAUU isoleucine aptamer loop.

Moreover, in this study we also used two sets of primer sequences. It is known that fixed sequences influence selection outcomes. Legiewicz and Yarus (2005) showed that primer sequences could disfavor a simpler motif and force selection toward a rarer, more complex aptamer by supplying its own sequence to be incorporated by the more complex site structure. Here all selections were dominated by the previously defined simplest motif, though primer sequences differentially influenced the abundance of structural variations.

RESULTS

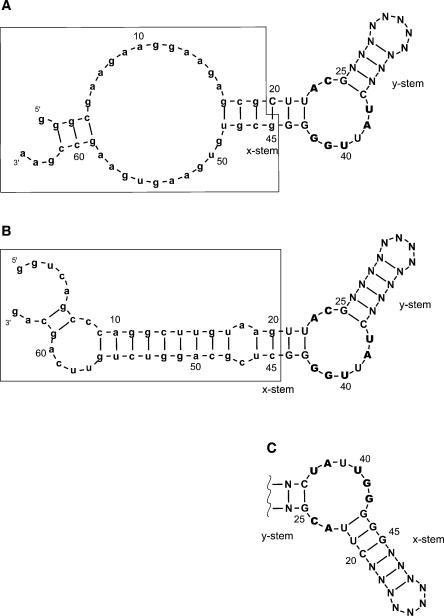
We applied the column affinity selection protocol (Lozupone et al. 2003) and carried out eight selections with contiguous randomized regions of 26, 50, 70, and 90 nt surrounded by either SC or ML primer site sequences (Fig. 1). The SC sequences (Fig. 1A) have been used before in search of the simplest isoleucine motif (Lozupone et al. 2003), and the results of two previous successful selections (with 22- and 26-nt randomized regions, called 22SCi and 26SCi, respectively) are included in this report. ML fixed sequences were newly designed and are predicted to form a long stable stem (Fig. 1B), thereby supporting selection of a coaxial helix within the randomized nucleotides. This contrasts with the SC primer sequences, which have a potentially less stable structure with a probable large bulge (Fig. 1A).

FIGURE 1.

Secondary structures of the UAUU motif in permutation P1 supported by either SC (A) or ML (B) pre-formed primer sequences folded by BayesFold (Knight et al. 2004). Conserved nucleotide positions of the motif are boldfaced. Primer sequences are in lowercase, and pre-existing structures are boxed. The N region in the y-stem has been counted as 10 nt for consistency of position numbering. (C) Permutation P2 of the UAUU motif. Position numbering has been broken in the middle for consistency.

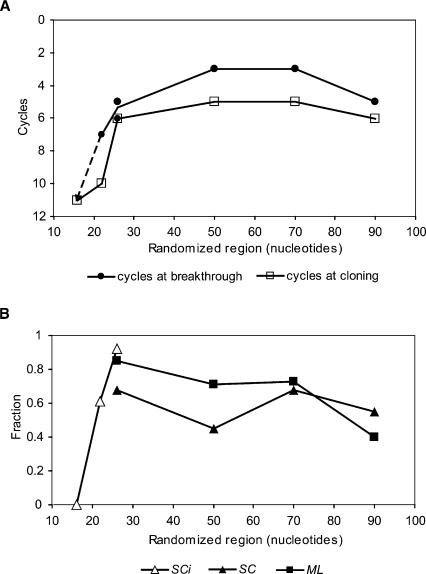
Selection completion is measured in two ways. The most sensitive and objective is breakthrough, which corresponds to the first appearance of an elution peak of functional aptamers during elution of RNA with isoleucine. Breakthrough occurred after three (50SC, 50ML, 70SC, 70ML), five (26SCi, 26ML, 90SC, 90ML), six (26SC), or seven (22SCi) cycles (Fig. 2A). The second quantity plotted in Figure 2A is cycles of selection at cloning, a more intuitive criterion corresponding to isolation of substantial numbers of active sequences among the cloned sub-population. RNA pools were cloned and sequenced after five (50SC, 50ML, 70SC, 70ML), six (26SCi, 26SC, 26ML, 90SC, 90ML), or 10 (22SCi) cycles of selections.

FIGURE 2.

(A) Number of cycles of selection at breakthrough and at cloning. (B) Fraction of the UAUU motif in cloned pools. The dashed line is hypothetical and intended to be illustrative because breakthrough was not observed at 16 randomized nucleotides.

In all eight new selections, as for the previous 22SCi and 26SCi sequences, we observe that the UAUU internal loop motif is the most abundant structure, as we had hoped. The frequencies of the UAUU motif among the cloned and sequenced population are shown in Figure 2B.

Randomized region length

In order to provide a more quantitative index of selection success, we estimated the initial apparent abundance of the functional UAUU motif, as follows. For a given fraction of the UAUU isoleucine motif, Pm, in the initial pool of a given cycle of selection, c, we can predict the fraction of the UAUU motif after a round of selection based on the efficiency of the UAUU motif recovery, Em, versus that for total RNA recovered, T. We estimated T for each cycle from the percent of RNA radioactivity added to the column recovered during elution with isoleucine. We estimated Em under the selection conditions by creating independent RNA pools from different representative UAUU clones, subjecting these pure populations to the selection criteria, and measuring the recovery, which averaged 0.35 (based on 21 columns with eight different sequences; not shown). We can estimate the fraction of the UAUU motif after selection Pm_{c + 1} as Pm_c × Em/T. This value also is taken as the starting abundance for the next cycle. Starting with an arbitrary value of Pm, the prediction can be propagated through all of the rounds of selection to determine the percent of the UAUU motif in the final rounds of selection. Our estimate for Pm is the value that predicts the experimentally measured fraction of UAUU RNA in the cloned and sequenced pool.

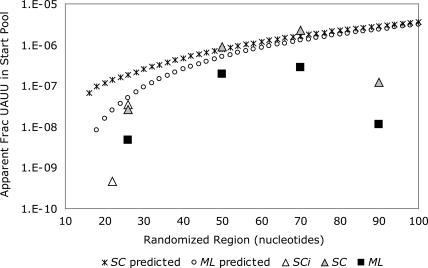
Estimated in this way the apparent initial abundance of the UAUU motif agrees with simpler estimates from breakthrough and cloning; it is optimum at ~50–70 nt (cf. Fig. 2A and Fig. 3). An increase of the randomized region from 22 to 26 nt makes the UAUU internal loop motif 67-fold more abundant. Increasing from 26- to 50-nt tracts makes the motif 30- or 43-fold more abundant, depending on the SC versus ML constant sequence set. Further increasing this region from 50 nt to 70 nt changes the UAUU loop frequency 2.5- or 1.4-fold for the SC or ML set, respectively. Finally, lengthening by 20 more nucleotides to 90 nt decreases apparent abundance 18- or 24-fold, for both SC and ML constant sequence sets (Fig. 3).

FIGURE 3.

Estimated initial abundance of functional UAUU loop motifs with SC (triangles) or ML (squares) primer sequences. The “predicted” curves are total probabilities for the UAUU motif calculated by summing those that are entirely in the random region, overlapping the 3^′ constant sequence, overlapping the 5^′ constant sequence, and overlapping both the 3^′ and 5^′ constant sequences (see Materials and Methods).

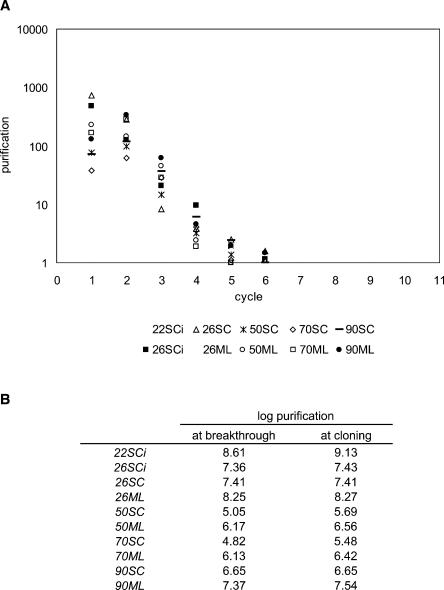
The calculation above also estimates the purification of the UAUU motif during each round of selection. We did a reconstruction experiment in which the UAUU motif was mixed with an excess of randomized RNA and subjected to the isoleucine affinity column. Reconstruction suggests that affinity chromatography purifies UAUU sequences 101-fold with respect to randomized RNA. This value is in approximate agreement with the previously determined purification, 131-fold (Lozupone et al. 2003), using a similar method. The reconstruction experiment notably also agrees with our calculation for early cycles of selection in which pool sequences that can survive selection have not yet become abundant (at cycle 1 and 2 in Fig. 4A). As the selection progresses, the estimated purification decreases dramatically (Fig. 4A). Figure 4B summarizes the purification required to detect breakthrough of the motif and at cloning. To detect the isoleucine UAUU loop aptamer selections with 50- and 70-nt randomized regions required more than one order of magnitude less apparent enrichment.

FIGURE 4.

(A) Estimated purification of the UAUU motif at particular selection cycles. (B) Calculated purification required to observe selection breakthrough and at cloning.

Moreover, we calculated how the abundance of the UAUU motif will change with randomized region length (see Materials and Methods for description). Specifically, we calculated the probability of recovery of the motif either entirely within the random region or using bases supplied by one or both primers. Because in Figure 3 the calculated lines’ courses (for the two primer sequences) track the observed rise in abundance, we conclude that the recovery of the UAUU aptamer in these experiments is explained potentially by 1) an increase in its frequency as the randomized region becomes long enough to contain it, and thereafter 2) the increase in frequency attributed to the statistical increase in efficiency of the search due to the longer randomized regions (Yarus and Knight 2004). Therefore, we believe we have observed the much-predicted statistical superiority of somewhat longer randomized regions for the first time. However, the expected continuous increase of abundance of the UAUU motif does not agree with our data. There is a substantial decrease in the UAUU motif in both longest investigated randomized regions (Fig. 3).

Primer sequences and the UAUU abundance

Calculated apparent initial abundance of the UAUU motif also depends on its flanking constant sequences, by up to an order of magnitude. Figure 3 shows that use of the less structured SC primer set instead of the ML set increases the apparent initial frequency of the UAUU motif 6.6-, 4.6-, 8.2-, or 10.6-fold in random regions of 26, 50, 70, or 90 nt, respectively. This is also consistent with calculated purifications; selections using SC primer sequences required one order less purification to detect activity at breakthrough (Fig. 4B). An explanation is suggested by the calculations for short random regions where the constant sequences interact strongly with the necessarily adjacent active site. However, calculation plausibly says (Fig. 3) that this effect should disappear when the random regions are longer (and the motif folds independently of its more distant constant flankers), and this expectation is not realized.

As in previous selections (22SCi and 26SCi) and also in current selections, we obtained sequences with the UAUU internal loop originating from many independent parents. Consequently, the simplest isoleucine UAUU internal loop aptamer has now been independently isolated 267 times; its sequence requirements are therefore known with substantial precision, perhaps more so than for any other RNA active site. In Table 1 we show a new consensus for the UAUU motif based on 258 independent isolations that are predicted to form the structures in Figure 1; calculation of the information content by our previous method now yields 32.7 bits, in agreement with our previous calculation (Legiewicz and Yarus 2005). However, observed structures with shortened stems suggest that both stems can be one nucleotide pair shorter than previously assumed (Fig. 1; Legiewicz and Yarus 2005). The length of the x-stem can be four nucleotide pairs and the y-stem three nucleotide pairs. In this case the information would be 30.2 bits, and this implies that a sequence just big enough to contain the UAUU motif (a minimal randomized region) would occur once in every 2^30.2 = 1.2 × 10⁹ randomized sequences, or ~15 pg of 22-mer RNA (cf. Fig. 3).

TABLE 1.

Sequence variation within the UAUU motif

Sequence variation is based on 258 sequences that are predicted to form the structures in Figure 1. Table includes both permutations presented as for permutation P1. Shaded regions indicate double-stranded regions. Conserved nucleotide positions of the UAUU motif are boldfaced. Nucleotide numbering is the same as in Figure 1.

The 267 parents include 14 sequences encountered in three additional selections using 35-, 50-, and 75-nt randomized regions that we have not presented. These were excluded because this particular isoleucine–Sepharose preparation yielded both a higher background from random RNA and lower recovery of a characterized pure UAUU aptamer RNA. Both differences reduce purification per cycle and thus increase the number of cycles for breakthrough, as was also observed in these three selections (not shown). Because these results differed from all others, they have not been included in these comparisons.

Primer sequences and permutations of the UAUU motif

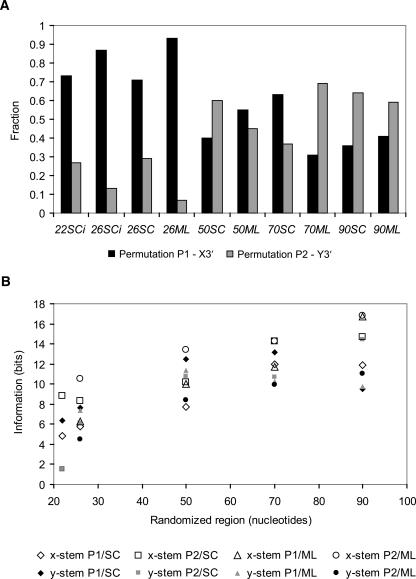
Because the two modules of the UAUU motif can be circularly permuted (Lozupone et al. 2003), we asked if the length of the randomized region affects permutation. Permutation P1 has the module UACG (the short side of the internal loop; Fig. 1A,B) 5^′ and the longer conserved sequence CUAUUGGG 3^′. From previous work (Lozupone et al. 2003), the x-stem (Fig. 1) is longer and shows higher conservation than the y-stem.

The results are clear: Permutation is affected in a consistent way by the length of the randomized tract. In short random regions, 22–26 nt, permutation P1 is 2.5- to 13-fold more prevalent (Fig. 5A). Because the two stems have different informational contents at each base pair, the information required to define the stems differs in the two permutations because one or another stem is pre-initiated by base pairs from fixed regions (boxed structure in Fig. 1). Permutation P2 (Fig. 1C) appears less favorable because the 4-base-pair x-stem then requires that 9 bits of information appear in a randomized region. In other words, it is statistically more advantageous when the short stem (y, with lower informational content) is defined in whole from the randomized region and the longer stem (x, with higher informational content) is supplied automatically from constant sequences.

FIGURE 5.

(A) Frequencies of both permutations of the conserved sequences within the UAUU motif. (B) Number of bits of information that was required in a randomized region to specify observed x- and y-stems around the UAUU motif in permutations P1 and P2.

In longer randomized regions, ≥50 nt, both permutations appear with indistinguishable frequencies, whichever primer set was used (Fig. 5A). Thus, in some respects, the effects of the terminal constant sequences do decrease as they become more distant from the selected active region, in accord with expectation.

Figure 5B shows that the apparent average helical stem length (in the calculated most stable conformation) increases with the length of the randomized region. Because these lengthened helices are less probable, their predominance means that they must be more functional. This in turn seems likely to be due to superior folding because of better resistance to the perturbed folds possible in longer random regions. Therefore, longer random regions evoke more stable versions of the selected motif. We can relate this to the permutation results above; as the motif’s folding strengthens, it is less affected by its context, ultimately making the particular permutation unimportant.

Primer sequences and RNA folding

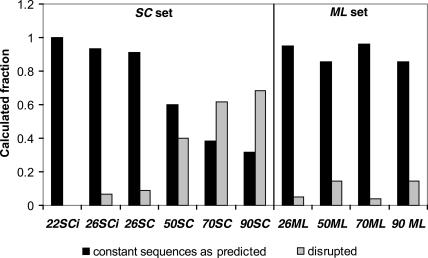
Presence of a weak (SC) or stable (ML) pre-existing structure involving constant sequences (Fig. 1A,B) can influence the folding of the randomized sequences. If primers do not form a very stable structure (SC set) there should be many possible folding solutions; in contrast, a stable pre-existing structure (ML set) limits folding to those structures compatible with the pre-structured constant sequences. To make the proper folding of the UAUU motif probable, its two modules have to appear in accessible positions in the sequence space. When the molecule is constrained due to presence of an initial stable structure, the probability that suitable modules exist in accessible positions is lower because the accessible sequence space is smaller. This probably explains why all selections are five- to 10-fold more successful with primer sequences that do not form a stable pre-existing structure (SC set; Fig. 3). This, in turn, is consistent with the observation that pre-existing predicted stable ML primer structures are preserved at all randomized lengths (Fig. 6). In contrast, the SC structure is preserved only with short regions, 22–26 randomized nucleotides, when there is not enough space for alternative solutions. With a randomized region length >50 nt (Fig. 6), the selected structures compete with and destabilize the less stable preexisting SC constant sequences.

FIGURE 6.

Calculated persistence of pre-existing structures involving SC or ML primer sequences in observed UAUU loop motifs.

DISCUSSION

The UAUU motif has again shown itself to be the most easily isolated isoleucine affinity motif (Lozupone et al. 2003), having now been independently isolated 267 times in randomized regions of 22, 26, 50, 70, and 90 nt in length. As a result it is an extremely well defined RNA active site, and we present a new consensus, consistent with all prior data, for its structure (Table 1). These results supply one detailed answer to Lehman’s question (2004) about whether an RNA motif can be repeatedly selected: When it is the smallest, most probable outcome, it appears reliably.

Using the appearance of the UAUU motif in investigated pools as an index of selection performance, we observe that this structure is found as soon as the RNA can accommodate an active site. This includes the proviso that constant nucleotides can be recruited for roles in the flanking helical sequences (Fig. 1A,B). Thus, the UAUU motif can appear in selections with 22 contiguous randomized nucleotides, though it does not reach its maximal abundance unless longer regions are used, which do not require that it alter preferred structures. In fact, it appears that 50 or 70 randomized nucleotides are optimal, and both selections with tracts of 90 randomized nucleotides are considerably worse. Estimated apparent initial abundances suggest an average 21-fold less initial motif at 90 nt (Fig. 3), instead of the twofold increase predicted from probability of motif appearance alone (Fig. 3). This 40-fold discrepancy persisted despite variation in the flanking constant sequences. It is also derived from two consistent sets of selections from the same person using the same materials. Further, it is visible by all criteria, including the simplest criteria of breakthrough and cloning. Finally, the optimum of only three cycles of selection to breakthrough is unusually few, suggesting that an optimal selection is exceptionally efficient, as would be expected. Despite the unavoidable statistical element in selection success, observed decreases are therefore thought to reliably indicate an optimum.

On the one hand, the optimum is probably produced by an increasing probability of finding the modules for the UAUU aptamer as randomized length increases. The similarity of the calculated curves in absolute value and slope to the estimated experimental abundance of the UAUU motif (Fig. 3) suggests that the rising limb of the recovery curve confirms the expected statistical superiority of longer sequences for finding a motif. The appearance of the calculated abundances just above the mean of the data (Fig. 3) is consistent with the moderate difficulty in folding expected from calculations (R.D. Knight, H.R.M. De Sterck, S. Smith, A. Oshmyansky, and M. Yarus, in prep.). However, in 90-mers there is a descending limb of 21-fold instead of the increase of approximately twofold expected from calculations (R.D. Knight, H.R.M. De Sterck, S. Smith, A. Oshmyansky, and M. Yarus, in prep.). Thus, either the disruption of the motif by alternative folding is much more dramatic than expected from folding calculations, or there is an another unexpected inhibitory effect decreasing apparent motif abundance ~40-fold in longer randomized tracts. Because the differences between SC and ML primers (see Fig. 1A,B) persist into this region (Fig. 3) instead of being minimized, the unexpected inhibitory effect probably varies among different primer sequences. For example, folding or aggregation both would likely have this property, and might (together or separately) explain the unexpected decrease in competence of longer randomized regions.

As an effect of smaller magnitude, it appears that strongly structured ML primer sequences reduce the frequency of the UAUU motif by a mean of 7.5-fold, in comparison with SC primer sequences (Fig. 3). This conclusion is supported by the reproducible observation of the calculated ML primer structure at all lengths of randomized region (Fig. 6). This idea is also supported by prediction of an effect of just this magnitude by statistical calculations based on short randomized tracts (Fig. 3). The more stable ML primer complements exert an experimentally reproducible sequence constraint, in our interpretation.

At a perhaps even more subtle level, the influence of the helical tendency of the flanking primers is visible in the selection of predominantly one permutation of the UAUU internal loop in short random regions (Fig. 5A). Conversely, supplying longer randomized tracts leads to the selection of, on average, more stable UAUU structures by lengthening their flanking helices (Fig. 5B) and moving potential disturbances from constant sequences to greater distance. Ultimately, these effects make the motif in longer initially randomized regions able to displace the more weakly structured primers (Fig. 6) and become independent of both weak and strong constant sequence structures (Fig. 5A).

Our results measure the frequency of functional RNAs that contain a relatively small motif. Clearly, bigger motifs might require much longer randomized regions. For example, a recently described complex RNA structure capable of high-affinity GTP binding (K_D = 9 nM) required 69 nt (Carothers et al. 2004). This motif would not occur at all unless an approximately threefold longer randomized region than the shortest possible for the UAUU motif was supplied. Thus, these results must be interpreted when reasoning about more complex RNA sites.

Finally, these results are very encouraging with regard to the selection of RNA activities in an RNA world with access to limited chain lengths. As shown in Figure 3, the rise in frequency of this active motif is very rapid at low tract lengths. As soon as the RNA will accommodate an active site it is found, and slightly longer randomized RNAs confer the expected statistical benefits. We and others have speculated that the RNA world might have begun with RNAs a few tens of nucleotides in length (Vlassov et al. 2004; Yarus and Knight 2004). Figure 3 shows that such pools would be nearly as capable as optimal randomized RNAs. Surprisingly, 26 randomized nucleotides are as useful as 90-nt randomized RNAs for the retrieval of isoleucine aptamers (Figs. 2, 3). These experimental data therefore provide non-trivial support for emergence of an RNA world as soon as short arbitrary-sequence RNAs became available.

MATERIALS AND METHODS

Isoleucine selection

Affinity chromatography selection for isoleucine-binding RNA was described previously (Lozupone et al. 2003). Two sets of primers were employed:

SC: 5^′-TAATACGACTCACTATAGGGCGAAGAAGGAAGAGCG (RR)GCGTGTGAAGTGAAGCCGAA-3^′ and

ML: 5^′-TAATACGACTCACTATAGGTCAGCCCAGGCTTGTAA G(RR)CTCGCAGGTCTGTTCAGCAG-3^′,

where RR is a randomized region of 26, 50, 70, or 90 adjacent nucleotides with equal initial nucleotide probabilities. Sixteen- and 22-nt randomized regions were done only with use of the SC set (Lozupone et al. 2003). The T7 promoter sequence is underlined. The initial PCR for all the selection sets in this study contained 8.4 × 10¹⁴ unique molecules of single-stranded DNA. All single-stranded DNA oligomers (synthesized by IDT) as well as transcribed RNAs were purified on 8% polyacryalmide gel in denaturing conditions.

Information content calculation

Information content for conserved positions of the internal loop of the UAUU motif and information for stems were calculated as described previously (Legiewicz and Yarus 2005). Stems surrounding the UAUU loop motif end when bulges of three or more nucleotides interrupt the helix; both standard and UG pairs were allowed.

Calculation of the probability of the UAUU motif

In order to compare theoretical results with experimental results, we devised a method of extending the probability calculations from Knight and Yarus (2003) to include the possibility of finding matches in one or both primers. In particular, we expected that when the random region is short any bases that can be supplied by the primer will outweigh the combinatorial disadvantage of fixing the position of one of the modules.

There are four mutually exclusive cases we needed to consider: (a) a match entirely within the random region; (b) a match in the 5^′ primer alone; (c) a match in the 3^′ primer alone; and (d) a match in both the 5^′ and the 3^′ primer. For each case, we used the Poisson approximation to derive the probability of finding at least one match as 1− exp(− np), where n is the number of possible ways of placing the modules in the longer sequence, and p is the probability of a match on a single trial. Thus, n and p need to be calculated for each case.

For matches entirely within the random region, n and p are calculated as follows. n is given by (s + 1)!/((s + 1 − m)!(m!)), where s is the amount of spacer, calculated as the difference between the length of the random region and the sum of the lengths of all the modules of the motif, and m is the number of modules in the motif (Knight and Yarus 2003). p is calculated, assuming equal base frequencies and GU wobble pairing, as (1/4)^{num fixed bases} × (6/16)^{num pairs}, reflecting the 1/4 probability of getting a specific base by chance, and the 6/16 probability of getting any of the six base pairs out of the 16 possible dinucleotides.

For matches that involve one or both primers, the probability needs to be recalculated to take into account the number of bases supplied by each primer. For each number of bases supplied by the 5^′ primer (from one up to the length of the first module), for each number of bases supplied by the 3^′ primer (from one up to the length of the last module), we first test whether there are any mismatches between the primer and the conserved bases in the motif. If there are mismatches, the probability of a match at that position is zero. We then check the positions that are required to pair with each other. If both partners of a pair are supplied by primers, the bases at those positions are examined. If they could not form a valid base pair, the probability of a match is zero. We then calculate p as before, with the following modifications: the probability of obtaining each base supplied by the primer is 1, so these bases do not enter the calculation. For conserved bases not supplied by the primer, the probability is 1/4; for base pairs not supplied by the primer, the probability is 6/16; and for base pairs in which one partner is supplied by the primer, the probability of finding a matching partner is 1/4 if the primer-supplied base is A or C, and 1/2 if the primer-supplied base is U or G. The single-trial probability is the product of the probabilities of these non-supplied bases. The number of modules is decreased by the number of modules partially supplied by the primer (i.e., a two-module motif is considered to have one free module if either the 5^′ or the 3^′ primer is involved, and no free modules if both primers are involved), and the amount of spacer is increased by the number of bases supplied by the primer (since these bases need no longer be found in the random region). For example, if the random region is 50 bases long, and there are two modules each 12 bases long, but six bases of the first module are supplied by the 5^′ primer, there will be one free module to find (i.e., m = 1), and there will be 50 − (12 + 12) + 6 = 32 bases of spacer (i.e., s = 32 in the equation above). We can then calculate n, and hence p, for each particular combination of bases supplied by the 5^′ and 3^′ primers.

Having calculated the probability of obtaining a match with each combination of bases supplied by the 5^′ and 3^′ primers, we need to find the probability that we got at least one match (there can be multiple matches in the same sequence). This probability is calculated as 1 − product(1 − p_ij), where i and j range from 0 to the length of the first and last module respectively; in other words, we calculate the complement of the probability that no combination of primer-supplied bases matched. To lessen the numerical difficulties in this calculation, we use the approximation that ln(1 − p) ~ − p when p is small (<0.01), allowing us to reach the same result as 1 − exp(∑(−p)) when all probabilities are small (when some probabilities are not small, the individual ln(p) terms are calculated directly). The result is the probability of obtaining at least one match in the sequence using any combination of bases supplied by primers, which can then be compared with the number of distinct sequence families representing starting sequences in the initial pool.