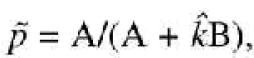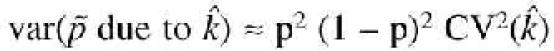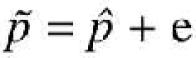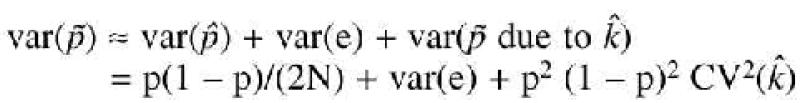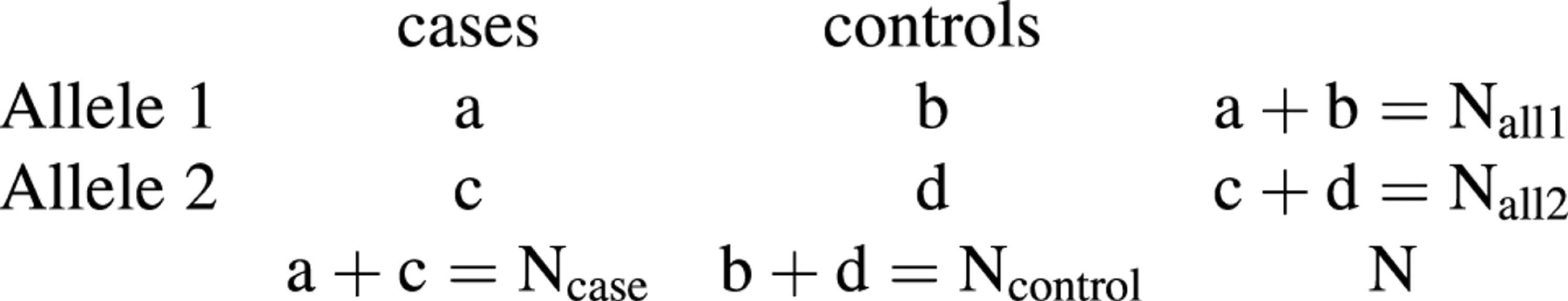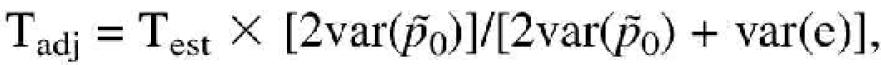Abstract
We have compared the accuracy, efficiency and robustness of three methods of genotyping single nucleotide polymorphisms on pooled DNAs. We conclude that (i) the frequencies of the two alleles in pools should be corrected with a factor for unequal allelic amplification, which should be estimated from the mean ratio of a set of heterozygotes (k); (ii) the repeatability of an assay is more important than pinpoint accuracy when estimating allele frequencies, and assays should therefore be optimised to increase the repeatability; and (iii) the size of a pool has a relatively small effect on the accuracy of allele frequency estimation. We therefore recommend that large pools are genotyped and replicated a minimum of four times. In addition, we describe statistical approaches to allow rigorous comparison of DNA pool results. Finally, we describe an extension to our ACeDB database that facilitates management and analysis of the data generated by association studies.
INTRODUCTION
Single nucleotide polymorphisms (SNPs) are the most common type of polymorphism in the human genome, with an approximate frequency of one every kilobase (1). These biallelic variants are relatively easy to genotype compared with VNTRs and microsatellites. For these reasons SNPs are thought to have a promising future in a wide range of human genetics applications including pharmacogenomics, the study of population evolution, analysis of forensic samples and the identification of susceptibility genes involved in complex diseases. Hence, a large proportion of the effort of genome centres is now focused on the identification and the mapping of a large collection of SNPs: to date about 1 260 000 have been mapped onto the human draft sequence (http://snp.cshl.org/).
The study of complex common diseases and quantitative traits is confounded by the effects of disease heterogeneity, gene–gene and gene–environment interactions. This means that large numbers of SNPs must be surveyed in large numbers of individuals in order to detect single gene variants with a small to moderate effect size (2,3). The use of pooled samples, comprised of equal amounts of genomic DNA from up to 1000 individuals, has been proposed as a means of reducing the number of genotyping reactions required. The method used to genotype SNPs in pooled DNAs must provide accurate estimates of allele frequencies, and must be time and cost effective. The spectra of methods currently available for genotyping SNPs in individual samples [for an extensive review of SNP genotyping methods see Syvanen (4)] can be divided into three classes. First, methods such as SSCP or dHPLC that are based on the physical–chemical properties of the alleles. Secondly, methods such as TAQMAN™ (Applied Biosystems); oligo-ligation assay; Invader assay™ (Third Wave Technologies Inc.); and allele-specific amplification and padlock probes that are based on hybridisation, amplification or ligation of an allele-specific probe. Thirdly, methods based on allele-specific extension or minisequencing from a primer adjacent to the site of the SNP such as SNaPshot™ (Applied Biosystems); primer extension read by dHPLC or by mass spectrometry; primer extension performed on microarrays; fluorescence polarisation; bioluminometric assay coupled with modified primer extension reactions (BAMPER) and Pyrosequencing™ (Pyrosequencing).
Previous studies have shown that allelic frequencies can be accurately estimated from pools using primer extension followed by dHPLC (5); TAQMAN™ and RFLP analysis (6); allele-specific amplification with real-time PCR (7); SSCP (8); BAMPER (9) and MassARRAY™ (10). In common with many other groups, we wish to screen a large candidate region for evidence of genetic association. The preferred strategy is to assay small numbers of pooled DNA samples with large numbers of SNPs. Consequently, methods such as Pyro sequencing™, TAQMAN™ or BAMPER that use modified primers are too expensive. Methods based on hybridisation or on physical–chemical properties are ruled out as each assay must be optimised. We therefore chose to compare the robustness, accuracy and cost of three methods based on minisequencing: SNaPshot™ (Applied Biosystems) and primer extension followed either by dHPLC, or mass spectrometry (MassARRAY™ system by Sequenom).
We have also addressed the important issues of how many DNAs can be pooled, and how many times pool genotypes should be replicated to optimise the accuracy of allele frequency estimation.
In addition, we suggest the use of a modified statistical method that allows rigorous analysis of allele frequencies estimated from pools. Classical association studies on individual DNA samples use the χ2 test to compare the frequencies of alleles in case and control populations. However, when pooled DNAs are used, allelic frequencies are estimated rather than directly counted from individual genotypes, which introduces extra sources of error. We have therefore modified the χ2 test to take these sources of error into account, diminishing the risks of type I error.
Finally, genotyping large numbers of SNPs on pools or on individual samples generates a large data set. We have set up an extension of our ACeDB database (11) to store and manage information on the pools, individuals and markers and to record and analyse genotyping results. Furthermore, we have created in ACeDB a model (‘Pop_pool_meta’) that allows the data of several pools or populations of individual samples to be merged and analysed as a single set. This option allows the pools or populations to be stratified on the basis of phenotypic traits, and then analysed independently or together. We have also developed a ‘user friendly’ web interface for submission of new data, which is fed automatically into an analysis pipeline, before being recorded in the database.
MATERIALS AND METHODS
DNA pool set up
All subjects gave written ethical consent to take part in these studies.
The concentration of the DNAs used to construct pools was measured using the PicoGreen dsDNA Quantitation Reagent (Molecular Probes) in a CytoFluor fluorimeter (Applied Biosystems). The DNAs were diluted to a final concentration of 8 ng/µl and equal amounts of DNAs were mixed to form the pools.
Range pools were constructed by mixing appropriate volumes of homozygote DNA. Five homozygote DNAs for each genotype were used for pooling. The concentrations ranged from 50–50% to 85–15%, with 5% increments.
Markers and PCR
SNPs RS643304, RS1402045, RS15020285, RS489009 and RS508509 were retrieved from the dbSNP database (http://www.ncbi.nlm.nih.gov/SNP). Primers were designed using Primer3 programme (http://www-genome.wi.mit.edu/cgi-bin/primer/primer3_www.cgi), and synthesised by Genosys Biotechnologies (Europe) Ltd. Sequences of PCR and genotyping primers are available upon request.
PCRs were carried out on a PTC225 (MJ Research) using 40 ng total DNA, 10 pmol of each primer, 80 µM dNTPs (Sigma), 1.5 mM MgCl2 and 1 U Taq (Sigma) in 1× PCR buffer [67 mM Tris–HCl, 16 mM enzyme grade (NH4)2SO4, 6.7 mM MgCl2 pH 8.8]. The programme used was an initial denaturation of 94°C for 3 min, followed by 10 cycles of 94°C for 15 s, touch down annealing from 65 to 55°C for 30 s over 10 cycles (–1°C/cycle) and 72°C for 45 s, followed by 30 cycles of 94°C for 15 s, 55°C for 30 s and 72°C for 45 s.
PCR clean up
After PCR, the products were checked on a 2% agarose gel. PCR primers and dNTPs were removed before genotyping: 5 µl of PCR product was incubated with 1 µl of ExoSapIT (Amersham Pharmacia) for 45 min at 37°C, followed by 20 min at 80°C for enzyme inactivation. For multiplexing of PCRs, 1 µl of each PCR product was pooled and treated with 1 µl of ExoSapIT.
Primer extension followed by dHPLC
Reactions were carried out as described in Hoogendoorn et al. (12).
SNaPshotTM reactions
The primers used for the extension reactions were designed according to the manufacturer’s recommendations. Additionally, we used the mfold server (http://bioinfo.math.rpi.edu/∼mfold/dna/form1.cgi) to assess the secondary structure of the PCR product and the accessibility of the SNP, in order to decide whether to use the forward or the reverse primer.
Reactions were carried out in a final volume of 10 µl, containing 2 µl of cleaned up PCR product, 1 µl of SNaPshot™ multiplex mix (Applied Biosystems), 2 µl of half term buffer (200 mM Tris–HCl, 5 mM MgCl2 pH 9), 2 pmol of genotyping primer. In multiplex reactions 2 µl of the cleaned PCR multiplex was used. The cycling programme was 25 cycles of 94°C for 10 s, 50°C for 5 s, 60°C for 30 s. After cycling, the unincorporated fluorescent ddNTPs were removed by adding 1 U of shrimp alkaline phosphatase (Amersham Pharmacia) and incubating for 45 min at 37°C, followed by 20 min at 80°C for enzyme inactivation. An aliquot of 9 µl formamide was added to 1 µl of SNaPshot™ reactions and loaded on ABI3700 sequencer (Applied Biosystems). Samples were run using the POP6 Polymer, with dye set E and analysed using the Genescan v3.5.2 program. The relative proportion of each allele was measured by the height of the corresponding peaks.
Primer extension on MassARRAYTM
Reactions were performed at Sequenom GmbH (Hamburg, Germany; http://www.sequenom.com). Assays were designed using Sequenom’s SpectroDESIGNER™ software (version 1.3.4). Genotypes were performed using MassARRAY™ system and SpectroTYPER™ software.
Statistical analysis
Correction for unequal allelic amplification and estimation of frequencies. Let k be the ratio of the two allele peak heights in heterozygotes. Following Hoogendoorn et al. (5), this factor is estimated from a number of independent heterozygotes, and we assume that the estimator ![]() is unbiased with a variance of σk2, i.e.
is unbiased with a variance of σk2, i.e. ![]() with
with ![]() . The error in estimating k arises from variation in the quality of the DNA from each heterozygote, and from a pure experimental error attached to each individual analysis. The estimate of the allele frequency in the pool is estimated as
. The error in estimating k arises from variation in the quality of the DNA from each heterozygote, and from a pure experimental error attached to each individual analysis. The estimate of the allele frequency in the pool is estimated as
with ![]() the estimated frequency in pools, and A and B the observed peak heights corresponding to the two alleles. The variance of the estimated allele frequency as a function of the variance of
the estimated frequency in pools, and A and B the observed peak heights corresponding to the two alleles. The variance of the estimated allele frequency as a function of the variance of ![]() is, approximately, following a Taylor series expansion,
is, approximately, following a Taylor series expansion,
with p the true frequency in the population, and CV the coefficient of variation. Furthermore we observed a pool specific error (e) which contributes to a difference between the allele frequency estimated from the pools and the estimate of the allele frequency from a direct count of alleles on individual genotypes (![]() ),
),
We assumed that these errors are normally distributed. This assumption was confirmed for the distribution of the frequencies for 10 replicates of the five markers we have tested in this study. Following these assumptions, the variance of the estimated allele frequency from a pool of N individuals is
Comparing freqencies between pools. The standard procedure to test whether the allele frequencies in two pools are significantly different from each other is to summarise the observed counts in a 2×2 table and to perform a χ2 test (13). For a case-control study we use the following notation,
In this notation Ncase is twice the number of case individuals and, for an equal number of cases (n) and controls (n), N = 2n + 2n = 4n. The standard test statistic of independence can be written as
T1 = (ad – bc)2N/(Ncase × Ncontrol × Nall1 × Nall2)
Under the null hypothesis of the same population allele frequencies in cases and controls, for large N and not too extreme population frequencies, this test is distributed as a χ2 with one degree of freedom. If estimated counts are substituted for the observed ones, this test is then Test
Test = (aede – bece)2N/(Ncase × Ncontrol × Nall1 × Nall2)
with ae, be, ce and de the estimates of a, b, c and d, respectively. The expected value of Test is, approximately,
with 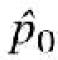 the estimate of the allele frequency across the two pools under the null hypothesis, i.e.
the estimate of the allele frequency across the two pools under the null hypothesis, i.e. 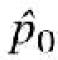 = (a + b)/N, and its variance is obtained from the binomial distribution [var(
= (a + b)/N, and its variance is obtained from the binomial distribution [var(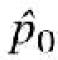 ) =
) = 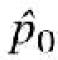 (1 –
(1 – 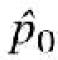 )/N]. Under the null hypothesis of equal allele frequencies, the expected value of the test statistic based upon observed counts is E(T1) = 1. Hence, the test statistic is inflated by the extra source of errors in estimating the allele frequencies and its use would lead to an inflated type I error rate. We suggest a simple adjusted test,
)/N]. Under the null hypothesis of equal allele frequencies, the expected value of the test statistic based upon observed counts is E(T1) = 1. Hence, the test statistic is inflated by the extra source of errors in estimating the allele frequencies and its use would lead to an inflated type I error rate. We suggest a simple adjusted test,
i.e. a shrunk version of the standard test statistic, with the estimate of the sampling variance of the allele frequency under the null hypothesis obtained from the estimated counts (i.e. 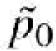 replacing
replacing 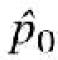 ).
).
A more detailed protocol is available online at our website (http://www.genetics.med.ed.ac.uk/protocols/).
Data management in ACeDB
Modified models. The ‘STS’ model was modified to cross-reference to the allele model for the markers (SNPs or microsatellites) that are present in the STS. The ‘allele’ model was modified to store information on the method used to genotype the marker (e.g. details of the extension primer and genotyping method used, and the experimental conditions); the pools, populations, metapopulations and metapools that have been typed with the marker and the statistical analysis of the results obtained.
New models. The ‘Individual’ model was created to store individual genotypes and indicate which pool or population, metapopulation and metapool an individual DNA sample belongs to.
The new ‘Pop_pool’ model stores the identities of the DNA samples that constitute the pool or the population, and provides links to the markers that have been genotyped on the pool/population and the genotyping results. It also stores the results of comparison of allele frequencies with those of other pools/populations, or metapools/metapopulations, and information regarding inclusion of the pool/population in a metapool/metapopulation.
The ‘Pop_pool_metapool’ model stores data on the set of pools/populations combined and provides links to the markers typed on the pools/populations, the statistical description of the data set obtained, and information on the comparison of allele frequencies with those of other samples (pools, populations, metapopulations and metapools).
The statistical description model ‘Stat_des’ stores the results of the statistical analysis of data obtained by genotyping specified markers on a given sample (mean frequencies of the two alleles, standard deviation, standard error).
Finally, the statistical comparison model ‘Stat_comp’ stores the results of association studies carried out by comparing allele frequencies in the samples or direct allele counts for a given marker, using the appropriate statistical test.
Web interface for submission of data and automation of statistical analysis
CGI/Perl scripts were produced to facilitate the submission of new data and to perform statistical description and χ2 tests. When entering new data or updating a given object, the tace program (Morris, J. 1994; http://www.acedb.org/Cornell/tace.html) is used by the script to retrieve existing information, e.g. names of the pool and the marker, and information on the genotyping experimental conditions. The user then selects parameters from pull-down lists that are either defined in the script or retrieved from the database (e.g. names of the pool and the marker), which ensures accurate data entry. Pool genotyping data are then automatically analysed using a script that computes descriptive statistics and runs the Shapiro–Wilk test for goodness-of-fit to normality.
Tests of association based on pools and metapools are automatically performed using a script that runs the modified χ2 test. The interface also allows classical association studies to be carried out based on genotypes of individuals. A ‘.ace’ file storing any new data submitted is generated and read into the database. All the models and scripts described here are available at http://www.genetics.med.ed.ac.uk.
RESULTS
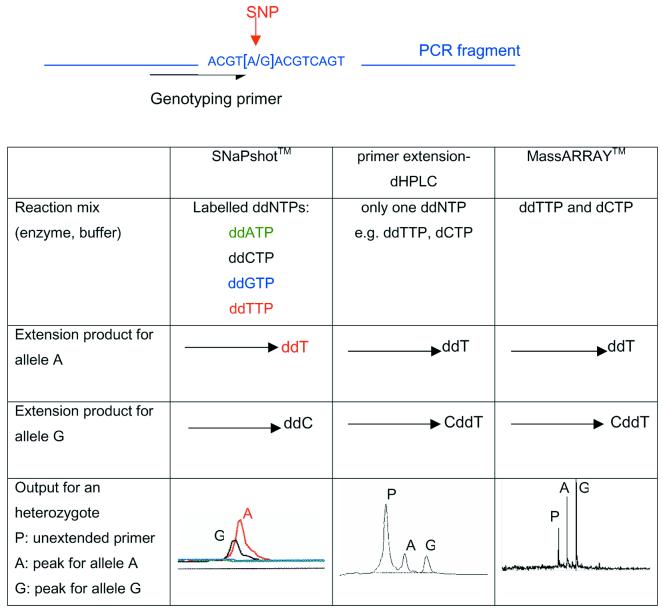
Figure 1 gives a brief description of the methods compared in this study.
Figure 1.
Genotyping a SNP with SNaPshot™, primer extension followed by dHPLC or mass spectrometry (MassArray™) analysis. The three methods are based on the allele specific extension of a genotyping primer adjacent to the SNP site (see below). The region containing the primer is first amplified by PCR.
Estimating allele frequency in pools: correction for unequal allele amplification
By definition, heterozygote individuals have an equal number of copies of the two alleles at any given locus. If genotyping was equally efficient for the two alleles, then the two amplified peaks would be the same height. However, in practice unequal peak heights is the norm. We genotyped individual heterozygotes 6–10 times and recorded the variation in peak height ratios between replicates. This indicated that the standard error of the mean (SEM) ratios were less than one-twentieth of the mean value (data not shown).
We observed greater variation in peak height ratios between different heterozygotes (SEM ranging from 0.003 to 0.147; Table 1). Hoogendoorn et al. (5) reported a SEM of 0.005– 0.06 when comparing the peak height ratios of different heterozygotes for nine markers genotyped by primer extension followed by dHPLC. It is possible that the variation observed between heterozygotes could be due to variable DNA quality. However, all of the DNAs used for this study were collected, extracted and stored under the same conditions. The observed variation is therefore more likely to be caused by factors specific to the experimental procedures. The maximum variation (SEM) between the ratios of different heterozygote individuals was within one-seventh of the mean ratio (Table 1). A mean ratio of unequal amplification (k) can therefore be accurately calculated for any given marker genotyped by a given method.
Table 1. Unequal allelic amplification.
| Marker | SNaPshot™ | dHPLC | MassARRAY™ |
|---|---|---|---|
| RS15020285 | 0.951 ± 0.272 (0.086) | 0.416 ± 0.272 (0.087) | 0.566 (nd) |
| RS508509 | 0.268 ± 0.085 (0.027) | 0.389 ± 0.016 (0.005) | 0.593 (nd) |
| RS1402045 | 0.447 ± 0.047 (0.015) | 0.911 ± 0.465 (0.147) | 0.754 (nd) |
| RS643304 | 0.648 ± 0.009 (0.003) | 0.748 ± 0.063 (0.020) | 0.564 (nd) |
| RS489009 | 0.813 ± 0.275 (0.087) | 0.569 ± 0.161 (0.051) | 0.515 (nd) |
Ten heterozygote individuals were genotyped for each of the five markers. The mean ratio of the two allele peaks across 10 different heterozygotes individuals ± standard deviation between the ratios of the heterozygotes (and standard error of the mean) is shown. nd, not determined.
When allele frequencies are estimated by genotyping a pooled sample the resultant peak heights must be corrected for unequal amplification by the factor k. If k is the mean ratio of the allele A and B peak heights (HA and HB, respectively) in heterozygote individuals, i.e. k = HA/HB, then the frequency of the allele A in the pools would be pApools = HApools/(HApools + kHBpools). If the unequal amplification of alleles is ignored and the ratios of peak heights are used in a χ2 statistic this will result in a biased test procedure, as the test statistic is not distributed as a χ2 under the null hypothesis of equal allele frequencies in the pools. To a first order approximation, the expected value of the test statistic based upon the unadjusted ratio of peak heights is
E(test statistic) = k/[1 + (k – 1)p]**2,
where p is the population frequency. This result was validated by computer simulation. Depending on the true value of k and the frequency (p), this test is either expected to be smaller or larger than 1.0 (which is the expected value from a proper χ2 test). For example, for p = 0.25 and k = 0.5, the expected value of the test statistic is ∼0.65, which will result in a test that is too conservative.
Hoogendoorn et al. (5) used the mean ratio from eight heterozygote individuals to determine k. We currently use a panel of 16 control individuals, which are genotyped for each marker. We then calculate a mean ratio from the heterozygote individuals of this panel—we always divide the height of the smaller allele peak by the height of the bigger allele peak to keep data homogenous. As long as the SEM of the ratio between the heterozygotes is less than one-tenth of the mean value, we use this mean value as k. If the SEM is greater than one-tenth of k, then either the assay must be optimised or the number of heterozygote genotypes must be increased appropriately until this criterion is met.
To avoid introducing any extra sources of variation, we perform all stages of the genotyping procedure simultaneously on all samples.
Effect of allele frequencies on unequal amplification in pools
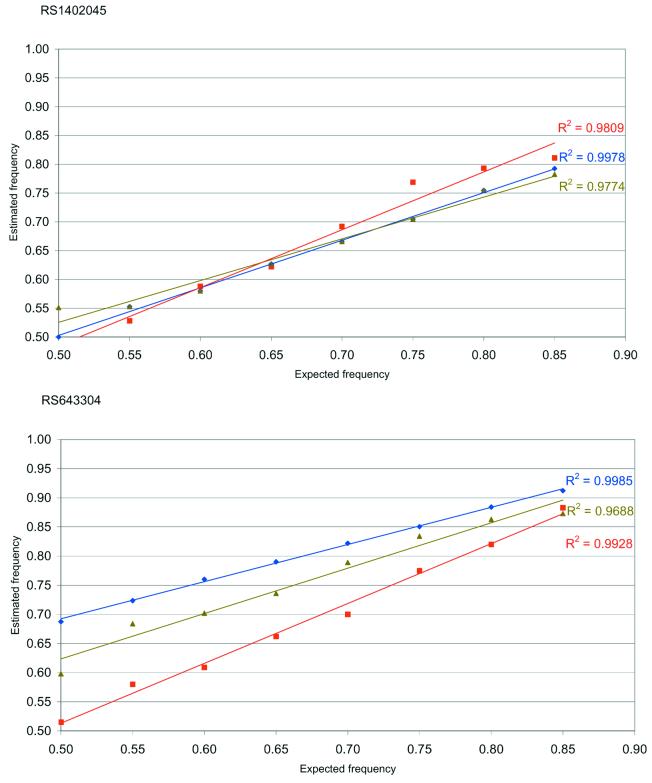
The allele frequencies in pools of cases and controls are both corrected with the same k factor. This approach is valid only if unequal amplification is linearly correlated with allele frequencies. To test this, we constructed two sets of artificial pools with a range of allele frequencies by mixing appropriate volumes of two homozygote DNAs for the markers RS1402045 and RS643304. The ratio of concentrations of alleles in both sets of pools ranged from 50–50% to 85–15%, at 5% increments. Each pool was genotyped 5–10 times. Results (Fig. 2) show that there is a linear correlation between the allele frequencies and the ratios for all three methods tested. These data indicate that variation in allele frequency does not affect the extent of unequal allele amplification, and that pools with different allele frequencies can be corrected with the same k factor.
Figure 2.
Test for linearity for the markers RS1402045 and RS643304 across artificial pools with allele frequencies ranging from 50–50% to 85–15% with 5% increments were constructed. Comparison of the three methods: SNaPshot™ (diamonds), dHPLC (triangles) and MassARRAY™ (squares).
<! COMMENT -- SGML op. please reinstate proper trademark SGML code twice in this title -- KB>Comparison of accuracy and repeatability of SNaPshotTM, primer extension followed by dHPLC, or by mass spectrometry (MassARRAYTM) methods
Five markers were genotyped on a set of 96 individual DNAs to obtain the sample allelic frequencies. The 96 DNAs were then pooled (Pool96), and the pool was genotyped 10 times with each of the five markers by the three methods. The k factors were obtained for the three methods and used to correct the estimate of allele frequencies within the pools. The estimated allele frequencies were in good agreement with the results of individual genotyping. This was true for all methods and markers tested (Table 2). Several parameters are important in comparing the efficiency of the different methods. First, the estimation of frequencies has to be close to the sample frequencies, as a large discrepancy would introduce a risk of type I and type II errors. However, as we demonstrate below, good repeatability (i.e. a smaller SEM) is more important than pinpoint accuracy. Poor repeatability necessitates a larger number of replications in order to lower the SEM of the estimated allele frequencies. The SEMs observed varied from 0.003 to 0.066 for SNaPshot™, 0.003 to 0.017 for primer extension followed by dHPLC and 0.003 to 0.004 for MassARRAY™. Thus, from a quantitative point of view, the three methods tested are all suitable for genotyping pools, with the MassARRAY™ method performing substantially better than the other two.
Table 2. Comparison of the accuracy of the three methods in estimating allele frequencies in a pool of 96 DNAs (Pool96).
| Marker | Sample frequency | Estimated frequency | ||
|---|---|---|---|---|
| SnaPshot™ | dHPLC | MassARRAY™ | ||
| RS15020285 | 0.658 | 0.666 ± 0.022 (0.007) | 0.633 ± 0.013 (0.004) | 0.727 ± 0.013 (0.004) |
| RS508509 | 0.714 | 0.702 ± 0.135 (0.043) | 0.711 ± 0.013 (0.004) | 0.761 ± 0.009 (0.003) |
| RS1402045 | 0.713 | 0.699 ± 0.047 (0.015) | 0.683 ± 0.047 (0.015) | 0.724 ± 0.009 (0.003) |
| RS643304 | 0.657 | 0.648 ± 0.032 (0.010) | 0.656 ± 0.022 (0.007) | 0.645 ± 0.013 (0.004) |
| RS489009 | 0.528 | 0.561 ± 0.063 (0.02) | 0.501 ± 0.054 (0.017) | 0.503 ± 0.009 (0.003) |
The sample allelic frequencies were obtained from genotyping the 96 individuals (using the SNaPshot™ method). A k correction factor for unequal amplification was obtained for each of the three methods and used to estimate the frequencies in the Pool96. Ten replicates of Pool96 were genotyped to test the repeatability of the method, which is expressed here as ± standard deviation (and SEM).
Ease of use and cost considerations
For all of the markers tested, the SNaPshot™ method was found to be robust and required little optimisation. However, multiplexing SNP assays was less straightforward, as the signal strength varied between assays. We circumvented this problem by multiplexing assays on the basis of signal strength, or by increasing the amount of genotyping primer for the weaker assays (14). We currently find that multiplexing four markers is relatively straightforward, although according to the manufacturer 10 SNPs can be successfully multiplexed.
In our hands, SNP genotyping using primer extension followed by dHPLC required extensive optimisation of the primer extension reaction. Optimisation of the gradient that is best suited to the elution of each product was also required and, furthermore, attempts to multiplex reactions were unsuccessful.
For the MassARRAY™ analysis, sequence files with information on the marker and localisation of the SNPs to be detected were provided to Sequenom who designed the assays using their ‘in house’ software. Coded samples and pools were provided, and highly satisfactory results returned promptly for each SNP assay.
The cost of genotyping pools (Table 3) is highly dependent on the ability to multiplex reactions and minimise reaction volume. For these reasons, primer extension followed by dHPLC or MassARRAY™ is not as cost effective as the SNaPshot™ method. However, as we demonstrate below, the MassARRAY™ requires less replicates per pool than the SNaPshot™, which makes MassARRAY™ as cost effective as SNaPshot™. Table 3 also provides a comparison of the throughputs of the different platforms.
Table 3. Comparison of cost and throughput of the methods.
| Cost per sample | Throughput/day/machine | |
|---|---|---|
| dHPLC | 157 cents | 192 |
| MassARRAY™ | 100 cents | 40 000 |
| SNaPshot™ | 87 cents | 7000a |
| 1500b |
The calculations include genotyping reagents and primers (on the basis of 100 reactions per primer), plastic consumables and the cost of running the assay on the detection platform. Salary costs are not included. PCR costs are not included, as they are the same for the three methods.
aWith a 96 capillary system (ABI37000).
bWith a 16 capillary system (ABI3100).
Effect of pool size
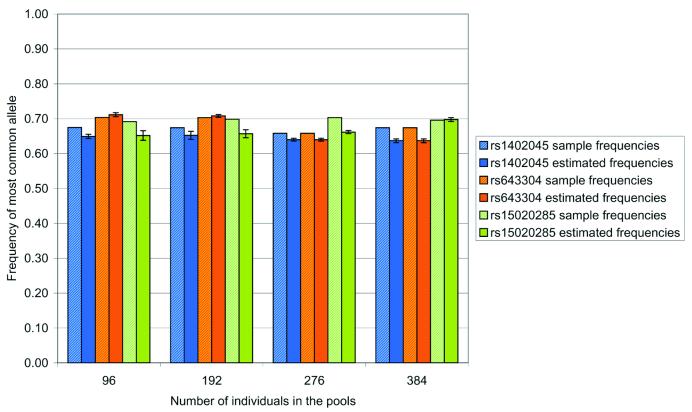
We wanted to determine whether the number of the samples in the pool would affect the accuracy of allele frequency estimation in pooled DNAs. We genotyped 384 individual DNAs to calculate the sample frequencies for the markers RS1402045, RS15020285 and RS643304. The same 384 individuals were then included in four pools of 96, two pools of 192, one pool of 288 and one pool of 384 individuals, and genotyped using the SNaPshot™ method (six replicates per pool). The frequencies estimated from the pools were compared with the sample frequencies (Fig. 3). We found that for the range tested, pool size had no significant effect on the accuracy of frequency estimations or on repeatability. This indicates that pooling larger numbers of samples does not result in a loss of power. We therefore recommend that larger pools are typed, minimising the number of genotyping reactions required.
Figure 3.
Estimation of allele frequency in different sized pools. Marker RS1402045, RS15020285 and RS643304 were typed on 384 individuals (using the SNaPshot™ method) to obtain sample allelic frequencies. 384 DNAs were combined in four pools of 96, two pools of 192, one pool of 276 and one pool of 384 individuals. Each pool was genotyped six times (using the SNaPshot™ method) and the frequencies were estimated from the mean frequency corrected for unequal amplification. The repeatability is expressed as the SEM estimated frequency.
Statistical comparison of two or more pools genotyped with a given marker
Estimating the allelic frequencies in pools. As we have demonstrated above, estimating allele frequencies in pooled DNAs introduces three potential sources of error: (i) error caused by sampling a finite number of individuals from a population (the standard sampling error); (ii) error in estimating the adjustment factor k; and (iii) a pool-specific measurement error. The first source of error is reduced by increasing the sample size; the second source of error is reduced by using the appropriate number of heterozygotes to estimate k (see above); and the third source of error is reduced by genotyping replicate samples of the pools. When allele frequencies from two (or more) pools are compared, a minor error in the estimation of k will induce a covariance between the estimates from the two pools, because the error in estimating k is the same for both pools. However, as the same error in estimating k is made for both pools, and as k is independent of the allelic frequency, the difference between the estimates of the frequency in both pools is not affected to a first order approximation. This was also observed by Hoogendoorn et al. (5).
Comparing frequencies between pools. We have modified the standard χ2 test, which is used in classical case-control association studies, to take into account the sources of error discussed above. The effect of a larger variance in allele frequencies from pools due to the use of estimated rather than observed counts was investigated using models that simulate observed and estimated counts. The results are shown in Tables 4 and 5. Generally, unless the sources of errors are large, the inflation in the type I error is small. However, if the pool-specific error is large [e.g. experimental error (σe) > 0.025], then the type I error can be substantially inflated. For example, for σe = 0.025 the type I error is at least doubled relative to the type I error rate on the observed counts.
Table 4. Empirical type I errors from 10 000 simulations, for 100 cases and 100 controls, and p = 0.5.
| |
|
Using observed counts |
Using estimated counts |
|
|---|---|---|---|---|
| αa | σeb | T1 | Test | Tadj |
| 0.10 | 0.01 | 0.099 | 0.113 | 0.093 |
| 0.025 | 0.098 | 0.180 | 0.094 | |
| 0.05 | 0.100 | 0.345 | 0.102 | |
| 0.05 | 0.01 | 0.051 | 0.060 | 0.048 |
| 0.025 | 0.051 | 0.112 | 0.053 | |
| 0.05 | 0.051 | 0.264 | 0.054 | |
| 0.01 | 0.01 | 0.011 | 0.015 | 0.011 |
| 0.025 | 0.011 | 0.039 | 0.011 | |
| 0.05 | 0.011 | 0.144 | 0.011 | |
aNominal type I error.
bSEM of estimated allele frequency.
T1 χ2 test on observed counts.
Test unadjusted test on estimated counts.
Tadj adjusted test on estimated counts.
Table 5. Power for a significance level of 0.05 and 100 cases and 100 controls, from 10 000 simulations.
| σea | p(cases) | p(controls) | T1b | Tadjc |
|---|---|---|---|---|
| 0.01 | 0.50 | 0.45 | 0.17 | 0.16 |
| 0.40 | 0.52 | 0.48 | ||
| 0.35 | 0.86 | 0.83 | ||
| 0.025 | 0.50 | 0.45 | 0.17 | 0.13 |
| 0.40 | 0.52 | 0.38 | ||
| 0.35 | 0.86 | 0.71 | ||
| 0.05 | 0.50 | 0.45 | 0.17 | 0.09 |
| 0.40 | 0.52 | 0.22 | ||
| 0.35 | 0.86 | 0.42 |
aSEM of estimated allele frequency.
bT1 χ2 test on observed counts.
cTadj adjusted test on estimated counts.
Regarding the type II error, power is reduced when using the adjusted statistical test relative to the power based upon observed counts (Table 5). For σe > 0.025, the reduction in power can be substantial. To achieve the same power for pooling and direct genotyping, the pool sample size must be increased by a factor of 1/[1 – 2var(e)/var(Δ)], with var(Δ) the variance of the difference in allele frequencies in the two groups obtained from observed counts, and var(e) the experimental pool-specific error. For example, for σe = 0.01 (which corresponds to a standard error of 0.01, as is typically seen in SNaPshot™ experiments) and σΔ = 0.03 (which corresponds to, for example, 200 case and 200 control individual populations with frequencies of 0.3 and 0.2, respectively), the sample size of the pool would have to be increased by a factor of 1/(1 – 0.0002/0.0009) = 1.3.
To achieve an experimental error of σe = 0.01 or less, replicate pools must be used. If the estimate of the between-replicate variation in the estimate of the allele frequency is in the range of 0.02–0.04 (standard deviation), then to achieve a SEM of <0.01, approximately 4–16 replicate pools would give the same power as tests based upon observations, assuming that there are no errors in determining individual genotypes. From the results in Table 2 we can conclude that most standard deviations are in this range, so that a minimum of four replicates appears to be appropriate.
Database development
We have previously used an ACeDB database (15) to manage the construction of a physical map of chromosome 4p16.1–15.3 (16). Although this database necessitates expert bio-informatics support, it possesses the flexible architecture required to adapt it to our current purpose. We were able to modify existing models and create new ones to allow storage of all information relevant to pool construction, populations and genotyping results. The new models facilitate storage of statistical analysis and of association data based on both pools and populations of individual samples. We have also created a model (‘Pop_pool_meta’) that allows the genotyping data obtained for a set of pools or populations to be merged and analysed as a single data set. The data from different pools can then be merged and the results analysed as a single group.
Submission and analysis of new genotyping data
Data submission via a web interface. CGI/Perl scripts were produced to facilitate the submission of new data and to perform direct statistical analysis. A web page with a graphical representation of a 96-well plate allows the submission of individual genotypes for use in classical association studies. This interface can also be used to enter peak heights obtained from heterozygote samples, which are used to calculate the correction factor k. Another form is used to submit the allele peak heights for the different pool replicates.
Statistical analysis and description of pool genotyping data. Once entered, peak height ratios are subjected to statistical analyses (the mean frequencies of the two alleles, standard deviation and SEM are calculated). The interface also allows the analysis of a data set produced by combining two or more pools. A table of results is displayed and a file containing the new data and their statistical description is automatically created and read into the database.
Association studies based on pools. The modified χ2 test is used to detect differences between the allele frequencies of selected pools. The results are displayed and stored in a new file that is then read into the database.
Association studies based on populations. For a specified marker, allele numbers in each selected population, or group of populations, are calculated from the genotypes of all individuals. A classical χ2 test is performed on these data to identify differences between populations. Results are displayed and automatically read into the database.
DISCUSSION
Pool allele frequencies can be estimated with a high degree of accuracy using SNaPshot™ and primer extension followed by either dHPLC or MassARRAY™. However, accurate estimation of allele frequencies requires calculation of a correction factor for unequal allelic amplification from the peak height ratios of a small set of heterozygotes. Of the three methods tested, the MassARRAY™ method gives the best repeatability, while primer extension followed by dHPLC requires more optimisation than the other methods and does not allow easy multiplexing. The number of samples in a pool has a negligible effect on the accuracy of frequency estimations. We therefore recommend the use of larger pools (we use pools of 384 individuals) and multiple replicates rather than smaller pools with fewer replicates. The ideal number of replicates required is dependent on the reliability of the marker, and the repeatability of the method. For example, for the majority of markers four replicates appeared to be sufficient when the MassARRAY™ method was used.
Choosing a method for genotyping, particularly if this implies the purchase of expensive equipment, is difficult and no golden rule can be applied. The deciding factors include the number of genes/SNPs to be typed, the need for single genotyping versus pool genotyping, the level of throughput required and whether there is a need for SNP detection as well as genotyping. For example, MassARRAY™ may be the best choice for a core facility that provides a very high throughput SNP genotyping service on pools and/or individuals, but a capillary electrophoresis instrument would provide more flexibility for a project that requires SNP detection and medium genotyping throughput.
We have expanded the ACeDB architecture to allow the storage, management and analysis of genotyping data and related information. The ACeDB database provides a graphical, multi-window interface and allows the user to navigate easily between objects. With the new models one can now navigate from a marker to the pools tested with the marker, to the data obtained, and to the results of the comparison of allele frequencies in that pool with those of other pools. Additionally, we have developed a web interface that allows easy and accurate submission of new data and their automatic examination, via descriptive statistical analysis and association studies. A useful future development of the analysis pipeline would be a graphical display of the association data along the DNA sequence of a genomic region. This would allow researchers to visualise the strength of the association in the context of other sequence annotation.
We have modified an existing statistical test to correct for extra sources of error introduced by the pooling methodology. Our test controls the type I error well, but at the expense of a slight decrease of power, which is expected because extra sources of error increase the random variation of the difference in allele frequencies between pools, so that a true difference is more difficult to detect. However, the power of the pooled sample can be maintained at a level equivalent to that obtained by individual genotypes by minimising the experimental error and slightly increasing the sample size.
Genotyping accuracy has not been systematically examined but recent studies (16; L. Peltonen, personal communication) have suggested that no genotyping method is 100% accurate, and that as many as 5% of individual genotypes could be mis-called. Such genotyping errors would decrease the power to detect quantitative trait loci (17) or could have serious effect on linkage disequilibrium measures (18). Most of the scoring errors are caused by ambiguities in the allele peaks, sample-to-sample contamination or mislabelling of DNAs. The use of pools should reduce all of these sources of error. Hence, the procedures described above can be used to perform very accurate association studies, saving valuable time and money compared with genotyping individual samples. Pooling studies should therefore be used to perform a fast, cheap and reliable preliminary screen of a candidate region.
Acknowledgments
ACKNOWLEDGEMENTS
We would particularly like to thank Christiane Honisch from Sequenom for leading the MassARRAY™ experiments, and Dirk van den Boom, Edvin N. Munk and Suzanne Müller, from Sequenom, for their support and comments. We would also like to thank Nadine Norton, Mick O’Donovan and Mike Owen (University of Wales College of Medicine) and Gerome Breen (University of Aberdeen) for sharing their useful expertise. We would like to thank Kenneth Humphreys from the Gastro-Intestinal Unit, University of Edinburgh, and the MRC Human Genetics Unit, for use of their equipment. This work was supported by grants from the UK Medical Research Council, the UK Biotechnology and Biological Sciences Research Council and Organon NV.
REFERENCES
- 1.The International SNP Map Working Group (2001) A map of human genome sequence variation containing 1.42 million single nucleotide polymorphisms. Nature, 409, 928–933. [DOI] [PubMed] [Google Scholar]
- 2.Risch N.J. (2000) Searching for genetic determinants in the new millennium. Nature, 405, 847–856. [DOI] [PubMed] [Google Scholar]
- 3.Cardon L.R. and Bell,J.I. (2001) Association study designs for complex diseases. Nature Rev. Genet., 2, 91–99. [DOI] [PubMed] [Google Scholar]
- 4.Syvanen A.C. (2001) Accessing genetic variation: genotyping single nucleotide polymorphisms. Nature Rev. Genet., 2, 930–942. [DOI] [PubMed] [Google Scholar]
- 5.Hoogendoorn B., Norton,N., Kirov,G., Williams,N., Hamshere,M.L., Spurlock,G., Austin,J., Stephens,M.K., Buckland,P.R., Owen,M.J. and O’Donovan,M.C. (2000) Cheap, accurate and rapid allele frequency estimation of single nucleotide polymorphisms by primer extension and DHPLC in DNA pools. Hum. Genet., 107, 488–493. [DOI] [PubMed] [Google Scholar]
- 6.Breen G., Harold,D., Ralston,S., Shaw,D. and St Clair,D. (2000) Determining SNP allele frequencies in DNA pools. Biotechniques, 28, 464–466, 468, 470. [DOI] [PubMed] [Google Scholar]
- 7.Germer S., Holland,M.J. and Higuchi,R. (2000) High-throughput SNP allele-frequency determination in pooled DNA samples by kinetic PCR. Genome Res., 10, 258–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sasaki T., Tahira,T., Suzuki,A., Higasa,K., Kukita,Y., Baba,S. and Hayashi,K. (2001) Precise estimation of allele frequencies of single-nucleotide polymorphisms by a quantitative SSCP analysis of pooled DNA. Am. J. Hum. Genet., 68, 214–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhou G., Kamahori,M., Okano,K., Chuan,G., Harada,K. and Kambara,H. (2001) Quantitative detection of single nucleotide polymorphisms for a pooled sample by a bioluminometric assay coupled with modified primer extension reactions (BAMPER). Nucleic Acids Res., 29, e93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Buetow K.H., Edmonson,M., MacDonald,R., Clifford,R., Yip,P., Kelley,J., Little,D.P., Strausberg,R., Koester,H., Cantor,C.R. and Braun,A. (2001) High-throughput development and characterization of a genomewide collection of gene-based single nucleotide polymorphism markers by chip-based matrix-assisted laser desorption/ionization time-of-flight mass spectrometry. Proc. Natl Acad. Sci. USA, 98, 581–584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Durbin R. and Thierry Mieg,J. (1991) A C. elegans Database. Documentation, code and data available from anonymous FTP servers at lirmm.lirmm.fr, cele.mrc-lmb.cam.ac.uk and ncbi.nlm.nih.gov.
- 12.Hoogendoorn B., Owen,M.J., Oefner,P.J., Williams,N., Austin,J. and O’Donovan,M.C. (1999) Genotyping single nucleotide polymorphisms by primer extension and high performance liquid chromatography. Hum. Genet., 104, 89–93. [DOI] [PubMed] [Google Scholar]
- 13.Sokal R.R. and Rohlf,F.J. (1995) Biometry. WH Freeman and Company, New York.
- 14.Norton N., Williams,N.G., Williams,H.J., Spurlock,J., Kirov,G., Morris,D.W., Hoogendoorn,B., Owen,M.J. and O’Donovan,M.C. (2002) Universal, robust, highly quantitative SNP allele frequency measurement in DNA pools. Hum. Genet., 110, 471–478. [DOI] [PubMed] [Google Scholar]
- 15.Evans K.L., Le Hellard,S., Morris,S.W., Lawson,D., Whitton,C., Semple,C.A.M., Fantes,J.A., Torrance,H.S., Malloy,M.P., Maule,J.C., Humphray,S.J., Ross,M.T., Bentley,D.R., Muir,W.J., Blackwood,D.H.R. and Porteous,D.J. (2001) A 6.9Mb high resolution BAC/PAC contig of human 4p15.3-p16.1, a candidate region for bipolar affective disorder. Genomics, 71, 315–323. [DOI] [PubMed] [Google Scholar]
- 16.Bray M.S., Boerwinkle,E. and Doris,P.A. (2001) High-throughput multiplex SNP genotyping with MALDI-TOF mass spectrometry: practice, problems and promise. Hum. Mutat., 17, 296–304. [DOI] [PubMed] [Google Scholar]
- 17.Abecasis G.R., Cherny,S.S. and Cardon,L.R. (2001) The impact of genotyping error on family-based analysis of quantitative traits. Eur. J. Hum. Genet., 9, 130–134. [DOI] [PubMed] [Google Scholar]
- 18.Akey J.M., Zhang,K., Xiong,M., Doris,P. and Jin,L. (2001) The effect that genotyping errors have on the robustness of common linkage-disequilibrium measures. Am. J. Hum. Genet., 68, 1447–1456. [DOI] [PMC free article] [PubMed] [Google Scholar]